по
дисциплине «Теория графов»
Студент
Фофанов Г.А. группы ИКН-311
Руководитель
проекта
Финк
Т.Ю.
Подпись,
дата
Исполнитель
студент
гр. ИКН-311
Фофанов
Г.А.
Подпись,
дата
Омск
2014
Лабораторная
работа 4. Эйлеровы
и гамильтоновы графы.
Метрические
характеристики графов.
Задание
1.
По алгоритму Флёри найти эйлеровы циклы
на графах. (Приложение
8).
Задание
2.
Найти
все гамильтоновы циклы графа. (Приложение
9).
Задание
3. Найти
матрицы фундаментальных циклов и
фундаментальных разрезов. Найти радиус,
диаметр и центр графа G.
Является ли изображенный граф эйлеровым?
Является ли изображенный граф планарным?
(Приложение
10).
Задание
1.
По алгоритму Флёри найти эйлеровы циклы
на графах. (Приложение
8).
Вариант 11

Вход:
эйлеров граф G.
Выход:
список ребер графа G в той последовательности,
в которой они
образуют
эйлеров цикл.
1.
Положить текущий граф равным G, а текущую
вершину — равной
произвольной
вершине v ∈
V(G).
2.
Выбрать произвольное ребро e
текущего
графа, инцидентное текущей вершине.
3.
Назначить текущей вторую вершину,
инцидентную e.
4.
Удалить e из текущего графа и внести в
список.
5.
Если в текущем графе еще остались ребра,
вернуться на шаг 2.
Выбираем
ребро 4,1 вносим его в список затем,
выбираем ребро 1,2 вносим его в список
затем, выбираем ребро 2,5 вносим его в
список затем, выбираем ребро 5,4 вносим
его в список затем, выбираем ребро 4,3
вносим его в список затем, выбираем
ребро 3,2 вносим его в список затем,
выбираем ребро 2,6 вносим его в список
затем, выбираем ребро 6,5 вносим его в
список затем, выбираем ребро 5,3 вносим
его в список затем, выбираем ребро 4,1
вносим его в список затем, выбираем
ребро 3,6 вносим его в список затем,
выбираем ребро 6,4.
Задание
2.
Найти
все гамильтоновы циклы графа. (Приложение
9).
Б
acdbg acbdg
Задание
3. Найти
матрицы фундаментальных циклов и
фундаментальных разрезов. Найти радиус,
диаметр и центр графа G.
Является ли изображенный граф эйлеровым?
Является ли изображенный граф планарным?
(Приложение
10).
Найти
матрицы фундаментальных циклов и
фундаментальных разрезов.
Для
построения матрицы фундаментальных
циклов нужно построить остовное дерево
и пронумеруем все ребра графа.

Всего
12 ребер ,5 из них не включены в дерево
следовательно у нас будет 12-8 +1 =5 циклов.
Матрица фундаментальных циклов
a
b c d e f g h k j l m
1
0 0 0 0 0 1 1 1 0 0 0 0
2
1 0 1 0 0 0 1 1 0 0 0 0
3
0 0 0 1 1 0 1 1 0 0 0 0
4
1 1 0 0 1 0 1 1 0 0 0 0
5
0 0 0 0 0 0 0 0 1 0 1 1
Матрица
фундаментальных разрезов.
a b c d e f g h k j l m
1
1 1 1 1 0 1 0 0 0 0 0 0
2
0 1 1 1 1 1 0 0 0 0 0 0
3
0 1 1 1 0 1 0 1 0 0 0 0
4
0 1 1 1 0 1 1 0 0 0 0 0
5
0 0 0 0 0 0 0 0 1 0 1 0
6
0 0 0 0 0 0 0 0 1 0 0 1
7
0 1 1 1 0 1 0 0 0 1 0 0
Найти
радиус, диаметр и центр графа G.
Является ли изображенный граф эйлеровым?

Составим
матрицу расстояний
1
2 3 4 5 6 7 8
1
0 1 4 3 4 2 1 1
2
1 0 3 2 3 1 1 1
3
4 3 0 1 1 2 3 4
4
3 2 1 0 1 1 2 3
5
4 3 1 1 0 2 3 4
6
2 1 2 1 2 0 1 2
7
1 1 3 2 3 1 0 1
8
1 1 4 3 4 2 1 0
Выпишем
максимальные эксцентриситеты каждой
вершины
4
3 4 3 4 2 3 4
Радиус
графа – минимальный эксцентриситет
вершин r
=2
Диаметр
графа – максимальный эксцентриситет
вершин d=4
Центр
графа – вершины с минимальным
эксцентриситетом = 6
Граф
не является эйлеровым т к он не содержит
эйлерова цикла потому что граф содержит
более 2 вершин с нечетной степенью. Граф
не является планарным т к при любой его
геометрической интерпретации будут
ребра которые будут пересекаться не
только в вершинах(граф нельзя уложить
на плоскость).
Для
решения задания применен представленный
ниже код программы, написанный на языке
C#:
using
System;
using
System.Collections.Generic;
namespace
ПоискГамильтоновыхЦиклов
{
class
ModifiedAdjacencyMatrix
{
private
List<string>[,]
_matrix;
private
readonly
List<string>[,]
_matrixB;
private
int
_size;
public
List<string>[,]
GetMatrix
{
get
{ return
_matrix; }
set
{ _matrix = value;
}
}
public
ModifiedAdjacencyMatrix(int[,]
matrix, int
n)
{
_size
= n;
_matrix
= new
List<string>[_size,_size];
_matrixB
= new
List<string>[_size,
_size];
for
(int
i = 0; i < n; i++)
for
(int
j = 0; j < n; j++)
{
_matrix[i,
j] = new
List<string>();
_matrixB[i,
j] = new
List<string>();
}
Initialize(matrix);
GetModifiedMatrix();
}
private
void
Initialize(int[,]
matrix)
{
for
(int
i = 0; i < matrix.GetLength(0); i++)
for
(int
j = 0; j < matrix.GetLength(0); j++)
_matrix[i,j].Add(matrix[i,j].ToString());
}
public
List<string>
this
[int
index1,int
index2]
{
get
{ return
_matrix[index1, index2]; }
set
{ _matrix[index1, index2] = value;
}
}
public
string
this
[int
index1,int
index2,int
index]
{
get
{ return
_matrix[index1, index2][index]; }
set
{
if(_matrix[index1,index2].Count<1)
_matrix[index1,
index2].Add(“”);
_matrix[index1,
index2][index] += value;
}
}
public
int
Size
{
get
{ return
_size; }
set
{ _size = value;
}
}
private
void
GetModifiedMatrix()
{
for(int
i=0;i<_matrixB.GetLength(0);i++)
for
(int
j = 0; j < _matrixB.GetLength(1); j++)
{
_matrixB[i,j]
= new
List<string>();
if
(_matrix[i, j][0] == “1”)
{
char
c = Convert.ToChar(65
+ j);
_matrixB[i,
j].Add(c.ToString());
}
else
{
_matrixB[i,
j].Add(0.ToString());
}
}
}
public
string[]
GetHamiltonCircuit()
{
string[,]
strings = ListMassiveToArray(_matrix);
Console.WriteLine(“Матрица
A:”);
for
(int
i = 0; i < strings.GetLength(0); i++)
{
for
(int
j = 0; j < strings.GetLength(1); j++)
Console.Write(strings[i,
j] + ”
t”);
Console.WriteLine();
}
Console.WriteLine();
strings
= ListMassiveToArray(_matrixB);
Console.WriteLine(“Матрица
B:”);
for
(int
i = 0; i < strings.GetLength(0); i++)
{
for
(int
j = 0; j < strings.GetLength(1); j++)
Console.Write(strings[i,
j] + ”
t”);
Console.WriteLine();
}
for(int
i=0;i<_size-1;i++)
{
_matrix
= Multiply(_matrixB, _matrix);
AddZero();
if(i
!= _size-2)
SetNull();
Console.WriteLine();
strings
= ListMassiveToArray(_matrix);
Console.WriteLine(“Матрица
P”+(i+2));
for
(int
k = 0; k < strings.GetLength(0); k++)
{
for
(int
j = 0; j < strings.GetLength(1); j++)
Console.Write(strings[k,
j] + ”
t”);
Console.WriteLine();
}
}
List<string>
temp = _matrix[0, 0];
string[]
str = temp.ToArray();
for(int
i=0;i<str.GetLength(0);i++)
{
string
del = str[i];
for(char
c = ‘A’;c<‘F’;c++)
{
int
begin = str[i].IndexOf(c);
int
end = str[i].LastIndexOf(c);
if(begin>-1
&& end >-1 && begin!=end)
{
temp.Remove(del);
}
}
}
for
(int
i = 0; i < temp.Count; i++)
temp[i]
= ‘A’
+ temp[i];
return
temp.ToArray();
}
private
string[,]
ListMassiveToArray(List<string>[,]
list )
{
string[,]
result = new
string[list.GetLength(0),
list.GetLength(1)];
for(int
i=0;i<list.GetLength(0);i++)
for(int
j=0;j<list.GetLength(1);j++)
{
for
(int
k = 0; k < list[i, j].Count; k++)
{
result[i,
j] += list[i,j][k];
if
(k != list[i, j].Count – 1)
result[i,
j] += “+”;
}
}
return
result;
}
private
List<string>[,]
Multiply(List<string>[,]
lhs, List<string>[,]
rhs)
{
List<string>[,]
result = new
List<string>[lhs.GetLength(0),
lhs.GetLength(1)];
for
(int
i = 0; i < lhs.GetLength(0); i++)
for
(int
j = 0; j < lhs.GetLength(1); j++)
{
result[i,
j] = new
List<string>();
for
(int
n = 0; n < lhs.GetLength(1); n++)
{
foreach
(string
ls in
lhs[i, n])
foreach
(string
rs in
rhs[n, j])
{
if
(ls != “0”
&& rs != “0”)
{
if
(rs == “1”)
{
result[i,
j].Add(ls);
continue;
}
result[i,
j].Add(ls + rs);
}
}
}
}
return
result;
}
private
void
AddZero()
{
for
(int
i = 0; i < _size; i++)
for
(int
j = 0; j < _size; j++)
if(_matrix[i,j].Count
== 0)
_matrix[i,j].Add(“0”);
}
private
void
SetNull()
{
for(int
i=0;i<_matrix.GetLength(0);i++)
for(int
j=0;j<_matrix.GetLength(1);j++)
{
if(i==j)
{
_matrix[i,j].Clear();
_matrix[i,j].Add(“0”);
}
}
}
}
}
using
System;
using
System.IO;
namespace
ПоискГамильтоновыхЦиклов
{
class
Program
{
static
void
Main(string[]
args)
{
StreamReader
fsRead = File.OpenText(“input.txt”);
int
n = Convert.ToInt32(fsRead.ReadLine());
int[,]
g = new
int[n,n];
for
(int
i = 0; i < n; i++)
for
(int
j = 0; j < n; j++)
g[i,
j] = Convert.ToInt32(fsRead.ReadLine());
ModifiedAdjacencyMatrix
matr = new
ModifiedAdjacencyMatrix(g,n);
string
[] str = matr.GetHamiltonCircuit();
Console.WriteLine(“rnГамильтоновы
циклы:”);
for(int
i=0;i<str.GetLength(0);i++)
Console.WriteLine(str[i]);
Console.ReadKey();
}
}
}
ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ
«Омский
государственный технический университет»
Кафедра
«Прикладная
математика и фундаментальная информатика»
Соседние файлы в папке Графы
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Элементы теории графов. Основные определения. Пример графа и его матрицы инциденций. Матрицы инциденций, фундаментальных разрезов, фундаментальных циклов
Страницы работы
Содержание работы
3 ЭЛЕМЕНТЫ ТЕОРИИ
ГРАФОВ
3.1 Основные определения
Граф G(V,E)– совокупность двух множеств V и E, причем множество вершин V=![]() непустое,
непустое,
а множество E=![]() представляет собою набор неупорядоченных или упорядоченных пар вершин,
представляет собою набор неупорядоченных или упорядоченных пар вершин,
то есть ![]() . Множество Е принято называть
. Множество Е принято называть
множеством ребер или дуг. Количество вершин и ребер можно обозначить n(G) и m(G) соответственно.
Граф, в
котором множество E=![]() представляет собою
представляет собою
набор неупорядоченных пар вершин, называют неориентированным.
Граф, в
котором множество E=![]() представляет собою
представляет собою
набор упорядоченных пар вершин, называют ориентированным или орграфом. В орграфе для каждого ребра
определены его начало ( первый элемент в паре вершин) и конец (второй элемент в
паре вершин).
Пара
вершин может быть соединена несколькими ребрами. Такие ребра в графе называют
кратными. Ребро может соединять вершину саму с собою, и такое ребро называют петлей. Вершины, соединенные ребром ,
называют смежными вершинами.
Ребра, имеющие общую вершину, тоже называют смежными.
Ребро инцидентно вершине, если эта вершина
является одним из его концов.
Граф без
кратных ребер и петель называется простым
графом.
Простой
граф, любые две вершины которого являются смежными, называется полным.
Подграфом графа G(V,E)
называется граф, все вершины и ребра которого содержатся среди вершин и ребер
исходного графа.
Степенью вершины ![]() неориентированного графа называется
неориентированного графа называется
количество ребер ![]() , инцидентных вершине.
, инцидентных вершине.
При этом петли учитываются дважды. Вершину со степенью ноль называют
изолированной.
Полустепенью исхода (захода ) вершины ![]() орграфа называется количество ребер
орграфа называется количество ребер ![]() , исходящих из вершины
, исходящих из вершины
( заходящих в вершину ![]() ). Петля,
). Петля,
инцидентная вершине, учитывается как в ![]() ,
,
так и в ![]() .
.
Теорема.
Для
неориентированного графа ![]() .
.
Для
орграфа ![]() .
.
Маршрутом в графе G(V,E)
называется последовательность вершин и ребер ![]() ,
,
причем любые соседние вершина и ребро ![]() в
в
этой последовательности инцидентны. Путь
( ориентированный маршрут ) представляет собою
последовательность вершин и ребер ![]() , где каждое
, где каждое
ребро ![]() является парой упорядоченных вершин
является парой упорядоченных вершин ![]() . Маршрут, в котором все ребра
. Маршрут, в котором все ребра
попарно различны, называется простым
маршрутом.
Замкнутый
маршрут, в котором все ребра попарно различны, называется циклом. Замкнутый путь, в котором все
ребра попарно различны, называется контуром.
Цикл ( контур ), в котором все вершины попарно различны,
называется простым циклом
( контуром ).
Два графа G(V,E) и G1(V1,E1)
называются изоморфными, если
существует взаимно – однозначное соответствие между множествами вершин V,V1 и
множествами ребер E,E1 , сохраняющее инцидентность. Изоморфизм можно определить иначе – граф G можно так перерисовать ( расположив его вершины и ребра по – другому
), что получится граф G1 .
Рисунки
3.1 и 3.2 иллюстрируют приведенные выше понятия.
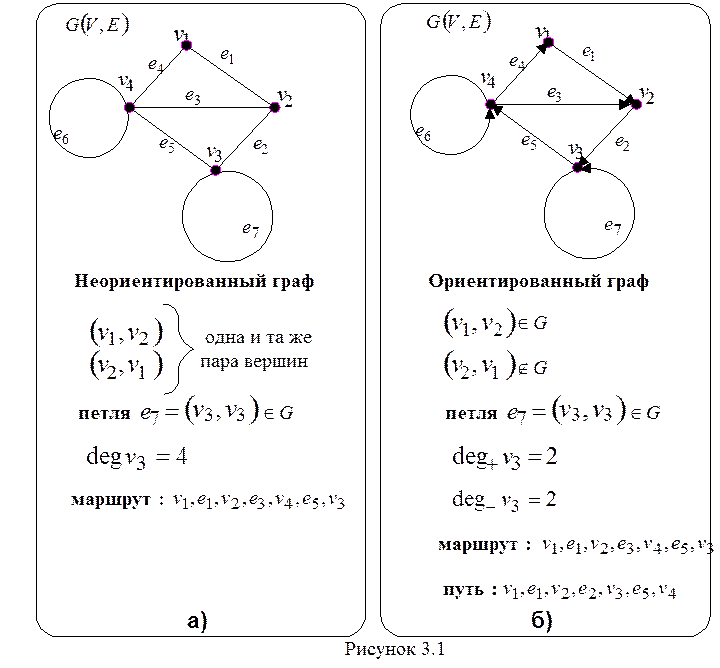

Неориентированный граф G(V,E) называется связным,
если в нем существует маршрут между каждой парой вершин. Например, граф на
рисунке 3.1 а) – связный. Ориентированный граф называется связным, если
связным является лежащий в его основе неориентированный граф.
Связный
граф без циклов называется деревом.
В дереве между любыми двумя вершинами существует только один простой маршрут.
Количество ребер в дереве на единицу меньше, чем количество вершин. Если
соединить ребром произвольные две несмежные вершины дерева, то получается
граф, имеющий только один цикл.
3.2 Матрица инциденций орграфа
Пусть имеется граф G(V,E) без
петель на n вершинах и m ребрах. Матрица инциденций ![]() графа G
графа G
имеет n строк (по одной на
каждую вершину) и m столбцов (по одному
на каждое ребро). Элемент ![]() матрицы
матрицы ![]() определяется следующим образом:
определяется следующим образом:
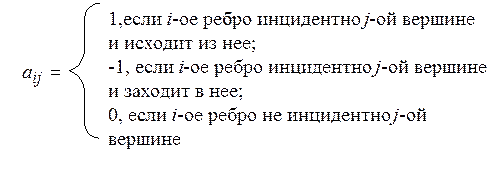
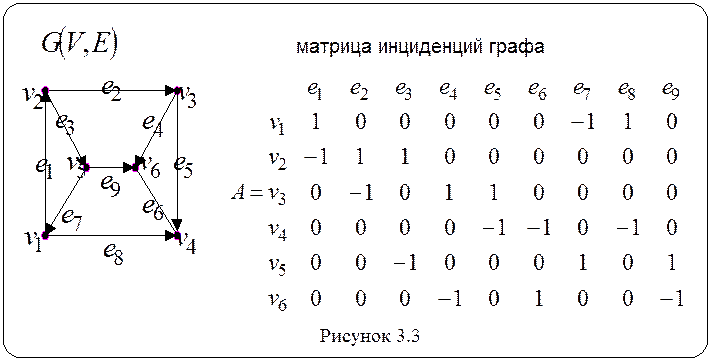 На рисунке 3.3 приведен пример
На рисунке 3.3 приведен пример
графа и его матрицы инциденций.
Из
определения следует, что сумма элементов каждого столбца матрицы инциденций
равна нулю.
3.3
Фундаментальные разрезы и фундаментальные циклы графа
Связный
ациклический подграф графа G на всех вершинах
называют остовом графа G. Ребра остова называют ветвями,
а остальные ребра графа G, на входящие в остов, называют хордами.
Если усечь
матрицу инциденций графа по какой – либо строке, то можно вычислить
количество остовов и выделить каждый остов графа.
Количество
остовов равно ![]() . Каждому ненулевому минору
. Каждому ненулевому минору
усеченной матрицы инциденций порядка n-1 ( n – количество вершин графа) соответствует остов. Ветви остова
соответствуют столбцам такого минора. Рисунок 3.4 иллюстрирует последние
утверждения.
Если из
остова T графа G
удалить одну ветвь ek, то множество его вершин V разбивается на
два не связанных между собой подмножества W1 и W2 . Все ребра графа G,
имеющие один конец в W1, а другой конец в W2, составляют фундаментальный
разрез для остова T. Направление разреза выбирают по
направлению породившей его ветви. Количество фундаментальных разрезов равно
количеству ветвей.
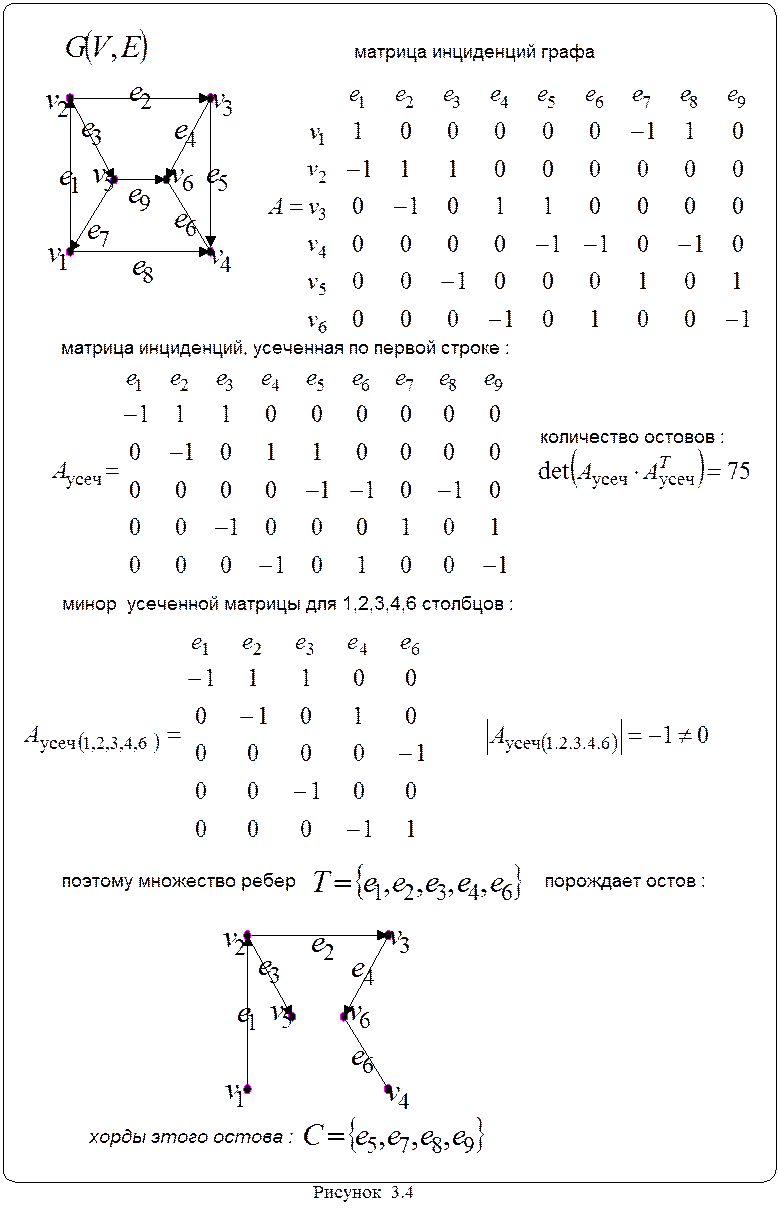
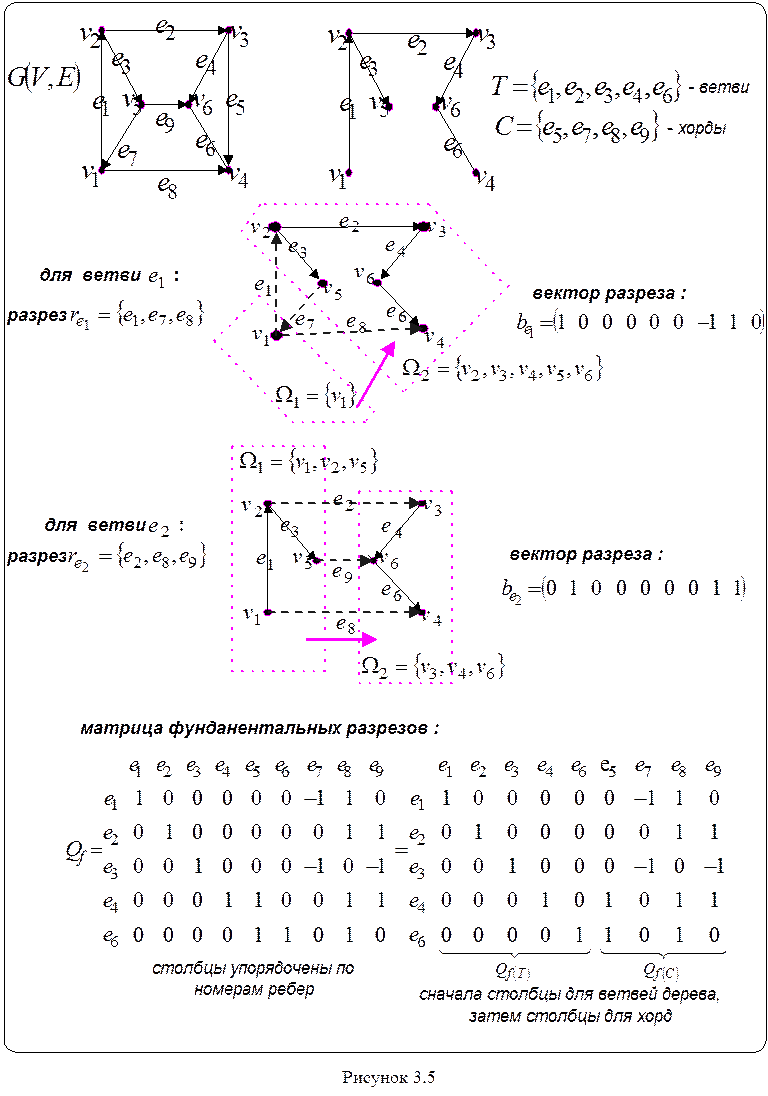
Каждому фундаментальному разрезу
можно поставить в соответствие вектор – строку, элементы которого
определяются по правилу:
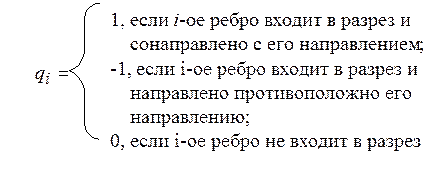
Из таких
векторов – строк составляется матрица фундаментальных разрезов![]() . Количество строк в ней совпадает с
. Количество строк в ней совпадает с
количеством ветвей остова, а количество столбцов равно количеству столбцов
исходного графа G. Процесс составления матрицы
фундаментальных разрезов показан на рисунке 3.5 .
Если к
остову T графа G добавить одну хорду
ek, то в результате
образуется только один цикл. Множество ребер, входящих в полученный цикл,
составляет фундаментальный цикл графа G для
остова T . Направление обхода цикла выбирается по
направлению породившей этот цикл хорды. Каждому фундаментальному циклу можно
поставить в соответствие вектор – строку, элементы которого
определяются по правилу:
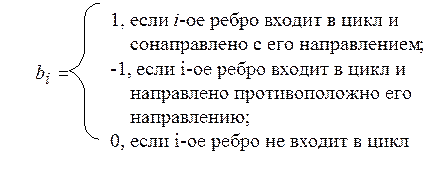
Из таких
векторов – строк составляется матрица фундаментальных циклов![]() . Количество строк в ней совпадает с
. Количество строк в ней совпадает с
количеством хорд остова, а количество столбцов равно количеству столбцов
исходного графа G. Процесс составления матрицы
фундаментальных циклов показан на рисунке 3.6 .
В матрицах
фундаментальных разрезов![]() и фундаментальных
и фундаментальных
циклов![]() можно выделить столбцы, соответствующие
можно выделить столбцы, соответствующие
ветвям (![]() ,
,![]() )
)
и хордам (![]() ,
,![]() )
)
остова. Матрицы связаны между собой соотношением :
![]() .
.
Этот факт
проиллюстрирован на рисунке 3.7 .
Матрицы
инциденций, фундаментальных разрезов, фундаментальных циклов используются при
исследовании электрических цепей. Эти матрицы входят в качестве коэффициентов в
уравнения Кирхгофа, описывающие цепь.
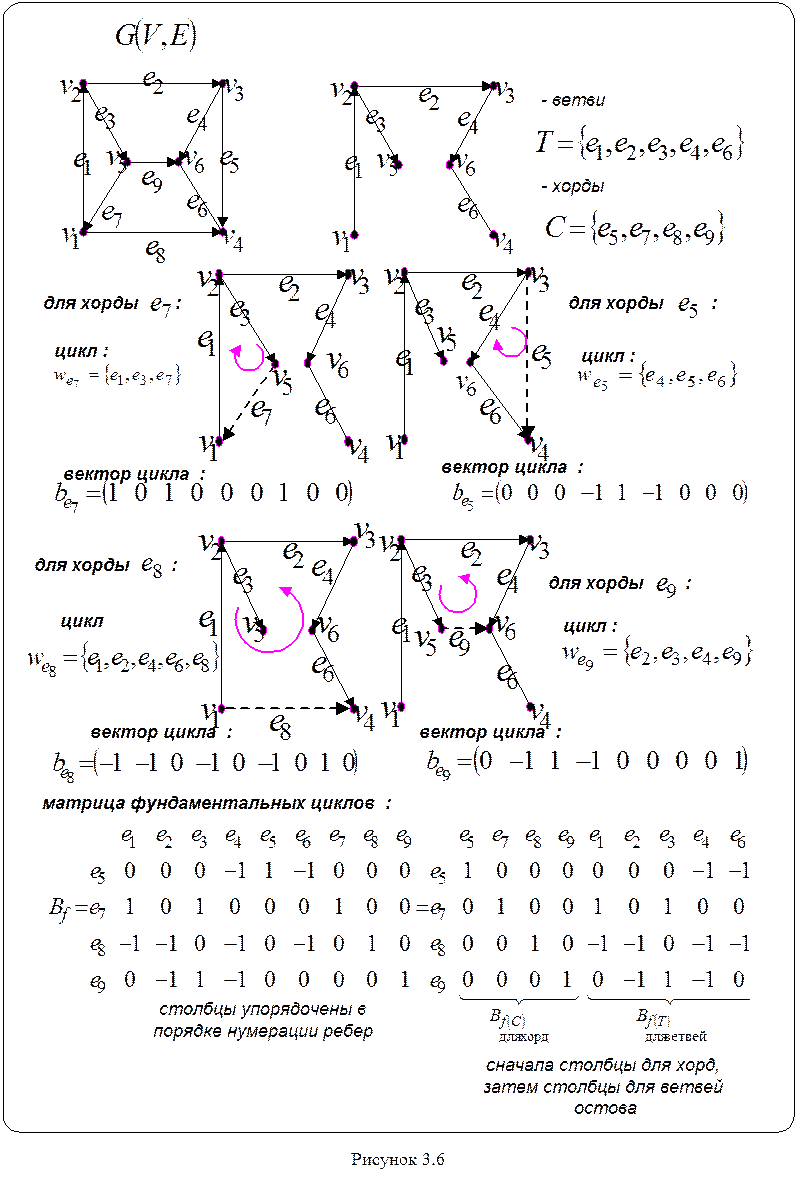
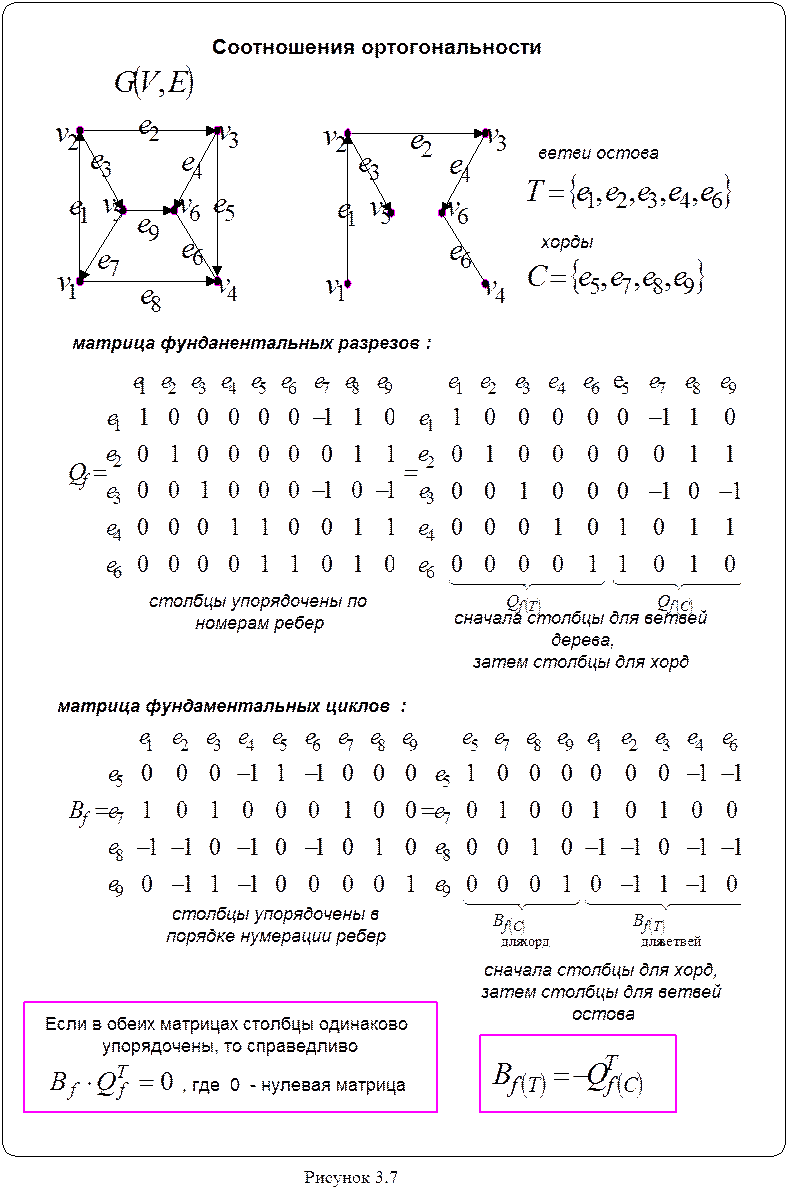
Похожие материалы
- Определение равенств, используя свойства операций над множествами
- Элементы теории множеств. Представление множеств в ЭВМ. Декартово произведение множеств. Отношения. Аналитическое представление функций алгебры логики
- Статистическое кодирование. Коэффициент избыточности. Ветвление кодовых комбинаций. Средняя длина кодовой комбинации
Информация о работе
В предыдущей главе мы обсуждали, как преобразовать электрическую цепь в эквивалентный граф. Теперь давайте обсудим Матрицы топологии сети, которые полезны для решения любой проблемы электрической цепи или сети с использованием их эквивалентных графов.
Матрицы, связанные с сетевыми графами
Ниже приведены три матрицы, которые используются в теории графов.
- Матрица заболеваемости
- Матрица фундаментальной петли
- Фундаментальный крой Set Matrix
Матрица заболеваемости
Матрица инцидентности представляет график данной электрической цепи или сети. Следовательно, можно нарисовать график той же электрической цепи или сети из матрицы инцидентности .
Мы знаем, что граф состоит из множества узлов, которые связаны между собой несколькими ветвями. Итак, соединение ветвей с узлом называется инцидентностью. Матрица инцидентности представлена буквой А. Она также называется матрицей инцидентности между узлами или матрицей узлов .
Если в ориентированном графе имеется «n» узлов и «b» ответвлений, то матрица инцидентности будет иметь «n» строк и «b» столбцов. Здесь строки и столбцы соответствуют узлам и ветвям ориентированного графа. Следовательно, порядок матрицы инцидентности будет n × b .
Элементы матрицы инцидентности будут иметь одно из этих трех значений: +1, -1 и 0.
-
Если ток ветви уходит из выбранного узла, то значение элемента будет +1.
-
Если ток ветви поступает в направлении выбранного узла, то значение элемента будет равно -1.
-
Если ток ветви не входит в выбранный узел и не выходит из выбранного узла, тогда значение элемента будет 0.
Если ток ветви уходит из выбранного узла, то значение элемента будет +1.
Если ток ветви поступает в направлении выбранного узла, то значение элемента будет равно -1.
Если ток ветви не входит в выбранный узел и не выходит из выбранного узла, тогда значение элемента будет 0.
Процедура поиска Матрицы заболеваемости
Выполните следующие действия, чтобы найти матрицу инцидентности ориентированного графа.
-
Выберите узел во время данного ориентированного графа и заполните значения элементов матрицы инцидентности, соответствующих этому узлу, в строке.
-
Повторите вышеуказанный шаг для всех узлов данного ориентированного графа.
Выберите узел во время данного ориентированного графа и заполните значения элементов матрицы инцидентности, соответствующих этому узлу, в строке.
Повторите вышеуказанный шаг для всех узлов данного ориентированного графа.
пример
Рассмотрим следующий ориентированный граф .
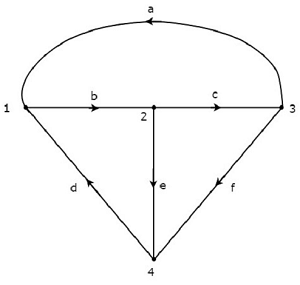
Матрица инцидентности, соответствующая приведенному выше ориентированному графу, будет
A = begin {bmatrix} -1 & 1 & 0 & -1 & 0 & 0 \ 0 & -1 & 1 & 0 & 1 & 0 \ 1 & 0 & -1 & 0 & 0 & 1 \ 0 & 0 & 0 & 1 & -1 & -1 end {bmatrix}
Строки и столбцы вышеприведенной матрицы представляют узлы и ветви данного ориентированного графа. Порядок этой матрицы инцидентности составляет 4 × 6.
Соблюдая приведенную выше матрицу инцидентности, можно сделать вывод, что сумма элементов столбца матрицы инцидентности равна нулю. Это означает, что ток ветвления выходит из одного узла и входит только в другой отдельный узел.
Примечание. Если данный граф является неориентированным типом, преобразуйте его в ориентированный граф, представив стрелки на каждой его ветви. Мы можем рассмотреть произвольное направление протекания тока в каждой ветви.
Матрица фундаментальной петли
Фундаментальный цикл или f-цикл представляет собой цикл, который содержит только одну ссылку и одну или несколько веток. Итак, количество f-циклов будет равно количеству ссылок. Матрица фундаментальной петли представлена буквой B. Она также называется матрицей фундаментальной цепи и матрицей Tie-set. Эта матрица дает соотношение между токами ветвления и токами звеньев.
Если в ориентированном графе имеется n узлов и ветви b присутствуют, то количество ссылок, присутствующих в совместном дереве, которое соответствует выбранному дереву данного графа, будет b-n + 1.
Таким образом, матрица основного цикла будет иметь строки «b-n + 1» и столбцы «b». Здесь строки и столбцы соответствуют ссылкам co-дерева и ветвей данного графа. Следовательно, порядок матрицы фундаментального цикла будет (b – n + 1) × b .
Элементы матрицы основного цикла будут иметь одно из этих трех значений: +1, -1 и 0.
-
Значение элемента будет +1 для ссылки выбранного f-цикла.
-
Значение элементов будет равно 0 для остальных ссылок и веток, которые не являются частью выбранного f-цикла.
-
Если направление тока ветки выбранного f-контура совпадает с направлением тока линии f-контура, то значение элемента будет +1.
-
Если направление тока ветки выбранного f-петли противоположно направлению тока звена f-петли, тогда значение элемента будет -1.
Значение элемента будет +1 для ссылки выбранного f-цикла.
Значение элементов будет равно 0 для остальных ссылок и веток, которые не являются частью выбранного f-цикла.
Если направление тока ветки выбранного f-контура совпадает с направлением тока линии f-контура, то значение элемента будет +1.
Если направление тока ветки выбранного f-петли противоположно направлению тока звена f-петли, тогда значение элемента будет -1.
Процедура поиска матрицы фундаментальных циклов
Выполните следующие шаги, чтобы найти матрицу фундаментального цикла данного ориентированного графа.
-
Выберите дерево заданного ориентированного графа.
-
Включая одну ссылку за раз, мы получим один f-цикл. Заполните значения элементов, соответствующих этому f-циклу, в строке матрицы фундаментального цикла.
-
Повторите вышеуказанный шаг для всех ссылок.
Выберите дерево заданного ориентированного графа.
Включая одну ссылку за раз, мы получим один f-цикл. Заполните значения элементов, соответствующих этому f-циклу, в строке матрицы фундаментального цикла.
Повторите вышеуказанный шаг для всех ссылок.
пример
Взгляните на следующее дерево ориентированного графа , которое рассматривается для матрицы инцидентности.
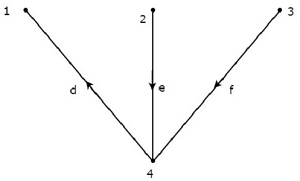
Вышеуказанное дерево содержит три ветви d, e & f. Следовательно, ветви a, b & c будут связями Co-Tree, соответствующими вышеуказанному дереву. Включая одну ссылку за раз на вышеуказанное дерево, мы получим один f-цикл . Таким образом, будет три f-петли , так как есть три ссылки. Эти три f-петли показаны на следующем рисунке.
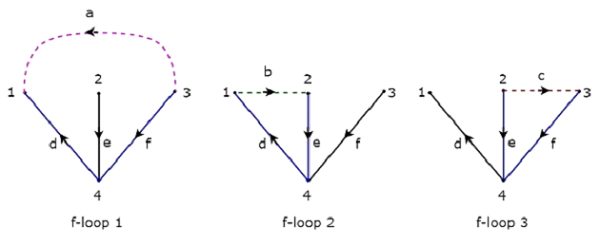
На рисунке выше ветви, которые представлены цветными линиями, образуют f-петли. Мы получим значения построчных элементов матрицы Tie-set из каждого f-цикла. Таким образом, матрица Tieset рассмотренного выше дерева будет
B = begin {bmatrix} 1 & 0 & 0 & -1 & 0 & -1 \ 0 & 1 & 0 & 1 & 1 & 0 \ 0 & 0 & 1 & 0 & -1 & 1 конец {bmatrix}
Строки и столбцы вышеприведенной матрицы представляют собой связи и ветви данного ориентированного графа. Порядок этой матрицы инцидентности составляет 3 × 6.
Количество матриц основного цикла ориентированного графа будет равно количеству деревьев этого ориентированного графа. Потому что каждое дерево будет иметь одну матрицу фундаментальных циклов.
Фундаментальная обрезная матрица
Фундаментальный набор срезов или набор f-срезов – это минимальное количество ветвей, которые удаляются из графа таким образом, что исходный граф станет двумя изолированными подграфами. Набор f-cut содержит только одну веточку и одну или несколько ссылок. Таким образом, количество наборов f-cut будет равно количеству веточек.
Матрица набора основных срезов обозначена буквой C. Эта матрица дает соотношение между напряжениями ответвления и напряжениями ветки.
Если в ориентированном графе имеется «n» узлов и «b» ветвей, то количество веток в выбранном дереве данного графа будет n-1. Таким образом, матрица основного набора сокращений будет иметь n-1 строки и столбцы b. Здесь строки и столбцы соответствуют веткам выбранного дерева и ветвям данного графа. Следовательно, порядок матрицы базового набора сечений будет (n-1) × b .
Элементы матрицы набора базовых сечений будут иметь одно из этих трех значений: +1, -1 и 0.
-
Значение элемента будет +1 для ветки выбранного f-cutset.
-
Значение элементов будет 0 для оставшихся веток и ссылок, которые не являются частью выбранного f-cutset.
-
Если направление тока связи выбранного набора f-отрезков такое же, как и у потока веток f-отрезков, то значение элемента будет +1.
-
Если направление тока связи выбранного набора f-cut противоположно направлению тока ветки f-cutset, то значение элемента будет -1.
Значение элемента будет +1 для ветки выбранного f-cutset.
Значение элементов будет 0 для оставшихся веток и ссылок, которые не являются частью выбранного f-cutset.
Если направление тока связи выбранного набора f-отрезков такое же, как и у потока веток f-отрезков, то значение элемента будет +1.
Если направление тока связи выбранного набора f-cut противоположно направлению тока ветки f-cutset, то значение элемента будет -1.
Процедура нахождения Фундаментальной Вырезанной Матрицы
Выполните следующие шаги, чтобы найти матрицу фундаментальных наборов сечений данного ориентированного графа.
-
Выберите дерево заданного ориентированного графа и представьте ссылки пунктирными линиями.
-
Удалив одну веточку и необходимые ссылки за раз, мы получим один набор f-cut. Заполните значения элементов, соответствующих этому набору f-сечений, в строке основной матрицы срезов.
-
Повторите вышеуказанный шаг для всех веток.
Выберите дерево заданного ориентированного графа и представьте ссылки пунктирными линиями.
Удалив одну веточку и необходимые ссылки за раз, мы получим один набор f-cut. Заполните значения элементов, соответствующих этому набору f-сечений, в строке основной матрицы срезов.
Повторите вышеуказанный шаг для всех веток.
пример
Рассмотрим тот же ориентированный граф , который мы обсуждали в разделе матрицы инцидентности. Выберите ветви d, e & f этого ориентированного графа в виде веточек. Таким образом, оставшиеся ветви a, b & c этого ориентированного графа будут ссылками.
Веточки d, e & f представлены сплошными линиями, а ссылки a, b и c представлены пунктирными линиями на следующем рисунке.
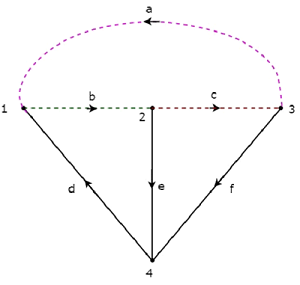
Удалив одну веточку и необходимые ссылки за раз, мы получим один набор f-cut. Итак, будет три набора f-cut, так как есть три веточки. Эти три набора f-cut показаны на следующем рисунке.
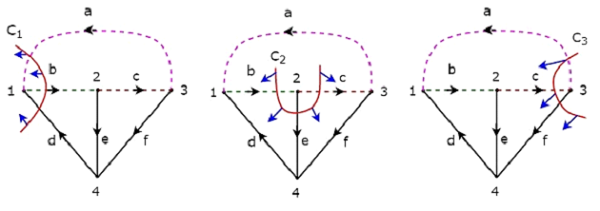
У нас будет три набора f-cut, удалив набор веток и звеньев C 1 , C 2 и C 3 . Мы получим значения построчных элементов матрицы фундаментальных наборов сечений из каждого набора f-срезов. Таким образом, основная матрица множества срезов рассмотренного выше дерева будет
C = begin {bmatrix} 1 & -1 & 0 & 1 & 0 & 0 \ 0 & -1 & 1 & 0 & 1 & 0 \ 1 & 0 & -1 & 0 & 0 & 1 конец {bmatrix}
Строки и столбцы вышеприведенной матрицы представляют собой веточки и ветви данного ориентированного графа. Порядок этой основной матрицы сечений равен 3 × 6.
Количество матриц Фундаментального набора сечений ориентированного графа будет равно количеству деревьев этого ориентированного графа. Потому что каждое дерево будет иметь одну матрицу Фундаментального среза.
