Как найти матрицу гессе онлайн - Сайт, где вы сможете решить свои вопросы

EMBED

Make your selections below, then copy and paste the code below into your HTML source.
* For personal use only.

Theme

Output Type

Lightbox
Popup
Inline

Widget controls displayed
Widget results displayed

To add the widget to Blogger, click here and follow the easy directions provided by Blogger.

To add the widget to iGoogle, click here. On the next page click the “Add” button. You will then see the widget on your iGoogle account.

To embed this widget in a post on your WordPress blog, copy and paste the shortcode below into the HTML source:

For self-hosted WordPress blogs

To add a widget to a MediaWiki site, the wiki must have the Widgets Extension installed, as well as the code for the Wolfram|Alpha widget.

To include the widget in a wiki page, paste the code below into the page source.

Источник

Матрица Гессе

Назначение сервиса. Онлайн-калькулятор используется для нахождения матрицы Гессе и определения вида функции (выпуклая или вогнутая). Решение оформляется в формате Word. Для функции одной переменной f(x) определяются интервалы выпуклости и вогнутости.

Решение онлайн
Видеоинструкция

Правила ввода функций:

Все переменные выражаются через x1,x2,x3

Дважды непрерывно дифференцируемая функция f(x) является выпуклой (вогнутой) тогда и только тогда, когда матрица Гессе функции f(x) по x положительно (отрицательно) полуопределена для всех x (см. точки локальных экстремумов функции многих переменных).

Критические точки функции:

если гессиан положительно определён, то x₀ — точка локального минимума функции f(x),
если гессиан отрицательно определён, то x₀ — точка локального максимума функции f(x),
если гессиан не является знакоопределённым (принимает как положительные, так и отрицательные значения) и невырожден (det G(f) ≠ 0), то x₀ — седловая точка функции f(x).

Критерии определенности матрицы (теорема Сильвестра)

Положительная определенность:

все диагональные элементы матрицы должны быть положительны;
все ведущие главные определители должны быть положительны.

Для положительно полуопределённых матриц критерий Сильвестра звучит подобным образом: Форма положительно полуопределена тогда и только тогда, когда все главные миноры неотрицательны. Если матрица Гессе в точке положительно полуопределена (все главные миноры неотрицательные), то это точка минимума (однако, если гессиан полуопределен, а один из миноров равен 0, то это может быть и седловая точка. Нужны дополнительные проверки).

Положительная полуопределенность:

все диагональные элементы неотрицательны;
все главные определители неотрицательны.

Главный определитель – это определитель главного минора.

Квадратная симметрическая матрица порядка n, элементами которой являются частные производные целевой функции второго порядка, называется матрицей Гессе и обозначается:

Для того, чтобы симметрическая матрица была положительно определена, необходимо и достаточно, чтобы все ее диагональные миноры были положительны, т.е.

для матрицы A= (a_ij) положительные.

Отрицательная определенность.
Для того чтобы симметрическая матрица была отрицательно определена, необходимо и достаточно, чтобы имели место неравенства:
(-1)^k D_k> 0, k =1,.., n.
Другими словами, для того, чтобы квадратичная форма была отрицательно определённой, необходимо и достаточно, чтобы знаки угловых миноров матрицы квадратичной формы чередовались, начиная со знака минус. Например, для двух переменных, D₁ < 0, D₂ > 0.

Если гессиан полуопределен, то это может быть и точка перегиба. Нужны дополнительные исследования, которые могут быть проведены по одному из следующих вариантов:

Понижение порядка. Делается замена переменных. Например, для функции двух переменных это y=x, в итоге получаем функцию одного переменного x. Далее исследуется поведение функции на прямых y=x и y=-x. Если в первом случае функция в исследуемой точке будет иметь минимум, а в другом случае максимум (или наоборот), то исследуемая точка представляет собой седловую точку.
Нахождение собственных значений гессиана. Если все значения положительные, функция в исследуемой точке имеет минимум, если все отрицательные – имеется максимум.
Исследование функции f(x) в окрестности точки ε. Переменные x заменяются на x₀+ε. Далее необходимо доказать, что функция f(x₀+ε) от одной переменной ε, либо больше нуля (тогда x₀ точка минимума), либо меньше нуля (тогда x₀ точка максимума).

Примечание. Чтобы найти обратный гессиан достаточно найти обратную матрицу.

Пример №1. Какие из следующих функций являются выпуклыми или вогнутыми: f(x) = 8x₁²+4x₁x₂+5x₂².
Решение. 1. Найдем частные производные.

2. Решим систему уравнений.
-4x₁+4x₂+2 = 0
4x₁-6x₂+6 = 0
Получим:
а) Из первого уравнения выражаем x₁ и подставляем во второе уравнение:
x₂ = x₂+¹/₂
-2x₂+8 = 0
Откуда x₂ = 4
Данные значения x₂ подставляем в выражение для x₁. Получаем: x₁ = ⁹/₂
Количество критических точек равно 1.
M₁(⁹/₂;4)
3. Найдем частные производные второго порядка.

4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀).
Вычисляем значения для точки M₁(⁹/₂;4)

Строим матрицу Гессе:

D₁ = a₁₁ < 0, D₂ = 8 > 0
Поскольку диагональные миноры имеют различные знаки, то о выпуклости или вогнутости функции ничего сказать нельзя.

Пример №2. Выяснить, является ли функция f(x) = 2x₁² + x₂² + sin(x₁ + x₂) выпуклой в пространстве R².
Решение. Дважды дифференцируемая функция является выпуклой в пространстве R², если главные угловые миноры матрицы Гессе неотрицательны. Запишем матрицу Гессе – матрицу вторых производных:

Угловые миноры Δ_i соответственно равны:

Таким образом, D₁> 0, D₂> 0 при всех значениях x∈R², т.е. функция f(x) выпукла.

Пример №3. Является ли функция f(x) = x1+2*x1*x2+4*x2 выпуклой, вогнутой?
Решение. 1. Найдем частные производные.

2. Решим систему уравнений.
2•x₂+1 = 0
2•x₁+4 = 0
Получим:
Количество критических точек равно 2.
M₁(0;^-1/₂), M₂(-2;0)
3. Найдем частные производные второго порядка.

4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀).
Вычисляем значения для точки M₁(0;^-1/₂)

Строим матрицу Гессе:

D₁ = a₁₁ = 0, то вопрос о вогнутости или выпуклости функции остается открытым.
Вычисляем значения для точки M₂(-2;0)

Строим матрицу Гессе:
D₁ = a₁₁ = 0, то вопрос о вогнутости или выпуклости функции остается открытым.

Пример №4. Выяснить, является ли функция выпуклой в пространстве R².
Решение. Запишем матрицу Гессе – матрицу вторых производных:

Угловые миноры равны:

Таким образом, D₁> 0, D₂> 0 при всех значениях x∈R², т.е. функция f(x) выпукла.

Источник

‹– Назад

Матрица Гессе

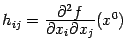
Двойная сумма в формуле (9.8) содержит в качестве коэффициентов значения всех частных производных второго порядка, вычисленные в точке . Эти значений можно объединить в квадратную матрицу размера . Эта матрица называется матрицей Гессе функции в точке .

Если все смешанные частные производные второго порядка непрерывны, то

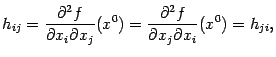
так что матрица Гессе в этом случае симметрична: (знак означает транспонирование матрицы).

Заметим, что линейную часть правой части формулы (9.8) можно представить в виде

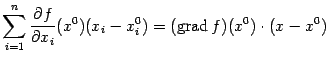
(точка означает скалярное произведение), а квадратичную часть, заданную двойной суммой в формуле (9.8), — в виде

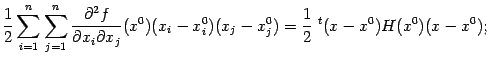
при этом мы считаем вектор записанным в виде матрицы-столбца, а транспонированный вектор — в виде матрицы-строки. Тем самым, получаем формулу квадратичного приближения в виде

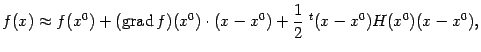
где — матрица Гессе.

В случае, когда — стационарная точка функции , градиент обращается в 0 в точке , так что получаем

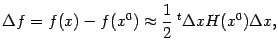
где — приращение аргумента в точке . Таким образом, в окрестности стационарной точки приращение функции ведёт себя как квадратичная функция приращения аргумента:

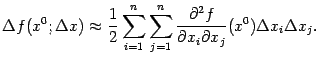
Пример 9.1 Рассмотрим функцию

Покажем, что начало координат — это стационарная точка функции , и найдём квадратичное приближение функции в окрестности начала координат.

Частные производные первого порядка равны

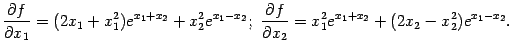
При и обе частные производные, действительно, обращаются в 0, так что точка — стационарная. Вычислим элементы матрицы Гессе функции в точке :

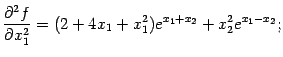
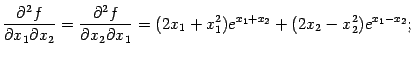
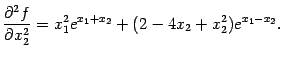
При и получаем:

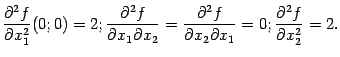
Значит,

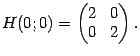
Так как значение равно 0, то квадратичное приближение функции в окрестности начала координат выглядит так:

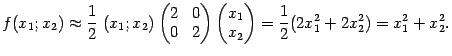
Таким образом, при небольших функция приближённо равна .

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Источник

Частные производные функций многих переменных

Частная
производная функции
по переменной

в точке

– предел отношения частного приращения
функции по переменной
к приращению

этой переменной при
:(аналогично определяется производная
по).

Обозначения:
частная производная по
:,,;частная
производная по
:
точке:,,.

Замечание.
Частная
производная по
– обычная производная попри фиксированном.
Частная производная по– обычная производная попри фиксированном значении.

Пример.
Для
имеем:
,.

Необходимое условие экстремума.Если функцияимеет непрерывные производные иэкстремумв точке
,
то.

Градиент

Градиент
функции –
вектор из ее частных производных –
характеризует направление и величину
максимальной скорости возрастания этой
функции в заданной точке.

Градиент
функции двух переменных

в точке

– это
.

Градиент
функции

в точке
перпендикулярен
линии уровня функции
,
проходящей через эту точку.

Пример.
Найти градиент функции

в точке
.

Решение.
1) Найдем частные производные:
,.

2)
Вычислим частные производные в точке

:
,.

3)
Составим из полученных значений градиент
.

Частные
производные второго порядка
– это производные от производных.

Для
функции двух переменных – это
,,,.

Матрица
Гессе –
матрица из вторых производных функции.

Для
функции двух переменных – это
.

Пример.
Построить
матрицу Гессе функции
в точке (-1, 1).

Решение.
1) Найдем частные производные первого
порядка:
,.

2)
Найдем частные производные второго
порядка:

,
,

,
.

3)
Строим матрицу Гессе
.
Вычисляем в заданной точке.

Достаточное
условие минимума (максимума) в точке
– главные миноры матрицы Гессе
положительны (чередуют знаки, начиная
со знака «минус»).

Алгоритм
поиска наибольшего и наименьшего
значений функции на множестве
1)
Построить множество
.

2)
Найти точки экстремума функции
,
выбрать из них те, которые попадают
внутрь множества,
и вычислить значение функции в этих
точках.

3) Последовательно
подставляя в функцию
уравнения линий,
ограничивающих множество, найти
наибольшие и наименьшие значения
получающихся функций одной переменной
на границе множества
и вычислить значения функциив этих точках.

4)
Из найденных значений функции
выбрать наибольшее и наименьшее.

Пример.
Найти max
и min
функции
на множестве

Решение.
1)
– прямоугольный треугольник, ограниченный
прямыми,,.

2) Функция
имеет стационарные точкиив области
,
, вычислим:,.

3)
Исследуем значения функции на границе
множества
.

Подставим
уравнение прямой
в функциюи уравнение границы.
Получится функция,.
Найдем ее наибольшее и наименьшее
значения на отрезке:,
тогда.
Обозначим точку.
Вычислим значение функции в этой
точке:.
При(точка)
значение функции.
При(точка);
значение функции.

Подставим
уравнение прямой
в функциюи уравнение границы.
Получится функция,.
Найдем ее наибольшее и наименьшее
значения на отрезке:,
тогда,
то есть получилась точка;.
При(точка)
значение функции:.
Приполучается точка,.

Подставим
уравнение прямой
в функцию,
тогда она примет вид,.
Найдем ее наибольшее и наименьшее
значения на отрезке.
Уравнениевещественных корней не имеет. Следовательно,
функцияна отрезкене имеет стационарных точек. Приполучается точка,.
Приполучается точка,.

4)
Выпишем полученные значения функций:
,,,,,.
Следовательно, наибольшего значенияфункция достигает в точке,
а наименьшегов точкахи.

Соседние файлы в папке Matematika_Abramov

Источник

Гессиан функции — симметрическая квадратичная форма^[1], описывающая поведение функции во втором порядке.

Для функции , дважды дифференцируемой в точке $xin mathbb{R} ^{n}$

$H(x)=sum _{{i=1}}^{n}sum _{{j=1}}^{n}a_{{ij}}x_{i}x_{j}$

или

$H(z)=sum _{{i=1}}^{n}sum _{{j=1}}^{n}a_{{ij}}z_{i}overline {z}_{j}$

где $a_{{ij}}=partial ^{2}f/partial x_{i}partial x_{j}$ (или $a_{{ij}}=partial ^{2}f/partial z_{i}partial overline {z}_{j}$ ) и функция задана на -мерном вещественном пространстве $mathbb {R} ^{n}$ (или комплексном пространстве $mathbb{C}^n$ ) с координатами $x_{1},ldots ,x_{n}$ (или $z_{1},ldots ,z_{n}$ ). В обоих случаях гессиан — квадратичная форма, заданная на касательном пространстве, не меняющаяся при линейных преобразованиях переменных. Гессианом также часто называют и определитель матрицы ${displaystyle (a_{ij}),}$ см. ниже.

Матрица Гессе[править | править код]

Матрица этой квадратичной формы образована вторыми частными производными функции. Если все производные существуют, то

$H(f)={begin{bmatrix}{frac {partial ^{2}f}{partial x_{1}^{2}}}&{frac {partial ^{2}f}{partial x_{1},partial x_{2}}}&cdots &{frac {partial ^{2}f}{partial x_{1},partial x_{n}}}\\{frac {partial ^{2}f}{partial x_{2},partial x_{1}}}&{frac {partial ^{2}f}{partial x_{2}^{2}}}&cdots &{frac {partial ^{2}f}{partial x_{2},partial x_{n}}}\\vdots &vdots &ddots &vdots \\{frac {partial ^{2}f}{partial x_{n},partial x_{1}}}&{frac {partial ^{2}f}{partial x_{n},partial x_{2}}}&cdots &{frac {partial ^{2}f}{partial x_{n}^{2}}}end{bmatrix}}$

Определитель этой матрицы называется определителем Гессе, или просто гессианом^{[источник не указан 3824 дня]}.

Матрицы Гессе используются в задачах оптимизации методом Ньютона.
Полное вычисление матрицы Гессе может быть затруднительно, поэтому были разработаны квазиньютоновские алгоритмы, основанные на приближённых выражениях для матрицы Гессе. Наиболее известный из них — алгоритм Бройдена — Флетчера — Гольдфарба — Шанно.

Симметрия матрицы Гессе[править | править код]

Смешанные производные функции f — это элементы матрицы Гессе, стоящие не на главной диагонали. Если они непрерывны, то порядок дифференцирования не важен:

${frac {partial }{partial x_{i}}}left({frac {partial f}{partial x_{j}}}right)={frac {partial }{partial x_{j}}}left({frac {partial f}{partial x_{i}}}right)$

Это можно также записать как

$f_{{x_{i}x_{j}}}=f_{{x_{j}x_{i}}},quad forall i,jin {1,ldots ,n}.$

В этом случае матрица Гессе симметрична.

Критические точки функции[править | править код]

Если градиент (её векторная производная) равен нулю в некоторой точке $x_{0}$ , то эта точка называется критической. Достаточным условием существования экстремума в этой точке является знакоопределённость гессиана f (понимаемого в данном случае как квадратичная форма), а именно:

Вариации и обобщения[править | править код]

Вектор-функции[править | править код]

Если — вектор-функция, то есть

$f=(f_{1},f_{2},dots ,f_{n}),$

то её вторые частные производные образуют не матрицу, а тензор ранга 3, который можно рассматривать как массив из матриц Гессе:

${displaystyle H(f)=left(H(f_{1}),ldots ,H(f_{n})right).}$

При n = 1 данный тензор вырождается в обычную матрицу Гессе.

Окаймлённый гессиан[править | править код]

При решении задачи нахождения условного экстремума функции ${displaystyle f:mathbb {R} ^{n}rightarrow mathbb {R} }$ с ограничениями

${displaystyle left{{begin{array}{c}g_{1}(x)=0,\vdots \g_{m}(x)=0,end{array}}right.}$

где $x in mathbb{R}^n$ , m<n , для проверки достаточных условий экстремума можно использовать так называемый окаймлённый гессиан функции Лагранжа , который будет иметь вид^[2]

${displaystyle left({begin{array}{cc}{dfrac {partial ^{2}L}{partial x^{2}}}&{dfrac {partial ^{2}L}{partial xpartial lambda }}\left({dfrac {partial ^{2}L}{partial xpartial lambda }}right)^{mathrm {T} }&{dfrac {partial ^{2}L}{partial lambda ^{2}}}end{array}}right)=left({begin{array}{cccccc}{dfrac {partial ^{2}L}{partial x_{1}^{2}}}&ldots &{dfrac {partial ^{2}L}{partial x_{1}partial x_{n}}}&{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{1}}}\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial ^{2}L}{partial x_{n}partial x_{1}}}&ldots &{dfrac {partial ^{2}L}{partial x_{n}^{2}}}&{dfrac {partial g_{1}}{partial x_{n}}}&ldots &{dfrac {partial g_{m}}{partial x_{n}}}\{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{1}}{partial x_{n}}}&0&ldots &0\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial g_{m}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{n}}}&0&ldots &0end{array}}right).}$

Проверка достаточных условий экстремума заключается в вычислении знаков детерминантов определённого набора подматриц окаймлённого гессиана. Именно, если существуют ${displaystyle x^{*}in mathbb {R} ^{n}}$ и ${displaystyle lambda ^{*}in mathbb {R} ^{m}}$ такие, что ${displaystyle nabla L(x^{*},lambda ^{*})=0}$ и

${displaystyle (-1)^{m}{mbox{det}}left({begin{array}{cccccc}{dfrac {partial ^{2}L}{partial x_{1}^{2}}}&ldots &{dfrac {partial ^{2}L}{partial x_{1}partial x_{p}}}&{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{1}}}\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial ^{2}L}{partial x_{p}partial x_{1}}}&ldots &{dfrac {partial ^{2}L}{partial x_{p}^{2}}}&{dfrac {partial g_{1}}{partial x_{p}}}&ldots &{dfrac {partial g_{m}}{partial x_{p}}}\{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{1}}{partial x_{p}}}&0&ldots &0\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial g_{m}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{p}}}&0&ldots &0end{array}}right)>0}$

для , то в точке $x^{*}$ функция имеет строгий условный минимум. Если же

${displaystyle (-1)^{p}{mbox{det}}left({begin{array}{cccccc}{dfrac {partial ^{2}L}{partial x_{1}^{2}}}&ldots &{dfrac {partial ^{2}L}{partial x_{1}partial x_{p}}}&{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{1}}}\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial ^{2}L}{partial x_{p}partial x_{1}}}&ldots &{dfrac {partial ^{2}L}{partial x_{p}^{2}}}&{dfrac {partial g_{1}}{partial x_{p}}}&ldots &{dfrac {partial g_{m}}{partial x_{p}}}\{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{1}}{partial x_{p}}}&0&ldots &0\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial g_{m}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{p}}}&0&ldots &0end{array}}right)>0}$

для , то в точке $x^{*}$ функция имеет строгий условный максимум^[3].

История[править | править код]

Понятие введено Людвигом Отто Гессе (1844), который использовал другое название. Термин «гессиан» был введён Джеймсом Джозефом Сильвестром.

См. также[править | править код]

Якобиан
Критическая точка (математика)
Лемма Морса
Критерий Сильвестра — критерий положительной или отрицательной определённости квадратной матрицы

Примечания[править | править код]

↑ Гессиан. Дата обращения: 2 апреля 2016. Архивировано 15 апреля 2016 года.
↑ Hallam, Arne Econ 500: Quantitative Methods in Economic Analysis I. Iowa State (7 октября 2004). Дата обращения: 14 апреля 2021. Архивировано 19 апреля 2021 года.
↑ Neudecker, Heinz. Matrix Differential Calculus with Applications in Statistics and Econometrics / Heinz Neudecker, Jan R. Magnus. — New York : John Wiley & Sons, 1988. — P. 136. — ISBN 978-0-471-91516-4.

Ссылки[править | править код]

Камынин Л.И. Математический анализ. Т. 1, 2. – 2001.
Кудрявцев Л.Д «Краткий курс математического анализа. Т.2. Дифференциальное и интегральное исчисления функций многих переменных. Гармонический анализ», ФИЗМАТЛИТ, 2002, — 424 с. — ISBN 5-9221-0185-4. Или любое другое издание.
Голубицкий М., Гийемин В. Устойчивые отображения и их особенности, — М.: Мир, 1977.

Источник

EMBED

Theme

Output Type

Матрица Гессе

Критерии определенности матрицы (теорема Сильвестра)

Матрица Гессе

Частные производные функций многих переменных

Градиент

Матрица Гессе[править | править код]

Симметрия матрицы Гессе[править | править код]

Критические точки функции[править | править код]

Вариации и обобщения[править | править код]

Вектор-функции[править | править код]

Окаймлённый гессиан[править | править код]

История[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Вам также может понравиться

Как найти пониженную скорость

Как найти неизвестный трек

Как найти уравнение прямой пример

Добавить комментарий Отменить ответ