Как найти матрицу гомографии

В этой заметке будет рассмотрено преобразование изображения в вид сверху с помощью матрицы гомографии. В жаргоне компьютерного зрения вид сверху называется вид с высоты птичьего полета (bird eye view).

Что такое матрица гомографии ?

Работа с планарными (плоскими) объектами — часто возникающая задача в компьютерном зрении. Преобразования для планарных объектов называются гомографией.

[x_i’ = frac{h_{11}x_i + h_{12}y_i + h_{13}}{h_{31}x_i + h_{32}y_i + h_{33}} \
y_i’ = frac{h_{21}x_i + h_{22}y_i + h_{23}}{h_{31}x_i + h_{32}y_i + h_{33}} ]

Выведем это преобразование:

Рассмотрим проекцию на первом изображении и проекцию на втором изображении. Во втором случае у нас другая проекционная матрица, потому что поза другая, соответственно точка тоже будет другая. Мы хотим найти преобразование между пикселями на изображении. Идея получения этого преобразования состоит в следующем: так как объект плоский, то мы можем выбрать такую систему координат, в которой начало координат расположено где-то на этой плоскости, ось (Z) будет направлена по нормали к этой плоскости. И как-то направлены оси (X), (Y) . В этой системе координат будут новые проекционные матрицы, которые всегда можно пересчитать. Главное, что координаты нашего объекта теперь вместо ((X,Y,Z,1)) будут ((X, Y, 0, 1)). При умножении такого вектора ((X, Y, 0, 1)) на проекционную матрицу размерности (3×4), то третий столбец будет все время умножаться на ноль. Поэтому на плоскости в качестве проекционной матрицы мы можем использовать матрицу (P) без третьего столбца и умножать ее на вектор ((X, Y, 1)). Тоже самое верно для второго изображения. Теперь новые проекционные матрицы (P1′) и (P2′) имеют размерность (3×3), дальнейшее просто. Мы можем слева умножить на обратную матрицу, получим, что

[ begin{bmatrix} w_i x_i′ \ w_i y_i′ \ w_i end{bmatrix} = H begin{bmatrix} x_i \ y_i \ 1 end{bmatrix}, ]

где (H) матрица гомографии размерностью (3×3)

Таким образом, если мы знаем координаты первого изображения на плоскости, то существует такая матрица размером (3×3), с помощью которой можно найти координаты на втором изображении, используя формулу приведенную выше. Результатом такого преобразования получается вектор в однородных координатах. Для перехода от однородных координат к мировым нужно результирующий вектор поделить на (w_i).

Выравнивание изображения с помощью матрицы гомографии

Рассмотрим 2 изображения, показанных на рисунке 1. На данном рисунке можно увидеть 4 соответствующие точки, помеченные разными цветами: синим, зеленым, черным и красным. Обычно соответствующие точки для выравнивания изображения обнаруживаются автоматически путем сопоставления между изображениями таких функций, как SIFT или SURF, но в данном разделе такие точки мы выделяли вручную.

Рассмотрим код на языке Python с использованием библиотек OpenCV и Numpy в котором указаны исходные и конечные точки на двух изображениях.

import cv2
import numpy as np

# Read source image.
im_src = cv2.imread('book1.jpg')
# Four corners of the book in source image
pts_src = np.float32([[1016, 1856], [1944, 1927], [1917, 2148], [998, 2081]])

# Read destination image.
im_dst = cv2.imread('book2.jpg')
# Four corners of the book in destination image.
pts_dst = np.float32([[1410, 1437], [2004, 2009], [1846, 2149], [1268, 1572]])<br />
Приведенное выше уравнение верно для всех наборов соответствующих точек, лежащих в одной плоскости в реальном мире. Другими словами, мы можем применить гомографию к первому изображению и книга на первом изображении выровняется с книгой на втором изображении. Смотрите рисунок 2.
Для расчета матрицы гомографии будем использовать библиотеку OpenCV, которая надежно оценит гомографию изображения, используя 4 начальные
и 4 конечные точки.
# Calculate the homography
M = cv2.getPerspectiveTransform(pts_src, pts_dst)

# Warp source image to destination
im_out = cv2.warpPerspective(im_src, M, (im_src.shape[1], im_src.shape[0])

# Show output
cv2.imshow("Warped Source Image", im_out)
cv2.imwrite("book_bird_eye_view.jpg", im_out)

cv2.waitKey(0)
Вид сверху
Преобразования изображения в вид сверху очень похоже на выравнивание изображения. Для этого также выделяется 4 точки на изображении, однако теперь удобнее выделить эти точки в углах книги. После чего нам нужно создать пустое изображение и задать новое положение найденным точкам в углах книги так, чтобы книга находилась по центру в вертикальном положении.
Для удобства будем задавать точки кликом мыши на изображении. Выделять точки стоит с левого верхнего угла. Исходя из разрешения исходного изображения, размер книги возьмем равным 1500×2000 пикселей. Вы можете изменить размер объекта на ваше усмотрение.
def mouse_handler(event, x, y, flags, data):
    if event == cv2.EVENT_LBUTTONDOWN:
        cv2.circle(data['im'], (x, y), 25, (0, 0, 255), -1)
        cv2.imshow("Image", data['im'])
        if len(data['points']) < 4:
            data['points'].append([x, y])


def get_four_points(im):
    data = {}
    data['im'] = im.copy()
    data['points'] = []

    cv2.imshow("Image", im)
    cv2.setMouseCallback("Image", mouse_handler, data)
    cv2.waitKey(0)

    points = np.float32(data['points'])
    return points


if __name__ == '__main__':

    # Read in the image.
    im_src = cv2.imread('book1.jpg')

    # Show image and wait for 4 clicks.
    pts_src = get_four_points(im_src)

    # Book size
    size = (1500, 2000)

    # Destination coordinates located in the center of the image
    pts_dst = np.float32(
        [                    
            [im.shape[1]/2 - size[0]/2, im.shape[0]/2 - size[1]/2],
            [im.shape[1]/2 + size[0]/2, im.shape[0]/2 - size[1]/2],
            [im.shape[1]/2 + size[0]/2, im.shape[0]/2 + size[1]/2],
            [im.shape[1]/2 - size[0]/2, im.shape[0]/2 + size[1]/2]
         ]
    )
Расчет матрицы гомографии производится аналогично предыдущему пункту.
На рисунке 3 мы преобразовали все исходное изображение в вид сверху, однако возможно произвести коррекцию перспективы. При этом в результирующем изображении будет видна только сама книжка, без лишней информации с исходного изображения. Для этого новое положение найденных точек задается в начале координат — левый верхний угол изображения.
Еще одним из самых интересных применений гомографии является создание панорам (сшивание двух изображений).



  


                       
  




Полный код программы на языке Python
Вместо заключения, приведем код программы для преобразования изображения в вид сверху. Вы можете изменять конечное положение точек на ваше усмотрение для достижения других результатов, главное не забывайте, что начало координат в компьютерной геометрии находится в левом верхнем углу.
import cv2
import numpy as np


def mouse_handler(event, x, y, flags, data):
    if event == cv2.EVENT_LBUTTONDOWN:
        cv2.circle(data['im'], (x, y), 25, (0, 0, 255), -1)
        cv2.imshow("Image", data['im'])
        if len(data['points']) < 4:
            data['points'].append([x, y])

def get_four_points(im):
    data = {}
    data['im'] = im.copy()
    data['points'] = []

    cv2.imshow("Image", im)
    cv2.setMouseCallback("Image", mouse_handler, data)
    cv2.waitKey(0)

    points = np.float32(data['points'])
    return points

if __name__ == '__main__':

    # Read in the image.
    im_src = cv2.imread('book1.jpg')

    # Show image and wait for 4 clicks.
    pts_src = get_four_points(im_src)

    # Book size
    size = (1500, 2000)

    # Destination coordinates located in the center of the image
    pts_dst = np.float32(
        [
            [im_src.shape[1]/2 - size[0]/2, im_src.shape[0]/2 - size[1]/2],
            [im_src.shape[1]/2 + size[0]/2, im_src.shape[0]/2 - size[1]/2],
            [im_src.shape[1]/2 + size[0]/2, im_src.shape[0]/2 + size[1]/2],
            [im_src.shape[1]/2 - size[0]/2, im_src.shape[0]/2 + size[1]/2]
         ]
    )

    # Calculate the homography
    M = cv2.getPerspectiveTransform(pts_src, pts_dst)

    # Warp source image to destination
    im_out = cv2.warpPerspective(im_src, M, (im_src.shape[1], im_src.shape[0])

    # Show output
    cv2.imshow("Warped Source Image", im_out)
    cv2.imwrite("book_bird_eye_view.jpg", im_out)

    cv2.waitKey(0)

1. Гомография

1 Концепция

Если сцена плоская, или приблизительно плоская, или с низким параллаксом, мы можем применить матрицу гомографии (гомография)

Преобразование гомографии – это преобразование двумерной проекции, которое отображает точки одной плоскости на другую. Здесь под плоскостью понимается изображение или плоская поверхность в трех измерениях.

Как показано на рисунке, красные точки на двух изображениях называются соответствующими парами точек.
Цель преобразования гомографии – получить матрицу гомографии через несколько заданных точек (обычно 4 пары точек).
использует матрицу 3×3 для представления гомографии, которую можно записать как

Рассмотрим первый набор соответствующих точек (X1, Y1) на первом изображении и (X2, Y2) на втором изображении. Тогда Homography H отображает их следующим образом

Преобразование координат:

Чтобы получить H-матрицу двух изображений, вы должны знать как минимум 4 точки в одной и той же соответствующей позиции. Обычно соответствие этих точек автоматически определяется путем сопоставления таких функций, как SIFT или Harris, между изображениями. из

Два, аффинное преобразование

1. Определение

Функция аффинного преобразования – это линейное преобразование из двухмерных координат в двухмерные координаты при сохранении «плоскостности» и «параллельности» двухмерной графики. Аффинное преобразование может быть реализовано путем комбинации ряда элементарных преобразований, включая перенос, масштабирование и вращение. Другими словами, когда существует разница смещения между двумя изображениями, величина перевода может быть рассчитана с помощью соответствующих параметров, и два изображения могут перекрываться.
Поскольку аффинное преобразование имеет 6 степеней свободы, для оценки матрицы необходимы три соответствующие пары точек.H。


Итак, проблема, которую необходимо решить, заключается в том, как решить (xt, yt)

2 Принцип

Используйте алгоритм просеивания или другие алгоритмы сопоставления, чтобы найти соответствующие точки двух изображений и координаты соответствующих точек, но проблема заключается в том, как найти разницу смещения группы соответствующих точек.
Предположим, что смещение i-й характерной точки равно


Поскольку количество уравнений больше, чем неизвестное, здесь мы используем решение методом наименьших квадратов.
Метод наименьших квадратов находит наилучшее совпадение функций данных путем минимизации суммы квадратов ошибок.
Для любой точки значения пикселя (Xi, Yi),

определяет остаток сопоставления как

Цель состоит в том, чтобы минимизировать остаточную сумму квадратов.

Метод, принятый методом наименьших квадратов, состоит в том, чтобы минимизировать дисперсию по обе стороны от знака равенства, то есть найти минимальное значение этой функции.

Метод наименьших квадратов аффинного преобразования

Искажение сцены во время процесса формирования изображения приведет к тому, что изображение будет вне масштаба. Для исправления искажения можно использовать аффинное преобразование. Параметры аффинного преобразования можно оценить методом наименьших квадратов.
Предположим, что исходное изображение – это f (x, y), а искаженное – F (X ‘, Y’). Чтобы восстановить F (X ‘, Y’) в f (x , y), заключается в нахождении отношения преобразования между координатами (X ‘, Y’) и координатами (x, y). Это отношение преобразования называется преобразованием координат и выражается как (x, y) = T (X ‘, Y’) .
Искажение сцены во время процесса формирования изображения приведет к тому, что изображение будет вне масштаба, и для исправления различных искажений можно использовать аффинное преобразование. Взаимодействие с другими людьми
Сначала вычислите коэффициент преобразования координат, выражение аффинного преобразования: R (x) = Px + Q, x = (x, y) – положение пикселя на плоскости, P – Матрица вращения 2×2, Q – вектор сдвига 2×1, P и Q – параметры аффинного преобразования, а именно:
　 　　　x= AX’ + BY’ + C
　　　　y= DX’ + EY’ + F
Следовательно, коррекция геометрического искажения – это, в конечном счете, решение коэффициентов преобразования координат A, B, C, D, E и F.
В этом процессе могут быть пустые пиксели. Это связано с тем, что при отображении изображения на одну и ту же точку могут быть сопоставлены два или более пикселей. В настоящее время около этой точки Пиксели будут пустыми, то есть появятся черные линии.
Как избежать этого явления, используйте билинейную разность, а затем обратное отображение.
Обратное сопоставление: для каждого пикселя x’in g (x ‘) вычислите соответствующую координату сопоставления x = h-1 (x’) в соответствии с моделью преобразования и установите x равным Значение пикселя присваивается g (x ‘). `

В-третьих, альфа-канал

Альфа-канал представляет собой 8-битный канал шкалы серого. Этот канал использует 256 уровней серого для записи информации о прозрачности изображения, определяя прозрачные, непрозрачные и полупрозрачные области, где белый означает непрозрачность, черный означает прозрачность, а серый означает полупрозрачность.
Метод наложения на исходное изображение состоит в том, чтобы удалить значение пикселя в соответствующей позиции наложенного изображения и смешать его со значением пикселя нижележащего изображения. Есть много способов микширования, но следует отметить, что значение альфа-канала должно быть преобразовано в тип с плавающей запятой.Этот процесс является нормализацией, и конечное изображение по-прежнему имеет 3 канала.

В-четвертых, осознайте

 # -*- coding: utf-8 -*-
from PCV.geometry import warp, homography
from PIL import  Image
from pylab import *
from scipy import ndimage

# example of affine warp of im1 onto im2
im1 = array(Image.open('../data/JMU/02.jpg').convert('L'))
im2 = array(Image.open('../data/JMU/03.jpg').convert('L'))
# set to points
tp = array([[120,260,260,120],[16,16,305,305],[1,1,1,1]])
#tp = array([[675,826,826,677],[55,52,281,277],[1,1,1,1]])
im3 = warp.image_in_image(im1,im2,tp)
figure()
gray()
subplot(141)
axis('off')
imshow(im1)
subplot(142)
axis('off')
imshow(im2)
subplot(143)
axis('off')
imshow(im3)

# set from points to corners of im1
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
# first triangle
tp2 = tp[:,:3]
fp2 = fp[:,:3]
# compute H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im3 = (1-alpha)*im2 + alpha*im1_t
# second triangle
tp2 = tp[:,[0,2,3]]
fp2 = fp[:,[0,2,3]]
# compute H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im4 = (1-alpha)*im3 + alpha*im1_t
subplot(144)
imshow(im4)
axis('off')
show()

Из экспериментальных результатов видно, что изображение 1 отображается на изображение 2, синтезируются два изображения разных размеров, а из другого изображения вычитается область. Здесь необходимо отметить, что сначала нужно удалить эту область из изображения, чтобы создать маленькое изображение, а затем указать область, в которую будет вставлено целевое изображение. Если размер двух изображений отличается, часть изображения будет обрезана.
Поскольку размер наложенного изображения не обязательно совпадает, например, при загрузке png и jpg, исходная прозрачная часть в png теперь черная, а видимая часть прозрачна Считается значением 0.

Мифическая сказка из Библии рассказывает о первой для людей инженерной катастрофе — Вавилонская башня^એ. У проекта было всё: ясная миссия, огромный человеческий ресурс, отсутствие временных ограничений и адекватные технологии (кирпичи и строительный раствор). Тем не менее, всё это эффектно провалилось, потому что Бог перепутал языки и люди больше не смогли общаться.

Такие термины, как «гомография», сбивают с толку и напоминают, как мы всё еще частенько боремся с общением. Гомография — такая простая концепция, но так странно называется!

Что есть гомография?

Рассмотрим два изображения на плоскости (обложка книги), показанные на рисунке 1. Красная точка представляет одну и ту же физическую точку на двух изображениях. В жаргоне компьютерного зрения они называются corresponding points (точки соответствия). На рисунке 1. показаны четыре точки соответствия в четырех разных цветах — красный, зеленый, желтый и оранжевый. Гомография — это преобразование (матрица 3 × 3), которое отображает точки одного изображения в точки соответствия другого изображения.

Теперь, поскольку гомография является матрицей 3 × 3, мы можем записать ее как

mathbf{H} = begin{pmatrix}h_{00}&h_{01}&h_{02}\h_{10}&h_{11}&h_{12}\h_{20}&h_{21}&h_{22}end{pmatrix}

Рассмотрим первый набор соответствующих точек — (x_1, y_1) в первом изображении и (x_2, y_2) во втором. Далее гомография H отображает их следующим образом:

begin{pmatrix}x_1\y_1\1end{pmatrix} = mathbf{H} times begin{pmatrix}x_2\y_2\1end{pmatrix} = begin{pmatrix}h_{00}&h_{01}&h_{02}\h_{10}&h_{11}&h_{12}\h_{20}&h_{21}&h_{22}end{pmatrix} times begin{pmatrix}x_2\y_2\1end{pmatrix}

Трансформация изображения с помощью гомографии

Приведенное выше уравнение верно для ВСЕХ наборов соответствующих точек, если в реальном мире они лежат на одной плоскости. Другими словами, применив гомографию к первому изображению, сделаете книгу на втором изображении такой же, как на первом! Смотрите рисунок 2.

Но как насчет точек, которые не находятся в плоскости? Ну, они НЕ будут выровнены с помощью гомографии, как вы можете видеть на рисунке 2. Но подождите, а что, если на изображении две плоскости? Ну, тогда у вас есть две гомографии — по одной на каждую плоскость.

Панорама есть приложение гомографии

В предыдущем разделе вы узнали, что при известной гомографией между двумя изображениями, можно трансформировать одно изображение в другое. Однако, есть одна тонкость. На изображении должна быть плоскость (обложка книги) и только фрагмент на плоскости может быть правильно трансформирован. Оказывается, если сделаеть снимок любой сцены (и не только плоской), а затем сделаете второй снимок, повернув камеру, то эти два изображения будут связаны гомографией! Другими словами, вы можете установить камеру на штатив и сделать снимок. Затем горизонтально сместить камеру и сделайте еще один снимок. Два изображения совершенно произвольной трехмерной сцены, которые вы только что сделали, будут связаны гомографией. На этих двух изображениях будут некоторые общие фрагменты, которые могут быть выровнены и сшиты так, что получится панорама из двух изображений. Что всё так просто? Нет! (извините, что разочаровал) На создание хорошей панорамы уходит много времени, но основной принцип заключается в том, чтобы с использованием гомографии выравнивать и сшивать так, чтобы швов было не видно. Созданию панорамы, безусловно, будет посвящена одна из следующих статей.

Как рассчитать гомографию?

Чтобы рассчитать гомографию между двумя изображениями, нужно знать как минимум 4 точки соответствия между двумя изображениями. Если таких точек больше, то это даже лучше. OpenCV надежно проведёт оценку гомографии по всем точкам соответствия самым наилучшим образом. Обычно эти точки соответствия обнаруживаются автоматически путем сопоставления между изображениями таких функций, как SIFT^એ или SURF, но здесь точки заданы вручную.

Посмотрим код.

'''
pts_src и pts_dst - это массивы точек
в исходных и конечных изображениях. Нам нужно как минимум
4 соответствующих пункта. 
'''
h, status = cv2.findHomography(pts_src, pts_dst)

''' 
Рассчитанная гомография может быть использована для деформации
исходного изображения до места назначения. Размер
размер (ширина, высота) im_dst
'''

im_dst = cv2.warpPerspective(im_src, h, size)

Пример гомографии с OpenCV на Python

Изображения на рисунке 2 созданы с использованием следующего кода Python, где используются четыре точки соответствия на двух изображениях и одно изображение трансформируется в другое.

import cv2
import numpy as np

if __name__ == '__main__' :

    # Прочитайте исходное изображение.
    im_src = cv2.imread('book2.jpg')
    # Четыре точки соответствия на обложке книги в исходном изображении
    pts_src = np.array([ [141, 131], [480, 159], [493, 630],[64, 601] ])


    # Прочитайте изображение для трансформации
    im_dst = cv2.imread('book1.jpg')
    # Четыре точки соответствия на обложке книги в изображении трансформации
    pts_dst = np.array([ [318, 256],[534, 372],[316, 670],[73, 473] ])

    # Рассчитайте гомографию
    h, status = cv2.findHomography(pts_src, pts_dst)
    
    # Трансформируем исходное изображение, используя полученную гомографию
    im_out = cv2.warpPerspective(im_src, h, (im_dst.shape[1],im_dst.shape[0]))
    
    # Покажите картинки
    cv2.imshow("Source Image", im_src)
    cv2.imshow("Destination Image", im_dst)
    cv2.imshow("Warped Source Image", im_out)

    cv2.waitKey(0)

Приложения гомографии

Самым интересным применением гомографии, несомненно, является создание панорам, например, мозаика и сшивание изображений. О панорамах по-позже. Посмотрим на некоторые другие интересные приложения.

Коррекция перспективы с помощью гомографии

Допустим, у вас есть фотография, показанная на рисунке 1. Не было бы здорово, если бы вы могли щелкнуть по четырем углам книги и быстро получить изображение, похожее на изображение, показанное на рисунке 3. Вы можете получить код для этого пример в разделе загрузки ниже. Вот шаги.

1. Напишите пользовательский интерфейс для сбора четырех углов книги. Давайте подсчитаем эти баллы pts_src
2. Нам нужно знать соотношение сторон книги. Для этой книги соотношение сторон (ширина/высота) составляет 3/4. Таким образом, мы можем выбрать размер выходного изображения 300 × 400, а наши конечные точки (pts_dst) равны (0,0), (299,0), (299,399) и (0,399)
3. Получите гомографию, используя pts_src и pts_dst.
4. Примените гомографию к исходному изображению, чтобы получить изображение на рисунке 3.

Виртуальный билборд

На многих телевизионных спортивных мероприятиях реклама практически вставляется в прямую трансляцию видео. Например. в футболе и бейсболе реклама, размещенная на небольших рекламных щитах прямо за границей поля, может быть практически изменена. Вместо того, чтобы показывать одно и то же объявление всем, рекламодатели могут выбирать, какие объявления показывать, исходя из демографических данных, местоположения и т. Д. В этих приложениях в ролике обнаруживаются четыре угла рекламного щита, которые служат точками назначения. Четыре угла объявления служат исходными точками. Гомография рассчитывается на основе этих четырех соответствующих точек и используется для деформации рекламы в видеокадр.

Прочитав этот пост, вы, вероятно, получите представление о том, как разместить изображение на виртуальном рекламном щите. Рисунок 4. показывает Исходное изображение, загруженное из интернета.

А на рисунке 5 показан Таймс-сквер.

Мы можем заменить один из рекламных щитов на Таймс-сквер нужным нам изображением. Вот шаги.

1. Напишите пользовательский интерфейс для сбора четырех углов рекламного щита на изображении. Давайте назовем эти точки pts_dst
2. Пусть размер изображения, которое вы хотите поместить на виртуальный рекламный щит, будет равен w x h. Поэтому углы изображения (pts_src) должны быть (0,0), (w-1,0), (w-1, h-1) и (0, h-1)
3. Получите гомографию, используя pts_src и pts_dst.
4. Примените гомографию к исходному изображению и смешайте его с целевым изображением, чтобы получить изображение на рисунке 6.

Обратите внимание на рисунок 6, где в изображение на Таймс-сквер мы вставили изображение, показанное на рисунке 4.

Кредиты изображений

1. Изображение на рисунке 4. было первым фотографическим изображением, загруженным в Интернет. Это квалифицируется как добросовестное использование. [ link ]
2. Изображение, использованное на рисунке 5. (Квадрат времени), лицензировано в рамках GFDL. [ ссылка ]

По мотивам Homography Examples using OpenCV (Python/ C++)

In this article, we are trying to track an object in the video with the image already given in it. We can also track the object in the image. Before seeing object tracking using homography let us know some basics.

What is Homography?

Homography is a transformation that maps the points in one point to the corresponding point in another image. The homography is a 3×3 matrix :

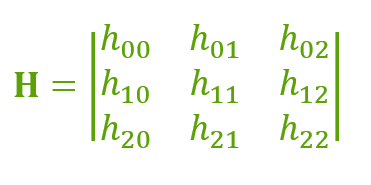
If 2 points are not in the same plane then we have to use 2 homographs. Similarly, for n planes, we have to use n homographs. If we have more homographs then we need to handle all of them properly. So that is why we use feature matching.

Importing Image Data : We will be reading the following image : 

Above image is the cover page of book and it is stored as ‘img.jpg’. 

Feature Matching : Feature matching means finding corresponding features from two similar datasets based on a search distance. Now will be using sift algorithm and flann type feature matching. 

Now, we also have to convert the video capture into grayscale and by using appropriate matcher we have to match the points from image to the frame.

Here, we may face exceptions when we draw matches because infinitely there will we many points on both planes. To handle such conditions we should consider only some points, to get some accurate points we can vary the distance barrier.

Homography : To detect the homography of the object we have to obtain the matrix and use function findHomography() to obtain the homograph of the object. 

Everything is done till now, but when we try to change or move the object in another direction then the computer cannot able to find its homograph to deal with this we have to use perspective transform. For example, humans can see near objects larger than far objects, here perspective is changing. This is called Perspective transform.

At the end, lets see the output 

Output : 

Last Updated :
03 Jan, 2023

Like Article

Save Article

[Let’s Know Series] – №1

Оценка гомографии

Этот небольшой фрагмент описывает уравнения для оценки матрицы гомографии 3 × 3. Сначала мы обсудим вычисление по внутренним и внешним параметрам камеры; и, где необходимо, свяжите формулировку с реальными техническими характеристиками камеры. Затем мы представляем методологию вычислений с использованием двух наборов соответствующих точек, которые копланарны в своих соответствующих плоскостях и избегают коллинеарных вырождений.

1 ⌉ ГОМОГРАФИЯ ПО ПАРАМЕТРАМ КАМЕРЫ

а. Базовая настройка

Давайте рассмотрим точку в 3D мировом пространстве как тройку

Затем мы можем сопоставить эту 3D точку с точкой в ​​произвольном пространстве следующим образом:

где C _int – это внутреннее, а C _ext – внешнее матрица камеры соответственно. Точка (x _a , y _a , z _a ) в произвольном пространстве, может быть сопоставлен с пространством 2D изображения с помощью следующего масштабного коэффициента:

Таким образом, когда у нас есть точка в произвольном пространстве, мы можем просто масштабировать ее координаты, чтобы получить координаты 2D в (захваченном) пространстве изображения.

б. Внутренняя матрица

Давайте теперь посмотрим на форму C _int. Рассмотрим камеру с фокусным расстоянием f (в мм) с фактическим размером сенсора (x _S, y _S) (в мм), а ширина и высота захваченного изображения (эффективный размер сенсора) как (w, h ) (в пикселях).
оптический центр (o _ x , o _ y) камеры тогда (w / 2 , h / 2). Теперь мы можем указать C _int следующим образом:

Таким образом, можно заметить, что все записи в C _int указаны в пикселях . Следующее может рассматриваться как эффективное фокусное расстояние в пикселях в направлениях x и y соответственно.

c. Внешняя матрица

C _ext состоит из матрицы поворота R и матрицы перевода T следующим образом:

Кортеж (T _x, T _y, T _z ) указывает на перевод камеры в мирово-пространственные координаты. Обычно мы можем считать, что камера не имеет перевода x и y (T _x = T _y = 0), а высота положения камеры от земли (в мм) равна T _z.

Если θ, φ, ψ быть ориентации камеры относительно осей x, y и z соответственно (как углы в радианах), мы можем получить r _ ij; i, j ∈ {1,2,3} следующим образом:

d. Гомография

Матрица гомографии H, которую необходимо оценить, представляет собой матрицу 3 × 3 и включает в себя части как внутренней, так и внешней матрицы камеры следующие:

Сказанное выше может быть непосредственно установлено из того факта, что когда мы ищем плоскую поверхность в мировоззрении для вычисления гомографии, Z _w = 0, и, следовательно, ,

Следовательно, гомография H отобразит точку зрения в произвольном пространстве. Этого пространства вполне достаточно, если нам просто нужно вычислить расстояния между любыми двумя заданными точками. Однако в действительности координаты в пиксельном пространстве будут вычисляться с учетом масштабного коэффициента, указанного в формуле. (2).

2⌉ ГОМОГРАФИЯ ИЗ ТОЧЕК КОПЛАНАРА

а. Базовая настройка

Гомография позволяет нам связать две камеры, наблюдающие одну и ту же плоскую поверхность; И камеры, и поверхность, которую они просматривают (создают изображения), расположены в координатах мировоззрения. Другими словами, два 2D изображения связаны между собой гомографией H, если оба смотрят на одну и ту же плоскость под другим углом . Отношения омографии не зависят от просматриваемой сцены.

Рассмотрим два таких изображения, просматривающих одну и ту же плоскость в мировоззрении.
Пусть (x _ 1, y _ 1) будет точкой на первом изображении, и (x ˆ_1, y ˆ_1) – соответствующая точка на втором изображении. Затем эти точки связаны оценкой гомографии H следующим образом:

Таким образом, любая точка на первом изображении может быть сопоставлена ​​с соответствующей точкой на втором изображении посредством гомографии, и операция может рассматриваться как операция деформации изображения.

б. Гомография

Давайте параметризуем матрицу гомографии 3 × 3 H следующим образом:

Таким образом, оценка H требует оценки 9 параметров. Другими словами, H имеет 9 степеней свободы. Если мы выберем два набора соответствующих точек, ☟ [копланарных] в их соответствующих плоскостях, следующим образом:

[co-planar] The homography relation is provable only under the co-planarity of the points, since everywhere, we are assuming that the z-coordinate of any point in any image is 1. In practice, for instance, one may thus choose four points on a floor, or a road, which indicate a nearly planar surface in the scene.

Затем из уравнения. (8, 9, 10), мы можем решить следующее, чтобы оценить H:

Где (x ˆ _ i, y ˆ _ i ) ∈ T ˆ _1 и (x _i, y _i) ∈ T _1 для i, j ∈ {1,2,3 , 4}. Затем это будет преобразовано в следующую систему уравнений, которую необходимо решить:

Теперь у нас есть 8 уравнений, которые можно использовать для оценки 8 степеней свободы H (кроме h _ 33). Для этого нам потребуется, чтобы указанная выше матрица 8 × 8 имела полный ранг (без избыточной информации) в том смысле, что ни одна из строк не является линейно зависимой. Это означает, что нет трех точек ни в T _1, ни в T ˆ _1 должен быть коллинеарным.

Затем нам нужно заняться h _33. Обратите внимание, что в формуле. (13), если h _33 предварительно приравнено к 1, мы просто сдвинем весь набор h _ij гиперплоскости к другой системе отсчета, но их направление не изменится. На практике, таким образом, мы просто увидели бы другое значение z _a при сопоставлении координат 2D изображения в соответствии с Уравнение (8), которые впоследствии будут разделены в формуле. (9). Следовательно, мы сохраняем h _33 = 1 в H, и уравнение. Затем уравнение (13) может быть решено с использованием оценки методом наименьших квадратов.

В OpenCV можно использовать функцию findHomography, которая делает то же самое, что описано выше. Он принимает два кортежа из четырех соответствующих точек и вычисляет гомографию H с h _33 всегда и строго 1. Любая точка изображения 2D будет затем сопоставлена ​​с z _a усиленной версией соответствующей точки в другой плоскости. .

c. Гомография с помощью гипотетической камеры

В различных приложениях, таких как виртуальная реклама, измерение абсолютного расстояния для умного планирования города, необходимо предположить наличие гипотетической камеры C и вычислить матрицу гомографии, которая может проецировать любую точку наблюдаемой сцены на плоскость изображения, захваченного с помощью C.

Представить C с высоты птичьего полета (вид сверху) – это ☟ [популярный выбор]. В таком случае можно выбрать T _1 с четырьмя копланарными точками в наблюдаемой сцене, в то время как соответствующий кортеж T ˆ _1 может просто иметь четыре точки в качестве углов гипотетического прямоугольника с евклидовой системой координат с центром вокруг (0, 0). Затем любую точку сцены можно сопоставить с ее видом с высоты птичьего полета, то есть как она может выглядеть сверху.

[popular choice] There has been a recent surge of research papers, which exploit the bird's eye view (BEV) for behavioural prediction and planning in autonmous driving.

Обратите внимание, что отображение на основе гомографии – это только искаженная версия наблюдаемого изображения, и что новая информация в сцене не синтезируется. Например, если мы наблюдали только фронтальный вид человека в сцене, его вид с высоты птичьего полета, на самом деле не начнем говорить о том, как у человека волосы сверху; но он будет деформировать только видимую часть его головы, видимую спереди, так, что это будет примерно похоже на вид сверху.

d. Отрицательные значения в проекциях с гомографией

Обратите внимание, что при решении для H нет ограничения, что точки проекции в произвольном пространстве должны быть положительными, то есть x _ a, y _ a и z _ a может быть отрицательным. После масштабирования на z _ a это будет означать, что сопоставленная точка (x ˆ_i , y ˆ_i) может быть отрицательным.

Это может показаться интуитивно нежелательным, поскольку координаты изображения обычно считаются положительными. Однако это можно рассматривать только как сдвиг опорной оси, и после сопоставления всего изображения величина сдвига может быть соответствующим образом решена.

💡 Remark - The treatment presented here, may not be akin to 3D reconstruction procedures, which may involve estimation of multiple-view homographies', sometimes via a hypothesized view projection. Multi-view homographies, have been shown to possess specific algebraic structures, but 3D reconstruction from 2D scenes largely remains an unsolved problem.