Пусть
в пространстве Rn
заданы два базиса е1,е2,
…
,еn
и f1,
f2,
f3…,
fn,
тогда каждый вектор из базиса f
можно разложить по базису e,
т.е.
![]()
![]()
Из
координатных столбцов векторов fj
в базисе e
можно составить квадратную матрицу
порядка n.
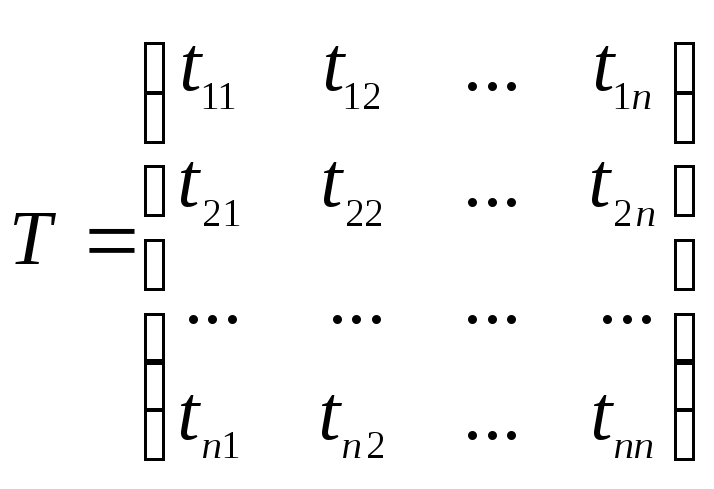 ,
,
которая называется, матрицей перехода
от базиса e
к базису f.
Она
является невырожденной, т.е. А0.
Значит, выражение
![]() можно записать в матричном виде
можно записать в матричном виде![]() .
.
Умножая это равенство наТ-1
справа, получаем
fT-1=e
или e
= fT-1,
т.е. Т-1
– матрица перехода от базиса f
к базису e.
Пример
5.
Найти координаты вектора
![]() в базисе
в базисе![]() если он задан в базисе
если он задан в базисе![]() .
.
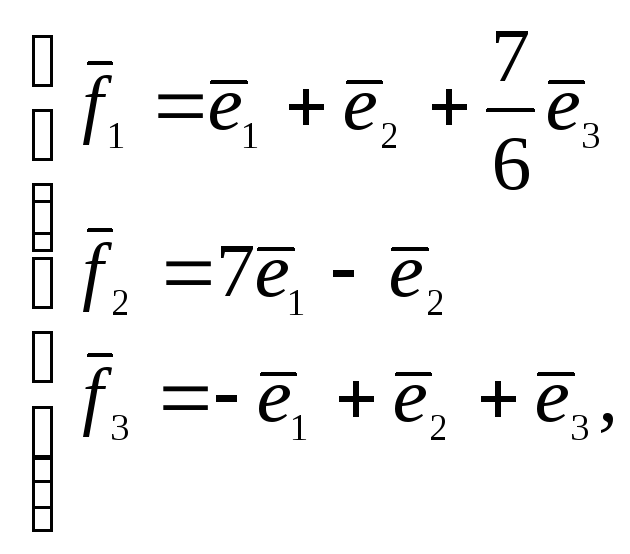
![]() .
.
Решение.
При
переходе от базиса e
к базису f
координаты одного и того же вектора
связаны формулами:
![]() ,
,
![]() ,
,
где
T
матрица перехода, которая находится
из равенства f
= eT.
Здесь
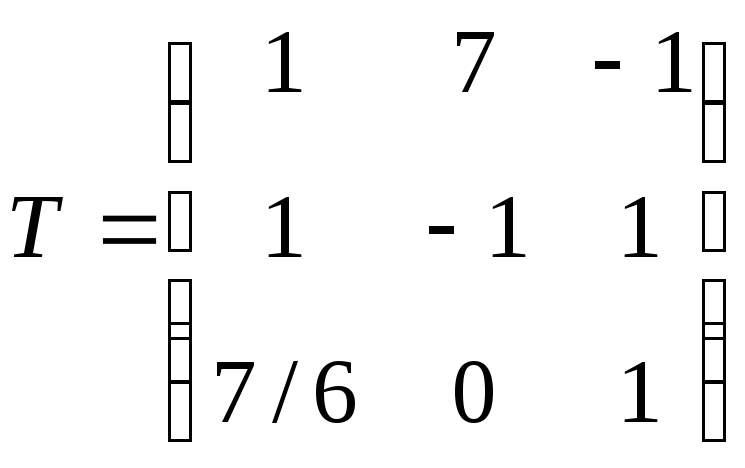 .
.
Найдем определитель матрицы:
![]()
(формула
разложения определителя по третьей
строке).
Найдем
алгебраические дополнения к элементам
матрицы T
и обратную матрицу по формуле
![]() :
:
![]()
![]()
![]() .
.
Таким
образом, обратная матрица будет
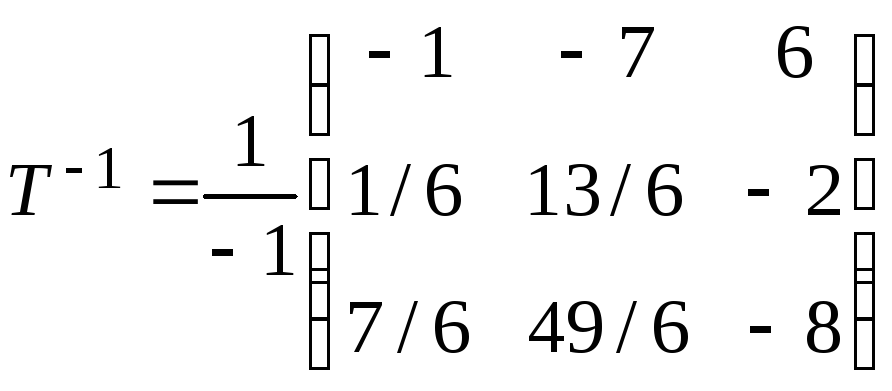 и, следовательно,
и, следовательно,
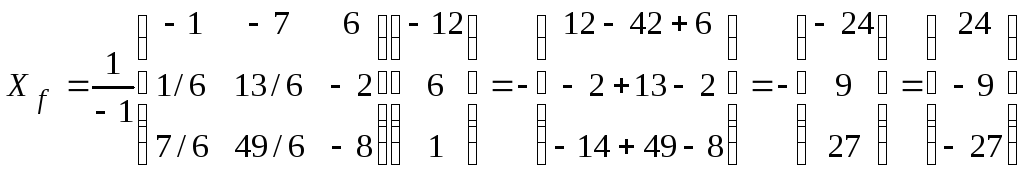 .
.
Окончательно
имеем в базисе f:
![]() .
.
Зависимость
между матрицами одного и того же оператора
в разных базисах выражается теоремой.
Теорема.
Матрицы
А
и
А*
линейного оператора А(х)
в
базисах
е1,е2,
…
,еn
и
f1,
f2,
f3…,
fn
связаны соотношением
A*
= Т-1∙A∙Т,
где
Т
— матрица перехода от старого базиса
к новому.
Пример
6.
В базисе e1,
e2
оператор А
имеет матрицу
![]() .
.
Найти матрицу этого же оператора в новом
базисеf1,
f2
, где
![]() .
.
Решение:
составим матрицу перехода (координаты
векторов нового базиса являются столбцами
матрицы перехода) т.е.
![]() и найдем обратную матрицу Т-1.
и найдем обратную матрицу Т-1.
Т=5,
![]() .
.
![]() –
–
матрица оператора А
в новом базисе.
Пример
7. Найти
матрицу линейного преобразования
![]() в базисе
в базисе![]() если она задана в базисе
если она задана в базисе![]()
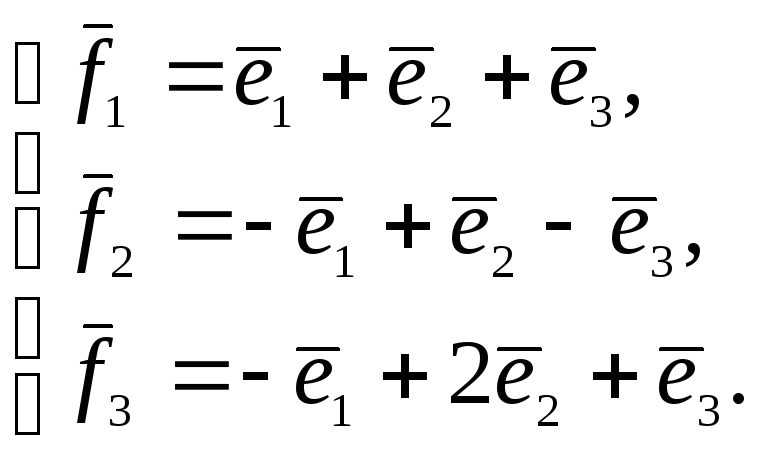 ,
,
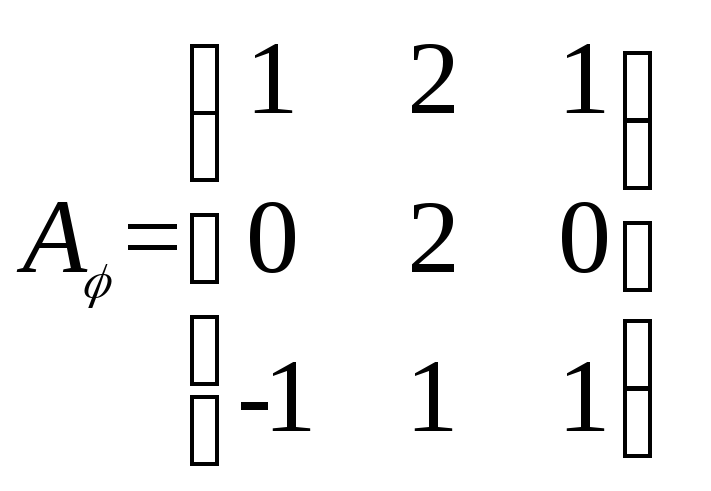 .
.
Решение.
При переходе
от базиса e
к базису f
матрица линейного преобразования, в
соответствии с определением, будет
иметь вид
![]() ,
,
где
T
матрица перехода, которая находится
из равенства f
= eT.
Здесь
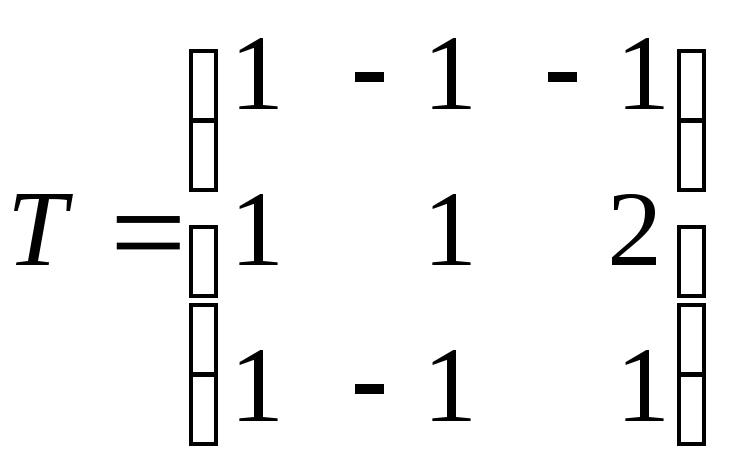 .
.
Найдем
определитель матрицы:
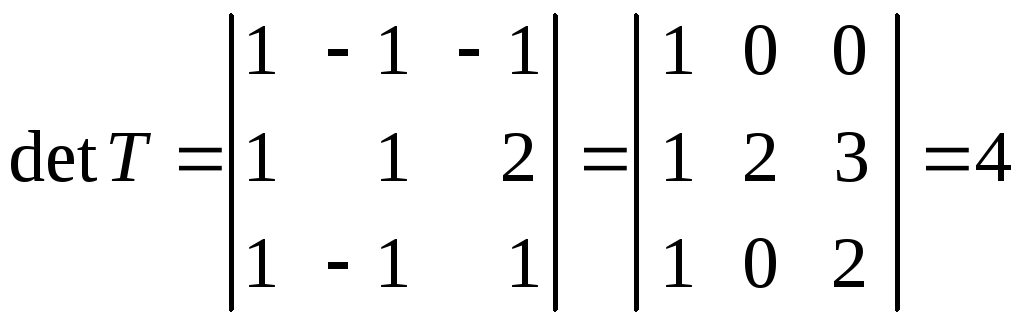
(прибавили к
элементам второго и третьего столбца
соответствующие элементы первого
столбца и записали формулу разложения
определителя по первой строке).
Найдем
алгебраические дополнения к элементам
матрицы T
и обратную матрицу по формуле
![]() :
:
![]()
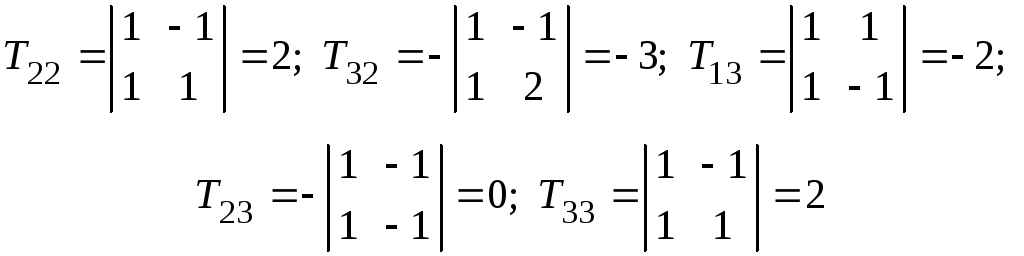 .
.
Таким
образом, обратная матрица будет
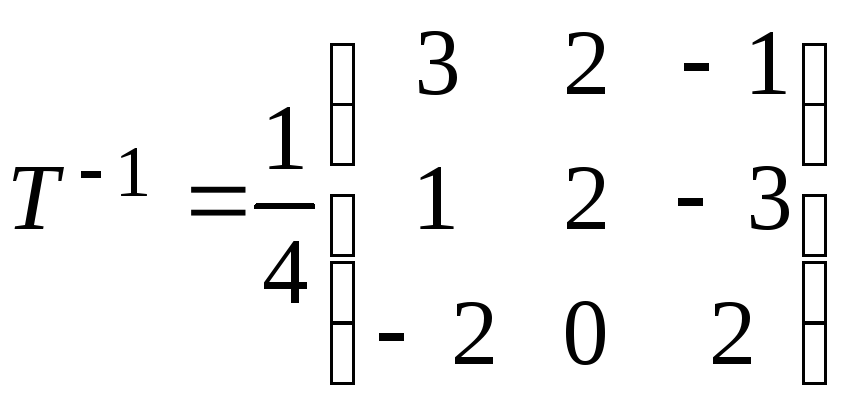 и, следовательно,
и, следовательно,

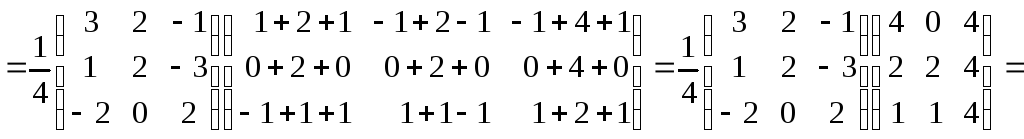
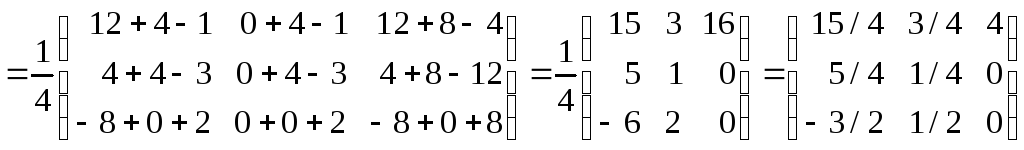 .
.
Лекция
14. Собственные значения и собственные
векторы линейного оператора.
ЗАДАЧА.
Найти
собственные значения и собственные
векторы линейного преобразования,
заданного в некотором базисе матрицей
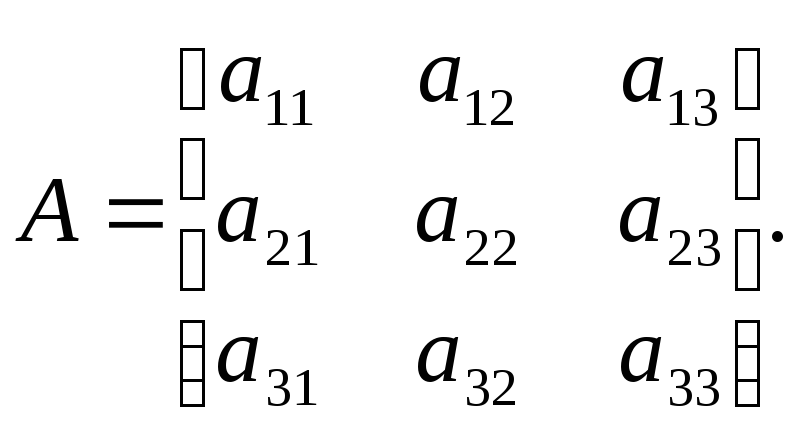
Определение
1.
Ненулевой
вектор X,
удовлетворяющий условию
AX=X
, (1)
называется
собственным вектором преобразования
A
. Число
в равенстве (1) называется собственным
значением.
Из
определения следует, что
собственный вектор под действием
линейного оператора А
переходит
в вектор, коллинеарный самому
себе, т.е. просто умножается на некоторое
число.
В то же время
несобственные векторы преобразуются
более сложным образом.
В связи с этим понятие собственного
вектора является очень
полезным и удобным при изучении многих
вопросов матричной
алгебры и ее приложений.
Равенство
(1) записано в матричной форме: АХ
= Х,
где
X
—
матрица-столбец
из координат вектора х,
или
в развернутом
виде
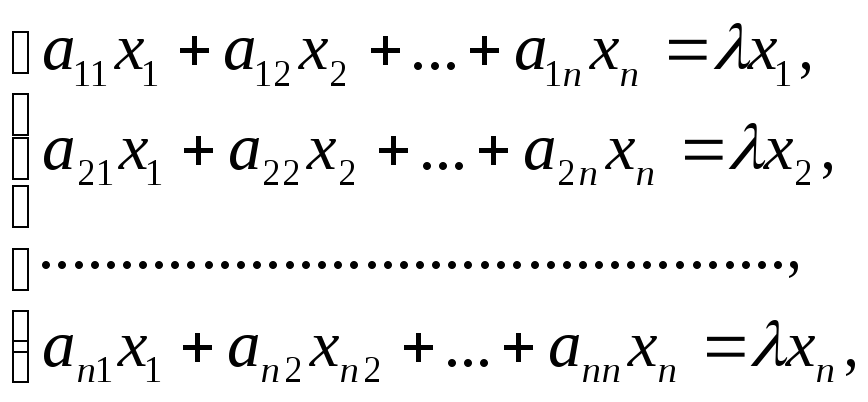 (1)
(1)
Перепишем
систему так, чтобы в правых частях были
нули:
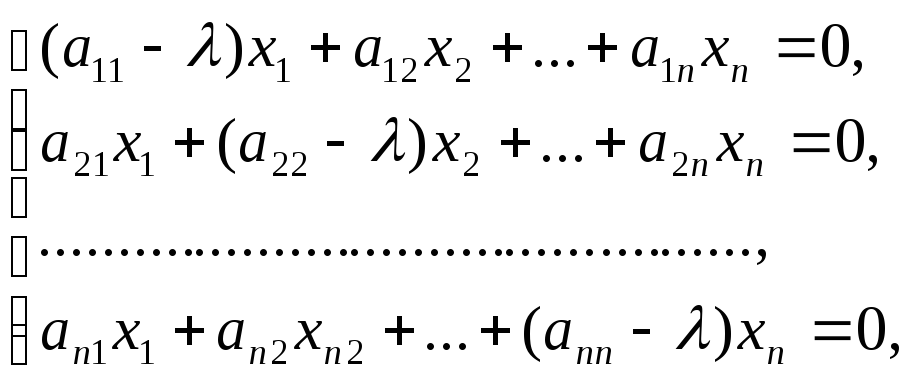 (2)
(2)
Или
в матричном виде (А
– Е)
= 0.
Полученная
однородная система всегда имеет нулевое
решение
х
=
0
= (0,0,…,0). Для существования ненулевого
решения необходимо
и достаточно, чтобы определитель системы
(2) был равен 0.
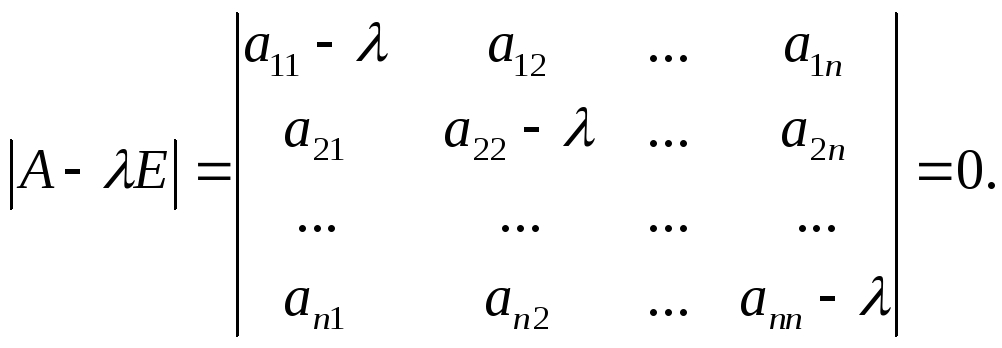 (3)
(3)
Определитель
|А
– ХЕ|
является
многочленом n-й
степени относительно
X.
Этот
многочлен называется характеристическим
многочленом
оператора А
или
матрицы А,
а
уравнение (3) —
характеристическим
уравнением оператора А
или
матрицы А.
Для
отыскания собственных векторов
необходимо:
1)
составить характеристическое уравнение
(3) и найти его корни 1,
2,
3
т.е. собственные значения;
2)
составить систему (2), положив
равным одному из найденных собственных
значений, например:
= 1,
и найти ненулевое решение
![]() этой системы;
этой системы;
3)
записать вектор
![]() который является собственным вектором
который является собственным вектором
данного преобразования, соответствующим
собственному значению1
;
4)
проделать шаги 2), 3) для
= 2
и
= 3.
Следует
иметь в виду, что собственные векторы
определяются с точностью до произвольного
множителя, т.е. если вектор X
– собственный, то и вектор
![]() – собственный.
– собственный.
Собственные
векторы, соответствующие различным
собственным значениям, линейно независимы.
Если
линейное преобразование имеет S
одинаковых собственных чисел 0
, то говорят, что 0
имеет кратность S.
Тогда ему соответствует не более S
линейно независимых собственных
векторов.
Пример
1. Найти
собственные значения и собственные
векторы линейного преобразования,
заданного в некотором базисе матрицей
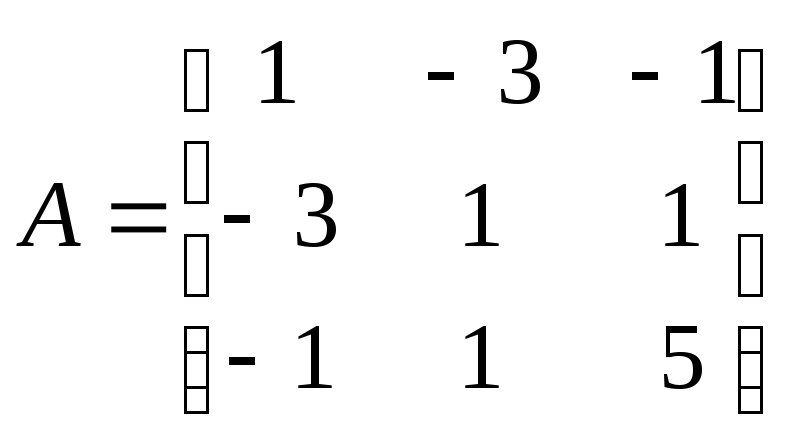 .
.
РЕШЕНИЕ.
-
Запишем
характеристическое уравнение данного
линейного преобразования и найдем его
корни:
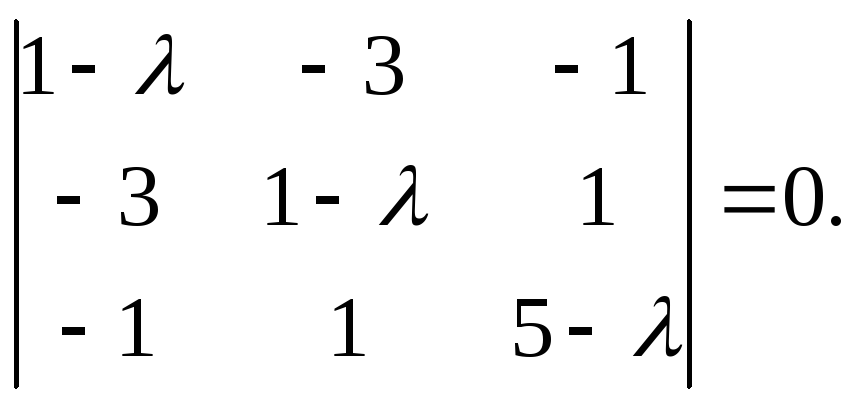
Чтобы
решить это уравнение, необходимо раскрыть
определитель. Для этого рекомендуется
разложить определитель по элементам
некоторой строки (столбца), предварительно
получив в этой строке (столбце) два нуля,
используя свойства определителей. В
нашем случае сначала к первой строке
прибавим вторую, получим
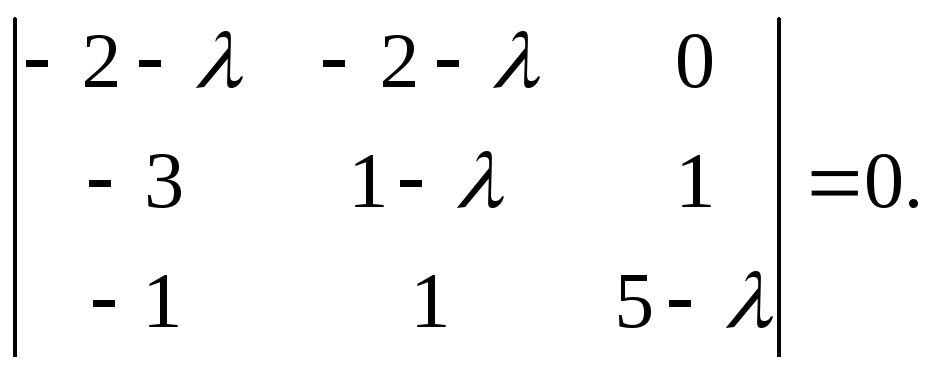
Теперь
ко второму столбцу прибавим первый,
умноженный на (-1):
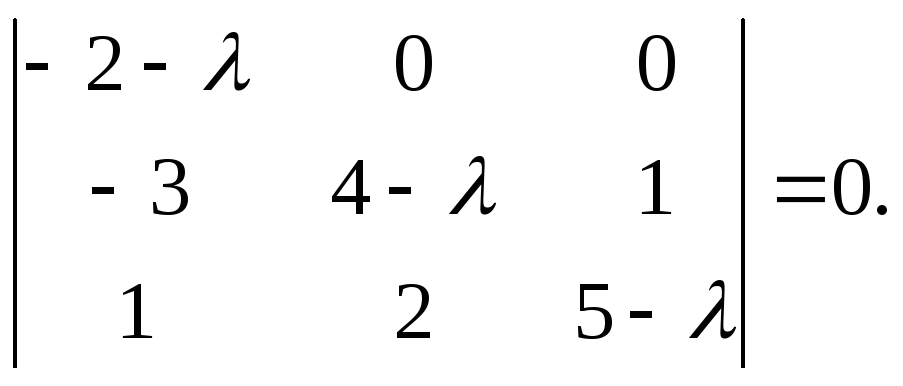
Раскладывая
этот определитель по элементам первой
строки, получаем:
![]()
или
![]()
Корнями
этого уравнения являются три числа,
1
= -2, 2
= 3, 3
= 6.
-
В
системе (2) положим
= 1
= -2, тогда она примет вид:
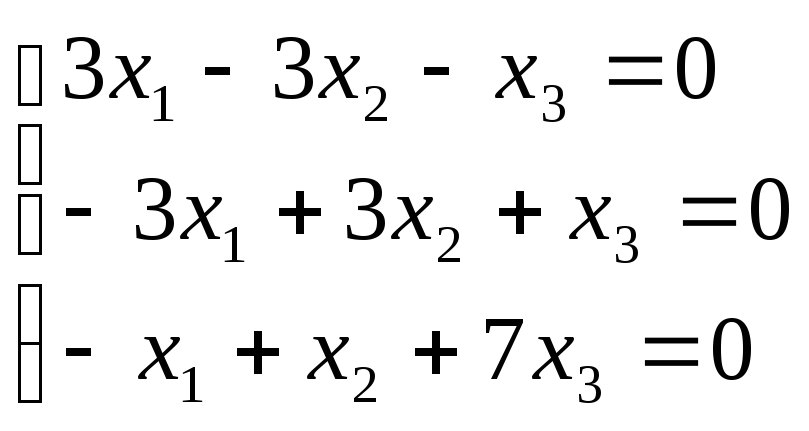
Здесь
первые два уравнения тождественны,
поэтому одно из них можно отбросить
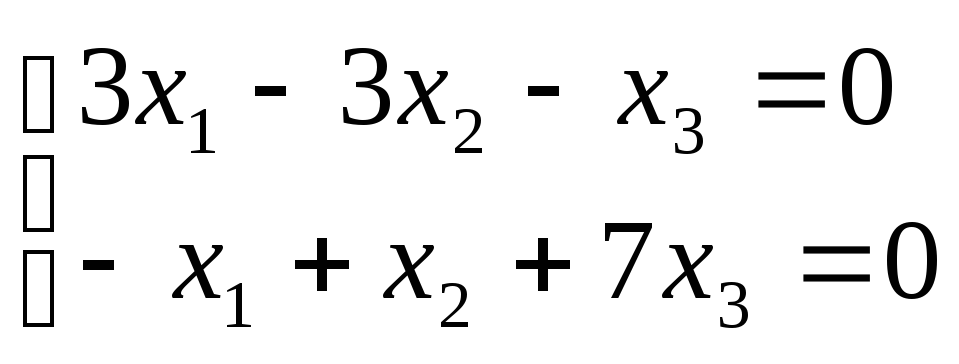
Применяя
метод Гаусса, найдем общее решение этой
системы:
![]()
-
Следовательно,
первым собственным вектором,
соответствующим
= -2, является X1
= (p1
, p1
, 0) = p1
(1,1,0), p1
0.
Меняя
p1
,будем получать различные векторы,
лежащие на одной прямой. Все они
собственные.
-
Аналогично
поступаем с собственными значениями
2
= 3, 3
=
6, т.е. находим соответствующие им
собственные векторы
X2
= p2(1
, -1 , 1); p2
0, (2
= 3);
X3
= p3(1
, -1 , -2); p3
0, (3
= 6).
Собственные
вектора X1,
X2,
X3
определены с точностью до произвольных
чисел p1
, p2
, p3
.
Пример
2.
Найти собственные значения и собственные
векторы линейного преобразования,
заданного в некотором базисе матрицей
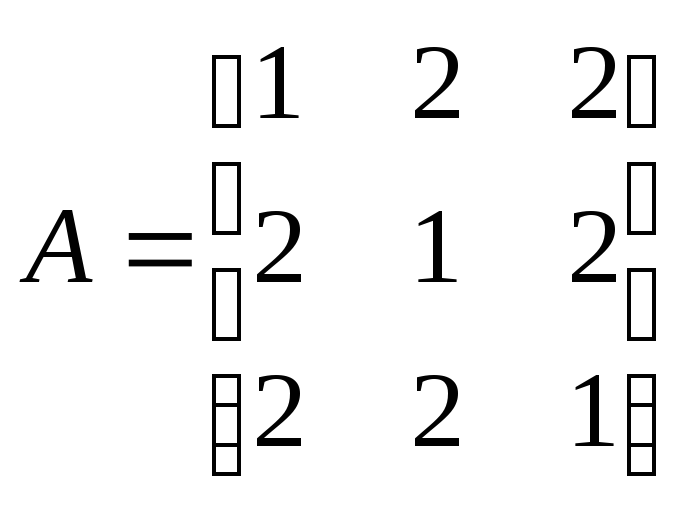 .
.
РЕШЕНИЕ
-
Характеристическое
уравнение данного преобразования имеет
вид
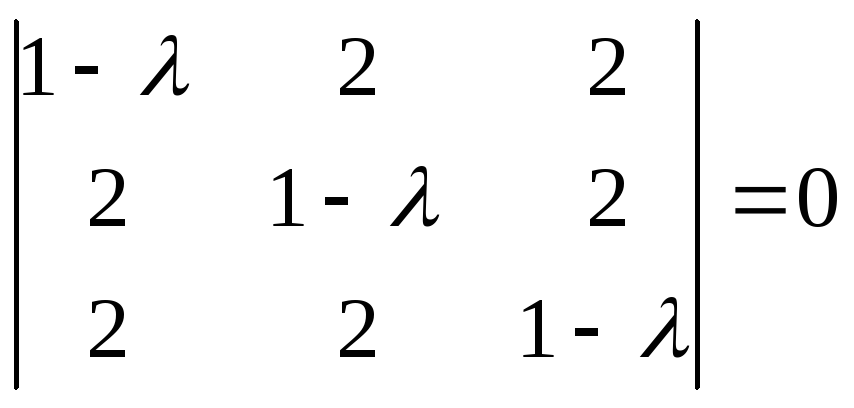 .
.
Корни
этого уравнения 1
= 2
= -1,
3
= 5 являются собственными значениями.
-
Чтобы
найти собственный вектор, соответствующий
1
= 2
= -1, полагаем в системе (2)
=
-1. Получим
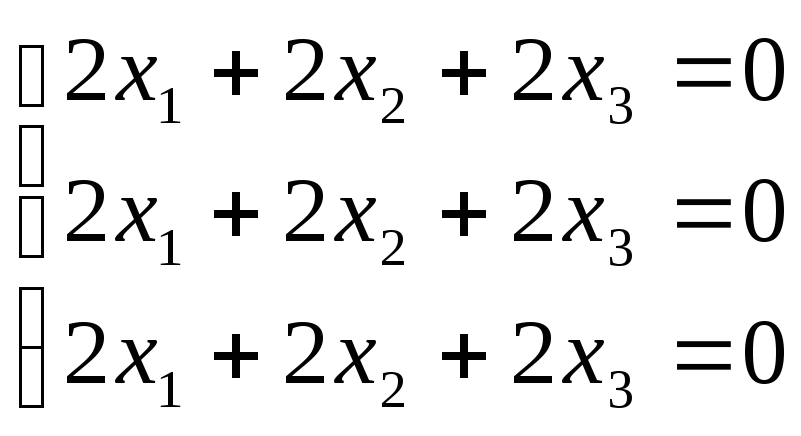
Все
три уравнения тождественны, поэтому
два из них могут быть отброшены. Оставшееся
уравнение
![]()
содержит три неизвестные. Полагая
![]() =p1
=p1
,
![]() =p2
=p2
, находим
![]()
= -p1
– p2
.
-
Вектор
X1
= (-p1
– p2
, p1
, p2
), где p1
и p2
– любые числа, одновременно не равные
нулю, является собственным вектором
линейного преобразования, соответствующим
1
= 2
= -1. -
Аналогично
находим, что вектор X2
= p3(1,
1, 1) является собственным вектором
данного преобразования, соответствующим
3=5.
Пример
3.
Найти собственные значения и собственные
векторы линейного преобразования,
заданного в некотором базисе матрицей
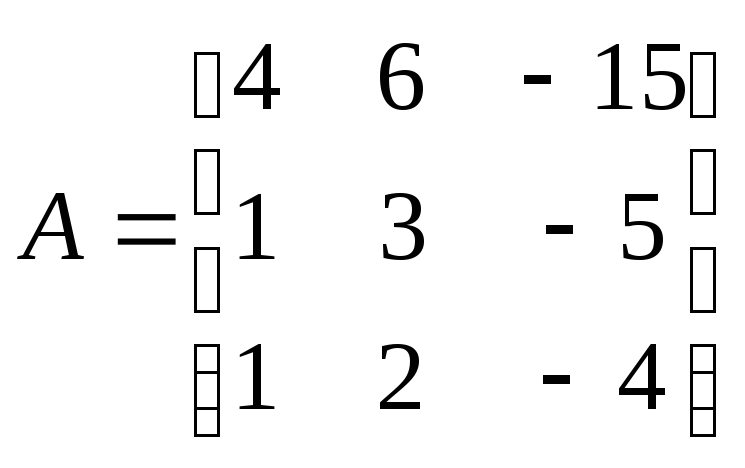
.
РЕШЕНИЕ.
-
Характеристическое
уравнение данного преобразования
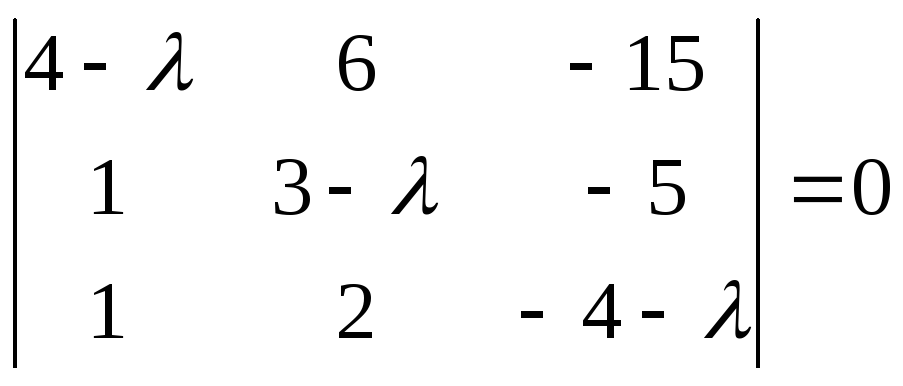 .
.
Корни
этого уравнения 1
= 2
= 3
= 1 являются собственными значениями.
-
Полагаем
в системе (2)
= 1:
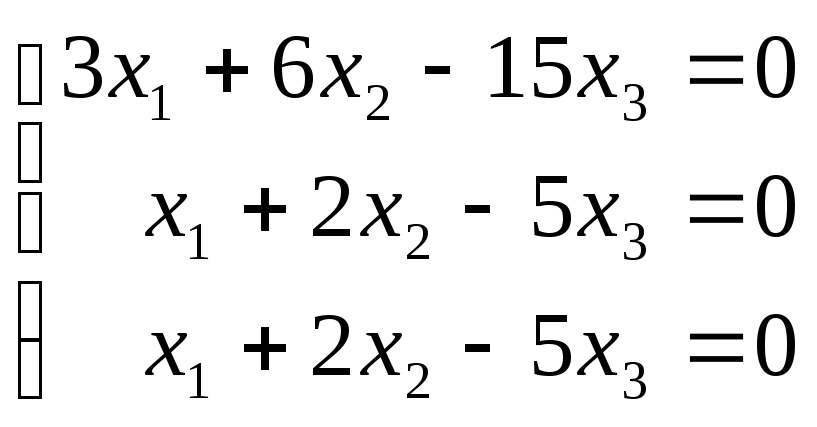
.
Все
три уравнения тождественны, поэтому,
отбросив два из них, имеем
![]()
.
Полагая
![]() ,
,
находим
![]() .
.
-
Вектор
X
= (5q
– 2p;
p;
q),
где p,
q
– любые числа, одновременно не равные
нулю, является собственным вектором
данного линейного преобразования.
Пример4. Найти собственные
значения и собственные векторы
преобразования![]() ,
,
заданного в некотором базисе матрицей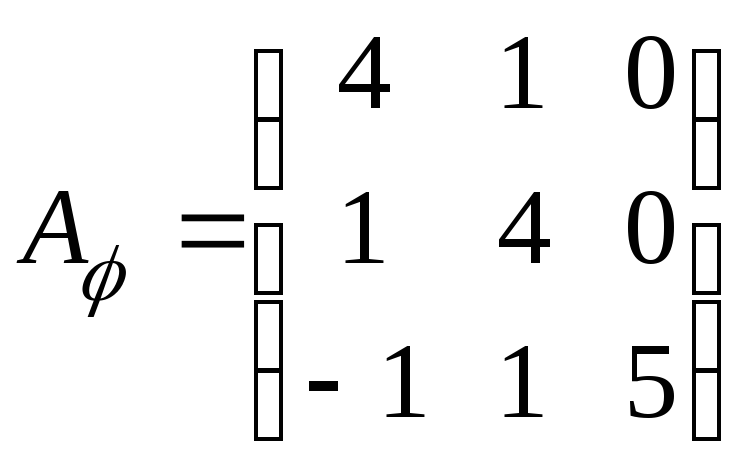 .
.
Решение.
Найдем
собственные числа этой матрицы, для
чего составим и решим характеристическое
уравнение:
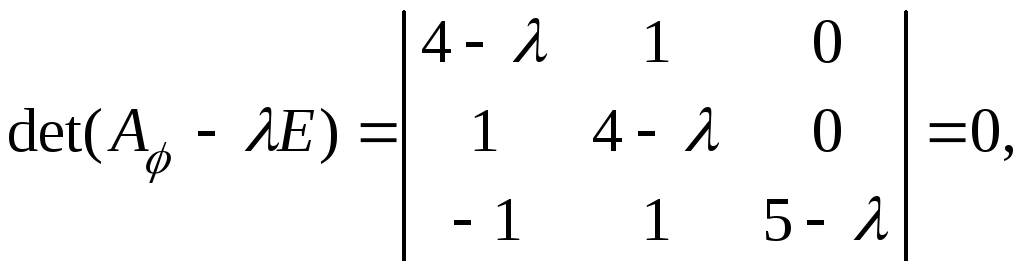
![]()
Приравняв к нулю это выражение, находим:
![]()
Находим
собственные векторы, соответствующие
найденным собственным значениям, для
чего при каждом
![]() составляем и решаем систему:
составляем и решаем систему:
а)
при
![]() ,
,
получаем
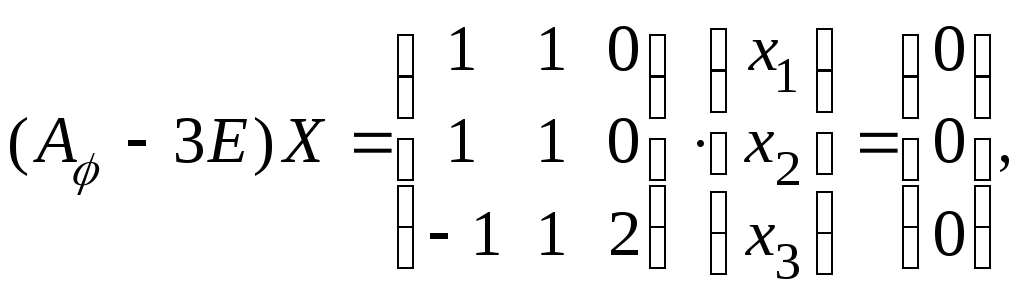
что
равносильно системе (здесь
![]() )
)
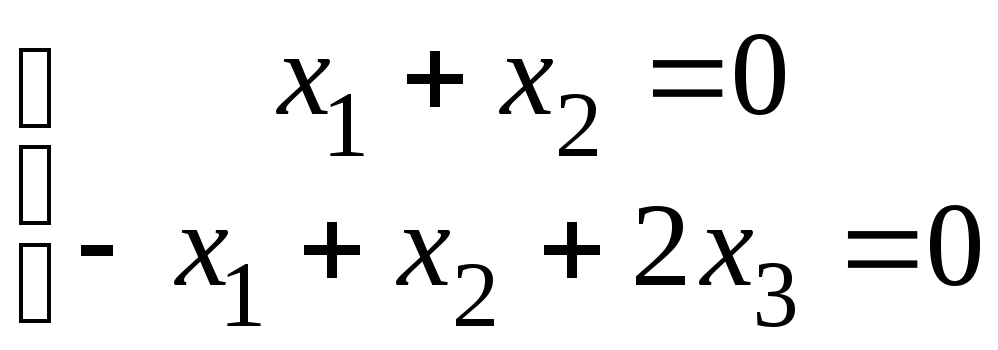 ,
,
полагая
в которой, например,
![]() ,находим
,находим![]() ,таким образом, собственный вектор,
,таким образом, собственный вектор,
соответствующий собственному значению
3 есть
![]()
б)
при
![]() ,
,
получаем
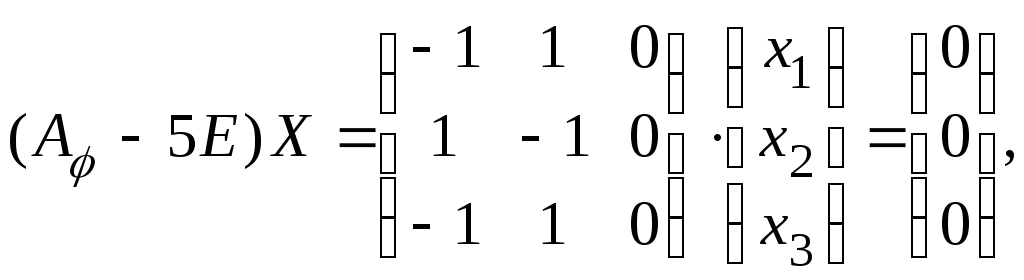
что
равносильно уравнению (здесь
![]() ):
):![]() ,
,
полагая
в котором сначала,
![]() ,а затем
,а затем
![]() получаем еще два линейно независимых
получаем еще два линейно независимых
собственных вектора:
![]() .
.
Лекция
15. Привидение квадратной матрицы к
диагональному виду.
Наиболее
простой вид принимает матрица А
линейного
оператора
А,
имеющего
n
линейно
независимых собственных векторов
el,e2,…,en
с
собственными значениями, соответственно
равными
1,
2,
3,
… n.
Векторы е1,
е2,
… , en
примем
за базисные.
Тогда
A(ei)
= iei
(i
= 1,2,…,
n)
или
A(еi)
=
a1ie1
+ a2ie2
+
… + aiiei
+
… +
anien
=
iei,
откуда
aij
= 0,
если i
j,
и
аij
= i,
если i
= j.
Таким
образом,
матрица
оператора А
в базисе, состоящем из его собственных
векторов,
является диагональной и
имеет вид:
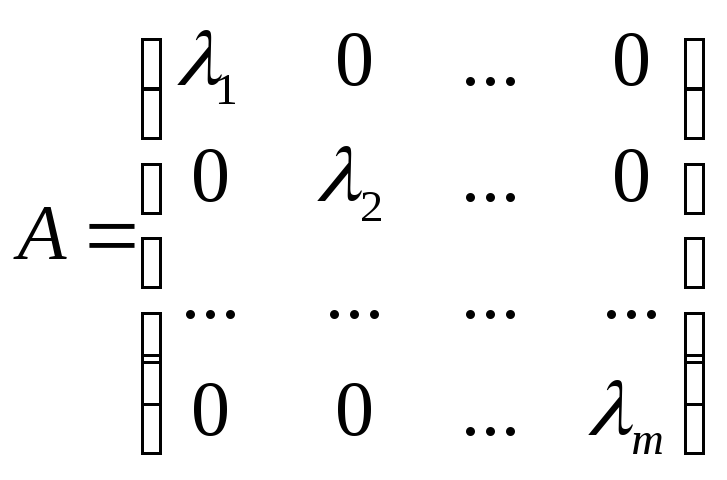 .
.
Верно
и обратное: если
матрица А
линейного оператора А
в некотором базисе является
диагональной,
то все векторы
этого базиса — собственные векторы
оператора А.
Можно
доказать, что если линейный
оператор имеет n
попарно различных
собственных значений, то отвечающие им
собственные векторы линейно независимы,
и матрица этого оператора в соответствующем
базисе имеет диагональный вид.
Пример
1.
Привести
матрицу А
=
![]()
линейного оператора
А
к
диагональному виду.
Решение.
Найдём собственные значения и
собственные векторы линейного оператора
А,
заданного матрицей
![]() .
.
Составляем
характеристическое уравнение
![]()
![]()
или
2
–
2
– 35
= 0 ,
откуда
собственные значения линейного оператора
А
1
= -5,
2
= 7.
Находим
собственный вектор х(1)
= (х1,
х2),
соответствующий собственному
значению 1
= -5.
Для
этого решаем матричное уравнение
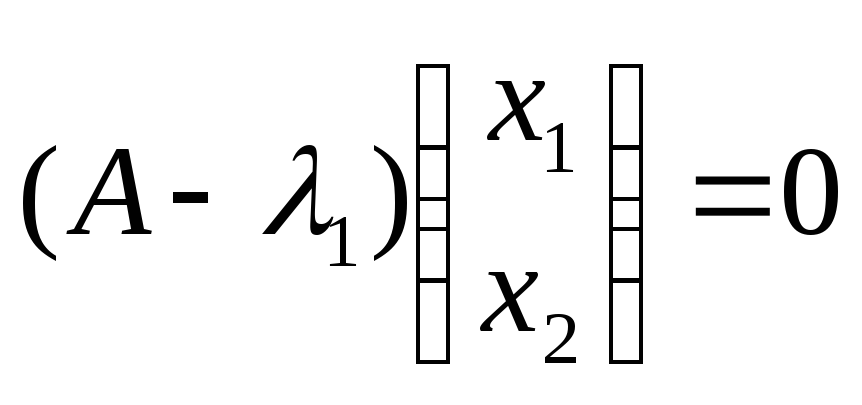 или
или
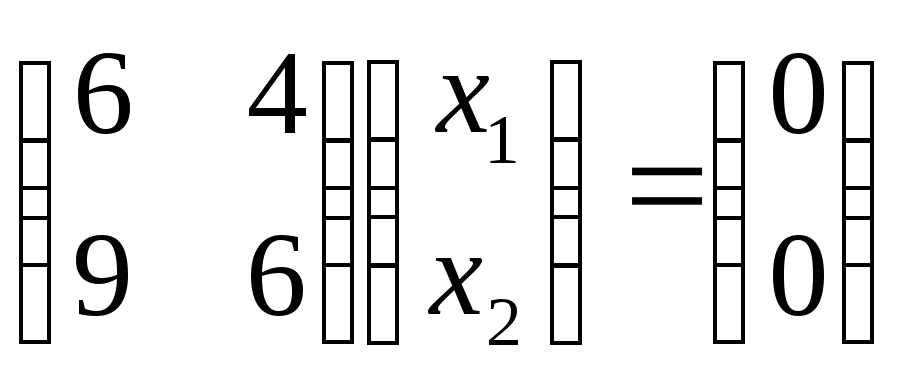 ,
,
откуда
находим х2
=
-1,5х1.
Положив
х1
= с,
получим,
что векторы
х(1)
= (с; -1,5с)
при любом с
0
являются собственными
векторами
линейного оператора А
с
собственным значением
1
=
-5.
Аналогично
можно убедиться в том, что векторы х(2)
=
![]()
при
любом с1
0
являются собственными векторами
линейного
оператора
А
с
собственным значением 2
= 7
.
Так
как координаты
векторов х(1
)и
x(2)
не пропорциональны, то векторы х(1)
и х(2)
линейно
независимы. Поэтому в базисе, состоящем
из любых
пар собственных векторов x(1)
= (с; -1,5с)
и х(2)
=
![]()
(т.е.
при любых с0,
c1
0,
например, при с
= 2,
c1
= 6 из векторов
x(1)
= (2; – 3) и х{2)
= (4;
6) и т.д.) матрица А
будет
иметь диагональный
вид:
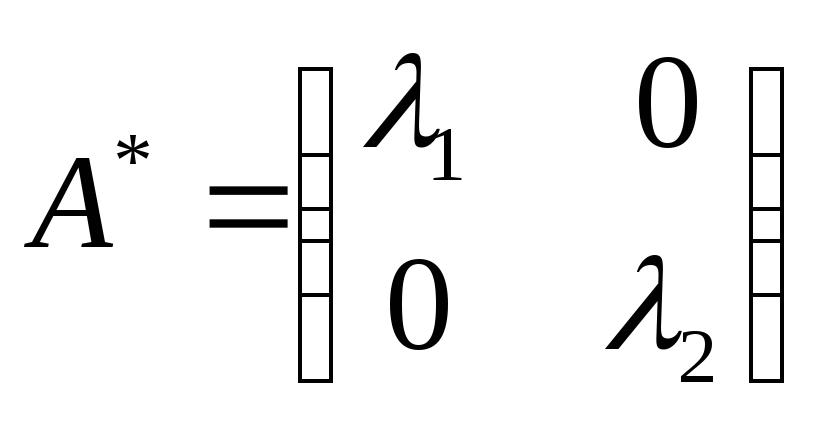 или
или
![]() .
.
Это
легко проверить, взяв, например, в
качестве нового базиса линейно
независимые собственные векторы х(1)
= (2; – 3) и x(2)
=
(4; 6). Действительно, матрица С
перехода от старого базиса
к новому в этом случае будет иметь
вид C
= (x(1),
x(2))
=
![]() .
.
Тогда
матрица А
в
новом
базисе х(1),
x(2)
примет вид:
![]() .
.
Или
после вычислений
![]() ,
,
т.е.
получим ту же диагональную матрицу,
элементы которой по главной диагонали
равны собственным значениям матрицы
А.
Пример2.Пусть линейный оператор![]() ,
,
действующий в евклидовом пространстве
![]() ,
,
имеет в ортонормированном базисе матрицу![]() .
.
Построить в этом векторов пространстве
базис из собственных оператора![]() и найти матрицу оператора
и найти матрицу оператора![]() в этом базисе.
в этом базисе.
 .
.
Решение.
1)
Найдем
собственные числа оператора
![]() ,
,
для чего составим и решим характеристическое
уравнение:
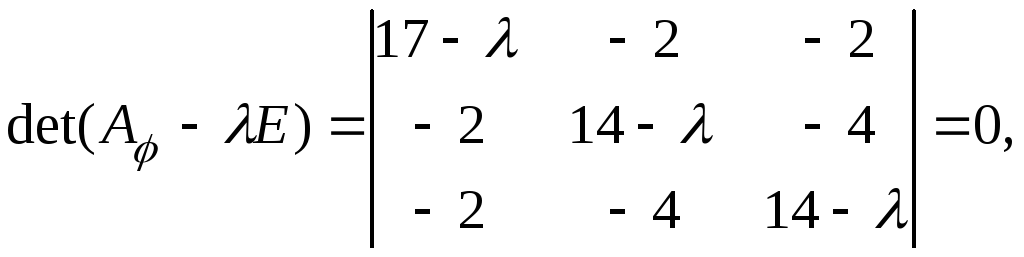
![]()
![]()
![]()
![]()
Приравняв
к нулю, находим:
![]()
2)
Находим собственные векторы, соответствующие
найденным собственным значениям, для
чего при каждом
![]() составляем и решаем систему:
составляем и решаем систему:
а)
при
![]() ,
,
получаем
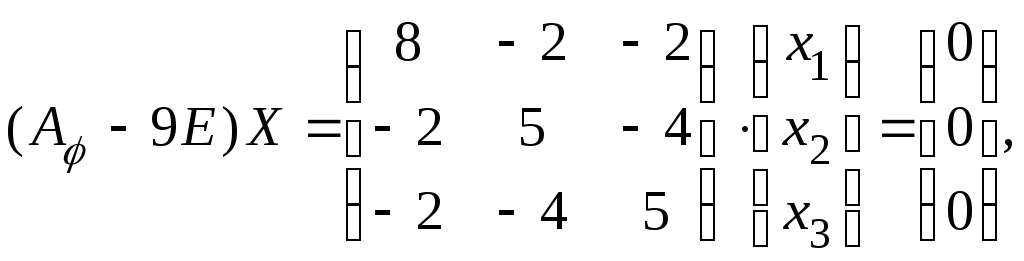
что
равносильно системе (здесь
![]() )
)
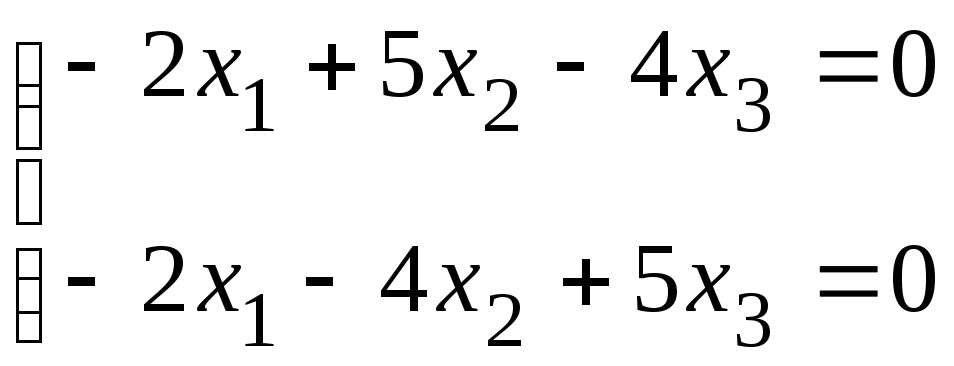 ,
,
полагая
в которой, например,
![]() ,
,
находим
![]() ,
,
таким образом, собственный вектор,
соответствующий собственному значению
9 есть
![]()
б) при
![]() ,получаем
,получаем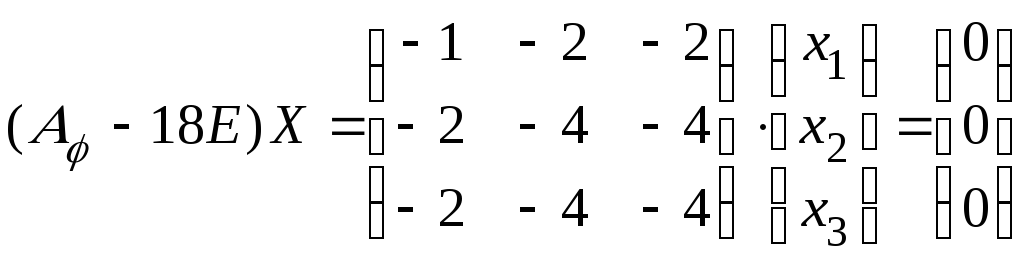 ,
,
что
равносильно уравнению (здесь
![]() )
)
![]() ,
,
полагая
в котором сначала,
![]() ,а затем
,а затем
![]() получаем еще два линейно независимых
получаем еще два линейно независимых
собственных вектора:
![]() .
.
3)
Находим матрицу перехода к базису из
собственных векторов и обратную к ней
(столбцами матрицы перехода являются
координатные столбцы векторов
![]()
(см. раздел
1)):
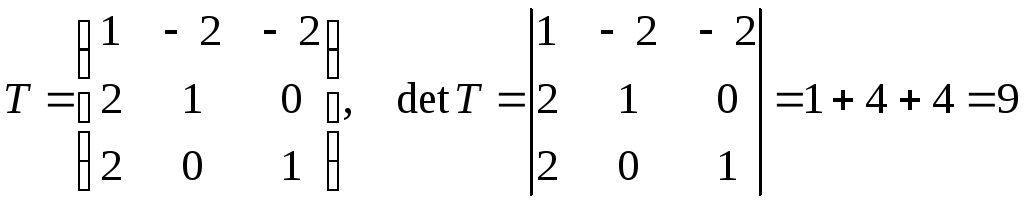 .
.
![]()
![]()
![]()
4)
Теперь по формуле (5.1) находим
![]()
– матрицу
линейного оператора в базисе из
собственных векторов

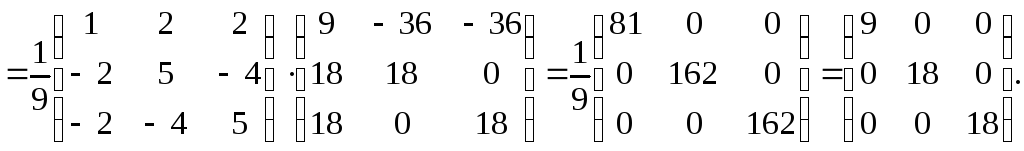
Таким образом,
матрица линейного оператора в базисе
из собственных векторов диагональная!
Лекция
16.
Квадратичные формы.
При
решении различных прикладных задач
часто приходится исследовать квадратичные
формы.
Определение
1.
Квадратичной
формой
L(х1,х2,…,хn)
от n
переменных
называется сумма, каждый член которой
является либо квадратом
одной из переменных, либо произведением
двух разных переменных,
взятых с некоторым коэффициентом:
L(х1,
х2,…,хn)
=
![]() .
.
Определение
2. Предполагаем,
что коэффициенты квадратичной формы
aij
— действительные
числа, причем aij
= aji.
Матрица А
=
(аij)
(i,
j
=
1, 2, …, n),
составленная
из этих коэффициентов, называется
матрицей
квадратичной формы.
Определение
3. Матрица,
у которой все элементы аij
= аji
,
называется симметрической.
В
матричной записи квадратичная форма
имеет вид:
L
=
ХТАХ,
где
X
—
матрица-столбец переменных.
или 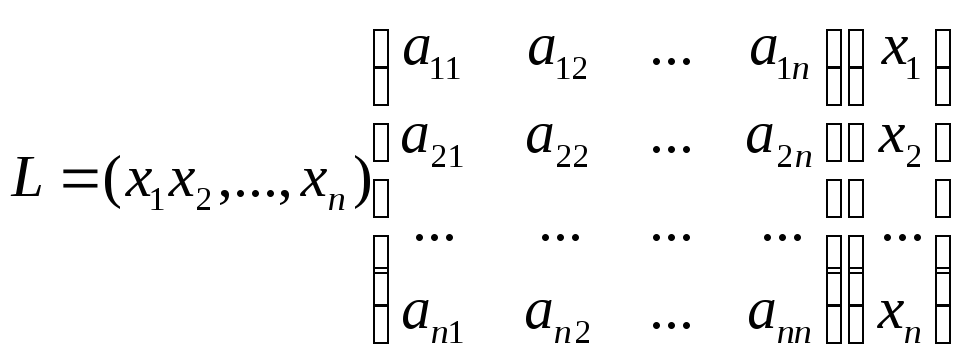 .
.
Пример
1.
Дана
квадратичная форма L(x1,
х2,
х3)
= 4х12
–
12х1х2
– 10х1х3
+ х22
–
3x32.
Записать
ее в матричном виде.
Решение.
Найдем матрицу квадратичной формы. Ее
диагональные
элементы равны коэффициентам при
квадратах переменных,
т.е. 4, 1, —3, а другие элементы — половинам
соответствующих
коэффициентов квадратичной формы.
Поэтому
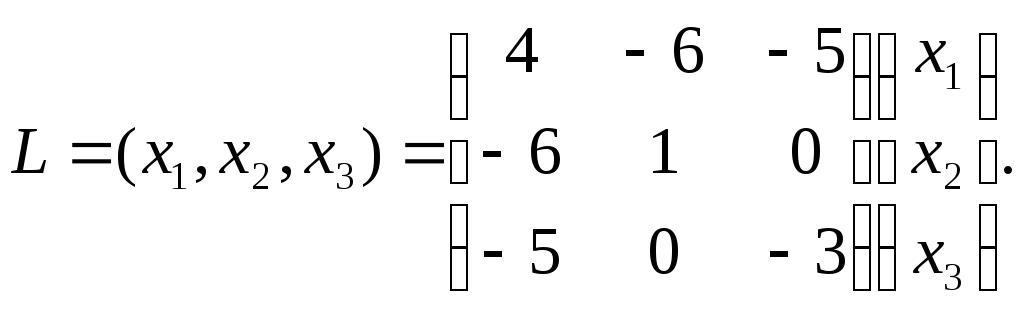 ►
►
Выясним,
как изменяется квадратичная форма при
невырожденном линейном преобразовании
переменных.
Пусть
матрицы-столбцы переменных X
=
(х1,х2,…,хn)Т
и
Y
= (y1,y2,
… ,yn)Т
связаны
линейным соотношением X
= CY,
где
С
= (cij)
(i,j
= 1,2,…,n)
есть некоторая невырожденная матрица
n-го
порядка.
Тогда
квадратичная форма
L
=
ХТАХ
= (CY)ТA(CY)
= (YТCТ)A(CY)
=
YТ(CТ
AC)Y.
Итак,
при
невырожденном линейном преобразовании
X
= CY
матрица
квадратичной формы принимает вид:
![]() .
.
Пример
2.
Дана
квадратичная форма L(х1,
х2)
= 2x12
+
4x1x2
– 3x22.
Найти квадратичную форму L(y1,
y2),
полученную из
данной линейным преобразованием х1
= 2y1
– 3y2,
x2
= y1
+ y2.
Решение.
Матрица
данной квадратичной формы
![]() ,
,
а матрица линейного преобразования С
=![]() .
.
Следовательно,
матрицу искомой квадратичной формы
находим по формуле:
 ,
,
Значит
квадратичная форма имеет вид L(y1,
y2)
=
13y12
–
34у1у2
+ 3у22.
►
Определение
4. Квадратичная
форма L
=![]()
называется
канонической
(или
имеет канонический
вид), если
все ее коэффициенты аij
=
0 при i
j:
L
= a11x12
+ a22x22
+ … + annxn2
=
![]() ,а
,а
ее матрица является диагональной.
Справедлива
следующая теорема.
Теорема.
Любая
квадратичная форма с помощью невырожденного
линейного преобразования переменных
может быть приведена к каноническому
виду.
Для
всякой квадратичной формы существует
такой базис, в котором она имеет
канонический (и даже нормальный) вид.
Познакомимся
с методами приведения квадратичной
формы к каноническому виду: метод
Лагранжа выделения полных квадратов и
методом собственных векторов.
Пример
3.
Найти ортогональное преобразование,
приводящее квадратичную форму
![]() ,
,
заданную в евклидовом пространстве![]() ,
,
к каноническому виду. Написать этот
канонический вид.
Решение:
матрица квадратичной формы имеет вид
 .
.
Найдем собственные числа этой матрицы:![]() .
.
Соответственно ортонормированные
собственные векторы:
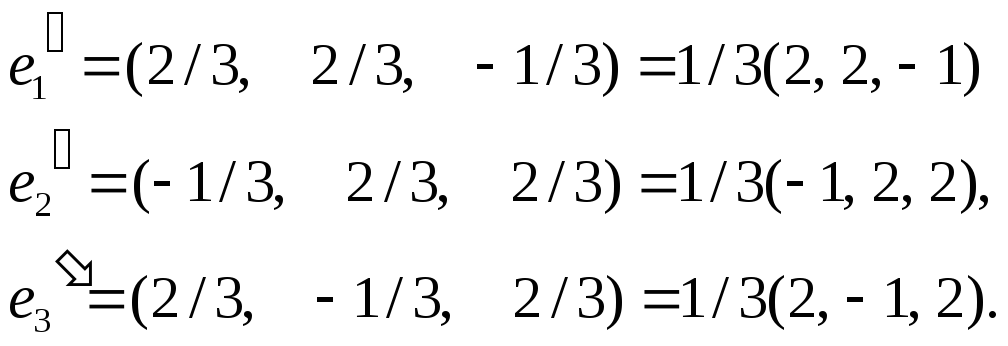
Следовательно,
в базисе из этих векторов, заданная
квадратичная форма имеет вид
 ,
,
где
соответствующие преобразования координат
имеют вид:
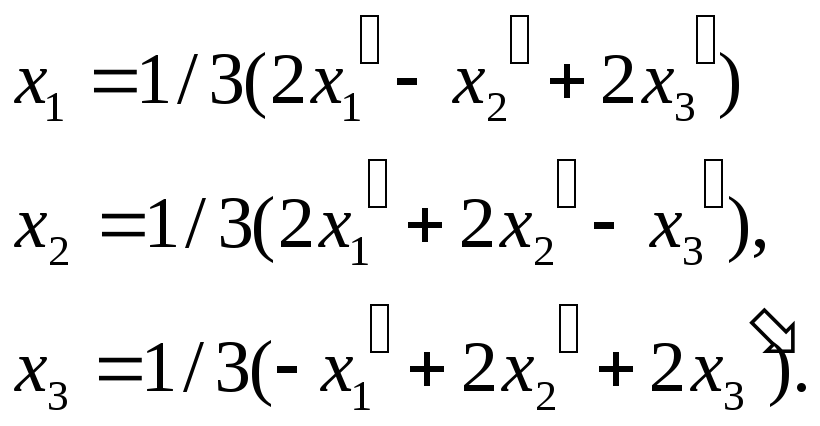 ►
►
Канонический
вид квадратичной формы не является
однозначно
определенным, так как одна и та же
квадратичная форма может
быть приведена к каноническому виду
многими способами. Однако полученные
различными способами канонические
формы
обладают рядом общих свойств. Одно из
этих свойств сформулируем в виде теоремы.
Теорема
(закон инерции квадратичных форм).
Число
слагаемых с
положительными (отрицательными)
коэффициентами квадратичной
формы не зависит от способа приведения
формы к этому виду.
Следует
отметить, что ранг
матрицы квадратичной формы, называемый
рангом квадратичной формы, равен
числу отличных от нуля
коэффициентов канонической формы и не
меняется при линейных
преобразованиях.
Лекция
17. Итоговое тестирование.
Лекция
18. Резерв.
Лекция
0. Входная контрольная работа за курс
средней школы.
Содержание:
- Линейные преобразования. Собственные векторы и собственные числа линейного оператора
- Собственные векторы и собственные числа линейного оператора: определение, свойства
- Нахождение собственных чисел и собственных векторов
- Базис пространства из собственных векторов линейного оператора
- Линейная модель обмена (модель международной торговли)
Линейные преобразования. Собственные векторы и собственные числа линейного оператора
Линейные преобразования (линейные операторы). Матрица линейного преобразования 
Пусть задано  -мерный пространство
-мерный пространство  . Если каждому вектору
. Если каждому вектору  поставлено в соответствие единственный вектор
поставлено в соответствие единственный вектор

этого же пространства, говорится, что в векторном пространстве  задано преобразование
задано преобразование  , или оператор
, или оператор  .
.
Вектор  – результат линейного преобразования – называют образом вектора
– результат линейного преобразования – называют образом вектора  , а выходной вектор
, а выходной вектор  – прообразом вектора
– прообразом вектора  .
.
Преобразование  называется линейным преобразованием, или линейным оператором, если для произвольных векторов
называется линейным преобразованием, или линейным оператором, если для произвольных векторов  и произвольного действительного скаляра
и произвольного действительного скаляра  выполняются условия:
выполняются условия:

То есть линейный оператор преобразует пространство  в то самое пространство. Это записывается следующим образом:
в то самое пространство. Это записывается следующим образом:

Примерами простейших линейных преобразований являются:
тождественное преобразование:  , когда каждый
, когда каждый  -мерный вектор пространства превращается в самого себя, то есть остается без изменения;
-мерный вектор пространства превращается в самого себя, то есть остается без изменения;
нулевой оператор  , когда каждый
, когда каждый  -мерный вектор пространства превращается в ноль-вектор этого же пространства, то есть
-мерный вектор пространства превращается в ноль-вектор этого же пространства, то есть 
Линейное преобразование  , с помощью которого осуществляется восстановление вектора
, с помощью которого осуществляется восстановление вектора  по его образу
по его образу  , называется обратным к
, называется обратным к  линейным преобразованием. В отличие от матрицы оператор записывают
линейным преобразованием. В отличие от матрицы оператор записывают  каллиграфическим
каллиграфическим шрифтом.
шрифтом.
Рассмотрим задачу об отыскании координат образа вектора  .
.
Пусть в пространстве  выбрано базис
выбрано базис  (не обязательно ортонормированный) и
(не обязательно ортонормированный) и  есть координатами вектора
есть координатами вектора  в этом базисе. Обозначим через
в этом базисе. Обозначим через  координаты вектора
координаты вектора  в выбранном базисе. по условию
в выбранном базисе. по условию  , тогда согласно линейностью оператора
, тогда согласно линейностью оператора  получим :
получим :

Но образы  тоже являются векторами с
тоже являются векторами с  , поэтому иx можно разложить по тому же базисом. Пусть
, поэтому иx можно разложить по тому же базисом. Пусть

где  коэффициенты разложения вектора
коэффициенты разложения вектора  по базису
по базису 
С учетом (5.5) соотношение (5.4) принимает вид:

Группируя члены правой части относительно векторов базиса, имеем:

С другой стороны, если  являются координатами вектора
являются координатами вектора  в базисе
в базисе  то его можно представить следующим образом:
то его можно представить следующим образом:

Сопоставляем (5.8) из (5.7) и получаем координаты вектора  :
:

Следовательно, при линейном преобразовании:

координаты образа вектора являются линейными комбинациями координат прообраза, коэффициенты при которых составляют матрицу  -го порядка (обозначим ее через
-го порядка (обозначим ее через  ):
):

Матрица  , которая в произведении (слева) с вектором с
, которая в произведении (слева) с вектором с  определяет координаты его образа при линейном преобразовании
определяет координаты его образа при линейном преобразовании  , Называется матрицей линейного преобразования
, Называется матрицей линейного преобразования  в базисе
в базисе  и пишут:
и пишут:

Каждый –  -й – столбец матрицы
-й – столбец матрицы  составляют коэффициенты разложения вектора
составляют коэффициенты разложения вектора  по базису
по базису  каждая –
каждая –  -я – строка определяет коэффициенты разложения координат вектора
-я – строка определяет коэффициенты разложения координат вектора  по координатам вектора
по координатам вектора  .
.
Обратите внимание, что  – нераздельный символ (обозначение вектораобраза), а
– нераздельный символ (обозначение вектораобраза), а  – произведение матрицы с вектором (прообразом).
– произведение матрицы с вектором (прообразом).
Каждому линейном оператору  -мерного пространства отвечает матрица
-мерного пространства отвечает матрица  -го порядка в данном базисе. И наоборот, каждой матрицы
-го порядка в данном базисе. И наоборот, каждой матрицы  -го порядка отвечает линейный оператор
-го порядка отвечает линейный оператор  -мерного пространства с определенным базисом.
-мерного пространства с определенным базисом.
Например, с помощью оператора линейных преобразований можно описать поворот произвольного вектора с пространства  вокруг начала координат на угол
вокруг начала координат на угол  против часовой стрелки. Формулы поворота осей координат (формулы перехода от исходных координат
против часовой стрелки. Формулы поворота осей координат (формулы перехода от исходных координат  и
и  к новым
к новым  и
и  , и наоборот ) определяют алгебраическую форму изображения линейного оператора поворота осей:
, и наоборот ) определяют алгебраическую форму изображения линейного оператора поворота осей:

где  оператор перехода от исходных (новых) координат к новым (исходных);
оператор перехода от исходных (новых) координат к новым (исходных);
 векторы, началом которых является точка
векторы, началом которых является точка  , а концами –
, а концами –
точки  и
и  , соответственно.
, соответственно.
По соотношению (5.12) матрица линейного преобразования}  , Описывающий поворот произвольного вектора из пространства
, Описывающий поворот произвольного вектора из пространства  вокруг начала координат на угол
вокруг начала координат на угол  против часовой стрелки, имеет вид:
против часовой стрелки, имеет вид:

а матрица обратного линейного преобразования  , то есть такого, что описывает поворот произвольного вектора из пространства
, то есть такого, что описывает поворот произвольного вектора из пространства  вокруг начала координат на угол
вокруг начала координат на угол  по часовой стрелке, имеет вид:
по часовой стрелке, имеет вид:

Теорема 5.1 (о связи между матрицами оператора в различных базисах).
Матрицы  и
и  линейного оператора
линейного оператора  в разных базисах
в разных базисах  и
и  связаны между собой соотношением:
связаны между собой соотношением:

где  матрица перехода от исходного к новому базису.
матрица перехода от исходного к новому базису.
Доказательство. Пусть линейный оператор  превращает вектор
превращает вектор  пространства
пространства  в вектор
в вектор  того самого пространства. Тогда в матричной форме связь между вектором
того самого пространства. Тогда в матричной форме связь между вектором  и его образом
и его образом  в исходном базисе можно записать как
в исходном базисе можно записать как  , а в новом – как
, а в новом – как  . Поскольку
. Поскольку  является матрицей перехода от исходного базиса к новому, то в соответствии с (4.18) имеем:
является матрицей перехода от исходного базиса к новому, то в соответствии с (4.18) имеем:

Умножим равенство (5.14) слева на матрицу  и получим
и получим  . Отсюда по определению линейного оператора имеем:
. Отсюда по определению линейного оператора имеем:  . С учетом (5.15):
. С учетом (5.15):

Сравнив соотношение  и
и  , получаем
, получаем 
Две квадратные матрицы  и
и  называются подобными, если существует такая невырожденная матрица
называются подобными, если существует такая невырожденная матрица  , матрицы
, матрицы  и
и  связанные соотношениями:
связанные соотношениями:

Соответствующие линейные операторы называются преобразованиями сходства.
Подобные матрицы описывают то же линейное преобразование, но в разных базисах, а матрица  является матрицей перехода от одного базиса к другому.
является матрицей перехода от одного базиса к другому.
Подобные матрицы имеют те же ранги, суммы элементов главной диагонали и определители.
В базисе  и
и  задана матрица линейного оператора
задана матрица линейного оператора  :
:

Определим матрицу  , которая отвечает том же оператору в базисе векторов
, которая отвечает том же оператору в базисе векторов  и
и  есть матрица
есть матрица  подобна матрице
подобна матрице  .
.
Предоставим расписание векторов нового базиса по векторам исходного базиса:  . Соответственно, матрица перехода от исходного к новому базису имеет вид:
. Соответственно, матрица перехода от исходного к новому базису имеет вид:

Ее определитель  , то есть матрица
, то есть матрица  невырожденная и имеет обратную:
невырожденная и имеет обратную:

По теореме 5.1 определяем матрицу оператора  в новом базисе:
в новом базисе:

Обратите внимание, что в новом базисе матрица оператора  оказалась диагональной.
оказалась диагональной.
Собственные векторы и собственные числа линейного оператора: определение, свойства
Рассмотрим  -мерных линейный пространство
-мерных линейный пространство  с определенным базисом и матрицу
с определенным базисом и матрицу  , некоторого линейного оператора
, некоторого линейного оператора  пространства.
пространства.
Ненулевой вектор  называют собственным, или характеристическим вектором линейного оператора
называют собственным, или характеристическим вектором линейного оператора  (или матрицы
(или матрицы  ), если существует такое действительное число
), если существует такое действительное число  , имеет место равенство:
, имеет место равенство:

Скаляр  называется собственным, или характеристическим, числом матрицы
называется собственным, или характеристическим, числом матрицы  , или ее собственным значением, соответствует собственному вектору
, или ее собственным значением, соответствует собственному вектору  :
:
Согласно определениями собственного числа и собственного вектора имеем:
1) Если  , то каждый ненулевой вектор из
, то каждый ненулевой вектор из  является собственным вектором матрицы
является собственным вектором матрицы  , при этом
, при этом  , ведь по свойству единичной матрицы имеем
, ведь по свойству единичной матрицы имеем  ;
;
2) любой ненулевой  -мерный вектор является собственным вектором нулевой матрицы
-мерный вектор является собственным вектором нулевой матрицы  , при этом
, при этом  , так как
, так как  .
.
Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы 
Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы



Запишем матричное уравнение (5.17) в развернутом виде:
Таким образом, задача сводится к решению однородной системы  линейных уравнений с
линейных уравнений с  неизвестными. Нас интересуют (по определению собственного вектора) только ненулевые векторы, то есть нетривиальные решения системы, поэтому определитель системы (5.18) должен быть равен нулю:
неизвестными. Нас интересуют (по определению собственного вектора) только ненулевые векторы, то есть нетривиальные решения системы, поэтому определитель системы (5.18) должен быть равен нулю:

Раскрытие определителя в соотношении (5.19) дает многочлен степени  относительно
относительно  , который называется характеристическим многочленом матрицы
, который называется характеристическим многочленом матрицы  , а соотношение (5.19), которое можно представить в виде
, а соотношение (5.19), которое можно представить в виде  , определяет уравнение для нахождения собственных чисел, которое называют характеристическим уравнением матрицы
, определяет уравнение для нахождения собственных чисел, которое называют характеристическим уравнением матрицы  .
.
По основной теореме алгебры уравнения  любой матрицы
любой матрицы  имеет
имеет  корней, если каждый из них считать столько раз, какова его кратность. Характеристическое уравнение матрицы может иметь только действительные, но и комплексные корни, то есть числа вида
корней, если каждый из них считать столько раз, какова его кратность. Характеристическое уравнение матрицы может иметь только действительные, но и комплексные корни, то есть числа вида  где
где  действительные числа,
действительные числа,  мнимая единица.
мнимая единица.
Множество всех собственных чисел матрицы называют спектром матрицы. Если в спектре матрицы то же собственное число повторяется  раз, то говорят, что кратность этого собственного числа равна
раз, то говорят, что кратность этого собственного числа равна  .
.
Теорема 5.2 (о единственности собственного чucлa, что соответствует собственному вектору). Если  – собственный вектор матрицы
– собственный вектор матрицы  , то существует единственный скаляр
, то существует единственный скаляр  , который удовлетворяет условие
, который удовлетворяет условие  .
.
Доказательство. Предположим, что кроме собственного числа  существует еще один
существует еще один
скаляр  , такой, что
, такой, что  . Тогда должно выполняться равенство
. Тогда должно выполняться равенство  . Поскольку по определению собственный вектор является ненулевым, то есть
. Поскольку по определению собственный вектор является ненулевым, то есть  , получим
, получим  .
.
Согласно теореме 5.2 говорят, что собственный вектор  из матрицы
из матрицы  принадлежит собственному числу
принадлежит собственному числу  .
.
Теорема 5.3 (о множестве собственных векторов, принадлежащих собственному числу). Если матрица имеет собственный вектор, принадлежащий собственному числу  , то таких векторов бесконечно много.
, то таких векторов бесконечно много.
Доказательство базируется на определении собственного вектора и свойствах ассоциативности и коммутативности операции умножения матрицы на скаляр.
Действительно, пусть  собственный вектор матрицы
собственный вектор матрицы  , тогда
, тогда  . Привлечем к рассмотрению вектор
. Привлечем к рассмотрению вектор  , коллинеарный вектору
, коллинеарный вектору  , то есть
, то есть  , где
, где  , и покажем, что в также является собственным вектором матрицы
, и покажем, что в также является собственным вектором матрицы  :
:

Поскольку равенство (5.19) выполняется для произвольного  , то существует множество собственных векторов, принадлежащих данному собственному числу.
, то существует множество собственных векторов, принадлежащих данному собственному числу.
Теорема 5.4 (критерий существования собственного вектора  , соответствующего собственному числу
, соответствующего собственному числу  ). Вектор
). Вектор  тогда и только тогда является собственным вектором матрицы
тогда и только тогда является собственным вектором матрицы  , соответствующим собственному числу
, соответствующим собственному числу  , когда его координаты
, когда его координаты  образуют ненулевое решение однородной квадратной системы линейных алгебраических уравнений
образуют ненулевое решение однородной квадратной системы линейных алгебраических уравнений 
 или
или 
Доказательство сводится к тождественных преобразований матричных уравнений.
Необходимость уже доказано переходом от соотношения  , к однородной системе линейных уравнений
, к однородной системе линейных уравнений  , представленной в развернутом виде (5 18).
, представленной в развернутом виде (5 18).
Достаточность. На основании свойств действий над матрицами с учетом условия  , осуществит переход от однородной системы уравнений в матричной форме с соотношением
, осуществит переход от однородной системы уравнений в матричной форме с соотношением  :
:

Теорема 5.5 (пpo линейную независимость собственных векторов). Собственные векторы, принадлежащие различным собственным числам, является линейно независимыми.
Доказательство проведем методом от противного. Пусть  два произвольные собственные векторы, принадлежащие соответственно собственным числам
два произвольные собственные векторы, принадлежащие соответственно собственным числам  и
и 
 . Необходимо показать, что линейная комбинация этих собственных векторов
. Необходимо показать, что линейная комбинация этих собственных векторов  ноль-вектор только тогда, когда
ноль-вектор только тогда, когда  , то есть
, то есть

Предположим обратное. Пусть (5.23) выполняется при условии, что одно из чисел  не является нулем, например,
не является нулем, например, 
Умножим левую и правую части (5.23) на собственное число  . Тогда
. Тогда

Левую и правую части равенства (5.23) умножим на матрицу  слева, и, учитывая свойства операций над матрицами, получим:
слева, и, учитывая свойства операций над матрицами, получим:

Сравним (5.25) и (5.24). Получаем:

По условию теоремы  . По определению вектор
. По определению вектор  является ненулевым, поэтому равенство (5.26) возможно только при
является ненулевым, поэтому равенство (5.26) возможно только при  , то есть предположение о линейной зависимости векторов
, то есть предположение о линейной зависимости векторов  и
и  ошибочно.
ошибочно.
Если есть более двух собственных векторов, принадлежащих попарно различным собственным числам, доведение аналогичное (с использованием метода математической индукции).
Заметим, что собственные векторы, принадлежащих различным собственным числам, можно использовать как базисные векторы пространства  .
.
Теорема 5.6 (пpo сумму и произведение собственных чисел). Если  собственные числа матрицы
собственные числа матрицы  , то:
, то:
1) сумма собственных чисел равна сумме элементов главной диагонали матрицы  :
:

2) произведение собственных чисел равна определителю матрицы  :
:

Доказательство основывается на формулах Виета, которые описывают соотношение между корнями и коэффициентами многочлена  -гo степени в случае, когда его старший коэффициент равен единице.
-гo степени в случае, когда его старший коэффициент равен единице.
Рассмотрим простейший случай  . Запишем характеристическое уравнение в развернутом виде:
. Запишем характеристическое уравнение в развернутом виде:

С (5.29) по теореме Виета (для квадратного уравнения) имеем:

Сумму всех диагональных элементов матрицы называют следом (от нем. spur – след) этой матрицы и обозначают  .
.
Для квадратной матрицы произвольного порядка  теорему 5.6 в символьном виде можно записать так:
теорему 5.6 в символьном виде можно записать так:

при этом собственное число  берем столько раз, какова его кратность как корня характеристического уравнения (5.29).
берем столько раз, какова его кратность как корня характеристического уравнения (5.29).
Нахождение собственных чисел и собственных векторов
Рассмотрим алгоритм нахождения собственных чисел матрицы  и собственных векторов, которые им принадлежат.
и собственных векторов, которые им принадлежат.
Согласно соотношениями (5.18) и (5.19) имеем такой порядок отыскания собственных чисел и собственных векторов матрицы.
1. Составляем по исходной матрицей  характеристическое уравнение (5.18) и решаем его, то есть находим спектр собственных чисел.
характеристическое уравнение (5.18) и решаем его, то есть находим спектр собственных чисел.
2. Подставляем поочередно каждое собственное число в систему (5.18) и находим все ее нетривиальные решения, что и дает множество собственных векторов, принадлежащих соответствующему собственному числу.
Замечания. Множество всех собственных векторов, принадлежащих определенному собственному числу, можно представить как линейную комбинацию фундаментальных решений однородной системы уравнений согласно (4.19), гл. 4.
Найдем собственные числа и собственные векторы матрицы

Характерным уравнением этой матрицы является квадратное уравнение:

Решив его, получим собственные числа  и
и 
Теперь описываем множества  и
и  всех собственных векторов, принадлежащих найденным собственным числам.
всех собственных векторов, принадлежащих найденным собственным числам.
Для этого в матрицу  вместо
вместо  подставим поочередно значения собственных чисел, запишем соответствующую систему однородных линейных уравнений (5.18) и решим ее:
подставим поочередно значения собственных чисел, запишем соответствующую систему однородных линейных уравнений (5.18) и решим ее:

Предоставляя параметру  произвольных значений, для данного собственного числа
произвольных значений, для данного собственного числа  получим совокупность коллинеарных между собой собственных векторов.
получим совокупность коллинеарных между собой собственных векторов.
Теорема 5.7 (про собственные числа и собственные векторы симметричной матрицы).
Симметричная матрица  имеет только действительные собственные числа. Собственные векторы, принадлежащие разным собственным числам, ортогональны и линейно независимы.
имеет только действительные собственные числа. Собственные векторы, принадлежащие разным собственным числам, ортогональны и линейно независимы.
Теорема приводим без доказательства.
Проиллюстрируем прав выводов данной теоремы на примере.
Пусть имеем симметричную матрицу

Найдем собственные числа и собственные векторы этой матрицы и докажем ортогональность собственных векторов, соответствующих различным собственным числам.
1. Составим характеристическое уравнение матрицы

2. Найдем корни полученного кубического уравнения относительно  . С элементарной алгебры известно, если многочлен со старшим коэффициентом, равным единице, имеет целые корни, то их следует искать среди делителей свободного члена. Перебирая делители числа 36, убеждаемся, что
. С элементарной алгебры известно, если многочлен со старшим коэффициентом, равным единице, имеет целые корни, то их следует искать среди делителей свободного члена. Перебирая делители числа 36, убеждаемся, что  является корнем уравнения (5.30).
является корнем уравнения (5.30).
Нахождение других двух корней сводится к решению квадратного уравнения:

3. Опишем множества  и
и  собственных векторов, принадлежащих найденным собственным числам.
собственных векторов, принадлежащих найденным собственным числам.
Для этого в матрицу  вместо
вместо  подставляем поочередно значения собственных чисел, записываем соответствующую систему однородных линейных уравнений (5.17) и решаем ее методом Жордана-Гаусса:
подставляем поочередно значения собственных чисел, записываем соответствующую систему однородных линейных уравнений (5.17) и решаем ее методом Жордана-Гаусса:

Аналогично находим собственные векторы  и
и 

Система векторов  и
и  является линейно независимой, поскольку
является линейно независимой, поскольку

Убеждаемся, что векторы  и
и  – попарно ортогональны.
– попарно ортогональны.
Для этого определим их скалярные произведения:

Поскольку скалярные произведения векторов равны нулю, то векторы попарно ортогональны.
Если в выражениях (5.31-5.33) положить  , то получим систему векторов:
, то получим систему векторов:

которая использовалась как базис пространства  в примере после теоремы
в примере после теоремы 
 и
и  . В таком базисе, то есть базисе из собственных векторов, матрица оператора
. В таком базисе, то есть базисе из собственных векторов, матрица оператора  оказалась диагональной, ее ненулевыми элементами являются собственные числа матрицы
оказалась диагональной, ее ненулевыми элементами являются собственные числа матрицы  .
.
Теорема 5.8 (о преобразовании матрицы к диагональному виду). Матрица линейного оператора  в базисе
в базисе  имеет диагональный вид тогда и только тогда, когда все векторы базиса являются собственными векторами матрицы
имеет диагональный вид тогда и только тогда, когда все векторы базиса являются собственными векторами матрицы  .
.
Теорему наводим без доказательств
Заметим, что при нахождении собственных чисел для заданной матрицы самой задачей является решение алгебраического уравнения  -й степени, что во многих случаях сделать невозможно без использования приближенных методов. Изучение приближенных методов выходит за пределы программы. Поэтому предлагаем воспользоваться известными программами MatLab, MathCad, Maple и др.
-й степени, что во многих случаях сделать невозможно без использования приближенных методов. Изучение приближенных методов выходит за пределы программы. Поэтому предлагаем воспользоваться известными программами MatLab, MathCad, Maple и др.
Следующий пример был решен в пакете MatLab, в котором конечный результат вычислений предоставляется без промежуточных выкладок.
Найдем собственные числа и соответствующие им собственные векторы матрицы

Характерным уравнением для нахождения собственных чисел является уравнение

корнями которого будут числа  а соответствующие им собственные векторы имеют вид:
а соответствующие им собственные векторы имеют вид:

Собственные числа и собственные векторы матриц имеют широкий спектр использования, в частности, в аналитической геометрии (Раздел 2), в задачах различных отраслей естественных наук и эконометрики.
Базис пространства из собственных векторов линейного оператора
По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Возникает вопрос, при каких условиях существует базис линейного пространства  , построенный из собственных векторов матрицы.
, построенный из собственных векторов матрицы.
Лема. Если  является собственным числом матрицы
является собственным числом матрицы  , то множество собственных векторов матрицы
, то множество собственных векторов матрицы  содержит
содержит  линейно независимых векторов, где
линейно независимых векторов, где  – ранг матрицы
– ранг матрицы  .
.
Доказательство. Согласно теореме 5.4 множество собственных векторов совпадает с множеством всех решений однородной системы линейных уравнений:

где  – собственный вектор матрицы
– собственный вектор матрицы  , что соответствует собственному числу
, что соответствует собственному числу  . По теореме 4.4 такая система имеет фундаментальную систему решений, количество векторов которой равна
. По теореме 4.4 такая система имеет фундаментальную систему решений, количество векторов которой равна  , то есть содержит
, то есть содержит  – линейно независимых векторов.
– линейно независимых векторов.
Теорема 5.9 (о существовании базиса из собственных векторов матрицы). Пусть числа  образуют множество всех различных собственных чисел матрицы
образуют множество всех различных собственных чисел матрицы  . Если сумма рангов матриц
. Если сумма рангов матриц  равна
равна  , то в пространстве
, то в пространстве  существует базис из собственных векторов матрицы
существует базис из собственных векторов матрицы  .
.
Доказательство. Согласно лемме каждое множество собственных векторов, соответствующих уравнению  , содержит независимые векторы в количестве
, содержит независимые векторы в количестве  . По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Тогда для матрицы
. По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Тогда для матрицы  общее количество линейно независимых собственных векторов составляет:
общее количество линейно независимых собственных векторов составляет:

Поскольку собственные векторы матрицы  в совокупности составляют систему
в совокупности составляют систему  линейно независимых векторов, то они образуют базис пространства
линейно независимых векторов, то они образуют базис пространства  .
.
Теорема 5.10 (о существовании базиса из собственных векторов симметричной матрицы). Если матрица  линейного оператора симметрична, то в пространстве
линейного оператора симметрична, то в пространстве  существует базис, образованный из собственных векторов матрицы
существует базис, образованный из собственных векторов матрицы  .
.
Теорему принимаем без доказательств.
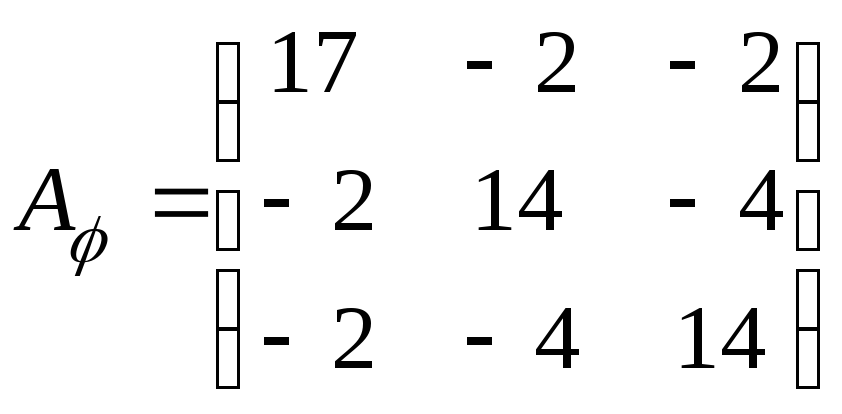
Построим ортонормированный базис пространства  , состоящий из собственных векторов матрицы
, состоящий из собственных векторов матрицы

линейного преобразования  , и найдем матрицу
, и найдем матрицу  заданного преобразования в этом базисе.
заданного преобразования в этом базисе.
Согласно теореме 5.9 такой базис существует, поскольку матрица  является симметричной матрицей. Составим характеристическое уравнение матрицы
является симметричной матрицей. Составим характеристическое уравнение матрицы  :
:

и решим его:  (собственное значение кратности
(собственное значение кратности  ) и
) и 
Для каждого из двух различных собственных чисел матрицы определим фундаментальную систему решений однородной системы уравнений:  . При
. При  в результате элементарных преобразований основной матрицы системы получаем:
в результате элементарных преобразований основной матрицы системы получаем:

По последним шагом элементарных преобразований матрицы записываем общее решение системы:

Определяем фундаментальную систему решений однородной системы уравнений 

Собственные векторы  и
и  являются ортогональными, поскольку их скалярное произведение равно нулю:
являются ортогональными, поскольку их скалярное произведение равно нулю: 
При  в результате элементарных преобразований основной матрицы системы получаем:
в результате элементарных преобразований основной матрицы системы получаем:

По последнем шагом элементарных преобразований матрицы записываем общее решение системы:

Возлагаем  и получаем фундаментальный решение однородной системы уравнений
и получаем фундаментальный решение однородной системы уравнений 

Поскольку  и
и  , то все три вектора попарно ортогональны. Объединив полученные фундаментальные системы решений, иметь систему собственных векторов матрицы
, то все три вектора попарно ортогональны. Объединив полученные фундаментальные системы решений, иметь систему собственных векторов матрицы  . Они образуют ортогональный базис пространства
. Они образуют ортогональный базис пространства  . После нормирования векторы приобретают вид:
. После нормирования векторы приобретают вид:

Это и есть ортогональный базис пространства  , состоящий из собственных векторов матрицы
, состоящий из собственных векторов матрицы  .
.
По соотношению (5.13) определим матрицу  , что соответствует оператору
, что соответствует оператору  в базисе из собственных векторов. Согласно теореме 5.8 эта матрица будет иметь диагональный вид, а элементами ее главной диагонали будут собственные числа этой матрицы. Заключим с собственными векторами
в базисе из собственных векторов. Согласно теореме 5.8 эта матрица будет иметь диагональный вид, а элементами ее главной диагонали будут собственные числа этой матрицы. Заключим с собственными векторами  ,
,  и
и  матрицу
матрицу  перехода к новому базису и найдем обратную к ней матрицу
перехода к новому базису и найдем обратную к ней матрицу  :
:

По матричным уравнением (5.13) находим матрицу  , что соответствует оператору
, что соответствует оператору  в базисе из собственных векторов:
в базисе из собственных векторов:

Следовательно, мы получили диагональную матрицу третьего порядка, элементами главной диагонали которой есть собственные числа матрицы  .
.
Далее приведен пример применения собственных векторов и собственных чисел в одной из многих задач экономики.
Линейная модель обмена (модель международной торговли)
Практически все страны кроме внутреннего товарообмена осуществляют внешний товарообмен, то есть занимаются внешней торговлей. Торговля считается сбалансированной, или бездефицитной, если для каждой страны прибыль от торговли не меньше объем средств, которые она вкладывает в товарооборот (внутренний и внешний).
Постановка задачи. Несколько стран осуществляют взаимный товарообмен. Известную долю бюджетных средств, тратит каждая страна на закупку товаров у другой страны, учитывая и внутренний товарооборот. Определить, каким должно быть соотношение бюджетов партнеров для того, чтобы обеспечить бездефицитность торговли.
Построение математической модели. Введем обозначения количественных характеристик, описывающих торговлю между странами, и определим связь между этими характеристиками. Пусть  – страны, участвующие в международной торговле. Доли средств, которые тратит страна
– страны, участвующие в международной торговле. Доли средств, которые тратит страна  на закупку товаров в стране
на закупку товаров в стране  , учитывая и внутренний товарооборот
, учитывая и внутренний товарооборот  , обозначим через
, обозначим через  . Понятно, что
. Понятно, что

Матрицу  , элементами которой являются числа
, элементами которой являются числа  , называют структурной матрицей торговли:
, называют структурной матрицей торговли:

Эта матрица описывает взаимодействие стран в процессе международной торговли. Соотношение (5.34) означает, что сумма элементов каждого столбца матрицы равна
1. Если объем средств, которые тратит каждая страна на торговлю, обозначить через  , соответственно, то прибыль
, соответственно, то прибыль  страны
страны  от внутренней и внешней торговли составит
от внутренней и внешней торговли составит

Чтобы торговля каждой страны была сбалансированной, по определению должно выполняться условие  , и
, и  , то есть прибыль от торговли не должна быть меньше расходов. Однако соблюдение этого требования в виде неравенства невозможно для всех стран в совокупности. Действительно, добавим левые и правые части указанных неровностей, изменяя
, то есть прибыль от торговли не должна быть меньше расходов. Однако соблюдение этого требования в виде неравенства невозможно для всех стран в совокупности. Действительно, добавим левые и правые части указанных неровностей, изменяя  от единицы до
от единицы до  :
:

Группируя в левой части слагаемые, содержащие каждое из  , получим:
, получим:

Учитывая соотношение (5.20), получим:

Отсюда следует, что сбалансированная торговля возможна только в случае знака равенства. Это, полагаем, понятно не только на основании аналитических выкладок, но и с экономической точки зрения (и даже просто с точки зрения здравого смысла): все страны в совокупности не могут получить прибыль. Более того, для одной из стран не может выполняться знак строгого неравенства  .
.
Итак, условием сбалансированной торговли является равенства  , и
, и  , из которых получим:
, из которых получим:

Введем в рассмотрение вектор (бюджетных) средств  и подадим систему (5.39) в матричной форме:
и подадим систему (5.39) в матричной форме:

С (5.40) следует, что при условии сбалансированности торговли между странами вектор средств  должен быть собственным вектором структурной матрицы торговли
должен быть собственным вектором структурной матрицы торговли  , который принадлежит собственному числу
, который принадлежит собственному числу  . Таким образом, решение задачи сводится к нахождению этого собственного вектора
. Таким образом, решение задачи сводится к нахождению этого собственного вектора  , компоненты которого устанавливают соотношение между бюджетами стран, участвующих в товарообмене.
, компоненты которого устанавливают соотношение между бюджетами стран, участвующих в товарообмене.
Рассмотрим товарообмен между тремя странами. Пусть структурная матрица торговли стран  , имеет вид:
, имеет вид:

Найдем вектор средств, компонентами которого являются доли от общего объема торговли, должна вкладывать каждая из стран во внешней товарооборот для того, чтобы торговля была сбалансированной.
Искомый вектор средств является собственным вектором структурной матрицы, принадлежащий собственному значению  . Его компоненты образуют ненулевое решение однородной СЛАУ:
. Его компоненты образуют ненулевое решение однородной СЛАУ:

Поскольку система является однородной, то расширенная матрица эквивалентна основной матрицы системы. Осуществим элементарные преобразования основной матрицы этой системы уравнений:

Находим общее решение системы, в котором  – базисные переменные,
– базисные переменные,  – свободная переменная:
– свободная переменная:

Отсюда следует, что для сбалансированности торговли необходимо, чтобы средства, которые вкладывает в внешний товарооборот каждая страна, соотносились как 
Лекции:
- Разложение в ряд Фурье четных и нечетных функций
- Функции многих переменных
- Наибольшее и наименьшее значение функции
- Уравнение плоскости
- Экстремум функции трёх переменных
- Как найти вероятность: пример решения
- Свойства определенного интеграла
- Комбинаторика
- Однородные дифференциальные уравнения
- Простейшие задачи аналитической геометрии
Линейные операторы (преобразования)
Определение линейных операторов (преобразований)
Линейным преобразованием (линейным оператором) линейного пространства называется линейное отображение
пространства
в себя.
Поскольку линейное преобразование является частным случаем линейного отображения, к нему применимы все понятия и свойства, рассмотренные для отображений: инъективность, сюръективность, биективность, обратимость, ядро, образ, дефект, ранг и т.д.
Матрицей линейного оператора (преобразования) в базисе
пространства
называется квадратная матрица
, составленная из координатных столбцов образов базисных векторов
, найденных относительно базиса
.
Матрица биективного линейного оператора (преобразования) обратима, т.е. невырождена. Поэтому биективное (обратимое) преобразование называют также невырожденным.
Примеры линейных операторов (преобразований)
1. Обозначим — нулевое преобразование n-мерного пространства
, которое ставит в соответствие любому вектору
нулевой элемент
пространства
. Это преобразование не является инъективным, сюръективным, биективным, обратимым. Матрица нулевого преобразования (в любом базисе) нулевая, ядро преобразования
, образ преобразования
, дефект
, ранг
.
2. Обозначим — тождественное преобразование n-мерного пространства
, которое ставит в соответствие каждому вектору
этот же вектор
. Это преобразование является инъективным, сюръективным, биективным, обратимым. Матрица тождественного преобразования (в любом базисе) единичная n-го порядка, ядро преобразования
, образ преобразования
, дефект
, ранг
.
3. Обозначим — центральную симметрию n-мерного пространства
(относительно нулевого вектора
), т.е. преобразование, которое каждому вектору ставит в соответствие противоположный ему вектор:
. Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Матрица преобразования противоположна единичной (в любом базисе):
; ядро преобразования
, образ преобразования
, дефект
, ранг
.
4. Обозначим — гомотетию n-мерного пространства
(с коэффициентом
), т.е. преобразование, которое каждому вектору ставит в соответствие коллинеарный ему вектор:
. Это преобразование линейное. При
оно инъективное, сюръективное, биективное, обратимое. Матрица преобразования пропорциональна единичной (в любом базисе):
, ядро преобразования
, образ преобразования
, дефект
, ранг
. При
(см. пункт 1); при
(см. пункт 2); при
(см. пункт 3).
5. Рассмотрим линейное пространство радиус-векторов (с общим началом в точке
), принадлежащих одной плоскости (рис. 9.1). Обозначим
— поворот вокруг точки
(на угол
в положительном направлении (против часовой стрелки)). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу поворота в стандартном ортонормированием базисе
. Раскладывая образы
базисных векторов по базису, получаем
Составляем матрицу (9.1) преобразования (оператора), записывая найденные координаты образов по столбцам:
Ядро оператора (преобразования) , образ преобразования
, дефект
, ранг
. При
(см. пункт 2); при
(см. пункт 3).
6. Обозначим — оператор дифференцирования, который каждому многочлену степени не выше и ставит в соответствие его производную, рассматриваемую как многочлен степени не выше
. Это преобразование линейное, неинъективное, несюръективное, небиективное, необратимое. Квадратная матрица ((n+l)-го порядка) преобразования в стандартном базисе имеет вид
Ядро преобразования — пространство многочленов нулевой степени, образ
— пространство многочленов степени не выше
, дефект
, ранг
.
Рассмотрим преобразование линейного пространства тригонометрических многочленов (частоты
) с действительными коэффициентами:
, т.е.
— множество функций вида
, где
. Заметим, что это множество является двумерным вещественным линейным пространством. Стандартный базис пространства
образуют функции
, поскольку они линейно независимы (тождественное равенство нулю
возможно только в тривиальном случае
). При дифференцировании функции
получаем функцию
того же вида. Следовательно, преобразование
определено. Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу преобразования в стандартном базисе
. Раскладывая образы базисных векторов, получаем
Составляем матрицу (9.1) преобразования, записывая найденные координаты образов по столбцам: . Ядро преобразования
— нулевое подпространство, образ
, дефект
, ранг
,
.
Аналогичными свойствами обладает преобразование , где
— множество функций вида
с комплексными коэффициентами
и
. Множество
является двумерным комплексным линейным пространством.
7. Пусть линейное пространство разлагается в прямую сумму подпространств . Обозначим
— оператор проектирования на подпространство
параллельно подпространству
, который каждому вектору
, где
, ставит в соответствие его составляющую (проекцию)
, т.е.
(рис.9.2). Это преобразование линейное. При
оно неинъективное, несюръективное, небиективное, необратимое. Ядро преобразования
, образ преобразования
, дефект
, Ранг
,. При
; при
.
8. Пусть линейное пространство разлагается в прямую сумму подпространств . Обозначим
— оператор отражения в подпространстве
параллельно подпространству
(или преобразование симметрии относительно подпространства
параллельно подпространству
), который каждому вектору
, где
, ставит в соответствие вектор
, т.е.
(рис. 9.3). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Ядро преобразования
, образ преобразования
, дефект
, ранг
. При
.
Матрицы линейного оператора (преобразования) в разных базисах
Найдем связь матриц одного и того же линейного оператора (преобразования) в разных базисах.
Пусть в базисе преобразование
имеет матрицу
, а в базисе
— матрицу
. Если
— матрица перехода от базиса
к базису
, то
(9.4)
Докажем формулу (9.4). Пусть векторы и
в базисах
и
имеют координатные столбцы
и
соответственно. Если
, то по формуле (9.2) имеем
Подставляя в первое равенство связи координат векторов в разных базисах
получаем
или, учитывая обратимость матрицы
. Сравнивая последнее равенство с
, убеждаемся в справедливости (9.4).
Замечания 9.2
1. Матрицы линейного преобразования в разных базисах оказываются подобными. И наоборот, любые две подобные матрицы являются матрицами некоторого линейного преобразования, найденными относительно разных базисов.
2. Для матриц преобразований справедливы свойства, рассмотренные ранее. В частности, при фиксированном базисе матрица суммы преобразований равна сумме их матриц, матрица произведения преобразования на число равна произведению матрицы преобразования на это же число, матрица композиции преобразований равна произведению матриц преобразований, матрица обратного преобразования является обратной для матрицы обратимого преобразования.
Алгебра линейных операторов (преобразований)
Рассмотрим множество — линейных преобразований (операторов) n-мерного линейного пространства
. Напомним, что два преобразования
и
называются равными, если
.
На множестве определены две линейные операции: сложение преобразований и умножение преобразования на число, поскольку в результате этих операций получается линейное преобразование.
Нетрудно показать, что эти операции удовлетворяют условиям:
1. ;
2. ;
3. существует нулевое преобразование такое, что
;
4. для каждого преобразования существует противоположное преобразование
такое, что
;
5. и любого числа
;
6. и любых чисел
;
7. и любых чисел
;
8. .
В условиях 5-7 говорится о числах из того же числового поля, над которым определено линейное пространство .
Условия 1-8 повторяют аксиомы линейного пространства. Поэтому множество с линейными операциями является линейным пространством. Если пространство
вещественное (комплексное), то и пространство
вещественное (комплексное).
Найдем размерность пространства . При фиксированном базисе имеется взаимно однозначное соответствие между линейными преобразованиями и их матрицами, причем это соответствие сохраняет линейные операции. Следовательно, пространство
изоморфно пространству
— квадратных матриц n-го порядка. Размерность пространства
равна
. По теореме 8.3:
то есть
Кроме линейных операций в множестве определена операция умножения элементов. Произведением преобразований
и
назовем их композицию, т.е.
. В результате композиции линейных преобразований получается линейное преобразование. Операция умножения удовлетворяет следующим условиям:
1. ;
2. ;
3. ;
4. существует тождественное преобразование такое, что
.
Первое условие выражает ассоциативность операции умножения, условия 2 и 3 — законы дистрибутивности, условие 4 — существование нейтрального элемента. Множество с операциями сложения и умножения элементов является кольцом с единицей (вообще говоря, некоммутативное, так как в общем случае
).
Операции умножения операторов (преобразований) и произведения операторов на число (из заданного числового поля) удовлетворяют условию:
5.
Линейное пространство, которое является кольцом, удовлетворяющим условию 5, называется алгеброй. Поэтому множество называют алгеброй линейных операторов (преобразований).
Многочлены от линейного оператора (преобразования)
В алгебре можно определить целую неотрицательную степень оператора
, полагая по определению
Пусть — многочлен переменной
. Многочленом
от линейного преобразования
называется преобразование
.
Многочлен называется аннулирующим для линейного преобразования
, если
— нулевое преобразование. Заметим, что у каждого линейного преобразования
n-мерного линейного пространства
существует аннулирующий многочлен степени не выше
. Действительно, система из
элементов
линейного пространства
линейно зависима (так как
). Поэтому существуют такие числа
, не все равные нулю одновременно, что
. Следовательно, многочлен
— аннулирующий для преобразования
.
Замечания 9.3
1. При фиксированном базисе каждому преобразованию (оператору) можно сопоставить его матрицу. Свойства линейных операций 1-8, записанные для матриц преобразований, повторяют свойства линейных операций с матрицами, а свойствам 1-5 произведения операторов отвечают свойства операции умножения матриц.
2. При фиксированном базисе многочлен от линейного преобразования
имеет матрицу
, где
— матрица преобразования
в том же базисе. Поэтому свойства многочленов от матриц переносятся на многочлены от линейного преобразования. В частности, многочлены от одного преобразования перестановочны:
3. Функции от матриц определяются при помощи многочленов от матриц. Поэтому можно определить функции от линейных преобразований.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Матрица перехода
3 июля 2022
Матрица перехода — это просто квадратная матрица, в столбцах которой записаны координаты новых базисных векторов. У такой матрицы много важных свойств, которые сформулированы и доказаны в первой части урока — теоретической. Этой теории хватит для любого экзамена или коллоквиума.
Вторая часть урока — практическая. В ней разобраны все типовые задачи, которые встречаются на контрольных, зачётах и экзаменах.
Содержание
- Определение матрицы перехода
- Свойства матрицы перехода
- Теорема о замене координат
- Задача 1. Базисы трёхмерного пространства
- Задача 2. Базисы в поле вычетов
- Задача 3. Пространство многочленов
- Задача 4. Матрица перехода при симметрии
- Задача 5. Матрица поворота
Если вы учитесь в серьёзном университете (МГУ, Бауманка и т.д.), то обязательно изучите первые три пункта. А если вам нужны только задачи, сразу переходите к пункта 4—6.
1. Определение матрицы перехода
Пусть дано $n$-мерное линейное пространство $L$. Пусть также $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — два базиса в $L$.
Определение. Матрица перехода ${{T}_{eto f}}$ от базиса $e=left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ к базису $f=left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — это квадратная матрица порядка $n$, где по столбцам записаны координаты нового базиса $f$ в старом базисе $e$:
[{{T}_{eto f}}=left[ begin{array}{c|c|c|c}{{t}_{1,1}} & {{t}_{2,1}} & cdots & {{t}_{n,1}} \{{t}_{1,2}} & {{t}_{2,2}} & cdots & {{t}_{n,1}} \cdots & cdots & cdots & cdots \{{t}_{1,n}} & {{t}_{2,n}} & cdots & {{t}_{n,n}} \end{array} right]]
Обратите внимание на нумерацию элементов ${{t}_{i,j}}$: первый индекс обозначает номер столбца, т.е. номер нового базисного вектора, а второй отвечает за координаты этого вектора в старом базисе. Так, во втором столбце записаны координаты вектора ${{f}_{2}}$:
[{{f}_{2}}={{left[ {{t}_{2,1}},{{t}_{2,2}},ldots ,{{t}_{2,n}} right]}^{T}}]
Или, что то же самое, разложение вектора ${{f}_{2}}$ по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:
[{{f}_{2}}={{t}_{2,1}}{{e}_{1}}+{{t}_{2,2}}{{e}_{2}}+ldots +{{t}_{2,n}}{{e}_{n}}]
Да, такая нумерация не является обязательной. Но она очень распространена именно в записи матриц перехода: первый индекс отвечает за номер базисного вектора, второй — за номер координаты этого вектора.
Пример 1. В некотором базисе $e=left{ {{e}_{1}},{{e}_{2}},{{e}_{3}} right}$ векторного пространства ${{mathbb{R}}^{3}}$ даны три вектора:
[{{f}_{1}}={{left( 1,0,1 right)}^{T}},quad {{f}_{2}}={{left( 2,1,0 right)}^{T}},quad {{f}_{3}}={{left( 0,3,1 right)}^{T}}]
[begin{align}{{f}_{1}} &={{left( 1,0,1 right)}^{T}}, \ {{f}_{2}} &={{left( 2,1,0 right)}^{T}}, \ {{f}_{3}} &={{left( 0,3,1 right)}^{T}} \ end{align}]
Убедитесь, что система векторов $f=left{ {{f}_{1}},{{f}_{2}},{{f}_{3}} right}$ образует базис в ${{mathbb{R}}^{3}}$, найдите матрицу перехода ${{T}_{eto f}}$.
Решение. Система векторов будет базисом, если эти векторы линейно независимы, а их количество совпадает с размерностью пространства. Поскольку у нас три вектора и $dim{{mathbb{R}}^{3}}=3$, осталось проверить линейную независимость. Составим матрицу из столбцов с координатами векторов ${{f}_{1}}$, ${{f}_{2}}$ и ${{f}_{3}}$:
[left[ begin{matrix}1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]]
Вообще-то это и есть матрица перехода ${{T}_{eto f}}$, но сначала надо установить линейную независимость. Поэтому выполним элементарные преобразования строк:
[left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]begin{matrix} \ \ -1cdot left[ 1 right] \ end{matrix}sim left[ begin{array}{crc} 1 & 2 & 0 \ 0 & 1 & 3 \ 0 & -2 & 1 \ end{array} right]begin{matrix} -2cdot left[ 2 right] \ \ +2cdot left[ 2 right] \ end{matrix}sim left[ begin{array}{ccr} 1 & 0 & -6 \ 0 & 1 & 3 \ 0 & 0 & 7 \ end{array} right]]
[begin{align} & left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]begin{matrix} \ \ -1cdot left[ 1 right] \ end{matrix} \ & left[ begin{array}{crc} 1 & 2 & 0 \ 0 & 1 & 3 \ 0 & -2 & 1 \ end{array} right]begin{matrix} -2cdot left[ 2 right] \ \ +2cdot left[ 2 right] \ end{matrix} \ & left[ begin{array}{ccr} 1 & 0 & -6 \ 0 & 1 & 3 \ 0 & 0 & 7 \ end{array} right] \ end{align}]
Получили верхнетреугольную матрицу без нулей на главной диагонали. Ранг такой матрицы равен 3, поэтому система $left{ {{f}_{1}},{{f}_{2}},{{f}_{3}} right}$ линейно независима и образует базис. Матрица перехода от базиса $e$ к базису $f$ уже известна:
[{{T}_{eto f}}=left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]]
1.1. Зачем нужна матрица перехода
Матрица перехода нужна для того, чтобы компактно и наглядно выражать новый базис через старый. В самом деле, разложим векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ нового базиса по старому базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:
[begin{align}{{f}_{1}} &={{x}_{1,1}}{{e}_{1}}+{{x}_{2,1}}{{e}_{2}}+ldots +{{x}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{x}_{1,2}}{{e}_{1}}+{{x}_{2,2}}{{e}_{2}}+ldots +{{x}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}} &={{x}_{1,n}}{{e}_{1}}+{{x}_{2,n}}{{e}_{2}}+ldots +{{x}_{n,n}}{{e}_{n}} \ end{align}]
Получили систему из $n$ уравнений, которые в матричном виде можно представить так:
[left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1,1}} & cdots & {{x}_{1,n}} \ cdots & cdots & cdots \ {{x}_{n,1}} & cdots & {{x}_{n,n}} \ end{matrix} right]]
[left[ {{f}_{1}} cdots {{f}_{n}} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1,1}} & cdots & {{x}_{1,n}} \ cdots & cdots & cdots \ {{x}_{n,1}} & cdots & {{x}_{n,n}} \ end{matrix} right]]
Обратите внимание: ${{f}_{1}},ldots ,{{f}_{n}}$ и ${{e}_{1}},ldots ,{{e}_{n}}$ — это именно векторы, а не числа. Такие наборы принято записывать строками — в отличие от вектор-столбцов, элементами которых как раз выступают обычные числа.
Последний множитель — это и есть матрица перехода ${{T}_{eto f}}$, поэтому всё произведение можно записать более компактно:
[left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}]
2. Свойства матрицы перехода
Мы разберём три простых свойства, а далее отдельным разделом будет ещё одно — уже более серьёзное.
2.1. Переход от базиса к этому же базису
Свойство 1. При переходе от базиса $e$ к этому же базису $e$ матрица перехода ${{T}_{eto e}}=E$.
Для доказательства достаточно рассмотреть формулы
[begin{align}{{f}_{1}} &={{x}_{1,1}}{{e}_{1}}+{{x}_{2,1}}{{e}_{2}}+ldots +{{x}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{x}_{1,2}}{{e}_{1}}+{{x}_{2,2}}{{e}_{2}}+ldots +{{x}_{n,2}}{{e}_{n}} \ &cdots \ {{f}_{n}} &={{x}_{1,n}}{{e}_{1}}+{{x}_{2,n}}{{e}_{2}}+ldots +{{x}_{n,n}}{{e}_{n}} \ end{align}]
А затем положить ${{f}_{1}}={{e}_{1}}$, ${{f}_{2}}={{e}_{2}}$, …, ${{f}_{n}}={{e}_{n}}$. Тогда:
[begin{align} {{f}_{1}} &={{e}_{1}}=1cdot {{e}_{1}}+0cdot {{e}_{2}}+ldots +0cdot {{e}_{n}} \ {{f}_{2}} &={{e}_{2}}=0cdot {{e}_{1}}+1cdot {{e}_{2}}+ldots +0cdot {{e}_{n}} \ &cdots \ {{f}_{n}} &={{e}_{n}}=0cdot {{e}_{1}}+0cdot {{e}_{2}}+ldots +1cdot {{e}_{n}} \ end{align}]
Указанное выражение однозначно, поскольку $e$ — базис. Следовательно, матрица перехода равна
[{{T}_{eto f}}=left[ begin{array}{c|c|c|c} 1 & 0 & cdots& 0 \ 0 & 1 & cdots& 0 \ cdots& cdots& cdots& cdots \ 0 & 0 & cdots& 1 \ end{array} right]=E]
Итак, ${{T}_{eto f}}=E$, что и требовалось доказать.
2.2. Обратный переход
Свойство 2. Если ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к базису $f$, то ${{T}_{fto e}}={{left( {{T}_{eto f}} right)}^{-1}}$ матрица обратного перехода, от базиса $f$ к базису $e$.
В самом деле, базисы $e$ и $f$ связаны с матрицей перехода по формуле
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}]
Поскольку матрица ${{T}_{eto f}}$ невырожденная, существует обратная к ней матрица ${{left( {{T}_{eto f}} right)}^{-1}}$. Домножим на эту матрицу обе части формулы, связывающей базисы $e$ и $f$:
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{left( {{T}_{eto f}} right)}^{-1}}=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}cdot {{left( {{T}_{eto f}} right)}^{-1}}]
[begin{align}left[ {{f}_{1}},ldots ,{{f}_{n}} right] &cdot {{left( {{T}_{eto f}} right)}^{-1}}= \ &=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}cdot {{left( {{T}_{eto f}} right)}^{-1}} \ end{align}]
Упрощаем эту формулу и получаем
[left[ {{e}_{1}},ldots ,{{e}_{n}} right]=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{left( {{T}_{eto f}} right)}^{-1}}]
Итак, мы получили формулу перехода от базиса $f$ к базису $e$. Следовательно, ${{left( {{T}_{eto f}} right)}^{-1}}$ — матрица такого перехода, что и требовалось доказать.
2.3. Переход через транзитный базис
Пусть ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к базису $f$ линейного пространства $L$, а ${{T}_{fto g}}$ — матрица перехода от базиса $f$ к базису $g$ того же линейного пространства $L$.
Тогда матрица перехода ${{T}_{eto g}}$ от базиса $e$ к базису $g$ находится по формуле
[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}]
Для доказательства достаточно записать формулы для выражения базисов $f$ и $g$, а затем подставить одну формулу в другую. По условию теоремы, базис $f$ выражается через базис $e$ по формуле
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}]
Кроме того, базис $g$ выражается через базис $f$ по формуле
[left[ {{g}_{1}},ldots ,{{g}_{n}} right]=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}]
Подставим первое выражение во второе и получим
[begin{align}left[ {{g}_{1}},ldots ,{{g}_{n}} right] &=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}= \ &=left( left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}} right)cdot {{T}_{fto g}}= \ & =left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot left( {{T}_{eto f}}cdot {{T}_{fto g}} right) end{align}]
[begin{align}& left[ {{g}_{1}},ldots ,{{g}_{n}} right]= \ =& left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}= \ =& left( left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}} right)cdot {{T}_{fto g}}= \ =& left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot left( {{T}_{eto f}}cdot {{T}_{fto g}} right) end{align}]
Мы получили прямое выражение базиса $g$ через базис $e$, причём матрица перехода равна
[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}]
Это именно та формула, которую и требовалось доказать.
2.4. Невырожденные матрицы
И ещё одно важное свойство:
Свойство 4. Пусть дана произвольная квадратная невырожденная матрица
[T=left[ begin{matrix}{{a}_{1,1}} & {{a}_{1,2}} & cdots & {{a}_{1,n}} \ {{a}_{2,1}} & {{a}_{2,2}} & cdots & {{a}_{2,n}} \ cdots & cdots & cdots & cdots \ {{a}_{n,1}} & {{a}_{n,2}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
Пусть $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ — произвольный базис линейного пространства $L$. Тогда система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$, полученных по формуле
[begin{align}{{f}_{1}}&={{a}_{1,1}}{{e}_{1}}+{{a}_{2,1}}{{e}_{2}}+ldots +{{a}_{n,1}}{{e}_{n}} \ {{f}_{2}}&={{a}_{1,2}}{{e}_{1}}+{{a}_{2,2}}{{e}_{2}}+ldots +{{a}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}}&={{a}_{1,n}}{{e}_{1}}+{{a}_{2,n}}{{e}_{2}}+ldots +{{a}_{n,n}}{{e}_{n}} \ end{align}]
тоже будет базисом $L$.
Иначе говоря, всякая квадратная невырожденная матрица $T$ является матрицей перехода от данного базиса $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ к некоторому новому базису $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ линейного пространства $L$.
Обратите внимание: поскольку изначально мы не знаем, что $T$ — матрица перехода, её элементы пронумерованы стандартным образом: первый индекс отвечает за строку, а второй — за столбец. Однако это нисколько не помешает нам доказать теорему.
Для доказательства того, что $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — базис линейного пространства $L$, нужно доказать два утверждения:
- 1.Система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — линейно независима.
- 2.Ранг этой системы векторов совпадает с размерностью пространства $L$.
Поскольку количество векторов в системе $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ совпадает с количеством базисных векторов $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$, т.е. равно $n=dim L$, достаточно лишь проверить линейную независимость.
Рассмотрим линейную комбинацию векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ и предположим, что она равна нулю:
[{{lambda }_{1}}{{f}_{1}}+{{lambda }_{2}}{{f}_{2}}+ldots +{{lambda }_{n}}{{f}_{n}}=0]
В матричном виде это выглядит так:
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot left[ begin{align}& {{lambda }_{1}} \ & cdots\ & {{lambda }_{n}} \ end{align} right]=0]
По условию теоремы векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ раскладываются по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ с коэффициентами, записанными в столбцах матрицы $T$. В матричном виде это выглядит так:
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot T]
Подставляем полученное выражение для $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ в предыдущее матричное уравнение и получаем
[left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot Tcdot left[ begin{align}& {{lambda }_{1}} \ & cdots \ & {{lambda }_{n}} \ end{align} right]=0]
Поскольку $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ — базис линейного пространства $L$, такое равенство возможно лишь при условии
[Tcdot left[ begin{matrix} {{lambda }_{1}} \ cdots \ {{lambda }_{n}} \ end{matrix} right]=left[ begin{matrix} 0 \ cdots \ 0 \ end{matrix} right]]
Это матричное уравнение можно рассматривать как систему из $n$ однородных уравнений относительно переменных ${{lambda }_{1}},ldots ,{{lambda }_{n}}$. И поскольку по условию теоремы матрица $T$ невырожденная, это СЛАУ имеет лишь одно решение — тривиальное:
[{{lambda }_{1}}={{lambda }_{2}}=ldots ={{lambda }_{n}}=0]
Получаем, что система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ линейно независима, а количество векторов совпадает с размерностью линейного пространства $L$. Следовательно, эта система — базис, что и требовалось доказать.
3. Замена координат в новом базисе
До сих пор мы рассуждали лишь о том, как координаты новых базисных векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ выражаются через координаты старых базисных векторов $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$. Но что будет с координатами одного и того же вектора линейного пространства $L$ при переходе от одного базиса к другому?
Ответ даёт следующая теорема.
3.1. Формулировка теоремы
Теорема. Пусть $e=left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $f=left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — базисы линейного пространства $L$ над полем $K$. Пусть ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к $f$:
[{{T}_{eto f}}=left[ begin{matrix}{{a}_{1,1}} & cdots& {{a}_{1,n}} \ cdots& cdots& cdots \ {{a}_{n,1}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
Тогда координаты произвольного вектора $hin L$ пересчитываются по формуле
[{{left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]}_{e}}={{T}_{eto f}}cdot {{left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]}_{f}}]
Ещё раз: если произвольный вектор $hin L$ в новом базисе $f$ имеет координаты
[{{left[ h right]}_{f}}=left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
то в старом базисе $e$ этот же вектор $hin L$ имеет координаты
[{{left[ h right]}_{e}}=left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]={{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Т.е. для векторов всё наоборот: не новые координаты выражаются через старые, а старые — через новые. Впрочем, никто не мешает найти матрицу $T_{eto f}^{-1}$ и записать
[left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]=T_{eto f}^{-1}cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]]
Но такая запись предполагает дополнительное действие — нахождение обратной матрицы.
3.2. Доказательство
Сначала «соберём» матрицу ${{T}_{eto f}}$. Для этого разложим векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:
[left{ begin{align}{{f}_{1}} &={{a}_{1,1}}{{e}_{1}}+{{a}_{2,1}}{{e}_{2}}+ldots +{{a}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{a}_{1,2}}{{e}_{1}}+{{a}_{2,2}}{{e}_{2}}+ldots +{{a}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}} &={{a}_{1,n}}{{e}_{1}} +{{a}_{2,n}}{{e}_{2}}+ldots +{{a}_{n,n}}{{e}_{n}} \ end{align} right.]
В матричной форме эту систему линейных уравнений можно записать так:
[left[ begin{matrix} {{f}_{1}} \ {{f}_{2}} \ cdots \ {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{a}_{1,1}} & {{a}_{2,1}} & cdots & {{a}_{n,1}} \ {{a}_{1,2}} & {{a}_{2,2}} & cdots & {{a}_{n,2}} \ cdots & cdots & cdots & cdots \ {{a}_{1,n}} & {{a}_{2,n}} & cdots & {{a}_{n,n}} \ end{matrix} right]cdot left[ begin{matrix} {{e}_{1}} \ {{e}_{2}} \ cdots \ {{e}_{n}} \ end{matrix} right]]
Транспонируем обе стороны равенства, учитывая, что произведение справа транспонируется по правилу ${{left( Acdot B right)}^{T}}={{B}^{T}}cdot {{A}^{T}}$:
[left[ begin{matrix}{{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{a}_{1,1}} & {{a}_{1,2}} & cdots & {{a}_{1,n}} \ {{a}_{2,1}} & {{a}_{2,2}} & cdots & {{a}_{2,n}} \ cdots & cdots & cdots & cdots \ {{a}_{n,1}} & {{a}_{n,2}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
[left[ {{f}_{1}} cdots {{f}_{n}} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{a}_{1,1}} & cdots & {{a}_{1,n}} \ cdots & cdots & cdots \ {{a}_{n,1}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
Квадратная матрица справа — это и есть матрица перехода ${{T}_{eto f}}$. Поэтому матричное уравнение можно переписать так:
[left[ begin{matrix}{{f}_{1}} & cdots& {{f}_{n}} \ end{matrix} right]=left[ begin{matrix}{{e}_{1}} & cdots& {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}]
Теперь возьмём произвольный вектор $hin L$ и разложим его по базисам $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$:
[begin{align}h &={{x}_{1}}{{e}_{1}}+{{x}_{2}}{{e}_{2}}+ldots +{{x}_{n}}{{e}_{n}}= \ &={{y}_{1}}{{f}_{1}}+{{y}_{2}}{{f}_{2}}+ldots +{{y}_{n}}{{f}_{n}} end{align}]
Вновь перейдём к матричной форме. Сначала учтём, что координаты векторов принято записывать в виде вектор-столбцов:
[{{left[ h right]}_{e}}=left[ begin{matrix} {{x}_{1}} \ {{x}_{2}} \ cdots \ {{x}_{n}} \ end{matrix} right]quad {{left[ h right]}_{f}}=left[ begin{matrix} {{y}_{1}} \ {{y}_{2}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Тогда левую и правую часть уравнения можно представить как произведение строк с базисными векторами и указанных вектор-столбцов с координатами:
[left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
[left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ {{f}_{1}} cdots {{f}_{n}} right]cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Но выше мы выражали строку векторов $left[ {{f}_{1}},ldots ,{{f}_{n}} right]$ через строку $left[ {{e}_{1}},ldots ,{{e}_{n}} right]$ и матрицу перехода ${{T}_{eto f}}$. Подставим это выражение в наше матричное уравнение:
[left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
[left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot {{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Уберём слева и справа первый множитель — строку $left[ {{e}_{1}},ldots ,{{e}_{n}} right]$. Получим уравнение, связывающее координаты вектора в разных базисах:
[left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]={{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Это именно та формула, которую и требовалось доказать.
Задача 1. Базисы трёхмерного пространства
Задача. Убедитесь, что системы векторов
[{{a}_{1}}={{left( 1,2,1 right)}^{T}},quad {{a}_{2}}={{left( 2,3,2 right)}^{T}},quad {{a}_{3}}={{left( 1,-1,2 right)}^{T}}]
[begin{align}{{a}_{1}} &={{left( 1,2,1 right)}^{T}}, \ {{a}_{2}} &={{left( 2,3,2 right)}^{T}}, \ {{a}_{3}} &={{left( 1,-1,2 right)}^{T}} \ end{align}]
и
[{{b}_{1}}={{left( 1,3,1 right)}^{T}},quad {{b}_{2}}={{left( 1,-1,3 right)}^{T}},quad {{b}_{3}}={{left( 2,2,1 right)}^{T}}]
[begin{align}{{b}_{1}} &={{left( 1,3,1 right)}^{T}}, \ {{b}_{2}} &={{left( 1,-1,3 right)}^{T}}, \ {{b}_{3}} &={{left( 2,2,1 right)}^{T}} \ end{align}]
являются базисами в векторном пространстве ${{mathbb{R}}^{3}}$. Найдите матрицу перехода ${{T}_{ato b}}$. Найдите координаты в базисе $a$ вектора $x$, который в базисе $b$ имеет координаты ${{left( 0,3,2 right)}^{T}}$.
Решение
Чтобы доказать, что система векторов образует базис, достаточно составить матрицу $A$ из координат этих векторов, а затем вычислить её определитель $det A$. И если $det Ane 0$, то векторы линейно независимы. А поскольку их количество совпадает с размерностью линейного пространства, такие векторы образуют базис.
Рассмотрим систему векторов $a=left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$. Составим из них матрицу, расположив координаты по столбцам. Получим матрицу перехода ${{T}_{eto a}}$ от некого исходного базиса $e$ (в котором как раз и даны координаты векторов ${{a}_{i}}$ и ${{b}_{i}}$ в условии задачи) к базису $a$:
[{{T}_{eto a}}=left[ begin{array}{ccr} 1 & 2 & 1 \ 2 & 3 & -1 \ 1 & 2 & 2 \ end{array} right]]
Определитель этой матрицы отличен от нуля:
[det {{T}_{eto a}}=-1ne 0]
Следовательно, $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ — базис пространства ${{mathbb{R}}^{3}}$.
Теперь составим матрицу из векторов $b=left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$. Получим матрицу перехода ${{T}_{eto b}}$:
[{{T}_{eto b}}=left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right]]
Определитель этой матрицы вновь отличен от нуля:
[det {{T}_{eto b}}=12ne 0]
Следовательно, $left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ — тоже базис пространства ${{mathbb{R}}^{3}}$.
Осталось найти матрицу перехода ${{T}_{ato b}}$. Заметим, что эту матрицу можно выразить так:
[begin{align}{{T}_{ato b}} &={{T}_{ato e}}cdot {{T}_{eto b}}= \ &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}end{align}]
Мы внедрили «транзитный» базис $e$ и вместо прямого перехода $ato b$ рассмотрели цепочку $ato eto b$. Это стандартный и очень распространённый приём, но из-за этого появился новый элемент $T_{eto a}^{-1}$ — матрица, обратная к ${{T}_{eto a}}$. Найдём $T_{eto a}^{-1}$ методом присоединённой матрицы:
[left[ {{T}_{eto a}}|E right]sim ldots sim left[ E|T_{eto a}^{-1} right]]
Напомню, что элементарные преобразования в присоединённых матрицах выполняются только над строками. Если вы забыли, как всё это работает, см. урок «Обратная матрица». В нашем случае получим:
[left[ begin{array}{ccr|ccc}1 & 2 & 1 & 1 & 0 & 0 \ 2 & 3 & -1 & 0 & 1 & 0 \ 1 & 2 & 2 & 0 & 0 & 1 \end{array} right]begin{matrix} , \ -2cdot left[ 1 right] \ -1cdot left[ 1 right] \ end{matrix}]
Мы «зачистили» первый столбец. Теперь «зачистим» последний:
[left[ begin{array}{crr|rcc} 1 & 2 & 1 & 1 & 0 & 0 \ 0 & -1 & -3 & -2 & 1 & 0 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]begin{matrix} -1cdot left[ 3 right] \ +3cdot left[ 3 right] \ , \ end{matrix}]
Остался лишь средний. Разберёмся и с ним:
[left[ begin{array}{crc|rcr} 1 & 2 & 0 & 2 & 0 & -1 \ 0 & -1 & 0 & -5 & 1 & 3 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]begin{matrix} +2cdot left[ 2 right] \ |cdot left( -1 right) \ , \ end{matrix}]
Получили единичную матрицу слева от вертикальной черты. Значит, справа стоит искомая матрица $T_{eto a}^{-1}$:
[left[ begin{array}{ccc|rrr} 1 & 0 & 0 & -8 & 2 & 5 \ 0 & 1 & 0 & 5 & -1 & -3 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]]
Теперь у нас есть всё, чтобы найти матрицу перехода ${{T}_{ato b}}$:
[{{T}_{ato b}}={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}=left[ begin{array}{rrr} -8 & 2 & 5 \ 5 & -1 & -3 \ -1 & 0 & 1 \ end{array} right]cdot left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right]]
[begin{align}{{T}_{ato b}} &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}= \ &=left[ begin{array}{rrr} -8 & 2 & 5 \ 5 & -1 & -3 \ -1 & 0 & 1 \ end{array} right]cdot left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right] end{align}]
После несложных вычислений получаем матрицу перехода от базиса $a$ к базису $b$:
[{{T}_{ato b}}=left[ begin{array}{rrr} 3 & 5 & -7 \ -1 & -3 & 5 \ 0 & 2 & -1 \ end{array} right]]
Осталось найти координаты вектора $x$, который в базисе $b$ имеет координаты ${{left( 0,3,2 right)}^{T}}$. Вспомним формулу, выражающую координаты в старом базисе через координаты в новом базисе:
[{{left[ x right]}_{a}}={{T}_{ato b}}cdot {{left[ x right]}_{b}}]
Подставляем в эту формулу матрицу ${{T}_{ato b}}$ и вектор-столбец ${{left[ x right]}_{b}}={{left[ 0,3,2 right]}^{T}}$:
[{{left[ x right]}_{a}}=left[ begin{array}{rrr} 3 & 5 & -7 \ -1 & -3 & 5 \ 0 & 2 & -1 \ end{array} right]cdot left[ begin{matrix} 0 \ 3 \ 2 \ end{matrix} right]=left[ begin{matrix} 1 \ 1 \ 4 \ end{matrix} right]]
Итак, вектор $x$ в базисе $a$ имеет координаты ${{left( 1,1,4 right)}^{T}}$. Задача решена.
Альтернативное решение
Можно найти матрицу ${{T}_{ato b}}$ заметно быстрее, если использовать алгоритм решения матричных уравнений. Заметим, что нам требуется найти произведение
[{{T}_{ato b}}={{A}^{-1}}cdot B]
С другой стороны, для нахождения такого произведения достаточно составить присоединённую матрицу вида $left[ A|B right]$ и цепочкой элементарных преобразований свести её к виду
[left[ A|B right]sim ldots sim left[ E|{{A}^{-1}}cdot B right]]
Другими словами, справа от вертикальной черты мы получим искомую матрицу перехода ${{T}_{ato b}}$!
На практике это выглядит так. Записываем присоединённую матрицу $left[ A|B right]$:
[left[ begin{array}{ccr|crc} 1 & 2 & 1 & 1 & 1 & 2 \ 2 & 3 & -1 & 3 & -1 & 2 \ 1 & 2 & 2 & 1 & 2 & 1 \ end{array} right]]
И после элементарных преобразований получим
[left[ begin{array}{ccc|rrr} 1 & 0 & 0 & 3 & 5 & -7 \ 0 & 1 & 0 & -1 & -3 & 5 \ 0 & 0 & 1 & 0 & 2 & -1 \ end{array} right]]
Для экономии места я пропустил промежуточные шаги. Попробуйте сделать их самостоятельно — это очень полезная практика.
Если же вы хотите разобраться, как это работает (и почему вдруг справа возникает матрица вида ${{A}^{-1}}cdot B$), см. урок «Матричные уравнения». А мы идём дальше.
Задача 2. Базисы в поле вычетов
Найдите матрицу перехода от базиса
[{{a}_{1}}={{left( 1,1,1 right)}^{T}},quad {{a}_{2}}={{left( 2,1,1 right)}^{T}},quad {{a}_{3}}={{left( 3,2,1 right)}^{T}}]
[begin{align}{{a}_{1}} &={{left( 1,1,1 right)}^{T}}, \ {{a}_{2}} &={{left( 2,1,1 right)}^{T}}, \ {{a}_{3}} &={{left( 3,2,1 right)}^{T}} \ end{align}]
к базису
[{{b}_{1}}={{left( 0,4,3 right)}^{T}},quad {{b}_{2}}={{left( 3,3,2 right)}^{T}},quad {{b}_{3}}={{left( 2,2,1 right)}^{T}}]
[begin{align}{{b}_{1}} &={{left( 0,4,3 right)}^{T}}, \ {{b}_{2}} &={{left( 3,3,2 right)}^{T}}, \ {{b}_{3}} &={{left( 2,2,1 right)}^{T}} \ end{align}]
арифметического линейного пространства $mathbb{Z}_{5}^{3}$.
Решение
Эта задача проще предыдущей, поскольку поле вычетов ${{mathbb{Z}}_{5}}$ является конечным и состоит всего из пяти элементов — представителей смежных классов:
[{{mathbb{Z}}_{5}}=left{ 0,1,2,3,4 right}]
Как и в предыдущей задаче, рассмотрим систему векторов $a=left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ и составим из них матрицу ${{T}_{eto a}}$:
[{{T}_{eto a}}=left[ begin{matrix} 1 & 2 & 3 \ 1 & 1 & 2 \ 1 & 1 & 1 \ end{matrix} right]]
Определитель $det {{T}_{eto a}}=1ne 0$, поэтому $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ — базис.
Аналогично, рассмотрим систему $b=left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ и составим матрицу ${{T}_{eto b}}$:
[{{T}_{eto b}}=left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]]
Определитель $det {{T}_{eto b}}=4ne 0$, поэтому $left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ — базис.
Выразим искомую матрицу ${{T}_{ato b}}$ через «транзитный» базис $e$:
[begin{align}{{T}_{ato b}} &={{T}_{ato e}}cdot {{T}_{eto b}}= \ &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}} end{align}]
Найдём $T_{eto a}^{-1}$ через присоединённую матрицу:
[left[ begin{array}{ccc|ccc} 1 & 2 & 3 & 1 & 0 & 0 \ 1 & 1 & 2 & 0 & 1 & 0 \ 1 & 1 & 1 & 0 & 0 & 1 \ end{array} right]]
После цепочки элементарных преобразований над строками (попробуйте выполнить их самостоятельно!) получим
[left[ begin{array}{ccc|ccc} 1 & 0 & 0 & 4 & 1 & 1 \ 0 & 1 & 0 & 1 & 3 & 1 \ 0 & 0 & 1 & 0 & 1 & 4 \ end{array} right]]
Итак, мы нашли матрицу $T_{eto a}^{-1}$:
[T_{eto a}^{-1}=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]]
Осталось вычислить искомую матрицу перехода ${{T}_{ato b}}$:
[{{T}_{ato b}}={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]cdot left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]=left[ begin{matrix} 2 & 2 & 1 \ 0 & 4 & 4 \ 1 & 1 & 1 \ end{matrix} right]]
[begin{align}{{T}_{ato b}} &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}= \ &=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]cdot left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]= \ &=left[ begin{matrix} 2 & 2 & 1 \ 0 & 4 & 4 \ 1 & 1 & 1 \ end{matrix} right] end{align}]
По аналогии с предыдущей задачей, матрицу ${{T}_{ato b}}$ можно найти и через элементарные преобразования присоединённой матрицы $left[ A|B right]$. Результат будет точно такой же, но мы сэкономим пару строк вычислений и несколько минут времени.
Задача 3. Пространство многочленов
Убедитесь, что системы многочленов
[begin{align}e &=left{ 1,t-1,{{left( t-1 right)}^{2}} right} \ f &=left( 1,t+1,{{left( t+1 right)}^{2}} right) \ end{align}]
являются базисами в пространстве ${{P}_{3}}$ многочленов степени не выше 2. Найдите матрицу перехода ${{T}_{eto f}}$. Разложите по степеням $left( t-1 right)$ многочлен ${{left( t+1 right)}^{2}}+left( t+1 right)+1$.
Решение
Стандартным базисом в пространстве многочленов является система многочленов $p=left{ {{p}_{1}},{{p}_{2}},{{p}_{3}} right}$, где
[{{p}_{1}}=1quad {{p}_{2}}=tquad {{p}_{3}}={{t}^{2}}]
Выразим через базис $p$ многочлены из системы $e$:
[begin{align} & {{e}_{1}}=1={{p}_{1}} \ & {{e}_{2}}=t-1={{p}_{2}}-{{p}_{1}} \ & {{e}_{3}}={{left( t-1 right)}^{2}}={{t}^{2}}-2t+1={{p}_{3}}-2{{p}_{2}}+{{p}_{1}} end{align}]
[begin{align}{{e}_{1}} &=1={{p}_{1}} \ {{e}_{2}} &=t-1={{p}_{2}}-{{p}_{1}} \ {{e}_{3}} &={{left( t-1 right)}^{2}}= \ &={{t}^{2}}-2t+1= \ &={{p}_{3}}-2{{p}_{2}}+{{p}_{1}} end{align}]
Следовательно, матрица перехода ${{T}_{pto e}}$ выглядит так:
[{{T}_{pto e}}=left[ begin{array}{crr} 1 & -1 & 1 \ 0 & 1 & -2 \ 0 & 0 & 1 \ end{array} right]]
Аналогично, выразим через базис $p$ многочлены из системы $f$:
[begin{align} & {{f}_{1}}=1={{p}_{1}} \ & {{f}_{2}}=t+1={{p}_{2}}+{{p}_{1}} \ & {{f}_{3}}={{left( t+1 right)}^{2}}={{t}^{2}}+2t+1={{p}_{3}}+2{{p}_{2}}+{{p}_{1}} end{align}]
[begin{align}{{f}_{1}} &=1={{p}_{1}} \ {{f}_{2}} &=t+1={{p}_{2}}+{{p}_{1}} \ {{f}_{3}} &={{left( t+1 right)}^{2}}= \ &={{t}^{2}}+2t+1= \ &={{p}_{3}}+2{{p}_{2}}+{{p}_{1}} end{align}]
Получим матрицу перехода ${{T}_{pto f}}$:
[{{T}_{pto f}}=left[ begin{matrix} 1 & 1 & 1 \ 0 & 1 & 2 \ 0 & 0 & 1 \ end{matrix} right]]
Обе матрицы оказались верхнетреугольными, их определители отличны от нуля:
[begin{align} det {{T}_{pto e}} &=1cdot 1cdot 1=1 \ det {{T}_{pto f}} &=1cdot 1cdot 1=1 \ end{align}]
Следовательно системы многочленов $e$ и $f$ действительно являются базисами пространства ${{P}_{3}}$.
Теперь найдём матрицу перехода ${{T}_{eto f}}$. Для этого нам даже не потребуется искать обратную матрицу. Достаточно заметить, что векторы ${{f}_{1}}$ и ${{f}_{2}}$ легко раскладываются по базису $e$:
[begin{align}{{f}_{1}} &=1={{e}_{1}} \ {{f}_{2}} &=t+1=left( t-1 right)+2={{e}_{2}}+2{{e}_{1}} \ end{align}]
С вектором ${{f}_{3}}$ вычислений будет чуть больше:
[begin{align}{{f}_{3}} &={{left( t+1 right)}^{2}}= \ &={{left( t-1 right)}^{2}}+4t= \ &={{left( t-1 right)}^{2}}+4left( t-1 right)+4= \ &={{e}_{3}}+4{{e}_{2}}+4{{e}_{1}} end{align}]
Итого матрица перехода ${{T}_{eto f}}$ примет вид
[{{T}_{eto f}}=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]]
Теперь разложим многочлен ${{left( t+1 right)}^{2}}+left( t+1 right)+1$ по базису $e$. Сначала перепишем этот многочлен так:
[begin{align}hleft( t right) &=1+left( t+1 right)+{{left( t+1 right)}^{2}}= \ &={{f}_{1}}+{{f}_{2}}+{{f}_{3}} end{align}]
Следовательно, в базисе $f$ многочлен $hleft( t right)$ имеет координаты ${{left( 1,1,1 right)}^{T}}$. Но тогда по теореме о замене координат этот же многочлен в базисе $e$ имеет координаты
[{{left[ h right]}_{e}}={{T}_{eto f}}cdot {{left[ h right]}_{f}}=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]cdot left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{matrix} 7 \ 5 \ 1 \ end{matrix} right]]
[begin{align}{{left[ h right]}_{e}} &={{T}_{eto f}}cdot {{left[ h right]}_{f}}= \ &=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]cdot left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{matrix} 7 \ 5 \ 1 \ end{matrix} right] end{align}]
Другими словами, многочлен $hleft( t right)$ имеет вид
[hleft( t right)={{left( t-1 right)}^{2}}+5left( t-1 right)+7]
Это и есть искомое разложение многочлена ${{left( t+1 right)}^{2}}+left( t+1 right)+1$ по степеням $left( t-1 right)$.
Альтернативное решение
Искомое разложение можно получить и без привлечения матриц перехода. Достаточно применить схему Горнера или выделить нужные степени напрямую:
[begin{align}hleft( t right) &={{left( t+1 right)}^{2}}+left( t+1 right)+1= \ &={{left( t-1 right)}^{2}}+4t+t+1+1= \ &={{left( t-1 right)}^{2}}+5left( t-1 right)+5+2= \ &={{left( t-1 right)}^{2}}+5left( t-1 right)+7 end{align}]
Как видим, результат получился тем же самым, а времени потрачено меньше. Однако уже в пространстве ${{P}_{4}}$ многочленов степени не выше 4 сложность решения через матрицы и через выделение степеней будет сопоставимой. А дальше матрицы начнут выигрывать.
Смысл линейной алгебры — дать универсальные алгоритмы, которые работают с объектами любой природы, если эти объекты подчиняются аксиомам линейного пространства.
Задача 4. Матрица перехода при симметрии
Базис $b$получается из базиса
[{{a}_{1}}={{left( 2,1,3 right)}^{T}},quad {{a}_{2}}={{left( 1,1,-1 right)}^{T}},quad {{a}_{3}}={{left( 2,-1,-1 right)}^{T}}]
[begin{align}{{a}_{1}} &={{left( 2,1,3 right)}^{T}}, \ {{a}_{2}} &={{left( 1,1,-1 right)}^{T}}, \ {{a}_{3}} &={{left( 2,-1,-1 right)}^{T}} \ end{align}]
пространства ${{V}_{3}}$ симметрией относительно плоскости $2x+y+3z=0$. Найти матрицу перехода ${{T}_{ato b}}$.
Решение
Из курса аналитической геометрии мы знаем, что если плоскость задана уравнением
[ax+by+cz+d=0]
то вектор-нормаль $n$ имеет координаты
[n=left( a,b,c right)]
Тогда для плоскости $2x+y+3z=0$ нормаль имеет координаты $n=left( 2,1,3 right)$, что в точности совпадает с вектором ${{a}_{1}}$. Следовательно, при симметрии относительно плоскости этот вектор просто перейдёт в противоположный: ${{b}_{1}}=-{{a}_{1}}$.
Далее заметим, что векторы ${{a}_{2}}$ и ${{a}_{3}}$ лежат в плоскости симметрии, поскольку при подстановке их координат уравнение плоскости обращается в верное числовое равенство:
[begin{align}{{a}_{2}}={{left( 1,1,-1 right)}^{T}} &Rightarrow 2cdot 1+1+3cdot left( -1 right)=0 \ {{a}_{3}}={{left( 2,-1,-1 right)}^{T}} &Rightarrow 2cdot 2-1+3cdot left( -1 right)=0 \ end{align}]
[begin{align}{{a}_{2}}=&{{left( 1,1,-1 right)}^{T}}Rightarrow \ & Rightarrow 2cdot 1+1+3cdot left( -1 right)=0 \ {{a}_{3}}=&{{left( 2,-1,-1 right)}^{T}}Rightarrow \ & Rightarrow 2cdot 2-1+3cdot left( -1 right)=0 \ end{align}]
Следовательно, при симметрии эти векторы переходят сами в себя: ${{b}_{2}}={{a}_{2}}$, ${{b}_{3}}={{a}_{3}}$. Матрица перехода имеет вид
[{{T}_{ato b}}=left[ begin{array}{rcc} -1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \ end{array} right]]
Важное замечание. симметрия предполагает использование проекций и углов, что в конечном счёте сводится к скалярному произведению. Однако мы пока не знаем, что такое скалярное произведение в линейном пространстве.
Полноценное определение скалярного произведения будет намного позже — см. урок «Евклидово пространство». А пока будем считать, что скалярное произведение векторов $a$ и $b$ определено стандартным образом:
[left( a,b right)=left| a right|cdot left| b right|cdot cos alpha ]
Геометрическая интерпретация
Симметрию на плоскости и в пространстве удобно представлять графически. Пусть $alpha $ — плоскость, относительно которой выполняется симметрия. Тогда векторы $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ будут выглядеть так:
Из приведённого рисунка сразу видно, что при симметрии вектор ${{a}_{1}}$ перейдёт в противоположный, а векторы ${{a}_{2}}$ и ${{a}_{3}}$ останутся на месте.
Задача 5. Матрица поворота
Базис $e=left{ i,j,k right}$ пространства ${{V}_{3}}$ поворачивается на 180° вокруг прямой $l$, заданной системой
[left{ begin{align}x-y &=0 \ z &=0 \ end{align} right.]
Затем полученный базис $f$ поворачивается на 90° в отрицательном направлении вокруг нового положения вектора $j$. В результате получается базис $g=left{ {{i}_{2}},{{j}_{2}},{{k}_{2}} right}$.
Найдите матрицу перехода ${{T}_{eto g}}$. Найдите в базисе $e$ координаты вектора $h$, который в новом базисе $g$ имеет координаты $left( 1,1,1 right)$.
Решение
Вращение базиса и матрица поворота — это очень важная тема, по которой есть отдельный урок — «Матрица поворота». Но сейчас вращение совсем простое, поэтому обойдёмся без специальных матриц.
Вновь обратимся к геометрической интерпретации. Рассмотрим исходный базис $e=left{ i,j,k right}$ трёхмерного пространства:
Также на этом рисунке изображена прямая $l$, которая задаётся требованиями $z=0$ и $x=y$. Эта лежит в плоскости $Oxy$ и является биссектрисой первой координатной четверти.
Очевидно, что при повороте пространства на 180° относительно прямой $l$ базисные векторы $i$ и $j$ просто поменяются местами, а вектор $k$ перейдёт в противоположный:
Другими словами, ${{i}_{1}}=j$, ${{j}_{1}}=i$, ${{k}_{1}}=-k$, поэтому матрица перехода от базиса $e=left{ i,j,k right}$ к базису $f=left{ {{i}_{1}},{{j}_{1}},{{k}_{1}} right}$ примет вид
[{{T}_{eto f}}=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]]
Далее поворот осуществляется вокруг нового положения вектора $j$, т.е. вокруг вектора ${{j}_{1}}$. Вновь обратимся к чертежу. В этот раз нам уже не нужны координатные оси — нас интересуют лишь векторы ${{i}_{1}}$, ${{j}_{1}}$ и ${{k}_{1}}$, а также ось вращения:
Обратите внимание: в задаче сказано, что базис вращается на 90° в отрицательном направлении. Если мы смотрим на плоскость, образованную векторами ${{i}_{1}}$ и ${{k}_{1}}$, с вершины вектора ${{j}_{1}}$ (как на картинке), то отрицательное направление — это по часовой стрелке (отмечено зелёным), а положительное —против часовой стрелки (отмечено красным).
Все эти тонкости (положительное и отрицательное направление, правые и левые тройки векторов) детально описаны в уроке про матрицы поворота. Сейчас не будем подробно разбираться в них, а просто нарисуем результат:
Итак, ${{i}_{2}}={{k}_{1}}$, ${{j}_{2}}={{j}_{1}}$ и ${{k}_{2}}=-{{i}_{1}}$, поэтому матрица перехода от базиса $f=left{ {{i}_{1}},{{j}_{1}},{{k}_{1}} right}$ к базису $g=left{ {{i}_{2}},{{j}_{2}},{{k}_{2}} right}$ имеет вид
[{{T}_{fto g}}=left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]]
Теперь мы можем найти матрицу ${{T}_{eto g}}$ через транзитный базис $f$:
[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]cdot left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right]]
[begin{align}{{T}_{eto g}} &={{T}_{eto f}}cdot {{T}_{fto g}}= \ &=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]cdot left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]= \ &=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right] end{align}]
Кроме того, нам известны координаты вектора $h$ в базисе $g$:
[h={{left( 1,1,1 right)}^{T}}]
Тогда в базисе $e$ координаты этого же вектора равны
[{{left[ h right]}_{e}}={{T}_{eto g}}cdot {{left[ h right]}_{g}}=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right].left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{array}{r} 1 \ -1 \ -1 \ end{array} right]]
[begin{align}{{left[ h right]}_{e}} &={{T}_{eto g}}cdot {{left[ h right]}_{g}}= \ &=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right].left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{array}{r} 1 \ -1 \ -1 \ end{array} right] end{align}]
Итак, мы нашли матрицу перехода ${{T}_{eto g}}$ и координаты вектора $h$ в исходном базисе. Задача решена.
Смотрите также:
- Критерий Сильвестра для квадратичных функций

- Работа с формулами в задаче B12

- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)

- Показательные функции в задаче B15

- Задача B5: площадь кольца

- Случай четырехугольной пирамиды

Задание 1. Линейный оператор ![]() преобразует векторы
преобразует векторы ![]() ,
, ![]() ,
, ![]() в векторы
в векторы ![]() ,
, ![]() ,
, ![]() . Найти матрицу
. Найти матрицу ![]() линейного оператора.
линейного оператора.
Решение. Матрицы
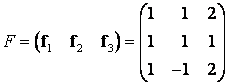 ,
, 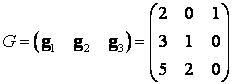 и
и ![]()
Связаны между собой соотношением ![]() , откуда
, откуда ![]() .
.
Так как ![]() , то
, то 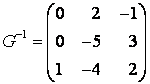 , а искомая матрица линейного оператора
, а искомая матрица линейного оператора 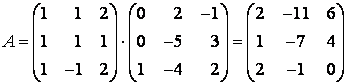 .
.
Ответ: .
Задание 2. Пусть линейный оператор ![]() в базисе
в базисе ![]() задан матрицей
задан матрицей 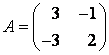 . Найти матрицу
. Найти матрицу ![]() этого линейного оператора в базисе
этого линейного оператора в базисе ![]() , если матрица
, если матрица 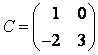 является матрицей перехода от базиса
является матрицей перехода от базиса ![]() к базису
к базису ![]() .
.
Решение. Матрицы ![]() и
и ![]() линейного оператора
линейного оператора ![]() , заданного в разных базисах, связаны между собой соотношением
, заданного в разных базисах, связаны между собой соотношением ![]() . Так как
. Так как 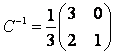 , то
, то
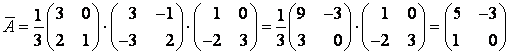 .
.
Ответ: 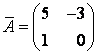 .
.
Задание 3. Линейный оператор ![]() в базисе
в базисе ![]() задан матрицей
задан матрицей 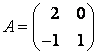 . Найти матрицу
. Найти матрицу ![]() этого линейного оператора в базисе
этого линейного оператора в базисе ![]() , если
, если ![]() ,
, ![]() .
.
Решение. Связь между матрицами ![]() и
и ![]() линейного оператора в разных базисах определяется формулой
линейного оператора в разных базисах определяется формулой ![]() , где
, где ![]() – матрица перехода от базиса
– матрица перехода от базиса ![]() к базису
к базису ![]() .
.
Составим матрицу ![]() :
: 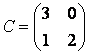 , тогда
, тогда 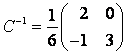 и, следовательно,
и, следовательно,
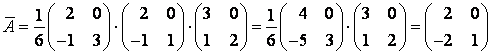 .
.
Ответ: 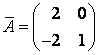 .
.
Задание 4. Линейный оператор ![]() в базисе
в базисе ![]() задан матрицей
задан матрицей  . Найти матрицу
. Найти матрицу ![]() этого линейного оператора в базисе
этого линейного оператора в базисе ![]() , если
, если ![]()
![]() ,
, ![]() .
.
Решение. Матрицы ![]() и
и ![]() связаны между собой соотношением
связаны между собой соотношением ![]() , где
, где ![]() – матрица перехода от базиса
– матрица перехода от базиса ![]() к базису
к базису ![]() .
.
Составим матрицу ![]() :
:  , тогда
, тогда  и, следовательно,
и, следовательно,


Ответ:  .
.
Задание 5. Найти собственные значения и собственные векторы линейного оператора ![]() , заданного в некотором базисе матрицей
, заданного в некотором базисе матрицей 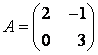 .
.
Решение. Для нахождения собственных значений линейного оператора составим характеристическое уравнение ![]() , т. е.
, т. е. 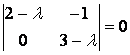 . Раскрывая определитель, получим
. Раскрывая определитель, получим ![]() , т. е.
, т. е. ![]() ,
, ![]() .
.
По определению ![]() называется собственным вектором линейного оператора
называется собственным вектором линейного оператора ![]() , соответствующим собственному значению
, соответствующим собственному значению ![]() , если
, если ![]() .
.
Найдём собственные векторы ![]() и
и ![]() , соответствующие собственным значениям
, соответствующие собственным значениям ![]() и
и ![]() .
.
При ![]() получим:
получим: 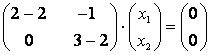 , что равносильно такой однородной системе уравнений:
, что равносильно такой однородной системе уравнений: 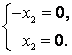
Если ![]() – базисная переменная, а
– базисная переменная, а ![]() – свободная, то
– свободная, то 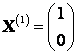 .
.
При ![]() :
: 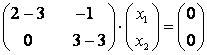 , что равносильно однородной системе уравнений
, что равносильно однородной системе уравнений 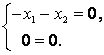
Пусть ![]() – базисная переменная,
– базисная переменная, ![]() – свободная. Примем
– свободная. Примем ![]() , тогда
, тогда ![]() , а следовательно,
, а следовательно,  .
.
Так как собственные векторы соответствуют различным собственным значениям, то они должны быть линейно независимы. Проверим линейную независимость полученных собственных векторов 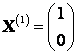 и
и  .
.
Составим матрицу  . Так как
. Так как ![]() , то собственные векторы
, то собственные векторы ![]() и
и ![]() линейно независимы.
линейно независимы.
Ответ: собственные числа ![]() ,
, ![]() ; собственные векторы
; собственные векторы 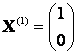 ,
,  .
.
Задание 6. Привести матрицу 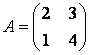 линейного оператора
линейного оператора ![]() к диагональному виду.
к диагональному виду.
Решение. Матрица линейного оператора будет диагональной в базисе из собственных векторов, если такой базис существует. Найдём собственные значения и собственные векторы линейного оператора.
Запишем характеристическое уравнение: 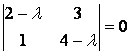 , т. е.
, т. е. ![]() или
или ![]() , откуда получаем
, откуда получаем ![]() ,
, ![]() .
.
Найдём собственные векторы ![]() И
И ![]() .
.
При ![]() получим:
получим:  , что соответствует следующей однородной системе уравнений:
, что соответствует следующей однородной системе уравнений: 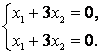
Пусть ![]() – базисная переменная,
– базисная переменная, ![]() – свободная. Полагая
– свободная. Полагая ![]() , получим
, получим 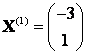 .
.
При ![]() :
: 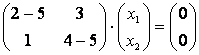 . Соответствующая однородная система уравнений имеет вид:
. Соответствующая однородная система уравнений имеет вид:
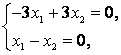
Откуда ![]() . Пусть
. Пусть ![]() – базисная переменная,
– базисная переменная, ![]() – свободная, примем
– свободная, примем ![]() тогда
тогда ![]() , а, следовательно,
, а, следовательно,  .
.
Собственные векторы ![]() и
и ![]() отвечают различным собственным значениям, поэтому они линейно независимы, т. е. могут составить базис. Матрица
отвечают различным собственным значениям, поэтому они линейно независимы, т. е. могут составить базис. Матрица ![]() линейного оператора в базисе из собственных векторов
линейного оператора в базисе из собственных векторов ![]() и
и ![]() имеет диагональный вид:
имеет диагональный вид: 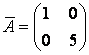 .
.
Можно проверить полученный результат. Так как ![]() , где матрица
, где матрица ![]() в случае перехода к базису из собственных векторов
в случае перехода к базису из собственных векторов 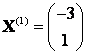 и
и  имеет вид
имеет вид  , следовательно,
, следовательно,
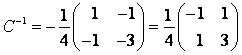 ,
,
Тогда
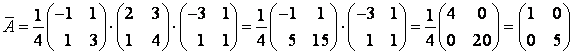 .
.
Ответ: 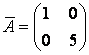 .
.
Задание 7. Найти собственные значения и собственные векторы линейного оператора ![]() , заданного в некотором базисе матрицей
, заданного в некотором базисе матрицей 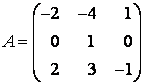 . Построить, если это возможно, базис из собственных векторов и найти матрицу
. Построить, если это возможно, базис из собственных векторов и найти матрицу ![]() этого линейного оператора в базисе из собственных векторов.
этого линейного оператора в базисе из собственных векторов.
Решение. Запишем характеристическое уравнение:
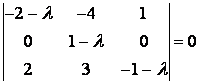 ,
,
Т. е. ![]() ,
, ![]()
![]() , откуда получаем
, откуда получаем ![]() ,
, ![]() ,
, ![]() .
.
Найдём собственные векторы линейного оператора.
При ![]() :
:  , тогда соответствующая однородная система уравнений примет вид:
, тогда соответствующая однородная система уравнений примет вид:
 или
или 
Что равносильно такой системе: 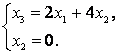
Пусть ![]() и
и ![]() – базисные переменные,
– базисные переменные, ![]() – свободная. Полагая
– свободная. Полагая ![]() , получим
, получим 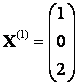 .
.
При ![]() :
: 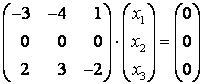 , или, переходя к однородной системе уравнений, получим
, или, переходя к однородной системе уравнений, получим
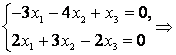
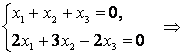
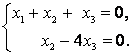
Пусть ![]() и
и ![]() – базисные переменные,
– базисные переменные, ![]() – свободная. Если
– свободная. Если ![]() , то
, то 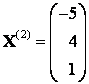 .
.
При ![]() получим:
получим: 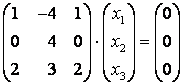 , и однородная система уравнений примет вид:
, и однородная система уравнений примет вид:


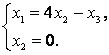
Пусть ![]() и
и ![]() – базисные переменные,
– базисные переменные, ![]() – свободная. Тогда если
– свободная. Тогда если ![]() , то
, то  . Найденные собственные векторы соответствуют различным собственным значениям, поэтому они линейно независимы, значит, существует базис из собственных векторов. Матрица перехода к такому базису
. Найденные собственные векторы соответствуют различным собственным значениям, поэтому они линейно независимы, значит, существует базис из собственных векторов. Матрица перехода к такому базису 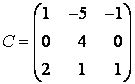 , тогда
, тогда
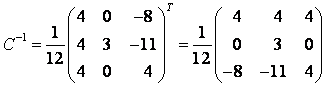 .
.
Матрица ![]() линейного оператора
линейного оператора ![]() в базисе из собственных векторов имеет вид:
в базисе из собственных векторов имеет вид:  .
.
Можно сделать проверку полученных результатов:
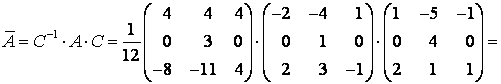

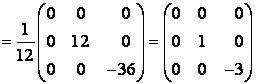 .
.
Ответ: ![]() ,
, ![]() ,
, ![]() ;
; 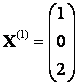 ,
, 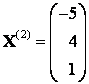 ,
,  ; матрица линейного оператора в базисе из собственных векторов
; матрица линейного оператора в базисе из собственных векторов  .
.
| < Предыдущая | Следующая > |
|---|





