Матрица перехода
3 июля 2022
Матрица перехода — это просто квадратная матрица, в столбцах которой записаны координаты новых базисных векторов. У такой матрицы много важных свойств, которые сформулированы и доказаны в первой части урока — теоретической. Этой теории хватит для любого экзамена или коллоквиума.
Вторая часть урока — практическая. В ней разобраны все типовые задачи, которые встречаются на контрольных, зачётах и экзаменах.
Содержание
- Определение матрицы перехода
- Свойства матрицы перехода
- Теорема о замене координат
- Задача 1. Базисы трёхмерного пространства
- Задача 2. Базисы в поле вычетов
- Задача 3. Пространство многочленов
- Задача 4. Матрица перехода при симметрии
- Задача 5. Матрица поворота
Если вы учитесь в серьёзном университете (МГУ, Бауманка и т.д.), то обязательно изучите первые три пункта. А если вам нужны только задачи, сразу переходите к пункта 4—6.
1. Определение матрицы перехода
Пусть дано $n$-мерное линейное пространство $L$. Пусть также $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — два базиса в $L$.
Определение. Матрица перехода ${{T}_{eto f}}$ от базиса $e=left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ к базису $f=left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — это квадратная матрица порядка $n$, где по столбцам записаны координаты нового базиса $f$ в старом базисе $e$:
[{{T}_{eto f}}=left[ begin{array}{c|c|c|c}{{t}_{1,1}} & {{t}_{2,1}} & cdots & {{t}_{n,1}} \{{t}_{1,2}} & {{t}_{2,2}} & cdots & {{t}_{n,1}} \cdots & cdots & cdots & cdots \{{t}_{1,n}} & {{t}_{2,n}} & cdots & {{t}_{n,n}} \end{array} right]]
Обратите внимание на нумерацию элементов ${{t}_{i,j}}$: первый индекс обозначает номер столбца, т.е. номер нового базисного вектора, а второй отвечает за координаты этого вектора в старом базисе. Так, во втором столбце записаны координаты вектора ${{f}_{2}}$:
[{{f}_{2}}={{left[ {{t}_{2,1}},{{t}_{2,2}},ldots ,{{t}_{2,n}} right]}^{T}}]
Или, что то же самое, разложение вектора ${{f}_{2}}$ по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:
[{{f}_{2}}={{t}_{2,1}}{{e}_{1}}+{{t}_{2,2}}{{e}_{2}}+ldots +{{t}_{2,n}}{{e}_{n}}]
Да, такая нумерация не является обязательной. Но она очень распространена именно в записи матриц перехода: первый индекс отвечает за номер базисного вектора, второй — за номер координаты этого вектора.
Пример 1. В некотором базисе $e=left{ {{e}_{1}},{{e}_{2}},{{e}_{3}} right}$ векторного пространства ${{mathbb{R}}^{3}}$ даны три вектора:
[{{f}_{1}}={{left( 1,0,1 right)}^{T}},quad {{f}_{2}}={{left( 2,1,0 right)}^{T}},quad {{f}_{3}}={{left( 0,3,1 right)}^{T}}]
[begin{align}{{f}_{1}} &={{left( 1,0,1 right)}^{T}}, \ {{f}_{2}} &={{left( 2,1,0 right)}^{T}}, \ {{f}_{3}} &={{left( 0,3,1 right)}^{T}} \ end{align}]
Убедитесь, что система векторов $f=left{ {{f}_{1}},{{f}_{2}},{{f}_{3}} right}$ образует базис в ${{mathbb{R}}^{3}}$, найдите матрицу перехода ${{T}_{eto f}}$.
Решение. Система векторов будет базисом, если эти векторы линейно независимы, а их количество совпадает с размерностью пространства. Поскольку у нас три вектора и $dim{{mathbb{R}}^{3}}=3$, осталось проверить линейную независимость. Составим матрицу из столбцов с координатами векторов ${{f}_{1}}$, ${{f}_{2}}$ и ${{f}_{3}}$:
[left[ begin{matrix}1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]]
Вообще-то это и есть матрица перехода ${{T}_{eto f}}$, но сначала надо установить линейную независимость. Поэтому выполним элементарные преобразования строк:
[left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]begin{matrix} \ \ -1cdot left[ 1 right] \ end{matrix}sim left[ begin{array}{crc} 1 & 2 & 0 \ 0 & 1 & 3 \ 0 & -2 & 1 \ end{array} right]begin{matrix} -2cdot left[ 2 right] \ \ +2cdot left[ 2 right] \ end{matrix}sim left[ begin{array}{ccr} 1 & 0 & -6 \ 0 & 1 & 3 \ 0 & 0 & 7 \ end{array} right]]
[begin{align} & left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]begin{matrix} \ \ -1cdot left[ 1 right] \ end{matrix} \ & left[ begin{array}{crc} 1 & 2 & 0 \ 0 & 1 & 3 \ 0 & -2 & 1 \ end{array} right]begin{matrix} -2cdot left[ 2 right] \ \ +2cdot left[ 2 right] \ end{matrix} \ & left[ begin{array}{ccr} 1 & 0 & -6 \ 0 & 1 & 3 \ 0 & 0 & 7 \ end{array} right] \ end{align}]
Получили верхнетреугольную матрицу без нулей на главной диагонали. Ранг такой матрицы равен 3, поэтому система $left{ {{f}_{1}},{{f}_{2}},{{f}_{3}} right}$ линейно независима и образует базис. Матрица перехода от базиса $e$ к базису $f$ уже известна:
[{{T}_{eto f}}=left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]]
1.1. Зачем нужна матрица перехода
Матрица перехода нужна для того, чтобы компактно и наглядно выражать новый базис через старый. В самом деле, разложим векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ нового базиса по старому базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:
[begin{align}{{f}_{1}} &={{x}_{1,1}}{{e}_{1}}+{{x}_{2,1}}{{e}_{2}}+ldots +{{x}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{x}_{1,2}}{{e}_{1}}+{{x}_{2,2}}{{e}_{2}}+ldots +{{x}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}} &={{x}_{1,n}}{{e}_{1}}+{{x}_{2,n}}{{e}_{2}}+ldots +{{x}_{n,n}}{{e}_{n}} \ end{align}]
Получили систему из $n$ уравнений, которые в матричном виде можно представить так:
[left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1,1}} & cdots & {{x}_{1,n}} \ cdots & cdots & cdots \ {{x}_{n,1}} & cdots & {{x}_{n,n}} \ end{matrix} right]]
[left[ {{f}_{1}} cdots {{f}_{n}} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1,1}} & cdots & {{x}_{1,n}} \ cdots & cdots & cdots \ {{x}_{n,1}} & cdots & {{x}_{n,n}} \ end{matrix} right]]
Обратите внимание: ${{f}_{1}},ldots ,{{f}_{n}}$ и ${{e}_{1}},ldots ,{{e}_{n}}$ — это именно векторы, а не числа. Такие наборы принято записывать строками — в отличие от вектор-столбцов, элементами которых как раз выступают обычные числа.
Последний множитель — это и есть матрица перехода ${{T}_{eto f}}$, поэтому всё произведение можно записать более компактно:
[left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}]
2. Свойства матрицы перехода
Мы разберём три простых свойства, а далее отдельным разделом будет ещё одно — уже более серьёзное.
2.1. Переход от базиса к этому же базису
Свойство 1. При переходе от базиса $e$ к этому же базису $e$ матрица перехода ${{T}_{eto e}}=E$.
Для доказательства достаточно рассмотреть формулы
[begin{align}{{f}_{1}} &={{x}_{1,1}}{{e}_{1}}+{{x}_{2,1}}{{e}_{2}}+ldots +{{x}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{x}_{1,2}}{{e}_{1}}+{{x}_{2,2}}{{e}_{2}}+ldots +{{x}_{n,2}}{{e}_{n}} \ &cdots \ {{f}_{n}} &={{x}_{1,n}}{{e}_{1}}+{{x}_{2,n}}{{e}_{2}}+ldots +{{x}_{n,n}}{{e}_{n}} \ end{align}]
А затем положить ${{f}_{1}}={{e}_{1}}$, ${{f}_{2}}={{e}_{2}}$, …, ${{f}_{n}}={{e}_{n}}$. Тогда:
[begin{align} {{f}_{1}} &={{e}_{1}}=1cdot {{e}_{1}}+0cdot {{e}_{2}}+ldots +0cdot {{e}_{n}} \ {{f}_{2}} &={{e}_{2}}=0cdot {{e}_{1}}+1cdot {{e}_{2}}+ldots +0cdot {{e}_{n}} \ &cdots \ {{f}_{n}} &={{e}_{n}}=0cdot {{e}_{1}}+0cdot {{e}_{2}}+ldots +1cdot {{e}_{n}} \ end{align}]
Указанное выражение однозначно, поскольку $e$ — базис. Следовательно, матрица перехода равна
[{{T}_{eto f}}=left[ begin{array}{c|c|c|c} 1 & 0 & cdots& 0 \ 0 & 1 & cdots& 0 \ cdots& cdots& cdots& cdots \ 0 & 0 & cdots& 1 \ end{array} right]=E]
Итак, ${{T}_{eto f}}=E$, что и требовалось доказать.
2.2. Обратный переход
Свойство 2. Если ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к базису $f$, то ${{T}_{fto e}}={{left( {{T}_{eto f}} right)}^{-1}}$ матрица обратного перехода, от базиса $f$ к базису $e$.
В самом деле, базисы $e$ и $f$ связаны с матрицей перехода по формуле
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}]
Поскольку матрица ${{T}_{eto f}}$ невырожденная, существует обратная к ней матрица ${{left( {{T}_{eto f}} right)}^{-1}}$. Домножим на эту матрицу обе части формулы, связывающей базисы $e$ и $f$:
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{left( {{T}_{eto f}} right)}^{-1}}=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}cdot {{left( {{T}_{eto f}} right)}^{-1}}]
[begin{align}left[ {{f}_{1}},ldots ,{{f}_{n}} right] &cdot {{left( {{T}_{eto f}} right)}^{-1}}= \ &=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}cdot {{left( {{T}_{eto f}} right)}^{-1}} \ end{align}]
Упрощаем эту формулу и получаем
[left[ {{e}_{1}},ldots ,{{e}_{n}} right]=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{left( {{T}_{eto f}} right)}^{-1}}]
Итак, мы получили формулу перехода от базиса $f$ к базису $e$. Следовательно, ${{left( {{T}_{eto f}} right)}^{-1}}$ — матрица такого перехода, что и требовалось доказать.
2.3. Переход через транзитный базис
Пусть ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к базису $f$ линейного пространства $L$, а ${{T}_{fto g}}$ — матрица перехода от базиса $f$ к базису $g$ того же линейного пространства $L$.
Тогда матрица перехода ${{T}_{eto g}}$ от базиса $e$ к базису $g$ находится по формуле
[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}]
Для доказательства достаточно записать формулы для выражения базисов $f$ и $g$, а затем подставить одну формулу в другую. По условию теоремы, базис $f$ выражается через базис $e$ по формуле
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}]
Кроме того, базис $g$ выражается через базис $f$ по формуле
[left[ {{g}_{1}},ldots ,{{g}_{n}} right]=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}]
Подставим первое выражение во второе и получим
[begin{align}left[ {{g}_{1}},ldots ,{{g}_{n}} right] &=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}= \ &=left( left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}} right)cdot {{T}_{fto g}}= \ & =left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot left( {{T}_{eto f}}cdot {{T}_{fto g}} right) end{align}]
[begin{align}& left[ {{g}_{1}},ldots ,{{g}_{n}} right]= \ =& left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}= \ =& left( left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}} right)cdot {{T}_{fto g}}= \ =& left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot left( {{T}_{eto f}}cdot {{T}_{fto g}} right) end{align}]
Мы получили прямое выражение базиса $g$ через базис $e$, причём матрица перехода равна
[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}]
Это именно та формула, которую и требовалось доказать.
2.4. Невырожденные матрицы
И ещё одно важное свойство:
Свойство 4. Пусть дана произвольная квадратная невырожденная матрица
[T=left[ begin{matrix}{{a}_{1,1}} & {{a}_{1,2}} & cdots & {{a}_{1,n}} \ {{a}_{2,1}} & {{a}_{2,2}} & cdots & {{a}_{2,n}} \ cdots & cdots & cdots & cdots \ {{a}_{n,1}} & {{a}_{n,2}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
Пусть $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ — произвольный базис линейного пространства $L$. Тогда система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$, полученных по формуле
[begin{align}{{f}_{1}}&={{a}_{1,1}}{{e}_{1}}+{{a}_{2,1}}{{e}_{2}}+ldots +{{a}_{n,1}}{{e}_{n}} \ {{f}_{2}}&={{a}_{1,2}}{{e}_{1}}+{{a}_{2,2}}{{e}_{2}}+ldots +{{a}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}}&={{a}_{1,n}}{{e}_{1}}+{{a}_{2,n}}{{e}_{2}}+ldots +{{a}_{n,n}}{{e}_{n}} \ end{align}]
тоже будет базисом $L$.
Иначе говоря, всякая квадратная невырожденная матрица $T$ является матрицей перехода от данного базиса $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ к некоторому новому базису $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ линейного пространства $L$.
Обратите внимание: поскольку изначально мы не знаем, что $T$ — матрица перехода, её элементы пронумерованы стандартным образом: первый индекс отвечает за строку, а второй — за столбец. Однако это нисколько не помешает нам доказать теорему.
Для доказательства того, что $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — базис линейного пространства $L$, нужно доказать два утверждения:
- 1.Система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — линейно независима.
- 2.Ранг этой системы векторов совпадает с размерностью пространства $L$.
Поскольку количество векторов в системе $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ совпадает с количеством базисных векторов $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$, т.е. равно $n=dim L$, достаточно лишь проверить линейную независимость.
Рассмотрим линейную комбинацию векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ и предположим, что она равна нулю:
[{{lambda }_{1}}{{f}_{1}}+{{lambda }_{2}}{{f}_{2}}+ldots +{{lambda }_{n}}{{f}_{n}}=0]
В матричном виде это выглядит так:
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot left[ begin{align}& {{lambda }_{1}} \ & cdots\ & {{lambda }_{n}} \ end{align} right]=0]
По условию теоремы векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ раскладываются по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ с коэффициентами, записанными в столбцах матрицы $T$. В матричном виде это выглядит так:
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot T]
Подставляем полученное выражение для $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ в предыдущее матричное уравнение и получаем
[left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot Tcdot left[ begin{align}& {{lambda }_{1}} \ & cdots \ & {{lambda }_{n}} \ end{align} right]=0]
Поскольку $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ — базис линейного пространства $L$, такое равенство возможно лишь при условии
[Tcdot left[ begin{matrix} {{lambda }_{1}} \ cdots \ {{lambda }_{n}} \ end{matrix} right]=left[ begin{matrix} 0 \ cdots \ 0 \ end{matrix} right]]
Это матричное уравнение можно рассматривать как систему из $n$ однородных уравнений относительно переменных ${{lambda }_{1}},ldots ,{{lambda }_{n}}$. И поскольку по условию теоремы матрица $T$ невырожденная, это СЛАУ имеет лишь одно решение — тривиальное:
[{{lambda }_{1}}={{lambda }_{2}}=ldots ={{lambda }_{n}}=0]
Получаем, что система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ линейно независима, а количество векторов совпадает с размерностью линейного пространства $L$. Следовательно, эта система — базис, что и требовалось доказать.
3. Замена координат в новом базисе
До сих пор мы рассуждали лишь о том, как координаты новых базисных векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ выражаются через координаты старых базисных векторов $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$. Но что будет с координатами одного и того же вектора линейного пространства $L$ при переходе от одного базиса к другому?
Ответ даёт следующая теорема.
3.1. Формулировка теоремы
Теорема. Пусть $e=left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $f=left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — базисы линейного пространства $L$ над полем $K$. Пусть ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к $f$:
[{{T}_{eto f}}=left[ begin{matrix}{{a}_{1,1}} & cdots& {{a}_{1,n}} \ cdots& cdots& cdots \ {{a}_{n,1}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
Тогда координаты произвольного вектора $hin L$ пересчитываются по формуле
[{{left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]}_{e}}={{T}_{eto f}}cdot {{left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]}_{f}}]
Ещё раз: если произвольный вектор $hin L$ в новом базисе $f$ имеет координаты
[{{left[ h right]}_{f}}=left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
то в старом базисе $e$ этот же вектор $hin L$ имеет координаты
[{{left[ h right]}_{e}}=left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]={{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Т.е. для векторов всё наоборот: не новые координаты выражаются через старые, а старые — через новые. Впрочем, никто не мешает найти матрицу $T_{eto f}^{-1}$ и записать
[left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]=T_{eto f}^{-1}cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]]
Но такая запись предполагает дополнительное действие — нахождение обратной матрицы.
3.2. Доказательство
Сначала «соберём» матрицу ${{T}_{eto f}}$. Для этого разложим векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:
[left{ begin{align}{{f}_{1}} &={{a}_{1,1}}{{e}_{1}}+{{a}_{2,1}}{{e}_{2}}+ldots +{{a}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{a}_{1,2}}{{e}_{1}}+{{a}_{2,2}}{{e}_{2}}+ldots +{{a}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}} &={{a}_{1,n}}{{e}_{1}} +{{a}_{2,n}}{{e}_{2}}+ldots +{{a}_{n,n}}{{e}_{n}} \ end{align} right.]
В матричной форме эту систему линейных уравнений можно записать так:
[left[ begin{matrix} {{f}_{1}} \ {{f}_{2}} \ cdots \ {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{a}_{1,1}} & {{a}_{2,1}} & cdots & {{a}_{n,1}} \ {{a}_{1,2}} & {{a}_{2,2}} & cdots & {{a}_{n,2}} \ cdots & cdots & cdots & cdots \ {{a}_{1,n}} & {{a}_{2,n}} & cdots & {{a}_{n,n}} \ end{matrix} right]cdot left[ begin{matrix} {{e}_{1}} \ {{e}_{2}} \ cdots \ {{e}_{n}} \ end{matrix} right]]
Транспонируем обе стороны равенства, учитывая, что произведение справа транспонируется по правилу ${{left( Acdot B right)}^{T}}={{B}^{T}}cdot {{A}^{T}}$:
[left[ begin{matrix}{{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{a}_{1,1}} & {{a}_{1,2}} & cdots & {{a}_{1,n}} \ {{a}_{2,1}} & {{a}_{2,2}} & cdots & {{a}_{2,n}} \ cdots & cdots & cdots & cdots \ {{a}_{n,1}} & {{a}_{n,2}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
[left[ {{f}_{1}} cdots {{f}_{n}} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{a}_{1,1}} & cdots & {{a}_{1,n}} \ cdots & cdots & cdots \ {{a}_{n,1}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
Квадратная матрица справа — это и есть матрица перехода ${{T}_{eto f}}$. Поэтому матричное уравнение можно переписать так:
[left[ begin{matrix}{{f}_{1}} & cdots& {{f}_{n}} \ end{matrix} right]=left[ begin{matrix}{{e}_{1}} & cdots& {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}]
Теперь возьмём произвольный вектор $hin L$ и разложим его по базисам $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$:
[begin{align}h &={{x}_{1}}{{e}_{1}}+{{x}_{2}}{{e}_{2}}+ldots +{{x}_{n}}{{e}_{n}}= \ &={{y}_{1}}{{f}_{1}}+{{y}_{2}}{{f}_{2}}+ldots +{{y}_{n}}{{f}_{n}} end{align}]
Вновь перейдём к матричной форме. Сначала учтём, что координаты векторов принято записывать в виде вектор-столбцов:
[{{left[ h right]}_{e}}=left[ begin{matrix} {{x}_{1}} \ {{x}_{2}} \ cdots \ {{x}_{n}} \ end{matrix} right]quad {{left[ h right]}_{f}}=left[ begin{matrix} {{y}_{1}} \ {{y}_{2}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Тогда левую и правую часть уравнения можно представить как произведение строк с базисными векторами и указанных вектор-столбцов с координатами:
[left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
[left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ {{f}_{1}} cdots {{f}_{n}} right]cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Но выше мы выражали строку векторов $left[ {{f}_{1}},ldots ,{{f}_{n}} right]$ через строку $left[ {{e}_{1}},ldots ,{{e}_{n}} right]$ и матрицу перехода ${{T}_{eto f}}$. Подставим это выражение в наше матричное уравнение:
[left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
[left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot {{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Уберём слева и справа первый множитель — строку $left[ {{e}_{1}},ldots ,{{e}_{n}} right]$. Получим уравнение, связывающее координаты вектора в разных базисах:
[left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]={{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Это именно та формула, которую и требовалось доказать.
Задача 1. Базисы трёхмерного пространства
Задача. Убедитесь, что системы векторов
[{{a}_{1}}={{left( 1,2,1 right)}^{T}},quad {{a}_{2}}={{left( 2,3,2 right)}^{T}},quad {{a}_{3}}={{left( 1,-1,2 right)}^{T}}]
[begin{align}{{a}_{1}} &={{left( 1,2,1 right)}^{T}}, \ {{a}_{2}} &={{left( 2,3,2 right)}^{T}}, \ {{a}_{3}} &={{left( 1,-1,2 right)}^{T}} \ end{align}]
и
[{{b}_{1}}={{left( 1,3,1 right)}^{T}},quad {{b}_{2}}={{left( 1,-1,3 right)}^{T}},quad {{b}_{3}}={{left( 2,2,1 right)}^{T}}]
[begin{align}{{b}_{1}} &={{left( 1,3,1 right)}^{T}}, \ {{b}_{2}} &={{left( 1,-1,3 right)}^{T}}, \ {{b}_{3}} &={{left( 2,2,1 right)}^{T}} \ end{align}]
являются базисами в векторном пространстве ${{mathbb{R}}^{3}}$. Найдите матрицу перехода ${{T}_{ato b}}$. Найдите координаты в базисе $a$ вектора $x$, который в базисе $b$ имеет координаты ${{left( 0,3,2 right)}^{T}}$.
Решение
Чтобы доказать, что система векторов образует базис, достаточно составить матрицу $A$ из координат этих векторов, а затем вычислить её определитель $det A$. И если $det Ane 0$, то векторы линейно независимы. А поскольку их количество совпадает с размерностью линейного пространства, такие векторы образуют базис.
Рассмотрим систему векторов $a=left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$. Составим из них матрицу, расположив координаты по столбцам. Получим матрицу перехода ${{T}_{eto a}}$ от некого исходного базиса $e$ (в котором как раз и даны координаты векторов ${{a}_{i}}$ и ${{b}_{i}}$ в условии задачи) к базису $a$:
[{{T}_{eto a}}=left[ begin{array}{ccr} 1 & 2 & 1 \ 2 & 3 & -1 \ 1 & 2 & 2 \ end{array} right]]
Определитель этой матрицы отличен от нуля:
[det {{T}_{eto a}}=-1ne 0]
Следовательно, $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ — базис пространства ${{mathbb{R}}^{3}}$.
Теперь составим матрицу из векторов $b=left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$. Получим матрицу перехода ${{T}_{eto b}}$:
[{{T}_{eto b}}=left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right]]
Определитель этой матрицы вновь отличен от нуля:
[det {{T}_{eto b}}=12ne 0]
Следовательно, $left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ — тоже базис пространства ${{mathbb{R}}^{3}}$.
Осталось найти матрицу перехода ${{T}_{ato b}}$. Заметим, что эту матрицу можно выразить так:
[begin{align}{{T}_{ato b}} &={{T}_{ato e}}cdot {{T}_{eto b}}= \ &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}end{align}]
Мы внедрили «транзитный» базис $e$ и вместо прямого перехода $ato b$ рассмотрели цепочку $ato eto b$. Это стандартный и очень распространённый приём, но из-за этого появился новый элемент $T_{eto a}^{-1}$ — матрица, обратная к ${{T}_{eto a}}$. Найдём $T_{eto a}^{-1}$ методом присоединённой матрицы:
[left[ {{T}_{eto a}}|E right]sim ldots sim left[ E|T_{eto a}^{-1} right]]
Напомню, что элементарные преобразования в присоединённых матрицах выполняются только над строками. Если вы забыли, как всё это работает, см. урок «Обратная матрица». В нашем случае получим:
[left[ begin{array}{ccr|ccc}1 & 2 & 1 & 1 & 0 & 0 \ 2 & 3 & -1 & 0 & 1 & 0 \ 1 & 2 & 2 & 0 & 0 & 1 \end{array} right]begin{matrix} , \ -2cdot left[ 1 right] \ -1cdot left[ 1 right] \ end{matrix}]
Мы «зачистили» первый столбец. Теперь «зачистим» последний:
[left[ begin{array}{crr|rcc} 1 & 2 & 1 & 1 & 0 & 0 \ 0 & -1 & -3 & -2 & 1 & 0 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]begin{matrix} -1cdot left[ 3 right] \ +3cdot left[ 3 right] \ , \ end{matrix}]
Остался лишь средний. Разберёмся и с ним:
[left[ begin{array}{crc|rcr} 1 & 2 & 0 & 2 & 0 & -1 \ 0 & -1 & 0 & -5 & 1 & 3 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]begin{matrix} +2cdot left[ 2 right] \ |cdot left( -1 right) \ , \ end{matrix}]
Получили единичную матрицу слева от вертикальной черты. Значит, справа стоит искомая матрица $T_{eto a}^{-1}$:
[left[ begin{array}{ccc|rrr} 1 & 0 & 0 & -8 & 2 & 5 \ 0 & 1 & 0 & 5 & -1 & -3 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]]
Теперь у нас есть всё, чтобы найти матрицу перехода ${{T}_{ato b}}$:
[{{T}_{ato b}}={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}=left[ begin{array}{rrr} -8 & 2 & 5 \ 5 & -1 & -3 \ -1 & 0 & 1 \ end{array} right]cdot left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right]]
[begin{align}{{T}_{ato b}} &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}= \ &=left[ begin{array}{rrr} -8 & 2 & 5 \ 5 & -1 & -3 \ -1 & 0 & 1 \ end{array} right]cdot left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right] end{align}]
После несложных вычислений получаем матрицу перехода от базиса $a$ к базису $b$:
[{{T}_{ato b}}=left[ begin{array}{rrr} 3 & 5 & -7 \ -1 & -3 & 5 \ 0 & 2 & -1 \ end{array} right]]
Осталось найти координаты вектора $x$, который в базисе $b$ имеет координаты ${{left( 0,3,2 right)}^{T}}$. Вспомним формулу, выражающую координаты в старом базисе через координаты в новом базисе:
[{{left[ x right]}_{a}}={{T}_{ato b}}cdot {{left[ x right]}_{b}}]
Подставляем в эту формулу матрицу ${{T}_{ato b}}$ и вектор-столбец ${{left[ x right]}_{b}}={{left[ 0,3,2 right]}^{T}}$:
[{{left[ x right]}_{a}}=left[ begin{array}{rrr} 3 & 5 & -7 \ -1 & -3 & 5 \ 0 & 2 & -1 \ end{array} right]cdot left[ begin{matrix} 0 \ 3 \ 2 \ end{matrix} right]=left[ begin{matrix} 1 \ 1 \ 4 \ end{matrix} right]]
Итак, вектор $x$ в базисе $a$ имеет координаты ${{left( 1,1,4 right)}^{T}}$. Задача решена.
Альтернативное решение
Можно найти матрицу ${{T}_{ato b}}$ заметно быстрее, если использовать алгоритм решения матричных уравнений. Заметим, что нам требуется найти произведение
[{{T}_{ato b}}={{A}^{-1}}cdot B]
С другой стороны, для нахождения такого произведения достаточно составить присоединённую матрицу вида $left[ A|B right]$ и цепочкой элементарных преобразований свести её к виду
[left[ A|B right]sim ldots sim left[ E|{{A}^{-1}}cdot B right]]
Другими словами, справа от вертикальной черты мы получим искомую матрицу перехода ${{T}_{ato b}}$!
На практике это выглядит так. Записываем присоединённую матрицу $left[ A|B right]$:
[left[ begin{array}{ccr|crc} 1 & 2 & 1 & 1 & 1 & 2 \ 2 & 3 & -1 & 3 & -1 & 2 \ 1 & 2 & 2 & 1 & 2 & 1 \ end{array} right]]
И после элементарных преобразований получим
[left[ begin{array}{ccc|rrr} 1 & 0 & 0 & 3 & 5 & -7 \ 0 & 1 & 0 & -1 & -3 & 5 \ 0 & 0 & 1 & 0 & 2 & -1 \ end{array} right]]
Для экономии места я пропустил промежуточные шаги. Попробуйте сделать их самостоятельно — это очень полезная практика.
Если же вы хотите разобраться, как это работает (и почему вдруг справа возникает матрица вида ${{A}^{-1}}cdot B$), см. урок «Матричные уравнения». А мы идём дальше.
Задача 2. Базисы в поле вычетов
Найдите матрицу перехода от базиса
[{{a}_{1}}={{left( 1,1,1 right)}^{T}},quad {{a}_{2}}={{left( 2,1,1 right)}^{T}},quad {{a}_{3}}={{left( 3,2,1 right)}^{T}}]
[begin{align}{{a}_{1}} &={{left( 1,1,1 right)}^{T}}, \ {{a}_{2}} &={{left( 2,1,1 right)}^{T}}, \ {{a}_{3}} &={{left( 3,2,1 right)}^{T}} \ end{align}]
к базису
[{{b}_{1}}={{left( 0,4,3 right)}^{T}},quad {{b}_{2}}={{left( 3,3,2 right)}^{T}},quad {{b}_{3}}={{left( 2,2,1 right)}^{T}}]
[begin{align}{{b}_{1}} &={{left( 0,4,3 right)}^{T}}, \ {{b}_{2}} &={{left( 3,3,2 right)}^{T}}, \ {{b}_{3}} &={{left( 2,2,1 right)}^{T}} \ end{align}]
арифметического линейного пространства $mathbb{Z}_{5}^{3}$.
Решение
Эта задача проще предыдущей, поскольку поле вычетов ${{mathbb{Z}}_{5}}$ является конечным и состоит всего из пяти элементов — представителей смежных классов:
[{{mathbb{Z}}_{5}}=left{ 0,1,2,3,4 right}]
Как и в предыдущей задаче, рассмотрим систему векторов $a=left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ и составим из них матрицу ${{T}_{eto a}}$:
[{{T}_{eto a}}=left[ begin{matrix} 1 & 2 & 3 \ 1 & 1 & 2 \ 1 & 1 & 1 \ end{matrix} right]]
Определитель $det {{T}_{eto a}}=1ne 0$, поэтому $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ — базис.
Аналогично, рассмотрим систему $b=left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ и составим матрицу ${{T}_{eto b}}$:
[{{T}_{eto b}}=left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]]
Определитель $det {{T}_{eto b}}=4ne 0$, поэтому $left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ — базис.
Выразим искомую матрицу ${{T}_{ato b}}$ через «транзитный» базис $e$:
[begin{align}{{T}_{ato b}} &={{T}_{ato e}}cdot {{T}_{eto b}}= \ &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}} end{align}]
Найдём $T_{eto a}^{-1}$ через присоединённую матрицу:
[left[ begin{array}{ccc|ccc} 1 & 2 & 3 & 1 & 0 & 0 \ 1 & 1 & 2 & 0 & 1 & 0 \ 1 & 1 & 1 & 0 & 0 & 1 \ end{array} right]]
После цепочки элементарных преобразований над строками (попробуйте выполнить их самостоятельно!) получим
[left[ begin{array}{ccc|ccc} 1 & 0 & 0 & 4 & 1 & 1 \ 0 & 1 & 0 & 1 & 3 & 1 \ 0 & 0 & 1 & 0 & 1 & 4 \ end{array} right]]
Итак, мы нашли матрицу $T_{eto a}^{-1}$:
[T_{eto a}^{-1}=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]]
Осталось вычислить искомую матрицу перехода ${{T}_{ato b}}$:
[{{T}_{ato b}}={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]cdot left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]=left[ begin{matrix} 2 & 2 & 1 \ 0 & 4 & 4 \ 1 & 1 & 1 \ end{matrix} right]]
[begin{align}{{T}_{ato b}} &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}= \ &=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]cdot left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]= \ &=left[ begin{matrix} 2 & 2 & 1 \ 0 & 4 & 4 \ 1 & 1 & 1 \ end{matrix} right] end{align}]
По аналогии с предыдущей задачей, матрицу ${{T}_{ato b}}$ можно найти и через элементарные преобразования присоединённой матрицы $left[ A|B right]$. Результат будет точно такой же, но мы сэкономим пару строк вычислений и несколько минут времени.
Задача 3. Пространство многочленов
Убедитесь, что системы многочленов
[begin{align}e &=left{ 1,t-1,{{left( t-1 right)}^{2}} right} \ f &=left( 1,t+1,{{left( t+1 right)}^{2}} right) \ end{align}]
являются базисами в пространстве ${{P}_{3}}$ многочленов степени не выше 2. Найдите матрицу перехода ${{T}_{eto f}}$. Разложите по степеням $left( t-1 right)$ многочлен ${{left( t+1 right)}^{2}}+left( t+1 right)+1$.
Решение
Стандартным базисом в пространстве многочленов является система многочленов $p=left{ {{p}_{1}},{{p}_{2}},{{p}_{3}} right}$, где
[{{p}_{1}}=1quad {{p}_{2}}=tquad {{p}_{3}}={{t}^{2}}]
Выразим через базис $p$ многочлены из системы $e$:
[begin{align} & {{e}_{1}}=1={{p}_{1}} \ & {{e}_{2}}=t-1={{p}_{2}}-{{p}_{1}} \ & {{e}_{3}}={{left( t-1 right)}^{2}}={{t}^{2}}-2t+1={{p}_{3}}-2{{p}_{2}}+{{p}_{1}} end{align}]
[begin{align}{{e}_{1}} &=1={{p}_{1}} \ {{e}_{2}} &=t-1={{p}_{2}}-{{p}_{1}} \ {{e}_{3}} &={{left( t-1 right)}^{2}}= \ &={{t}^{2}}-2t+1= \ &={{p}_{3}}-2{{p}_{2}}+{{p}_{1}} end{align}]
Следовательно, матрица перехода ${{T}_{pto e}}$ выглядит так:
[{{T}_{pto e}}=left[ begin{array}{crr} 1 & -1 & 1 \ 0 & 1 & -2 \ 0 & 0 & 1 \ end{array} right]]
Аналогично, выразим через базис $p$ многочлены из системы $f$:
[begin{align} & {{f}_{1}}=1={{p}_{1}} \ & {{f}_{2}}=t+1={{p}_{2}}+{{p}_{1}} \ & {{f}_{3}}={{left( t+1 right)}^{2}}={{t}^{2}}+2t+1={{p}_{3}}+2{{p}_{2}}+{{p}_{1}} end{align}]
[begin{align}{{f}_{1}} &=1={{p}_{1}} \ {{f}_{2}} &=t+1={{p}_{2}}+{{p}_{1}} \ {{f}_{3}} &={{left( t+1 right)}^{2}}= \ &={{t}^{2}}+2t+1= \ &={{p}_{3}}+2{{p}_{2}}+{{p}_{1}} end{align}]
Получим матрицу перехода ${{T}_{pto f}}$:
[{{T}_{pto f}}=left[ begin{matrix} 1 & 1 & 1 \ 0 & 1 & 2 \ 0 & 0 & 1 \ end{matrix} right]]
Обе матрицы оказались верхнетреугольными, их определители отличны от нуля:
[begin{align} det {{T}_{pto e}} &=1cdot 1cdot 1=1 \ det {{T}_{pto f}} &=1cdot 1cdot 1=1 \ end{align}]
Следовательно системы многочленов $e$ и $f$ действительно являются базисами пространства ${{P}_{3}}$.
Теперь найдём матрицу перехода ${{T}_{eto f}}$. Для этого нам даже не потребуется искать обратную матрицу. Достаточно заметить, что векторы ${{f}_{1}}$ и ${{f}_{2}}$ легко раскладываются по базису $e$:
[begin{align}{{f}_{1}} &=1={{e}_{1}} \ {{f}_{2}} &=t+1=left( t-1 right)+2={{e}_{2}}+2{{e}_{1}} \ end{align}]
С вектором ${{f}_{3}}$ вычислений будет чуть больше:
[begin{align}{{f}_{3}} &={{left( t+1 right)}^{2}}= \ &={{left( t-1 right)}^{2}}+4t= \ &={{left( t-1 right)}^{2}}+4left( t-1 right)+4= \ &={{e}_{3}}+4{{e}_{2}}+4{{e}_{1}} end{align}]
Итого матрица перехода ${{T}_{eto f}}$ примет вид
[{{T}_{eto f}}=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]]
Теперь разложим многочлен ${{left( t+1 right)}^{2}}+left( t+1 right)+1$ по базису $e$. Сначала перепишем этот многочлен так:
[begin{align}hleft( t right) &=1+left( t+1 right)+{{left( t+1 right)}^{2}}= \ &={{f}_{1}}+{{f}_{2}}+{{f}_{3}} end{align}]
Следовательно, в базисе $f$ многочлен $hleft( t right)$ имеет координаты ${{left( 1,1,1 right)}^{T}}$. Но тогда по теореме о замене координат этот же многочлен в базисе $e$ имеет координаты
[{{left[ h right]}_{e}}={{T}_{eto f}}cdot {{left[ h right]}_{f}}=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]cdot left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{matrix} 7 \ 5 \ 1 \ end{matrix} right]]
[begin{align}{{left[ h right]}_{e}} &={{T}_{eto f}}cdot {{left[ h right]}_{f}}= \ &=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]cdot left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{matrix} 7 \ 5 \ 1 \ end{matrix} right] end{align}]
Другими словами, многочлен $hleft( t right)$ имеет вид
[hleft( t right)={{left( t-1 right)}^{2}}+5left( t-1 right)+7]
Это и есть искомое разложение многочлена ${{left( t+1 right)}^{2}}+left( t+1 right)+1$ по степеням $left( t-1 right)$.
Альтернативное решение
Искомое разложение можно получить и без привлечения матриц перехода. Достаточно применить схему Горнера или выделить нужные степени напрямую:
[begin{align}hleft( t right) &={{left( t+1 right)}^{2}}+left( t+1 right)+1= \ &={{left( t-1 right)}^{2}}+4t+t+1+1= \ &={{left( t-1 right)}^{2}}+5left( t-1 right)+5+2= \ &={{left( t-1 right)}^{2}}+5left( t-1 right)+7 end{align}]
Как видим, результат получился тем же самым, а времени потрачено меньше. Однако уже в пространстве ${{P}_{4}}$ многочленов степени не выше 4 сложность решения через матрицы и через выделение степеней будет сопоставимой. А дальше матрицы начнут выигрывать.
Смысл линейной алгебры — дать универсальные алгоритмы, которые работают с объектами любой природы, если эти объекты подчиняются аксиомам линейного пространства.
Задача 4. Матрица перехода при симметрии
Базис $b$получается из базиса
[{{a}_{1}}={{left( 2,1,3 right)}^{T}},quad {{a}_{2}}={{left( 1,1,-1 right)}^{T}},quad {{a}_{3}}={{left( 2,-1,-1 right)}^{T}}]
[begin{align}{{a}_{1}} &={{left( 2,1,3 right)}^{T}}, \ {{a}_{2}} &={{left( 1,1,-1 right)}^{T}}, \ {{a}_{3}} &={{left( 2,-1,-1 right)}^{T}} \ end{align}]
пространства ${{V}_{3}}$ симметрией относительно плоскости $2x+y+3z=0$. Найти матрицу перехода ${{T}_{ato b}}$.
Решение
Из курса аналитической геометрии мы знаем, что если плоскость задана уравнением
[ax+by+cz+d=0]
то вектор-нормаль $n$ имеет координаты
[n=left( a,b,c right)]
Тогда для плоскости $2x+y+3z=0$ нормаль имеет координаты $n=left( 2,1,3 right)$, что в точности совпадает с вектором ${{a}_{1}}$. Следовательно, при симметрии относительно плоскости этот вектор просто перейдёт в противоположный: ${{b}_{1}}=-{{a}_{1}}$.
Далее заметим, что векторы ${{a}_{2}}$ и ${{a}_{3}}$ лежат в плоскости симметрии, поскольку при подстановке их координат уравнение плоскости обращается в верное числовое равенство:
[begin{align}{{a}_{2}}={{left( 1,1,-1 right)}^{T}} &Rightarrow 2cdot 1+1+3cdot left( -1 right)=0 \ {{a}_{3}}={{left( 2,-1,-1 right)}^{T}} &Rightarrow 2cdot 2-1+3cdot left( -1 right)=0 \ end{align}]
[begin{align}{{a}_{2}}=&{{left( 1,1,-1 right)}^{T}}Rightarrow \ & Rightarrow 2cdot 1+1+3cdot left( -1 right)=0 \ {{a}_{3}}=&{{left( 2,-1,-1 right)}^{T}}Rightarrow \ & Rightarrow 2cdot 2-1+3cdot left( -1 right)=0 \ end{align}]
Следовательно, при симметрии эти векторы переходят сами в себя: ${{b}_{2}}={{a}_{2}}$, ${{b}_{3}}={{a}_{3}}$. Матрица перехода имеет вид
[{{T}_{ato b}}=left[ begin{array}{rcc} -1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \ end{array} right]]
Важное замечание. симметрия предполагает использование проекций и углов, что в конечном счёте сводится к скалярному произведению. Однако мы пока не знаем, что такое скалярное произведение в линейном пространстве.
Полноценное определение скалярного произведения будет намного позже — см. урок «Евклидово пространство». А пока будем считать, что скалярное произведение векторов $a$ и $b$ определено стандартным образом:
[left( a,b right)=left| a right|cdot left| b right|cdot cos alpha ]
Геометрическая интерпретация
Симметрию на плоскости и в пространстве удобно представлять графически. Пусть $alpha $ — плоскость, относительно которой выполняется симметрия. Тогда векторы $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ будут выглядеть так:
Из приведённого рисунка сразу видно, что при симметрии вектор ${{a}_{1}}$ перейдёт в противоположный, а векторы ${{a}_{2}}$ и ${{a}_{3}}$ останутся на месте.
Задача 5. Матрица поворота
Базис $e=left{ i,j,k right}$ пространства ${{V}_{3}}$ поворачивается на 180° вокруг прямой $l$, заданной системой
[left{ begin{align}x-y &=0 \ z &=0 \ end{align} right.]
Затем полученный базис $f$ поворачивается на 90° в отрицательном направлении вокруг нового положения вектора $j$. В результате получается базис $g=left{ {{i}_{2}},{{j}_{2}},{{k}_{2}} right}$.
Найдите матрицу перехода ${{T}_{eto g}}$. Найдите в базисе $e$ координаты вектора $h$, который в новом базисе $g$ имеет координаты $left( 1,1,1 right)$.
Решение
Вращение базиса и матрица поворота — это очень важная тема, по которой есть отдельный урок — «Матрица поворота». Но сейчас вращение совсем простое, поэтому обойдёмся без специальных матриц.
Вновь обратимся к геометрической интерпретации. Рассмотрим исходный базис $e=left{ i,j,k right}$ трёхмерного пространства:
Также на этом рисунке изображена прямая $l$, которая задаётся требованиями $z=0$ и $x=y$. Эта лежит в плоскости $Oxy$ и является биссектрисой первой координатной четверти.
Очевидно, что при повороте пространства на 180° относительно прямой $l$ базисные векторы $i$ и $j$ просто поменяются местами, а вектор $k$ перейдёт в противоположный:
Другими словами, ${{i}_{1}}=j$, ${{j}_{1}}=i$, ${{k}_{1}}=-k$, поэтому матрица перехода от базиса $e=left{ i,j,k right}$ к базису $f=left{ {{i}_{1}},{{j}_{1}},{{k}_{1}} right}$ примет вид
[{{T}_{eto f}}=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]]
Далее поворот осуществляется вокруг нового положения вектора $j$, т.е. вокруг вектора ${{j}_{1}}$. Вновь обратимся к чертежу. В этот раз нам уже не нужны координатные оси — нас интересуют лишь векторы ${{i}_{1}}$, ${{j}_{1}}$ и ${{k}_{1}}$, а также ось вращения:
Обратите внимание: в задаче сказано, что базис вращается на 90° в отрицательном направлении. Если мы смотрим на плоскость, образованную векторами ${{i}_{1}}$ и ${{k}_{1}}$, с вершины вектора ${{j}_{1}}$ (как на картинке), то отрицательное направление — это по часовой стрелке (отмечено зелёным), а положительное —против часовой стрелки (отмечено красным).
Все эти тонкости (положительное и отрицательное направление, правые и левые тройки векторов) детально описаны в уроке про матрицы поворота. Сейчас не будем подробно разбираться в них, а просто нарисуем результат:
Итак, ${{i}_{2}}={{k}_{1}}$, ${{j}_{2}}={{j}_{1}}$ и ${{k}_{2}}=-{{i}_{1}}$, поэтому матрица перехода от базиса $f=left{ {{i}_{1}},{{j}_{1}},{{k}_{1}} right}$ к базису $g=left{ {{i}_{2}},{{j}_{2}},{{k}_{2}} right}$ имеет вид
[{{T}_{fto g}}=left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]]
Теперь мы можем найти матрицу ${{T}_{eto g}}$ через транзитный базис $f$:
[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]cdot left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right]]
[begin{align}{{T}_{eto g}} &={{T}_{eto f}}cdot {{T}_{fto g}}= \ &=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]cdot left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]= \ &=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right] end{align}]
Кроме того, нам известны координаты вектора $h$ в базисе $g$:
[h={{left( 1,1,1 right)}^{T}}]
Тогда в базисе $e$ координаты этого же вектора равны
[{{left[ h right]}_{e}}={{T}_{eto g}}cdot {{left[ h right]}_{g}}=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right].left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{array}{r} 1 \ -1 \ -1 \ end{array} right]]
[begin{align}{{left[ h right]}_{e}} &={{T}_{eto g}}cdot {{left[ h right]}_{g}}= \ &=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right].left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{array}{r} 1 \ -1 \ -1 \ end{array} right] end{align}]
Итак, мы нашли матрицу перехода ${{T}_{eto g}}$ и координаты вектора $h$ в исходном базисе. Задача решена.
Смотрите также:
- Критерий Сильвестра для квадратичных функций
- Работа с формулами в задаче B12
- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
- Показательные функции в задаче B15
- Задача B5: площадь кольца
- Случай четырехугольной пирамиды
В линейной алгебре базис векторного пространства размерности 


Определение[править | править код]
Если векторы 

.
.
.
.
то матрица перехода от базиса 

Использование[править | править код]
При умножении матрицы, обратной к матрице перехода, на столбец, составленный из коэффициентов разложения вектора по базису 

Пример[править | править код]
Для того, чтобы повернуть вектор на угол θ против часовой стрелки, можно умножить матрицу поворота на него:
| Матрицы наиболее распространённых преобразований | ||||
|---|---|---|---|---|
| В двумерных координатах | В однородных двумерных координатах | В однородных трёхмерных координатах | ||
| Масштабирование
При a, b и c — коэффициенты масштабирования соответственно по осям OX, OY и OZ: |
|
|
|
|
| Поворот
При φ — угол поворота изображения в двухмерном пространстве |
По часовой стрелке |
|
Относительно OX на угол φ |
Относительно OY на угол ψ |
|
Против часовой стрелки |
Относительно OZ на угол χ |
|||
| Перемещение
При a, b и c — смещение соответственно по осям OX, OY и OZ. |
В неоднородных координатах не имеет матричного представления. |
|
|
Свойства[править | править код]
- Матрица перехода является невырожденной. То есть определитель этой матрицы не равен нулю.
Пример поиска матрицы[править | править код]
Найдём матрицу перехода от базиса 
путём элементарных преобразований
следовательно

См. также[править | править код]
- Цепи Маркова
- Стохастическая матрица
- Матрица поворота
Ссылки[править | править код]
- Матрицы перехода от базиса к базису
Время на прочтение
9 мин
Количество просмотров 9.4K
Под преобразованием базиса системы координат понимается замена одного набора базовых вершин (реперов) на другой. По сравнению с обычной системой координат на векторах изменение системы координат на точечном базисе имеет особенности, связанные с тем, что базисы могут принадлежать разным пространствам.
В предыдущей части было рассмотрено определение базиса низкой размерности в пространстве высокой размерности и показано, каким образом можно определять дистанции между вершинами, не принадлежащими пространству базиса. При замене базиса требование сохранения метрических свойств системы координат также является ключевым.
Основные матрицы
Под матрицами преобразования (матрицами перехода) обычно понимают такие матрицы, при умножении на которые координат элемента (вершины) в старом базисе, получаются ее координаты в новом. На основании данных матриц преобразуются также метрические тензоры из одного базиса в другой.
Матрицы преобразования базисов содержат сравнительные характеристики двух базисов. Среди данных матриц выделятся инвариантные матрицы — их значения не зависят от выбора базиса. Например, матрица дистанций между вершинами является инвариантной.
Прямые матрицы перехода
Набор исходных базовых вершин обозначим как
(старый базис), новый набор как
(новый базис). Для преобразования координат должна быть задана матрица перехода — описание координат вершин нового базиса в старом. Такими координатами могут быть как ди-координаты вершин, так и би-координаты. Матрицу перехода в ди-координатах обозначим как
. Строка матрицы — это координаты вершины нового базиса
в старом
, соответственно столбец — это ди-координаты вершины старого базиса относительно нового.
Матрица перехода должна быть квадратной, следовательно одних координат вершин недостаточно — их количество меньше, чем количество компонент координат (из-за наличия скалярной компоненты в координатах). Поэтому необходимо добавить в данную матрицу ди-координаты вектора нормали [0; 1, 1,… 1]. После чего матрица перехода в ди-координатах становится похожей по форме на мажорный грамиан. Назовем матрицу
дистанционным тензором преобразования координат (ДТП):
Дистанционный тензор преобразования является инвариантом — его значения не зависят от базиса. При обратном переходе (от
к
) значения даной матрицы просто транспонируются (строки и столбцы меняются местами).
Поскольку ДТП — это ди-координаты, то умножая их на лапласиан (ЛМТ), можно получить би-координаты
. Структура би-координат матрицы перехода:
Первая строка данной матрицы — это би-координаты нормали:
.
В отличие от ДТП значения би-координат матрицы перехода зависят от того, для какого базиса они получены — для старого или нового. Выбор базиса определяет матрицу ЛМТ. Для определенности би-координаты перехода в базисе
обозначим как
, а в базисе
как
. Тогда имеют место следующие тождества. Для исходного базиса:
,
и для нового:
,
Здесь
и
— лапласиан и грамиан исходного базиса. Соответственно
и
— метрические тензоры нового базиса.
При переходе от одного базиса к другому требуется определить метрические тензоры нового базиса, если заданы матрицы преобразования.
Обратные матрицы перехода
Матрицы перехода
и
обратимы при условии отличного от нуля детерминанта матрицы перехода:
или
Нулевой детерминант матрицы преобразования означает ортогональность базисов. В ортогональном базисе невозможно выразить метрику проекций. Будем считать базисы неортогональными. Тогда обратные матрицы перехода выражаются через прямые следующим образом:
Матрица
— представляет собой би-координаты вершин старого базиса
относительно вершин нового
. То есть обращение би-координат дает взаимные би-координаты.
Матрица
— это лапласовский тензор преобразования базиса (ЛТП). Ее структура аналогична структуре лапласиана (ЛМТ):
Здесь главный минор
— это симметричный лапласиан. В окаймлении барицентрические координаты обратных проекций ортоцентров двух базисов (симплексов). Ортоцентр исходного базиса выражена в барицентрических координатах нового —
, а ортоцентр нового в координатах исходного —
.
Что понимается под «обратными проекциями», будет пояснено далее.
В углу лапласовского тензора находится скаляр
. Его значение отражает скалярное произведение двух базисов — нового и старого. Чтобы раскрыть его смысл, рассмотрим две ситуации — 1) базисы принадлежат одному и тому же пространству и 2) базисы принадлежат разным пространствам.
Скалярное произведение базисов одного пространства
В общем пространстве скалярное произведение базисов выражается через нормы ортоцентров (
и
) и расстояния между ортоцентрами (
):
Данная формула подобна выражению для скалярного произведения пар с общей вершиной (3.8). Поэтому можно считать соотношение (5.5) определением скалярного произведения ортоцентров.
На рисунке показана геометрическая интерпретация скалярного произведения ортоцентров (окружностей). Слева — определение через скалярное произведение смежных пар
и
. Если окружности пересекаются, то у них есть общий элемент
— элемент смежности пар.
Скалярное произведение элементов можно определить через их взаимные степени (показано на рисунке справа). Геометрическое определение степени точки дано во 2-й части. Согласно (2.9) степень точки
относительно элемента выражается через дистанцию от точки до элемента
и норму элемента
:
Можно обобщить данное определение, если вместо точки использовать другой элемент. Тогда взаимной степенью двух элементов
и
является следующая скалярная величина
:
Данная формула известна как произведение Дарбу. На правом рисунке показано построение точек, значение дистанции между которыми равно взаимной степени элементов:
По своим свойствам взаимная степень элементов обобщает свойства степени точки, то есть определяет их взаимное расположение. Если элементы находятся вне друг друга, то их взаимная степень положительна, если пересекаются — отрицательна. Под пересечением здесь понимается ситуация, при которой точки касания
(или
) находятся внутри элемента
(или
соответственно) (на рисунке взаимная степень элементов положительна).
Тогда скалярное произведение (5.5) — это взаимная полустепень элементов (и наоборот). Напомним (2.10), что под полустепенью понимается степень, деленная на (-2):
Если центры элементов совпадают (
), то их скалярное произведение будет равно их средней норме:
Скалярное произведение базисов разных пространств
Если базисы принадлежат разным пространствам, то геометрическая интерпретация их скалярного произведения
усложняется. Приведем вначале алгебраические тождества. Они аналогичны подобным для составляющих лапласовского тензора, приведенных в первой части.
Скалярное произведение базисов может выражено через отношение детерминантов дистанционной матрицы перехода и ее главного минора (см. 5.1.1):
Связь взаимной нормы базисов и барицентрических координат обратных проекций их ортоцентров:
— для вершин базиса
.
— для вершин базиса
.
Разберемся, что такое обратная проекция точки. Допустим, что у нас есть точка
, принадлежащая базису
. Тогда ее обратной проекцией на базис
будет такая точка
, что перпендикуляр, опущенный из нее на базис
, пересекается с ним в исходной точке
.
На рисунке обратной проекцией точки
на пространство
является точка
, а обратной проекцией точки
на пространство
— точка
. Точки
и
— это ортоцентры базисов
и
соответственно.
Понятие обратной проекции применимо также к нормам элементов. Норма при обратной проекции становится больше исходной (в отличие от прямой проекции). На рисунке дистанция
— это норма ортоцентра базиса
. Обратной проекцией на базис
будет дистанция:
.
Соответственно обратной проекцией нормы базиса
на базис
будет дистанция
.
Обозначая дистанцию между обратными проекциями центров как
, получаем следующее выражение для скалярного произведения базисов разных пространств:
Видим, что по форме оно совпадает со взаимной нормой базисов одного пространства (5.5), но вместо дистанций используются их обратные проекции на взаимный базис. Если базисы принадлежат одному пространству, то угол между пространствами становится нулевым, и формула (5.9) переходит в (5.5).
Все приведенные формулы применимы также и к пространству графа. В графе нет описанных сфер (базиса), но есть связность. Тогда скалярное произведение базисов графа должно отражать их взаимную связность.
Расчет нового базиса
Здесь также рассмотрим две ситуации: 1) новый и старый базис принадлежат одному и тому же пространству и 2) принадлежат разным пространствам. Первый случай как правило относится к обычному геометрическому пространству (при смене базиса тут редко меняется его пространство), второй — к пространству графа.
Определить принадлежность элемента (вершины) пространству базиса можно по его норме в данном пространстве. Если равна нулю, то элемент принадлежит пространству.
Единое пространство базисов
Для получения грамиана нового базиса
необходимо умножить ди-координаты элементов нового базиса
на би-координаты
. Полученная матрица будет матрицей скалярных произведений в новом базисе
(см. 4.4.2 в предыдущей части). Таким образом если пространства базисов совпадают, то матрица норм вершин нового базиса относительно старого — это и есть грамиан нового базиса:
Мы пометили данный грамиан штрихом, чтобы помнить об условии общего пространства базисов. Лапласиан нового базиса (ЛМТ) можно получить обращением грамиана (ДМТ):
Координаты элемента в новом базисе могут быть выражены через координаты в старом и матрицы перехода. Ди-координаты
:
Би-координаты элемента в новом базисе
:
Все приведенные выражения аналогичны формулам изменения координат и в обычных (векторных) системах координат. В пределах общего пространства использование точечного базиса аналогично использованию векторного.
Пример преобразования базиса
На КДПВ показан основной базис
из 3-х вершин (A, B, C) и новый базис
, образованный вершинами (P, Q, R). Значения ДМТ основного базиса есть в первой статье:
begin{array}{c | c c c c}
Gm_{aa} & * & A & B & C \
hline
* & 0 & 1 & 1 & 1 \
A & 1 & 0 & -4.5 & -8 \
B & 1 & -4.5 & 0 & -12.5 \
C & 1 & -8 & -12.5 & 0 \
end{array}
Звездочкой обозначена скалярная компонента. Значение лапласиана (ЛМТ) можно получить обращением грамиана (ДМТ).
Дистанционную матрицу перехода считаем заданной. Ее вид:
begin{array}{c | c c c c}
Dm_{pa} & * & A & B & C \
hline
* & 0 & 1 & 1 & 1 \
P & 1 & -1.0 & -2.5 & -13.0 \
Q & 1 & -6.5 & -2.0 & -6.5 \
R & 1 & -12.5 & -2.0 & -20.5 \
end{array}
Значения би-координат матрицы перехода получаем по формуле (5.2.1):
begin{array}{c | c c c c}
Ba_p{}^a & * & A & B & C \
hline
* & 1 & 0 & 0 & 0 \
P & -1.5 & 0.91(6) & 0.(3) & -0.25 \
Q & 2.0 & -0.5 & 1.0 & 0.50 \
R & -5.0 & -0.(6) & 1.(6) & 0.0 \
end{array}
Скалярной компонентой (значения первого столбца) би-координат являются орбитали. Сумма барицентрических компонент равна 1.
Лапласовский тензор преобразования (5.3.1):
begin{array}{c | c c c c}
Lt^{ap} & * & P & Q & R \
hline
* & 2.15 & 0.30 & 1.15 & -0.45 \
A & 0.058(3) & 0.11(6) & -0.0(6) & -0.05 \
B & 0.9(6) & -0.0(6) & -0.0(3) & 0.10 \
C & -0.025 & -0.05 & 0.10 & -0.05 \
end{array}
Вектор
— это барицентрические координаты ортоцентра старого базиса (симплекса ABC) относительно вершин нового (PQR). Соответственно, вектор
— наоборот, барицентрические координаты ортоцентра симплекса PQR относительно вершин старого базиса.
Используя (5.10.1), получаем грамиан нового базиса:
begin{array}{c | c c c c}
Gm’_{pp} & * & P & Q & R \
hline
* & 0 & 1 & 1 & 1 \
P & 1 & 0 & -6.5 & -8.5 \
Q & 1 & -6.5 & 0 & -4.0 \
R & 1 & -8.5 & -4.0 & 0 \
end{array}
Базисы в разных пространствах
Если базисы находятся в разных пространствах, то формула (5.10.1) будет давать неверные значения полудистанций между вершинами нового базиса. В предыдущей части было показано, что в общем случае для нахождения правильных дистанций между вершинами необходимо к матрице норм прибавить фундаментальную матрицу
(4.5):
Следовательно, при преобразовании базиса к базису из другого пространства необходимо наряду с матрицами перехода задать фундаментальную матрицу нового базиса (относительно исходного).
Для задания фундаментальной матрицы полезно вспомнить ее геометрический смысл (см. 4.6.1). Элемент фундаментальной матрицы — это скалярное произведение нормалей, направленных к вершинам из их проекций на пространство базиса. В частном (но практически важном) случае общего надпространства элемент фундаментальной матрицы вычисляется как произведение расстояний от заданных элементов до пространства базиса.
Скалярное произведение обратных проекций
В пространстве графа значения фундаментальной матрицы можно получить через матрицу смежности между старым и новым базисом
. Элементами данной матрицы является вес связей между вершинами двух базисов. Если матрица известна и обратима, то можно получить обратную матрицу смежности:
Полученная матрица (как и матрица смежности) является инвариантом — ее значения не зависят от выбора базиса. Значения элементов матрицы
отражают скалярное произведение обратных проекций между вершинами двух базисов. На рисунке представлена поясняющая схема.
Здесь точка A принадлежит базису
, а точка P — базису
. Штрихами помечены обратные проекции точек на смежный базис. Тогда значение элемента матрицы — это скалярное произведение векторов
и
:
Можно выразить данное соотношение через расстояния от вершин до гиперплоскости пересечения пространств (на рисунке — точка O) и угол между пространствами
:
Из формулы (5.13.2′) видно, что если базисы ортогональны
, то элементы скалярного произведения обращаются в бесконечность.
Итоговые формулы преобразования базисов
Удобно привести размерность матрицы скалярных произведений проекций
к размерности остальных матриц перехода, окаймив ее нулями. Тогда фундаментальная матрица базиса
определяется как
Объединяя все вместе, получаем конечное выражение для грамиана нового базиса
:
Симметричным образом выражается исходный базис при заданных матрицах преобразования:
Здесь
и
— би-координаты матриц перехода (5.2.1) и (5.2.2).
— общая дистанционная матрица преобразования:
Данная матрица является инвариантом, состоит из двух частей — дистанционного тензора преобразования
и добавки, связанной с некомпланарностью пространств базисов, — матрицы скалярных произведений проекций
.
Лапласовский тензор базисов получается обращением ДМТ (5.15). Задача определения связи базисов решена.
Подводим итоги. Тяжелая формульная часть серии в целом завершена. Приведены основные понятия и тождества. Точечные базисы — это полезный и мощный инструмент для различных прикладных задач. В заключительной статье рассмотрим базис простейшей структуры — в виде звезды.
Пусть задан в линейном
пространстве
некоторый базис
.
Тогда любой векторможет быть разложен единственным образом
по базису (материал первого семестра!):
Введем новый базис
.
В этом базисе тот же самый векторбудет иметь уже другие координаты:
Возникает задача:
связать между собой координаты
произвольного вектора в двух различных
базисах. Эту задачу будем называть
задачей
преобразования базисов.
Чтобы технически
удобно решить эту задачу и подобные ей,
введем в рассмотрение новый объект –
векторную
матрицу-строку.
Это обычная матрица-строка, но ее
элементами являются не числа, а векторы
(из некоторого линейного пространства).
Любую систему векторов можно задать в
виде векторной матрицы строки.
Для векторной
матрицы-строки
определим умножение ее справа на обычную
числовую матрицуразмера
для данного
,
равного числу векторов строки и
произвольногоследующим образом:
Таким образом, по
определению, результатом умножения
векторной матрицы строки справа на
числовую матрицу будет новая векторная
матрица-строка, число компонент которой
равно числу столбцов матрицы
,
и каждая компонента вычисляется как
умножение векторной строки на
соответствующий столбец числовой
матрицы по тому же правилу, что и в
обычном матричном умножении, но только
вместо числового умножения используется
умножение вектора на число.
Легко доказать (по
аналогии с доказательством ассоциативности
умножения числовых матриц) следующее
равенство:
(каковы бы ни были
числовые матрицы
и
,
произведение которых существует).
С использованием
векторных матриц-строк удобно записывать
разложение произвольных систем векторов
по данному базису.
Пусть дан базис (в
виде векторной матрицы-строки)
и система векторов
.
Запишем разложение векторов системыпо базису
:
Или, с использованием
векторных матриц-строк:
Нетрудно сообразить,
что j-ый
столбец матрицы
– это столбец координат вектора
в базисе
.
Утверждение 1.3
Если система
линейно независима, то столбцы матрицы
линейно независимы.
Доказательство.
Предположим противное – тогда найдутся
числа
,
не все равные нулю, такие, что
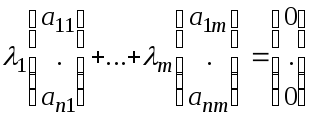
или, покомпонентно:
С учетом этих равенств
рассмотрим линейную комбинацию
Подставляя вместо
каждого вектора
,
его разложение по базису,
получим:
Итак, мы получили
нетривиальную линейную комбинацию
линейно независимых векторов, равную
нулю, что невозможно.
Можно заметить, что,
проводя рассуждения доказательства
утверждения 1.3 в обратном порядке,
получим, что верно и обратное: если
столбцы матрицы
линейно
независимы, то система векторовлинейно
независима. Следовательно, для
распознавания линейной независимости
произвольной системы векторов
конечномерного линейного пространства
достаточно составить матрицу из столбцов
координат векторов системы в произвольном
фиксированном базисе и доказать линейную
независимость этих столбцов, используя,
например, метод элементарных преобразований
(т.е., вычислив ранг составленной
матрицы).
Для одного вектора
его разложение по базису задается в
виде:
,
где
–
столбец координат векторав базисе
.
Вернемся к задаче
преобразования базисов. Запишем
разложение нового («штрихованного»)
базиса в старом (не «штрихованном»):
Матрица
(квадратная порядка
)
называетсяматрицей
перехода от
базиса
к
базису.
Каждый ее столбец есть, как мы только
что доказали, столбец координат
соответствующего вектора нового базиса
в старом базисе. В силу утверждения 1.3
столбцы матрицылинейно
независимы, тем самым ее ранг равен,
и матрицаявляется
невырожденной.
Тогда для разложения
вектора
в новом базисе получим:
Отсюда по теореме
о единственности разложения вектора
по базису (первый семестр!)
Так как матрица
не вырождена, то
Итак, чтобы
вычислить столбец координат вектора в
новом базисе, достаточно матрицу,
обратную к матрице перехода, умножить
на столбец координат вектора в старом
базисе.
По контрасту заметим,
что для того, чтобы получить сам
новый базис (как векторную матрицу-строку),
нужно старый базис умножить на саму
матрицу перехода.
Таким образом, можно
заметить, что сами базисы и координаты
векторов в базисах при переходе от
базиса к базису перевычисляются
«зеркально» по отношению к друг другу.
Утверждение 1.4
1) Если
–
матрица перехода от базисак
базису,
то обратная матрицаявляется матрицей перехода от базиса
к базису
.
-
Если
–
матрица перехода от базисак
базису,
а–
матрица перехода от базисак
базису,
то–
матрица перехода от базисак базису
.
Схематически:
Т
T
S

-1
TS
Доказательство.
Упражнение.
Со сложными
преобразованиями базисов связана
следующая задача: пусть векторы базисов
и
заданы
своими координатами в некотором базисе(который
сам может быть явно и не определен).
Требуется найти матрицуперехода от
к
.
Составляем матрицы
перехода от
к
и
отк
(по
столбцам координат векторов базисови
).
Пусть это будут матрицыи
соответственно. Тогда используя
утверждение 1.4, легко получим (см. рис.
1.2):
A
B
T
рис.
1.2
1В приведенном доказательстве нулевой
вектор обозначен как0.
Соседние файлы в папке Linal
- #
- #
- #
- #
- #
- #
Матрица перехода
Пусть 


Матрица 




Определитель матрицы перехода отличен от нуля:
Пример с решением
Пример 183.
Определим матрицу перехода от базиса 
Запишем координаты векторов в виде строк матрицы и приведем полученную матрицу к ступенчатому виду.
Справа от матрицы указываются векторы и регистрируются проводимые преобразования матрицы.
Нулевым строкам ступенчатого вида матрицы соответствуют равенства 

Получено разложение векторов 



По этой ссылке вы найдёте полный курс лекций по высшей математике:
Мы ограничимся далее изложением простейших фактов для однородных цепей Маркова, в которых условная вероятность появления события 




Полная вероятностная картина возможных изменений, осуществляющихся при переходе от одного испытания непосредственно к следующему, задается матрицей
составленной из вероятностей перехода, которую мы будем называть матрицей перехода.
Отметим, каким условиям должны удовлетворять элементы этой матрицы. Прежде всего, они, как вероятности, должны быть неотрицательными числами, т.е. при всех 
Далее из того, что при переходе из состояний 

система обязательно переходит в одно и только в одно из состояний 

Таким образом, сумма элементов в каждой строке матрицы перехода равна единице.
Возможно вам будут полезны данные страницы:
Наша первая задача в теории цепей Маркова состоит в определении вероятности перехода из состояния 



Рассмотрим какое-нибудь промежуточное испытание с номером 





Обозначим через 
Согласно (1) между матрицами 
В частности, при
находим, что
при
и вообще при любом
Отметим частный случай формулы (1): при
Преобразование координат. Матрица перехода.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Пусть $L_n -$ произвольное мерное пространство, $B=(e_1, . e_n) -$ фиксированный базис в нем. Тогда всякому вектору $xin L_n$ взаимно однозначно соответствует столбец его координат в этом базисе.
$$x=x_1e_1+. +x_ne_nLeftrightarrow X=beginx_1\ vdots\x_nend$$
При этом линейные комбинации над векторами в координатной форме выглядят следующим образом:
$y=lambda xLeftrightarrow Y=lambda X.$
Пусть $B=(e_1, e_2, . e_n)$ и $B’=(e_1′, e_2′, . e_n’) -$ два различных базиса в $L_n.$ Каждый из векторов базиса $B’$ разложим по базису $B:$
Матрицей перехода $T_$ от базиса $B$ к базису $B’$ называется матрица
$T_=begint_&. &t_\. &. &. \t_&. &t_end$ $k$-й столбец которой есть столбец $E’_k$ координат вектора $e’_k$ в базисе $B.$ Если $x -$ произвольный вектор из $L_n,$ $X$ и $X’ -$ столбцы его координат в базисах $B$ и $B’$ соответственно то имеет место равенство $$X’=(T_)^X$$ (формула преобразования координат при преобразовании базиса).
Примеры.
4.15. В постранстве $V_3$ заданы векторы $e_1’=i+j, $ $e_2’=i-j, $ $e_3’=-i+2j-k.$ Доказать, что система $B’=(e_1′, e_2′, e_3′)$ базис в $R_3 $ и написать матрицу перехода $T_$ где $B=(e_1=i, e_2=j, e_3=k).$ Найти координаты вектора $x=i-2j+2k$ в базисе $B’.$
Решение.
Для того, чтобы показать, что система векторов $B’=(e_1′, e_2′, e_3′)$ базис в $R_3, $ достаточно показать, что эти вектора не компланарны.
Из условия мы имеем $e_1’=i+j=(1, 1, 0),$ $e_2’=i-j=(1, -1, 0),$ $e_3’=-i+2j-k=(-1, 2, -1).$ Вектора $e_1′, e_2′, e_3’$ не компланарны, если $begin1&1&0\1&-1&0\-1&2&-1endneq 0.$ Проверим это:
Далее запишем матрицу перехода $T_$
Подставляя этот результат в формулу $X’=(T_)^X,$ получаем:
4.17. Пусть $B=(i, j, k)$ и $B’=(i’, j’, k’) -$ прямоугольные базисы в $R_3.$ Написать матрицу перехода $T_,$ и выписать столбец координат вектора $x=i-2j+k$ в базисе $B’.$
Базис $B’$ получен перестановкой $i’=j,$ $j’=k,$ $k’=i.$
Решение.
Из условия мы имеем $e_1=i, e_2-j, e_3=k;$ $e_1’=j=(0, 1, 0),$ $e_2’=k=(0, 0, 1),$ $e_3’=i=(1, 0, 0).$
Подставляя этот результат в формулу $X’=(T_)^X,$ получаем:
Домашнее задание.
Пусть $B=(i, j, k)$ и $B’=(i’, j’, k’) -$ прямоугольные базисы в $R_3.$ Написать матрицу перехода $T_,$ и выписать столбец координат вектора $x=i-2j+k$ в базисе $B’.$
4.16. Базис $B’$ получен изменением на противоположное направление всех трех базисных ортов $B.$
4.18. Базис $B’$ получен поворотом базиса $B$ на угол $varphi$ вокруг орта $i.$
Геометрия данных 5. Преобразование базиса
Под преобразованием базиса системы координат понимается замена одного набора базовых вершин (реперов) на другой. По сравнению с обычной системой координат на векторах изменение системы координат на точечном базисе имеет особенности, связанные с тем, что базисы могут принадлежать разным пространствам.
Основные матрицы
Под матрицами преобразования (матрицами перехода) обычно понимают такие матрицы, при умножении на которые координат элемента (вершины) в старом базисе, получаются ее координаты в новом. На основании данных матриц преобразуются также метрические тензоры из одного базиса в другой.
Матрицы преобразования базисов содержат сравнительные характеристики двух базисов. Среди данных матриц выделятся инвариантные матрицы — их значения не зависят от выбора базиса. Например, матрица дистанций между вершинами является инвариантной.
Прямые матрицы перехода
Набор исходных базовых вершин обозначим как (старый базис), новый набор как (новый базис). Для преобразования координат должна быть задана матрица перехода — описание координат вершин нового базиса в старом. Такими координатами могут быть как ди-координаты вершин, так и би-координаты. Матрицу перехода в ди-координатах обозначим как . Строка матрицы — это координаты вершины нового базиса в старом , соответственно столбец — это ди-координаты вершины старого базиса относительно нового.
Матрица перехода должна быть квадратной, следовательно одних координат вершин недостаточно — их количество меньше, чем количество компонент координат (из-за наличия скалярной компоненты в координатах). Поэтому необходимо добавить в данную матрицу ди-координаты вектора нормали [0; 1, 1,… 1]. После чего матрица перехода в ди-координатах становится похожей по форме на мажорный грамиан. Назовем матрицу дистанционным тензором преобразования координат (ДТП):
Дистанционный тензор преобразования является инвариантом — его значения не зависят от базиса. При обратном переходе (от к ) значения даной матрицы просто транспонируются (строки и столбцы меняются местами).
Поскольку ДТП — это ди-координаты, то умножая их на лапласиан (ЛМТ), можно получить би-координаты . Структура би-координат матрицы перехода:
Первая строка данной матрицы — это би-координаты нормали: .
В отличие от ДТП значения би-координат матрицы перехода зависят от того, для какого базиса они получены — для старого или нового. Выбор базиса определяет матрицу ЛМТ. Для определенности би-координаты перехода в базисе обозначим как , а в базисе как . Тогда имеют место следующие тождества. Для исходного базиса:
Здесь и — лапласиан и грамиан исходного базиса. Соответственно и — метрические тензоры нового базиса.
При переходе от одного базиса к другому требуется определить метрические тензоры нового базиса, если заданы матрицы преобразования.
Обратные матрицы перехода
Матрицы перехода и обратимы при условии отличного от нуля детерминанта матрицы перехода:
Нулевой детерминант матрицы преобразования означает ортогональность базисов. В ортогональном базисе невозможно выразить метрику проекций. Будем считать базисы неортогональными. Тогда обратные матрицы перехода выражаются через прямые следующим образом:
Матрица — представляет собой би-координаты вершин старого базиса относительно вершин нового . То есть обращение би-координат дает взаимные би-координаты.
Матрица — это лапласовский тензор преобразования базиса (ЛТП). Ее структура аналогична структуре лапласиана (ЛМТ):
Здесь главный минор — это симметричный лапласиан. В окаймлении барицентрические координаты обратных проекций ортоцентров двух базисов (симплексов). Ортоцентр исходного базиса выражена в барицентрических координатах нового — , а ортоцентр нового в координатах исходного — .
Что понимается под «обратными проекциями», будет пояснено далее.
В углу лапласовского тензора находится скаляр . Его значение отражает скалярное произведение двух базисов — нового и старого. Чтобы раскрыть его смысл, рассмотрим две ситуации — 1) базисы принадлежат одному и тому же пространству и 2) базисы принадлежат разным пространствам.
Скалярное произведение базисов одного пространства
В общем пространстве скалярное произведение базисов выражается через нормы ортоцентров ( и ) и расстояния между ортоцентрами ():
Данная формула подобна выражению для скалярного произведения пар с общей вершиной (3.8). Поэтому можно считать соотношение (5.5) определением скалярного произведения ортоцентров.
На рисунке показана геометрическая интерпретация скалярного произведения ортоцентров (окружностей). Слева — определение через скалярное произведение смежных пар и . Если окружности пересекаются, то у них есть общий элемент — элемент смежности пар.
Скалярное произведение элементов можно определить через их взаимные степени (показано на рисунке справа). Геометрическое определение степени точки дано во 2-й части. Согласно (2.9) степень точки относительно элемента выражается через дистанцию от точки до элемента и норму элемента :
Можно обобщить данное определение, если вместо точки использовать другой элемент. Тогда взаимной степенью двух элементов и является следующая скалярная величина :
Данная формула известна как произведение Дарбу. На правом рисунке показано построение точек, значение дистанции между которыми равно взаимной степени элементов:
По своим свойствам взаимная степень элементов обобщает свойства степени точки, то есть определяет их взаимное расположение. Если элементы находятся вне друг друга, то их взаимная степень положительна, если пересекаются — отрицательна. Под пересечением здесь понимается ситуация, при которой точки касания (или ) находятся внутри элемента (или соответственно) (на рисунке взаимная степень элементов положительна).
Тогда скалярное произведение (5.5) — это взаимная полустепень элементов (и наоборот). Напомним (2.10), что под полустепенью понимается степень, деленная на (-2):
Если центры элементов совпадают (), то их скалярное произведение будет равно их средней норме:
Скалярное произведение базисов разных пространств
Если базисы принадлежат разным пространствам, то геометрическая интерпретация их скалярного произведения усложняется. Приведем вначале алгебраические тождества. Они аналогичны подобным для составляющих лапласовского тензора, приведенных в первой части.
Скалярное произведение базисов может выражено через отношение детерминантов дистанционной матрицы перехода и ее главного минора (см. 5.1.1):
Связь взаимной нормы базисов и барицентрических координат обратных проекций их ортоцентров:
— для вершин базиса .
— для вершин базиса .
Разберемся, что такое обратная проекция точки. Допустим, что у нас есть точка , принадлежащая базису . Тогда ее обратной проекцией на базис будет такая точка , что перпендикуляр, опущенный из нее на базис , пересекается с ним в исходной точке .
На рисунке обратной проекцией точки на пространство является точка , а обратной проекцией точки на пространство — точка . Точки и — это ортоцентры базисов и соответственно.
Понятие обратной проекции применимо также к нормам элементов. Норма при обратной проекции становится больше исходной (в отличие от прямой проекции). На рисунке дистанция — это норма ортоцентра базиса . Обратной проекцией на базис будет дистанция:
.
Соответственно обратной проекцией нормы базиса на базис будет дистанция
.
Обозначая дистанцию между обратными проекциями центров как , получаем следующее выражение для скалярного произведения базисов разных пространств:
Видим, что по форме оно совпадает со взаимной нормой базисов одного пространства (5.5), но вместо дистанций используются их обратные проекции на взаимный базис. Если базисы принадлежат одному пространству, то угол между пространствами становится нулевым, и формула (5.9) переходит в (5.5).
Все приведенные формулы применимы также и к пространству графа. В графе нет описанных сфер (базиса), но есть связность. Тогда скалярное произведение базисов графа должно отражать их взаимную связность.
Расчет нового базиса
Здесь также рассмотрим две ситуации: 1) новый и старый базис принадлежат одному и тому же пространству и 2) принадлежат разным пространствам. Первый случай как правило относится к обычному геометрическому пространству (при смене базиса тут редко меняется его пространство), второй — к пространству графа.
Определить принадлежность элемента (вершины) пространству базиса можно по его норме в данном пространстве. Если равна нулю, то элемент принадлежит пространству.
Единое пространство базисов
Для получения грамиана нового базиса необходимо умножить ди-координаты элементов нового базиса на би-координаты . Полученная матрица будет матрицей скалярных произведений в новом базисе (см. 4.4.2 в предыдущей части). Таким образом если пространства базисов совпадают, то матрица норм вершин нового базиса относительно старого — это и есть грамиан нового базиса:
Мы пометили данный грамиан штрихом, чтобы помнить об условии общего пространства базисов. Лапласиан нового базиса (ЛМТ) можно получить обращением грамиана (ДМТ):
Координаты элемента в новом базисе могут быть выражены через координаты в старом и матрицы перехода. Ди-координаты :
Би-координаты элемента в новом базисе :
Все приведенные выражения аналогичны формулам изменения координат и в обычных (векторных) системах координат. В пределах общего пространства использование точечного базиса аналогично использованию векторного.
На КДПВ показан основной базис из 3-х вершин (A, B, C) и новый базис , образованный вершинами (P, Q, R). Значения ДМТ основного базиса есть в первой статье:
begin
Gm_ & * & A & B & C \
hline
* & 0 & 1 & 1 & 1 \
A & 1 & 0 & -4.5 & -8 \
B & 1 & -4.5 & 0 & -12.5 \
C & 1 & -8 & -12.5 & 0 \
end
Звездочкой обозначена скалярная компонента. Значение лапласиана (ЛМТ) можно получить обращением грамиана (ДМТ).
Дистанционную матрицу перехода считаем заданной. Ее вид:
begin
Dm_ & * & A & B & C \
hline
* & 0 & 1 & 1 & 1 \
P & 1 & -1.0 & -2.5 & -13.0 \
Q & 1 & -6.5 & -2.0 & -6.5 \
R & 1 & -12.5 & -2.0 & -20.5 \
end
Значения би-координат матрицы перехода получаем по формуле (5.2.1):
begin
Ba_p^a & * & A & B & C \
hline
* & 1 & 0 & 0 & 0 \
P & -1.5 & 0.91(6) & 0.(3) & -0.25 \
Q & 2.0 & -0.5 & 1.0 & 0.50 \
R & -5.0 & -0.(6) & 1.(6) & 0.0 \
end
Скалярной компонентой (значения первого столбца) би-координат являются орбитали. Сумма барицентрических компонент равна 1.
Лапласовский тензор преобразования (5.3.1):
begin
Lt^ & * & P & Q & R \
hline
* & 2.15 & 0.30 & 1.15 & -0.45 \
A & 0.058(3) & 0.11(6) & -0.0(6) & -0.05 \
B & 0.9(6) & -0.0(6) & -0.0(3) & 0.10 \
C & -0.025 & -0.05 & 0.10 & -0.05 \
end
Вектор — это барицентрические координаты ортоцентра старого базиса (симплекса ABC) относительно вершин нового (PQR). Соответственно, вектор — наоборот, барицентрические координаты ортоцентра симплекса PQR относительно вершин старого базиса.
Базисы в разных пространствах
Если базисы находятся в разных пространствах, то формула (5.10.1) будет давать неверные значения полудистанций между вершинами нового базиса. В предыдущей части было показано, что в общем случае для нахождения правильных дистанций между вершинами необходимо к матрице норм прибавить фундаментальную матрицу (4.5):
Следовательно, при преобразовании базиса к базису из другого пространства необходимо наряду с матрицами перехода задать фундаментальную матрицу нового базиса (относительно исходного).
Для задания фундаментальной матрицы полезно вспомнить ее геометрический смысл (см. 4.6.1). Элемент фундаментальной матрицы — это скалярное произведение нормалей, направленных к вершинам из их проекций на пространство базиса. В частном (но практически важном) случае общего надпространства элемент фундаментальной матрицы вычисляется как произведение расстояний от заданных элементов до пространства базиса.
Скалярное произведение обратных проекций
В пространстве графа значения фундаментальной матрицы можно получить через матрицу смежности между старым и новым базисом . Элементами данной матрицы является вес связей между вершинами двух базисов. Если матрица известна и обратима, то можно получить обратную матрицу смежности:
Полученная матрица (как и матрица смежности) является инвариантом — ее значения не зависят от выбора базиса. Значения элементов матрицы отражают скалярное произведение обратных проекций между вершинами двух базисов. На рисунке представлена поясняющая схема.
Здесь точка A принадлежит базису , а точка P — базису . Штрихами помечены обратные проекции точек на смежный базис. Тогда значение элемента матрицы — это скалярное произведение векторов и :
Можно выразить данное соотношение через расстояния от вершин до гиперплоскости пересечения пространств (на рисунке — точка O) и угол между пространствами :
Из формулы (5.13.2′) видно, что если базисы ортогональны , то элементы скалярного произведения обращаются в бесконечность.
Итоговые формулы преобразования базисов
Удобно привести размерность матрицы скалярных произведений проекций к размерности остальных матриц перехода, окаймив ее нулями. Тогда фундаментальная матрица базиса определяется как
Объединяя все вместе, получаем конечное выражение для грамиана нового базиса :
Симметричным образом выражается исходный базис при заданных матрицах преобразования:
Здесь и — би-координаты матриц перехода (5.2.1) и (5.2.2). — общая дистанционная матрица преобразования:
Данная матрица является инвариантом, состоит из двух частей — дистанционного тензора преобразования и добавки, связанной с некомпланарностью пространств базисов, — матрицы скалярных произведений проекций .
Лапласовский тензор базисов получается обращением ДМТ (5.15). Задача определения связи базисов решена.
Подводим итоги. Тяжелая формульная часть серии в целом завершена. Приведены основные понятия и тождества. Точечные базисы — это полезный и мощный инструмент для различных прикладных задач. В заключительной статье рассмотрим базис простейшей структуры — в виде звезды.

























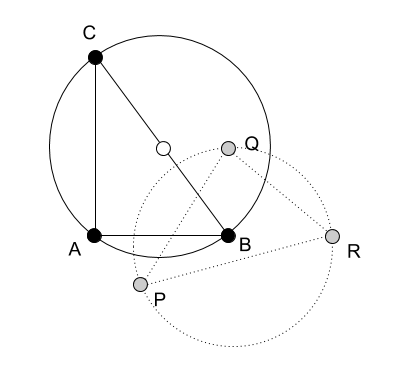

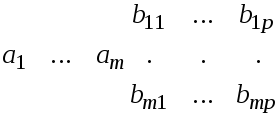



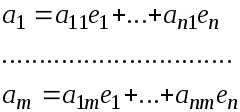
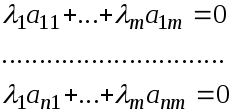


























 находим, что
находим, что







