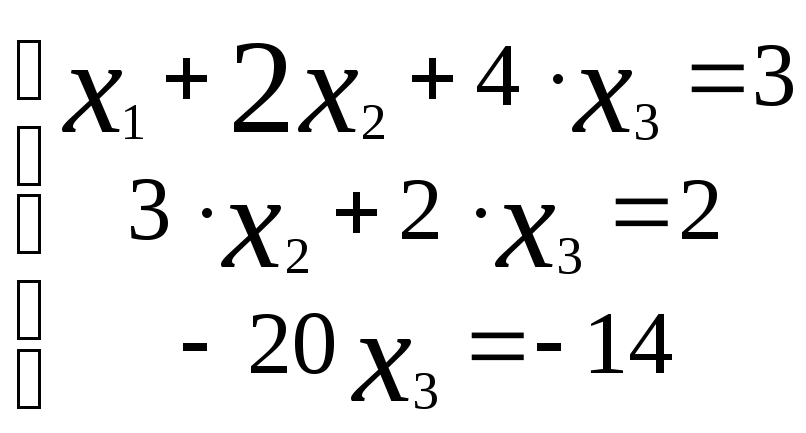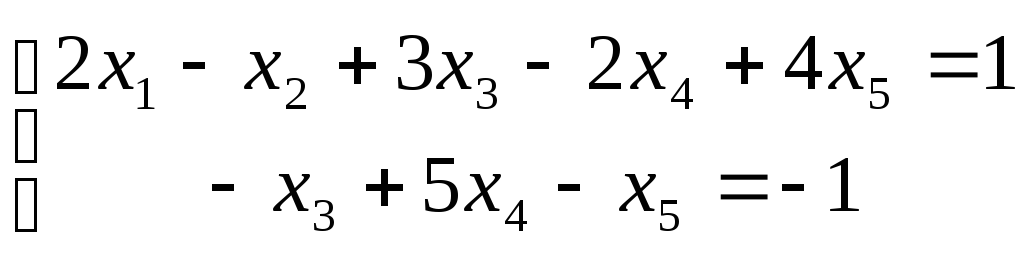Решение систем линейных алгебраических уравнений с помощью обратной матрицы.
Решение систем линейных алгебраических уравнений (СЛАУ) с помощью обратной матрицы (иногда этот способ именуют ещё матричным методом или методом обратной матрицы) требует предварительного ознакомления с таким понятием как матричная форма записи СЛАУ. Метод обратной матрицы предназначен для решения тех систем линейных алгебраических уравнений, у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода обратной матрицы можно выразить в трёх пунктах:
- Записать три матрицы: матрицу системы $A$, матрицу неизвестных $X$, матрицу свободных членов $B$.
- Найти обратную матрицу $A^{-1}$.
- Используя равенство $X=A^{-1}cdot B$ получить решение заданной СЛАУ.
Почему $X=A^{-1}cdot B$? показатьскрыть
Перед переходом к чтению примеров рекомендую ознакомиться с методами вычисления обратных матриц, изложенными здесь.
Пример №1
Решить СЛАУ $
left { begin{aligned}
& -5x_1+7x_2=29;\
& 9x_1+8x_2=-11.
end{aligned} right.$ с помощью обратной матрицы.
Решение
Запишем матрицу системы $A$, матрицу свободных членов $B$ и матрицу неизвестных $X$.
$$
A=left(begin{array} {cc} -5 & 7\ 9 & 8 end{array}right);;
B=left(begin{array} {c} 29\ -11 end{array}right);;
X=left(begin{array} {c} x_1\ x_2 end{array}right).
$$
Найдём обратную матрицу к матрице системы, т.е. вычислим $A^{-1}$. В примере №2 на странице, посвящённой нахождению обратных матриц, обратная матрица была уже найдена. Воспользуемся готовым результатом и запишем $A^{-1}$:
$$
A^{-1}=-frac{1}{103}cdotleft(begin{array}{cc} 8 & -7\ -9 & -5end{array}right).
$$
Теперь подставим все три матрицы ($X$, $A^{-1}$, $B$) в равенство $X=A^{-1}cdot B$. Затем выполним умножение матриц в правой части данного равенства.
$$
left(begin{array} {c} x_1\ x_2 end{array}right)=
-frac{1}{103}cdotleft(begin{array}{cc} 8 & -7\ -9 & -5end{array}right)cdot
left(begin{array} {c} 29\ -11 end{array}right)=\
=-frac{1}{103}cdot left(begin{array} {c} 8cdot 29+(-7)cdot (-11)\ -9cdot 29+(-5)cdot (-11) end{array}right)=
-frac{1}{103}cdot left(begin{array} {c} 309\ -206 end{array}right)=left(begin{array} {c} -3\ 2end{array}right).
$$
Итак, мы получили равенство $left(begin{array} {c} x_1\ x_2 end{array}right)=left(begin{array} {c} -3\ 2end{array}right)$. Из этого равенства имеем: $x_1=-3$, $x_2=2$.
Ответ: $x_1=-3$, $x_2=2$.
Пример №2
Решить СЛАУ $
left{begin{aligned}
& x_1+7x_2+3x_3=-1;\
& -4x_1+9x_2+4x_3=0;\
& 3x_2+2x_3=6.
end{aligned}right.$ методом обратной матрицы.
Решение
Запишем матрицу системы $A$, матрицу свободных членов $B$ и матрицу неизвестных $X$.
$$
A=left(begin{array} {ccc} 1 & 7 & 3\ -4 & 9 & 4 \0 & 3 & 2end{array}right);;
B=left(begin{array} {c} -1\0\6end{array}right);;
X=left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right).
$$
Теперь настал черёд найти обратную матрицу к матрице системы, т.е. найти $A^{-1}$. В примере №3 на странице, посвящённой нахождению обратных матриц, обратная матрица была уже найдена. Воспользуемся готовым результатом и запишем $A^{-1}$:
$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$
Теперь подставим все три матрицы ($X$, $A^{-1}$, $B$) в равенство $X=A^{-1}cdot B$, после чего выполним умножение матриц в правой части данного равенства.
$$
left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right)=
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)cdot
left(begin{array} {c} -1\0\6end{array}right)=\
=frac{1}{26}cdot left(begin{array} {c} 6cdot(-1)+(-5)cdot 0+1cdot 6 \ 8cdot (-1)+2cdot 0+(-16)cdot 6 \ -12cdot (-1)+(-3)cdot 0+37cdot 6 end{array}right)=frac{1}{26}cdot left(begin{array} {c} 0\-104\234end{array}right)=left(begin{array} {c} 0\-4\9end{array}right)
$$
Итак, мы получили равенство $left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right)=left(begin{array} {c} 0\-4\9end{array}right)$. Из этого равенства имеем: $x_1=0$, $x_2=-4$, $x_3=9$.
Ответ: $x_1=0$, $x_2=-4$, $x_3=9$.
Естественно, что решение систем линейных уравнений с помощью обратной матрицы без применения специальных программ вроде Mathcad возможно лишь при сравнительно небольшом количестве переменных. Если СЛАУ содержит четыре и более переменных, то гораздо удобнее в таком случае применить метод Гаусса или метод Гаусса-Жордана.
Обратная матрица. Вычисление обратной матрицы методом присоединённой матрицы. Решение систем линейных уравнений методом обратной матрицы.
Определение. Матрица А-1называется обратной к матрице А, если
выполняется условие: АА-1= А-1А=Е,
где Е – единичная матрица того же порядка,
что и матрица А. Обратная А-1матрица имеет ту же размерность, что и
матрица А.
Определение. Квадратная матрица
А=
определитель неравен нулю, в противном
случае матрица называется вырожденной.
Теорема.Всякая невырожденная
матрица имеет обратную.
Определение. Присоединенной матрицейк матрице А называется матрица вида:
=

где Аij-алгебраическое
дополнение элемента аij.
Находят обратную матрицу по формуле:
А-1=.
Пример 3.1
Найти обратную матрицу методом
присоединенной матрицы.
А=
Решение.
-
Выясним, является ли данная матрица
невырожденной. Для этого найдем
определитель матрицы:
=3(-1)1+1
+0(-1)2+1
+1(-1)3+1
=3(12-4)+0+(2-6)=24-4=20.
Т.к.
0,
следовательно, данная матрица имеет
обратную.
-
Найдем транспонированную матрицу.
АТ=
-
Вычислим присоединенную матрицу. Для
этого найдем алгебраическое дополнение
каждого элемента матрицы.
=
(-1)1+1=12-4=8
=
(-1)1+2=
-(4-4)= 0
=
(-1)1+3=
2-6= -4
=
(-1)2+1=
-(0-2)=2
=
(-1)2+2=
12-2=10
=
(-1)2+3=
-(6-0)= -6
=
(-1)3+1=
0-3= -3
=
(-1)3+2=
-(6-1)= -5
=
(-1)3+3=
9-0=9.
=
4. Воспользуемся формулой: А-1=.
А-1=

Решение систем линейных уравнений
методом обратной матрицы
Пусть дана система линейных уравнений
Обозначим её через (1). Выпишим основную
матрицу данной системы: А=
вектор-столбец неизвестных:X=и
вектор-столбец свободных членов:B=.
Теперь перепишем систему (1) в матричной
форме:AX=BX=A-1B-
решение системы (1).
Пример 3.2
Решить систему линейных уравнений:

Решение.
Формула, по которой будем находить
решение системы: X=A-1B.
Основная матрица системы А=
вектор-столбец неизвестных:X=и
вектор-столбец свободных членов:B=.
Найдем определитель
=3(-1)1+1
+0(-1)2+1
+1(-1)3+1
=3(12-4)+0+(2-6)=24-4=20.
Т.к.
0,
следовательно, данная матрица имеет
обратную.
Найдем обратную матрицу с помощью
присоединенной матрицы (см. пример 3.1):
А-1=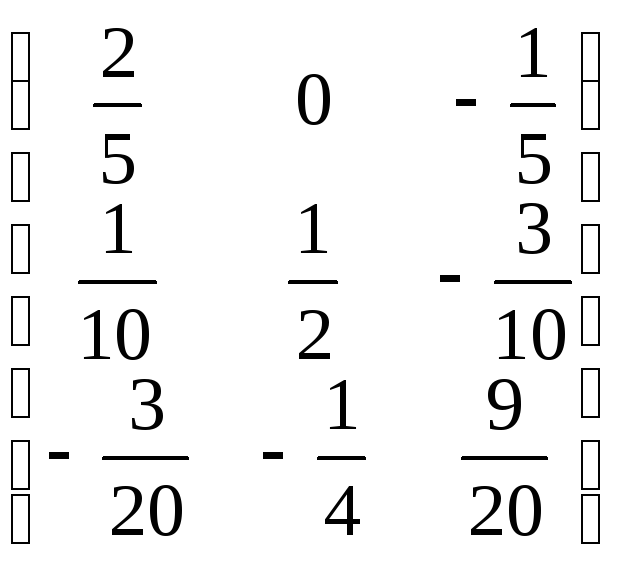
Подставим в формулу X=A-1B,
получим:X=
=

Ответ:
=
,
,
.
Правильность решения легко проверить,
подставив полученные результаты,
,
в данную систему уравнения.
Решение систем линейных уравнений методом Гаусса и Крамера
Пусть дана система линейных уравнений
Обозначим её через (1). Основная матрица
данной системы: А=
вектор-столбец неизвестных:X=и
вектор-столбец свободных членов:B=.
Теперь запишем систему (1) в матричной
форме:AX=B.
Теорема Крамера. Пусть
–определитель
матрицы А,
j–определитель матрицы, получаемой из А
заменойj-го столбца
столбцом свободных членов. Тогда, если0,
то система имеет единственное решение:,
(1jn).
Пример 4.1
Решить систему линейных уравнений:

Решение.
Основная матрица системы А=
.
Найдем определитель
=
=3(-1)1+1
+0(-1)2+1
+1(-1)3+1
=3(12-4)+0+(2-6)=24-4=20. Т.к.
0,
следовательно, можно применить формулы
Крамера.
Найдем определители
,
,
,
полученные заменой соответствующих
столбцов столбцом свободных членов:
=

-4;
=

=

Тогда, по формуле Крамера:
=
=
–=
;
=
;
=
.
Ответ:
=
,
,
.
Решение систем линейных уравнений
методом Гаусса
Пусть дана система линейных уравнений
Рассмотрим расширенную матрицу (АВ)
данной системы и с помощью элементарных
преобразований приведем её к ступенчатому
виду, в результате получим расширенную
матрицу (АВ).
Если ранг основной матрицы системы
меньше ранга расширенной матрицы
r(A)<r(АВ),
то система несовместна. Еслиr(A)=r(АВ)=n,
гдеn-число неизвестных,
то система совместна и определена. Еслиr(A)=r(АВ)<n,
гдеn-число неизвестных,
то система совместна и неопределенна.
Записываем систему линейных уравнений
из полученной ступенчатой матрицы.
Определяем базисные и свободные
переменные, и выражая базисные переменные
через свободные получаем решение
системы.
Пример 4.2
Решить систему линейных уравнений:

Решение.
r(A)=r(АВ)=nсистема совместна и определена.
Отсюда, запишем эквивалентную систему
уравнений, имеем:
Решая её, получаем:
Ответ:
=
,
,
.
Пример 4.3
Найти общее решение системы:

Решение.
Составим матрицу системы: А=
Приведем её к треугольному виду:
r(A)=2. Запишем
эквивалентную систему уравнений:
Примем за базисные переменные
и
,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (3-2)=1, т. е. у нас одна свободная
переменная это.
Выразим базисные переменные через
свободные:

Обозначая свободную переменную:=
,
получаем общее решение в виде:
Пример
4.4
Найти общее решение системы:
Решение.
Приведем расширенную матрицу системы
к ступенчатому виду:
АВ=
r(A)=r(AВ)=2<n,
гдеn-число неизвестных,
то система совместная и неопределенная.
Запишем эквивалентную систему уравнений:
Примем за базисные переменные
и
,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (5-2)=3, значит,
-свободные
переменные.
Выразим базисные переменные через
свободные:

=
,
,
получаем
общее решение в виде:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решаем СЛАУ методом обратной матрицы:
2×1-4×2+3×3=1×1-2×2+4×3=33×1-x2+5×3=2
Как решить?
- Записываем систему в виде матричного уравнения АX=B, где
А=2-431-243-15, X=x1x2x3, B=132.
- Выражаем из этого уравнения X:
X=A-1×B
- Находим определитель матрицы А:
det A= 2-431-243-15=2×(-2)×5+3×(-4)×4+3×(-1)×1-3×(-2)×3–1×(-4)×5-2×4-(-1)=-20-48-3+18+20+8=-25
det А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.
- Находим обратную матрицу А-1 при помощи союзной матрицы. Вычисляем алгебраические дополнения Аij к соответствующим элементам матрицы А:
А11=(-1)(1+1)-24-15=-10+4=-6,
А12=(-1)1+21435=-(5-12)=7,
А13=(-1)1+31-23-1=-1+6=5,
А21=(-1)2+1-43-15=-(-20+3)=17,
А22=(-1)2+22335-10-9=1,
А23=(-1)2+32-43-1=-(-2+12)=-10,
А31=(-1)3+1-43-24=-16+6=-10,
А32=(-1)3+22314=-(8-3)=-5,
А33=(-1)3+32-41-2=-4+4=0.
- Записываем союзную матрицу А*, которая составлена из алгебраических дополнений матрицы А:
А*=-675171-10-10-50
- Записываем обратную матрицу согласно формуле:
A-1=1detA(A*)T: А-1=-125-617-1071-55-100,
- Умножаем обратную матрицу А-1 на столбец свободных членов В и получаем решение системы:
X=A-1×B=-125-617-1071-55-100132=-125-6+51-207+3-105-30+0=-101
Ответ: x1=-1; x2=0; x3=1
Матрица BB является обратной матрицей к квадратной матрице AA, если AB=BA=EAB = BA = E.
Из определения можно понять, что обратная матрица BB будет квадратной матрицей аналогичного порядка, какой имеет матрица AA (иначе какое-либо из произведений ABAB или BABA будет не определено).
Обратная матрица для исходной матрицы AA определяется так: A−1A^{-1}. Можно утверждать, что если A−1A^{-1} существует, то AA−1=A−1A=EAA^{-1} = A^{-1} A= E.
Также легко видеть, что (A−1)−1=A(A^{-1})^{-1} = A.
Если детерминант матрицы является нулем, то обратную к ней матрицу нельзя получить.
Онлайн-калькулятор
Квадратную матрицу AA можно назвать вырожденной матрицей тогда, когда определитель матрицы AA равен нулю, и невырожденной, если определитель не равен нулю.
В том случае, если обратная матрица может существовать, то она будет единственной.
Формула для вычисления обратной матрицы
Обратную матрицу A−1A^{-1} к матрице AA можно найти по формуле:
A−1=1detA⋅A∗A^{-1}=frac{1}{det A}cdot A^*
detAdet A — определитель матрицы A,A,
A∗A^* — транспонированая матрица алгебраических дополнений к матрице A.A.
Нужно найти обратную матрицу для следующей матрицы:
A=(1−20 342 −131)A = begin{pmatrix}
1& -2 & 0\
3 & 4 & 2\
-1& 3& 1 \
end{pmatrix}
Решение
Вычислим детерминант:
detA=∣1−20342−131∣=1∣4231∣−(−2)∣32−11∣+0∣34−13∣=8det A = begin{vmatrix}
1 & -2 & 0 \
3 & 4 & 2 \
-1 & 3 & 1 \
end{vmatrix} = 1 begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} – (-2) begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} +0 begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 8
Так как detA≠0det A neq 0, то матрица – невырожденная, и обратная для нее существует.
Посчитаем алгебраические дополнение:
A11=(−1)1+1∣4231∣=−2,A_{11} = (-1)^{1+1} begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} = -2,
A12=(−1)1+2∣32−11∣=−5,A_{12} = (-1)^{1+2} begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} = -5,
A13=(−1)1+3∣34−13∣=13A_{13} = (-1)^{1+3} begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 13,
A21=(−1)2+1∣−2031∣=2A_{21} = (-1)^{2+1} begin{vmatrix}
-2 & 0 \
3 & 1 \
end{vmatrix} = 2,
A22=(−1)2+2∣10−11∣=1A_{22} = (-1)^{2+2} begin{vmatrix}
1 & 0 \
-1 & 1 \
end{vmatrix} = 1,
A23=(−1)2+3∣1−2−13∣=−1A_{23} = (-1)^{2+3} begin{vmatrix}
1 & -2 \
-1 & 3 \
end{vmatrix} = -1,
A31=(−1)3+1∣−2042∣=−4A_{31} = (-1)^{3+1} begin{vmatrix}
-2 & 0 \
4 & 2 \
end{vmatrix} = -4,
A32=(−1)3+2∣1032∣=−2A_{32} = (-1)^{3+2} begin{vmatrix}
1 & 0 \
3 & 2 \
end{vmatrix} = -2,
A33=(−1)3+3∣1−234∣=10.A_{33} = (-1)^{3+3} begin{vmatrix}
1 & -2 \
3 & 4 \
end{vmatrix} = 10.
Обратная матрица:
A−1=18(−22−4−51−213−110)A^{-1} = frac{1}{8} begin{pmatrix}
-2 & 2 & -4 \
-5 & 1 & -2 \
13 & -1 & 10 \
end{pmatrix}
Чтобы избежать ошибок, необходимо сделать проверку: для этого нужно посчитать произведение первоначальной матрицы на конечную. Если в результате получится единичная матрица, то вы нашли обратную матрицу безошибочно.
Найдите обратную матрицу для матрицы:
A=(13−25)A = begin{pmatrix}
1 & 3\
-2 & 5 \
end{pmatrix}
Решение
detA=11≠0→A−1det A= 11 neq 0 rightarrow A^{-1} – существует.
A11=(−1)1+1⋅5=5A_{11} = (-1)^ {1+1} cdot 5 = 5,
A12=(−1)1+2⋅(−2)=2A_{12} = (-1)^ {1+2} cdot (-2) = 2,
A21=(−1)2+1⋅3=−3A_{21} = (-1)^ {2+1} cdot 3 = -3,
A22=(−1)2+2⋅1=1.A_{22} = (-1)^ {2+2} cdot 1 = 1.
Ответ:
A−1=111(5−321)A^{-1} = frac{1}{11} begin{pmatrix}
5 & -3 \
2 & 1 \
end{pmatrix}
Нами был рассмотрен способ нахождения матрицы с помощью алгебраических дополнений. Существует еще один способ, который называется методом элементарных преобразований.
Метод элементарных преобразований
Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:
- перестановка местами любых двух рядов (строк или столбцов) матрицы;
- умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
- прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.
Рассмотрим алгоритм нахождения обратной матрицы данным методом.
Алгоритм нахождения обратной матрицы методом элементарных преобразований
- Из исходной матрицы AA и единичной матрицы EE того же порядка составить расширенную матрицу, т.е. матрицу вида (A∣E)begin{pmatrix}A|Eend{pmatrix}.
- С помощью элементарных преобразований над строками расширенной матрицы получить единичную матрицу слева от черты: (E∣A−1)begin{pmatrix}E|A^{-1}end{pmatrix}.
- Выписать обратную матрицу, которая находится справа от черты.
Найти матрицу K−1K^{-1}, если K=(1301)K=begin{pmatrix}1&3\0&1end{pmatrix}.
Из матрицы KK второго порядка и единичной матрицы второго порядка составим расширенную матрицу:
(1301∣1001)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №3, умноженную на -3:
(1301∣1001)∼(1001∣1−301)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}1&-3\0&1end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
K−1=(1−301)K^{-1}=begin{pmatrix}1&-3\0&1end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
K⋅K−1=(1301)⋅(1−301)=(1⋅1+3⋅01⋅(−3)+3⋅10⋅1+1⋅00⋅(−3)+1⋅1)=(1001)Kcdot K^{-1}=begin{pmatrix}1&3\0&1end{pmatrix}cdotbegin{pmatrix}1&-3\0&1end{pmatrix}=begin{pmatrix}1cdot1+3cdot0&1cdot(-3)+3cdot1\0cdot1+1cdot0&0cdot(-3)+1cdot1end{pmatrix}=begin{pmatrix}1&0\0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Найти матрицу F−1F^{-1}, если F=(110010033)F=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}.
Из матрицы FF третьего порядка и единичной матрицы третьего порядка составим расширенную матрицу:
(110010033∣100010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №2, умноженную на -1:
(110010033∣100010001)∼(100010033∣1−10010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на -3:
(100010033∣1−10010001)∼(100010003∣1−100100−31)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}.
Умножим строку №3 на 13frac{1}{3}:
(100010003∣1−100100−31)∼(100010001∣1−100100−113)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
F−1=(1−100100−113)F^{-1}=begin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
F⋅F−1=(110010033)⋅(1−100100−113)=(100010001)Fcdot F^{-1}=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}cdotbegin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}=begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Выполнение контрольных работ на заказ недорого от профильных авторов на бирже Студворк!
Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву и другим 200 предметам можно здесь всего за 10 минут.
Метод обратной матрицы (матричный способ)
Пусть задана система линейных алгебраических уравнений $$begin{cases} a_{11}x_1 + a_{12}x_2 + a_{13}x_3 = b_1 \ a_{21}x_1 + a_{22}x_2 + a_{23}x_3 = b_2 \ a_{31}x_1 + a_{32}x_2 + a_{33}x_3 = b_3 end{cases}.$$
Метод обратной матрицы подходит для решения систем линейных алгебраических уравнений в которых число строк совпадает с числом неизвестных переменных. Формула матричного метода выглядит следующим образом $$X = A^{-1} cdot B$$
Здесь $A^{-1}$ – это обратная матрица к матрице $A$, составленной из коэфициентов $a_{ij}$ в системе уравнений. $B$ – это вектор свободных членов, взятых из системы $$begin{pmatrix} x_1\x_2\x_3 end{pmatrix} = A^{-1} cdot begin{pmatrix} b_1 \ b_2 \ b_3 end{pmatrix}.$$
Важное замечание!
Для данного метода определитель матрицы $A$ не должен равняться нулю $det A neq 0$, так как это условие для существования обратной матрицы $A^{-1}$.
| Пример 1 |
| Решить систему уравнений методом обратной матрицы $$begin{cases} x_1+2x_2-x_3=2 \ 2x_1-3x_2 + 2x_3 = 2 \ 3x_1 + x_2 + x_3 = 8 end{cases}.$$ |
| Решение |
|
Составляем матрицу $$A = begin{pmatrix} 1&2&-1 \ 2&-3&2 \ 3&1&1 end{pmatrix}.$$ Прежде чем искать обратную матрицу, необходимо вычислить определитель и проверить то, что он неравен нулю. $$det A = begin{vmatrix} 1&2&-1 \ 2&-3&2 \ 3&1&1 end{vmatrix} = -3+12-2-9-2-4=-8 neq 0$$ Найдем обратную матрицу $A^{-1}$ с помощью единичной матрицы. Добавляем её к основной матрице сбоку. $$begin{pmatrix} 1&2&-1&|&1&0&0 \ 2&-3&2&|&0&1&0 \ 3&1&1&|&0&0&1 end{pmatrix}$$ Выполняем элементарные преобразования со строками приводим матрицу $A$ слева к единичной, а справа получаем обратную матрицу. Из второй строки вычитаем первую строчку, умноженную на 2. Из третьей строки вычитаем первую, умноженную на 3. $$begin{pmatrix} 1&2&-1&|&1&0&0 \ 2&-3&2&|&0&1&0 \ 3&1&1&|&0&0&1 end{pmatrix} sim begin{pmatrix} 1&2&-1&|&1&0&0 \ 0&-7&4&|&-2&1&0 \ 0&-5&4&|&-3&0&1 end{pmatrix}$$ Умножаем третью строку на 7 и вычитаем из неё вторую строчку, умноженную на 5. $$begin{pmatrix} 1&2&-1&|&1&0&0 \ 0&-7&4&|&-2&1&0 \ 0&0&8&|&-11&-5&7 end{pmatrix}$$ Теперь запускаем обратный ход. Умножаем вторую строку на 2 и вычитаем из неё третью. Умножаем первую строку на 8 и прибавляем к ней третью. $$begin{pmatrix} 8&16&0&|&-3&-5&7 \ 0&-14&0&|&7&7&-7 \ 0&0&8&|&-11&-5&7 end{pmatrix}$$ Умножаем первую строчку на 14 и прибавляем к ней вторую строчку, умноженную на 16. $$begin{pmatrix} 112&0&0&|&70&42&-14 \ 0&-14&0&|&7&7&-7 \ 0&0&8&|&-11&-5&7 end{pmatrix}$$ Теперь делим кажду строку на элемент стоящий на главной диагонали левой матрицы, чтобы получилась единичная. Первую строку делим на 112, вторую на (-14) и третью на 8. $$begin{pmatrix} 1&0&0&|&frac{70}{112}&frac{42}{112}&frac{-14}{112} \ 0&1&0&|&-frac{7}{14}&-frac{7}{14}&frac{7}{14} \ 0&0&1&|&-frac{11}{8}&-frac{5}{8}&frac{7}{8} end{pmatrix}$$ Итак, слева получилась обратная матрица $$A^{-1} = begin{pmatrix} frac{70}{112}&frac{42}{112}&frac{-14}{112} \ -frac{7}{14}&-frac{7}{14}&frac{7}{14} \ -frac{11}{8}&-frac{5}{8}&frac{7}{8} end{pmatrix}.$$ Теперь воспользуемся формулой $X = A^{-1} cdot B$, чтобы найти $x_1,x_2,x_3$ и тем самым решить поставленную задачу. Производим умножение обратной матрицы на столбец свободных членов $$begin{pmatrix} x_1\x_2\x_3 end{pmatrix} = begin{pmatrix} frac{70}{112}&frac{42}{112}&frac{-14}{70} \ -frac{7}{14}&-frac{7}{14}&frac{7}{14} \ -frac{11}{8}&-frac{5}{8}&frac{7}{8} end{pmatrix} cdot begin{pmatrix} 2\2\8 end{pmatrix} =$$ Произведение ищем по правилу умножения двух матриц. Напоминаем, находим сумму произведения элементов строк на столбец. $$=begin{pmatrix} frac{2cdot70}{112} + frac{2cdot42}{112} -frac{8cdot14}{112} \ -frac{2cdot7}{14} – frac{2cdot7}{14} + frac{8cdot7}{14} \ -frac{2cdot11}{8} -frac{2cdot5}{8} + frac{8cdot7}{8} end{pmatrix} = begin{pmatrix} 1\2\3 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x_1 = 1, x_2=2, x_3=3$$ |
| Пример 2 |
| Решить систему уравнений матричным методом $$begin{cases} x_1+2x_2=10 \ 3x_1+2x_2+x_3=23 \ x_2+2x_3=13 end{cases}.$$ |
| Решение |
|
Составляем матрицу из коэффициентов $$A = begin{pmatrix} 1&2&0 \ 3&2&1 \ 0&1&2 end{pmatrix}$$ Находим обратную матрицу с помощью единичной матрицы. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 3&2&1 &|& 0&1&0 \ 0&1&2 &|& 0&0&1 end{pmatrix}$$ Из второй строки вычитаем первую, умноженную на 3. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 0&-4&1 &|& -3&1&0 \ 0&1&2 &|& 0&0&1 end{pmatrix}$$ Умножаем третью строчку на 4 и прибавляем к ней вторую. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 0&-4&1 &|& -3&1&0 \ 0&0&9 &|& -3&1&4 end{pmatrix}$$ Начинаем обратный ход элементарных преобразований. Умножаем вторую строку на 9 и вычитаем третью. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 0&-36&0 &|& -24&8&-4 \ 0&0&9 &|& -3&1&4 end{pmatrix}$$ Умножаем первую строку на 18 и прибавляем к ней вторую. $$begin{pmatrix} 18&0&0 &|& -6&8&-4 \ 0&-36&0 &|& -24&8&-4 \ 0&0&9 &|& -3&1&4 end{pmatrix}$$ Остаётся получить единицы на главной диагонали. Для этого делим первую строку на 18, вторую на (-36) и третью 9. $$begin{pmatrix} 1&0&0 &|& -frac{6}{18}&frac{8}{18}&-frac{4}{18} \ 0&1&0 &|& frac{24}{36}&-frac{8}{36}&frac{4}{36} \ 0&0&1 &|& -frac{3}{9}&frac{1}{9}&frac{4}{9} end{pmatrix}$$ Итак, выписываем полученную обратную матрицу $$A^{-1} = begin{pmatrix} -frac{6}{18}&frac{8}{18}&-frac{4}{18} \ frac{24}{36}&-frac{8}{36}&frac{4}{36} \ -frac{3}{9}&frac{1}{9}&frac{4}{9} end{pmatrix}.$$ Теперь пользуйся формулой $X = A^{-1} cdot B$ вычисляем $$begin{pmatrix} x_1\x_2\x_3 end{pmatrix} = begin{pmatrix} -frac{6}{18}&frac{8}{18}&-frac{4}{18} \ frac{24}{36}&-frac{8}{36}&frac{4}{36} \ -frac{3}{9}&frac{1}{9}&frac{4}{9} end{pmatrix} cdot begin{pmatrix} 10\23\13 end{pmatrix} = $$ Умножение производится по правилу произведения двух матриц: сумма произведений элементов строк первой матрицы на элементы второй матрицы. $$ = begin{pmatrix} -frac{6cdot10}{18}+frac{8cdot23}{18}-frac{4cdot13}{18} \ frac{24cdot10}{36}-frac{8cdot23}{36}+frac{4cdot13}{36} \ -frac{3cdot10}{9}+frac{23}{9}+frac{4cdot13}{9} end{pmatrix} = begin{pmatrix} 4\3\5 end{pmatrix}$$ Вот таким вот образом матричный метод помогает решать системы линейных алгебраических уравнений. Главное не забывать что данный способ работает, если определитель матрицы $A$ не равен нулю и число переменных в системе совпадает с числом уравнений. |
| Ответ |
| $$x_1 = 4, x_2 = 3, x_3 = 5$$ |