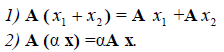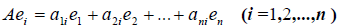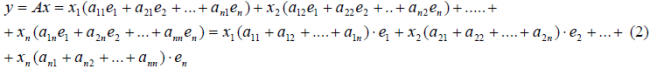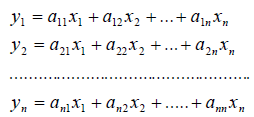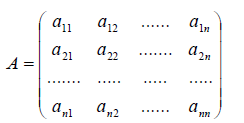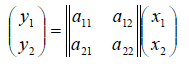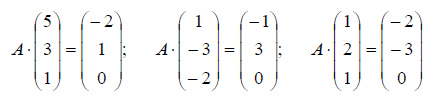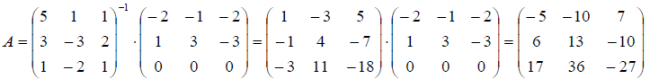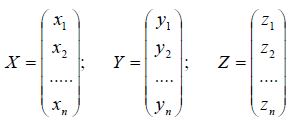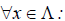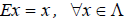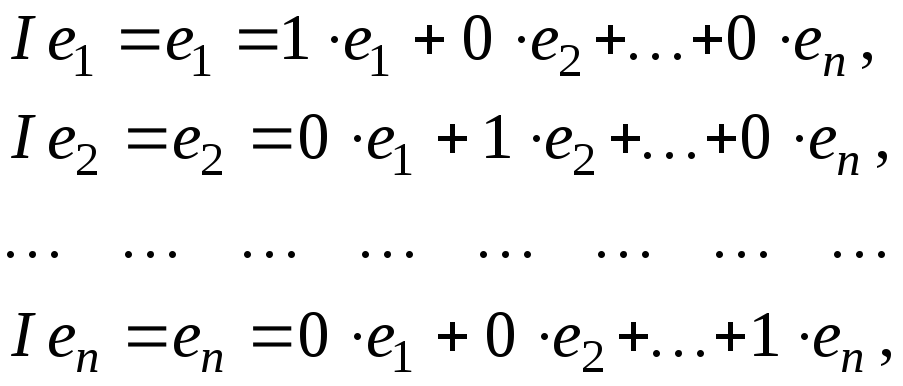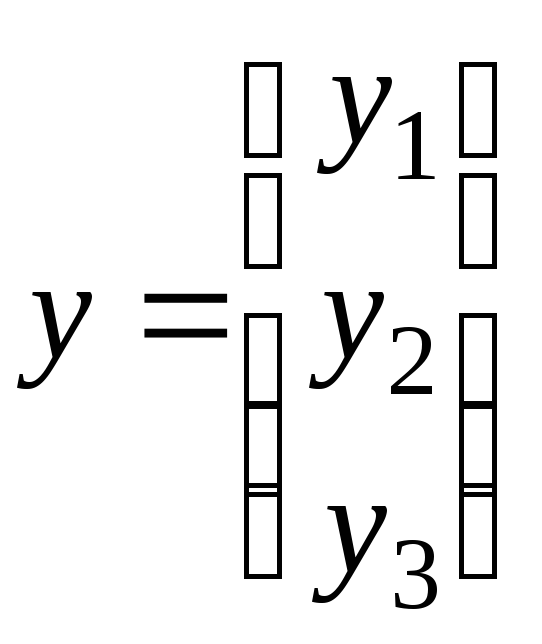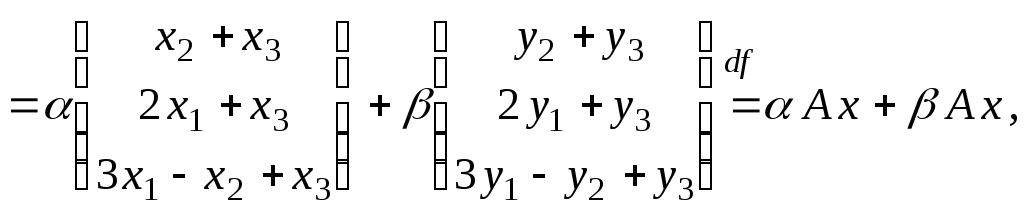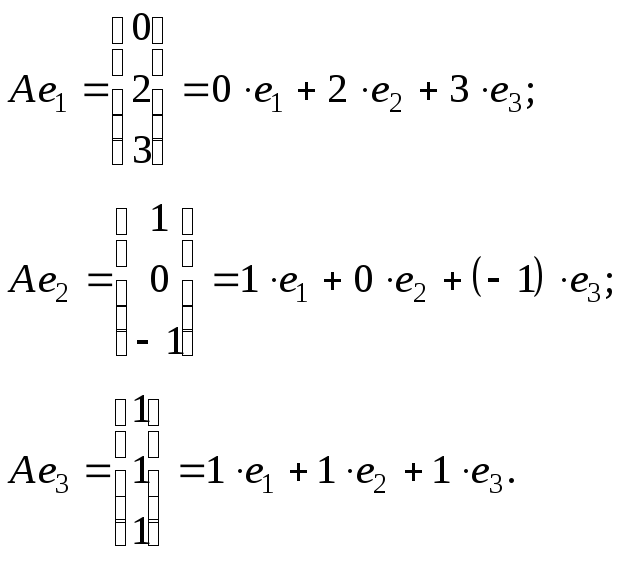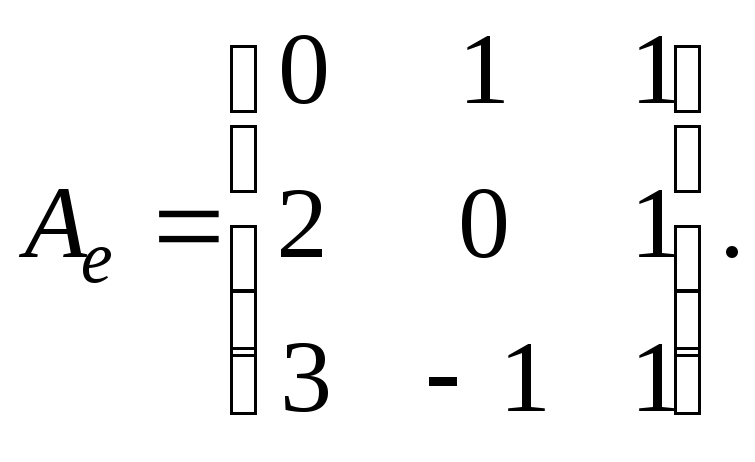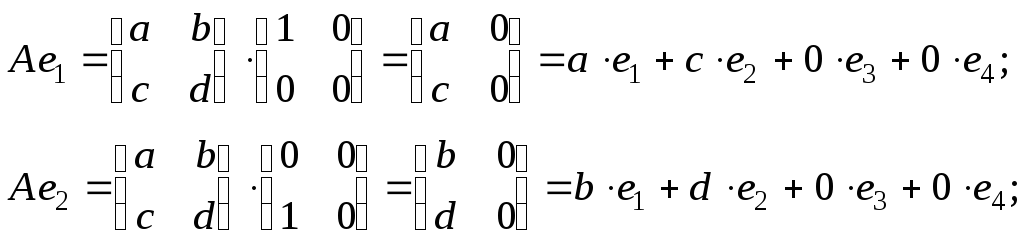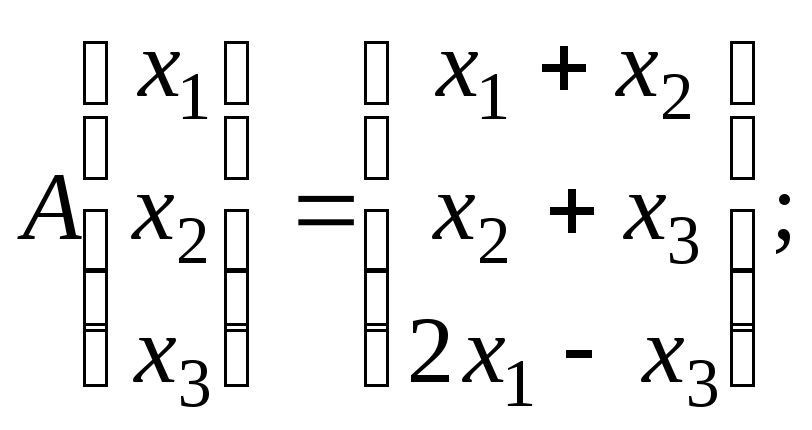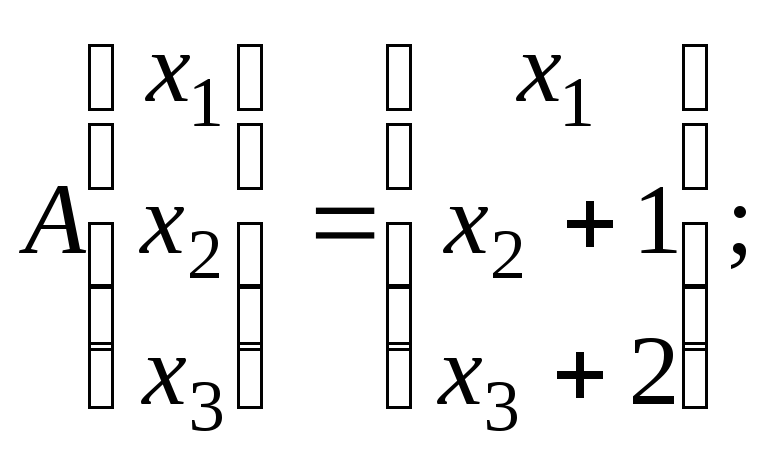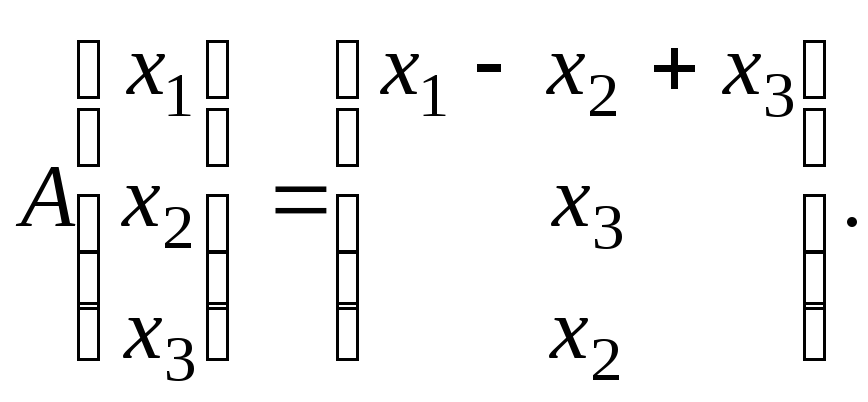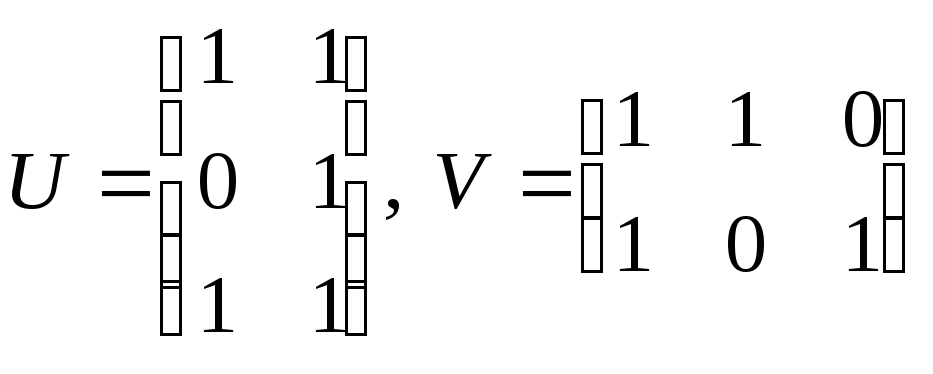4.3.5 Линейный оператор и его матрица
Определение. Пусть даны два пространства 




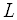
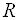

Обозначение: 
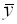
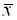
Определение. Если для любых 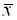
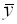
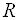
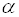


Произвольные отображения линейных пространств изучаются в курсе математического анализа. В курсе линейной алгебры изучаются лишь линейные отображения.
Пример 6. Оператор 
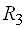
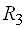


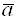


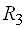
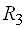

Пример 7. Линеен ли оператор 
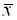
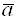
Решение. 



Пусть даны два пространства 








Подействовав оператором 




Строим матрицу 



Матрица 




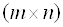
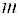
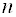
Замечание. Если в 

Из определения матрицы линейного оператора следует, что, зная закон (оператор), по которому вектору 

Пример 8. Построить матрицу линейного оператора, действующего из 
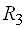



Решение. Подействуем оператором на базисные векторы 



Таким, образом, 
Пример 9. Пусть в 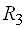
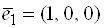
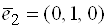
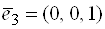



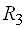



Решение. 



Пример 10. Дана матрица 
Решение. Матрица 

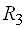


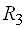





Пусть 





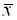

Учитывая (1), имеем:

Таким образом, оператор 

Зная матрицу оператора 
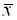

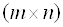



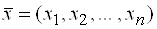


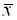

Где 

Пример 11. Операторы 






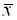


Решение. Координаты вектора 
А) найдем матрицу 
Строим матрицу 




Строим матрицу 






Этот способ решения называется матричным;
Б) операторный способ.






Для самостоятельной работы.
1. Оператор 

Найти его матрицу в каноническом базисе.
Ответ: 
2. Оператор 


Ответ: 
3. Дана матрица 
А) Найти оператор, матрицей которого является матрица 
Б) Найти образ вектора 
Ответ: 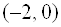
Как найти матрицу линейного оператора в базисе
Построение матрицы по заданной формуле отображения.
Пусть отображение задано с помощью формулы:
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор , найдём его образ, это будет вектор . Для этого в формуле, задающей образ вектора, полагаем , ,…, . Аналогично находим образы для ,…, . Из координат образа вектора составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.
Пример 1. Пусть оператор задан с помощью формулы:
Прежде всего, докажем, что это отображение – действительно линейный оператор.
Отобразим сумму векторов:
Теперь каждую координату получившегося вектора можем преобразовать:
Аналогично для умножения на константу:
Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x1 = 1, x2 = 0, а затем x1 = 0, x2 = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).
Поэтому матрица линейного оператора будет иметь вид:
Аналогичным способом решается задача и для 3 и большего количества переменных.
Пример 2. .
Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).
Матрица линейного оператора:
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.
Если задана система из n векторов, образующих базис, и какая-нибудь произвольная система n векторов (возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.
Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.
Пусть — матрица оператора в базисе . По условию, для всех индексов . Данные n равенств можно записать в виде одного матричного равенства: , при этом столбцы матрицы — это векторы , а столбцы матрицы — векторы . Тогда матрица может быть найдена в виде .
Пример. Найти матрицу линейного оператора, отображающего базис
в систему векторов .
Здесь , , , и получаем:
Проверка осуществляется умножением получившейся матрицы на каждый вектор: .
Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.
2.3. Прочие способы нахождения матрицы оператора.
Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида и . Построим матрицу одного из этих операторов, . Для этого найдём образы всех трёх базисных векторов линейного пространства.
Координаты полученных векторов запишем в виде столбцов матрицы оператора.
Аналогично можно построить матрицу линейного оператора :
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы , , ,…, .
Матрица этого линейного оператора:
Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8829 — | 7543 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Матрица линейного оператора
Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:
Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:
Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .
Разложим векторы x и y по базису e 1 ,e 2 . e n :
В силу линейности оператора A можно написать
Заметим, что каждый вектор 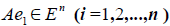
В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:
Получили, что линейному оператору A в данном базисе соответствует квадратная матрица
которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .
Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .
Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .
Примеры линейных операторов
1. В пространстве 2-мерных векторов линейным оператором является правило
связывающее вектор-прообраз 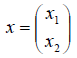
2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.
3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .
Пример: Известны образы базисных векторов E 3 под действием оператора A :
Найти матрицу этого оператора в исходном базисе.
Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем
Действия над операторами
Сложение линейных операторов. Пусть x?E n , A и B — два линейных оператора в этом пространстве.
Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .
Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B — матрицы линейных операторов A и B .
Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? — некоторое число.
Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством 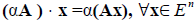
?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.
Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .
Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .
Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .
Рассмотрим матрицы – столбцы:
и обозначим через A, B и C — соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.
a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y
б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x
Свойства умножения линейных операторов вытекают из свойств умножения матриц.
Определение 4. Линейные операторы A и В называются равными, если 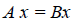
Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 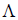
        7.31 .
Решение
        Составим матрицу перехода из координатных столбцов векторов         в базисе         . Получим . Найдём обратную матрицу, используя метод элементарных преобразований над строками. Припишем единичную матрицу справа от матрицы перехода         Первую строку прибавим ко второй и вычтем из третьей, получим         Вторую строку прибавим к первой и дважды вычтем из третьей, получим         Третью строку умножим на (-1). Третью строку, умноженную на (-1) прибавим к первой, получим         Поменяем местами вторую и третью строки         Получилась матрица, которая содержит единичную матрицу слева. Следовательно, в правой части стоит искомая обратная матрица         Сделаем проверку:         Следовательно, обратная матрица найдена верно.
        Матрицу преобразования в базисе         найдём по формуле        
        Ищем произведение
        Тогда
ВНИМАНИЕ! Обратная матрица для всех задач найдена на этой странице. См. выше.
    Вариант 3     Вариант 4     Вариант 6     Вариант 7     Вариант 9     Вариант 11
    Вариант 14     Вариант 18     Вариант 19     Вариант 20     Вариант 21     Вариант 24
    Вариант 25     Вариант 26     Вариант 30     Вариант 31
Линейный оператор
Линейное отображение линейного (векторного) пространства $ mathbb V_ $ в себя $$ mathcal A : mathbb V longmapsto mathbb V $$ называется линейным преобразованием $ mathbb V_ $ или линейным оператором 1) на $ mathbb V_ $.
Напомню свойство линейности: $$ mathcal A (X_1 +X_2)= mathcal A(X_1) + mathcal A(X_2),quad mathcal A (alpha_1 X_1)= alpha_1 mathcal A (X_1), $$ или, в эквивалентном виде: $$ mathcal A(alpha_1 X_1 + alpha_2 X_2)= alpha_1 mathcal A(X_1) + alpha_2 mathcal A(X_2) $$ для $ forall subset mathbb V, forall subset mathbb R mbox mathbb C $ (здесь $ alpha_1,alpha_ 2 $ — константы из $ mathbb R_ $ если $ mathbb V_ $ вещественное пространство, и из $ mathbb C_ $, если оно комплексное).
Примеры линейных операторов
Бóльшую часть примеров пункта ☞ ПРИМЕРЫ ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ представляют именно линейные операторы. Укажу еще несколько, к которым буду часто обращаться.
Все это — примеры линейных операторов. Но вот отображение сдвига $ (x,y,z) mapsto (x+1,y,z+2) $ оператором не является поскольку $$ alpha > (x,y,z) = ( alpha > x, alpha > y, alpha > z) mapsto ( alpha > x+1, alpha > y, alpha > z+2) ne alpha > (x+1,y,z+2) . $$
Пример 2. В пространстве $ mathbb R^ $ отображение ортогонального проецирования на плоскость $ x+y-7, z=0 $ будет линейным оператором (а вот на плоскость $ x+y-7, z=1 $ — не будет!). Вообще, в произвольном пространстве $ mathbb V_ $ разбитом в прямую сумму нетривиальных подпространств $ mathbb V= mathbb V_1 oplus mathbb V_2 $ отображение, сопоставляющее вектору $ X_ $ его проекцию на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_2 $, будет оператором.
Пример 3. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степеней $ le 3 $ отображение $ mathcal A_ $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ т.е. полином $ f_(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Это отображение будет оператором в $ mathbb P_3 $. Действительно, если $$ beginf_1(x)(x^2-2) equiv q_1(x)(x^4-x^3-x^2+x)+ r_1(x), , \ f_2(x)(x^2-2) equiv q_2(x)(x^4-x^3-x^2+x)+ r_2(x) , end $$ при $ subset mathbb R[x], deg r_1(x) le 3, deg r_2(x) le 3 $, то $$ (alpha_1 f_1(x)+alpha_2 f_2(x)) (x^2-2) equiv (alpha_1 q_1(x)+alpha_2 q_2(x))(x^4-x^3-x^2+x)+ (alpha_1 r_1(x)+alpha_2 r_2(x)) ; $$ очевидно, что $ deg (alpha_1 r_1(x)+alpha_2 r_2(x)) le 3 $. ♦
Пример 4. Задачу интерполяции можно интерпретировать как построение некоторого отображения. В интерполяционной таблице
$$ beginx & x_1 & x_2 & dots & x_n \ hline y & y_1 & y_2 &dots & y_n end qquad npu qquad , dots, x_, y_,dots,y_ > subset mathbb C $$ будем считать узлы $ _^n $ фиксированными, а значения $ _^n $ — переменными. Эта таблица однозначно определяет интерполяционный полином $ f(x)=A_+A_1x+dots+A_x^ $ со свойством $ f(x_j)=y_j $ при $ j in $. При этом $ >_^ subset mathbb C $. Будет ли получившееся отображение $$ (y_1,dots,y_n) mapsto (A_0,A_1,dots,A_) $$ оператором на $ mathbb C^n $? Покажем, что отображение $$ mathcal A(y_1,dots,y_n) = f(x) in mathbb C[x] $$ является линейным отображением. Действительно, решением задачи интерполяции для таблицы $$ beginx & x_1 & x_2 & dots & x_n \ hline y & alpha y_1 & alpha y_2 &dots & alpha y_n end qquad npu qquad forall alpha in mathbb C $$ является полином $ alpha f(x) $. Если же, вдобавок, решением задачи интерполяции для таблицы $$ beginx & x_1 & x_2 & dots & x_n \ hline y & z_1 & z_2 &dots & z_n end qquad npu qquad ,dots,z_ > subset mathbb C $$ является полином $ g(x)in mathbb C[x], deg g(x) le n-1 $, то решением задачи интерполяции для таблицы $$ beginx & x_1 & x_2 & dots & x_n \ hline y & y_1+z_1 & y_2+z_2 &dots & y_n+z_n end qquad $$ будет полином $ f(x)+g(x) $ и этот полином будет единственным решением среди полиномов степеней $ le n-1 $. Таким образом, линейность отображения $ mathcal A $ установлена. Далее, множество $ mathbb P_ $ полиномов из $ mathbb C[x] $ степеней $ le n-1 $ изоморфно пространству $ mathbb C^n $. Следовательно, «сложное» отображение $$ (y_1,dots,y_n) mapsto f(x)=A_+A_1x+dots+A_x^ mapsto (A_0,A_1,dots,A_) $$ является линейным отображением из $ mathbb C^n $ в $ mathbb C^n $, т.е. оператором на $ mathbb C^n $.
По аналогии с задачей алгебраической интерполяции, можно поставить и задачу тригонометрической интерполяции. Имеем здесь «точку входа» в теорию дискретного преобразования Фурье. ♦
В пространстве $ mathbb P_2 $ оператор действует следующим образом:
$$ mathcal A (x^2+x+1) =2,x+1, mathcal A (x^2-x-1) =2,x^2-1, mathcal A (x+1) =-x^2+x+1 . $$ Вычислить $ mathcal A (x^2) $ и $ mathcal A (x^2+1) $.
Пример 5. В пространстве полиномов степени не выше $ n_ $ с вещественными коэффициентами от $ m_ $ переменных $ x_1,x_2,dots,x_ $ отображение
$$ f(x_1,x_2,dots,x_m) mapsto frac +frac+ dots+ frac $$ яыляется линейным оператором. Этот оператор известен как оператор Лапласа и для него используется символьное обозначение $$ Delta = frac +frac+ dots+ frac , . $$
Пример 6. В линейном пространстве квадратных матриц порядка $ n_ $ с вещественными элементами рассмотрим коммутирующее отображение
$$ mathcal K (X) = AX-XA , $$ а также отображение Ляпунова $$ mathcal V (X) = A^X+XA $$ при произвольной фиксированной квадратной матрице $ A_ $ и $ ^ $ означающем транспонирование. Легко проверить, что оба отображения $ mathcal K $ и $ mathcal V $ являются операторами. ♦
Основные определения
Все введенные для линейного отображения понятия переносятся на этот частный случай. Например, ядром оператора называется множество векторов, отображаемых оператором в нулевой вектор: $$mathcaler (mathcal A)= left ; $$ а образом оператора называется множество всех векторов из $ mathbb V_ $, для каждого из которых существует прообраз в том же пространстве: $$mathcalm (mathcal A)= left .$$
Теорема 1. Множества $ mathcaler (mathcal A) $ и $ mathcalm (mathcal A) $ являются подпространствами пространства $ mathbb V_ $.
Доказать, что для оператора в $ mathbb R^4 $
$$ mathcal A left(beginx_1 \ x_2 \ x_3 \ x_4 end right)= left(beginx_3 \ x_4 \ 0 \ 0 end right) $$ имеет место равенство $ mathcaler (mathcal A) = mathcalm (mathcal A) $.
Для оператора $ mathcal A_ $ его дефектом его называется размерность ядра, а его рангом — размерность образа: $$ operatorname(mathcal A )=dim (mathcaler (mathcal A )) , operatorname(mathcal A )= dim (mathcalm (mathcal A )) . $$ Оператор называется невырожденным если $ operatorname(mathcal A )=0 $.
Пример. В пространстве $ mathbb R^ $ оператор проецирования на плоскость:
$$ mathcal A left(x, y, zright) longmapsto left(x, y, 0 right) $$ является вырожденным поскольку его ядро нетривиально: $ mathcaler (mathcal A)= $. ♦
Следующий результат является следствием теоремы $ 4 $ из ☞ ПУНКТА.
Теорема 2. Имеет место равенство:
$$ dim mathbb V=dim left( mathcaler (mathcal A) right) + dim left( mathcalm (mathcal A) right) = operatorname(mathcal A )+ operatorname(mathcal A ) .$$
Отображение $ mathcal P: mathbb V longmapsto mathbb V $ называется произведением оператора $ mathcal A $ на оператор $ mathcal B $ если $ mathcal P(X)=mathcal A (mathcal B(X)) $ для любого $ Xin mathbb V_ $. Записывать этот факт будем в виде $ mathcal P=mathcal A , mathcal B $.
Теорема 3. Произведение операторов является оператором на $ mathbb V_ $. Операция произведения ассоциативна.
Доказательство. Имеем на основании свойства линейности $$mathcal P (alpha_1X_1+alpha_2X_2)= mathcal A (mathcal B(alpha_1X_1+alpha_2X_2))=mathcal A (alpha_1mathcal B(X_1)+ alpha_2mathcal B(X_2))=$$ $$=alpha_1mathcal A (mathcal B(X_1))+ alpha_2mathcal A (mathcal B(X_2))=alpha_1mathcal P(X_1)+alpha_2(X_2).$$
Далее, для любого вектора $ X_ $: $$mathcal A_1(mathcal A_2mathcal A_3(X))= mathcal A_1(mathcal A_2(mathcal A_3(X)))=mathcal A_1mathcal A_2(_3(X)) ,$$ откуда и следует ассоциативность. ♦
Говорят, что операторы $ mathcal A $ и $ mathcal B $ коммутируют если $ mathcal A , mathcal B = mathcal B , mathcal A $.
Пример. В пространстве полиномов $ mathbb P_ $ рассмотрим дифференциальный оператор
$$mathcal A = xfractimes Box — 1times Box : mathcal A(p(x)) = x p'(x) — p(x) .$$ Этот оператор не коммутирует с обычным оператором дифференцирования $ displaystyle mathcal B= frac$: $$mathcal A (x^2)=x^2, quad mathcal B (mathcal A(x^2))=2,x, quad mathcal B (x^2)=2,x, quad mathcal A (mathcal B (x^2))=0 .$$ ♦
Оператор $ mathcal E $, отображающий произвольный вектор $ Xin mathbb V_ $ в себя : $ mathcal E(X)= X $, называется тождественным на $ mathbb V_ $. Оператор $ mathcal B $ называется (левым) обратным оператору $ mathcal A_ $, если $ mathcal Bmathcal A=mathcal E $. В этом случае оператор $ mathcal A_ $ называют обратимым и записывают: $ mathcal B=mathcal A^ $.
Не всякий оператор обратим.
Пример. В пространстве $ mathbb R^ $ для оператора проецирования на плоскость:
$$ mathcal A left(x, y, zright) longmapsto left(x, y, 0 right) $$ обратного не существует, т.к. $ mathcal A(0,0,1)=(0,0,0) $ и ни при каком выборе оператора $ mathcal B $ нельзя добиться выполнения равенства $ mathcal B(0,0,0)=(0,0,1) $. ♦
Показать, что обратным для оператора
$$fracint_0^x : p(x) longmapsto fracint_^ p(t) d, t ,$$ на $ mathbb P_ $ является оператор $$ fracleft(xtimes Box right) : p(x) longmapsto (xp(x))’ .$$
Теорема 4. Оператор $ mathcal A_ $ обратим тогда и только тогда, когда когда он невырожден: $ operatorname (mathcal A) =0 $. В этом случае $ mathcal A^ $ единствен и коммутирует с $ mathcal A $.
При $ Kin mathbb N $ и $ K>1 $, $ K_ $-я степень оператора $ mathcal A $ определяется рекурсивной формулой $$mathcal A^=mathcal A (mathcal A^) .$$ Если, вдобавок, $ mathcal A $ невырожден, то отрицательная степень оператора определяется формулой $$mathcal A^=left(mathcal A^right)^K . $$ Полагают также $ mathcal A^= $ для любого $ mathcal A ne $.
Теорема 5. Степени оператора $ mathcal A $ коммутируют:
$$mathcal A^ mathcal A^=mathcal A^mathcal A^=mathcal A^ .$$
Пример. $ K_ $-й степенью оператора дифференцирования в пространстве полиномов $ mathbb P_ $ будет оператор нахождения $ K_ $-й производной:
$$left( fracright)^K = frac .$$ Очевидно, что при $ K_>n $ этот оператор будет нулевым. ♦
Пример. В произвольном пространстве $ mathbb V_ $ разбитом в прямую сумму нетривиальных подпространств $ mathbb V= mathbb V_1 oplus mathbb V_2 $ оператор проецирования $ mathcal P $ на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_2 $ обладает свойством $ mathcal P^2 = mathcal P $ (проецирование проекции оставляет ее на месте). ♦
Оператор $ mathcal A $, обладающий свойством $ mathcal A^2 = mathcal A $, называется идемпотентным 3) .
Пример. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ отображение $ mathcal A_ $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ т.е. полином $ f_(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Для этого оператора $ K_ $-й его степенью является оператор $$ mathcal B (f(x)) = f(x) (x^2-2)^K pmod . $$ Действительно, если $$ f(x)(x^2-2) equiv q(x)(x^4-x^3-x^2+x)+ r(x) $$ при $ subset mathbb R[x] $ и $ deg r(x) le 3 $, то $$ f(x)(x^2-2)^2 equiv q(x)(x^4-x^3-x^2+x)(x^2-2)+ r(x)(x^2-2) . $$ Но тогда $$ mathcal A^2 (f(x))= mathcal A (r(x)) = r(x) (x^2-2) pmod equiv $$ $$ equiv f(x)(x^2-2)^2 pmod . $$ Завершает доказательство святая индукция по степени $ K_ $… ♦
Пусть задан произвольный полином $ g(x)=b_x^m+b_1x^+dots+b_m $ из $ mathbb R[x] $ или $ mathbb C[x] $. Выражение $$g(mathcal A )= b_0mathcal A^+b_1mathcal A^+dots+b_m$$ будем называть операторным полиномом.
Доказать, что операторные полиномы коммутируют: $ g_1(mathcal A )g_2(mathcal A )=g_2(mathcal A )g_1(mathcal A ) $.
Доказать, что для любого $ mathcal A in om(mathbb V,mathbb V) $ всегда найдется полином $ g_(x) $, $ deg g le n^2+1 $ такой, что $ g(mathcal A)= $.
Сформулируем еще один результат, являющийся частным случаем приведенного в пункте ☞ СВОЙСТВА ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ.
Теорема 6. Пусть $ $ — произвольный базис $ mathbb V_ $, а $ Y_1,Y_2,dots,Y_n $ — произвольные векторы того же пространства. Существует единственный оператор $ mathcal A: mathbb V longmapsto mathbb V $ такой, что
$$ mathcal A(X_1)=Y_1,mathcal A(X_2)=Y_2, dots,mathcal A(X_n)=Y_n .$$
Доказательство. Искомый оператор строится следующим образом. Если $ X=x_1X_1+x_2X_2+dots+x_nX_n $ — разложение произвольного вектора $ X in mathbb V $ по базису, то $$ mathcal A(X)=x_1 Y_1+x_2Y_2+dots+ x_nY_n . $$ Единственность этого оператора доказывается от противного. Любой другой оператор $ mathcal B $, удовлетворяющий условиям $ _^n $, будет действовать на тот же вектор $ X_ $ с тем же результатом: $$ mathcal B(X)=x_1 mathcal B(X_1)+x_2mathcal B(X_2) +dots+ x_nmathcal B(X_n)= x_1 Y_1+x_2Y_2+dots+ x_nY_n= mathcal A(X) . $$ ♦
Таким образом, оператор — как функция, действующая в $ n_ $-мерном линейном пространстве, однозначно определяется заданием на $ n_ $ линейно независимых векторах. В доказательстве теоремы дается и конструктивный способ представления оператора по этим значениям (т.е. строится его “интерполяционная формула” ).
Матрица оператора
Рассмотрим оператор $ mathcal A $ на $ mathbb V_ $ и пусть $ $ — базис $ mathbb V_ $. Являясь частным случаем линейного отображения, оператор должен обладать и соответствующей матрицей. Существенной особенностью, отличающей наш случай от рассмотренного в пункте ☞ МАТРИЦА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ, является невозможность произвола при выборе базиса для $ mathcalm (mathcal A) $. Поскольку $ mathcalm (mathcal A) $ является подпространством $ mathbb V_ $, то было бы слишком большой роскошью иметь два разных базиса для одного и того же пространства.
Найдем координаты образов базисных векторов $ mathcal A (X_1),dots,mathcal A (X_n) $ в том же базисе $ $: $$ left mathcal A(X_1)&=& alpha >>_X_1+ alpha >>_X_2+dots+ alpha >>_X_n, \ mathcal A(X_2)&=& alpha >>_X_1+ alpha >>_X_2+dots+ alpha >>_X_n, \ dots & & qquad dots , \ mathcal A(X_n)&=&alpha_X_1+alpha_X_2+dots+alpha_X_n. end right. $$ Матрица $$ mathbf A= left(beginalpha >>_ & alpha >>_& dots & alpha_ \ alpha >>_ & alpha >>_& dots & alpha_ \ dots & & & dots \ alpha >>_ & alpha >>_& dots & alpha_ end right)_, $$ в столбцах которой стоят координаты образов базисных векторов, называется матрицей оператора $ mathcal A_ $ в базисе $ $.
Пример. Известны образы базисных векторов $ mathbb R^ $ под действием оператора $ mathcal A_ $:
$$mathcal A left( begin5 \ 3 \ 1 endright)= left( begin-2 \ 1 \ 0 endright) , mathcal A left( begin1 \ -3 \ -2 endright) = left( begin-1 \ 3 \ 0 endright) , mathcal A left( begin1\ 2 \ 1 endright)= left( begin-2 \ -3 \ 0 endright) . $$ Найти матрицу этого оператора в исходном базисе.
Решение. Элементы матрицы $ $ ищутся по формулам из определения, которые можно переписать в матричном виде: $$left[ X_1,dots,X_n right] =left[ mathcal A (X_1),dots,mathcal A (X_n) right] .$$ Откуда $$= left[ X_1,dots,X_n right]^ left[ mathcal A (X_1),dots,mathcal A (X_n) right] ,$$ и для нашего примера эта формула дает $$ = left(begin5&1&1 \ 3&-3&2 \ 1&-2&1 endright)^ left(begin-2&-1&-2 \ 1&3&-3 \ 0&0&0 endright) = $$ $$ =left(begin1&-3&5\ -1&4&-7\ -3&11&-18 endright) left(begin-2&-1&-2 \ 1&3&-3 \ 0&0&0 endright) = left(begin-5&-10&7\ 6&13&-10\ 17&36&-27 end right). $$ ♦
В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ оператор $ mathcal A_ $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^3+2,x^2+1) pmod , $$ т.е. полином $ f_(x) $ отображается в остаток от деления произведения $ f(x) (x^3+2,x^2+1) $ на $ x^4+4 $. Найти матрицу оператора $ mathcal A_ $ в базисе $ $.
Ответ. $$ left(begin1 & -4 & -8 & 0 \ 0 & 1 & -4 & -8 \ 2& 0 & 1 & -4 \ 1 & 2 & 0 & 1 end right) . $$
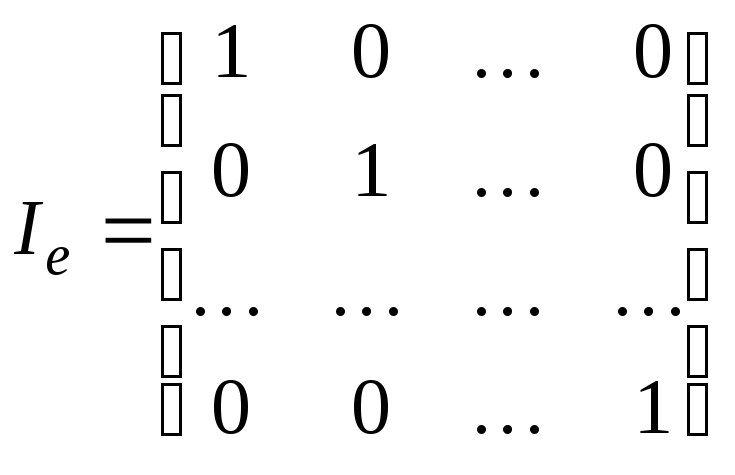
Теорема 1. Координаты произвольного вектора $ X=x_1X_1+dots+x_nX_n $ и его образа $ Y=mathcal A(X)=y_1X_1+dots+y_nX_n $ связаны формулой
$$ left(beginy_1 \ vdots \ y_n end right) = left(beginx_1 \ vdots \ x_n end right) . $$
Как изменяется матрица оператора при переходе к новому базису?
Доказательство ☞ ЗДЕСЬ.
Пример. Оператор $ mathcal A $ в базисе пространства $ mathbb R^ $
Матрицы $ $ и $ $, связанные соотношением $ =C^cdot cdot C $ при какой-то неособенной матрице $ C_ $, называются подобными, этот факт будем записывать: $ doteq $.
Доказать, что отношение подобия есть отношение эквивалентности, и если $ doteq $ то $ g()doteq g() $ при любом полиноме $ g_(x) $.
Теорема 3. Для оператора $ mathcal A_ $ ранг его матрицы является инвариантом, т.е. не зависит от выбора базиса пространства. Этот ранг совпадает с рангом оператора $ mathcal A_ $.
Доказательство. Если $ $ и $ $ — матрицы оператора в двух разных базисах, то они являются подобными: $ =C^ C $. По свойству ранга матрицы имеем: $ operatorname( )= operatorname() $. ♦
Дефект оператора $ mathcal A_ $ совпадает с дефектом его матрицы в произвольном базисе пространства.
Теорема 4. Для оператора $ mathcal A_ $ определитель и след его матрицы являются инвариантами, т.е. не зависят от выбора базиса пространства.
Доказательство. Действительно, для подобных матриц $ $ и $ $, на основании теоремы Бине-Коши имеем: $$ det () = det (C^ C) = det (C^) cdot det () cdot det (C) =det () . $$ Далее, по свойству следа матрицы: $$ operatorname() = operatorname(C^ C)=operatorname( cdot C cdot C^)=operatorname() . $$ ♦
Этот результат позволяет ввести понятие определителя и следа оператора $ mathcal A_ $ — посредством матрицы этого оператора в произвольном базисе пространства. Такое определение оказывается корректным поскольку оба значения не зависят от выбора базиса.
— Для ответа на этот вопрос рассмотрим оператор в $ mathbb R^2 $, заданный формулой: $$ left(beginy_1 \ y_2 end right)= left(begin1 & — 3 \ 1 & -1 end right) left(beginx_1 \ x_2 end right) . $$ Свойство линейности оператора как отображения плоскости проявляется в том, что параллельные отрезки он отображает в параллельные же отрезки (см. упражнение к теореме 2 из ☞ ПУНКТА ), и, следовательно, любой параллелограмм отображается им в параллелограмм. Площади соответствующих параллелограммов оказываются связанными через определитель матрицы — более точно, через модуль этого определителя. В частном случае настоящего примера это проверяется непосредственно; что касается обобщения на произвольное евклидово пространство, в котором понятие объема вводится аксиоматически то сошлюсь на упражнение 3 ☞ ЗДЕСЬ.
Иными словами: «физический» смысл определителя оператора заключается в том, что модуль его значения представляет коэффициент расширения 4) объема (в настоящем примере — площади) тела (соответственно, плоской фигуры) под воздействием этого оператора.
Теорема 5. Оператор обратим тогда и только тогда, когда когда его определитель отличен от нуля.
Теорема 6. Линейное пространство $ om(mathbb V,mathbb V) $ операторов на $ mathbb V_, dim mathbb V = n $ изоморфно линейному пространству квадратных матриц порядка $ n_ $ (с элементами из $ mathbb R_ $ или из $ mathbb C_ $).
Это утверждение является простым следствием теоремы 2, приведенной в пункте ☞ МАТРИЦА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ. Однако в случае операторов установленный изоморфизм сохранит не только результат операции сложения, но и результат операции умножения: $$ . mbox mathcal A_1 leftrightarrow mathbf A_1, mathcal A_2 leftrightarrow mathbf A_2, mbox mathcal A_1+ mathcal A_2 leftrightarrow mathbf A_1 + mathbf A_2, lambda mathcal A_1 leftrightarrow lambda mathbf A_1 , mathcal A_1 mathcal A_2 leftrightarrow mathbf A_1 mathbf A_2 . $$ Я сформулирую этот «усиленный вариант» изоморфизма в виде набора свойств, которыми буду пользоваться по мере возникновения потребности.
Теорема 7. В любом базисе пространства
а) матрица нулевого оператора $ mathcal O $ является нулевой матрицей $ mathbb O_ $, а матрица тождественного оператора $ mathcal E $ является единичной матрицей $ E_ $; обратно: если матрица оператора в этом базисе — нулевая (единичная), то оператор является нулевым (соответственно, тождественным);
б) матрица произведения операторов совпадает с произведением матриц этих операторов 5) ;
в) коммутирующим операторам соответствуют коммутирующие матрицы;
г) если $ $ — матрица оператора, то $ ^ $ — матрица обратного оператора;
д) если $ $ — матрица оператора $ mathcal A $, то матрицей операторного полинома $ g (mathcal A) $ является матрица $ g() $ .
Матрица оператора и матрица перехода от базиса к базису
Эти матрицы как-то взаимодействовали между собой в предыдущем пункте, хотя вторая была определена совершенно в другом разделе. Обе матрицы квадратные, обе имеют в определении «завязку» на базис пространства $ mathbb V_ $. У начинающих изучать теорию часто возникает путаница при различении этих определений.
«Физический» смысл этих понятий различен. Образно говоря, если рассматривать оператор как процесс (точнее: установленную связь между входными и выходными значениями процесса), то выбор базиса можно интерпретировать как выбор точки зрения на этот процесс (можно трактовать эти слова как формализацию выражения «рассмотрим этот процесс под другим углом»).
Тем не менее, с чисто формальной точки зрения, матрица $ C_ $ перехода от базиса $ $ пространства $ mathbb V_ $ к какому-то другому базису $ $ того же пространства может считаться матрицей некоторого оператора, действующего в этом пространстве. В самом деле, на основании теоремы, приведенной в конце ☞ ПУНКТА, существует единственный оператор $ mathcal C $, переводящий старые базисные векторы в новые, взятые в той же последовательности: $$ mathcal C (X_1)=mathfrak X_1, mathcal C (X_2)= mathfrak X_2, dots, mathcal C (X_n)= mathfrak X_n . $$ Но тогда, по определению, матрица оператора $ mathcal C $ в базисе $ $ совпадает с матрицей $ C_ $ перехода от базиса $ $ к базису $ $.
Я буду записывать матрицы операторов и матрицы переходов от базиса к базису в разных стилях: $ mathbf A, mathbf B,dots $ и, соответственно, $ C, P, T, dots $ — с целью быстрого распознавания их «физической» сущности.
Матрица оператора проецирования
Настоящий пункт может быть пропущен при первоначальном чтении.
Теорема. Рассмотрим линейную оболочку линейно независимой системы столбцов $ subset mathbb R^n $.
$$ mathbb M =left subset mathbb R right>= mathcal L (Y_1,dots,Y_k) , . $$ Пусть скалярное произведение векторов $ X_ $ и $ Y_ $ задается стандартным способом, т.е. $ langle X,Y rangle =x_1y_1+dots+x_ny_n $. Ближайшей к точке $ X_0 subset mathbb R^n $ точкой многообразия (или ортогональной проекцией точки $ X_0 $ на многообразие) $ mathbb M_ $ является $$ X_ = mathbf L (mathbf L^ mathbf L )^ mathbf L^ X_0 , . $$ Здесь $ mathbf L=[Y_1 |dots |Y_k]_ $.
Доказательство. Пусть $ X_0=X_0^>+X_0^> $, где $ X_0^> $ — ортогональная проекция точки $ X_0 $ на $ mathbb M $, а $ X_0^> $ — ортогональная составляющая. Тогда $$ mathbf L^ X_0^>=mathbb O $$ поскольку $ Y_1^ X_0^>=0,dots, Y_k^ X_0^>=0 $. Далее, $ X_0^> $ можно разложить по базису $ $: $$ X_0^>=alpha_1 Y_1+dots+ alpha_k Y_k quad npu quad subset mathbb R , . $$ Следовательно, $$ mathbf L^ X_0=mathbf L^ (X_0^>+X_0^>)=mathbf L^ X_0^>= mathbf L^ (alpha_1 Y_1+dots+ alpha_k Y_k)= $$ $$ =left( beginalpha_1 Y_1^ Y_1 +dots + alpha_k Y_1^ Y_k \ alpha_1 Y_2^ Y_1 +dots + alpha_k Y_2^ Y_k \ dots \ alpha_1 Y_k^ Y_1 +dots + alpha_k Y_k^ Y_k end right)= mathbf L^ mathbf L left( beginalpha_1 \ alpha_2 \ vdots \ alpha_k end right), . $$ Тогда $$ mathbf L (mathbf L^ mathbf L )^ mathbf L^ X_0= mathbf L left( beginalpha_1 \ alpha_2 \ vdots \ alpha_k end right) =alpha_1 Y_1+dots+ alpha_k Y_k= X_0^> , . $$ На основании теорем $ 1_ $ и $ 2_ $, приведенных ☞ ЗДЕСЬ, точка $ X_0^> $ является ближайшей точкой многообразия $ mathbb M $ к точке $ X_ $. ♦
Матрица $ P=mathbf L (mathbf L^ mathbf L )^ mathbf L^ $ является матрицей оператора ортогонального проецирования на многообразие $ mathbb M_ $ в стандартном базисе $$ bigg_j = big[underbrace_,0,dots,0big]^ bigg>_^n , . $$ Она симметрична и идемпотентна, т.е. обладает свойством $ P^2=P $.
Пример. В $ mathbb R^ $ найти матрицу проецирования на плоскость $ x+y+z=0 $.
Решение. Параметрическое задание плоскости: $$ mathbb M=>_ + lambda_2 underbrace>_ big| subset mathbb R > , . $$ Имеем: $$ mathbf L= left(begin1 & 0 \ -1 & 1 \ 0 & -1 end right) Rightarrow mathbf L^ mathbf L= left(begin2 & -1 \ -1 & 2 end right) Rightarrow (mathbf L^ mathbf L )^= left(begin2/3 & 1/3 \ 1/3 & 2/3 end right) Rightarrow $$ $$ Rightarrow mathbf L (mathbf L^ mathbf L )^ mathbf L^= frac left(begin2 & -1 & -1 \ -1& 2 & -1 \ -1 & -1 & 2 end right) , . $$ ♦
Матрица оператора отражения (оператора Хаусхолдера)
Настоящий пункт может быть пропущен при первоначальном чтении.
В пространстве $ mathbb R^n $ со стандартным скалярным произведением рассмотрим плоскость, заданную уравнением $$ C^X= c_1x_1+c_2x_2+dots+c_nx_n = 0 $$ при векторе нормали $ C^=(c_1,c_2,dots,c_n) $ единичной длины: $ |C|^2= C^C=1 $. Действие оператора зеркального отражения или оператора Хаусхолдера 6) относительно этой плоскости на вектор (точку) $ X in mathbb R^n $ определим правилом $$ mathcal H( X^> + X^>)= X^> — X^> ; $$ здесь $ X^> $ — ортогональная проекция вектора $ X_ $ на заданную плоскость, а $ X^> $ — ортогональная составляющая вектора $ X_ $ относительно этой плоскости.
Теорема. Оператор $ mathcal H $ задается уравнением
$$ mathcal H(X)=X-2, langle X,C rangle C=X-2, C (C^X)= X-2, C^XC , . $$
Доказательство. $$ mathcal H( X^> + X^>)=X^> + X^>-2, langle X^>,C rangle C-2, langle X^>,C rangle C = $$ Поскольку $ X^> $ ортогонален, а вектор $ X^> $ коллинеарен вектору $ C $ единичной длины, то $$= X^> + X^> — 2, X^> = X^> — X^> , . $$ ♦
Теорема. Матрица оператора $ mathcal H $ в стандартном базисе
$$ bigg_j = big[underbrace_,0,dots,0big]^ bigg>_^n , . $$ имеет вид $$ mathbf H_= E-2, C cdot C^ = left( begin1-2c_1^2 & -2,c_1c_2 & dots & — 2 c_1 c_n \ -2,c_1c_2 & 1-2c_2^2 & dots & — 2 c_2 c_n \ vdots & & & vdots \ — 2 c_1 c_n & — 2 c_2 c_n & dots & 1-2c_n^2 end right) , . $$
Пример. Найти зеркальное отражение точки $ [3,2,3] $ относительно плоскости $ 2,x-2,y+z = 0 $.
Решение. Здесь $ C^=[2/3,-2/3,1/3] $ и $$ mathcal H(X)= left( begin3 \ 2 \ 3 end right) — 2([3,2,3],[2/3,-2/3,1/3]) left( begin2/3\ -2/3 \ 1/3 end right)= left( begin7/9 \ 38/9 \ 17/9 end right) , . $$ Проверим результат посредством матричного представления: $$ mathbf H_C= left( begin1/9 & 8/9 & -4/9 \ 8/9 & 1/9 & 4/9 \ -4/9 & 4/9 & 7/9 end right) quad Rightarrow quad mathbf H left( begin3 \ 2 \ 3 end right)= left( begin7/9 \ 38/9 \ 17/9 end right) , . $$ ♦
Матрица $ mathbf H_ $ одновременно симметрична и ортогональна, и $ det mathbf H_=-1 $. Следовательно, ей обратная существует и совпадает с ней самой: $$ mathbf H_^= mathbf H_ , . $$
Инвариантное подпространство
Задача. Подобрать базис пространства $ mathbb V_ $ так, чтобы матрица заданного оператора $ mathcal A_ $ имела наиболее простой вид.
Исследуем действие оператора $ mathcal A $ на произвольное подпространство $ mathbb V_1 subset mathbb V $: $$mathcal A (mathbb V_1)= left .$$ Вообще говоря, множества $ mathbb V_1 $ и $ mathcal A (mathbb V_1) $ будут различными, т.е. $ exists X_1 in mathbb V_1 $ такой, что $ mathcal A (X_1)notin mathbb V_1 $.
Подпространство $ mathbb V_1 $ называется инвариантным подпространством оператора $ mathcal A $, если оно отображается этим оператором в себя: $$ mathcal A(mathbb V_1)subset mathbb V_1 .$$
$ mathbb V_1= $ и $ mathbb V_1=mathbb V $ — тривиальные инвариантные подпространства произвольного оператора $ mathcal A $.
Нас будут интересовать нетривиальные инвариантные подпространства.
Пример. Оператор
$$left(beginx \ y \ z end right) longmapsto left(begin/ & —/ & 0 \ / & / & 0 \ 0 & 0 & 1 end right) left(beginx \ y \ z end right) $$ задает в пространстве поворот вокруг оси $ mathbb O z $ на угол $ +pi /4 $. Нетривиальными инвариантными подпространствами будут
а) ось вращения $ mathbb V_1=> mid z in mathbb R> $, $ dim mathbb V_1=1 $ и
б) плоскость, перпендикулярная оси вращения $ mathbb V_2=> mid subset mathbb R> $, $ dim mathbb V_2= 2 $. ♦
Пример. Оператор
$$left(beginx \ y end right) longmapsto left(beginlambda_1 x \ lambda_2 y end right) $$ задает на плоскости «растяжение»: $ x_ $-компонента увеличивается в $ lambda_ $ раз, а $ y_ $-компонента — в $ lambda_ $ раз. При любой комбинации коэффициентов растяжения координатные оси будут инвариантными подпространствами. Однако в частном случае $ lambda_1=lambda_2 $ инвариантной будет также любая прямая, проходящая через начало координат. ♦
Пример. Оператор в $ mathbb R^_ $ задан блочной матрицей
$$X longmapsto left( begin_1 & \ mathbb O & _2 end right) X $$ где $ _1 $ — $ n_1times n_1 $-матрица, $ _2 $ — $ (n-n_1)times (n-n_1) $-матрица. Множество столбцов $$mathbb V_1=left,0,dots,0]^> bigg| > subset mathbb R right>$$ образует инвариантное подпространство, $ dim mathbb V_1=n_1 $. Если же, вдобавок, матрица, обозначенная $ $ — нулевая, то вторым инвариантным подпространством будет $$ mathbb V_2=left,dots,x_n]^> bigg| ,dots, x_n > subset mathbb R right> .$$ ♦
Теорема. $ mathcaler (mathcal A) $ и $ mathcalm(mathcal A) $ — инвариантные подпространства оператора $ mathcal A $.
Доказать, что сумма двух инвариантных подпространств является инвариантным подпространством.
Теорема. Если пространство $ mathbb V_ $ раскладывается в прямую сумму подпространств, инвариантных относительно оператора $ mathcal A $, то существует базис пространства, в котором матрица оператора будет блочно-диагональной.
Теорема обобщается очевидным образом на произвольное число слагаемых подпространств: $ mathbb V=mathbb V_1oplus mathbb V_2 oplus dots oplus mathbb V_k $. Если при этом $ dim mathbb V_1= dots = dim mathbb V_k=1 $, то матрица оператора в базисе, полученном объединением базисных векторов слагаемых подпространств, становится диагональной — это и является решением задачи, поставленной в начале пункта.
Собственное число и собственный вектор
Задача. Найти одномерные инвариантные подпространства оператора.
Вектор $ X_in mathbb V $ называется собственным вектором оператора $ mathcal A_ $, если $$ X ne mathbb O, quad u quad exists lambda in mathbb C qquad mbox qquad mathcal A(X)=lambda X .$$ В этом случае число $ lambda_ $ называется собственным или характеристическим числом оператора, соответствующим (или принадлежащим) данному собственному вектору; обратно, говорят, что вектор $ X_ $ принадлежит собственному числу $ lambda_ $.
Пример. Оператор
$$left(beginx \ y end right) longmapsto left(begin1 & — 5/2 \ -1/2 & 2 end right) left(beginx \ y end right) $$ задает отображение плоскости $ mathbb R^2 $. На рисунке показан результат действия этого отображения на единичную окружность. Все точки плоскости, за исключением начала координат $ mathbb O_ $, изменят свое положение — ни одна не останется на месте.
Если рассмотреть эти точки как концы векторов, имеющих начало в $ mathbb O_ $, то смещения точек под действием оператора можно представить в виде двух составляющих: растяжения (т.е. увеличения расстояния до начала координат) и поворота вокруг начала координат на некоторый угол. И только по двум направлениям плоскости поворота не происходит. Точки окружности с координатами $$ pm left( 0.823, -0.568 right)^ quad u quad pm left( 0.960, 0.278 right)^ $$ будут смещаться без поворота. Эти точки и задают координаты конца собственного вектора. А соответствующие им собственные числа $ 2.725 $ и $ 0.275 $ определяют коэффициенты сдвига. Если вообразить оператор как деформацию физической среды, заполняющей плоскость, то можно сказать, что cобственный вектор задает направление, на котором действие оператора сводится к растяжению, при этом коэффициент растяжения и будет собственным числом.
Анимация процесса ☞ ЗДЕСЬ (1500 Kb, gif).
Пример другого оператора $$ left(beginx \ y end right) longmapsto left(begin1 & — 3 \ 1 & -1 end right) left(beginx \ y end right) $$ показывает, что существование вещественных собственных чисел вовсе не гарантировано даже в случае оператора в вещественном пространстве: в этом примере все точки плоскости повернутся вокруг начала координат. ♦
Доказать, что $ operatorname (mathcal A) ne 0 $ тогда и только тогда, когда оператор $ mathcal A_ $ имеет собственное число, равное нулю.
Теорема. Любой собственный вектор оператора порождает его одномерное инвариантное подпространство, и обратно: любой ненулевой вектор одномерного инвариантного подпространства оператора является собственным вектором.
Пример. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ оператор $ mathcal A_ $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ т.е. полином $ f_(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Найти собственные векторы этого оператора.
Решение. В пространстве $ mathbb P_3 $ векторами являются полиномы, а условие того, что полином $ f_(x) $ является собственным, принадлежащим числу $ lambda_ $, записывается в виде: $$ f(x)(x^2-2)equiv lambda f(x) pmod quad iff $$ $$ iff quad f(x)(x^2-2-lambda)equiv 0 pmod . $$ Поскольку $ deg f le 3 $, то последнее может выполняться тогда и только тогда, когда полином $ x^2-2-lambda $ имеет общие корни с $ x^4-x^3-x^2+x equiv x(x+1)(x-1)^2 $. Из этого условия вытекает, что число $ lambda_ $ может принимать только два значения: $ lambda_1=-2 $ и $ lambda_2=-1 $. Если $ lambda_1=-2 $ является собственным числом, то ему соответствующий собственный вектор — полином степени $ le 3 $ — должен определяться из условия делимости $ f(x)x^2 $ на $ x(x+1)(x-1)^2 $. Такой полином имеет вид $ t(x+1)(x-1)^2 $ при произвольной константе $ t_ $. Следовательно множество $$ $$ является множеством собственных векторов, принадлежащих $ lambda_1=-2 $.
С числом $ lambda_2=-1 $ поступаем аналогично. Условие делимости полинома $ f(x)(x^2-1) $ на $ x(x+1)(x-1)^2 $ дает также бесконечное множество: $$ subset mathbb R > . $$ Однако в этом случае бесконечность множества качественно иная, чем в предыдущем случае; она — «двумерная». ♦
Задача. Для произвольного оператора выяснить условия существования его собственного числа и разработать конструктивный метод его нахождения.
Теорема. В комплексном линейном пространстве любой оператор имеет по крайней мере один собственный вектор.
Доказательство. Пусть $ > $ — произвольный базис пространства $ mathbb V_ $ и $ mathbf A_ $ — матрица оператора $ mathcal A_ $ в этом базисе. Тогда для того чтобы вектор $ X=x_1X_1+cdots+x_nX_n ne mathbb O $ был собственным, принадлежащим собственному числу $ lambda_ $, необходимо и достаточно чтобы выполнялось равенство $$ left(beginx_1 \ x_2 \ vdots \ x_n end right) = lambda left(beginx_1 \ x_2 \ vdots \ x_n end right) quad Longleftrightarrow quad left(beginalpha_ — lambda & alpha_& dots & alpha_ \ alpha_ & alpha_— lambda& dots & alpha_ \ dots & & & dots \ alpha_ & alpha_& dots & alpha_— lambda end right) left(beginx_1 \ x_2 \ vdots \ x_n end right) = mathbb O_ $$ Покажем, что существуют комплексные числа $ lambda_ $ и не все нулевые $ x_1,dots,x_ $, удовлетворяющие этой системе. Необходимым и достаточным условием существования нетривиального решения у однородной системы линейных уравнений с квадратной матрицей является равенство нулю определителя этой матрицы: $$ det (-lambda E)=left|beginalpha_ — lambda & alpha_& dots & alpha_ \ alpha_ & alpha_— lambda& dots & alpha_ \ dots & & & dots \ alpha_ & alpha_& dots & alpha_— lambda end right|=0 . $$ Этот определитель является полиномом степени $ n_ $ по $ lambda_ $. По основной теореме высшей алгебры этот полином имеет по крайней мере один комплексный корень $ lambda=lambda_ $. Подставив его в систему, получаем однородную систему уравнений с нулевым определителем. Находим нетривиальное решение этой системы: $$ x_1=x_^,dots,x_n=x_^, quad exists x_^ ne 0 ; $$ но тогда вектор $ _= x_^X_1+cdots+x_^X_n $ будет собственным вектором оператора $ mathcal A_ $, принадлежащим $ lambda_^ $. ♦
Уравнение $ det (-lambda E)= 0 $ называется характеристическим или вековым уравнением, а полином в левой его части — характеристическим полиномом матрицы $ $. Любой корень характеристического полинома матрицы называется собственным числом этой матрицы. Набор всех собственных чисел матрицы (корней характеристического полинома с учетом кратностей) называется спектром матрицы. Ненулевой вектор $ X in mathbb C^n $, удовлетворяющий условию $ X= lambda X $, где $ lambda $ — собственное число матрицы, называется собственным вектором матрицы, соответствующим (или принадлежащим) данному собственному числу.
Пример. Применим полученный результат для получения альтернативного решения предыдущего примера.
Решение. Базисом в пространстве $ mathbb P_3 $ выберем $ $. Образы базисных векторов под действием оператора $ mathcal A (f(x)) = f(x) (x^2-2) pmod $: $$ left mathcal A (1) =&-2& &+x^2& ,\ mathcal A (x) =&&-2,x &&+x^3 ,\ mathcal A (x^2) =& &-x &-x^2 &+x^3, \ mathcal A (x^2) =& &-x & & , end right. qquad Rightarrow qquad = left(begin-2 & 0 & 0 & 0 \ 0 & -2 & -1 & -1 \ 1& 0 & -1 & 0 \ 0 & 1 & 1 & 0 end right) . $$ Характеристический полином матрицы $ $: $$ left|begin-2-lambda & 0 & 0 & 0 \ 0 & -2-lambda & -1 & -1 \ 1& 0 & -1-lambda & 0 \ 0 & 1 & 1 & -lambda end right|equiv (lambda+2)(lambda^3+3,lambda^2+3,lambda+1)equiv (lambda+2)(lambda+1)^3 . $$ Собственные числа $ lambda_1=-2 $ и $ lambda_2=-1 $, спектр матрицы $ $. Подставляем каждое из собственных чисел в матрицу $ -lambda E $ и решаем получившиеся системы однородных уравнений. Поскольку каждая из них должна иметь бесконечное множество решений, то мы строим фундаментальные системы решений (ФСР) $$ begin& (-lambda E)X=mathbb O & \ swarrow > & & searrow > \ lambda_1=-2 & & lambda_2=-1 \ Downarrow & & Downarrow \ left(begin0 & 0 & 0 & 0 \ 0 & 0 & -1 & -1 \ 1& 0 & 1 & 0 \ 0 & 1 & 1 & 2 end right) left(beginx_1 \ x_2 \ x_3 \ x_4 end right)= mathbb O & & left(begin-1 & 0 & 0 & 0 \ 0 & -1 & -1 & -1 \ 1& 0 & 0 & 0 \ 0 & 1 & 1 & 1 end right) left(beginx_1 \ x_2 \ x_3 \ x_4 end right)= mathbb O . \ Downarrow > & & Downarrow > \ x_1=1,x_2=-1,x_3=-1,x_4=1 & & left x_1=0,x_2=-1,x_3=1,x_4=0 \ x_1=0,x_2=-1,x_3=0,x_4=1 end right> end $$ Таким образом, собственному числу $ lambda_1=-2 $ соответствует собственнный вектор — полином $ 1-x-x^2+x^3 $, и он полностью совпадает с полученным при решении предыдущего примера. В то же время собственному числу $ lambda_2=-1 $ соответствует два линейно независимых собственнных вектора — полиномы $ -x+x^2 $ и $ -x+x^3 $. Любой (не тождественно нулевой) полином множества $$ subset mathbb R > $$ будет также являться собственным, принадлежащим $ lambda_2=-1 $. Это множество также совпадает с полученным при решении предыдущего примера. ♦
Итак, два формально различных подхода к решению одного и того же примера не привели к противоречию. Хотелось бы, однако, гарантировать глобальную непротиворечивость определения собственных чисел и векторов — т.е. независимость (инвариантность) этих объектов относительно способов их нахождения, и, в частности, от выбора базиса пространства $ mathbb V_ $.
Теорема. Характеристические полиномы подобных матриц одинаковы.
Доказательство. $ doteq iff exists $ неособенная матрица $ C_ $, такая что $ =C^ C $. Имеем: $$det (-lambda E)=det (C^ C-lambda E)=$$ $$= det (C^ C-lambda C^EC)=det left[ C^ ( -lambda E)C right] = det (-lambda E) .$$ ♦
Иначе говоря, для оператора $ mathcal A_ $ характеристический полином его матрицы не зависит от выбора базиса пространства. Поэтому можно говорить о характеристическом полиноме оператора $ mathcal A_ $.
Теорема [Гамильтон, Кэли]. Результатом подстановки оператора в собственный характеристический полином будет нулевой оператор.
Пример. Для рассмотренного в предыдущих примерах оператора
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ действующего в $ mathbb P_3 $, характеристический полином равен
$$ lambda^4+5,lambda^3+9,lambda^2+7,lambda+2 , .$$ Проверим утверждение теоремы Гамильтона-Кэли — должно быть выполнено условие $$ mathcal A^4+5,mathcal A^3+9,mathcal A^2+7,mathcal A +2, mathcal E = mathcal O . $$ Степени данного оператора $ mathcal A_ $ обсуждались в примере ☞ ПУНКТА. Переписанное в терминах остатков, последнее условие превращается в $$ (x^2-2)^4f(x)+5,(x^2-2)^3f(x)+9,(x^2-2)^2f(x)+7,(x^2-2)f(x) + $$ $$+2,f(x) equiv 0 pmod , $$ т.е. полином, стоящий в левой части сравнения, должен делиться нацело на $ x^4-x^3-x^2+x $ при любом выборе полинома $ f_(x) $. Проверяем: $$ (x^2-2)^4+5,(x^2-2)^3+9,(x^2-2)^2+7,(x^2-2)+2 equiv $$ $$equiv x^8-3,x^6+3,x^4-x^2 equiv (x^4+x^3-x^2-x)(x^4-x^3-x^2+x) , $$ т.е. утверждение оказывается справедливым. ♦
Диагонализуемость матрицы оператора
Теорема 1. Собственные векторы оператора, принадлежащие различным собственным числам, линейно независимы.
Теорема 2. Если оператор имеет $ n=dim mathbb V $ линейно независимых собственных векторов, то в базисе ими образуемом матрица оператора диагональна. Обратно: если матрица оператора в некотором базисе диагональна, то каждый вектор этого базиса является собственным для оператора.
Базис линейного пространства, состоящий из собственных векторов оператора $ mathcal A_ $, называется каноническим.
[Матричная версия теоремы]. Пусть $ A_ $ — квадратная матрица. Неособенная матрица $ C_ $, удовлетворяющая равенству
$$C^ A C= A_ quad mbox A_ quad mbox $$ существует тогда и только тогда, когда существует базис пространства $ mathbb C^_ $, состоящий из собственных векторов матрицы $ A_ $. Тогда матрица $ C_ $ является матрицей перехода от стандартного базиса $$ bigg_j = big[underbrace_,0,dots,0big]^ bigg>_^n $$ к каноническому, а на диагонали $ A_ $ стоят собственные числа матрицы $ A_ $: $$ A_= left( beginlambda_1 & 0 & dots & 0 \ 0 & lambda_2 & dots & 0 \ & & ddots & \ 0 & 0 & dots & lambda_n end right) . $$
Доказательство. Проведем формальное доказательство данного конкретного частного случая. Рассмотрим матричное равенство $$ A C= CA_ $$ при некоторой диагональной матрице $ A_ $. Легко видеть, что оно эквивалентно системе равенств относительно столбцов матрицы $ C_ $: $$ AC_=d_1 C_,dots, AC_=d_n C_ , . $$ Если все столбцы $ >_^n $ ненулевые, то тогда они являются собственными векторами для матрицы $ A_ $, а числа $ >_^n $ — собственными числами, соответствующими этим собственным векторам. Если матрица $ C_ $ невырождена, то все ее столбцы линейно независимы. Но тогда они образуют базис пространства $ mathbb C^n $, состоящий из собственных векторов. Обратное тоже верно. ♦
При выполнении условия предыдущего следствия говорят, что матрица $ A_ $ диагонализуема или приводится к диагональной форме 7) .
Теорема позволяет сформулировать достаточное условие диагонализуемости.
Теорема 3. Если характеристический полином оператора не имеет кратных корней, то матрица оператора диагонализуема.
Это условие не является необходимым, как показывает пример тождественного оператора .
Случай существования кратного корня у характеристического полинома является «пограничным»: существуют примеры как диагонализуемых, так и недиагонализуемых матриц. Так, для матриц $$ A= left( begin0 &1 \ -1 &2 end right) quad mbox quad A= left( begin1 &0 \ 1&1 end right) $$ при попытке подобрать матрицу $ C_ $, удовлетворяющую равенству $$AC=C left( beginalpha_1 &0 \ 0 & alpha_2 end right) qquad npu forall subset mathbb C $$ получим: $ det C=0 $.
В случае наличия у характеристического полинома оператора кратного корня, анализ оператора на возможность диагонализуемости его матрицы усложняется.
Теорема 4. Множество собственных векторов оператора, принадлежащих его собственному числу $ lambda_^ $ , дополненное нулевым вектором, образует линейное подпространство пространства $ mathbb V_ $.
Это подпространство $$ mathbb V_ = mathcaler (mathcal A- lambda_ mathcal E) $$ пространства $ mathbb V_ $ называется собственным подпространством оператора, соответствующим $ lambda_^ $. Величина $$ dim (mathcaler (mathcal A- lambda_ mathcal E)) $$ называется геометрической кратностью собственного числа $ lambda_^ $. Можно доказать, что геометрическая кратность собственного числа не превосходит кратности собственного числа в характеристическом полиноме. Для акцентирования различий в определениях двух кратностей, кратность собственного числа в характеристическом полиноме называют еще алгебраической кратностью собственного числа.
Если оператор (в некотором базисе пространства) задан своей матрицей $ mathbf A^ $, то базисные векторы собственного подпространства $ mathbb V_ $ вычисляются посредством нахождения фундаментальной системы решений (ФСР) системы линейных уравнений $$ (mathbf A- lambda_ E) X=mathbb O . $$
Теорема 5. Матрица оператора диагонализуема тогда и только тогда, когда для каждого ее собственного числа алгебраическая кратность равна геометрической кратности:
Диагонализуема ли матрица оператора
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ рассмотренного в примерах предыдущего пункта?
Пример. Найти все вещественные значения параметра $ > $, при которых матрица
Решение. Характеристический полином $ f(lambda)=-lambda^3+3, lambda-2,(3, > -1) $ имеет кратные корни только тогда когда его дискриминант $ mathcal D(f)=-324, > (3, > -2) $ обращается в нуль. При $ > =0 $ корень $ lambda=-1 $ имеет алгебраическую кратность $ 2_ $. Найдем дефект матрицы $ A+E $: $$left( begin2 &0 & -2 \ -1 &3 &1 \ 2 & 0 & -2 end right) longrightarrow left( begin1 &0 & -1 \ 0 &3 &0 \ 0 & 0 & 0 end right) Longrightarrow operatorname (A+E) =2 Longrightarrow operatorname (A+E)=1 . $$ Таким образом, геометрическая кратность собственного числа $ lambda=-1 $ равна $ 1_ $ и условие теоремы $ 5 $ не выполнено. Оно не будет выполнено и при $ > = 2/3 $ (здесь корень $ lambda=1 $ имеет кратность $ 2_ $).
Ответ. Матрица диагонализуема при всех значениях параметра, за исключением $ > = 0 $ и $ > = 2/3 $.
Диагонализуемость матрицы оператора над полем вещественных чисел
В предыдущем пункте мы рассматривали операторы, не всегда акцентируя внимания на поле, над которым они были определены — над $ mathbb R_ $ или над $ mathbb C_ $. Сама теорема существования собственного числа гарантирует нам только лишь наличие этих чисел в поле $ mathbb C_ $. Как следствие, даже если рассматриваются операторы над полем $ mathbb R_ $ (что чаще всего и случается на практике), то существование для них вещественного канонического базиса вовсе не гарантировано.
Задача. Найти условия диагонализуемости матрицы оператора $ mathcal A $ над полем вещественных чисел.
Необходимое условие следует из теоремы $ 2 $ предыдущего пункта: все собственные числа матрицы должны быть вещественными.
Теорема $ 3 $ позволяет сформулировать и достаточный критерий диагонализуемости матрицы оператора $ mathcal A $ над $ mathbb R_ $.
Теорема. Если характеристический полином оператора имеет только простые вещественные корни, то матрица оператора диагонализуема над $ mathbb R_ $.
Условие различности и вещественности корней произвольного полинома $ f(lambda)=lambda^n+a_1lambda^+dots+ a_n in mathbb R[x] $ можно проверить по коэффициентам этого полинома «чисто алгебраически», т.е. за конечное число элементарных алгебраических операций над этими коэффициентами. Воспользуемся, например, теоремой Якоби из раздела ☞ ЛОКАЛИЗАЦИЯ КОРНЕЙ ПОЛИНОМА. По коэффициентам $ a_1,dots,a_n $ можно определить сумму Ньютона полинома $ f(lambda) $, т.е. величину $$ s_k=sum_ lambda_j^k . $$ Далее, после нахождения всех этих сумм для значений $ k in $, из них составляется ганкелева матрица $$ S=left[ s_ right]_^ $$ и вычисляются ее главные миноры $ S_1,dots, S_ $. Для различности всех корней полинома необходимо и достаточно выполнение условия $ S_n ne 0 $ (этот минор совпадает с дискриминантом $ mathcal D(f) $ полинома $ f(lambda) $); для различности и вещественности всех корней необходимо и достаточно, чтобы были выполнены неравенства $$ S_1ge 0,dots,S_ ge 0,S_n > 0 . $$
Пример. Найти все вещественные значения параметра $ > $, при которых матрица
Решение. На основании теоремы нам нужно установить условия вещественности корней характеристического полинома $ f(lambda)=-lambda^3+3, lambda-2,(3, > -1) $. Вычисляем суммы Ньютона: $ s_0=3, s_1= 0, s_2=6, s_3=18, > -6, s_4=18 $, составляем матрицу: $$ S=left(begin3 & 0 & 6 \ 0 & 6 & 18, > -6 \ 6 & 18, > -6 & 18 end right) $$ и вычисляем ее главные миноры: $$S_1=3, S_2=18, S_3=-324, > , (3, > -2)=mathcal D(f) . $$ При $ > ne 0 $ и $ > ne 2/3 $ все собственные числа различны, условие теоремы выполняется при $ > in ]0,, 2/3[ $. Граничные точки последнего интервала следовало бы исследовать отдельно: хотя этим значениям параметра и соответствует случай кратных вещественных корней характеристического полинома, но матрица $ A_ $ может оказаться диагонализуемой на основании теоремы 5 предыдущего пункта. Но при решении примера в предыдущем пункте мы уже установили, что это условие не выполняется.
Ответ. Матрица диагонализуема над $ mathbb R_ $ при $ > in ]0,, 2/3[ $.
Жорданова нормальная форма
Если матрица оператора оказывается недиагонализуемой над $ mathbb C_ $, то к какому простейшему виду ее можно привести ? — Этим видом является, например, ☞ ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА.
Задачи
Источники
[1]. Гантмахер Ф.Р. Теория матриц. 4-е изд. М.Наука. 1988.
[2]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ.1960
[3]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989
[4]. Мишина А.П., Проскуряков И.В. Высшая алгебра. М.Наука. 1965
Светлой
памяти
Чубича
Михаила Петровича
посвящается
§ 7.1. Определение линейного оператора.
Матрица линейного оператора
Пусть
и
– линейные пространства над одним и тем
же полем .
Будем говорить, что из
пространства
в пространство
действует оператор
или, что то же самое, отображение
,
преобразование
,
если каждому вектору
по какому – либо правилу поставлен в
соответствии определенный вектор
из .
Наиболее
простыми являются линейные операторы.
Отображение
называется линейным
оператором
(линейным
преобразованием),
действующим из
в ,
если оно удовлетворяет следующим двум
условиям:
;
,
.
Совокупность
условий 1 и 2 равносильна следующему
условию:
.
(7.1.1)
Обозначим
через
множество всех линейных операторов,
действующих из линейного пространства
в линейное пространство .
Два линейных оператора
и
из
называются равными,
если
.
(7.1.2)
Множество
будет линейным пространством над полем
,
если определить сумму
операторов
и произведение
оператора
на число
соотношениями
(7.1.3)
(7.1.4)
Нулевым
вектором пространства
будет нулевой
оператор
из
в
,
т.е. оператор, переводящий любой вектор
линейного пространства
в нулевой вектор линейного пространства
.
В
случае, когда ,
линейный оператор
называется линейным преобразованием
пространства .
Пусть
–
оператор из ,
и пусть и
–
фиксированные базисы линейных пространств
и
соответственно.
Разложим векторы
по базису :
,
,
(7.1.5)
.
Из
коэффициентов этих разложений составим
–
матрицу

(7.1.6)
Матрица
называется матрицей
линейного оператора
в паре базисов и
.
Заметим, что столбцами матрицы
служат столбцы координат векторов
в базисе ,
т.е. строки коэффициентов из разложений
(7.1.5).
Если
,
то при нахождении матрицы линейного
оператора фиксируются векторы одного
базиса ,
по которому раскладываются .
Записанные столбцами коэффициенты
разложений образуют квадратную матрицу
порядка .
Равные
линейные операторы в одном и том же
базисе имеют одинаковые матрицы.
Матрицей
суммы линейных операторов в фиксированных
базисах является сумма матриц слагаемых
операторов в тех же базисах.
При
умножении линейного оператора на число
его матрица умножается на то же число.
Если
и
–
соответственно,
–
и
–
мерное линейные пространства над одним
полем
,
то линейное пространство
изоморфно
линейному пространству
–
матриц с элементами из
с
операциями сложения матриц и умножения
их на числа из поля
.
Пример
1.
Оператор
называется
тождественным
(единичным)
оператором,
если
.
(7.1.7)
Покажите
линейность оператора
и постройте его матрицу в базисе .
Решение.
В силу того, что
,
убеждаемся
в линейности тождественного оператора.
Поскольку
получаем,
что
В
любом базисе тождественный оператор
имеет единичную матрицу.
Пример
2.
Докажите, что преобразование
пространства
линейно и найдите его матрицу в
каноническом базисе.
Решение.
Пусть
– произвольные векторы из .
Тогда
т.
е. преобразование
пространства
линейно. Канонический базис линейного
пространства
составляют векторы
.
Из определения оператора
вытекает, что
Таким
образом,
Пример
3.
Покажите, что умножение квадратных
матриц второго порядка слева на данную
матрицу
является линейным преобразованием
пространства
и найдите матрицу этого преобразования
в базисе, состоящем из матриц
Решение.
По определению преобразования
для любых матриц
и любых чисел
имеем:
.
Перейдем
к построению матрицы оператора
в данном базисе. В силу того, что
получаем:
7.1.1.
Какую матрицу имеет нулевой оператор
в любых базисах пространств
и ?
7.1.2.
Линейное пространство
является прямой суммой подпространств
и .
Докажите, что оператор
пространства ,
который каждому вектору
с разложением ,
где ,
ставит в соответствие вектор
этого разложения, является линейным.
Оператор
называется оператором
проектирования
пространства
на
параллельно .
Найдите
матрицу этого оператора в базисе,
полученном объединением базисов
подпространств
и .
7.1.3.
Линейное пространство
является прямой суммой подпространств
и .
Докажите, что оператор ,
который каждому вектору
с разложением ,
где ,
ставит в соответствие вектор ,
является линейным. Оператор
называется отражением
пространства
в
параллельно .
Найдите
матрицу этого оператора в базисе,
полученном объединением базисов
подпространств
и .
7.1.4.
Докажите, что всякий линейный оператор,
действующий в одномерном пространстве,
сводится к умножению всех векторов
пространства на фиксированное (для
данного оператора) число.
7.1.5.
Верно ли, что линейный оператор переводит:
а)
линейно зависимую систему векторов в
линейно зависимую;
б)
линейно независимую систему векторов
в линейно независимую?
7.1.6.
Выясните, какие из следующих преобразований
пространства
линейны, и в случае линейности найдите
их матрицы в каноническом базисе:
а)
б)
в)
г)
7.1.7.
Укажите, какие из приведенных преобразований
пространства
являются линейными операторами, и
найдите их матрицы в базисе .
Каждое преобразование описывается
своим действием на произвольный многочлен
:
а)
б)
в)
,
где
и
– фиксированные числа, причем ;
г)
Этот оператор в дальнейшем называется
оператором
дифференцирования.
7.1.8.
Какова матрица оператора дифференцирования,
действующего в линейном пространстве
,
в базисе ,
где
– действительное число?
7.1.9.
Покажите, что умножение квадратных
матриц второго порядка справа на данную
матрицу
является линейным преобразованием
пространства ,
и найдите матрицу этого преобразования
в базисе, состоящем из матриц :
7.1.10.
Проверьте линейность оператора ,
заданного формулой ,
где
и постройте матрицу этого оператора в
базисах
и
7.1.11.
В пространстве
фиксирован базис, состоящий из матриц
(в
указанном порядке). Запишите в этом
базисе матрицу оператора транспонирования,
т.е. оператора, который каждой матрице
ставит в соответствие транспонированную
матрицу.
Как
изменится эта матрица, если в базисе
поменять местами векторы
и ?
Соседние файлы в папке Задачник-2
- #
- #
- #
- #
- #
- #
Канонический вид линейного оператора (преобразования)
Матрица линейного преобразования n-мерного линейного пространства определяется относительно его базиса. Выбирая разные базисы, получаем разные матрицы одного и того же преобразования. Поэтому возникает задача приведения линейного преобразования к каноническому виду: требуется найти такой базис пространства
, в котором матрица преобразования имеет наиболее простой вид. Упрощение матрицы преобразования позволяет выяснить его структуру, представить в виде композиции простых преобразований. Например, если в некотором базисе матрица преобразования оказывается диагональной, то с геометрической точки зрения это преобразование сводится к гомотетиям вдоль каждого из направлений базисных векторов. Кроме того, приведение преобразований к каноническому виду позволяет сравнивать различные преобразования. Все преобразования, которые имеют одинаковый канонический вид, эквивалентны, так как обладают одинаковыми свойствами.
Ранее были рассмотрены задачи приведения матрицы к диагональному виду и к жордановой нормальной форме при помощи преобразования подобия. В этом разделе аналогичные задачи рассматриваются для линейного преобразования.
Приведение линейного оператора (преобразования) к диагональному виду
Говорят, что линейное преобразование n-мерного линейного пространства
приводится к диагональному виду, если существует базис, в котором матрица
преобразования диагональная, т.е.
, где
— некоторые числа, среди которых могут быть равные. Если преобразование
приводится к диагональному виду, то оно называется диагонализируемым.
Ранее было сформулировано необходимое и достаточное условие приводимости матрицы к диагональному виду. Переформулируем это условие для линейного преобразования: линейное преобразование приводится к диагональному виду тогда и только тогда, когда в пространстве
существует базис из собственных векторов.
Действительно, предположим, что в базисе матрица преобразования имеет диагональный вид
Найдем образ . Умножая матрицу
на координатный столбец
базисного вектора
, получаем
. Значит,
, т.е. вектор
является собственным, а преобразование
действует в подпространстве
как гомотетия (с коэффициентом
). Аналогичный вывод можно сделать и про другие базисные векторы. Следовательно, базис пространства состоит из собственных векторов
. Необходимость доказана. Достаточность доказывается путем приведения тех же рассуждений, но в обратном порядке.
Критерий диагонализируемости линейного преобразования можно сформулировать иначе.
Теорема (9.7) о диагонализируемости линейного преобразования (оператора)
Для того чтобы линейное преобразование (оператор) приводилось к диагональному виду, необходимо и достаточно, чтобы все корни характеристического многочлена являлись собственными значениями преобразования и геометрическая кратность каждого собственного значения была равна его алгебраической кратности.
Достаточность следует из теорем 9.5 и 9.6. Действительно, если для каждого из различных собственных значений геометрическая кратность равна алгебраической кратности, то
, т.е.
для всех
. Поэтому в равенстве (9.9) корневые подпространства можно заменить собственными:
. Выбрав в каждом собственном подпространстве базис и объединив все эти базисы в единую систему, получим базис всего пространства, составленный из собственных векторов. Достаточность доказана. Необходимость доказывается путем приведения тех же рассуждений, но в обратном порядке.
Ранее было доказано, что существование линейно независимых собственных векторов необходимо и достаточно для диагонализируемости матрицы при помощи преобразования подобия. Теорема 9.7 дает более тонкое условие диагонализируемости матрицы линейного преобразования. Отмечалось также, что не всякую матрицу можно привести к диагональному виду при помощи преобразования подобия (см. пример 7.9). Аналогичный вывод справедлив и для линейного преобразования.
Следствие 1. Если характеристическое уравнение линейного преобразования комплексного (вещественного) пространства имеет попарно различных комплексных (действительных) корней (короче говоря, преобразование имеет простой спектр), то это преобразование приводится к диагональному виду.
Действительно, в этом случае алгебраическая и геометрическая кратности каждого собственного значения равны единице.
Следствие 2. Если сумма размерностей всех собственных подпространств линейного преобразования равна размерности линейного пространства
, то линейное преобразование приводится к диагональному виду.
Пример 9.2. Линейное преобразование в базисе
имеет матрицу
. Привести это преобразование к диагональному виду, т.е. найти базис
, в котором матрица преобразования имеет диагональный вид, и найти эту диагональную матрицу.
Решение. Задача сводится к нахождению собственных векторов и собственных значений преобразования. Применяем для их нахождения алгоритм, рассмотренный ранее.
1. Выбираем базис , в котором задана матрица преобразования.
2-5. Собственные значения и собственные векторы этой матрицы, а также ее диагональный вид были найдены в примере 7.10:
Осталось по координатным столбцам записать искомый базис
Приведение линейного преобразования к каноническому виду
Говорят, что линейное преобразование n-мерного линейного пространства
приводится к каноническому виду, если существует базис, в котором матрица
преобразования имеет нормальную жорданову форму. Такой базис называется жордановым.
Напомним, что жордановой клеткой r-то порядка, соответствующей собственному значению , называют квадратную матрицу r-го порядка (7.35):
(9.10)
Жордановой матрицей называют блочно-диагональную матрицу вида (7.38):
(9.11)
на диагонали которой стоят жордановы клетки (9.10), причем среди собственных значений могут быть равные, порядки
жордановых клеток (всех или некоторых) могут совпадать.
Существование и структура жорданова базиса
Пусть преобразование имеет собственный вектор
, соответствующий собственному значению
. Вектор
, удовлетворяющий условию
, называется присоединенным вектором 1-го порядка. Вектор
, удовлетворяющий условию
, называется присоединенным вектором 2-го порядка и т.д. Присоединенный вектор
p-го порядка определяется соотношением
, где
— присоединенный вектор (p-l)-го порядка.
Определение присоединенных векторов можно записать эквивалентным образом, используя преобразование (характеристическое преобразование для преобразования
): вектор
является присоединенным p-го порядка, если
, где
— собственный вектор преобразования
.
Действительно, при из условия
получаем
, то есть
. При
из условия
имеем
. Отсюда
, то есть
и т.д. Заметим, что присоединенный вектор
p-го порядка по определению удовлетворяет одновременно двум условиям:
и
, так как собственный вектор
ненулевой,
, поскольку
.
Необходимость рассмотрения присоединенных векторов объясняется следующим свойством: жорданов базис состоит из собственных и присоединенных векторов линейного преобразования, взятых в определенном порядке.
Предположим, что в базисе пространства
матрица
преобразования
имеет жорданову форму (9.11). Рассмотрим преобразование первых
базисных векторов (
— порядок первой жордановой клетки
в (9.11)). Умножая координатный столбец
базисного вектора
на матрицу
с учетом (9.10), получаем
, то есть
. Следовательно, вектор
— собственный. Умножая матрицу
на координатный столбец
базисного вектора
, получаем
, то есть
. Следовательно,
— присоединенный вектор (1-го порядка). Аналогично заключаем, что векторы
также присоединенные (от второго до (
)-гo порядков соответственно). Для других жордановых клеток выводы аналогичные.
Таким образом, жорданов базис составляют собственные и присоединенные векторы, взятые в следующем порядке (базисные векторы удобно обозначить иначе):
(9.12)
где — собственные векторы, а остальные векторы — соответственно присоединенные к ним,
. Каждой из
жордановых клеток в (9.11) отвечает одна группа векторов в (9.12). Количество собственных векторов в (9.12) равно количеству жордановых клеток в (9.11). Перестановке групп векторов в базисе (9.12) соответствует перестановка жордановых клеток в (9.11), при этом форма матрицы остается жордановой.
Докажем существование жорданова базиса для преобразования n-мерного линейного пространства
при условии, что все корни характеристического уравнения являются собственными значениями преобразования
.
Сначала рассмотрим случай, когда преобразование имеет единственное собственное значение
. В этом случае в прямой сумме (9.9) имеется одно слагаемое
(см. теорему 9.5), а цепочка (9.8) инвариантных подпространств имеет вид
где , а
— наименьшее натуральное число, при котором
. Здесь, как и ранее,
— характеристическое преобразование для преобразования
.
Каждое подпространство , состоит из собственных векторов (которые образуют собственное подпространство
) и присоединенных векторов первого, второго и т.д. до (p-l)-ro порядка включительно. Действительно, присоединенный вектор
определяется равенством
, где
— собственный вектор. Тогда
, то есть
.
Будем строить базис корневого подпространства следующим образом. Так как
не совпадает с
, то существует максимальная линейно независимая над подпространством
система
присоединенных векторов (m-)-го порядка (которая дополняет любой базис подпространства
до базиса подпространства
,
). Напомним, что векторы
называются линейно независимыми над подпространством
, если любая нетривиальная линейная комбинация этих векторов не принадлежит
.
Векторы являются присоединенными (m-2)-го порядка, принадлежат
и линейно независимы над подпространством
. Дополним их присоединенными векторами
(m-2)-го порядка
до максимальной линейно независимой над подпространством
системы
. Применяя к этим векторам преобразование
, получаем линейно независимые над подпространством
векторы
Дополняем их векторами до максимальной линейно независимой над подпространством
системы. Продолжая аналогично, приходим к следующей таблице базисов:
(9.13)
В таблице базисов (9.13) указаны следующие базисы:
в последней строке — базис собственного подпространства ;
в двух последних строках — базис подпространства и т.д.;
вся таблица — базис корневого подпространства .
По таблице (9.13) составим базис корневого подпространства. Записываем векторы, стоящие в первом столбце, один за другим снизу вверх, начиная с собственного вектора:
К ним приписываем в таком же порядке векторы, стоящие во втором столбце, и т.д. Получим жорданов базис корневого подпространства, состоящий из собственных и присоединенных векторов, взятых в определенном порядке, как это указано в (9.12). Все клетки жордановой формы (9.11) соответствуют собственному значению . Каждому из первых
столбцов таблицы (9.13) соответствует жорданова клетка m-го порядка, каждому из
следующих столбцов соответствует жорданова клетка (m-1)-гo порядка и т.д. Общее число жордановых клеток равно количеству собственных векторов в последней строке таблицы (9.13).
Таким образом, доказано существование жорданова базиса в случае единственного собственного значения.
Рассмотрим теперь случай, когда имеется несколько различных собственных значений . В этом случае по теореме 9.5 пространство разлагается в прямую сумму инвариантных (корневых) подпространств
. При объединении жордановых базисов корневых подпространств получаем жорданов базис всего пространства. Таким образом, справедливо следующее утверждение.
Теорема (9.8) о приведении линейного преобразования к каноническому виду
Если все корни характеристического уравнения являются собственными значениями преобразования, то это преобразование приводится к каноническому виду, т.е. существует базис пространства, в котором матрица преобразования имеет жорданову форму.
Из теоремы следует, что любое линейное преобразование комплексного линейного пространства приводится к каноническому виду, а преобразование вещественного линейного пространства приводится к каноническому виду только тогда, когда все корни характеристического уравнения действительные.
Замечания 9.5
1. По таблице (9.13) нетрудно выразить количество жордановых клеток порядка
через ранги преобразований
, учитывая, что
. Количество
жордановых клеток порядка
равно количеству векторов
в первой строке таблицы (9.13):
Количество жордановых клеток порядка равно количеству векторов
во второй строке таблицы (9.13):
Продолжая вычисления аналогичным образом, получаем следующий результат: количество жордановых клеток порядка
находится по формуле
(9.14)
где
— наименьшее натуральное число, при котором
.
2. Число в (9.14) равно кратности корня
минимального многочлена матрицы
линейного преобразования.
3. Из пункта 1 следует единственность жордановой формы матрицы линейного преобразования (с точностью до перестановок жордановых клеток), так как состав жордановых клеток (количество и порядки) полностью определяется по размерностям инвариантных подпространств (9.8), (9.9). От выбора базиса зависит расположение жордановых клеток на главной диагонали матрицы (9.11). Поэтому жордановы формы, отличающиеся перестановкой жордановых клеток, считаются одинаковыми.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Решение:
Линейность оператора следует из линейности матричных операций умножения на скаляр, транспонирования и умножения на матрицу.
Если в каноническом базисе пространства М22
то
т.е. матрица данного оператора в каноническом базисе имеет вид:

Находим ядро данного оператора:
Для получения базиса образа данного линейного оператора находим:



Полученные векторы линейно независимы:

и могут быть выбраны в качестве базиса образа данного оператора, т.е.
Данный оператор имеет ненулевое ядро, следовательно, он необратим.
3.17. Оператор А действует на матрицы второго порядка по правилу , где
. Показать, что А – линейный оператор. Составить его матрицу в каноническом базисе. Найти ядро и образ оператора. Существует ли обратный оператор?
Решение:
Линейность оператора следует из линейности матричных операций умножения на скаляр, транспонирования и умножения на матрицу.
Если в каноническом базисе пространства М22
то
т.е. матрица данного оператора в каноническом базисе имеет вид:

Поскольку detA=-34≠0, то KerA=0, ImA=M22.
Данный оператор имеет нулевое ядро, следовательно, он обратим.
3.18. В пространстве Р2 многочленов степени не выше 2 оператор А действует по правилу . Показать линейность оператора. Найти его матрицу в каноническом базисе. Найти образ многочлена
. Найти ядро и образ оператора. Существует ли обратный оператор?
Решение:
Проверяем линейность оператора:
Свойства линейности выполнены – оператор линеен.
Если в базисе пространства P2
то
т.е. матрица данного оператора в базисе имеет вид:

Для данного многочлена получаем:

Находим ядро оператора:

Образ оператора находим как дополнение ядра до всего пространства L, для этого выбираем базисные векторы с нулями в тех координатах, которые отличны от нуля в уже выбранном векторе (1;0;0): .
Данный оператор имеет ненулевое ядро, следовательно, он необратим.
3.19. В пространстве Р3 многочленов степени не выше 3 оператор А действует по правилу . Показать линейность оператора. Найти его матрицу в каноническом базисе. Найти ядро и образ оператора. Существует ли обратный оператор?
Решение:
Проверяем линейность оператора:
Свойства линейности выполнены – оператор линеен.
Если в базисе пространства P3
то
т.е. матрица данного оператора в базисе имеет вид:

Находим ядро оператора:

Образ оператора находим как дополнение ядра до всего пространства L, для этого выбираем базисные векторы с нулями в тех координатах, которые отличны от нуля в уже выбранном векторе (0;0;0;1): .
Данный оператор имеет ненулевое ядро, следовательно, он необратим.
3.20. В пространстве Р2 многочленов степени не выше 2 оператор А действует по правилу . Показать линейность оператора. Найти его матрицу в каноническом базисе и в базисе
.
Решение:
Проверяем линейность оператора:
Свойства линейности выполнены – оператор линеен.
Если в базисе пространства P2
то
т.е. матрица данного оператора в каноническом базисе имеет вид:

Матрица перехода от базиса к базису
имеет вид:

следовательно, матрица данного оператора в базисе S имеет вид:

3.21. Показать, что оператор А, действующий на функции f(t) по правилу , является линейным оператором в пространстве функций
. Найти матрицу оператора в каком-нибудь базисе пространства. Обратим ли оператор? Найти ядро и образ оператора.
Решение:
Проверяем линейность оператора:
Свойства линейности выполнены – оператор линеен.
Если в базисе пространства L
то
т.е. матрица данного оператора в базисе имеет вид:

При этом detA=0, следовательно, данный оператор необратим.
Находим ядро оператора:

Образ оператора находим как дополнение ядра до всего пространства L, для этого выбираем базисные векторы с нулями в тех координатах, которые отличны от нуля в уже выбранном векторе (-1;1;0):
3.22. Показать, что оператор дифференцирования является линейным оператором в пространстве функций . Найти матрицу оператора в каком-нибудь базисе пространства. Существует ли обратный оператор? Найти ядро и образ оператора.
Решение:
Если то
т.е. и матрица оператора в базисе
имеет вид:

Поскольку detA=0, то данный оператор не имеет обратного.
Находим ядро данного оператора:

т.е. KerA = L{(0;0;1)} =
Отсюда получаем образ данного оператора как дополнения ядра до полного пространства L, для этого выбираем базисные векторы с нулями в тех координатах, которые отличны от нуля в уже выбранном векторе (0;0;1):
ImA = L{(1;0;0).(0;1;0)} =
3.23. Показать, что оператор сдвига является линейным оператором в пространстве функций
. Найти матрицу оператора в каком-нибудь базисе пространства. Существует ли обратный оператор? Найти ядро и образ оператора.
Решение:
Данный оператор линеен, поскольку выполнены свойства
Если , то
т.е. и матрица оператора в базисе
имеет вид:

Поскольку detA≠0, то данный оператор имеет обратный.
Находим ядро данного оператора:

т.е. KerA = 0 и поэтому ImA = L.
3.24. Линейный оператор А в пространстве V3 имеет в базисе матрицу

Решение:
Матрица линейного оператора из задачи 3.24 в базисе имеет вид:

Находим собственные значения и собственные векторы матрицы:

Для
Для
Т.е. собственному значению соответствуют два собственных вектора
собственному значению
– один собственный вектор
.
По определению, линейный оператор называется оператором простого типа (или простым оператором), если из собственных векторов этого оператора можно составить базис линейного пространства. Собственные векторы данного оператора образуют базис пространства V3, следовательно, это оператор простого типа.
3.25. В пространстве V3 оператор линейный оператор А – зеркальное отражение относительно плоскости YOZ. Найти собственные значения и собственные векторы оператора А.
Решение:
Зеркальное отражение относительно плоскости YOZ в пространстве V3 переводит точку с координатами (a;b;c) в точку с координатами (-a;b;c), т.е. матрица данного оператора имеет вид:

Находим собственные значения и собственные векторы матрицы оператора:

Для
Для
Получаем два собственных значения , первому соответствует один собственный вектор
, второму – два собственных вектора:
.
3.26. В пространстве V3 оператор линейный оператор А – проекция на ось OY. Найти собственные значения и собственные векторы оператора А.
Решение:
Проекция на ось OY в пространстве V3 переводит точку с координатами (a;b;c) в точку с координатами (0;b;0), т.е. матрица данного оператора имеет вид:

Находим собственные значения и собственные векторы матрицы оператора:

Для
Для
Получаем два собственных значения , первому соответствуют два собственных вектора:
, второму – один собственный вектор
.
3.27. Линейный оператор А – проекция на ось . Найти собственные значения и собственные векторы оператора А.
Решение:
Проекция на ось переводит точку с координатами (a;b) в точку с координатами (a–b;b–a):

т.е. матрица данного оператора имеет вид:
Находим собственные значения и собственные векторы матрицы оператора:
Для
Получаем единственное собственное значение , которому соответствует один собственный вектор:
.
3.28. В пространстве V3 оператор действует по правилу , где
. Найти собственные значения и собственные векторы оператора А.
Решение:
Если , то
т.е. матрица данного оператора имеет вид:

Находим собственные значения и собственные векторы матрицы оператора:

Для
Для
Получаем два собственных значения , первому соответствуют два собственных вектора:
, второму – один собственный вектор
.
3.29. В каноническом базисе пространства R3 оператор А действует по правилу . Найти собственные значения и собственные векторы оператора А.
Решение:
Матрица данного оператора в каноническом базисе имеет вид:

Находим собственные значения и собственные векторы матрицы оператора:

Для
Для
Получаем два собственных значения , которым соответствуют собственные вектора:
.
3.30. Найти
Решение:
Находим собственные значения и собственные векторы матрицы оператора:
Для
Для
Отсюда получаем представление данной матрицы в виде
Тогда
=

3.31. Линейный оператор А в каноническом базисе пространства Р2 многочленов степени не выше 2 имеет матрицу 
Решение:
Находим собственные значения и собственные векторы матрицы оператора:

Для
Получаем единственное собственное значение , которому соответствуют два собственных вектора:
.
По определению, линейный оператор называется оператором простого типа (или простым оператором), если из собственных векторов этого оператора можно составить базис линейного пространства. Данный оператор имеет всего два собственных вектора, размерность пространства Р2 равна 3, следовательно, данный оператор не является оператором простого типа.
Содержание
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом
ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
Линейный оператор
Линейное отображение линейного (векторного) пространства $ mathbb V_{} $ в себя
$$ mathcal A : mathbb V longmapsto mathbb V $$
называется линейным преобразованием $ mathbb V_{} $ или линейным оператором1) на $ mathbb V_{} $.
В дальнейшем под выражением оператор понимается исключительно линейный оператор (и линейное пространство $ mathbb V_{} $ предполагается конечномерным!).
Напомню свойство линейности:
$$
mathcal A (X_1 +X_2)= mathcal A(X_1) + mathcal A(X_2),quad mathcal A (alpha_1 X_1)=
alpha_1 mathcal A (X_1),
$$
или, в эквивалентном виде:
$$
mathcal A(alpha_1 X_1 + alpha_2 X_2)= alpha_1 mathcal A(X_1) + alpha_2 mathcal A(X_2)
$$
для $ forall {X_1,X_2} subset mathbb V,
forall {alpha_1,alpha_2 } subset mathbb R mbox{ или } mathbb C $
(здесь $ alpha_1,alpha_ 2 $ — константы из $ mathbb R_{} $ если $ mathbb V_{} $
вещественное пространство, и из $ mathbb C_{} $, если оно комплексное).
Примеры линейных операторов
Бóльшую часть примеров пункта
☞
ПРИМЕРЫ ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ представляют именно линейные операторы. Укажу еще несколько, к которым буду часто обращаться.
П
Пример 1. В пространстве $ mathbb R^{3} $ рассмотрим следующие действия над вектором2) $ (x_{},y,z) $:
-
поворот вокруг прямой $ x=y=2,z $ на угол $ pi/3 $;
-
зеркальное отражение относительно плоскости $ 3,x-y+z = 0 $;
-
растяжение в $ 3.14 $ раза.
Все это — примеры линейных операторов. Но вот отображение сдвига $ (x,y,z) mapsto (x+1,y,z+2) $ оператором не является поскольку
$$ {color{RubineRed} alpha } (x,y,z) = ( {color{RubineRed} alpha } x, {color{RubineRed} alpha } y, {color{RubineRed} alpha } z) mapsto ( {color{RubineRed} alpha } x+1, {color{RubineRed} alpha } y, {color{RubineRed} alpha } z+2) ne {color{RubineRed} alpha } (x+1,y,z+2) . $$
П
Пример 2. В пространстве $ mathbb R^{3} $ отображение ортогонального проецирования на плоскость $ x+y-7, z=0 $ будет линейным оператором (а вот на плоскость $ x+y-7, z=1 $ — не будет!). Вообще, в произвольном пространстве $ mathbb V_{} $ разбитом в прямую сумму нетривиальных подпространств $ mathbb V= mathbb V_1 oplus mathbb V_2 $ отображение, сопоставляющее вектору $ X_{} $ его проекцию на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_2 $, будет оператором.
П
Пример 3. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степеней $ le 3 $ отображение $ mathcal A_{} $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} , $$
т.е. полином $ f_{}(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Это отображение будет оператором в $ mathbb P_3 $. Действительно, если
$$
begin{array}{l}
f_1(x)(x^2-2) equiv q_1(x)(x^4-x^3-x^2+x)+ r_1(x), , \
f_2(x)(x^2-2) equiv q_2(x)(x^4-x^3-x^2+x)+ r_2(x) ,
end{array}
$$
при $ {q_1(x),q_2(x),r_1(x),r_2(x)} subset mathbb R[x], deg r_1(x) le 3, deg r_2(x) le 3 $,
то
$$ (alpha_1 f_1(x)+alpha_2 f_2(x)) (x^2-2) equiv (alpha_1 q_1(x)+alpha_2 q_2(x))(x^4-x^3-x^2+x)+ (alpha_1 r_1(x)+alpha_2 r_2(x)) ;
$$
очевидно, что $ deg (alpha_1 r_1(x)+alpha_2 r_2(x)) le 3 $.
♦
П
Пример 4. Задачу интерполяции можно интерпретировать как построение некоторого отображения. В интерполяционной таблице
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & y_1 & y_2 &dots & y_n
end{array} qquad npu qquad { x_{1}, dots, x_{n}, y_{1},dots,y_{n} } subset mathbb C
$$
будем считать узлы $ { x_j}_{j=1}^n $ фиксированными, а значения $ { y_j}_{j=1}^n $ — переменными. Эта таблица однозначно определяет интерполяционный полином $ f(x)=A_{0}+A_1x+dots+A_{n-1}x^{n-1} $ со свойством $ f(x_j)=y_j $ при $ j in {1,dots,n} $. При этом $ {A_{j} }_{j=0}^{n-1} subset mathbb C $. Будет ли получившееся отображение
$$ (y_1,dots,y_n) mapsto (A_0,A_1,dots,A_{n-1}) $$
оператором на $ mathbb C^n $? Покажем, что отображение
$$ mathcal A(y_1,dots,y_n) = f(x) in mathbb C[x] $$
является линейным отображением. Действительно, решением задачи интерполяции для таблицы
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & alpha y_1 & alpha y_2 &dots & alpha y_n
end{array}
qquad npu qquad forall alpha in mathbb C
$$
является полином $ alpha f(x) $. Если же, вдобавок, решением задачи интерполяции для таблицы
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & z_1 & z_2 &dots & z_n
end{array}
qquad npu qquad { z_{1},dots,z_{n} } subset mathbb C
$$
является полином $ g(x)in mathbb C[x], deg g(x) le n-1 $, то
решением задачи интерполяции для таблицы
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & y_1+z_1 & y_2+z_2 &dots & y_n+z_n
end{array}
qquad
$$
будет полином $ f(x)+g(x) $ и этот полином будет единственным решением среди полиномов степеней $ le n-1 $. Таким образом, линейность отображения $ mathcal A $ установлена. Далее, множество $ mathbb P_{n-1} $ полиномов из $ mathbb C[x] $ степеней $ le n-1 $ изоморфно пространству $ mathbb C^n $. Следовательно, «сложное» отображение
$$
(y_1,dots,y_n) mapsto f(x)=A_{0}+A_1x+dots+A_{n-1}x^{n-1} mapsto (A_0,A_1,dots,A_{n-1})
$$
является линейным отображением из $ mathbb C^n $ в $ mathbb C^n $, т.е. оператором на $ mathbb C^n $.
По аналогии с задачей алгебраической интерполяции, можно поставить и задачу тригонометрической интерполяции. Имеем здесь «точку входа» в теорию дискретного преобразования Фурье.
♦
Этот пример можно «развернуть»: НИЖЕ будет показано, что произвольный оператор,
действующий в пространстве размерности $ n_{} $ полностью определяется своими значениями в $ n_{} $ точках пространства. Важное отличие от традиционной, числовой интерполяции: условие различности этих точек не является достаточным для однозначного определения оператора
!
?
В пространстве $ mathbb P_2 $ оператор действует следующим образом:
$$ mathcal A (x^2+x+1) =2,x+1, mathcal A (x^2-x-1) =2,x^2-1, mathcal A (x+1) =-x^2+x+1 . $$
Вычислить $ mathcal A (x^2) $ и $ mathcal A (x^2+1) $.
П
Пример 5. В пространстве полиномов степени не выше $ n_{} $ с вещественными коэффициентами от $ m_{} $ переменных $ x_1,x_2,dots,x_{m} $ отображение
$$ f(x_1,x_2,dots,x_m) mapsto frac{partial^2 f}{partial x_1^2} +frac{partial^2 f}{partial x_2^2}+ dots+ frac{partial^2 f}{partial x_m^2}
$$
яыляется линейным оператором. Этот оператор известен как оператор Лапласа и для него используется символьное обозначение
$$ Delta = frac{partial^2 }{partial x_1^2} +frac{partial^2 }{partial x_2^2}+ dots+ frac{partial^2 }{partial x_m^2} , .
$$
П
Пример 6. В линейном пространстве квадратных матриц порядка $ n_{} $ с вещественными элементами рассмотрим коммутирующее отображение
$$ mathcal K (X) = AX-XA , $$
а также отображение Ляпунова
$$ mathcal V (X) = A^{top}X+XA $$
при произвольной фиксированной квадратной матрице $ A_{} $ и $ {}^{top} $ означающем транспонирование. Легко проверить, что оба отображения $ mathcal K $ и $ mathcal V $ являются операторами.
♦
Основные определения
Все введенные для линейного отображения понятия переносятся на этот частный случай. Например, ядром оператора называется множество векторов, отображаемых оператором в нулевой вектор:
$$mathcal{K}er (mathcal A)= left{Xin mathbb V big| mathcal A(X)=mathbb O right} ; $$
а образом оператора называется множество всех векторов из
$ mathbb V_{} $, для каждого из которых существует прообраз в том же пространстве:
$$mathcal{I}m (mathcal A)= left{Yin mathbb V mid exists X in mathbb V, mathcal A(X)= Y
right} .$$
Т
Теорема 1. Множества $ mathcal{K}er (mathcal A) $ и $ mathcal{I}m (mathcal A) $ являются подпространствами пространства $ mathbb V_{} $.
?
Доказать, что для оператора в $ mathbb R^4 $
$$
mathcal A
left(begin{array}{c}
x_1 \ x_2 \ x_3 \ x_4
end{array}
right)=
left(begin{array}{c}
x_3 \ x_4 \ 0 \ 0
end{array}
right)
$$
имеет место равенство $ mathcal{K}er (mathcal A) = mathcal{I}m (mathcal A) $.
Для оператора $ mathcal A_{} $ его дефектом его называется размерность ядра,
а его рангом — размерность образа:
$$ operatorname{dfc}(mathcal A )=dim (mathcal{K}er (mathcal A )) ,
operatorname{rank}(mathcal A )= dim (mathcal{I}m (mathcal A )) .
$$
Оператор называется невырожденным если $ operatorname{dfc}(mathcal A )=0 $.
П
Пример. В пространстве $ mathbb R^{3} $ оператор проецирования на плоскость:
$$ mathcal A left(x, y, zright) longmapsto left(x, y, 0 right)
$$
является вырожденным поскольку его ядро нетривиально: $ mathcal{K}er (mathcal A)={(0,0,z) | z in mathbb R } $.
♦
Следующий результат является следствием теоремы $ 4 $ из
☞
ПУНКТА.
Т
Теорема 2. Имеет место равенство:
$$ dim mathbb V=dim left( mathcal{K}er (mathcal A) right) + dim left( mathcal{I}m (mathcal A) right) = operatorname{dfc}(mathcal A )+ operatorname{rank}(mathcal A ) .$$
В чем смысл свойства вырожденности оператора? — В том, что такой оператор «схлопывает» пространство, в котором действует: $ dim left( mathcal{I}m (mathcal A) right) < dim mathbb V $. Происходит уменьшение размерности подобное тому, что описано в предыдущем примере: трехмерное пространство прообразов оператором проецирования отображается в двухмерное пространство всевозможных образов.
Отображение $ mathcal P: mathbb V longmapsto mathbb V $ называется произведением оператора $ mathcal A $ на оператор $ mathcal B $ если
$ mathcal P(X)=mathcal A (mathcal B(X)) $ для любого $ Xin mathbb V_{} $. Записывать этот факт будем в виде $ mathcal P=mathcal A , mathcal B $.
Фактически, произведение операторов — частный случай понятия сложной функции.
Т
Теорема 3. Произведение операторов является оператором на $ mathbb V_{} $.
Операция произведения ассоциативна.
Доказательство. Имеем на основании свойства линейности
$$mathcal P (alpha_1X_1+alpha_2X_2)=
mathcal A (mathcal B(alpha_1X_1+alpha_2X_2))=mathcal A (alpha_1mathcal B(X_1)+
alpha_2mathcal B(X_2))=$$
$$=alpha_1mathcal A (mathcal B(X_1))+
alpha_2mathcal A (mathcal B(X_2))=alpha_1mathcal P(X_1)+alpha_2{mathcal P}(X_2).$$
Далее, для любого вектора $ X_{} $:
$$mathcal A_1(mathcal A_2mathcal A_3(X))= mathcal A_1(mathcal A_2(mathcal A_3(X)))=mathcal A_1mathcal A_2({mathcal A}_3(X))
,$$
откуда и следует ассоциативность.
♦
Говорят, что операторы $ mathcal A $ и $ mathcal B $ коммутируют если $ mathcal A , mathcal B = mathcal B , mathcal A $.
П
Пример. В пространстве полиномов $ mathbb P_{n} $ рассмотрим
дифференциальный оператор
$$mathcal A = xfrac{d}{d, x}times Box – 1times Box :
mathcal A(p(x)) = x p'(x) – p(x) .$$
Этот оператор не коммутирует с обычным оператором дифференцирования
$ displaystyle mathcal B= frac{d}{d, x} $:
$$mathcal A (x^2)=x^2, quad mathcal B (mathcal A(x^2))=2,x, quad
mathcal B (x^2)=2,x, quad mathcal A (mathcal B (x^2))=0 .$$
♦
Оператор $ mathcal E $, отображающий произвольный вектор $ Xin mathbb V_{} $ в себя : $ mathcal E(X)= X $, называется тождественным на $ mathbb V_{} $. Оператор $ mathcal B $ называется (левым)
обратным оператору $ mathcal A_{} $, если $ mathcal Bmathcal A=mathcal E $.
В этом случае оператор $ mathcal A_{} $ называют обратимым и записывают:
$ mathcal B=mathcal A^{-1} $.
Не всякий оператор обратим.
П
Пример. В пространстве $ mathbb R^{3} $ для оператора проецирования на плоскость:
$$ mathcal A left(x, y, zright) longmapsto left(x, y, 0 right)
$$
обратного не существует, т.к. $ mathcal A(0,0,1)=(0,0,0) $ и ни при каком выборе оператора $ mathcal B $ нельзя добиться выполнения равенства $ mathcal B(0,0,0)=(0,0,1) $.
♦
?
Показать, что обратным для оператора
$$frac{1}{x}int_0^x : p(x) longmapsto frac{1}{x}int_{0}^{x}
p(t) d, t ,$$
на $ mathbb P_{n} $ является оператор
$$ frac{d}{d,x}left(xtimes Box right) : p(x) longmapsto
(xp(x))’ .$$
Т
Теорема 4. Оператор $ mathcal A_{} $ обратим тогда и только тогда, когда
когда он невырожден: $ operatorname{dfc} (mathcal A) =0 $. В этом случае $ mathcal A^{-1} $ единствен и коммутирует с $ mathcal A $.
Из теоремы следует, что левый обратный оператор к оператору $ mathcal A_{} $ — если он существует — совпадает с правым обратным оператором. Это утверждение не будет справедливым для бесконечномерных пространств. См. задачу
7
☞
ЗДЕСЬ.
При $ Kin mathbb N $ и $ K>1 $, $ K_{} $-я степень оператора $ mathcal A $ определяется
рекурсивной формулой
$$mathcal A^{, K}=mathcal A (mathcal A^{, K-1}) .$$
Если, вдобавок, $ mathcal A $ невырожден, то отрицательная степень оператора определяется формулой
$$mathcal A^{-K}=left(mathcal A^{-1}right)^K . $$
Полагают также $ mathcal A^{, 0}= {mathcal E} $ для любого $ mathcal A ne {mathcal O} $.
Т
Теорема 5. Степени оператора $ mathcal A $ коммутируют:
$$mathcal A^{, K} mathcal A^{, L}=mathcal A^{, L}mathcal A^{, K}=mathcal A^{, K+L} .$$
П
Пример. $ K_{} $-й степенью оператора дифференцирования в пространстве полиномов $ mathbb P_{n} $ будет оператор нахождения $ K_{} $-й производной:
$$left( frac{d}{d,x} right)^K = frac{d^K}{d,x^K} .$$
Очевидно, что при $ K_{}>n $ этот оператор будет нулевым.
♦
П
Пример. В произвольном пространстве $ mathbb V_{} $ разбитом в прямую сумму нетривиальных подпространств $ mathbb V= mathbb V_1 oplus mathbb V_2 $ оператор проецирования $ mathcal P $ на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_2 $ обладает свойством $ mathcal P^2 = mathcal P $ (проецирование проекции оставляет ее на месте).
♦
Оператор $ mathcal A $, обладающий свойством $ mathcal A^2 = mathcal A $, называется идемпотентным3).
П
Пример. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ отображение $ mathcal A_{} $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} , $$
т.е. полином $ f_{}(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Для этого оператора $ K_{} $-й его степенью является оператор
$$ mathcal B (f(x)) = f(x) (x^2-2)^K pmod{x^4-x^3-x^2+x} . $$
Действительно, если
$$
f(x)(x^2-2) equiv q(x)(x^4-x^3-x^2+x)+ r(x)
$$
при $ {q(x),r(x)} subset mathbb R[x] $ и $ deg r(x) le 3 $, то
$$
f(x)(x^2-2)^2 equiv q(x)(x^4-x^3-x^2+x)(x^2-2)+ r(x)(x^2-2) .
$$
Но тогда
$$ mathcal A^2 (f(x))= mathcal A (r(x)) = r(x) (x^2-2) pmod{x^4-x^3-x^2+x} equiv
$$
$$
equiv f(x)(x^2-2)^2 pmod{x^4-x^3-x^2+x} .
$$
Завершает доказательство святая индукция по степени $ K_{} $…
♦
Пусть задан произвольный полином
$ g(x)=b_{0}x^m+b_1x^{m-1}+dots+b_m $ из $ mathbb R[x] $ или $ mathbb C[x] $. Выражение
$$g(mathcal A )= b_0mathcal A^{m}+b_1mathcal A^{m-1}+dots+b_m{mathcal E}$$
будем называть операторным полиномом.
?
Доказать, что операторные полиномы коммутируют:
$ g_1(mathcal A )g_2(mathcal A )=g_2(mathcal A )g_1(mathcal A ) $.
?
Доказать, что для любого $ mathcal A in {mathcal H}om(mathbb V,mathbb V) $
всегда найдется полином $ g_{}(x) $, $ deg g le n^2+1 $ такой, что
$ g(mathcal A)={mathcal O} $.
Сформулируем еще один результат, являющийся частным случаем приведенного в пункте
☞
СВОЙСТВА ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ.
Т
Теорема 6. Пусть $ {X_1,X_2,dots,X_n} $ — произвольный базис $ mathbb V_{} $,
а $ Y_1,Y_2,dots,Y_n $ — произвольные векторы того же пространства. Существует единственный оператор $ mathcal A: mathbb V longmapsto mathbb V $ такой, что
$$ mathcal A(X_1)=Y_1,mathcal A(X_2)=Y_2, dots,mathcal A(X_n)=Y_n .$$
Доказательство. Искомый оператор строится следующим образом. Если $ X=x_1X_1+x_2X_2+dots+x_nX_n $ — разложение произвольного вектора $ X in mathbb V $ по базису, то
$$ mathcal A(X)=x_1 Y_1+x_2Y_2+dots+ x_nY_n . $$
Единственность этого оператора доказывается от противного. Любой другой оператор $ mathcal B $, удовлетворяющий условиям $ {mathcal B(X_j)=Y_j}_{j=1}^n $, будет действовать на тот же вектор $ X_{} $ с тем же результатом:
$$ mathcal B(X)=x_1 mathcal B(X_1)+x_2mathcal B(X_2) +dots+ x_nmathcal B(X_n)=
x_1 Y_1+x_2Y_2+dots+ x_nY_n= mathcal A(X) . $$
♦
Таким образом, оператор — как функция, действующая в $ n_{} $-мерном линейном пространстве, однозначно определяется заданием на $ n_{} $ линейно независимых векторах. В доказательстве теоремы дается и конструктивный способ представления оператора по этим значениям (т.е. строится его “интерполяционная формула” ).
Матрица оператора
Рассмотрим оператор $ mathcal A $ на $ mathbb V_{} $ и пусть $ {X_1,dots,X_n} $ — базис $ mathbb V_{} $. Являясь частным случаем линейного отображения, оператор должен обладать и соответствующей матрицей. Существенной особенностью, отличающей наш случай от
рассмотренного в пункте
☞
МАТРИЦА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ, является невозможность произвола при выборе базиса для $ mathcal{I}m (mathcal A) $. Поскольку $ mathcal{I}m (mathcal A) $ является
подпространством $ mathbb V_{} $, то было бы слишком большой роскошью
иметь два разных базиса для одного и того же пространства.
Найдем координаты образов базисных векторов
$ mathcal A (X_1),dots,mathcal A (X_n) $ в том же базисе $ {X_1,dots,X_n} $:
$$
left{ begin{array}{ccc}
mathcal A(X_1)&=&{{color{RubineRed} alpha }}_{11}X_1+{{color{RubineRed} alpha }}_{21}X_2+dots+{{color{RubineRed} alpha }}_{n1}X_n, \
mathcal A(X_2)&=&{{color{Green} alpha }}_{12}X_1+{{color{Green} alpha }}_{22}X_2+dots+{{color{Green} alpha }}_{n2}X_n, \
dots & & qquad dots , \
mathcal A(X_n)&=&alpha_{1n}X_1+alpha_{2n}X_2+dots+alpha_{nn}X_n.
end{array} right.
$$
Матрица
$$
mathbf A= left(begin{array}{cccc}
{{color{RubineRed} alpha }}_{11} & {{color{Green} alpha }}_{12}& dots & alpha_{1n} \
{{color{RubineRed} alpha }}_{21} & {{color{Green} alpha }}_{22}& dots & alpha_{2n} \
dots & & & dots \
{{color{RubineRed} alpha }}_{n1} & {{color{Green} alpha }}_{n2}& dots & alpha_{nn}
end{array}
right)_{ntimes n},
$$
в столбцах которой стоят координаты образов базисных векторов,
называется матрицей оператора $ mathcal A_{} $ в базисе $ {X_1,dots,X_n} $.
П
Пример. Известны образы базисных векторов $ mathbb R^{3} $
под действием оператора $ mathcal A_{} $:
$$mathcal A left( begin{array}{r}
5 \ 3 \ 1
end{array}right)=
left( begin{array}{r}
-2 \ 1 \ 0
end{array}right)
,
mathcal A left( begin{array}{r}
1 \ -3 \ -2
end{array}right) =
left( begin{array}{r}
-1 \ 3 \ 0
end{array}right)
,
mathcal A
left( begin{array}{r}
1\ 2 \ 1
end{array}right)=
left( begin{array}{r}
-2 \ -3 \ 0
end{array}right) .
$$
Найти матрицу этого оператора в исходном базисе.
Решение. Элементы матрицы $ {mathbf A} $ ищутся по формулам из определения, которые можно переписать в матричном виде:
$$left[ X_1,dots,X_n right] {mathbf A}=left[ mathcal A (X_1),dots,mathcal A (X_n) right]
.$$
Откуда
$${mathbf A}= left[ X_1,dots,X_n right]^{-1} left[ mathcal A (X_1),dots,mathcal A (X_n)
right] ,$$
и для нашего примера эта формула дает
$$
{mathbf A}=
left(begin{array}{rrr}
5&1&1 \
3&-3&2 \
1&-2&1
end{array}right)^{-1}
left(begin{array}{rrr}
-2&-1&-2 \
1&3&-3 \
0&0&0
end{array}right)
=
$$
$$
=left(begin{array}{rrr} 1&-3&5\
-1&4&-7\
-3&11&-18
end{array}right)
left(begin{array}{rrr}
-2&-1&-2 \
1&3&-3 \
0&0&0
end{array}right)
=
left(begin{array}{rrr}
-5&-10&7\
6&13&-10\
17&36&-27
end{array}
right).
$$
♦
?
В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ оператор $ mathcal A_{} $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^3+2,x^2+1) pmod{x^4+4} , $$
т.е. полином $ f_{}(x) $ отображается в остаток от деления произведения $ f(x) (x^3+2,x^2+1) $ на $ x^4+4 $. Найти матрицу оператора $ mathcal A_{} $ в базисе $ {1,x,x^2,x^3} $.
Ответ.
$$
left(begin{array}{rrrr}
1 & -4 & -8 & 0 \
0 & 1 & -4 & -8 \
2& 0 & 1 & -4 \
1 & 2 & 0 & 1
end{array}
right) .
$$
Т
Теорема 1. Координаты произвольного вектора $ X=x_1X_1+dots+x_nX_n $ и его образа $ Y=mathcal A(X)=y_1X_1+dots+y_nX_n $ связаны формулой
$$
left(begin{array}{c}
y_1 \ vdots \ y_n
end{array}
right) =
{mathbf A}left(begin{array}{c}
x_1 \ vdots \ x_n
end{array}
right) .
$$
Как изменяется матрица оператора при переходе к новому базису?
Т
Теорема 2. Если $ C_{} $ — матрица перехода от старого базиса
к новому, то матрицы $ {mathbf A} $ и $ {mathbf B} $ оператора в старом и новом
базисах связаны формулой:
$$
{mathbf B}=C^{-1}cdot {mathbf A} cdot C .
$$
Доказательство
☞
ЗДЕСЬ.
П
Пример. Оператор $ mathcal A $ в базисе пространства $ mathbb R^{3} $
$$
underbrace{left( begin{array}{r}
8 \ -6 \ 7
end{array}right)}_{X_1},
underbrace{left( begin{array}{r}
-16 \ 7 \ -13
end{array}right)}_{X_2} ,
underbrace{left( begin{array}{r}
9\ -3 \ 7
end{array}right)}_{X_3}
qquad
mbox{ имеет матрицу }
qquad
left( begin{array}{rrr}
1&-18&15\
-1&-22&20\
1&-25 &22
end{array}right).
$$
Найти его матрицу в базисе
$$
underbrace{left( begin{array}{r}
1\ -2 \ 1
end{array}right)}_{mathfrak X_1} ,
underbrace{left( begin{array}{r}
3\ -1 \ 2
end{array}right)}_{mathfrak X_2} ,
underbrace{left( begin{array}{r}
2\ 1 \ 2
end{array}right)}_{mathfrak X_3}.
$$
Решение. Матрица $ C_{} $ перехода от старого базиса к новому
находится по
☞
формуле
$$ C= left[X_1|X_2|X_3right]^{-1} cdot left[{mathfrak X}_1|{mathfrak X}_2|{mathfrak X}_3right]= $$
$$
=left( begin{array}{rrr}
8&-16&9\
-6&7&-3\
7&-13 &7
end{array}right)^{-1}
left( begin{array}{rrr}
1&3&2\
-2&-1&1\
1&2 &2
end{array}right)
=
$$
$$
=left (begin{array}{rrr}
2&-1&-3\
{scriptstyle 21}/{scriptstyle 5}& -{scriptstyle 7}/{scriptstyle 5}&-6\
{scriptstyle 29}/{scriptstyle 5}&-{scriptstyle 8}/{scriptstyle 5}&-8
end{array}right)
left( begin{array}{rrr}
1&3&2\
-2&-1&1\
1&2 &2
end{array}right)=
left(begin{array}{rrr}
1&1&-3\
1&2&-5\
1&3&-6
end{array}right) .
$$
По теореме:
$$
{mathbf B}=C^{-1} {mathbf A} C=
left(begin{array}{rrr}
3&-3&1\
1&-3&2\
1&-2&1
end{array}right)
left( begin{array}{rrr}
1&-18&15\
-1&-22&20\
1&-25 &22
end{array}right)
left(begin{array}{rrr}
1&1&-3\
1&2&-5\
1&3&-6
end{array}right)=
$$
$$
=left(begin{array}{rrr}
7&-13&7\
6&-2&-1\
4&1&-3
end{array}right)
left(begin{array}{rrr}
1&1&-3\
1&2&-5\
1&3&-6
end{array}right)=left(begin{array}{rrr}
1&2&2\
3&-1&-2 \
2&-3&1
end{array}right).
$$
♦
Матрицы $ {mathbf A} $ и $ {mathbf B} $, связанные соотношением
$ {mathbf B}=C^{-1}cdot {mathbf A} cdot C $ при какой-то неособенной матрице $ C_{} $, называются подобными, этот факт будем записывать: $ {mathbf A}doteq {mathbf B} $.
?
Доказать, что отношение подобия есть отношение эквивалентности, и если $ {mathbf A}doteq {mathbf B} $ то $ g({mathbf A})doteq g({mathbf B}) $ при любом полиноме $ g_{}(x) $.
Т
Теорема 3. Для оператора $ mathcal A_{} $ ранг его матрицы является инвариантом, т.е. не зависит от выбора базиса пространства. Этот ранг совпадает с рангом оператора $ mathcal A_{} $.
Доказательство. Если $ {mathbf A} $ и $ {mathbf B} $ — матрицы оператора в двух разных базисах, то они являются подобными: $ {mathbf B}=C^{-1}{mathbf A} C $. По свойству ранга матрицы имеем:
$ operatorname{rank}( {mathbf B})= operatorname{rank}({mathbf A}) $.
♦
=>
Дефект оператора $ mathcal A_{} $ совпадает с дефектом его матрицы в произвольном базисе пространства.
Т
Теорема 4. Для оператора $ mathcal A_{} $ определитель и след его матрицы являются инвариантами, т.е. не зависят от выбора базиса пространства.
Доказательство. Действительно, для подобных матриц $ {mathbf A} $ и $ {mathbf B} $, на основании теоремы Бине-Коши имеем:
$$ det ({mathbf B}) = det (C^{-1}{mathbf A} C) = det (C^{-1}) cdot det ({mathbf A}) cdot det (C) =det ({mathbf A}) . $$
Далее, по свойству следа матрицы:
$$ operatorname{Sp}({mathbf B}) = operatorname{Sp}(C^{-1}{mathbf A} C)=operatorname{Sp}({mathbf A} cdot C cdot C^{-1})=operatorname{Sp}({mathbf A}) . $$
♦
Этот результат позволяет ввести понятие определителя и следа оператора $ mathcal A_{} $ — посредством матрицы этого оператора в произвольном базисе пространства. Такое определение оказывается корректным поскольку оба значения не зависят от выбора базиса.
Каков “физический” смысл определителя оператора?
— Для ответа на этот вопрос рассмотрим оператор в $ mathbb R^2 $, заданный формулой:
$$
left(begin{array}{l} y_1 \ y_2 end{array} right)=
left(begin{array}{rr} 1 & – 3 \ 1 & -1 end{array} right)
left(begin{array}{l} x_1 \ x_2 end{array} right) .
$$
Свойство линейности оператора как отображения плоскости проявляется в том, что параллельные отрезки он отображает в параллельные же отрезки (см. упражнение к теореме 2 из
☞
ПУНКТА ), и, следовательно, любой параллелограмм отображается им в параллелограмм. Площади соответствующих параллелограммов оказываются связанными через определитель матрицы — более точно, через модуль этого определителя. В частном случае настоящего примера это проверяется непосредственно; что касается обобщения на произвольное евклидово пространство, в котором понятие объема вводится аксиоматически то сошлюсь на упражнение 3
☞
ЗДЕСЬ.

Иными словами: «физический» смысл определителя оператора заключается в том, что модуль его значения представляет коэффициент расширения4)объема (в настоящем примере — площади) тела (соответственно, плоской фигуры) под воздействием этого оператора.
А вот объяснить «физический» смысл следа оператора посложнее будет…
Т
Теорема 5. Оператор обратим тогда и только тогда, когда когда его определитель отличен от нуля.
Т
Теорема 6. Линейное пространство $ {mathcal H}om(mathbb V,mathbb V) $ операторов на $ mathbb V_{}, dim mathbb V = n $ изоморфно линейному пространству квадратных матриц порядка $ n_{} $ (с элементами из $ mathbb R_{} $ или из $ mathbb C_{} $).
Это утверждение является простым следствием теоремы 2, приведенной в пункте
☞
МАТРИЦА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ.
Однако в случае операторов установленный изоморфизм сохранит не только результат операции сложения, но и результат операции умножения:
$$ . mbox{ если } mathcal A_1 leftrightarrow mathbf A_1,
mathcal A_2 leftrightarrow mathbf A_2, mbox{ то } mathcal A_1+ mathcal A_2 leftrightarrow mathbf A_1 + mathbf A_2, lambda mathcal A_1
leftrightarrow lambda mathbf A_1 , mathcal A_1 mathcal A_2 leftrightarrow mathbf A_1 mathbf A_2 .
$$
Я сформулирую этот «усиленный вариант» изоморфизма в виде набора свойств, которыми буду пользоваться по мере возникновения потребности.
Т
Теорема 7. В любом базисе пространства
а) матрица нулевого оператора $ mathcal O $ является нулевой матрицей $ mathbb O_{} $, а матрица тождественного оператора $ mathcal E $ является единичной матрицей $ E_{} $; обратно: если матрица оператора в этом базисе — нулевая (единичная), то оператор является нулевым (соответственно, тождественным);
б) матрица произведения операторов совпадает с произведением матриц этих операторов5);
в) коммутирующим операторам соответствуют коммутирующие матрицы;
г) если $ {mathbf A} $ — матрица оператора, то $ {mathbf A}^{-1} $ — матрица обратного оператора;
д) если $ {mathbf A} $ — матрица оператора $ mathcal A $, то матрицей операторного полинома $ g (mathcal A) $ является матрица $ g({mathbf A}) $ .
Матрица оператора и матрица перехода от базиса к базису
Эти матрицы как-то взаимодействовали между собой в предыдущем пункте, хотя вторая была определена совершенно в другом разделе. Обе матрицы квадратные, обе имеют в определении «завязку» на базис пространства $ mathbb V_{} $. У начинающих изучать теорию часто возникает путаница при различении этих определений.
«Физический» смысл этих понятий различен. Образно говоря, если рассматривать оператор как процесс (точнее: установленную связь между входными и выходными значениями процесса), то выбор базиса можно интерпретировать как выбор точки зрения на этот процесс (можно трактовать эти слова как формализацию выражения «рассмотрим этот процесс под другим углом»).
Тем не менее, с чисто формальной точки зрения, матрица $ C_{} $ перехода от базиса $ {X_1,X_2,dots,X_n } $ пространства $ mathbb V_{} $ к какому-то другому базису $ {mathfrak X_1,mathfrak X_2,dots,mathfrak X_n } $ того же пространства может считаться матрицей некоторого оператора, действующего в этом пространстве. В самом деле, на основании теоремы 6, существует единственный оператор $ mathcal C $, переводящий старые базисные векторы в новые, взятые в той же последовательности:
$$ mathcal C (X_1)=mathfrak X_1, mathcal C (X_2)= mathfrak X_2, dots, mathcal C (X_n)= mathfrak X_n . $$
Но тогда матрица оператора $ mathcal C $ в базисе $ {X_1,X_2,dots,X_n } $ совпадает с матрицей $ C_{} $ перехода от базиса $ {X_1,X_2,dots,X_n } $ к базису $ {mathfrak X_1,mathfrak X_2,dots,mathfrak X_n } $.
Я буду записывать матрицы операторов и матрицы переходов от базиса к базису в разных стилях: $ mathbf A, mathbf B,dots $ и, соответственно, $ C, P, T, dots $ —
с целью быстрого распознавания их «физической» сущности.
Матрица оператора проецирования
Настоящий пункт может быть пропущен при первоначальном чтении.
T
Теорема. Рассмотрим линейную оболочку линейно независимой системы столбцов $ {Y_1,dots, Y_k } subset mathbb R^n $.
$$ mathbb M =left{ lambda_1 Y_1 + dots + lambda_k Y_k big| {lambda_1,dots,lambda_k} subset mathbb R right}= mathcal L (Y_1,dots,Y_k) , . $$
Пусть скалярное произведение векторов $ X_{} $ и $ Y_{} $ задается стандартным способом, т.е. $ langle X,Y rangle =x_1y_1+dots+x_ny_n $.
Ближайшей к точке $ X_0 subset mathbb R^n $ точкой многообразия (или ортогональной проекцией точки $ X_0 $ на многообразие) $ mathbb M_{} $ является
$$ X_{ast} = mathbf L (mathbf L^{top} mathbf L )^{-1} mathbf L^{top} X_0 , . $$
Здесь $ mathbf L=[Y_1 |dots |Y_k]_{ntimes k} $.
Матрица $ mathbf L^{top} mathbf L $ невырождена, поскольку является матрицей Грама
$$
mathbf L^{top} mathbf L=
left(begin{array}{cccc}
Y_1^{top} Y_1 & Y_1^{top} Y_2 & dots & Y_1^{top} Y_k \
Y_2^{top} Y_1 & Y_2^{top} Y_2 & dots & Y_2^{top} Y_k \
dots & & & dots \
Y_k^{top} Y_1 & Y_k^{top} Y_2 & dots & Y_k^{top} Y_k
end{array}
right)
$$
системы линейно независимых столбцов $ {Y_1,dots, Y_k } $.
Доказательство. Пусть $ X_0=X_0^{^{parallel}}+X_0^{^{bot}} $, где $ X_0^{^{parallel}} $ — ортогональная проекция точки $ X_0 $ на $ mathbb M $, а $ X_0^{^{bot}} $ — ортогональная составляющая.
Тогда
$$ mathbf L^{top} X_0^{^{bot}}=mathbb O $$
поскольку $ Y_1^{top} X_0^{^{bot}}=0,dots, Y_k^{top} X_0^{^{bot}}=0 $. Далее, $ X_0^{^{parallel}} $ можно разложить по базису $ {Y_1,dots, Y_k } $:
$$ X_0^{^{parallel}}=alpha_1 Y_1+dots+ alpha_k Y_k quad npu quad {alpha_1,dots,alpha_k} subset mathbb R , .
$$
Следовательно,
$$
mathbf L^{top} X_0=mathbf L^{top} (X_0^{^{parallel}}+X_0^{^{bot}})=mathbf L^{top} X_0^{^{parallel}}=
mathbf L^{top} (alpha_1 Y_1+dots+ alpha_k Y_k)=
$$
$$
=left(
begin{array}{c}
alpha_1 Y_1^{top} Y_1 +dots + alpha_k Y_1^{top} Y_k \
alpha_1 Y_2^{top} Y_1 +dots + alpha_k Y_2^{top} Y_k \
dots \
alpha_1 Y_k^{top} Y_1 +dots + alpha_k Y_k^{top} Y_k
end{array}
right)= mathbf L^{top} mathbf L
left(
begin{array}{c}
alpha_1 \
alpha_2 \
vdots \
alpha_k
end{array}
right), .
$$
Тогда
$$
mathbf L (mathbf L^{top} mathbf L )^{-1} mathbf L^{top} X_0=
mathbf L
left(
begin{array}{c}
alpha_1 \
alpha_2 \
vdots \
alpha_k
end{array}
right)
=alpha_1 Y_1+dots+ alpha_k Y_k= X_0^{^{parallel}} , .
$$
На основании теорем $ 1_{} $ и $ 2_{} $, приведенных
☞
ЗДЕСЬ,
точка $ X_0^{^{parallel}} $ является ближайшей точкой многообразия $ mathbb M $ к точке $ X_{0} $.
♦
Матрица $ P=mathbf L (mathbf L^{top} mathbf L )^{-1} mathbf L^{top} $ является матрицей оператора ортогонального проецирования на многообразие $ mathbb M_{} $
в стандартном базисе
$$ bigg{{mathfrak e}_j = big[underbrace{0,dots,0,1}_{j},0,dots,0big]^{top} bigg}_{j=1}^n , . $$
Она симметрична и идемпотентна, т.е. обладает свойством $ P^2=P $.
П
Пример. В $ mathbb R^{3} $ найти матрицу проецирования на плоскость $ x+y+z=0 $.
Решение. Параметрическое задание плоскости:
$$
mathbb M={ lambda_1 underbrace{[1,-1,0]^{top}}_{Y_1} + lambda_2 underbrace{[0,1,-1]^{top}}_{Y_2} big| {lambda_1,lambda_2} subset mathbb R } , .
$$
Имеем:
$$
mathbf L=
left(begin{array}{rr}
1 & 0 \
-1 & 1 \
0 & -1
end{array}
right) Rightarrow
mathbf L^{top} mathbf L=
left(begin{array}{rr}
2 & -1 \
-1 & 2
end{array}
right) Rightarrow (mathbf L^{top} mathbf L )^{-1}=
left(begin{array}{rr}
2/3 & 1/3 \
1/3 & 2/3
end{array}
right) Rightarrow
$$
$$
Rightarrow mathbf L (mathbf L^{top} mathbf L )^{-1} mathbf L^{top}=
frac{1}{3} left(begin{array}{rrr}
2 & -1 & -1 \
-1& 2 & -1 \
-1 & -1 & 2
end{array}
right) , .
$$
♦
В общем случае отображение точки $ X_{0} $ на ближайшую к ней точку произвольного многобразия
$$ mathbb M =left{ Y_0+lambda_1 Y_1 + dots + lambda_k Y_k big| {lambda_1,dots,lambda_k} subset mathbb R right} $$
при $ Y_0 $ линейно независимом от $ {Y_1,dots,Y_k} $ не является линейным оператором, а относится к типу аффинных отображений. Выражение для этого отображения см. в разделе
☞
ВЫЧИСЛЕНИЕ РАССТОЯНИЙ МЕЖДУ ГЕОМЕТРИЧЕСКИМИ ОБЪЕКТАМИ.
Матрица оператора отражения (оператора Хаусхолдера)
Настоящий пункт может быть пропущен при первоначальном чтении.
В пространстве $ mathbb R^n $ со стандартным скалярным произведением рассмотрим плоскость, заданную уравнением
$$ C^{top}X= c_1x_1+c_2x_2+dots+c_nx_n = 0 $$
при векторе нормали $ C^{top}=(c_1,c_2,dots,c_n) $ единичной длины: $ |C|^2= C^{top}C=1 $. Действие оператора зеркального отражения или оператора Хаусхолдера6) относительно этой плоскости на вектор (точку) $ X in mathbb R^n $ определим правилом
$$ mathcal H( X^{^{parallel}} + X^{^{bot}})= X^{^{parallel}} – X^{^{bot}} ; $$
здесь $ X^{^{parallel}} $ — ортогональная проекция вектора $ X_{} $ на заданную плоскость, а $ X^{^{bot}} $ — ортогональная составляющая вектора $ X_{} $ относительно этой плоскости.

Т
Теорема. Оператор $ mathcal H $ задается уравнением
$$ mathcal H(X)=X-2, langle X,C rangle C=X-2, C (C^{top}X)= X-2, C^{top}XC , . $$
Последний вариант формулы никогда не встречал, но он имеет формальное право на существование!
Доказательство.
$$ mathcal H( X^{^{parallel}} + X^{^{bot}})=X^{^{parallel}} + X^{^{bot}}-2, langle X^{^{parallel}},C rangle C-2,
langle X^{^{bot}},C rangle C = $$
Поскольку $ X^{^{parallel}} $ ортогонален, а вектор $ X^{^{bot}} $ коллинеарен вектору $ C $ единичной длины, то
$$= X^{^{parallel}} + X^{^{bot}} – 2, X^{^{bot}} = X^{^{parallel}} – X^{^{bot}} , . $$
♦
Т
Теорема. Матрица оператора $ mathcal H $ в стандартном базисе
$$ bigg{{mathfrak e}_j = big[underbrace{0,dots,0,1}_{j},0,dots,0big]^{top} bigg}_{j=1}^n , . $$
имеет вид
$$ mathbf H_{C}= E-2, C cdot C^{top} =
left( begin{array}{cccc}
1-2c_1^2 & -2,c_1c_2 & dots & – 2 c_1 c_n \
-2,c_1c_2 & 1-2c_2^2 & dots & – 2 c_2 c_n \
vdots & & & vdots \
– 2 c_1 c_n & – 2 c_2 c_n & dots & 1-2c_n^2
end{array}
right) , .
$$
П
Пример. Найти зеркальное отражение точки $ [3,2,3] $ относительно плоскости $ 2,x-2,y+z = 0 $.
Решение. Здесь $ C^{top}=[2/3,-2/3,1/3] $ и
$$ mathcal H(X)= left( begin{array}{r} 3 \ 2 \ 3 end{array} right) – 2langle [3,2,3],[2/3,-2/3,1/3] rangle
left( begin{array}{r} 2/3\ -2/3 \ 1/3 end{array} right)=
left( begin{array}{r} 7/9 \ 38/9 \ 17/9 end{array} right) , .
$$
Проверим результат посредством матричного представления:
$$
mathbf H_C=
left( begin{array}{rrr}
1/9 & 8/9 & -4/9 \
8/9 & 1/9 & 4/9 \
-4/9 & 4/9 & 7/9
end{array}
right) quad Rightarrow quad mathbf H left( begin{array}{r} 3 \ 2 \ 3 end{array} right)=
left( begin{array}{r} 7/9 \ 38/9 \ 17/9 end{array} right) , .
$$
♦
=>
Матрица $ mathbf H_{C} $ одновременно симметрична и ортогональна, и $ det mathbf H_{C}=-1 $. Следовательно, ей обратная существует и совпадает с ней самой:
$$ mathbf H_{C}^{-1}= mathbf H_{C} , . $$
Инвариантное подпространство
Задача. Подобрать базис пространства $ mathbb V_{} $ так, чтобы матрица заданного оператора $ mathcal A_{} $ имела наиболее простой вид.
Исследуем действие оператора $ mathcal A $ на произвольное подпространство
$ mathbb V_1 subset mathbb V $:
$$mathcal A (mathbb V_1)= left{Yin mathbb V mid Y=mathcal A (X), X in mathbb V_1
right} .$$
Вообще говоря, множества $ mathbb V_1 $ и $ mathcal A (mathbb V_1) $ будут различными, т.е.
$ exists X_1 in mathbb V_1 $ такой, что $ mathcal A (X_1)notin mathbb V_1 $.
Подпространство $ mathbb V_1 $ называется инвариантным подпространством оператора $ mathcal A $, если оно отображается этим оператором в себя:
$$ mathcal A(mathbb V_1)subset mathbb V_1 .$$
$ mathbb V_1={mathbb O } $ и $ mathbb V_1=mathbb V $ — тривиальные инвариантные подпространства произвольного оператора $ mathcal A $.
Нас будут интересовать нетривиальные инвариантные подпространства.
П
Пример. Оператор
$$left(begin{array}{c}
x \ y \ z
end{array}
right) longmapsto
left(begin{array}{rrr}
{scriptstyle 1}/{scriptstyle sqrt 2} &
-{scriptstyle 1}/{scriptstyle sqrt 2} & 0 \
{scriptstyle 1}/{scriptstyle sqrt 2} &
{scriptstyle 1}/{scriptstyle sqrt 2} & 0 \
0 & 0 & 1
end{array}
right)
left(begin{array}{c}
x \ y \ z
end{array}
right)
$$
задает в пространстве поворот вокруг оси $ mathbb O z $ на угол
$ +pi /4 $.
Нетривиальными инвариантными подпространствами будут
а) ось вращения $ mathbb V_1={(0,0,z)^{^{top}} mid z in mathbb R} $, $ dim mathbb V_1=1 $ и
б) плоскость, перпендикулярная оси вращения $ mathbb V_2={(x,y,0)^{^{top}} mid {x,y} subset mathbb R} $, $ dim mathbb V_2= 2 $.
♦
П
Пример. Оператор
$$left(begin{array}{c}
x \ y
end{array}
right) longmapsto
left(begin{array}{c}
lambda_1 x \ lambda_2 y
end{array}
right)
$$
задает на плоскости «растяжение»: $ x_{} $-компонента увеличивается
в $ lambda_{1} $ раз, а $ y_{} $-компонента — в $ lambda_{2} $ раз.
При любой комбинации коэффициентов растяжения координатные оси будут инвариантными подпространствами. Однако в частном случае $ lambda_1=lambda_2 $ инвариантной будет также любая
прямая, проходящая через начало координат.
♦
П
Пример. Оператор в $ mathbb R^{n}_{} $ задан блочной матрицей
$$X longmapsto left( begin{array}{cc}
{mathbf A}_1 & {mathbf *}\
mathbb O & {mathbf A}_2
end{array}
right) X
$$
где $ {mathbf A}_1 $ — $ n_1times n_1 $-матрица, $ {mathbf A}_2 $ —
$ (n-n_1)times (n-n_1) $-матрица. Множество столбцов
$$mathbb V_1=left{X=[x_1,dots,x_{n_1},0,dots,0]^{^{top}} bigg| { x_1,
dots, x_{n_1} } subset mathbb R right}$$
образует инвариантное подпространство, $ dim mathbb V_1=n_1 $. Если же, вдобавок,
матрица, обозначенная $ {mathbf *} $ — нулевая, то вторым инвариантным
подпространством будет
$$ mathbb V_2=left{X=[0,dots,0,x_{n_1+1},dots,x_n]^{^{top}} bigg| {x_{n_1+1},dots, x_n } subset mathbb R right} .$$
♦
Т
Теорема. $ mathcal{K}er (mathcal A) $ и $ mathcal{I}m(mathcal A) $ —
инвариантные подпространства оператора $ mathcal A $.
?
Доказать, что сумма двух инвариантных подпространств является инвариантным подпространством.
Т
Теорема. Если пространство $ mathbb V_{} $ раскладывается в прямую сумму подпространств, инвариантных относительно оператора $ mathcal A $, то существует базис пространства, в котором матрица оператора будет блочно-диагональной.
Теорема обобщается очевидным образом на произвольное число слагаемых
подпространств: $ mathbb V=mathbb V_1oplus mathbb V_2 oplus dots oplus mathbb V_k $.
Если при этом $ dim mathbb V_1= dots = dim mathbb V_k=1 $, то матрица оператора в базисе, полученном объединением базисных векторов слагаемых подпространств, становится диагональной — это и является решением задачи, поставленной в начале пункта.
Собственное число и собственный вектор
Задача. Найти одномерные инвариантные подпространства оператора.
Вектор $ X_{}in mathbb V $ называется собственным вектором оператора $ mathcal A_{} $, если
$$ {mathbf a)} X ne mathbb O, quad u quad {mathbf b)} exists lambda in mathbb C qquad mbox{ такое, что } qquad
mathcal A(X)=lambda X .$$
В этом случае число $ lambda_{} $ называется
собственным или характеристическим числом оператора, соответствующим (или принадлежащим) данному собственному вектору; обратно, говорят, что вектор $ X_{} $ принадлежит собственному числу $ lambda_{} $.
Вопрос существования хотя бы одного собственного числа для произвольного оператора $ mathcal A_{} $ остается пока открытым. Однако, свойство линейности оператора гарантирует, что если это число существует, то ему соответствует бесконечное множество собственных векторов:
$$ mathcal A(X)=lambda X quad Rightarrow quad mathcal A(t,X)=t mathcal A(X)= tlambda, X , $$
т.е. если вектор $ X in mathbb V_{} $ является собственным, то и вектор $ t, X $ будет собственным при любом скаляре $ tne 0 $. Заметим, что собственное число разыскивается во множестве комплексных чисел: вопрос о существовании вещественного собственного числа — даже в случае вещественного пространства $ mathbb V_{} $ — остается открытым. Геометрический смысл вещественных собственных чисел и векторов проясняет следующий пример.
П
Пример. Оператор
$$left(begin{array}{c}
x \ y
end{array}
right) longmapsto
left(begin{array}{rr}
1 & – 5/2 \
-1/2 & 2
end{array}
right)
left(begin{array}{c}
x \ y
end{array}
right)
$$
задает отображение плоскости $ mathbb R^2 $. На рисунке показан результат действия этого отображения на единичную окружность. Все точки плоскости, за исключением начала координат $ mathbb O_{} $, изменят свое положение — ни одна не останется на месте.

Если рассмотреть эти точки как концы векторов, имеющих начало в $ mathbb O_{} $, то смещения точек под действием оператора можно представить в виде двух составляющих: растяжения (т.е. увеличения расстояния до начала координат) и поворота вокруг начала координат на некоторый угол. И только по двум направлениям плоскости поворота не происходит. Точки окружности с координатами
$$
pm left( 0.823, -0.568 right)^{top} quad u quad
pm left( 0.960, 0.278 right)^{top}
$$
будут смещаться без поворота. Эти точки и задают координаты конца собственного вектора. А соответствующие им собственные числа $ 2.725 $ и $ 0.275 $ определяют коэффициенты сдвига.
Если вообразить оператор как деформацию физической среды, заполняющей плоскость, то можно сказать, что cобственный вектор задает направление, на котором действие оператора сводится к растяжению, при этом коэффициент растяжения и будет собственным числом.
А
Анимация процесса
☞
ЗДЕСЬ (1500 Kb, gif).
Пример другого оператора
$$
left(begin{array}{l} x \ y end{array} right) longmapsto
left(begin{array}{rr} 1 & – 3 \ 1 & -1 end{array} right)
left(begin{array}{l} x \ y end{array} right)
$$
показывает, что существование вещественных собственных чисел вовсе не гарантировано даже в случае оператора в вещественном пространстве: в этом примере все точки плоскости повернутся вокруг начала координат.
♦
Я «замыливаю» ответ на вопрос какой физический смысл имеют отрицательные собственные числа…
?
Доказать, что $ operatorname{dfc} (mathcal A) ne 0 $ тогда и только тогда, когда оператор $ mathcal A_{} $ имеет собственное число, равное нулю.
Т
Теорема. Любой собственный вектор оператора порождает его одномерное инвариантное подпространство, и обратно: любой ненулевой вектор одномерного инвариантного подпространства
оператора является собственным вектором.
П
Пример. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ оператор $ mathcal A_{} $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} , $$
т.е. полином $ f_{}(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Найти собственные векторы этого оператора.
Решение. В пространстве $ mathbb P_3 $ векторами являются полиномы, а условие того, что полином $ f_{}(x) $ является собственным, принадлежащим числу $ lambda_{} $, записывается в виде:
$$ f(x)(x^2-2)equiv lambda f(x) pmod{x^4-x^3-x^2+x} quad iff $$
$$ iff quad f(x)(x^2-2-lambda)equiv 0 pmod{x^4-x^3-x^2+x} . $$
Поскольку $ deg f le 3 $, то последнее может выполняться тогда и только тогда, когда полином
$ x^2-2-lambda $ имеет общие корни с $ x^4-x^3-x^2+x equiv x(x+1)(x-1)^2 $. Из этого условия вытекает, что число $ lambda_{} $ может принимать только два значения: $ lambda_1=-2 $ и
$ lambda_2=-1 $. Если $ lambda_1=-2 $ является собственным числом, то ему соответствующий собственный вектор — полином степени $ le 3 $ — должен определяться из условия делимости $ f(x)x^2 $ на $ x(x+1)(x-1)^2 $. Такой полином имеет вид $ t(x+1)(x-1)^2 $ при произвольной константе $ t_{} $. Следовательно множество
$$ { t(x^3-x^2-x+1)= t(x+1)(x-1)^2 mid tne 0 } $$
является множеством собственных векторов, принадлежащих $ lambda_1=-2 $.
С числом $ lambda_2=-1 $ поступаем аналогично. Условие делимости полинома $ f(x)(x^2-1) $ на $ x(x+1)(x-1)^2 $ дает также бесконечное множество:
$$ { (t_1x+t_2)x(x-1) mid {t_1,t_2} subset mathbb R } . $$
Однако в этом случае бесконечность множества качественно иная, чем в предыдущем случае; она — «двумерная».
♦
Задача. Для произвольного оператора выяснить условия существования его собственного числа и разработать конструктивный метод его нахождения.
Т
Теорема. В комплексном линейном пространстве любой оператор имеет по крайней мере один собственный вектор.
Доказательство. Пусть $ {X_1,dots,X_{n} } $ — произвольный базис пространства $ mathbb V_{} $ и
$ mathbf A_{} $ — матрица оператора $ mathcal A_{} $ в этом базисе. Тогда для
того чтобы вектор $ X=x_1X_1+cdots+x_nX_n ne mathbb O $ был собственным,
принадлежащим собственному числу $ lambda_{} $, необходимо и достаточно чтобы выполнялось
равенство
$$
{mathbf A}left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) =
lambda left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) quad
Longleftrightarrow quad
left(begin{array}{cccc}
alpha_{11} – lambda & alpha_{12}& dots & alpha_{1n} \
alpha_{21} & alpha_{22}- lambda& dots & alpha_{2n} \
dots & & & dots \
alpha_{n1} & alpha_{n2}& dots & alpha_{nn}- lambda
end{array}
right)
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) = mathbb O_{ntimes 1}
$$
Покажем, что существуют комплексные числа $ lambda_{} $ и не все нулевые $ x_1,dots,x_{n} $, удовлетворяющие этой системе. Необходимым и достаточным
условием существования нетривиального решения у однородной системы линейных уравнений с квадратной матрицей является равенство нулю определителя этой матрицы:
$$
det ({mathbf A}-lambda E)=left|begin{array}{cccc}
alpha_{11} – lambda & alpha_{12}& dots & alpha_{1n} \
alpha_{21} & alpha_{22}- lambda& dots & alpha_{2n} \
dots & & & dots \
alpha_{n1} & alpha_{n2}& dots & alpha_{nn}- lambda
end{array}
right|=0 .
$$
Этот определитель является полиномом степени $ n_{} $ по $ lambda_{} $. По
основной теореме высшей алгебры этот полином имеет по крайней мере один комплексный корень $ lambda=lambda_{ast} $. Подставив его в
систему, получаем однородную систему уравнений с нулевым
определителем. Находим нетривиальное решение этой системы:
$$ x_1=x_{1}^{ast},dots,x_n=x_{n}^{ast}, quad exists x_{j}^{ast} ne 0 ; $$
но тогда вектор
$ {mathfrak X}_{ast}= x_{1}^{ast}X_1+cdots+x_{n}^{ast}X_n $ будет собственным вектором оператора $ mathcal A_{} $, принадлежащим $ lambda_{ast}^{} $.
♦
Уравнение $ det ({mathbf A}-lambda E)= 0 $ называется характеристическим или вековым уравнением, а полином в левой его части — характеристическим полиномом матрицы $ {mathbf A} $. Любой корень характеристического полинома матрицы называется собственным числом этой матрицы. Набор всех собственных чисел матрицы (корней характеристического полинома с учетом кратностей) называется спектром матрицы. Ненулевой вектор $ X in mathbb C^n $, удовлетворяющий условию $ {mathbf A} X= lambda X $, где $ lambda $ — собственное число матрицы, называется собственным вектором матрицы, соответствующим (или принадлежащим) данному собственному числу.
П
Пример. Применим полученный результат для получения альтернативного решения предыдущего примера.
Решение. Базисом в пространстве $ mathbb P_3 $ выберем $ {1,,x,,x^2,, x^3} $. Образы базисных векторов под действием оператора $ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} $:
$$
left{begin{array}{lrrrr}
mathcal A (1) =&-2& &+x^2& ,\
mathcal A (x) =&&-2,x &&+x^3 ,\
mathcal A (x^2) =& &-x &-x^2 &+x^3, \
mathcal A (x^2) =& &-x & & ,
end{array} right. qquad Rightarrow qquad {mathbf A}=
left(begin{array}{rrrr}
-2 & 0 & 0 & 0 \
0 & -2 & -1 & -1 \
1& 0 & -1 & 0 \
0 & 1 & 1 & 0
end{array}
right) .
$$
Характеристический полином матрицы $ {mathbf A} $:
$$
left|begin{array}{cccc}
-2-lambda & 0 & 0 & 0 \
0 & -2-lambda & -1 & -1 \
1& 0 & -1-lambda & 0 \
0 & 1 & 1 & -lambda
end{array}
right|equiv (lambda+2)(lambda^3+3,lambda^2+3,lambda+1)equiv (lambda+2)(lambda+1)^3 .
$$
Собственные числа $ lambda_1=-2 $ и $ lambda_2=-1 $, спектр матрицы $ {-1,-1,-1,-2} $. Подставляем каждое из собственных чисел в матрицу $ {mathbf A}-lambda E $ и решаем получившиеся системы однородных уравнений. Поскольку каждая из них должна иметь бесконечное множество решений, то мы строим фундаментальные системы решений (ФСР)
$$
begin{array}{ccc}
& ({mathbf A}-lambda E)X=mathbb O & \
{color{Red} swarrow } & & {color{Red} searrow } \
lambda_1=-2 & & lambda_2=-1 \
Downarrow & & Downarrow \
left(begin{array}{rrrr}
0 & 0 & 0 & 0 \
0 & 0 & -1 & -1 \
1& 0 & 1 & 0 \
0 & 1 & 1 & 2
end{array}
right)
left(begin{array}{l}
x_1 \ x_2 \ x_3 \ x_4
end{array}
right)= mathbb O
& &
left(begin{array}{rrrr}
-1 & 0 & 0 & 0 \
0 & -1 & -1 & -1 \
1& 0 & 0 & 0 \
0 & 1 & 1 & 1
end{array}
right) left(begin{array}{l}
x_1 \ x_2 \ x_3 \ x_4
end{array}
right)= mathbb O . \
{color{Red} Downarrow } & & {color{Red} Downarrow } \
x_1=1,x_2=-1,x_3=-1,x_4=1 & & left{begin{array}{c}
x_1=0,x_2=-1,x_3=1,x_4=0 \
x_1=0,x_2=-1,x_3=0,x_4=1
end{array} right}
end{array}
$$
Таким образом, собственному числу $ lambda_1=-2 $ соответствует собственнный вектор — полином $ 1-x-x^2+x^3 $, и он полностью совпадает с полученным при решении предыдущего примера. В то же время собственному числу $ lambda_2=-1 $ соответствует два линейно независимых собственнных вектора — полиномы $ -x+x^2 $ и $ -x+x^3 $. Любой (не тождественно нулевой) полином множества
$$ { tau_1(-x+x^2) +tau_2(-x+x^3) mid {tau_1,tau_2 } subset mathbb R } $$
будет также являться собственным, принадлежащим $ lambda_2=-1 $. Это множество также совпадает с полученным при решении предыдущего примера.
♦
Итак, два формально различных подхода к решению одного и того же примера не привели к противоречию. Хотелось бы, однако, гарантировать глобальную непротиворечивость определения собственных чисел и векторов — т.е. независимость (инвариантность) этих объектов относительно способов их нахождения, и, в частности, от выбора базиса пространства $ mathbb V_{} $.
Т
Теорема. Характеристические полиномы подобных матриц одинаковы.
Доказательство. $ {mathbf A}doteq {mathbf B} {color{Red} iff } exists $ неособенная матрица $ C_{} $,
такая что $ {mathbf B}=C^{-1} {mathbf A} C $. Имеем:
$$det ({mathbf B}-lambda E)=det (C^{-1} {mathbf A} C-lambda E)=$$
$$=
det (C^{-1} {mathbf A} C-lambda C^{-1}EC)=det left[ C^{-1} ({mathbf A} -lambda
E)C right] = det ({mathbf A}-lambda E) .$$
♦
Иначе говоря, для оператора $ mathcal A_{} $ характеристический полином его матрицы не
зависит от выбора базиса пространства. Поэтому можно говорить о характеристическом полиноме оператора $ mathcal A_{} $.
Характеристический полином матрицы подробнее исследуется
☞
ЗДЕСЬ. В частности, в указанном разделе приведен результат, на основании которого (а также на основании пунктов а) и д) теоремы 7, приведенной в пункте
☞
МАТРИЦА ОПЕРАТОРА ) выводится следующее нетривиальное утверждение:
Т
Теорема [Гамильтон, Кэли]. Результатом подстановки оператора в собственный характеристический полином будет нулевой оператор.
П
Пример. Для рассмотренного в предыдущих примерах оператора
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} , $$
действующего в $ mathbb P_3 $,
характеристический полином равен
$$ lambda^4+5,lambda^3+9,lambda^2+7,lambda+2 , .$$
Проверим утверждение теоремы Гамильтона-Кэли — должно быть выполнено условие
$$ mathcal A^4+5,mathcal A^3+9,mathcal A^2+7,mathcal A +2, mathcal E = mathcal O . $$
Степени данного оператора $ mathcal A_{} $ обсуждались в примере
☞
ПУНКТА. Переписанное в терминах остатков, последнее условие превращается в
$$ (x^2-2)^4f(x)+5,(x^2-2)^3f(x)+9,(x^2-2)^2f(x)+7,(x^2-2)f(x) + $$
$$+2,f(x) equiv 0 pmod{x^4-x^3-x^2+x} , $$
т.е. полином, стоящий в левой части сравнения, должен делиться нацело на $ x^4-x^3-x^2+x $ при любом выборе полинома $ f_{}(x) $. Проверяем:
$$ (x^2-2)^4+5,(x^2-2)^3+9,(x^2-2)^2+7,(x^2-2)+2 equiv $$
$$equiv x^8-3,x^6+3,x^4-x^2 equiv (x^4+x^3-x^2-x)(x^4-x^3-x^2+x) , $$
т.е. утверждение оказывается справедливым.
♦
Диагонализуемость матрицы оператора
Т
Теорема 1. Собственные векторы оператора, принадлежащие различным собственным числам, линейно независимы.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема 2. Если оператор имеет $ n=dim mathbb V $ линейно независимых собственных векторов, то в базисе ими образуемом матрица оператора диагональна. Обратно: если матрица оператора в некотором базисе диагональна, то каждый вектор этого базиса является собственным для оператора.
Базис линейного пространства, состоящий из собственных векторов оператора $ mathcal A_{} $, называется каноническим.
=>
[Матричная версия теоремы]. Пусть $ A_{} $ — квадратная матрица. Неособенная матрица
$ C_{} $, удовлетворяющая равенству
$$C^{-1} A C= A_{diag} quad mbox{ при матрице } A_{diag} quad mbox{ – диагональной} $$
существует тогда и только тогда, когда существует базис пространства $ mathbb C^{n}_{} $,
состоящий из собственных векторов матрицы $ A_{} $. Тогда матрица $ C_{} $ является матрицей перехода от
стандартного базиса
$$ bigg{{mathfrak e}_j = big[underbrace{0,dots,0,1}_{j},0,dots,0big]^{top} bigg}_{j=1}^n $$
к каноническому, а на диагонали $ A_{diag} $ стоят собственные числа матрицы $ A_{} $:
$$
A_{diag}=
left(
begin{array}{cccc}
lambda_1 & 0 & dots & 0 \
0 & lambda_2 & dots & 0 \
vdots & & ddots & vdots \
0 & 0 & dots & lambda_n
end{array}
right) .
$$
Доказательство. Проведем формальное доказательство данного конкретного частного случая. Рассмотрим матричное равенство
$$ A C= CA_{diag} $$
при некоторой диагональной матрице $ A_{diag} $.
Легко видеть, что оно эквивалентно системе равенств относительно столбцов матрицы $ C_{} $:
$$
AC_{[1]}=d_1 C_{[1]},dots, AC_{[n]}=d_n C_{[n]} , .
$$
Если все столбцы $ { C_{[j]} }_{j=1}^n $ ненулевые, то тогда они являются собственными векторами для матрицы $ A_{} $, а числа $ { d_{[j]} }_{j=1}^n $ — собственными числами, соответствующими этим собственным векторам. Если матрица $ C_{} $ невырождена, то все ее столбцы линейно независимы. Но тогда они образуют базис пространства $ mathbb C^n $, состоящий из собственных векторов. Обратное тоже верно.
♦
При выполнении условия предыдущего следствия говорят, что матрица $ A_{} $ диагонализуема или приводится к диагональной форме7).
Теорема позволяет сформулировать достаточное условие диагонализуемости.
Т
Теорема 3. Если характеристический полином оператора не имеет кратных корней, то матрица оператора диагонализуема.
Для проверки условия теоремы не требуется явного вычисления корней: оно проверяется по коэффициентам характеристического полинома «чисто алгебраически» (т.е. за конечное число элементарных алгебраических операций). Оно эквивалентно отличию от нуля дискриминанта характеристического полинома.
Это условие не является необходимым, как показывает пример тождественного оператора.
Случай существования кратного корня у характеристического полинома является
«пограничным»: существуют примеры как диагонализуемых, так и недиагонализуемых матриц. Так, для матриц
$$ A= left( begin{array}{rr}
0 &1 \
-1 &2
end{array}
right) quad mbox{ или } quad
A= left( begin{array}{cc}
1 &0 \
1&1
end{array}
right)
$$
при попытке подобрать матрицу $ C_{} $, удовлетворяющую равенству
$$AC=C left( begin{array}{cc}
alpha_1 &0 \
0 & alpha_2
end{array}
right) qquad npu forall {alpha_1 , alpha_2 } subset mathbb C
$$
получим: $ det C=0 $.
В случае наличия у характеристического полинома оператора кратного корня, анализ оператора на возможность диагонализуемости его матрицы усложняется.
Т
Теорема 4. Множество собственных векторов оператора, принадлежащих его собственному числу $ lambda_{ast}^{} $ , дополненное нулевым вектором, образует линейное подпространство пространства $ mathbb V_{} $.
Это подпространство
$$ mathbb V_{ast} = mathcal{K}er (mathcal A- lambda_{ast} mathcal E) $$
пространства $ mathbb V_{} $ называется собственным подпространством оператора, соответствующим $ lambda_{ast}^{} $.
Величина
$$ dim (mathcal{K}er (mathcal A- lambda_{ast} mathcal E)) $$
называется геометрической кратностью собственного числа $ lambda_{ast}^{} $.
Можно доказать, что геометрическая кратность собственного числа не превосходит кратности собственного числа в характеристическом полиноме. Для акцентирования различий в определениях двух кратностей, кратность собственного числа в характеристическом полиноме называют еще алгебраической кратностью собственного числа.
Если оператор (в некотором базисе пространства) задан своей матрицей $ mathbf A^{} $, то базисные векторы собственного подпространства $ mathbb V_{ast} $ вычисляются посредством нахождения фундаментальной системы решений (ФСР) системы линейных уравнений
$$ (mathbf A- lambda_{ast} E) X=mathbb O . $$
Т
Теорема 5. Матрица оператора диагонализуема тогда и только тогда,
когда для каждого ее собственного числа алгебраическая кратность равна геометрической кратности:
$$
operatorname{dfc} ({mathbf A}-lambda_{ast}, E)= mbox{ кратность } lambda_{ast} .
$$
?
Диагонализуема ли матрица оператора
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} , $$
рассмотренного в примерах предыдущего пункта?
П
Пример. Найти все вещественные значения параметра $ {color{Red}{ alpha} } $, при которых матрица
$$
left( begin{array}{rcc}
1 &2, {color{Red}{ alpha} } & {color{Red}{ alpha} } -2 \
-1 &2 &1 \
2 & 0 & -3
end{array}
right)
$$
диагонализуема.
Решение. Характеристический полином
$ f(lambda)=-lambda^3+3, lambda-2,(3, {color{Red}{ alpha} } -1) $
имеет кратные корни только тогда когда его дискриминант $ mathcal D(f)=-324, {color{Red}{ alpha} }
(3, {color{Red}{ alpha} } -2) $ обращается в нуль. При $ {color{Red}{ alpha} } =0 $ корень $ lambda=-1 $
имеет алгебраическую кратность $ 2_{} $. Найдем дефект матрицы $ A+E $:
$$left( begin{array}{rrr}
2 &0 & -2 \
-1 &3 &1 \
2 & 0 & -2
end{array}
right) longrightarrow
left( begin{array}{rrr}
1 &0 & -1 \
0 &3 &0 \
0 & 0 & 0
end{array}
right) {color{Red} Longrightarrow } operatorname{rank} (A+E) =2 Longrightarrow operatorname{dfc} (A+E)=1 .
$$
Таким образом, геометрическая кратность собственного числа $ lambda=-1 $ равна $ 1_{} $ и
условие теоремы $ 5 $ не выполнено. Оно не будет выполнено
и при $ {color{Red}{ alpha} } = 2/3 $ (здесь корень $ lambda=1 $ имеет кратность $ 2_{} $).
Ответ. Матрица диагонализуема при всех значениях параметра, за исключением $ {color{Red}{ alpha} } = 0 $ и $ {color{Red}{ alpha} } = 2/3 $.
Диагонализуемость матрицы оператора над полем вещественных чисел
В предыдущем пункте мы рассматривали операторы, не всегда акцентируя внимания на поле, над которым они были определены — над $ mathbb R_{} $ или над $ mathbb C_{} $. Сама теорема существования собственного числа гарантирует нам только лишь наличие этих чисел в поле $ mathbb C_{} $. Как следствие, даже если рассматриваются операторы над полем $ mathbb R_{} $ (что чаще всего и случается на практике), то существование для них вещественного канонического базиса вовсе не гарантировано.
Задача. Найти условия диагонализуемости матрицы оператора $ mathcal A $ над полем вещественных чисел.
Необходимое условие следует из теоремы $ 2 $ предыдущего пункта: все собственные числа
матрицы должны быть вещественными.
Теорема $ 3 $ позволяет сформулировать и достаточный критерий диагонализуемости матрицы оператора $ mathcal A $ над $ mathbb R_{} $.
Т
Теорема. Если характеристический полином оператора имеет только простые вещественные корни, то матрица оператора диагонализуема над $ mathbb R_{} $.
Условие различности и вещественности корней произвольного полинома $ f(lambda)=lambda^n+a_1lambda^{n-1}+dots+ a_n in mathbb R[x] $
можно проверить по коэффициентам этого полинома «чисто алгебраически», т.е. за конечное число элементарных алгебраических операций над этими коэффициентами. Воспользуемся, например,
теоремой Якоби из раздела
☞
ЛОКАЛИЗАЦИЯ КОРНЕЙ ПОЛИНОМА. По коэффициентам $ a_1,dots,a_n $ можно определить сумму Ньютона полинома
$ f(lambda) $, т.е. величину
$$
s_k=sum_{1le j le n} lambda_j^k .
$$
Далее, после нахождения всех этих сумм для значений $ k in {0,dots,2n-2} $, из них составляется ганкелева матрица
$$
S=left[ s_{j+k} right]_{j,k=0}^{n-1}
$$
и вычисляются ее главные миноры $ S_1,dots, S_{n} $.
Для различности всех корней полинома необходимо и достаточно выполнение условия $ S_n ne 0 $ (этот минор совпадает с дискриминантом $ mathcal D(f) $ полинома $ f(lambda) $); для различности и вещественности всех корней необходимо и достаточно, чтобы были выполнены неравенства
$$
S_1ge 0,dots,S_{n-1} ge 0,S_n > 0 .
$$
П
Пример. Найти все вещественные значения параметра $ {color{Red}{ alpha} } $, при которых матрица
$$
left( begin{array}{rcc}
1 &2, {color{Red}{ alpha} } & {color{Red}{ alpha} } -2 \
-1 &2 &1 \
2 & 0 & -3
end{array}
right)
$$
диагонализуема над $ mathbb R_{} $.
Решение. На основании теоремы нам нужно установить условия вещественности корней характеристического полинома $ f(lambda)=-lambda^3+3, lambda-2,(3, {color{Red}{ alpha} } -1) $.
Вычисляем суммы Ньютона:
$ s_0=3, s_1= 0, s_2=6, s_3=18, {color{Red}{ alpha} } -6, s_4=18 $, составляем матрицу:
$$ S=left(begin{array}{ccc}
3 & 0 & 6 \
0 & 6 & 18, {color{Red}{ alpha} } -6 \
6 & 18, {color{Red}{ alpha} } -6 & 18
end{array}
right)
$$
и вычисляем ее главные миноры:
$$S_1=3, S_2=18, S_3=-324, {color{Red}{ alpha} } , (3, {color{Red}{ alpha} } -2)=mathcal D(f) . $$
При $ {color{Red}{ alpha} } ne 0 $ и $ {color{Red}{ alpha} } ne 2/3 $ все собственные числа различны,
условие теоремы выполняется при $ {color{Red}{ alpha} } in ]0,, 2/3[ $. Граничные
точки последнего интервала следовало бы исследовать отдельно: хотя этим
значениям параметра и соответствует случай кратных вещественных корней
характеристического полинома, но матрица $ A_{} $ может оказаться диагонализуемой на
основании теоремы 5 предыдущего пункта. Но при решении примера в предыдущем пункте мы уже установили, что это условие не выполняется.
Ответ. Матрица диагонализуема над $ mathbb R_{} $ при $ {color{Red}{ alpha} } in ]0,, 2/3[ $.
Примером гарантировано диагонализуемых над $ mathbb R_{} $ матриц являются вещественные симметричные матрицы. См.
☞
ЗДЕСЬ.
Жорданова нормальная форма
Если матрица оператора оказывается недиагонализуемой над $ mathbb C_{} $, то к какому простейшему виду ее можно привести
?
— Этим видом является, например,
☞
ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА.
Задачи
Источники
[1]. Гантмахер Ф.Р. Теория матриц. 4-е изд. М.Наука. 1988.
[2]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ.1960
[3]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989
[4]. Мишина А.П., Проскуряков И.В. Высшая алгебра. М.Наука. 1965