Как найти матрицу ортогонального преобразования

Оглавление — Линейная алгебра

---

Канонический вид ортогонального преобразования евклидова пространства

Рассмотрим инвариантные подпространства ортогонального преобразования евклидова пространства. По теореме 9.4 линейное преобразование вещественного пространства имеет одномерное или двумерное инвариантное подпространство. Выясним геометрический смысл сужения ортогонального преобразования на инвариантное подпространство.

1. Пусть [math]L[/math] — одномерное инвариантное подпространство с базисом [math]boldsymbol{e}_1[/math]. Тогда [math]boldsymbol{e}_1[/math] — собственный вектор преобразования: [math]mathcal{A}(boldsymbol{e}_1)=lambda boldsymbol{e}_1[/math]. По свойству [math]lambda=pm1[/math]. Следовательно, ортогональное преобразование [math]mathcal{A}colon Lto L[/math] одномерного пространства — это либо тождественное преобразование [math]mathcal{A}(boldsymbol{e}_1)= boldsymbol{e}_1[/math] либо отражение (симметрия) [math]mathcal{A}(boldsymbol{e}_1)= -boldsymbol{e}_1[/math].

2. Пусть [math]L[/math] — двумерное инвариантное подпространство с ортонормированным базисом [math]boldsymbol{e}_1, boldsymbol{e}_2[/math]. Запишем для матрицы [math]A=begin{pmatrix} a&b\ c&d end{pmatrix}[/math] ортогонального преобразования [math]mathcal{A}colon Lto L[/math] равенство [math]A^T=A^{-1}:[/math]

[math]begin{pmatrix}a&c\ b&d end{pmatrix}= frac{1}{det{A}}! begin{pmatrix} d&-b\ -c&a end{pmatrix}!.[/math]

По свойству 6 для собственного преобразования [math]det{A}=1[/math], поэтому [math]d=a,~ c=-b,[/math] [math]det{A}=a^2+b^2=1[/math], т.е. [math]a=cosvarphi[/math] и [math]b=sinvarphi[/math], где [math]varphi[/math] — некоторый угол. Следовательно, матрица собственного ортогонального преобразования двумерного пространства совпадает с матрицей поворота на угол [math](-varphi)colon[/math] [math]A=R_{varphi}= begin{pmatrix} cosvarphi& sinvarphi\ -sinvarphi& cosvarphi end{pmatrix}[/math]. Для несобственного преобразования [math]det{A}=-1[/math] (см. свойство 6), поэтому [math]d=-a,~ c=b,[/math] [math]det{A}=-a^2-b^2=-1[/math]. Матрица [math]A=begin{pmatrix}a&b\ b&-aend{pmatrix}[/math] имеет два действительных собственных значения [math](lambda_1=1,~ lambda_2=-1)[/math], так как

[math]det(A-lambda E)= begin{vmatrix}a-lambda&b\ b&-a-lambda end{vmatrix}=(a-lambda)cdot(-a-lambda)-bcdot b= lambda^2-a^2-b^2=lambda^2-1.[/math]

Поэтому несобственное ортогональное преобразование имеет два одномерных инвариантных подпространства (см. пункт 1).

Получим канонический вид преобразования. Пусть [math]L[/math] — одномерное или двумерное инвариантное подпространство для ортогонального преобразования [math]mathcal{A}colon mathbb{E}to mathbb{E}[/math]. Представим пространство в виде прямой суммы [math]mathbb{E}= Lplus L^{perp}[/math]. Выберем в [math]L[/math] ортонормированный базис и дополним его до ортонормированного базиса всего пространства. В этом базисе матрица [math]A[/math] преобразования будет иметь блочно-диагональный вид [math]A=operatorname{diag} (A_L,A_{L^{perp}})[/math], где [math]A_{L}[/math] — матрица сужения [math]mathcal{A}_L[/math] преобразования [math]mathcal{A}[/math] на [math]L[/math], а [math]A_{L^{perp}}[/math] — матрица сужения [math]mathcal{A}_{L^{perp}}[/math] преобразования [math]mathcal{A}[/math] на [math]L^{perp}[/math]. Согласно пунктам 1, 2: [math]A_L=(1)[/math] или [math]A_L=-1[/math] при [math]dim{L}=1[/math], либо [math]A_L= R_{varphi}= begin{pmatrix} cosvarphi&sinvarphi\ -sinvarphi& cosvarphi end{pmatrix}[/math] при [math]dim{L}=2[/math]. Следовательно, в матрице [math]A=operatorname{diag} (A_L,A_{L^{perp}})[/math] ортогонального преобразования блок [math]A_L[/math] имеет один из указанных трех видов. Поскольку подпространство [math]L^{perp}[/math] инвариантно относительно ортогонального преобразования [math]mathcal{A}[/math] (см. свойство 7), то к матрице [math]A_{L^{perp}}[/math] применимы те же выводы, что и к матрице [math]A[/math]. Таким образом, справедливо следующее утверждение.

---

Теорема (9.9) о каноническом виде ортогонального преобразования

Для каждого ортогонального преобразования [math]mathcal{A}colon mathbb{E}to mathbb{E}[/math] n-мерного евклидова пространства [math]mathbb{E}[/math] существует ортонормированный базис, в котором матрица преобразования имеет канонический вид:

На главной диагонали матрицы стоят либо числа 1 или (–1), либо блоки вида [math]R_{varphi}= begin{pmatrix}cosvarphi&sinvarphi\ -sinvarphi&cosvarphi end{pmatrix}[/math], а остальные элементы матрицы равны нулю.

Базис [math](boldsymbol{s})=(boldsymbol{s}_1,ldots,boldsymbol{s}_n)[/math], в котором матрица преобразования имеет вид (9.20), называется каноническим. Заметим, что канонический базис определяется неоднозначно.

---

Приведение ортогонального преобразования к каноническому виду

Задача приведения ортогонального преобразования к каноническому виду формулируется следующим образом: требуется найти базис (канонический), в котором матрица ортогонального преобразования имеет канонический вид (9.20). Для приведения ортогонального преобразования к каноническому виду нужно выполнить следующие действия.

Нахождение канонического вида ортогонального преобразования (первый этап).

1. Выбрать базис [math]boldsymbol{e}_1,ldots, boldsymbol{e}_n[/math] евклидова пространства [math]mathbb{E}[/math] и найти матрицу [math]A[/math] преобразования в этом базисе.

2. Составить характеристическое уравнение [math]det(A-lambda E)=0[/math] и найти различные его корни [math]lambda_1,ldots, lambda_k[/math] (а также их алгебраические кратности).

3. Записать блочно-диагональную матрицу (9.20) канонического вида ортогонального преобразования:

— каждый действительный корень [math]lambda_1[/math] кратности [math]n_1[/math] поместить на главной диагонали [math]n_1[/math] раз;

— для каждой пары [math]lambda=alphapmbeta i[/math] комплексных сопряженных корней кратности [math]m[/math] записать [math]m[/math] блоков вида [math]R_{varphi}= begin{pmatrix} alpha&beta\ -beta&alpha end{pmatrix}[/math] (см. доказательство свойства 8 ортогональных преобразований).

Нахождение канонического базиса (второй этап).

4. Для действительного корня [math]lambda_1[/math] кратности [math]n_1[/math] найти фундаментальную систему [math]x_1,ldots,x_{n_1}[/math] решений однородной системы [math](A-lambda_1E)x=o[/math]. Линейно независимую систему [math]boldsymbol{x}_1,ldots, boldsymbol{x}_{n_1}[/math] векторов (пространства [math]mathbb{R}^n[/math]) ортогонализировать и нормировать. Получим векторы [math]boldsymbol{s}_1,ldots, boldsymbol{s}_{n_1}[/math].

5. Для пары [math]lambda=alphapmbeta i[/math] комплексных сопряженных корней кратности [math]m[/math] найти фундаментальную систему [math]z_1,ldots,z_{m}[/math] решений однородной системы [math](A+(alpha+beta i)E)z=o[/math]. Выделяя действительные [math]x_j=operatorname{Re}z_j[/math] и мнимые части [math]y_j=operatorname{Im}z_j,[/math] [math]j=1,ldots,m[/math], комплексных столбцов [math]z_1,ldots,z_{m}[/math], получить [math]m[/math] пар ортогональных векторов [math]boldsymbol{x}_1,boldsymbol{y}_1; boldsymbol{x}_2, boldsymbol{y}_2;ldots; boldsymbol{x}_m,boldsymbol{y}_m[/math] (пространства [math]mathbb{R}^n[/math]). Эту систему векторов ортогонализировать и нормировать. Получим [math]2m[/math] векторов [math]boldsymbol{s}_1,ldots,boldsymbol{s}_{2m}[/math].

6. Выполнить пункт 4 или пункт 5 для всех различных корней характеристического уравнения. Получаемые в результате группы столбцов последовательно записать в матрицу [math]S[/math] перехода от базиса [math]boldsymbol{e}_1,ldots,boldsymbol{e}_n[/math] к искомому каноническому базису [math]boldsymbol{s}_1,ldots, boldsymbol{s}_n colon,(boldsymbol{s})= (boldsymbol{e})S[/math]. Матрица [math]S^{-1}AS[/math] преобразования [math]mathcal{A}[/math] будет иметь канонический вид (9.20), полученный в пункте 3.

Замечания 9.7

1. Собственные векторы ортогональной матрицы, принадлежащие различным собственным значениям, ортогональны.

2. Из пункта 1 следует, что для получения ортонормированного базиса достаточно ортонормировать отдельно каждую группу векторов, получаемых в пункте 4 или пункте 5 алгоритма, причем по свойству 8 столбцы [math]x_j,y_j[/math] в пункте 5 будут ортогональными.

3. Матрицу вида (9.20) можно представить в виде произведения матриц, каждая из которых есть либо матрица [math]operatorname{diag}(1,ldots,1,-1,1,ldots,1)[/math] простого отражения относительно гиперплоскости, либо матрица math]operatorname{diag}(1,ldots,1, R_{varphi},1,ldots,1)[/math] простого вращения двумерной плоскости. Поэтому любое ортогональное преобразование можно представить в виде композиции простых отражений и простых вращений.

---

Пример 9.5. Ортогональное преобразование [math]mathcal{A}colon Vto V[/math] в базисе [math]boldsymbol{e}_1,boldsymbol{e}_2,boldsymbol{e}_3[/math] имеет матрицу [math]A=begin{pmatrix} 2/3&-1/3&2/3\ 2/3&2/3&-1/3\ -1/3&2/3&2/3 end{pmatrix}[/math]. Привести это преобразование к каноническому виду, т.е. найти базис [math]boldsymbol{s}_1, boldsymbol{s}_2, boldsymbol{s}_3[/math], в котором матрица преобразования имеет канонический вид (9.20).

Решение. Первый этап. Нахождение канонического вида преобразования.

1. Выбираем базис [math]boldsymbol{e}_1, boldsymbol{e}_2, boldsymbol{e}_3[/math], в котором задана матрица преобразования.

2. Составляем характеристическое уравнение

[math]det(A-lambda E)= begin{vmatrix}dfrac{2}{3}-lambda&-dfrac{1}{3}&dfrac{2}{3}\[8pt] dfrac{2}{3}&dfrac{2}{3}-lambda&-dfrac{1}{3}\[8pt] -dfrac{1}{3}&dfrac{2}{3}&dfrac{2}{3}-lambda end{vmatrix}= (1-lambda)(lambda^2-lambda+1)=0.[/math]

Уравнение имеет три простых (кратности 1) корня: один действительный [math]lambda_1=1[/math] и пару комплексных сопряженных [math]lambda_{2,3}= frac{1}{2}pmfrac{sqrt{3}}{2},i,~ alpha=frac{1}{2},~ beta=frac{sqrt{3}}{2}[/math].

3. Записываем искомый канонический вид (9.20), указывая на главной диагонали действительный корень [math]lambda_1=1[/math] и блок [math]R_{varphi}= begin{pmatrix}1/2&sqrt{3}/2\ -sqrt{3}/2&1/2 end{pmatrix}!,~ varphi=frac{pi}{3}:[/math]

[math]mathop{A}limits_{(boldsymbol{s})}= operatorname{diag}(1,,R_{varphi})= operatorname{diag}!!leftlgroup 1, begin{pmatrix} dfrac{1}{2}&dfrac{sqrt{3}}{2}\[7pt] -dfrac{sqrt{3}}{2}&dfrac{1}{2} end{pmatrix}!!rightrgroup= begin{pmatrix}1&0&0\[1pt] 0&dfrac{1}{2}&dfrac{sqrt{3}}{2}\[7pt] 0&-dfrac{sqrt{3}}{2}& dfrac{1}{2} end{pmatrix}!.[/math]

Второй этап. Нахождение канонического базиса. Найдем матрицу [math]S[/math] перехода от данного базиса [math]boldsymbol{e}_1,boldsymbol{e}_2,boldsymbol{e}_3[/math] к каноническому [math]boldsymbol{s}_1, boldsymbol{s}_2, boldsymbol{s}_3[/math].

4. Для действительного корня [math]lambda_1=1[/math] кратности 1 находим фундаментальную систему решений однородной системы [math](A-lambda_1E)x=o[/math]. Приводим матрицу системы к упрощенному виду:

[math]A-lambda_1E=A-E= left(!! begin{array}{rrr}dfrac{2}{3}&-dfrac{1}{3}&dfrac{2}{3}\[9pt] dfrac{2}{3}& dfrac{2}{3}&-dfrac{1}{3}\[9pt] -dfrac{1}{3}&dfrac{2}{3}&dfrac{2}{3} end{array}!!right)- begin{pmatrix}1&0&0\[2pt] 0&1&0\[2pt] 0&0&1end{pmatrix}= left(!! begin{array}{rrr} -dfrac{1}{3}&-dfrac{1}{3}&dfrac{2}{3}\[9pt] dfrac{2}{3}&-dfrac{1}{3}&-dfrac{1}{3}\[9pt] -dfrac{1}{3}&dfrac{2}{3}& -dfrac{1}{3}end{array} !!right)sim begin{pmatrix}1&0&-1\ 0&1&-1\ 0&0&0 end{pmatrix}!.[/math]

Следовательно, фундаментальная система содержит одно решение [math]x=begin{pmatrix} 1&1&1 end{pmatrix}^T[/math]. Нормируя это решение (поделив координаты на норму [math]|x|= sqrt{1^2+1^2+1^2}=sqrt{3}[/math]), получаем столбец [math]s_1=begin{pmatrix} dfrac{sqrt{3}}{3}& dfrac{sqrt{3}}{3}& dfrac{sqrt{3}}{3}end{pmatrix}^T[/math].

5. Для пары комплексных сопряженных корней [math]lambda_{2,3}= frac{1}{2}pm frac{sqrt{3}}{2},i[/math] находим фундаментальную систему решений однородной системы [math](A-lambda_2E)z=o[/math]. Приводим матрицу системы к упрощенному виду

[math]A-left(dfrac{1}{2}+dfrac{sqrt{3}}{2},iright)!E= begin{pmatrix} dfrac{1}{6}-dfrac{sqrt{3}}{2},i&-dfrac{1}{3}&dfrac{2}{3}\[9pt] dfrac{2}{3}&dfrac{1}{6}-dfrac{sqrt{3}}{2},i&-dfrac{1}{3}\[8pt] -dfrac{1}{3}&dfrac{2}{3}&dfrac{1}{6}-dfrac{sqrt{3}}{2},i end{pmatrix}sim begin{pmatrix}1&0&dfrac{1}{2}+dfrac{sqrt{3}}{2},i\[8pt] 0&1&dfrac{1}{2}-dfrac{sqrt{3}}{2},i\[8pt] 0&0&0 end{pmatrix}!.[/math]

Следовательно, фундаментальная система содержит одно решение. Полагая [math]z_3=1[/math], получаем решение:

[math]z=begin{pmatrix}z_1&z_2&z_3 end{pmatrix}^T=begin{pmatrix}-dfrac{1}{2}-dfrac{sqrt{3}}{2},i&-dfrac{1}{2}+ dfrac{sqrt{3}}{2},i &1end{pmatrix}^T.[/math]

Выделяем действительную и мнимую части:

[math]x=operatorname{Re}z= begin{pmatrix}-dfrac{1}{2}&-dfrac{1}{2}& 1end{pmatrix}^T, quad y=operatorname{Im}z= begin{pmatrix}-dfrac{sqrt{3}}{2}& dfrac{sqrt{3}}{2}& 0 end{pmatrix}^T.[/math]

Нормируя столбцы, поделив координаты вектора [math]boldsymbol{x}[/math] на его длину

[math]|boldsymbol{x}|=sqrt{{left(-frac{1}{2}right)!}^2+ {left(-frac{1}{2}right)!}^2+1^2}= sqrt{dfrac{3}{2}},,[/math] а координаты вектора [math]boldsymbol{y}[/math] — на [math]|boldsymbol{y}|= frac{sqrt{6}}{2}[/math], получаем

[math]s_2=begin{pmatrix}-dfrac{sqrt{6}}{6}&-dfrac{sqrt{6}}{6}&dfrac{sqrt{6}}{3} end{pmatrix}^T,quad s_3=begin{pmatrix}-dfrac{sqrt{2}}{2}& dfrac{sqrt{2}}{2}& 0end{pmatrix}^T.[/math]

6. Записываем полученные в пункт 4, 5 столбцы [math]s_1,,s_2,,s_3[/math] в искомую матрицу перехода

[math]S= begin{pmatrix}s_1&s_2&s_3end{pmatrix}= begin{pmatrix}dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}&-dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}& dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{3}&0 end{pmatrix}!.[/math]

Проверим равенство [math]Smathop{A}limits_{(boldsymbol{s})}=AS[/math] (равносильное [math]mathop{A}limits_{(boldsymbol{s})}=S^{-1}AS[/math]), находя произведения

[math]begin{aligned}Scdot mathop{A}limits_{(boldsymbol{s})}&= begin{pmatrix} dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}&-dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}& dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{3}&0 end{pmatrix}!cdot! begin{pmatrix}1&0&0\[1pt] 0&dfrac{1}{2}&dfrac{sqrt{3}}{2}\[8pt] 0&-dfrac{sqrt{3}}{2}&dfrac{1}{2} end{pmatrix}= begin{pmatrix} dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{6}&-dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{3}& 0\[9pt] dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{6}& dfrac{sqrt{2}}{2}end{pmatrix}!,\[5pt] Acdot S&= left(!! begin{array}{rrr}dfrac{2}{3}&-dfrac{1}{3}&dfrac{2}{3}\[9pt] dfrac{2}{3}& dfrac{2}{3}&-dfrac{1}{3}\[9pt] -dfrac{1}{3}&dfrac{2}{3}&dfrac{2}{3} end{array}!!right)!cdot! begin{pmatrix} dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}&-dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}& dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{3}&0 end{pmatrix}= begin{pmatrix} dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{6}&-dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{3}& 0\[9pt] dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{6}& dfrac{sqrt{2}}{2} end{pmatrix}!. end{aligned}[/math]

Результаты совпадают.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Ортогональное преобразование — линейное преобразование евклидова пространства , сохраняющее длины или (что эквивалентно) скалярное произведение векторов. Это означает, что для любых двух векторов выполняется равенство

где треугольными скобками обозначено скалярное произведение
в пространстве .

Свойства[править | править код]

где  — сопряжённое, а  — обратное преобразования.

Размерность 2[править | править код]

В случае евклидовой плоскости всякое собственное ортогональное преобразование является поворотом на некоторый угол , и его матрица в любом ортонормированном базисе имеет вид

Матрица несобственного ортогонального преобразования имеет вид

Она симметрична, имеет собственными числами 1 и −1 и, следовательно, является инволюцией.
В подходящем ортонормированном базисе матрица несобственного ортогонального преобразования имеет вид

то есть оно является отражением относительно некоторой прямой. Собственное ортогональное преобразование есть произведение двух отражений:

Размерность 3[править | править код]

В трёхмерном пространстве всякое собственное ортогональное преобразование
есть поворот вокруг некоторой оси, а всякое несобственное — композиция поворота вокруг оси и отражения в перпендикулярной плоскости.

Размерность n[править | править код]

Имеет место следующая общая теорема:

В терминах матрицы преобразования эту теорему можно сформулировать следующим образом:

Такая запись матрицы ортогонального преобразования иногда называется приведением к каноническому виду.

См. также[править | править код]

• Ортогональная матрица
• Дискретное ортогональное преобразование

Литература[править | править код]

• Мальцев А. И. Основы линейной алгебры. М.: Наука, 1975.
• Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
• Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
• В. А. Ильин, Э. Г. Позняк Линейная алгебра. — Физматлит, Москва, 1999.
• Гантмахер Ф. Р. Теория матриц, — М.: Наука, 1966.
• Гельфанд И. М., Линейная алгебра. Курс лекций.
• Кострикин А. И., Манин Ю. И. Линейная алгебра и геометрия, — М.: Наука, 1986.
• Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.

Как мы установили (см. 8.2), матрица А квадратичной формы при переходе к новому базису изменяется по формуле А’ = U^TAU, где U – матрица перехода. Бели рассматривается евклидово пространство, а старый и новый базисы выбраны ортонормированными, то матрица перехода U является ортогональной и мы имеем дело с ортогональным преобразованием квадратичной формы, т.е, преобразованием А’ = U^TAU, в котором матрица U ортогональна.

Теорема 8.1. При ортогональном преобразовании квадратичной формы характеристическое уравнение ее матрицы не изменяется.

◄ Пусть А – матрица заданной квадратичной формы. При ортогональном преобразовании эта матрица изменяется по формуле А’ = U^TAU, где U – ортогональная матрица. Согласно свойству 7.2, ортогональная матрица U имеет обратную, причем U^-1 = U^T. Поэтому А’ = U^TAU = U^-1AU, И мы видим, что матрицы А’ и А подобны. Согласно теореме 5.2, характеристи-ческие уравнения подобных матриц совпадают. ►

Теорема 8.2. Любую квадратичную форму ортогональным преобразованием можно привести к каноническому виду.

◄ Матрица А данной квадратичной формы является симме-трической. Но любая симметрическая матрица, согласно следствию 6.4, подобна диагональной, т.е. существует такая невырожденная матрица Р, что матрица А’ = Р^-1 АР является диагональной. Нам надо лишь убедиться, что в качестве Р можно выбрать ортогональную матрицу. Тогда А’ = Р^TАР и диагональная матрица А’ является матрицей квадратичной формы, полученной из исходной при помощи ортогонального преобразования. Диагональный вид А’ равнозначен каноническому виду квадратичной формы. Чтобы выяснить характер матрицы Р, нужно вспомнить теорему 6.5, из которой и было выведено упомянутое следствие 6.4.

Рассмотрим произвольное n-мерное евклидово пространство Ε (n – количество переменных в квадратичной форме) и некоторый ортонормированный базис b в этом пространстве. Матрица А является матрицей некоторого самосопряженного оператора А в базисе b. Согласно теореме 6.6, существует такой ортонормированный базис е, что матрица А’ оператора А в этом базисе является диагональной. Согласно формуле преобразования матрицы линейного оператора, имеем А’ = Р^-1АР (см. теорему 4.6), где Р – матрица перехода из базиса b в базис е. Так как оба базиса ортонормированные, матрица Р является ортогональной. ►

Теорема доказана, но подход, который мы использовали в доказательстве, позволяет сделать и другие выводы, о которых в формулировке теоремы речь не идет. Во-первых, диагональными элементами матрицы А’ квадратичной формы канонического вида, получающейся в результате ортогонального преобразования, являются собственные значения матрицы А квадратичной формы. Из этого следует, что мы можем записать матрицу А’ канонического вида, не находя соответствующего ортогонального преобразования.

Во-вторых, находя ортогональное преобразование, приводящее квадратичную форму к каноническому виду, мы фактически ищем базис из собственных векторов соответствующего самосопряженного оператора. Действительно, если квадратичная форма и самосопряженный оператор имели в исходном ортонормированием базисе одинаковую матрицу, то и в новом ортонормированием базисе их матрицы будут совпадать.

Мы предполагаем, что квадратичная форма представляет собой запись функции, заданной в евклидовом пространстве, через координаты вектора в некотором ортонормированном базисе. На самом деле такая интерпретация носит чисто вспомогательный характер, помогающий смотреть на процесс с геометрической точки зрения, но она никак не используется в самом алгоритме построения ортогонального преобразования. Достаточно лишь записать матрицу квадратичной формы и применить к этой матрице процедуру приведения к диаго-нальному виду (см. 7.4).

Проиллюстрируем на примерах процедуру практического вычисления ортогонального преобразования, приводящего квадратичную форму к каноническому виду.

Пример 8.4. Квадратичную форму f(x,у) = х²₁ – 4x₁x₂ от двух переменных мы приводили к каноническому виду методом Лагранжа (см. пример 8.3). Теперь попробуем привести ее к каноническому виду ортогональным преобразованием.

Матрица нашей квадратичной формы имеет вид

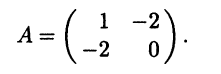
Найдем характеристическое уравнение этой матрицы:

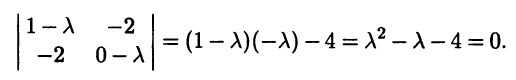
Вычисляем корни характеристического уравнения, они же собственные значения матрицы А:

λ_1,2 = (1 ± √17)/2.

Теперь можем записать канонический вид назраей квадратичной формы:

(1 + √17)/2 y²₁ + (1 + √17)/2 y²₂.

Пример 8.5. Найдем канонический вид квадратичной формы

f(x₁,x₂) = 5x²₁ + 8х₁x₂ + 5x²₂,

к которому она приводится ортогональным преобразованием, и укажем одно из таких ортогональных преобразований.

Квадратичная форма имеет матрицу

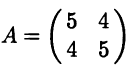
с характеристическим уравнением матрицы

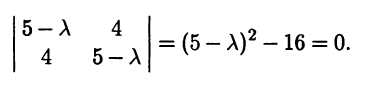
Собственными значениями матрицы квадратичной формы являются λ₁ = 1, λ₂ = 9, т.е. квадратичная форма приводится ортогональным преобразованием к каноническому виду

f(y₁,y₂) = y²₁ + 9y²₂.

Для построения ортогонального преобразования найдем собственные векторы матрицы рассматриваемой квадратичной формы. Из однородной системы линейных алгебраических уравнений (А – λЕ)х = 0 при λ = 1 находим собственный вектор е₁ = (1 – 1)^T . Тогда вектор e₂ = (1 1)^T , ортогональный вектору e₁, будет собственным вектором с соответствующим собственным значением λ₂ = 9 (см. 7.4). Пронормировав эти векторы, составляем из столбцов их координат матрицу ортогонального преобразования

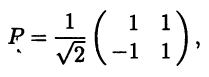
которой соответствует линейная замена переменных х = Ру. #

Единообразное поведение самосопряженных операторов и квадратичных форм при замене ортонормированного базиса объясняется следующей связью.

Теорема 8.3. Пусть А: Ε → Ε – самосопряженный oneратор, действующий в евклидовом пространстве Ε. Функция f(x) = (Аx, x), определенная на евклидовом пространстве, является квадратичной формой. Наоборот, для любой квадратичной формы f(x) на евклидовом пространстве Ε существует такой самосопряженный оператор А, что f(x) = (Аx, x). Этот оператор определен однозначно.

◄ Чтобы доказать первое утверждение теоремы, вспомним, как записывается скалярное произведение в ортонормированном базисе (см. 3.7). Используя такую запись и учитывая самосопряженность оператора, получаем

(Аx, x) = (x, Аx) = x^2TАx,

где х – столбец координат вектора x; А – матрица линейного оператора А. Мы пришли к координатной записи х^TАх некоторой квадратичной формы.

Пусть f(x) – квадратичная форма, которая в данном ортонормированном базисе е имеет вид f(x) = х^TАх. Взяв самосопряженный оператор А, который в базисе е имеет матрицу А, получаем

f(x) = х^TАх = х^T(Ах) = (x, Аx) = (Аx, x).

Наконец, докажем, что если для Двух самосопряженных операторов А и В выполняется равенство (Аx, x) = (Вx, x) для любого вектора x ∈ Ε, то А = В. Записав указанное равенство в координатах (А, В – матрицы операторов, х – столбец координат вектора x), получаем х^TАх = х^TВх, т.е. равенство двух многочленов второй степени от n переменных. Такое равенство возможно лишь в том случае, когда все коэффициенты этих многочленов при одинаковых слагаемых равны, но это эквивалентно равенству матриц А = В и, следовательно, равенству самосопряженных операторов. ►

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ

1. Ортогональные и симметрические матрицы линейных преобразований

Матрица
А является симметрической, если она не
меняется при транспонировании, то есть
А=

Например, следующие матрицы симметрические

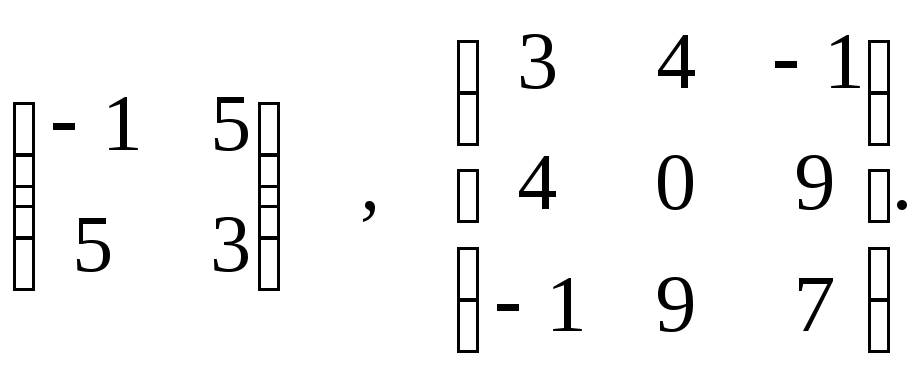
Свойства
симметрических матриц:

1. Собственные
   значения симметрической матрицы –
   действительные числа.

2. Любая симметрическая матрица имеет по
   крайней мере один набор попарно
   перпендикулярных собственных векторов.

3. Симметрическая матрица может быть
   приведена к диагональному виду.

Матрица
Q называется ортогональной, если при
транспонировании она совпадает со своей
обратной матрицей, то есть Q^-1=.

Свойства ортогональных матриц Q:

1. Если
   матрица ортогональная, то Q^-1
   также ортогональная.

2. Столбцы
   матрицы Q образуют ортонормированную
   систему векторов.

3. Для
   каждой симметрической матрицы
   существует такая ортогональная матрица
   Q, что матрица
   
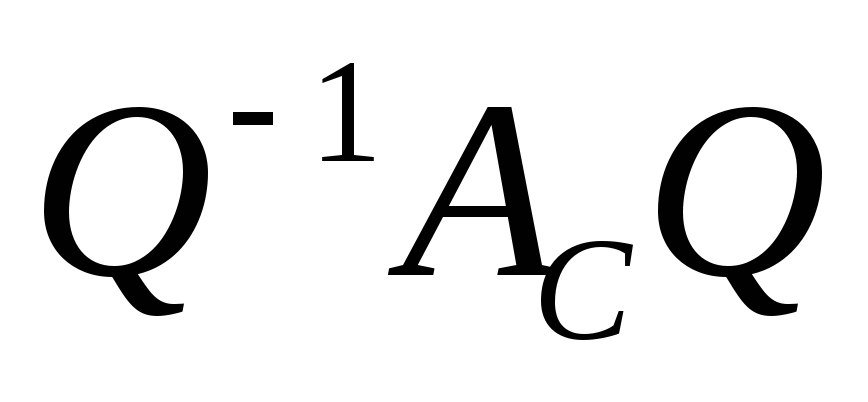
   является диагональной.

На основании перечисленных свойств
симметрических и ортогональных матриц
(преобразований) можно составить план
приведения симметрической матрицы к
диагональному виду:

1. Найти
   собственные значения матрицы.

2. Сформировать
   базис из ортогональных собственных
   векторов.

3. Составить матрицу перехода С к базису
   из собственных векторов.

4. Столбцы матрицы С подвергнуть
   нормализации

(т.е. каждый собственный вектор
разделить на его длину), в результате
получится матрица Q.

1. Транспонируя
   матрицу Q, получим обратную матрицу
   Q^-1.

2. Вычислим
   произведение
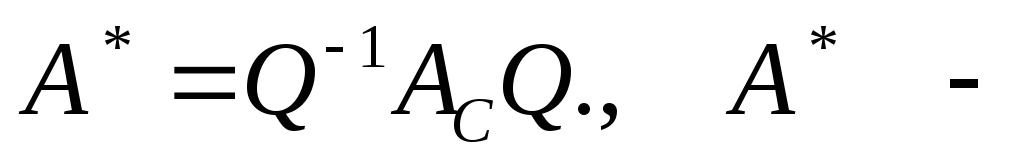   диагональная
   матрица.

Пример.
Привести симметрическую матрицу А к
диагональному виду с помощью ортогональной
матрицы Q, если

А=.

Решение.
Составим характеристическое уравнение
det(A-λE)=0,

Корни
характеристического уравнения

действительные
и различные числа. Определим собственные
векторы. В систему уравнений

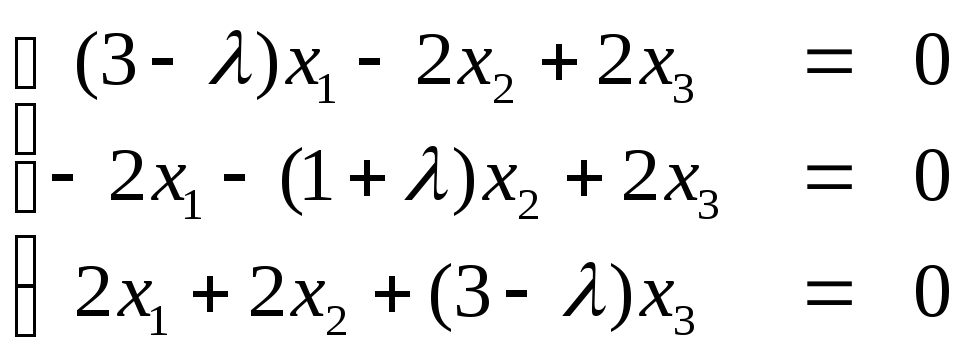
подставим собственные
значения.

1)
λ=λ₁=-3
получим

х₃ –
любое число, и не равно нулю. Пусть
х₃=-1.,
тогда имеем собственный вектор е₁=(1,
2, -1).

1. Возьмем
   λ=λ₂=3.

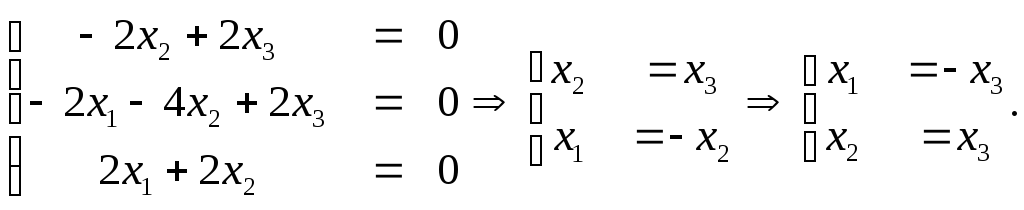
Пусть
х₃ =1.
Второй собственный вектор е₂=(-1,
1, 1).

3)
Подставим λ=λ₃=5.

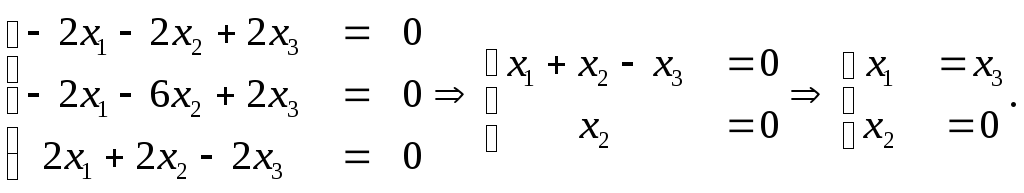
Если
х₃=1,
то е₃=(1,
0, 1). Полученные собственные векторы
попарно ортогональны:

Имеем ортогональный
базис

Матрица перехода к
этому базису.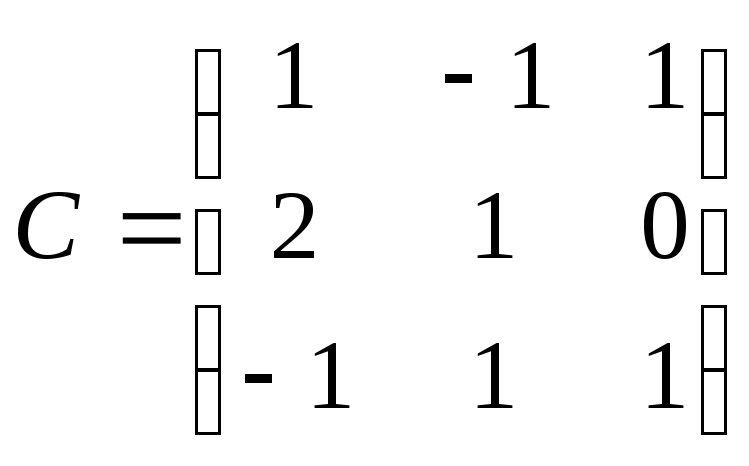
Можно было бы найти С^-1
и тогда
диагональная матрица

Однако быстрее нормировать базис,
разделив каждый вектор на его длину и
составить матрицу Q. Действительно

–
это ортонормированный базис. Матрица

Q=–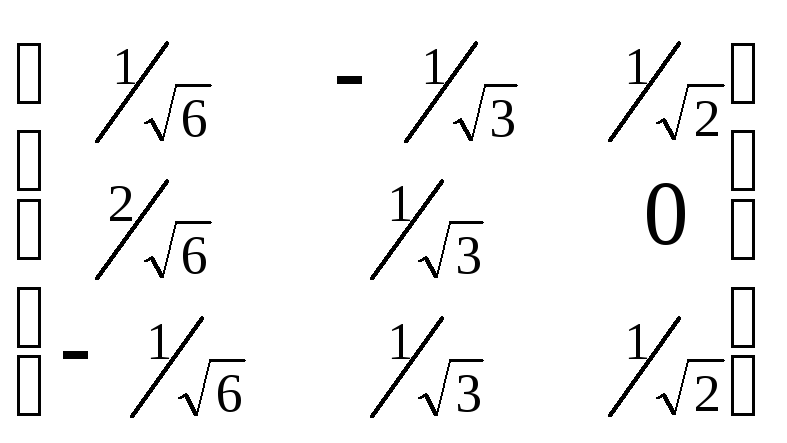
ортогональная матрица.

По
свойству

запишем обратную матрицу

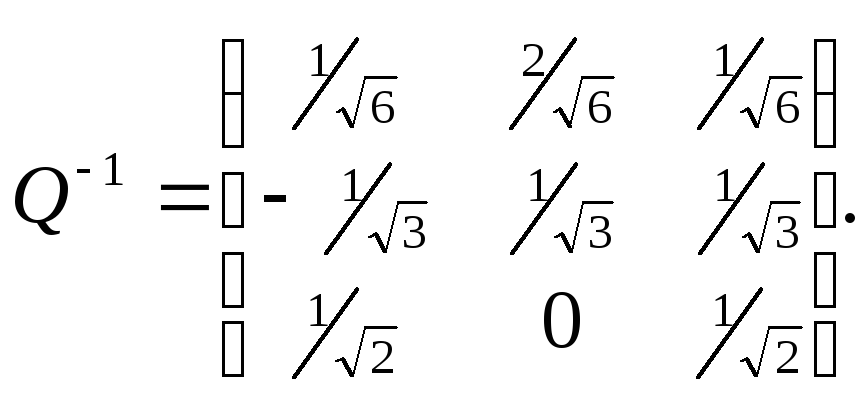
Вычислив произведение
трех матриц, получим диагональную
матрицу

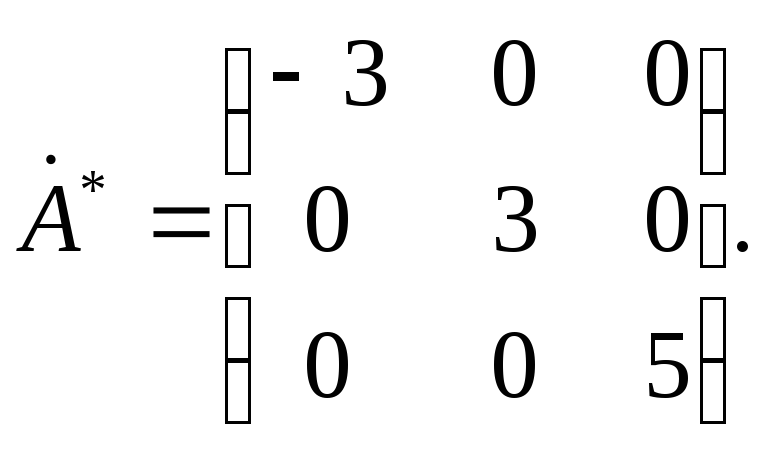
Рассмотрим теперь пример, в котором
собственные числа не все различны.

Пример.
Привести к диагональному виду матрицу
А, определяющую линейное преобразование
в ортогональном базисе:.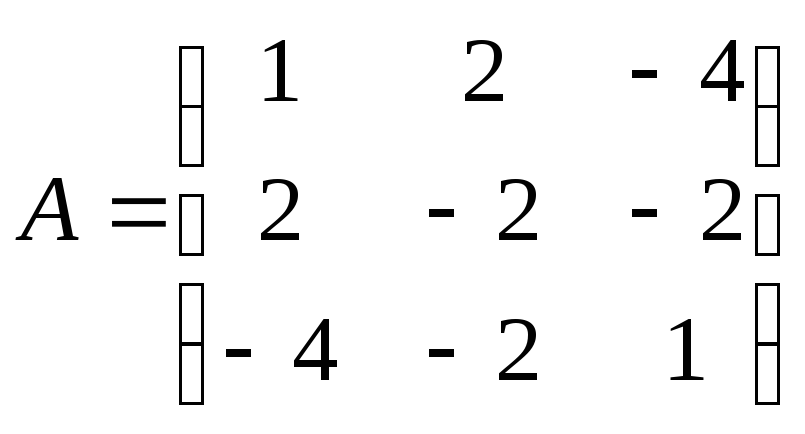

Решение.
Составим характеристическое уравнение.

(*)

Решая
уравнение, найдем собственные значения

Для нахождения собственных векторов
в систему уравнений

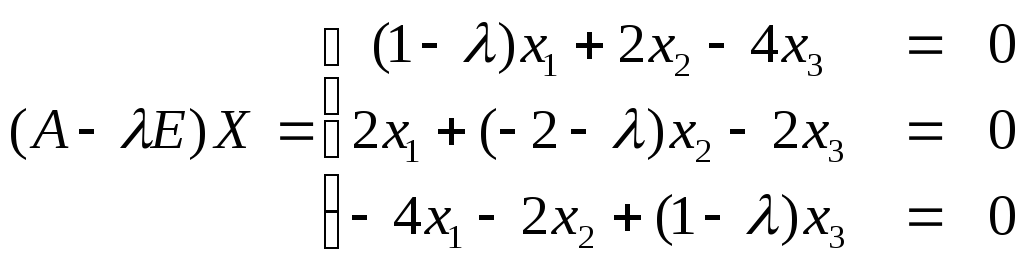
подставим сначала
двукратный корень λ=λ₁=λ₂=-3.
Получим следующую систему

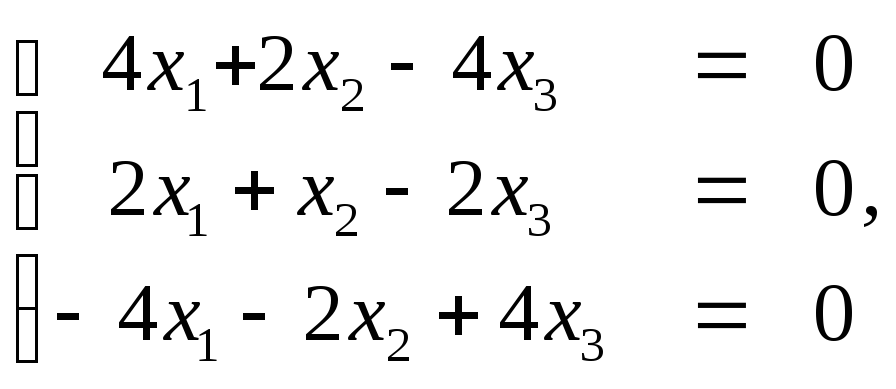
которая сводится к одному уравнению:

2х₁+х₂-2х₃=0
(**)

Из
последнего уравнения можно сделать
вывод, считая его скалярным произведением,
что все собственные векторы е₁,
е₂
, соответствующие кратному собственному
значению λ=-3, лежат в одной плоскости
и ортогональны вектору е=(2,1,-2), координаты
которого есть коэффициенты уравнения
(**). Следовательно, вектор е принадлежит
множеству собственных векторов,
соответствующих λ₃=6.
Этот факт можно проверить следующим
образом: подставим λ₃=6
в систему (*), а затем подставим туда
координаты вектора е. Получим
.
При х₁=2
х₂=1,
х₃=-2:
-10+2+8=0 4-8+4=0, -8-2+10=0. Поэтому е₃=е=(2,
1, -2). Теперь, пользуясь уравнением (**),
подберем решение х₁=1,
х₂=2,
х₃=2
и обозначим собственный вектор е₂=(1,
2, 2). Чтобы найти еще один собственный
вектор из бесчисленного множества
векторов, соответствующих λ=-3, примем
во внимание, что искомый вектор должен
быть ортогонален векторам е₂
и е₃
. Следовательно, его можно вычислить
как векторное произведение, т.е. е₁=.
В координатной форме это выглядит
следующим образом:

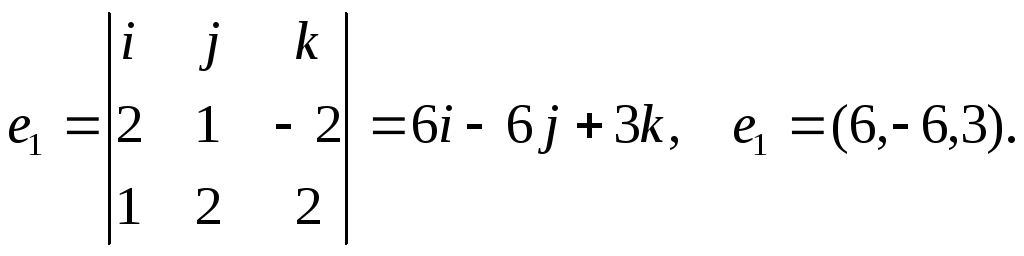
Таким
образом, новый ортогональный базис из
собственных векторов: е₁=(6,-6,3),
е₂=(1,2,2),
е₃=(2,1,-2).
Разделим каждый вектор на его длину
и
получим ортонормированный базис

Ортогональная
матрица:

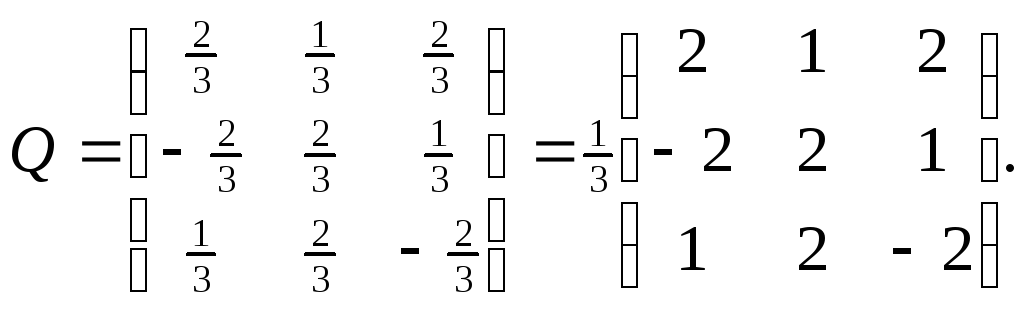
Обратная
матрица:Q^-1=Q^т=

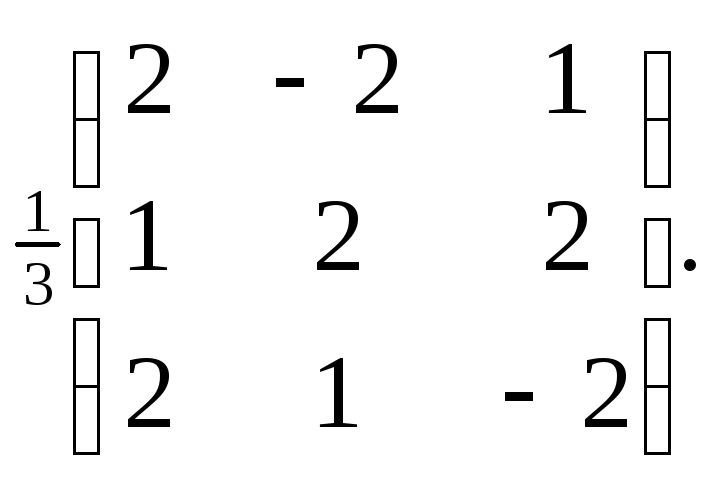
Диагональная
матрица, определяющая преобразование
в новом ортонормированном базисе,
найдется по формуле:

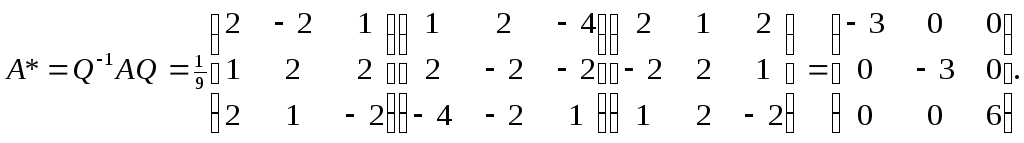
Ответ:

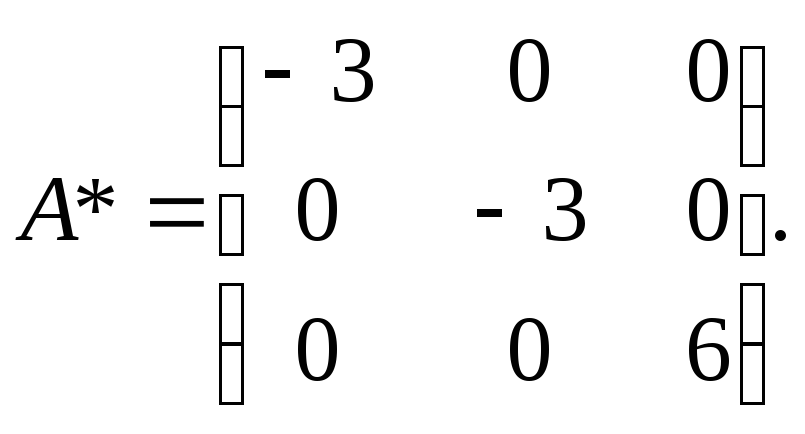
Если
собственные значения симметрической
матрицы в трехмерном линейном
пространстве все одинаковы λ₁=λ₂=λ₃=λ,
то матрица определяет преобразование
подобия с коэффициентом λ. В этом случае
все векторы пространства являются
собственными векторами. В качестве
нового базиса можно взять любую тройку
единичных попарно ортогональных
векторов, например е₁=(1,0,0),
е₂=(0,1,0),
е₃=(0,0,1).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #