Как найти матрицу отражения относительно прямой

Макеты страниц

Автор	Сообщение
	Заголовок сообщения: Найти матрицу оператора отражения Добавлено: 12 май 2021, 21:20
Начинающий Зарегистрирован: 11 май 2021, 12:21 Сообщений: 6 Cпасибо сказано: 1 Спасибо получено: 0 раз в 0 сообщении Очков репутации: 1	Всем добрый день. Помогите решить задачу, пожалуйста. Пусть в геометрическом пространстве V3 задана прямоугольная ск {O,e1,e2,e3}. В базисе e1,e2,e3 найти матрицу оператора отражения относительно прямой x-2y=0 параллельно прямой 3x-y=0. Решая задачу, нашел матрицу оператора отражения относительно прямой x-2y=0. Подскажите, как дорешать задачу. Заранее спасибо
Вернуться к началу

searcher	Заголовок сообщения: Re: Найти матрицу оператора отражения Добавлено: 13 май 2021, 10:43
	Mark512 писал(а): Решая задачу, нашел матрицу оператора отражения относительно прямой x-2y=0. Подскажите, как дорешать задачу. Может для начала покажете свои попытки решения?
Вернуться к началу

Mark512	Заголовок сообщения: Re: Найти матрицу оператора отражения Добавлено: 14 май 2021, 11:53
	searcher Нашел матрицу оператора отражения относительно x-2y=0. Получилось [math]begin{pmatrix} 3/5 & 4/5 \ 4/5 & -3/5 end{pmatrix}[/math]
Вернуться к началу

searcher	Заголовок сообщения: Re: Найти матрицу оператора отражения Добавлено: 14 май 2021, 13:16
	searcher писал(а): Может для начала покажете свои попытки решения? Mark512 писал(а): Нашел матрицу оператора отражения То, что вы нашли матрицу этого оператора, было ясно из первого поста. Может вы расскажете, каким образом вы сделали это?
Вернуться к началу

Mark512	Заголовок сообщения: Re: Найти матрицу оператора отражения Добавлено: 14 май 2021, 20:23
	searcher Нашел по формуле A=[math]frac{ 1 }{ 1+m^{2} }[/math][math]begin{pmatrix} 1-m^2 & 2m \ 2m & m^2 -1 end{pmatrix}[/math], где m=y/x
Вернуться к началу

searcher	Заголовок сообщения: Re: Найти матрицу оператора отражения Добавлено: 15 май 2021, 10:09
	Mark512 писал(а): Подскажите, как дорешать задачу. На этом пути дорешать задачу не получится никак. Эта формула никакого отношения к решению задачи не имеет. Дорешать можно было бы, если бы вы матрицу оператора строили исходя из её определения. Поэтому предлягаю начать всё сначала. Возьмите базисные векторы и изучите, как они преобразуются при нашем отражении. Если никакие идеи в голову не придут, смотрите подсказку в офф-топе. Подсказка:
Вернуться к началу

В то
время, как полный поворот на плоскости
ху обычно осуществляется в двумерном
пространстве относительно нормали к
плоскости, отражение представляет собой
тот же поворот на угол 180º
в трехмерном пространстве и обратно на
плоскость относительно оси, лежащей на
плоскости ху. На рис. 4.6 приведены
примеры двух отражений на плоскости
треугольника DEF.
Отражение относительно прямой у =
0 (ось х) получено с использованием
матрицы

(4.39)

В этом
случае новые вершины треугольника
D^*E^*F^*
будут определяться преобразованием

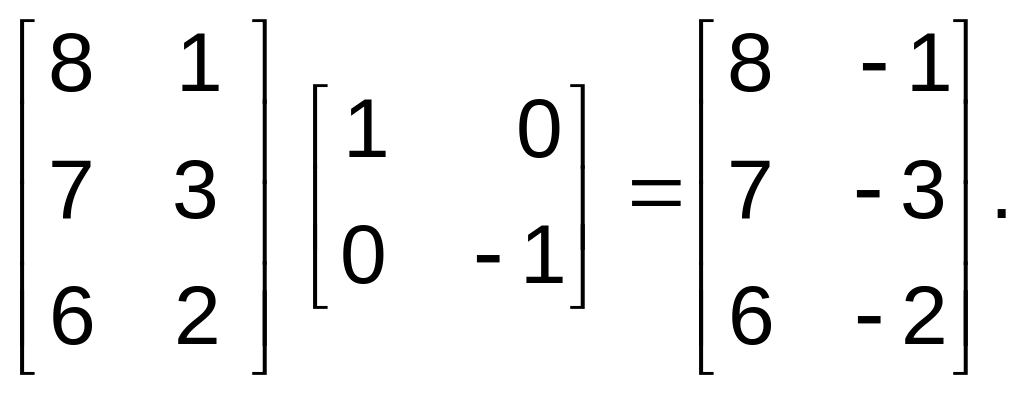
Подобным
образом отражение относительно оси у
при х = 0 будет иметь вид

(4.40)

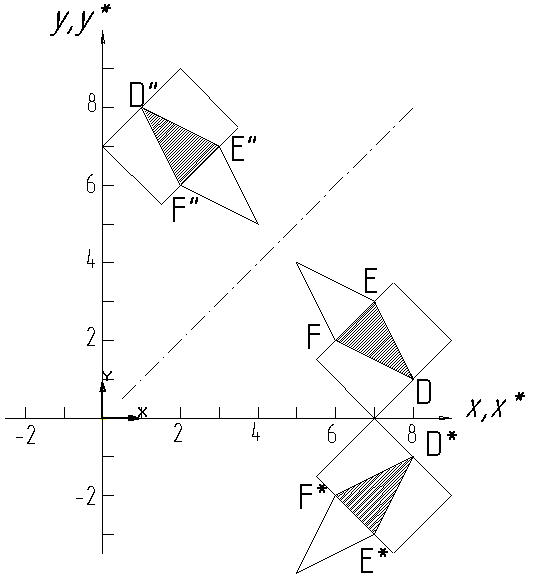
Рис. 4.6

Отражение
относительно прямой у = х осуществляется
с помощью матрицы

.
(4.41)

Выполнив преобразования,
получим координаты вершин треугольника
D^*E^*F^*

.

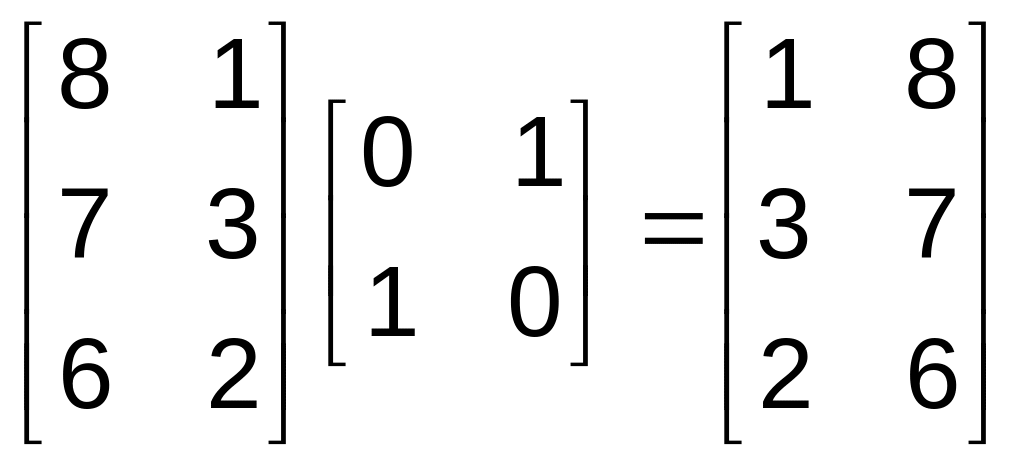
Аналогичным
образом отражение относительно оси х
будет иметь вид

.
(4.42)

У каждой
из этих матриц определитель равен –1.
В общем случае, если определитель равен
–1, то преобразование дает полное
отражение.

Если
оба полных отражения осуществляются
последовательно относительно прямых,
проходящих через начало координат, то
результатом будет полный поворот
относительно начала координат. Это
можно увидеть, обратившись к следующему
примеру.

Пример 3. Отражение и вращение

Рассмотрим
плоскость треугольника АВС, показанную
на рис. 4.7. Первоначально отобразим
относительно оси х (уравнение
(4.39)), а затем относительно прямой у =
–х (см. выражение (4.42)). Результатом
первого отображения будет

.

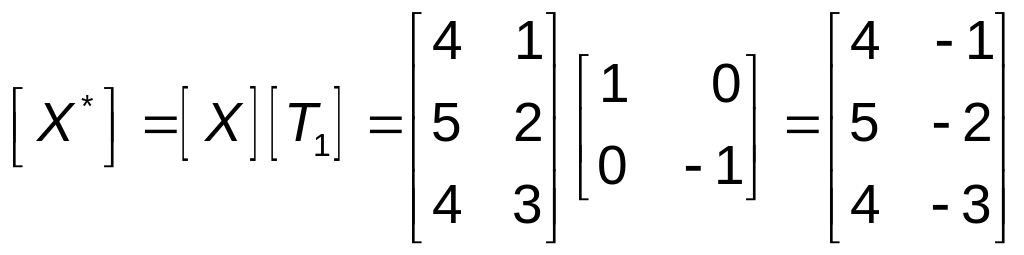
Результатом
второго будет

.

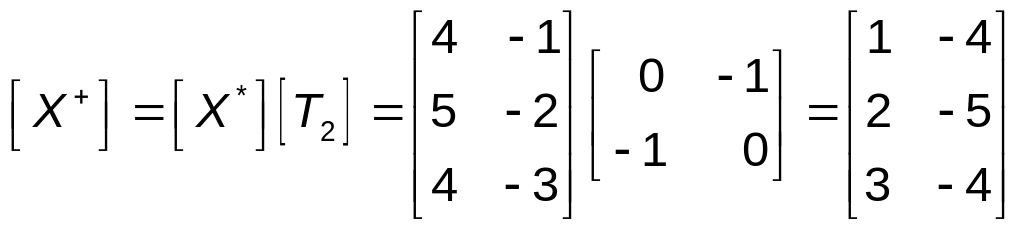
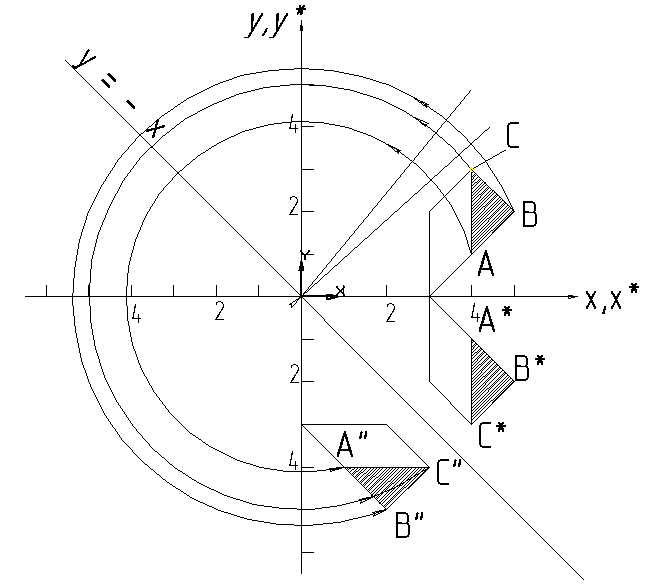
Рис. 4.7

Повернем
треугольник относительно начала
координат на угол θ
= 270º (4.35)
и получим аналогичный результат

Отметим,
что матрицы отражения из (4.39) и (4.42)
ортогональны,

т. е. транспонированная
матрица одновременно является обратной.

Например,

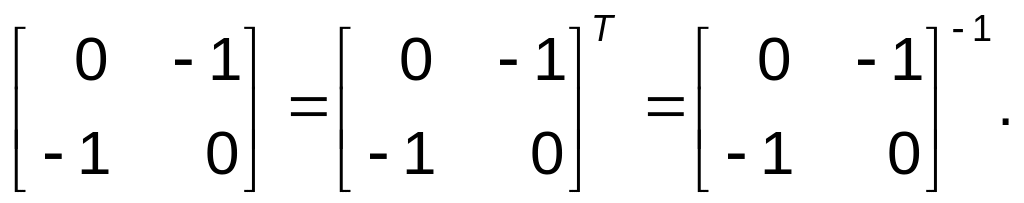
4.1.3.3. Масштабирование

Из
рассуждений относительно преобразования
точек следует, что величина масштабирования
определяется значением элементов
исходной диагональной матрицы. Если
матрица

используется
в качестве оператора воздействия на
вершины треугольника, то имеет место
«двукратное» расширение или равномерное
масштабирование относительно точки
начала координат. Если значения элементов
не равны, то треугольник искажается,
что проиллюстрировано на рис. 4.8.

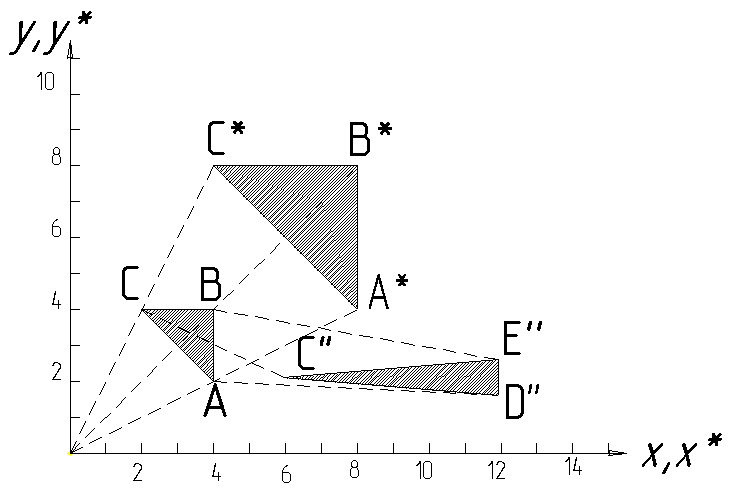
Рис. 4.8

Треугольник
АВС, преобразованный с помощью
матрицы

,

переходит
в пропорционально увеличенный треугольник
А^*В^*С^*.
Тот же треугольник, но преобразованный
с помощью матрицы

переходит
в треугольник D^*E^*F^*,
имеющий искажение, вызванное разными
коэффициентами масштабирования.

В общем
случае при матрице

, (4.43)

в которой
а = d, b
= c = 0, выполняется
пропорциональное масштабирование; если
a ≠ d,
b = c
= 0, то масштабирование будет проведено
непропорционально. В первом случае для
a = d
> 1 происходит расширение, т. е.
увеличение изображения. Если a
= d < 1, то
происходит равномерное сжатие, т. е.
фигура уменьшается. Непропорциональное
расширение и сжатие возникают в
зависимости от значений a
и d, которые могут быть
меньше либо больше, чем 1, независимо
друг от друга.

Из рис.
4.8 видно также, что на первый взгляд
преобразование треугольника является
перемещением. Это объясняется тем, что
относительно начала координат
масштабируются координатные векторы,
а не точки.

Для
того чтобы лучше понять этот факт,
рассмотрим преобразования АВС в
D^*E^*F^*
более внимательно. В частности,

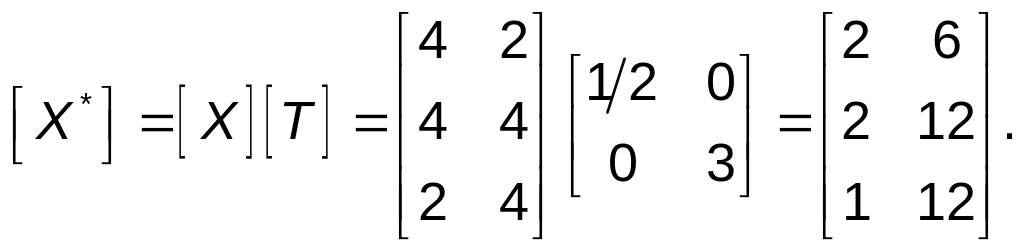
Заметим,
что каждая из компонент х
координатных векторов треугольника
DEF
умножалась на масштабный коэффициент
3, а компоненты у
– на 2.

Для
того чтобы получить чистое масштабирование
без эффекта перемещения, центр фигуры
надо поместить в начало координат. Это
видно на рис. 4.9, на котором треугольник
АВС
увеличивается в два раза при масштабировании
относительно его центра с координатами,
равными 1/3 основания и 1/3 высоты. Конкретная
матрица преобразования имеет вид

.

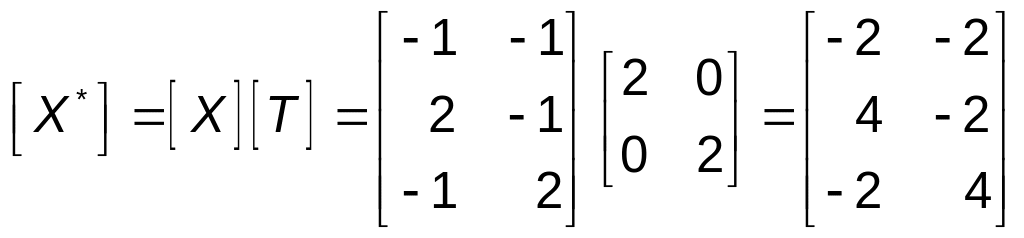
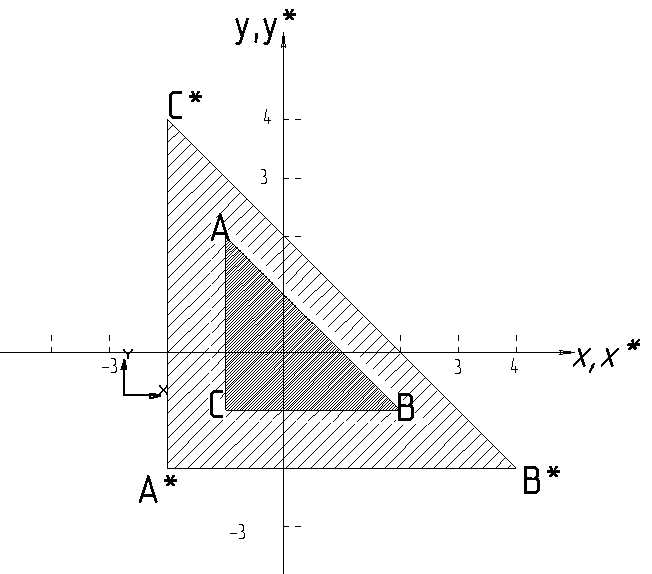
Рис. 4.9

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как матрица отражения известна в линейной алгебре , в матрице , отражение есть. Самый простой пример – отражение от прямой через начало координат в плоскости с углом наклона . Отображение отражения получается как произведение матрицы на вектор матрицы с соответствующим вектором .

Отражение на плоской прямой через начало координат

Матрица отражения на прямой, проходящей через начало координат с углом к положительной оси x, имеет следующий вид:

.

Например, матрица отражения S по оси x имеет вид:

.

Отражение на любой прямой

Это также позволяет представить отражение вектора на любой прямой с углом наклона . Для этого необходимо выполнить два шага:

1. Это приписывается отражению на прямой, проходящей через начало координат . Это происходит путем перехода к достижению . Вектор теперь зеркальный:
   

   

2. Сдвиг по опорному вектору стартовой линии

   

Более общие размышления

Матрицы отражения являются ортогональными матрицами и имеют определитель -1.

Представления отражений на гиперплоскостях в вычислительной математике называются матрицами Хаусхолдера .

литература

• Вольфганг Маккенс, Генрих Восс: математика. Для студентов инженерных специальностей. Том 1. HECO-Verlag, Aachen 1993, ISBN 3-930121-00-X .

Given: A function $y=f(x)$ from $mathbb{R}$ into $mathbb{R}$.

Find: The set $f^*$ of points consisting of the reflections of points of $f$ in the line $L$ defined by the equation $y=mx+c$.

Let $(x(t),y(t))in f$ and let $(x^*(t),y^*(t)$ denote its reflection in the line $L$.

Then the line containing $(x(t),y(t))$ and $(x^*(t),y^*(t))$ has slope $-dfrac{1}{m}$ and the midpoint of the line segment connecting the two points lies on $L$.

These two facts can be stated as equations.

begin{eqnarray}
dfrac{y^*(t)-y(t)}{x^*(t)-x(t)}&=&-dfrac{1}{m}\
dfrac{y(t)+y^*(t)}{2}&=&mleft(dfrac{x(t)+x^*(t)}{2}right)+c
end{eqnarray}

With a bit of algebra, these can be re-written as a system of two linear equations in $x^*(t)$ and $y^*(t)$.

begin{eqnarray}
x^*(t)+my^*(t)&=&x(t)+my(t)\
-mx^*(t)+y^*(t)&=&mx(t)-y(t)+2c
end{eqnarray}

Using the elimination method and replacing $y(t)$ with $f(a)$ we find that

begin{eqnarray}
x^*(t)&=&-dfrac{(m^2-1)x(t)-2m(y(t)-c)}{m^2+1} \
y^*(t)&=&dfrac{(m^2-1)y(t)+2(mx(t)+c)}{m^2+1}
end{eqnarray}

Example: Let $y=x$ so that $m=1$ and $c=0$. Substituting into these last two equations gives the result

begin{eqnarray}
x^*(t)&=&y(t)\
y^*(t)&=&x(t)
end{eqnarray}

which we know is correct since reflecting about $y=x$ inverts the function.

For a more complex example, find parametric equations for $y=x^2$ reflected about the line $y=-2x+1$.

Substituting into the equations and simplifying gives

begin{eqnarray}
x^*(t)&=&-frac{1}{5}left(4t^2+3t-4right)\
y^*(t)&=&frac{1}{5}left(3t^2-4t+2right)
end{eqnarray}

Desmos graph at this link:

https://www.desmos.com/calculator/hou5bqgopb