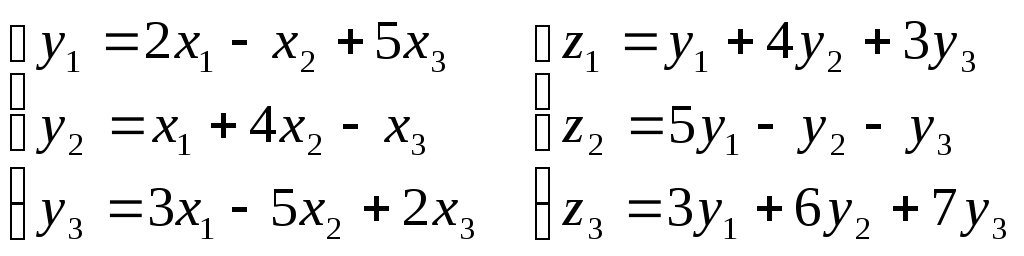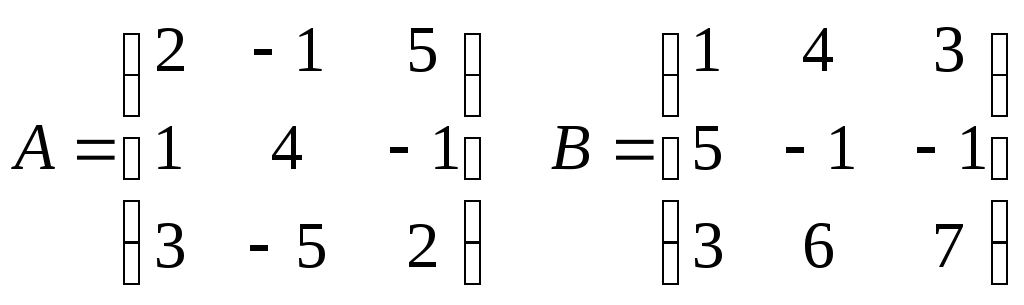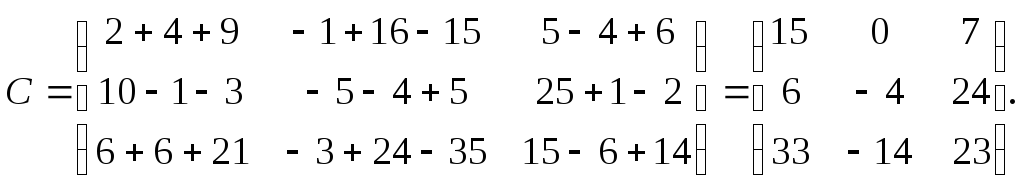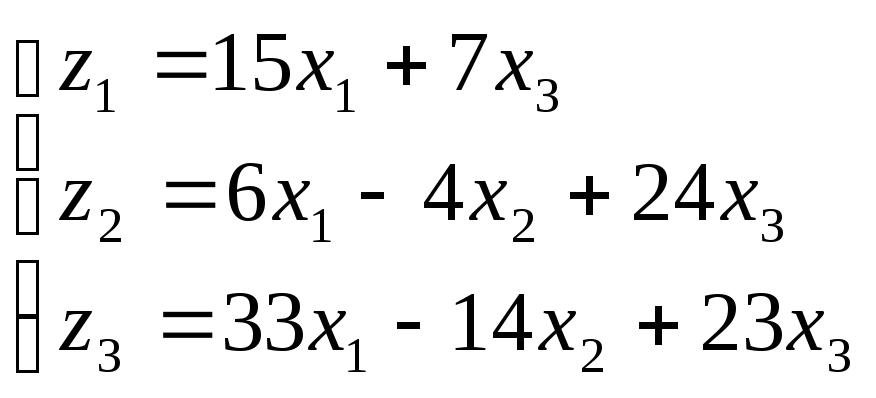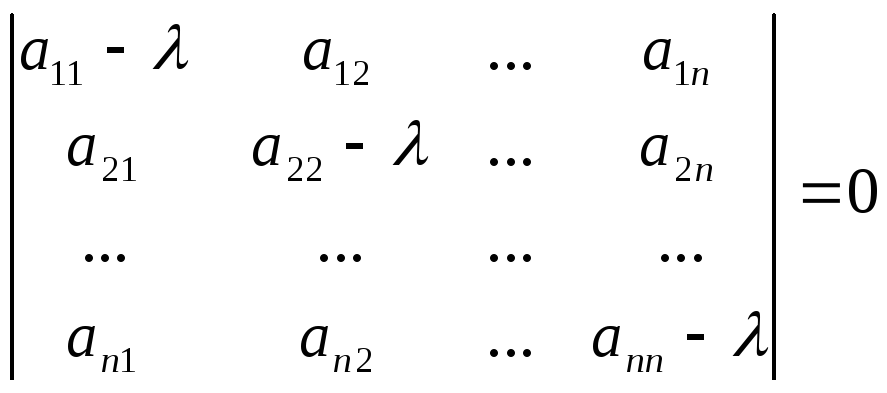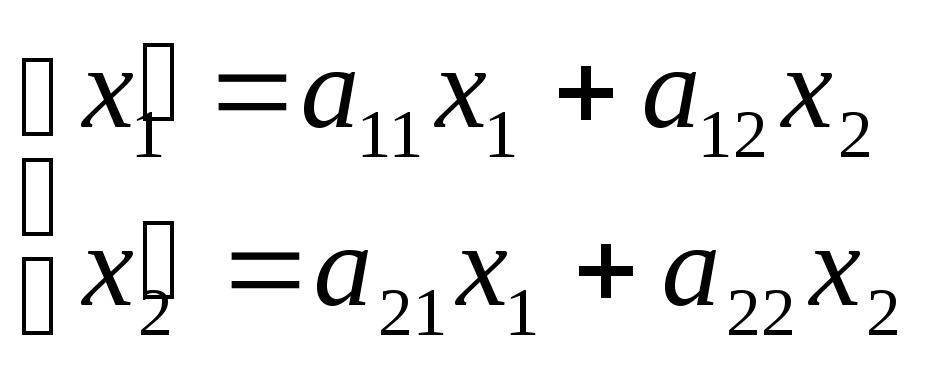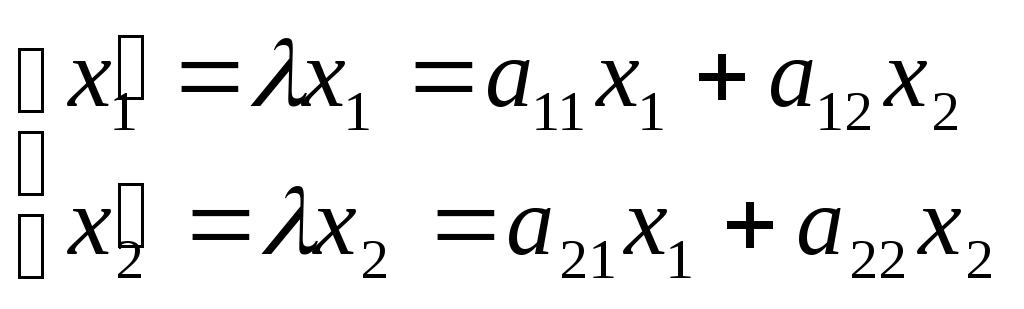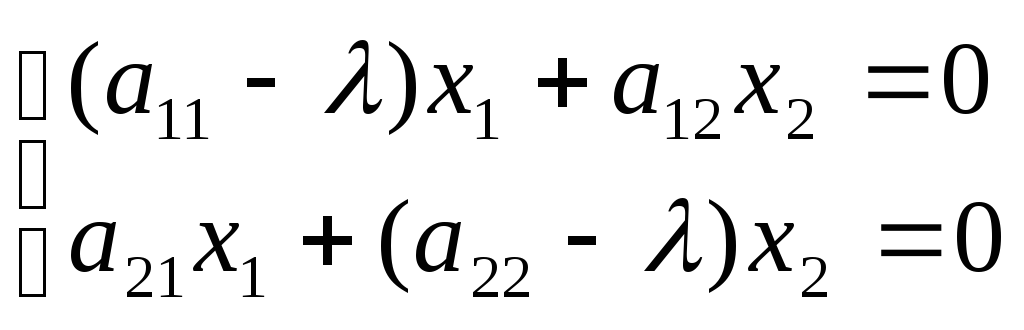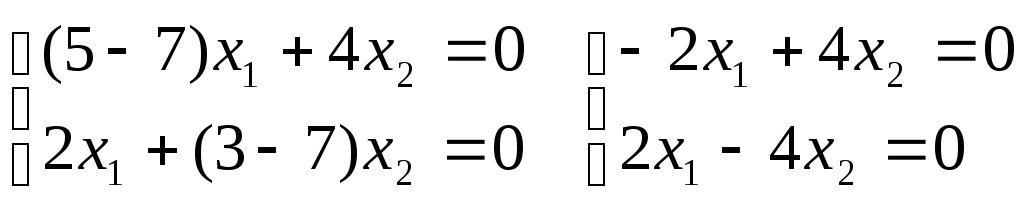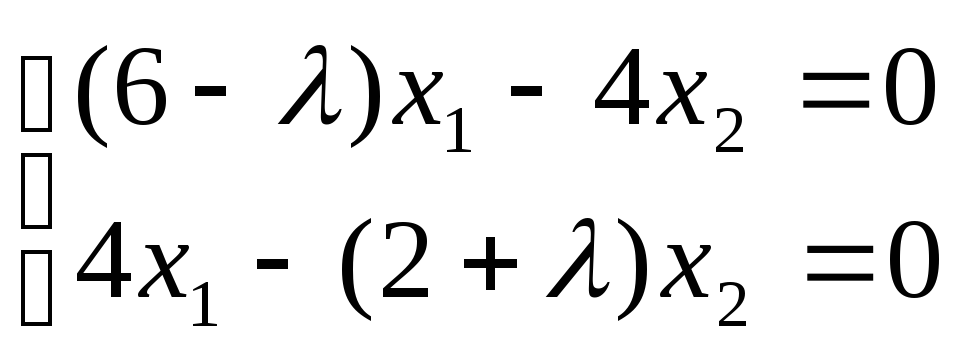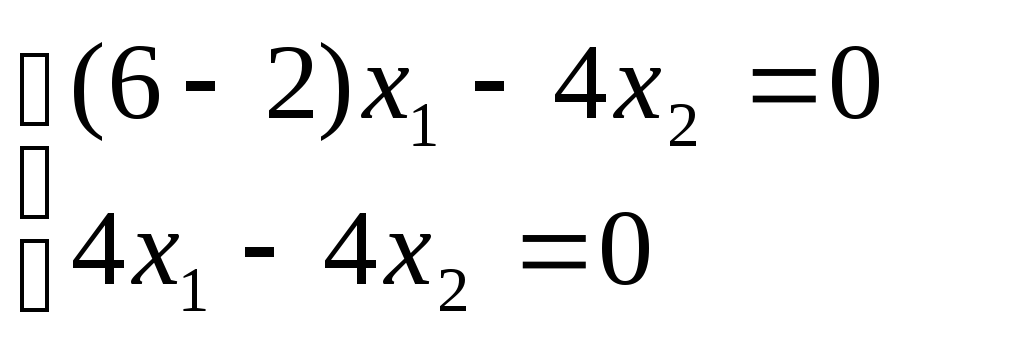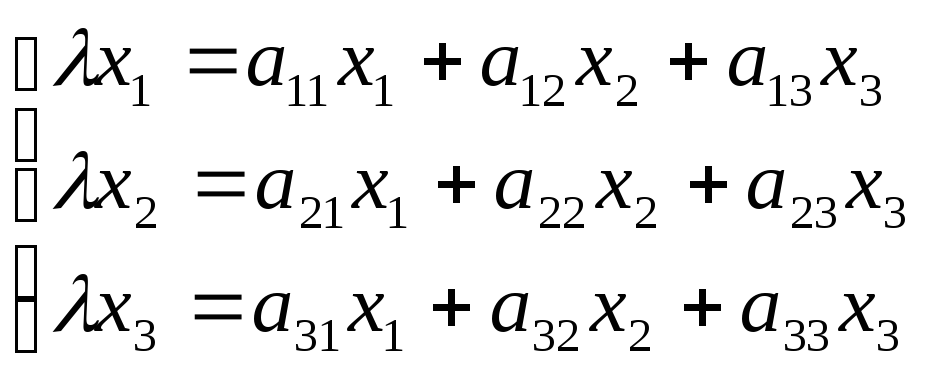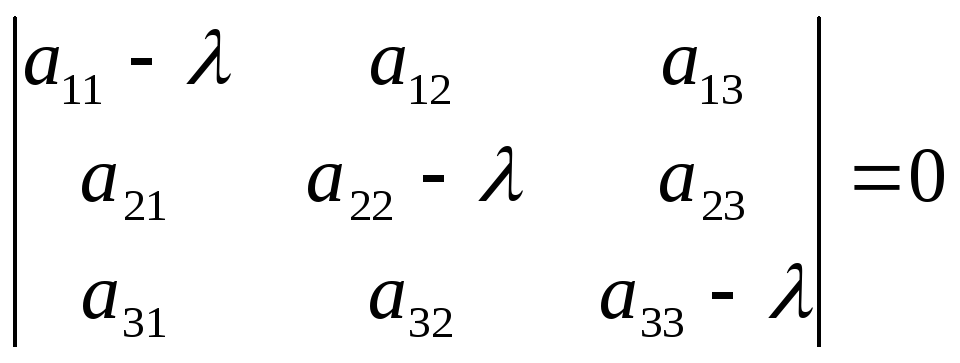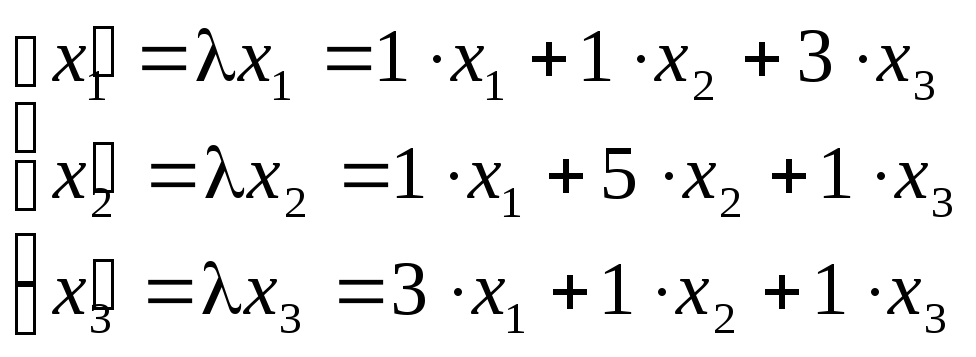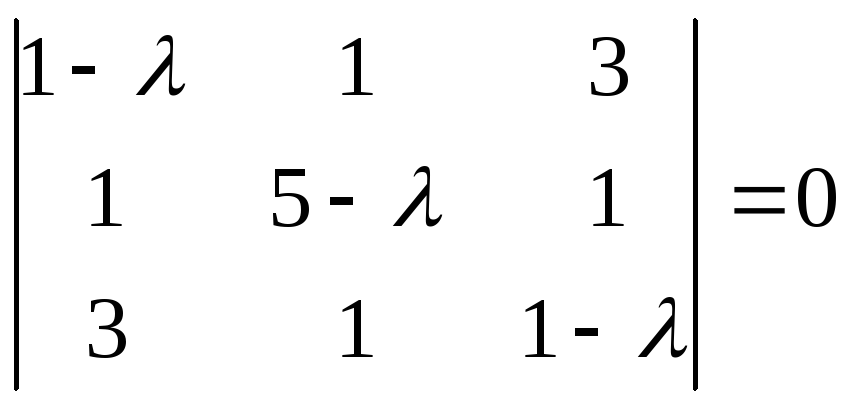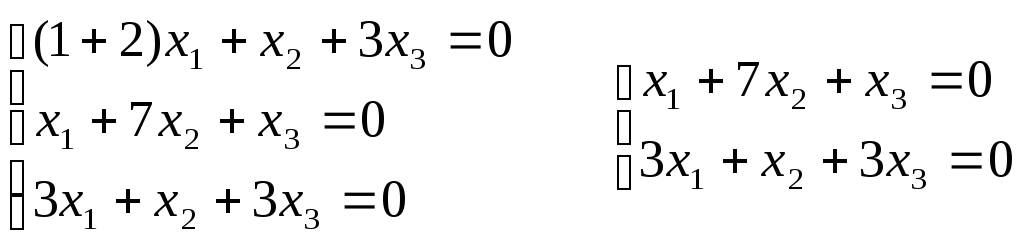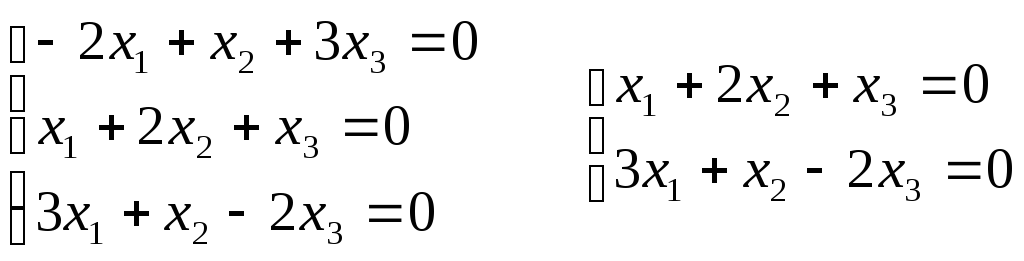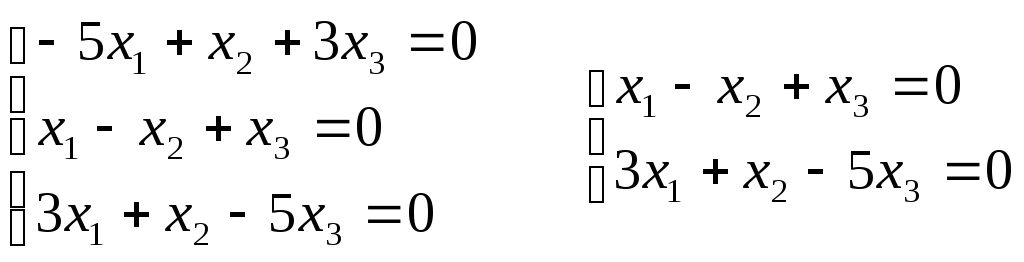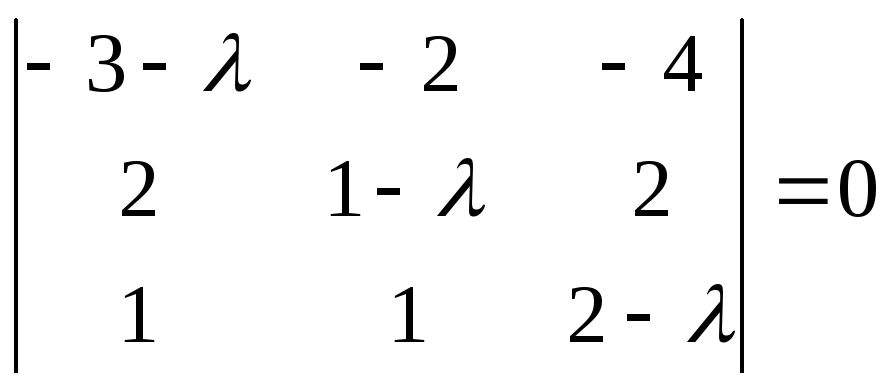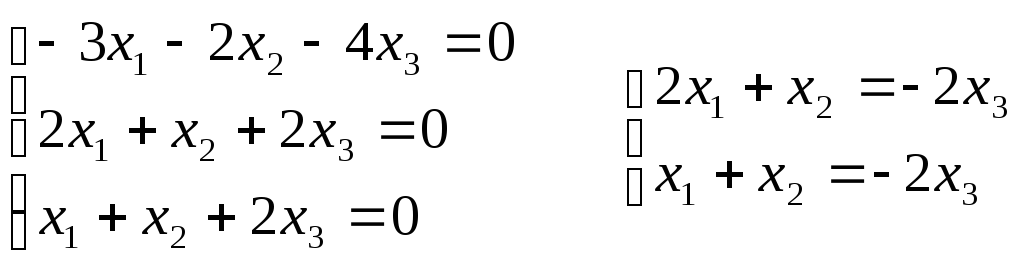Как найти матрицу преобразования координат

Все курсы > Линейная алгебра > Занятие 3

На прошлых занятиях мы поговорили про векторы и векторные пространства. Сегодня рассмотрим матрицы и линейные преобразования.

Ноутбук к сегодняшнему занятию⧉

Как матрицы преобразовывают пространство

Посмотрим, как матрица может изменить положение вектора.

Преобразование базисных векторов

Начнем с базисных векторов. Возьмем матрицу $A$ и два базисных вектора $mathbf i$ и $mathbf j$.

A = np.array([[2, 3],               [10, 1]]) i = np.array([1, 0]) j = np.array([0, 1])

Если поочередно умножить матрицу на каждый из векторов, то первый столбец матрицы $A$ определит новые координаты вектора $mathbf i$, второй столбец — вектора $mathbf j$.

$$ begin{bmatrix} 2 & 3 \ 10 & 1 end{bmatrix} cdot begin{bmatrix} 1 \ 0 end{bmatrix} = begin{bmatrix} 2 \ 10 end{bmatrix} $$

$$ begin{bmatrix} 2 & 3 \ 10 & 1 end{bmatrix} cdot begin{bmatrix} 0 \ 1 end{bmatrix} = begin{bmatrix} 3 \ 1 end{bmatrix} $$

Так трансформационная матрица (transformation matrix, левый множитель) оказывает влияние на базисные (и все остальные) векторы и, таким образом, меняет пространство.

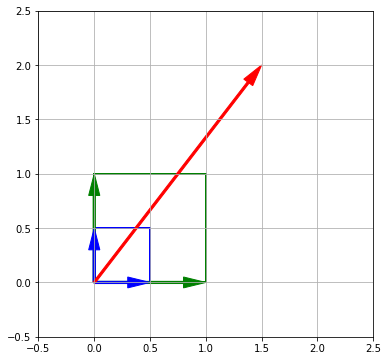
Посмотрим на результат на графике.

ax = plt.axes() plt.xlim([–0.5, 5]) plt.ylim([–0.5, 6]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) # найдем координаты с помощью произведения arrow_a = ax.arrow(0, 0, np.dot(A, i)[0], np.dot(A, i)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) arrow_b = ax.arrow(0, 0, np.dot(A, j)[0], np.dot(A, j)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.show()

Продемонстрируем, что при преобразовании любого вектора, мы по сути меняем базисные векторы, умноженные на скаляр. Рассмотрим, как в результате умножения матрицы A на вектор $mathbf r$, мы получим новый вектор $mathbf r’$.

$$A cdot mathbf r = mathbf r’ $$

Очевидно, мы можем умножать векторы $mathbf r$ и $mathbf r’$ на скаляр $n$ или представить их в виде суммы двух (базисных) векторов.

$$A cdot n mathbf r = n mathbf r’ $$

$$A cdot (mathbf i + mathbf j) = (mathbf i + mathbf j)’ $$

Тогда справедливо, что

$$A cdot (n mathbf i+m mathbf j) = (n mathbf i+m mathbf j)’ $$

Выполним умножение.

$$ A cdot (n mathbf i + m mathbf j) = (nA mathbf i+mA mathbf j) = n mathbf i’ + m mathbf j’ $$

Обратите внимание, что умножение матрицы на скаляр коммутативно, то есть $A n mathbf i = n A mathbf i $.

Таким образом, можно сказать, что при преобразовании пространства матрица преобразует масштабированные (scaled) базисные векторы. Приведем пример.

$$  begin{bmatrix} 2 & 3 \ 10 & 1 end{bmatrix} begin{bmatrix} 2 \ 3 end{bmatrix} = begin{bmatrix} 12 \ 32 end{bmatrix} $$

$$  begin{bmatrix} 2 & 3 \ 10 & 1 end{bmatrix} left( 2 begin{bmatrix} 1 \ 0 end{bmatrix} + 3 begin{bmatrix} 0 \ 1 end{bmatrix} right)  = begin{bmatrix} 12 \ 32 end{bmatrix} $$

$$ 2 begin{bmatrix} 2 & 3 \ 10 & 1 end{bmatrix} begin{bmatrix} 1 \ 0 end{bmatrix} + 3 begin{bmatrix} 2 & 3 \ 10 & 1 end{bmatrix} begin{bmatrix} 0 \ 1 end{bmatrix} = begin{bmatrix} 12 \ 32 end{bmatrix} $$

$$ 2 begin{bmatrix} 2 \ 10 end{bmatrix} + 3 begin{bmatrix} 3 \ 1 end{bmatrix} = begin{bmatrix} 12 \ 32 end{bmatrix} $$

Иначе говоря, «новые», преобразованные векторы будут иметь те же координаты относительно нового базиса, что и исходный вектор, относительно исходного базиса (потому что $n$ и $m$ или 2 и 3 в примере выше не изменяются при преобразовании).

Свойства преобразований

Вначале дадим описательное определение линейной трансформации пространства.

При линейном преобразовании начало координат не смещается, а линии координатной сетки остаются параллельными и сохраняют исходное расстояние друг от друга (origin remains fixed, grid lines remain parallel and evenly spaced).

Более формально свойства трансформации ($T$), которую также можно назвать функцией (function) или отображением (mapping) относительно векторов $mathbf v$ и $mathbf w$ можно выразить через две заданные в линейном пространстве операции сложения и умножения на скаляр.

1. $ T(mathbf v + mathbf w) = T(mathbf v) + T(mathbf w) $
2. $ T(c mathbf v) = c T(mathbf v) $

Примечение. Несмещение начала координат можно рассматривать как частный случай свойства 2, так как преобразование нулевого вектора должно дать нулевой вектор $T(mathbf 0) = mathbf 0 $. Приведем пример линейного и нелинейного преобразований.

Пример 1. Проекция

Рассмотрим проекцию $T: mathbb R^2 rightarrow mathbb R^2 $.

Проверим приведенные выше свойства:

• $ T(mathbf v + mathbf w) = T(mathbf v) + T(mathbf w) $
• если, например, вектор $mathbf v$ увеличить в два раза, то и проекция увеличится в два раза
• начало координат при проекции не смещается, то есть $T(mathbf 0) = mathbf 0 $

Пример 2. Нелинейное преобразование

Предположим, что мы хотим сместить каждый вектор проскости (в частности, вектор $ mathbf v $) на некоторый вектор $ mathbf d $.

Очевидно нарушается второе свойство, например, $ T(2 mathbf v) not= 2T(mathbf v) $. Более того, смещается начало координат, $T(mathbf 0) = mathbf d $.

Умножение матрицы на вектор

Важно, что умножение матрицы $A$ на векторы $mathbf v$ и $mathbf w$, т.е. $T(mathbf v) = A mathbf v$ и $T(mathbf w) = A mathbf w$ всегда линейно, так как

• $ A(mathbf v + mathbf w) = A(mathbf v) + A(mathbf w) $
• $ A(c mathbf v) = c A(mathbf v) $

Соответственно, задача линейного преобразования сводится к нахождению правильной трансформационной матрицы (причем в известной, заданной системе координат).

Например, если мы хотим перейти от трех измерений к двум, $T: mathbb R^3 rightarrow mathbb R^2$, то нам потребуется матрица $2 times 3$:

В общем случае матрица $A$ размерностью $m times n$ соответствует $ T: R^n rightarrow R^m $.

Смена базиса

Как уже было сказано, если линейное преобразование задано матрицей, то введена система координат (базис).

• На вход матрица получает базис $ mathbf v_1,…, mathbf v_n in R^n $
• На выходе выдает $ mathbf w_1,…, mathbf w_m in R^m $

Другими словами, при преобразовании линейной комбинации $mathbf v_1,…, mathbf v_n$ в линейную комбинацию $mathbf w_1,…, mathbf w_m$ происходит смена базиса. Например,

$$ mathbf v = c_1 mathbf v_1 + c_2 mathbf v_2 rightarrow T(mathbf v) = c_1 mathbf w_1 + c_2 mathbf w_2 $$

Пример 3. Производная как линейное преобразование

Интересно, что взятие производной линейно. Предположим, что у нас есть некоторая функция $ f(x) = c_1 + c_2 x + c_3 x^2 $. Ее базис: ${ 1, x, x^2 }$. Тогда производной будет $f'(x) = c_2 + 2 c_3 x $ с базисом ${ 1, x }$. Найти производную можно с помощью матрицы

$$ begin{bmatrix} 0 & 1 & 0 \ 0 & 0 & 2 end{bmatrix} begin{bmatrix} c_1 \ c_2 \ c_3 end{bmatrix} = begin{bmatrix} c_2 \ 2c_3 end{bmatrix} $$

Решение системы уравнений как преобразование

Теперь рассмотрим решение системы линейных уравнений (simultaneous equations) с точки зрения трансформации пространства.

$$ begin{bmatrix} 2 & 3 \ 10 & 1 end{bmatrix} begin{bmatrix} a \ b end{bmatrix} = begin{bmatrix} 8 \ 13 end{bmatrix}$$

По сути, нам нужно найти такой вектор $begin{bmatrix} a \ b end{bmatrix}$, при умножении матрицы на который мы окажемся в точке $ begin{bmatrix} 8 \ 13 end{bmatrix} $.

Виды преобразований

Можно выделить некоторые часто встречающиеся виды преобразований. Создадим вектор $mathbf x$.

Единичная матрица

Если умножить единичную матрицу (identity matrix) на вектор $mathbf x$, ничего не произойдет.

I = np.array([[1, 0],               [0, 1]]) np.dot(I, x)

Обратите внимание, мы легко можем догадаться, что с вектором после преобразования ничего не произойдет, потому что столбцы трансформационной матрицы в точности повторяют векторы базиса $mathbf i$ и $mathbf j$.

Сжатие и растяжение

При сжатии или растяжении (scaling) координаты вектора соответственно уменьшаются или увеличиваются в размере. В случае базисных векторов, они не меняют направления. Приведем пример растяжения.

# столбцы – это тот же базис, но # единицы увеличены в три и два раза соответственно Scale = np.array([[3, 0],                   [0, 2]]) np.dot(Scale, x)

Посмотрим, как это выглядит на графике.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

ax = plt.axes() plt.xlim([–0.5, 9.5]) plt.ylim([–0.5, 9.5]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, np.dot(Scale, i)[0], np.dot(Scale, i)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.arrow(0, 0, np.dot(Scale, j)[0], np.dot(Scale, j)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2)) ax.add_patch(Rectangle((0, 0), 3, 2, fill = False, edgecolor = ‘b’, lw = 2)) ax.arrow(0, 0, np.dot(Scale, x)[0], np.dot(Scale, x)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.show()

Дадим некоторые пояснения. Преобразования пространства удобно описывать с помощью площади, образованной двумя (в пространстве $R^2$) векторами.

• Зеленый квадрат: площадь базисных векторов
• Синий квадрат: площадь масштабированных базисных векторов
• Красный вектор: масштабированный вектор $mathbf x$

Обратите внимание, векторы базиса $mathbf i$ и $mathbf j$ после трансформации сохранили направление, вектор $ mathbf r $ сместился выше. Понимание того, что некоторые векторы сохраняют направление, а некоторые — нет, очень пригодится позднее.

Приведем пример сжатия. Для этого нужно, чтобы ненулевые координаты матрицы были меньше единицы.

Squish = np.array([[.5, 0],                    [0, .5]]) np.dot(Squish, x)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

ax = plt.axes() plt.xlim([–0.5, 2.5]) plt.ylim([–0.5, 2.5]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, np.dot(Squish, i)[0], np.dot(Squish, i)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.arrow(0, 0, np.dot(Squish, j)[0], np.dot(Squish, j)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2)) ax.add_patch(Rectangle((0, 0), .5, .5, fill = False, edgecolor = ‘b’, lw = 2)) ax.arrow(0, 0, np.dot(Squish, x)[0], np.dot(Squish, x)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.show()

Отражение

Отражение (reflection) как бы «перекидывает» вектор на другую сторону от осей координат. Посмотрим на отражение относительно оси y (то есть «перекидывать» мы будем вектор $mathbf i$). Для этого в первом столбце трансформационной матрицы 1 меняется на $-1$.

Reflect_y = np.array([[–1, 0],                       [0, 2]]) # посмотрим, где окажется вектор x np.dot(Reflect_y, x)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

ax = plt.axes() plt.xlim([–1.5, 1.5]) plt.ylim([–0.2, 2.5]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) # отражается относительно оси y ax.arrow(0, 0, np.dot(Reflect_y, i)[0], np.dot(Reflect_y, i)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) # вектор j мы растягиваем ax.arrow(0, 0, np.dot(Reflect_y, j)[0], np.dot(Reflect_y, j)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2)) ax.add_patch(Rectangle((0, 0), –1, 2, fill = False, edgecolor = ‘b’, lw = 2)) plt.show()

Выполним отражение относительно обеих осей.

Invert = np.array([[–1, 0],                    [0, –1]]) np.dot(Invert, x)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

ax = plt.axes() plt.xlim([–1.5, 1.5]) plt.ylim([–1.5, 1.5]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) # отражается относительно оси y ax.arrow(0, 0, np.dot(Invert, i)[0], np.dot(Invert, i)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) # отражается относительно оси x ax.arrow(0, 0, np.dot(Invert, j)[0], np.dot(Invert, j)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2)) ax.add_patch(Rectangle((0, 0), –1, –1, fill = False, edgecolor = ‘b’, lw = 2)) plt.show()

Матрица перестановки

Матрица перестановки (permutation matrix) позволяет поменять векторы $mathbf i$ и $mathbf j$ местами.

P = np.array([[0, 1],               [1, 0]]) # посмотрим, где окажется вектор x np.dot(P, x)

# а также базисные векторы np.dot(P, i), np.dot(P, j)

(array([0, 1]), array([1, 0]))

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

ax = plt.axes() plt.xlim([–0.5, 1.5]) plt.ylim([–0.5, 1.5]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) # i и j меняются местами ax.arrow(0, 0, np.dot(P, i)[0], np.dot(P, i)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.arrow(0, 0, np.dot(P, j)[0], np.dot(P, j)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2)) ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘b’, lw = 1)) plt.show()

Сдвиг (трансвекция)

Сдвиг или трансвекция (shear) предполагает, что один из базисных векторов остается на месте, второй сдвигается.

# вектор i остается на месте, j сдвигается Shear = np.array([[1, 1],                   [0, 1]]) np.dot(Shear, x)

ax = plt.axes() plt.xlim([–0.5, 2.5]) plt.ylim([–0.5, 1.5]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, np.dot(Shear, i)[0], np.dot(Shear, i)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.arrow(0, 0, np.dot(Shear, j)[0], np.dot(Shear, j)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2)) ax.add_patch(Polygon([[0, 0], [1, 0], [2, 1], [1, 1]], fill = False, edgecolor = ‘b’, lw = 2)) plt.show()

Вращение

Посмотрим, как можно повернуть (rotate) базисные векторы на 90 градусов против часовой стрелки.

# поворот на 90 градусов против часовой стрелки Rotate = np.array([[0, –1],                    [1, 0]]) np.dot(Rotate, x)

ax = plt.axes() plt.xlim([–1.5, 1.5]) plt.ylim([–0.5, 1.5]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, np.dot(Rotate, i)[0], np.dot(Rotate, i)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.arrow(0, 0, np.dot(Rotate, j)[0], np.dot(Rotate, j)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2)) ax.add_patch(Rectangle((0, 0), –1, 1, fill = False, edgecolor = ‘b’, lw = 2)) plt.show()

Поворот на определенный угол против часовой стрелки.

theta = np.radians(90) Rotate = np.array([[np.cos(theta), –np.sin(theta)],                    [np.sin(theta), np.cos(theta)]]) np.dot(Rotate, x)

Смысл такой трансформации представлен на схеме ниже. Для поворота на 90 градусов против часовой стрелки вспомним, что

• для вектора $mathbf i quad cos(90^{circ}) = 0, quad -sin(90^{circ}) = -1$
• для вектора $mathbf j quad sin(90^{circ}) = 1, quad cos(90^{circ}) = 0$

Видео про линейные преобразования⧉.

Композиция преобразований

Посмотрим, что произойдет, если применить сначала поворот на 90 градусов по часовой стрелке, затем отражение относительно оси y.

Так как матрица преобразования стоит слева от преобразуемого вектора, то для применения двух преобразований, матрица второго преобразования будет стоять слева от матрицы первого.

$$ Reflect_y cdot (Rotate cdot mathbf x ) $$

Подготовим матрицы.

# поворот по часовой стрелки theta = np.radians(90) Rotate = np.array([[np.cos(theta), np.sin(theta)],                    [–np.sin(theta), np.cos(theta)]]).round() Rotate

array([[ 0.,  1.],        [-1.,  0.]])

# отражение относительно оси y Reflect_y = np.array([[–1, 0],                       [0, 1]]) Reflect_y

array([[-1,  0],        [ 0,  1]])

Выполним преобразование.

np.dot(Reflect_y, np.dot(Rotate, i)), np.dot(Reflect_y, np.dot(Rotate, j))

(array([ 0., -1.]), array([-1.,  0.]))

Посмотрим на этот процесс графически. Вначале первое преобразование (вращение).

ax = plt.axes() plt.xlim([–1.5, 1.5]) plt.ylim([–1.5, 1.5]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) # поворот по часовой стрелке ax.arrow(0, 0, np.dot(Rotate, i)[0], np.dot(Rotate, i)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.arrow(0, 0, np.dot(Rotate, j)[0], np.dot(Rotate, j)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.show()

Теперь применим второе преобразование (отражение) к результату первого.

ax = plt.axes() plt.xlim([–1.5, 1.5]) plt.ylim([–1.5, 1.5]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) # отображение относительно оси y ax.arrow(0, 0, np.dot(Reflect_y, np.dot(Rotate, i))[0], np.dot(Reflect_y, np.dot(Rotate, i))[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.arrow(0, 0, np.dot(Reflect_y, np.dot(Rotate, j))[0], np.dot(Reflect_y, np.dot(Rotate, j))[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.show()

Запишем, где оказались векторы $mathbf i$ и $mathbf j$ после второго преобразования и соединим эти координаты в матрицу. Затем умножим на исходные векторы $mathbf i$ и $mathbf j$.

Composition = np.array([[0, –1],                         [–1, 0]]) np.dot(Composition, i), np.dot(Composition, j)

(array([ 0, -1]), array([-1,  0]))

Результат аналогичен последовательному применению предыдущих преобразований.

# то же самое мы получим, перемножив матрицы преобразований np.dot(Reflect_y, Rotate)

array([[ 0., -1.],        [-1.,  0.]])

Обратите внимание, что порядок операций важен. Поменяв матрицы преобразований местами, мы получим другой результат.

# выполнив отражение, а затем поворот, # мы вернем векторы в исходное положение np.dot(Rotate, np.dot(Reflect_y, i)), np.dot(Rotate, np.dot(Reflect_y, j))

(array([0., 1.]), array([1., 0.]))

Это еще раз демонстрирует некоммутативность, но ассоциативность умножения матриц.

Приведем ссылки на видео:

• Умножение матриц как последовательность преобразований⧉
• Линейные преобразования в трехмерном пространстве⧉

Подведем итог

Мы посмотрели, как матрицы преобразовывают пространство и на примерах изучили, чем линейные преобразования отличаются от нелинейных. Кроме того, мы познакомились с основными видами линейных преобразований.

Рассмотрим системы линейных уравнений.

Матрица перехода

3 июля 2022

Матрица перехода — это просто квадратная матрица, в столбцах которой записаны координаты новых базисных векторов. У такой матрицы много важных свойств, которые сформулированы и доказаны в первой части урока — теоретической. Этой теории хватит для любого экзамена или коллоквиума.

Вторая часть урока — практическая. В ней разобраны все типовые задачи, которые встречаются на контрольных, зачётах и экзаменах.

Содержание

1. Определение матрицы перехода
2. Свойства матрицы перехода
3. Теорема о замене координат
4. Задача 1. Базисы трёхмерного пространства
5. Задача 2. Базисы в поле вычетов
6. Задача 3. Пространство многочленов
7. Задача 4. Матрица перехода при симметрии
8. Задача 5. Матрица поворота

Если вы учитесь в серьёзном университете (МГУ, Бауманка и т.д.), то обязательно изучите первые три пункта. А если вам нужны только задачи, сразу переходите к пункта 4—6.

1. Определение матрицы перехода

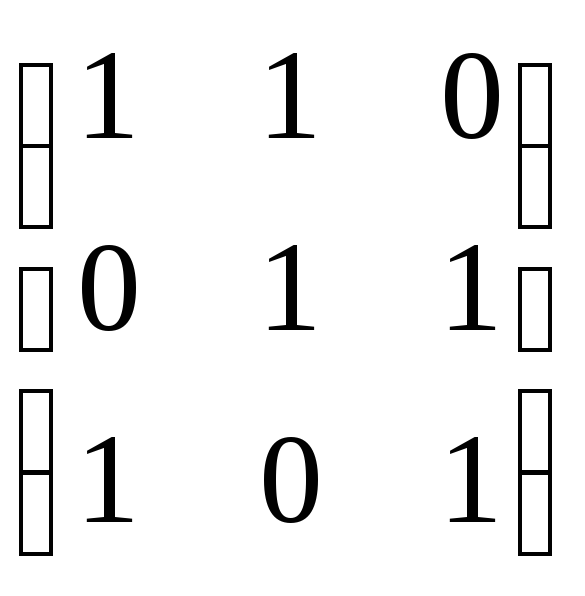
Пусть дано $n$-мерное линейное пространство $L$. Пусть также $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — два базиса в $L$.

Определение. Матрица перехода ${{T}_{eto f}}$ от базиса $e=left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ к базису $f=left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — это квадратная матрица порядка $n$, где по столбцам записаны координаты нового базиса $f$ в старом базисе $e$:

[{{T}_{eto f}}=left[ begin{array}{c|c|c|c}{{t}_{1,1}} & {{t}_{2,1}} & cdots & {{t}_{n,1}} \{{t}_{1,2}} & {{t}_{2,2}} & cdots & {{t}_{n,1}} \cdots & cdots & cdots & cdots \{{t}_{1,n}} & {{t}_{2,n}} & cdots & {{t}_{n,n}} \end{array} right]]

Обратите внимание на нумерацию элементов ${{t}_{i,j}}$: первый индекс обозначает номер столбца, т.е. номер нового базисного вектора, а второй отвечает за координаты этого вектора в старом базисе. Так, во втором столбце записаны координаты вектора ${{f}_{2}}$:

[{{f}_{2}}={{left[ {{t}_{2,1}},{{t}_{2,2}},ldots ,{{t}_{2,n}} right]}^{T}}]

Или, что то же самое, разложение вектора ${{f}_{2}}$ по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:

[{{f}_{2}}={{t}_{2,1}}{{e}_{1}}+{{t}_{2,2}}{{e}_{2}}+ldots +{{t}_{2,n}}{{e}_{n}}]

Да, такая нумерация не является обязательной. Но она очень распространена именно в записи матриц перехода: первый индекс отвечает за номер базисного вектора, второй — за номер координаты этого вектора.

Пример 1. В некотором базисе $e=left{ {{e}_{1}},{{e}_{2}},{{e}_{3}} right}$ векторного пространства ${{mathbb{R}}^{3}}$ даны три вектора:

[{{f}_{1}}={{left( 1,0,1 right)}^{T}},quad {{f}_{2}}={{left( 2,1,0 right)}^{T}},quad {{f}_{3}}={{left( 0,3,1 right)}^{T}}]

[begin{align}{{f}_{1}} &={{left( 1,0,1 right)}^{T}}, \ {{f}_{2}} &={{left( 2,1,0 right)}^{T}}, \ {{f}_{3}} &={{left( 0,3,1 right)}^{T}} \ end{align}]

Убедитесь, что система векторов $f=left{ {{f}_{1}},{{f}_{2}},{{f}_{3}} right}$ образует базис в ${{mathbb{R}}^{3}}$, найдите матрицу перехода ${{T}_{eto f}}$.

Решение. Система векторов будет базисом, если эти векторы линейно независимы, а их количество совпадает с размерностью пространства. Поскольку у нас три вектора и $dim{{mathbb{R}}^{3}}=3$, осталось проверить линейную независимость. Составим матрицу из столбцов с координатами векторов ${{f}_{1}}$, ${{f}_{2}}$ и ${{f}_{3}}$:

[left[ begin{matrix}1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]]

Вообще-то это и есть матрица перехода ${{T}_{eto f}}$, но сначала надо установить линейную независимость. Поэтому выполним элементарные преобразования строк:

[left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]begin{matrix} \ \ -1cdot left[ 1 right] \ end{matrix}sim left[ begin{array}{crc} 1 & 2 & 0 \ 0 & 1 & 3 \ 0 & -2 & 1 \ end{array} right]begin{matrix} -2cdot left[ 2 right] \ \ +2cdot left[ 2 right] \ end{matrix}sim left[ begin{array}{ccr} 1 & 0 & -6 \ 0 & 1 & 3 \ 0 & 0 & 7 \ end{array} right]]

[begin{align} & left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]begin{matrix} \ \ -1cdot left[ 1 right] \ end{matrix} \ & left[ begin{array}{crc} 1 & 2 & 0 \ 0 & 1 & 3 \ 0 & -2 & 1 \ end{array} right]begin{matrix} -2cdot left[ 2 right] \ \ +2cdot left[ 2 right] \ end{matrix} \ & left[ begin{array}{ccr} 1 & 0 & -6 \ 0 & 1 & 3 \ 0 & 0 & 7 \ end{array} right] \ end{align}]

Получили верхнетреугольную матрицу без нулей на главной диагонали. Ранг такой матрицы равен 3, поэтому система $left{ {{f}_{1}},{{f}_{2}},{{f}_{3}} right}$ линейно независима и образует базис. Матрица перехода от базиса $e$ к базису $f$ уже известна:

[{{T}_{eto f}}=left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]]

1.1. Зачем нужна матрица перехода

Матрица перехода нужна для того, чтобы компактно и наглядно выражать новый базис через старый. В самом деле, разложим векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ нового базиса по старому базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:

[begin{align}{{f}_{1}} &={{x}_{1,1}}{{e}_{1}}+{{x}_{2,1}}{{e}_{2}}+ldots +{{x}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{x}_{1,2}}{{e}_{1}}+{{x}_{2,2}}{{e}_{2}}+ldots +{{x}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}} &={{x}_{1,n}}{{e}_{1}}+{{x}_{2,n}}{{e}_{2}}+ldots +{{x}_{n,n}}{{e}_{n}} \ end{align}]

Получили систему из $n$ уравнений, которые в матричном виде можно представить так:

[left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1,1}} & cdots & {{x}_{1,n}} \ cdots & cdots & cdots \ {{x}_{n,1}} & cdots & {{x}_{n,n}} \ end{matrix} right]]

[left[ {{f}_{1}} cdots {{f}_{n}} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1,1}} & cdots & {{x}_{1,n}} \ cdots & cdots & cdots \ {{x}_{n,1}} & cdots & {{x}_{n,n}} \ end{matrix} right]]

Обратите внимание: ${{f}_{1}},ldots ,{{f}_{n}}$ и ${{e}_{1}},ldots ,{{e}_{n}}$ — это именно векторы, а не числа. Такие наборы принято записывать строками — в отличие от вектор-столбцов, элементами которых как раз выступают обычные числа.

Последний множитель — это и есть матрица перехода ${{T}_{eto f}}$, поэтому всё произведение можно записать более компактно:

[left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}]

2. Свойства матрицы перехода

Мы разберём три простых свойства, а далее отдельным разделом будет ещё одно — уже более серьёзное.

2.1. Переход от базиса к этому же базису

Свойство 1. При переходе от базиса $e$ к этому же базису $e$ матрица перехода ${{T}_{eto e}}=E$.

Для доказательства достаточно рассмотреть формулы

[begin{align}{{f}_{1}} &={{x}_{1,1}}{{e}_{1}}+{{x}_{2,1}}{{e}_{2}}+ldots +{{x}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{x}_{1,2}}{{e}_{1}}+{{x}_{2,2}}{{e}_{2}}+ldots +{{x}_{n,2}}{{e}_{n}} \ &cdots \ {{f}_{n}} &={{x}_{1,n}}{{e}_{1}}+{{x}_{2,n}}{{e}_{2}}+ldots +{{x}_{n,n}}{{e}_{n}} \ end{align}]

А затем положить ${{f}_{1}}={{e}_{1}}$, ${{f}_{2}}={{e}_{2}}$, …, ${{f}_{n}}={{e}_{n}}$. Тогда:

[begin{align} {{f}_{1}} &={{e}_{1}}=1cdot {{e}_{1}}+0cdot {{e}_{2}}+ldots +0cdot {{e}_{n}} \ {{f}_{2}} &={{e}_{2}}=0cdot {{e}_{1}}+1cdot {{e}_{2}}+ldots +0cdot {{e}_{n}} \ &cdots \ {{f}_{n}} &={{e}_{n}}=0cdot {{e}_{1}}+0cdot {{e}_{2}}+ldots +1cdot {{e}_{n}} \ end{align}]

Указанное выражение однозначно, поскольку $e$ — базис. Следовательно, матрица перехода равна

[{{T}_{eto f}}=left[ begin{array}{c|c|c|c} 1 & 0 & cdots& 0 \ 0 & 1 & cdots& 0 \ cdots& cdots& cdots& cdots \ 0 & 0 & cdots& 1 \ end{array} right]=E]

Итак, ${{T}_{eto f}}=E$, что и требовалось доказать.

2.2. Обратный переход

Свойство 2. Если ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к базису $f$, то ${{T}_{fto e}}={{left( {{T}_{eto f}} right)}^{-1}}$ матрица обратного перехода, от базиса $f$ к базису $e$.

В самом деле, базисы $e$ и $f$ связаны с матрицей перехода по формуле

[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}]

Поскольку матрица ${{T}_{eto f}}$ невырожденная, существует обратная к ней матрица ${{left( {{T}_{eto f}} right)}^{-1}}$. Домножим на эту матрицу обе части формулы, связывающей базисы $e$ и $f$:

[left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{left( {{T}_{eto f}} right)}^{-1}}=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}cdot {{left( {{T}_{eto f}} right)}^{-1}}]

[begin{align}left[ {{f}_{1}},ldots ,{{f}_{n}} right] &cdot {{left( {{T}_{eto f}} right)}^{-1}}= \ &=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}cdot {{left( {{T}_{eto f}} right)}^{-1}} \ end{align}]

Упрощаем эту формулу и получаем

[left[ {{e}_{1}},ldots ,{{e}_{n}} right]=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{left( {{T}_{eto f}} right)}^{-1}}]

Итак, мы получили формулу перехода от базиса $f$ к базису $e$. Следовательно, ${{left( {{T}_{eto f}} right)}^{-1}}$ — матрица такого перехода, что и требовалось доказать.

2.3. Переход через транзитный базис

Пусть ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к базису $f$ линейного пространства $L$, а ${{T}_{fto g}}$ — матрица перехода от базиса $f$ к базису $g$ того же линейного пространства $L$.

Тогда матрица перехода ${{T}_{eto g}}$ от базиса $e$ к базису $g$ находится по формуле

[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}]

Для доказательства достаточно записать формулы для выражения базисов $f$ и $g$, а затем подставить одну формулу в другую. По условию теоремы, базис $f$ выражается через базис $e$ по формуле

[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}]

Кроме того, базис $g$ выражается через базис $f$ по формуле

[left[ {{g}_{1}},ldots ,{{g}_{n}} right]=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}]

Подставим первое выражение во второе и получим

[begin{align}left[ {{g}_{1}},ldots ,{{g}_{n}} right] &=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}= \ &=left( left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}} right)cdot {{T}_{fto g}}= \ & =left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot left( {{T}_{eto f}}cdot {{T}_{fto g}} right) end{align}]

[begin{align}& left[ {{g}_{1}},ldots ,{{g}_{n}} right]= \ =& left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}= \ =& left( left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}} right)cdot {{T}_{fto g}}= \ =& left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot left( {{T}_{eto f}}cdot {{T}_{fto g}} right) end{align}]

Мы получили прямое выражение базиса $g$ через базис $e$, причём матрица перехода равна

[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}]

Это именно та формула, которую и требовалось доказать.

2.4. Невырожденные матрицы

И ещё одно важное свойство:

Свойство 4. Пусть дана произвольная квадратная невырожденная матрица

[T=left[ begin{matrix}{{a}_{1,1}} & {{a}_{1,2}} & cdots & {{a}_{1,n}} \ {{a}_{2,1}} & {{a}_{2,2}} & cdots & {{a}_{2,n}} \ cdots & cdots & cdots & cdots \ {{a}_{n,1}} & {{a}_{n,2}} & cdots & {{a}_{n,n}} \ end{matrix} right]]

Пусть $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ — произвольный базис линейного пространства $L$. Тогда система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$, полученных по формуле

[begin{align}{{f}_{1}}&={{a}_{1,1}}{{e}_{1}}+{{a}_{2,1}}{{e}_{2}}+ldots +{{a}_{n,1}}{{e}_{n}} \ {{f}_{2}}&={{a}_{1,2}}{{e}_{1}}+{{a}_{2,2}}{{e}_{2}}+ldots +{{a}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}}&={{a}_{1,n}}{{e}_{1}}+{{a}_{2,n}}{{e}_{2}}+ldots +{{a}_{n,n}}{{e}_{n}} \ end{align}]

тоже будет базисом $L$.

Иначе говоря, всякая квадратная невырожденная матрица $T$ является матрицей перехода от данного базиса $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ к некоторому новому базису $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ линейного пространства $L$.

Обратите внимание: поскольку изначально мы не знаем, что $T$ — матрица перехода, её элементы пронумерованы стандартным образом: первый индекс отвечает за строку, а второй — за столбец. Однако это нисколько не помешает нам доказать теорему.

Для доказательства того, что $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — базис линейного пространства $L$, нужно доказать два утверждения:

• 1.Система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — линейно независима.
• 2.Ранг этой системы векторов совпадает с размерностью пространства $L$.

Поскольку количество векторов в системе $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ совпадает с количеством базисных векторов $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$, т.е. равно $n=dim L$, достаточно лишь проверить линейную независимость.

Рассмотрим линейную комбинацию векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ и предположим, что она равна нулю:

[{{lambda }_{1}}{{f}_{1}}+{{lambda }_{2}}{{f}_{2}}+ldots +{{lambda }_{n}}{{f}_{n}}=0]

В матричном виде это выглядит так:

[left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot left[ begin{align}& {{lambda }_{1}} \ & cdots\ & {{lambda }_{n}} \ end{align} right]=0]

По условию теоремы векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ раскладываются по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ с коэффициентами, записанными в столбцах матрицы $T$. В матричном виде это выглядит так:

[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot T]

Подставляем полученное выражение для $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ в предыдущее матричное уравнение и получаем

[left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot Tcdot left[ begin{align}& {{lambda }_{1}} \ & cdots \ & {{lambda }_{n}} \ end{align} right]=0]

Поскольку $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ — базис линейного пространства $L$, такое равенство возможно лишь при условии

[Tcdot left[ begin{matrix} {{lambda }_{1}} \ cdots \ {{lambda }_{n}} \ end{matrix} right]=left[ begin{matrix} 0 \ cdots \ 0 \ end{matrix} right]]

Это матричное уравнение можно рассматривать как систему из $n$ однородных уравнений относительно переменных ${{lambda }_{1}},ldots ,{{lambda }_{n}}$. И поскольку по условию теоремы матрица $T$ невырожденная, это СЛАУ имеет лишь одно решение — тривиальное:

[{{lambda }_{1}}={{lambda }_{2}}=ldots ={{lambda }_{n}}=0]

Получаем, что система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ линейно независима, а количество векторов совпадает с размерностью линейного пространства $L$. Следовательно, эта система — базис, что и требовалось доказать.

3. Замена координат в новом базисе

До сих пор мы рассуждали лишь о том, как координаты новых базисных векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ выражаются через координаты старых базисных векторов $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$. Но что будет с координатами одного и того же вектора линейного пространства $L$ при переходе от одного базиса к другому?

Ответ даёт следующая теорема.

3.1. Формулировка теоремы

Теорема. Пусть $e=left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $f=left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — базисы линейного пространства $L$ над полем $K$. Пусть ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к $f$:

[{{T}_{eto f}}=left[ begin{matrix}{{a}_{1,1}} & cdots& {{a}_{1,n}} \ cdots& cdots& cdots \ {{a}_{n,1}} & cdots & {{a}_{n,n}} \ end{matrix} right]]

Тогда координаты произвольного вектора $hin L$ пересчитываются по формуле

[{{left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]}_{e}}={{T}_{eto f}}cdot {{left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]}_{f}}]

Ещё раз: если произвольный вектор $hin L$ в новом базисе $f$ имеет координаты

[{{left[ h right]}_{f}}=left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

то в старом базисе $e$ этот же вектор $hin L$ имеет координаты

[{{left[ h right]}_{e}}=left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]={{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

Т.е. для векторов всё наоборот: не новые координаты выражаются через старые, а старые — через новые. Впрочем, никто не мешает найти матрицу $T_{eto f}^{-1}$ и записать

[left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]=T_{eto f}^{-1}cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]]

Но такая запись предполагает дополнительное действие — нахождение обратной матрицы.

3.2. Доказательство

Сначала «соберём» матрицу ${{T}_{eto f}}$. Для этого разложим векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:

[left{ begin{align}{{f}_{1}} &={{a}_{1,1}}{{e}_{1}}+{{a}_{2,1}}{{e}_{2}}+ldots +{{a}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{a}_{1,2}}{{e}_{1}}+{{a}_{2,2}}{{e}_{2}}+ldots +{{a}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}} &={{a}_{1,n}}{{e}_{1}} +{{a}_{2,n}}{{e}_{2}}+ldots +{{a}_{n,n}}{{e}_{n}} \ end{align} right.]

В матричной форме эту систему линейных уравнений можно записать так:

[left[ begin{matrix} {{f}_{1}} \ {{f}_{2}} \ cdots \ {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{a}_{1,1}} & {{a}_{2,1}} & cdots & {{a}_{n,1}} \ {{a}_{1,2}} & {{a}_{2,2}} & cdots & {{a}_{n,2}} \ cdots & cdots & cdots & cdots \ {{a}_{1,n}} & {{a}_{2,n}} & cdots & {{a}_{n,n}} \ end{matrix} right]cdot left[ begin{matrix} {{e}_{1}} \ {{e}_{2}} \ cdots \ {{e}_{n}} \ end{matrix} right]]

Транспонируем обе стороны равенства, учитывая, что произведение справа транспонируется по правилу ${{left( Acdot B right)}^{T}}={{B}^{T}}cdot {{A}^{T}}$:

[left[ begin{matrix}{{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{a}_{1,1}} & {{a}_{1,2}} & cdots & {{a}_{1,n}} \ {{a}_{2,1}} & {{a}_{2,2}} & cdots & {{a}_{2,n}} \ cdots & cdots & cdots & cdots \ {{a}_{n,1}} & {{a}_{n,2}} & cdots & {{a}_{n,n}} \ end{matrix} right]]

[left[ {{f}_{1}} cdots {{f}_{n}} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{a}_{1,1}} & cdots & {{a}_{1,n}} \ cdots & cdots & cdots \ {{a}_{n,1}} & cdots & {{a}_{n,n}} \ end{matrix} right]]

Квадратная матрица справа — это и есть матрица перехода ${{T}_{eto f}}$. Поэтому матричное уравнение можно переписать так:

[left[ begin{matrix}{{f}_{1}} & cdots& {{f}_{n}} \ end{matrix} right]=left[ begin{matrix}{{e}_{1}} & cdots& {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}]

Теперь возьмём произвольный вектор $hin L$ и разложим его по базисам $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$:

[begin{align}h &={{x}_{1}}{{e}_{1}}+{{x}_{2}}{{e}_{2}}+ldots +{{x}_{n}}{{e}_{n}}= \ &={{y}_{1}}{{f}_{1}}+{{y}_{2}}{{f}_{2}}+ldots +{{y}_{n}}{{f}_{n}} end{align}]

Вновь перейдём к матричной форме. Сначала учтём, что координаты векторов принято записывать в виде вектор-столбцов:

[{{left[ h right]}_{e}}=left[ begin{matrix} {{x}_{1}} \ {{x}_{2}} \ cdots \ {{x}_{n}} \ end{matrix} right]quad {{left[ h right]}_{f}}=left[ begin{matrix} {{y}_{1}} \ {{y}_{2}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

Тогда левую и правую часть уравнения можно представить как произведение строк с базисными векторами и указанных вектор-столбцов с координатами:

[left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

[left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ {{f}_{1}} cdots {{f}_{n}} right]cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

Но выше мы выражали строку векторов $left[ {{f}_{1}},ldots ,{{f}_{n}} right]$ через строку $left[ {{e}_{1}},ldots ,{{e}_{n}} right]$ и матрицу перехода ${{T}_{eto f}}$. Подставим это выражение в наше матричное уравнение:

[left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

[left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot {{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

Уберём слева и справа первый множитель — строку $left[ {{e}_{1}},ldots ,{{e}_{n}} right]$. Получим уравнение, связывающее координаты вектора в разных базисах:

[left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]={{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

Это именно та формула, которую и требовалось доказать.

Задача 1. Базисы трёхмерного пространства

Задача. Убедитесь, что системы векторов

[{{a}_{1}}={{left( 1,2,1 right)}^{T}},quad {{a}_{2}}={{left( 2,3,2 right)}^{T}},quad {{a}_{3}}={{left( 1,-1,2 right)}^{T}}]

[begin{align}{{a}_{1}} &={{left( 1,2,1 right)}^{T}}, \ {{a}_{2}} &={{left( 2,3,2 right)}^{T}}, \ {{a}_{3}} &={{left( 1,-1,2 right)}^{T}} \ end{align}]

и

[{{b}_{1}}={{left( 1,3,1 right)}^{T}},quad {{b}_{2}}={{left( 1,-1,3 right)}^{T}},quad {{b}_{3}}={{left( 2,2,1 right)}^{T}}]

[begin{align}{{b}_{1}} &={{left( 1,3,1 right)}^{T}}, \ {{b}_{2}} &={{left( 1,-1,3 right)}^{T}}, \ {{b}_{3}} &={{left( 2,2,1 right)}^{T}} \ end{align}]

являются базисами в векторном пространстве ${{mathbb{R}}^{3}}$. Найдите матрицу перехода ${{T}_{ato b}}$. Найдите координаты в базисе $a$ вектора $x$, который в базисе $b$ имеет координаты ${{left( 0,3,2 right)}^{T}}$.

Решение

Чтобы доказать, что система векторов образует базис, достаточно составить матрицу $A$ из координат этих векторов, а затем вычислить её определитель $det A$. И если $det Ane 0$, то векторы линейно независимы. А поскольку их количество совпадает с размерностью линейного пространства, такие векторы образуют базис.

Рассмотрим систему векторов $a=left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$. Составим из них матрицу, расположив координаты по столбцам. Получим матрицу перехода ${{T}_{eto a}}$ от некого исходного базиса $e$ (в котором как раз и даны координаты векторов ${{a}_{i}}$ и ${{b}_{i}}$ в условии задачи) к базису $a$:

[{{T}_{eto a}}=left[ begin{array}{ccr} 1 & 2 & 1 \ 2 & 3 & -1 \ 1 & 2 & 2 \ end{array} right]]

Определитель этой матрицы отличен от нуля:

[det {{T}_{eto a}}=-1ne 0]

Следовательно, $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ — базис пространства ${{mathbb{R}}^{3}}$.

Теперь составим матрицу из векторов $b=left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$. Получим матрицу перехода ${{T}_{eto b}}$:

[{{T}_{eto b}}=left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right]]

Определитель этой матрицы вновь отличен от нуля:

[det {{T}_{eto b}}=12ne 0]

Следовательно, $left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ — тоже базис пространства ${{mathbb{R}}^{3}}$.

Осталось найти матрицу перехода ${{T}_{ato b}}$. Заметим, что эту матрицу можно выразить так:

[begin{align}{{T}_{ato b}} &={{T}_{ato e}}cdot {{T}_{eto b}}= \ &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}end{align}]

Мы внедрили «транзитный» базис $e$ и вместо прямого перехода $ato b$ рассмотрели цепочку $ato eto b$. Это стандартный и очень распространённый приём, но из-за этого появился новый элемент $T_{eto a}^{-1}$ — матрица, обратная к ${{T}_{eto a}}$. Найдём $T_{eto a}^{-1}$ методом присоединённой матрицы:

[left[ {{T}_{eto a}}|E right]sim ldots sim left[ E|T_{eto a}^{-1} right]]

Напомню, что элементарные преобразования в присоединённых матрицах выполняются только над строками. Если вы забыли, как всё это работает, см. урок «Обратная матрица». В нашем случае получим:

[left[ begin{array}{ccr|ccc}1 & 2 & 1 & 1 & 0 & 0 \ 2 & 3 & -1 & 0 & 1 & 0 \ 1 & 2 & 2 & 0 & 0 & 1 \end{array} right]begin{matrix} , \ -2cdot left[ 1 right] \ -1cdot left[ 1 right] \ end{matrix}]

Мы «зачистили» первый столбец. Теперь «зачистим» последний:

[left[ begin{array}{crr|rcc} 1 & 2 & 1 & 1 & 0 & 0 \ 0 & -1 & -3 & -2 & 1 & 0 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]begin{matrix} -1cdot left[ 3 right] \ +3cdot left[ 3 right] \ , \ end{matrix}]

Остался лишь средний. Разберёмся и с ним:

[left[ begin{array}{crc|rcr} 1 & 2 & 0 & 2 & 0 & -1 \ 0 & -1 & 0 & -5 & 1 & 3 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]begin{matrix} +2cdot left[ 2 right] \ |cdot left( -1 right) \ , \ end{matrix}]

Получили единичную матрицу слева от вертикальной черты. Значит, справа стоит искомая матрица $T_{eto a}^{-1}$:

[left[ begin{array}{ccc|rrr} 1 & 0 & 0 & -8 & 2 & 5 \ 0 & 1 & 0 & 5 & -1 & -3 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]]

Теперь у нас есть всё, чтобы найти матрицу перехода ${{T}_{ato b}}$:

[{{T}_{ato b}}={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}=left[ begin{array}{rrr} -8 & 2 & 5 \ 5 & -1 & -3 \ -1 & 0 & 1 \ end{array} right]cdot left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right]]

[begin{align}{{T}_{ato b}} &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}= \ &=left[ begin{array}{rrr} -8 & 2 & 5 \ 5 & -1 & -3 \ -1 & 0 & 1 \ end{array} right]cdot left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right] end{align}]

После несложных вычислений получаем матрицу перехода от базиса $a$ к базису $b$:

[{{T}_{ato b}}=left[ begin{array}{rrr} 3 & 5 & -7 \ -1 & -3 & 5 \ 0 & 2 & -1 \ end{array} right]]

Осталось найти координаты вектора $x$, который в базисе $b$ имеет координаты ${{left( 0,3,2 right)}^{T}}$. Вспомним формулу, выражающую координаты в старом базисе через координаты в новом базисе:

[{{left[ x right]}_{a}}={{T}_{ato b}}cdot {{left[ x right]}_{b}}]

Подставляем в эту формулу матрицу ${{T}_{ato b}}$ и вектор-столбец ${{left[ x right]}_{b}}={{left[ 0,3,2 right]}^{T}}$:

[{{left[ x right]}_{a}}=left[ begin{array}{rrr} 3 & 5 & -7 \ -1 & -3 & 5 \ 0 & 2 & -1 \ end{array} right]cdot left[ begin{matrix} 0 \ 3 \ 2 \ end{matrix} right]=left[ begin{matrix} 1 \ 1 \ 4 \ end{matrix} right]]

Итак, вектор $x$ в базисе $a$ имеет координаты ${{left( 1,1,4 right)}^{T}}$. Задача решена.

Альтернативное решение

Можно найти матрицу ${{T}_{ato b}}$ заметно быстрее, если использовать алгоритм решения матричных уравнений. Заметим, что нам требуется найти произведение

[{{T}_{ato b}}={{A}^{-1}}cdot B]

С другой стороны, для нахождения такого произведения достаточно составить присоединённую матрицу вида $left[ A|B right]$ и цепочкой элементарных преобразований свести её к виду

[left[ A|B right]sim ldots sim left[ E|{{A}^{-1}}cdot B right]]

Другими словами, справа от вертикальной черты мы получим искомую матрицу перехода ${{T}_{ato b}}$!

На практике это выглядит так. Записываем присоединённую матрицу $left[ A|B right]$:

[left[ begin{array}{ccr|crc} 1 & 2 & 1 & 1 & 1 & 2 \ 2 & 3 & -1 & 3 & -1 & 2 \ 1 & 2 & 2 & 1 & 2 & 1 \ end{array} right]]

И после элементарных преобразований получим

[left[ begin{array}{ccc|rrr} 1 & 0 & 0 & 3 & 5 & -7 \ 0 & 1 & 0 & -1 & -3 & 5 \ 0 & 0 & 1 & 0 & 2 & -1 \ end{array} right]]

Для экономии места я пропустил промежуточные шаги. Попробуйте сделать их самостоятельно — это очень полезная практика.

Если же вы хотите разобраться, как это работает (и почему вдруг справа возникает матрица вида ${{A}^{-1}}cdot B$), см. урок «Матричные уравнения». А мы идём дальше.

Задача 2. Базисы в поле вычетов

Найдите матрицу перехода от базиса

[{{a}_{1}}={{left( 1,1,1 right)}^{T}},quad {{a}_{2}}={{left( 2,1,1 right)}^{T}},quad {{a}_{3}}={{left( 3,2,1 right)}^{T}}]

[begin{align}{{a}_{1}} &={{left( 1,1,1 right)}^{T}}, \ {{a}_{2}} &={{left( 2,1,1 right)}^{T}}, \ {{a}_{3}} &={{left( 3,2,1 right)}^{T}} \ end{align}]

к базису

[{{b}_{1}}={{left( 0,4,3 right)}^{T}},quad {{b}_{2}}={{left( 3,3,2 right)}^{T}},quad {{b}_{3}}={{left( 2,2,1 right)}^{T}}]

[begin{align}{{b}_{1}} &={{left( 0,4,3 right)}^{T}}, \ {{b}_{2}} &={{left( 3,3,2 right)}^{T}}, \ {{b}_{3}} &={{left( 2,2,1 right)}^{T}} \ end{align}]

арифметического линейного пространства $mathbb{Z}_{5}^{3}$.

Решение

Эта задача проще предыдущей, поскольку поле вычетов ${{mathbb{Z}}_{5}}$ является конечным и состоит всего из пяти элементов — представителей смежных классов:

[{{mathbb{Z}}_{5}}=left{ 0,1,2,3,4 right}]

Как и в предыдущей задаче, рассмотрим систему векторов $a=left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ и составим из них матрицу ${{T}_{eto a}}$:

[{{T}_{eto a}}=left[ begin{matrix} 1 & 2 & 3 \ 1 & 1 & 2 \ 1 & 1 & 1 \ end{matrix} right]]

Определитель $det {{T}_{eto a}}=1ne 0$, поэтому $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ — базис.

Аналогично, рассмотрим систему $b=left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ и составим матрицу ${{T}_{eto b}}$:

[{{T}_{eto b}}=left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]]

Определитель $det {{T}_{eto b}}=4ne 0$, поэтому $left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ — базис.

Выразим искомую матрицу ${{T}_{ato b}}$ через «транзитный» базис $e$:

[begin{align}{{T}_{ato b}} &={{T}_{ato e}}cdot {{T}_{eto b}}= \ &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}} end{align}]

Найдём $T_{eto a}^{-1}$ через присоединённую матрицу:

[left[ begin{array}{ccc|ccc} 1 & 2 & 3 & 1 & 0 & 0 \ 1 & 1 & 2 & 0 & 1 & 0 \ 1 & 1 & 1 & 0 & 0 & 1 \ end{array} right]]

После цепочки элементарных преобразований над строками (попробуйте выполнить их самостоятельно!) получим

[left[ begin{array}{ccc|ccc} 1 & 0 & 0 & 4 & 1 & 1 \ 0 & 1 & 0 & 1 & 3 & 1 \ 0 & 0 & 1 & 0 & 1 & 4 \ end{array} right]]

Итак, мы нашли матрицу $T_{eto a}^{-1}$:

[T_{eto a}^{-1}=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]]

Осталось вычислить искомую матрицу перехода ${{T}_{ato b}}$:

[{{T}_{ato b}}={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]cdot left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]=left[ begin{matrix} 2 & 2 & 1 \ 0 & 4 & 4 \ 1 & 1 & 1 \ end{matrix} right]]

[begin{align}{{T}_{ato b}} &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}= \ &=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]cdot left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]= \ &=left[ begin{matrix} 2 & 2 & 1 \ 0 & 4 & 4 \ 1 & 1 & 1 \ end{matrix} right] end{align}]

По аналогии с предыдущей задачей, матрицу ${{T}_{ato b}}$ можно найти и через элементарные преобразования присоединённой матрицы $left[ A|B right]$. Результат будет точно такой же, но мы сэкономим пару строк вычислений и несколько минут времени.

Задача 3. Пространство многочленов

Убедитесь, что системы многочленов

[begin{align}e &=left{ 1,t-1,{{left( t-1 right)}^{2}} right} \ f &=left( 1,t+1,{{left( t+1 right)}^{2}} right) \ end{align}]

являются базисами в пространстве ${{P}_{3}}$ многочленов степени не выше 2. Найдите матрицу перехода ${{T}_{eto f}}$. Разложите по степеням $left( t-1 right)$ многочлен ${{left( t+1 right)}^{2}}+left( t+1 right)+1$.

Решение

Стандартным базисом в пространстве многочленов является система многочленов $p=left{ {{p}_{1}},{{p}_{2}},{{p}_{3}} right}$, где

[{{p}_{1}}=1quad {{p}_{2}}=tquad {{p}_{3}}={{t}^{2}}]

Выразим через базис $p$ многочлены из системы $e$:

[begin{align} & {{e}_{1}}=1={{p}_{1}} \ & {{e}_{2}}=t-1={{p}_{2}}-{{p}_{1}} \ & {{e}_{3}}={{left( t-1 right)}^{2}}={{t}^{2}}-2t+1={{p}_{3}}-2{{p}_{2}}+{{p}_{1}} end{align}]

[begin{align}{{e}_{1}} &=1={{p}_{1}} \ {{e}_{2}} &=t-1={{p}_{2}}-{{p}_{1}} \ {{e}_{3}} &={{left( t-1 right)}^{2}}= \ &={{t}^{2}}-2t+1= \ &={{p}_{3}}-2{{p}_{2}}+{{p}_{1}} end{align}]

Следовательно, матрица перехода ${{T}_{pto e}}$ выглядит так:

[{{T}_{pto e}}=left[ begin{array}{crr} 1 & -1 & 1 \ 0 & 1 & -2 \ 0 & 0 & 1 \ end{array} right]]

Аналогично, выразим через базис $p$ многочлены из системы $f$:

[begin{align} & {{f}_{1}}=1={{p}_{1}} \ & {{f}_{2}}=t+1={{p}_{2}}+{{p}_{1}} \ & {{f}_{3}}={{left( t+1 right)}^{2}}={{t}^{2}}+2t+1={{p}_{3}}+2{{p}_{2}}+{{p}_{1}} end{align}]

[begin{align}{{f}_{1}} &=1={{p}_{1}} \ {{f}_{2}} &=t+1={{p}_{2}}+{{p}_{1}} \ {{f}_{3}} &={{left( t+1 right)}^{2}}= \ &={{t}^{2}}+2t+1= \ &={{p}_{3}}+2{{p}_{2}}+{{p}_{1}} end{align}]

Получим матрицу перехода ${{T}_{pto f}}$:

[{{T}_{pto f}}=left[ begin{matrix} 1 & 1 & 1 \ 0 & 1 & 2 \ 0 & 0 & 1 \ end{matrix} right]]

Обе матрицы оказались верхнетреугольными, их определители отличны от нуля:

[begin{align} det {{T}_{pto e}} &=1cdot 1cdot 1=1 \ det {{T}_{pto f}} &=1cdot 1cdot 1=1 \ end{align}]

Следовательно системы многочленов $e$ и $f$ действительно являются базисами пространства ${{P}_{3}}$.

Теперь найдём матрицу перехода ${{T}_{eto f}}$. Для этого нам даже не потребуется искать обратную матрицу. Достаточно заметить, что векторы ${{f}_{1}}$ и ${{f}_{2}}$ легко раскладываются по базису $e$:

[begin{align}{{f}_{1}} &=1={{e}_{1}} \ {{f}_{2}} &=t+1=left( t-1 right)+2={{e}_{2}}+2{{e}_{1}} \ end{align}]

С вектором ${{f}_{3}}$ вычислений будет чуть больше:

[begin{align}{{f}_{3}} &={{left( t+1 right)}^{2}}= \ &={{left( t-1 right)}^{2}}+4t= \ &={{left( t-1 right)}^{2}}+4left( t-1 right)+4= \ &={{e}_{3}}+4{{e}_{2}}+4{{e}_{1}} end{align}]

Итого матрица перехода ${{T}_{eto f}}$ примет вид

[{{T}_{eto f}}=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]]

Теперь разложим многочлен ${{left( t+1 right)}^{2}}+left( t+1 right)+1$ по базису $e$. Сначала перепишем этот многочлен так:

[begin{align}hleft( t right) &=1+left( t+1 right)+{{left( t+1 right)}^{2}}= \ &={{f}_{1}}+{{f}_{2}}+{{f}_{3}} end{align}]

Следовательно, в базисе $f$ многочлен $hleft( t right)$ имеет координаты ${{left( 1,1,1 right)}^{T}}$. Но тогда по теореме о замене координат этот же многочлен в базисе $e$ имеет координаты

[{{left[ h right]}_{e}}={{T}_{eto f}}cdot {{left[ h right]}_{f}}=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]cdot left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{matrix} 7 \ 5 \ 1 \ end{matrix} right]]

[begin{align}{{left[ h right]}_{e}} &={{T}_{eto f}}cdot {{left[ h right]}_{f}}= \ &=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]cdot left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{matrix} 7 \ 5 \ 1 \ end{matrix} right] end{align}]

Другими словами, многочлен $hleft( t right)$ имеет вид

[hleft( t right)={{left( t-1 right)}^{2}}+5left( t-1 right)+7]

Это и есть искомое разложение многочлена ${{left( t+1 right)}^{2}}+left( t+1 right)+1$ по степеням $left( t-1 right)$.

Альтернативное решение

Искомое разложение можно получить и без привлечения матриц перехода. Достаточно применить схему Горнера или выделить нужные степени напрямую:

[begin{align}hleft( t right) &={{left( t+1 right)}^{2}}+left( t+1 right)+1= \ &={{left( t-1 right)}^{2}}+4t+t+1+1= \ &={{left( t-1 right)}^{2}}+5left( t-1 right)+5+2= \ &={{left( t-1 right)}^{2}}+5left( t-1 right)+7 end{align}]

Как видим, результат получился тем же самым, а времени потрачено меньше. Однако уже в пространстве ${{P}_{4}}$ многочленов степени не выше 4 сложность решения через матрицы и через выделение степеней будет сопоставимой. А дальше матрицы начнут выигрывать.

Смысл линейной алгебры — дать универсальные алгоритмы, которые работают с объектами любой природы, если эти объекты подчиняются аксиомам линейного пространства.

Задача 4. Матрица перехода при симметрии

Базис $b$получается из базиса

[{{a}_{1}}={{left( 2,1,3 right)}^{T}},quad {{a}_{2}}={{left( 1,1,-1 right)}^{T}},quad {{a}_{3}}={{left( 2,-1,-1 right)}^{T}}]

[begin{align}{{a}_{1}} &={{left( 2,1,3 right)}^{T}}, \ {{a}_{2}} &={{left( 1,1,-1 right)}^{T}}, \ {{a}_{3}} &={{left( 2,-1,-1 right)}^{T}} \ end{align}]

пространства ${{V}_{3}}$ симметрией относительно плоскости $2x+y+3z=0$. Найти матрицу перехода ${{T}_{ato b}}$.

Решение

Из курса аналитической геометрии мы знаем, что если плоскость задана уравнением

[ax+by+cz+d=0]

то вектор-нормаль $n$ имеет координаты

[n=left( a,b,c right)]

Тогда для плоскости $2x+y+3z=0$ нормаль имеет координаты $n=left( 2,1,3 right)$, что в точности совпадает с вектором ${{a}_{1}}$. Следовательно, при симметрии относительно плоскости этот вектор просто перейдёт в противоположный: ${{b}_{1}}=-{{a}_{1}}$.

Далее заметим, что векторы ${{a}_{2}}$ и ${{a}_{3}}$ лежат в плоскости симметрии, поскольку при подстановке их координат уравнение плоскости обращается в верное числовое равенство:

[begin{align}{{a}_{2}}={{left( 1,1,-1 right)}^{T}} &Rightarrow 2cdot 1+1+3cdot left( -1 right)=0 \ {{a}_{3}}={{left( 2,-1,-1 right)}^{T}} &Rightarrow 2cdot 2-1+3cdot left( -1 right)=0 \ end{align}]

[begin{align}{{a}_{2}}=&{{left( 1,1,-1 right)}^{T}}Rightarrow \ & Rightarrow 2cdot 1+1+3cdot left( -1 right)=0 \ {{a}_{3}}=&{{left( 2,-1,-1 right)}^{T}}Rightarrow \ & Rightarrow 2cdot 2-1+3cdot left( -1 right)=0 \ end{align}]

Следовательно, при симметрии эти векторы переходят сами в себя: ${{b}_{2}}={{a}_{2}}$, ${{b}_{3}}={{a}_{3}}$. Матрица перехода имеет вид

[{{T}_{ato b}}=left[ begin{array}{rcc} -1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \ end{array} right]]

Важное замечание. симметрия предполагает использование проекций и углов, что в конечном счёте сводится к скалярному произведению. Однако мы пока не знаем, что такое скалярное произведение в линейном пространстве.

Полноценное определение скалярного произведения будет намного позже — см. урок «Евклидово пространство». А пока будем считать, что скалярное произведение векторов $a$ и $b$ определено стандартным образом:

[left( a,b right)=left| a right|cdot left| b right|cdot cos alpha ]

Геометрическая интерпретация

Симметрию на плоскости и в пространстве удобно представлять графически. Пусть $alpha $ — плоскость, относительно которой выполняется симметрия. Тогда векторы $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ будут выглядеть так:

Из приведённого рисунка сразу видно, что при симметрии вектор ${{a}_{1}}$ перейдёт в противоположный, а векторы ${{a}_{2}}$ и ${{a}_{3}}$ останутся на месте.

Задача 5. Матрица поворота

Базис $e=left{ i,j,k right}$ пространства ${{V}_{3}}$ поворачивается на 180° вокруг прямой $l$, заданной системой

[left{ begin{align}x-y &=0 \ z &=0 \ end{align} right.]

Затем полученный базис $f$ поворачивается на 90° в отрицательном направлении вокруг нового положения вектора $j$. В результате получается базис $g=left{ {{i}_{2}},{{j}_{2}},{{k}_{2}} right}$.

Найдите матрицу перехода ${{T}_{eto g}}$. Найдите в базисе $e$ координаты вектора $h$, который в новом базисе $g$ имеет координаты $left( 1,1,1 right)$.

Решение

Вращение базиса и матрица поворота — это очень важная тема, по которой есть отдельный урок — «Матрица поворота». Но сейчас вращение совсем простое, поэтому обойдёмся без специальных матриц.

Вновь обратимся к геометрической интерпретации. Рассмотрим исходный базис $e=left{ i,j,k right}$ трёхмерного пространства:

Также на этом рисунке изображена прямая $l$, которая задаётся требованиями $z=0$ и $x=y$. Эта лежит в плоскости $Oxy$ и является биссектрисой первой координатной четверти.

Очевидно, что при повороте пространства на 180° относительно прямой $l$ базисные векторы $i$ и $j$ просто поменяются местами, а вектор $k$ перейдёт в противоположный:

Другими словами, ${{i}_{1}}=j$, ${{j}_{1}}=i$, ${{k}_{1}}=-k$, поэтому матрица перехода от базиса $e=left{ i,j,k right}$ к базису $f=left{ {{i}_{1}},{{j}_{1}},{{k}_{1}} right}$ примет вид

[{{T}_{eto f}}=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]]

Далее поворот осуществляется вокруг нового положения вектора $j$, т.е. вокруг вектора ${{j}_{1}}$. Вновь обратимся к чертежу. В этот раз нам уже не нужны координатные оси — нас интересуют лишь векторы ${{i}_{1}}$, ${{j}_{1}}$ и ${{k}_{1}}$, а также ось вращения:

Обратите внимание: в задаче сказано, что базис вращается на 90° в отрицательном направлении. Если мы смотрим на плоскость, образованную векторами ${{i}_{1}}$ и ${{k}_{1}}$, с вершины вектора ${{j}_{1}}$ (как на картинке), то отрицательное направление — это по часовой стрелке (отмечено зелёным), а положительное —против часовой стрелки (отмечено красным).

Все эти тонкости (положительное и отрицательное направление, правые и левые тройки векторов) детально описаны в уроке про матрицы поворота. Сейчас не будем подробно разбираться в них, а просто нарисуем результат:

Итак, ${{i}_{2}}={{k}_{1}}$, ${{j}_{2}}={{j}_{1}}$ и ${{k}_{2}}=-{{i}_{1}}$, поэтому матрица перехода от базиса $f=left{ {{i}_{1}},{{j}_{1}},{{k}_{1}} right}$ к базису $g=left{ {{i}_{2}},{{j}_{2}},{{k}_{2}} right}$ имеет вид

[{{T}_{fto g}}=left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]]

Теперь мы можем найти матрицу ${{T}_{eto g}}$ через транзитный базис $f$:

[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]cdot left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right]]

[begin{align}{{T}_{eto g}} &={{T}_{eto f}}cdot {{T}_{fto g}}= \ &=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]cdot left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]= \ &=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right] end{align}]

Кроме того, нам известны координаты вектора $h$ в базисе $g$:

[h={{left( 1,1,1 right)}^{T}}]

Тогда в базисе $e$ координаты этого же вектора равны

[{{left[ h right]}_{e}}={{T}_{eto g}}cdot {{left[ h right]}_{g}}=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right].left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{array}{r} 1 \ -1 \ -1 \ end{array} right]]

[begin{align}{{left[ h right]}_{e}} &={{T}_{eto g}}cdot {{left[ h right]}_{g}}= \ &=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right].left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{array}{r} 1 \ -1 \ -1 \ end{array} right] end{align}]

Итак, мы нашли матрицу перехода ${{T}_{eto g}}$ и координаты вектора $h$ в исходном базисе. Задача решена.

Смотрите также:

1. Критерий Сильвестра для квадратичных функций
2. Работа с формулами в задаче B12
3. Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
4. Показательные функции в задаче B15
5. Задача B5: площадь кольца
6. Случай четырехугольной пирамиды

Будем рассматривать двумерный случай.

Матрица преобразования – это некоторая матрица . Мы будем рассматривать матрицы вида

Допустим есть какое-то преобразование , и (к точке применили преобразование и получили точку ).

Тогда матрица преобразования , умноженная на однородные координаты , даёт однородные координаты .

В каком-то смысле, любое линейное преобразование одновременно является матрицей, так же как точка — это набор координат.

Посмотрим как меняются координаты при преобразовании.

.

То есть новые координаты как-то линейно зависят от старых.

Рассмотрим частные случаи преобразований.

Базовые преобразования

Параллельный перенос

Задаёт преобразование .

Обозначается , где — вектор параллельного переноса.

Пример
Задача: Найдите новые координаты точки после параллельного переноса плоскости на вектор .

Решение:

Вполне ожидаемый ответ.

Масштабирование вдоль осей

Задаёт преобразование .

Будем обозначать как . Числа и называются коэффициентами масштабирования.

Пример

Задача: Найдите новые координаты точки после масштабирования по оси с коэффициентом 2 (по оси масштаб остаётся таким же).

Решение:

Поворот относительно начала координат

Обозначается , где — угол поворота.
Как обычно, при повороте против часовой стрелки, и при повороте по часовой стрелке.

Пример
Задача: Найдите новые координаты точки после поворота плоскости на °.

Решение:

Замечание

, то есть центральная симметрия относительно начала координат меняет координаты точки на противоположные.

Тождественное преобразование

Это преобразование, оставляющее все точки неподвижными.

Его матрица:

Композиция преобразований

Задача: к точке применили осевую симметрию относительно , и затем применили параллельный перенос на . Какие новые координаты у точки?

Решение: обозначим нашу точку за , новую точку за

Посчитаем двумя способами.

1)

2) Воспользуемся ассоциативностью умножения матриц (сочетательный закон)

Заметим, что — тоже какая-то матрица преобразования, в данном случае “осевая симметрия относительно , с последующим параллельным переносом на ”

Действительно,

Тогда матрица для будет .

Получается, при композиции преобразований их матрицы перемножаются.

Содержание:

1. Линейные преобразования. Собственные векторы и собственные числа линейного оператора
2. Собственные векторы и собственные числа линейного оператора: определение, свойства
3. Нахождение собственных чисел и собственных векторов
4. Базис пространства из собственных векторов линейного оператора
5. Линейная модель обмена (модель международной торговли)

Линейные преобразования. Собственные векторы и собственные числа линейного оператора

Линейные преобразования (линейные операторы). Матрица линейного преобразования

Пусть задано -мерный пространство . Если каждому вектору поставлено в соответствие единственный вектор

этого же пространства, говорится, что в векторном пространстве  задано преобразование , или оператор .

Вектор – результат линейного преобразования – называют образом вектора , а выходной вектор  – прообразом вектора .

Преобразование называется линейным преобразованием, или линейным оператором, если для произвольных векторов и произвольного действительного скаляра выполняются условия:

То есть линейный оператор преобразует пространство  в то самое пространство. Это записывается следующим образом:

Примерами простейших линейных преобразований являются:
тождественное преобразование: , когда каждый -мерный вектор пространства превращается в самого себя, то есть остается без изменения;

нулевой оператор , когда каждый -мерный вектор пространства превращается в ноль-вектор этого же пространства, то есть

Линейное преобразование , с помощью которого осуществляется восстановление вектора  по его образу , называется обратным к линейным преобразованием. В отличие от матрицы оператор записывают каллиграфическим шрифтом.

Рассмотрим задачу об отыскании координат образа вектора .

Пусть в пространстве  выбрано базис (не обязательно ортонормированный) и есть координатами вектора в этом базисе. Обозначим через координаты вектора в выбранном базисе. по условию , тогда согласно линейностью оператора  получим :

Но образы тоже являются векторами с , поэтому иx можно разложить по тому же базисом. Пусть

где  коэффициенты разложения вектора  по базису  

С учетом (5.5) соотношение (5.4) принимает вид:

Группируя члены правой части относительно векторов базиса, имеем:

С другой стороны, если  являются координатами вектора  в базисе  то его можно представить следующим образом:

Сопоставляем (5.8) из (5.7) и получаем координаты вектора :

Следовательно, при линейном преобразовании:

координаты образа вектора являются линейными комбинациями координат прообраза, коэффициенты при которых составляют матрицу -го порядка (обозначим ее через ):

Матрица , которая в произведении (слева) с вектором с  определяет координаты его образа при линейном преобразовании , Называется матрицей линейного преобразования  в базисе  и пишут:

Каждый – -й – столбец матрицы составляют коэффициенты разложения вектора  по базису каждая – -я – строка определяет коэффициенты разложения координат вектора по координатам вектора .

Обратите внимание, что – нераздельный символ (обозначение вектораобраза), а – произведение матрицы с вектором (прообразом).

Каждому линейном оператору -мерного пространства отвечает матрица -го порядка в данном базисе. И наоборот, каждой матрицы -го порядка отвечает линейный оператор -мерного пространства с определенным базисом.

Например, с помощью оператора линейных преобразований можно описать поворот произвольного вектора с пространства вокруг начала координат на угол  против часовой стрелки. Формулы поворота осей координат (формулы перехода от исходных координат и к новым  и , и наоборот ) определяют алгебраическую форму изображения линейного оператора поворота осей:

где  оператор перехода от исходных (новых) координат к новым (исходных);

 векторы, началом которых является точка , а концами –
точки и , соответственно.

По соотношению (5.12) матрица линейного преобразования} , Описывающий поворот произвольного вектора из пространства вокруг начала координат на угол против часовой стрелки, имеет вид:

а матрица обратного линейного преобразования , то есть такого, что описывает поворот произвольного вектора из пространства вокруг начала координат на угол  по часовой стрелке, имеет вид:

Теорема 5.1 (о связи между матрицами оператора в различных базисах).

Матрицы и  линейного оператора в разных базисах и связаны между собой соотношением:

где  матрица перехода от исходного к новому базису.

Доказательство. Пусть линейный оператор превращает вектор пространства  в вектор того самого пространства. Тогда в матричной форме связь между вектором и его образом в исходном базисе можно записать как , а в новом – как . Поскольку является матрицей перехода от исходного базиса к новому, то в соответствии с (4.18) имеем:

Умножим равенство (5.14) слева на матрицу и получим . Отсюда по определению линейного оператора имеем: . С учетом (5.15):

Сравнив соотношение  и , получаем 

Две квадратные матрицы и называются подобными, если существует такая невырожденная матрица , матрицы и связанные соотношениями:

Соответствующие линейные операторы называются преобразованиями сходства.

Подобные матрицы описывают то же линейное преобразование, но в разных базисах, а матрица является матрицей перехода от одного базиса к другому.

Подобные матрицы имеют те же ранги, суммы элементов главной диагонали и определители.

В базисе и задана матрица линейного оператора :

Определим матрицу , которая отвечает том же оператору в базисе векторов  и  есть матрица  подобна матрице .

Предоставим расписание векторов нового базиса по векторам исходного базиса: . Соответственно, матрица перехода от исходного к новому базису имеет вид:

Ее определитель , то есть матрица невырожденная и имеет обратную: 

По теореме 5.1 определяем матрицу оператора в новом базисе:

Обратите внимание, что в новом базисе матрица оператора оказалась диагональной.

Собственные векторы и собственные числа линейного оператора: определение, свойства

Рассмотрим -мерных линейный пространство  с определенным базисом и матрицу , некоторого линейного оператора пространства.

Ненулевой вектор называют собственным, или характеристическим вектором линейного оператора (или матрицы ), если существует такое действительное число , имеет место равенство:

Скаляр называется собственным, или характеристическим, числом матрицы , или ее собственным значением, соответствует собственному вектору :

Согласно определениями собственного числа и собственного вектора имеем:

1) Если , то каждый ненулевой вектор из  является собственным вектором матрицы , при этом , ведь по свойству единичной матрицы имеем ;
2) любой ненулевой -мерный вектор является собственным вектором нулевой матрицы , при этом , так как .

Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы 

Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы

Запишем матричное уравнение (5.17) в развернутом виде:

Таким образом, задача сводится к решению однородной системы линейных уравнений с  неизвестными. Нас интересуют (по определению собственного вектора) только ненулевые векторы, то есть нетривиальные решения системы, поэтому определитель системы (5.18) должен быть равен нулю:

Раскрытие определителя в соотношении (5.19) дает многочлен степени относительно , который называется характеристическим многочленом матрицы , а соотношение (5.19), которое можно представить в виде , определяет уравнение для нахождения собственных чисел, которое называют характеристическим уравнением матрицы .

По основной теореме алгебры уравнения любой матрицы  имеет корней, если каждый из них считать столько раз, какова его кратность. Характеристическое уравнение матрицы может иметь только действительные, но и комплексные корни, то есть числа вида где действительные числа, мнимая единица.

Множество всех собственных чисел матрицы называют спектром матрицы. Если в спектре матрицы то же собственное число повторяется раз, то говорят, что кратность этого собственного числа равна .

Теорема 5.2 (о единственности собственного чucлa, что соответствует собственному вектору). Если – собственный вектор матрицы , то существует единственный скаляр , который удовлетворяет условие .

Доказательство. Предположим, что кроме собственного числа существует еще один
скаляр , такой, что . Тогда должно выполняться равенство . Поскольку по определению собственный вектор является ненулевым, то есть , получим .

Согласно теореме 5.2 говорят, что собственный вектор  из матрицы принадлежит собственному числу . 

Теорема 5.3 (о множестве собственных векторов, принадлежащих собственному числу). Если матрица имеет собственный вектор, принадлежащий собственному числу , то таких векторов бесконечно много.

Доказательство базируется на определении собственного вектора и свойствах ассоциативности и коммутативности операции умножения матрицы на скаляр.

Действительно, пусть собственный вектор матрицы , тогда . Привлечем к рассмотрению вектор , коллинеарный вектору , то есть ,  где , и покажем, что в также является собственным вектором матрицы :

Поскольку равенство (5.19) выполняется для произвольного , то существует множество собственных векторов, принадлежащих данному собственному числу.

Теорема 5.4 (критерий существования собственного вектора , соответствующего собственному числу ). Вектор тогда и только тогда является собственным вектором матрицы , соответствующим собственному числу , когда его координаты образуют ненулевое решение однородной квадратной системы линейных алгебраических уравнений

 или 

Доказательство сводится к тождественных преобразований матричных уравнений.

Необходимость уже доказано переходом от соотношения , к однородной системе линейных уравнений , представленной в развернутом виде (5 18).

Достаточность. На основании свойств действий над матрицами с учетом условия , осуществит переход от однородной системы уравнений в матричной форме с соотношением :

Теорема 5.5 (пpo линейную независимость собственных векторов). Собственные векторы, принадлежащие различным собственным числам, является линейно независимыми.

Доказательство проведем методом от противного. Пусть два произвольные собственные векторы, принадлежащие соответственно собственным числам и . Необходимо показать, что линейная комбинация этих собственных векторов ноль-вектор только тогда, когда , то есть

Предположим обратное. Пусть (5.23) выполняется при условии, что одно из чисел не является нулем, например,

Умножим левую и правую части (5.23) на собственное число . Тогда

Левую и правую части равенства (5.23) умножим на матрицу слева, и, учитывая свойства операций над матрицами, получим:

Сравним (5.25) и (5.24). Получаем:

По условию теоремы . По определению вектор  является ненулевым, поэтому равенство (5.26) возможно только при , то есть предположение о линейной зависимости векторов и  ошибочно.

Если есть более двух собственных векторов, принадлежащих попарно различным собственным числам, доведение аналогичное (с использованием метода математической индукции).

Заметим, что собственные векторы, принадлежащих различным собственным числам, можно использовать как базисные векторы пространства .

Теорема 5.6 (пpo сумму и произведение собственных чисел). Если собственные числа матрицы , то:
1) сумма собственных чисел равна сумме элементов главной диагонали матрицы :

2) произведение собственных чисел равна определителю матрицы :

Доказательство основывается на формулах Виета, которые описывают соотношение между корнями и коэффициентами многочлена -гo степени в случае, когда его старший коэффициент равен единице.

Рассмотрим простейший случай . Запишем характеристическое уравнение в развернутом виде:

С (5.29) по теореме Виета (для квадратного уравнения) имеем:

Сумму всех диагональных элементов матрицы называют следом (от нем. spur – след) этой матрицы и обозначают .

Для квадратной матрицы произвольного порядка теорему 5.6 в символьном виде можно записать так:

при этом собственное число берем столько раз, какова его кратность как корня характеристического уравнения (5.29).

Нахождение собственных чисел и собственных векторов

Рассмотрим алгоритм нахождения собственных чисел матрицы и собственных векторов, которые им принадлежат.
Согласно соотношениями (5.18) и (5.19) имеем такой порядок отыскания собственных чисел и собственных векторов матрицы.
1. Составляем по исходной матрицей характеристическое уравнение (5.18) и решаем его, то есть находим спектр собственных чисел.
2. Подставляем поочередно каждое собственное число в систему (5.18) и находим все ее нетривиальные решения, что и дает множество собственных векторов, принадлежащих соответствующему собственному числу.

Замечания. Множество всех собственных векторов, принадлежащих определенному собственному числу, можно представить как линейную комбинацию фундаментальных решений однородной системы уравнений согласно (4.19), гл. 4.

Найдем собственные числа и собственные векторы матрицы

Характерным уравнением этой матрицы является квадратное уравнение:

Решив его, получим собственные числа  и 

Теперь описываем множества и всех собственных векторов, принадлежащих найденным собственным числам.

Для этого в матрицу вместо подставим поочередно значения собственных чисел, запишем соответствующую систему однородных линейных уравнений (5.18) и решим ее:

Предоставляя параметру произвольных значений, для данного собственного числа получим совокупность коллинеарных между собой собственных векторов.

Теорема 5.7 (про собственные числа и собственные векторы симметричной матрицы).

Симметричная матрица имеет только действительные собственные числа. Собственные векторы, принадлежащие разным собственным числам, ортогональны и линейно независимы.

Теорема приводим без доказательства.
Проиллюстрируем прав выводов данной теоремы на примере.

Пусть имеем симметричную матрицу

Найдем собственные числа и собственные векторы этой матрицы и докажем ортогональность собственных векторов, соответствующих различным собственным числам.

1. Составим характеристическое уравнение матрицы

2. Найдем корни полученного кубического уравнения относительно . С элементарной алгебры известно, если многочлен со старшим коэффициентом, равным единице, имеет целые корни, то их следует искать среди делителей свободного члена. Перебирая делители числа 36, убеждаемся, что является корнем уравнения (5.30).

Нахождение других двух корней сводится к решению квадратного уравнения:

3. Опишем множества и собственных векторов, принадлежащих найденным собственным числам.

Для этого в матрицу  вместо подставляем поочередно значения собственных чисел, записываем соответствующую систему однородных линейных уравнений (5.17) и решаем ее методом Жордана-Гаусса:

Аналогично находим собственные векторы  и 

Система векторов  и  является линейно независимой, поскольку 

Убеждаемся, что векторы  и  – попарно ортогональны.
Для этого определим их скалярные произведения:

Поскольку скалярные произведения векторов равны нулю, то векторы попарно ортогональны.
Если в выражениях (5.31-5.33) положить , то получим систему векторов:

которая использовалась как базис пространства в примере после теоремы   и . В таком базисе, то есть базисе из собственных векторов, матрица оператора оказалась диагональной, ее ненулевыми элементами являются собственные числа матрицы .

Теорема 5.8 (о преобразовании матрицы к диагональному виду). Матрица линейного оператора в базисе имеет диагональный вид тогда и только тогда, когда все векторы базиса являются собственными векторами матрицы .
Теорему наводим  без доказательств

Заметим, что при нахождении собственных чисел для заданной матрицы самой задачей является решение алгебраического уравнения -й степени, что во многих случаях сделать невозможно без использования приближенных методов. Изучение приближенных методов выходит за пределы программы. Поэтому предлагаем воспользоваться известными программами MatLab, MathCad, Maple и др.

Следующий пример был решен в пакете MatLab, в котором конечный результат вычислений предоставляется без промежуточных выкладок.
Найдем собственные числа и соответствующие им собственные векторы матрицы

Характерным уравнением для нахождения собственных чисел является уравнение

корнями которого будут числа  а соответствующие им собственные векторы имеют вид: 

Собственные числа и собственные векторы матриц имеют широкий спектр использования, в частности, в аналитической геометрии (Раздел 2), в задачах различных отраслей естественных наук и эконометрики.

Базис пространства из собственных векторов линейного оператора

По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Возникает вопрос, при каких условиях существует базис линейного пространства , построенный из собственных векторов матрицы.
Лема. Если является собственным числом матрицы , то множество собственных векторов матрицы содержит линейно независимых векторов, где – ранг матрицы .

Доказательство. Согласно теореме 5.4 множество собственных векторов совпадает с множеством всех решений однородной системы линейных уравнений: 

где – собственный вектор матрицы , что соответствует собственному числу . По теореме 4.4 такая система имеет фундаментальную систему решений, количество векторов которой равна , то есть содержит – линейно независимых векторов.

Теорема 5.9 (о существовании базиса из собственных векторов матрицы). Пусть числа образуют множество всех различных собственных чисел матрицы . Если сумма рангов матриц равна , то в пространстве существует базис из собственных векторов матрицы .

Доказательство. Согласно лемме каждое множество собственных векторов, соответствующих уравнению , содержит независимые векторы в количестве . По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Тогда для матрицы общее количество линейно независимых собственных векторов составляет:

Поскольку собственные векторы матрицы  в совокупности составляют систему линейно независимых векторов, то они образуют базис пространства .

Теорема 5.10 (о существовании базиса из собственных векторов симметричной матрицы). Если матрица линейного оператора симметрична, то в пространстве существует базис, образованный из собственных векторов матрицы .

Теорему принимаем без доказательств.
Построим ортонормированный базис пространства , состоящий из собственных векторов матрицы

линейного преобразования , и найдем матрицу заданного преобразования в этом базисе.

Согласно теореме 5.9 такой базис существует, поскольку матрица является симметричной матрицей. Составим характеристическое уравнение матрицы :

и решим его: (собственное значение кратности ) и

Для каждого из двух различных собственных чисел матрицы определим фундаментальную систему решений однородной системы уравнений: . При в результате элементарных преобразований основной матрицы системы получаем:

По последним шагом элементарных преобразований матрицы записываем общее решение системы:

Определяем фундаментальную систему решений однородной системы уравнений 

Собственные векторы и являются ортогональными, поскольку их скалярное произведение равно нулю: 

При в результате элементарных преобразований основной матрицы системы получаем:

По последнем шагом элементарных преобразований матрицы записываем общее решение системы:

Возлагаем и получаем фундаментальный решение однородной системы уравнений 

Поскольку и , то все три вектора попарно ортогональны. Объединив полученные фундаментальные системы решений, иметь систему собственных векторов матрицы  . Они образуют ортогональный базис пространства . После нормирования векторы приобретают вид:

Это и есть ортогональный базис пространства , состоящий из собственных векторов матрицы .

По соотношению (5.13) определим матрицу , что соответствует оператору в базисе из собственных векторов. Согласно теореме 5.8 эта матрица будет иметь диагональный вид, а элементами ее главной диагонали будут собственные числа этой матрицы. Заключим с собственными векторами , и матрицу перехода к новому базису и найдем обратную к ней матрицу :

По матричным уравнением (5.13) находим матрицу , что соответствует оператору в базисе из собственных векторов:

Следовательно, мы получили диагональную матрицу третьего порядка, элементами главной диагонали которой есть собственные числа матрицы .

Далее приведен пример применения собственных векторов и собственных чисел в одной из многих задач экономики.

Линейная модель обмена (модель международной торговли)

Практически все страны кроме внутреннего товарообмена осуществляют внешний товарообмен, то есть занимаются внешней торговлей. Торговля считается сбалансированной, или бездефицитной, если для каждой страны прибыль от торговли не меньше объем средств, которые она вкладывает в товарооборот (внутренний и внешний).

Постановка задачи. Несколько стран осуществляют взаимный товарообмен. Известную долю бюджетных средств, тратит каждая страна на закупку товаров у другой страны, учитывая и внутренний товарооборот. Определить, каким должно быть соотношение бюджетов партнеров для того, чтобы обеспечить бездефицитность торговли.  

Построение математической модели. Введем обозначения количественных характеристик, описывающих торговлю между странами, и определим связь между этими характеристиками. Пусть – страны, участвующие в международной торговле. Доли средств, которые тратит страна на закупку товаров в стране , учитывая и внутренний товарооборот , обозначим через . Понятно, что

Матрицу , элементами которой являются числа , называют структурной матрицей торговли:

Эта матрица описывает взаимодействие стран в процессе международной торговли. Соотношение (5.34) означает, что сумма элементов каждого столбца матрицы равна
1. Если объем средств, которые тратит каждая страна на торговлю, обозначить через , соответственно, то прибыль страны от внутренней и внешней торговли составит

Чтобы торговля каждой страны была сбалансированной, по определению должно выполняться условие , и , то есть прибыль от торговли не должна быть меньше расходов. Однако соблюдение этого требования в виде неравенства невозможно для всех стран в совокупности. Действительно, добавим левые и правые части указанных неровностей, изменяя от единицы до :

Группируя в левой части слагаемые, содержащие каждое из , получим:

Учитывая соотношение (5.20), получим:

Отсюда следует, что сбалансированная торговля возможна только в случае знака равенства. Это, полагаем, понятно не только на основании аналитических выкладок, но и с экономической точки зрения (и даже просто с точки зрения здравого смысла): все страны в совокупности не могут получить прибыль. Более того, для одной из стран не может выполняться знак строгого неравенства .

Итак, условием сбалансированной торговли является равенства , и , из которых получим:

Введем в рассмотрение вектор (бюджетных) средств и подадим систему (5.39) в матричной форме:

С (5.40) следует, что при условии сбалансированности торговли между странами вектор средств должен быть собственным вектором структурной матрицы торговли , который принадлежит собственному числу . Таким образом, решение задачи сводится к нахождению этого собственного вектора , компоненты которого устанавливают соотношение между бюджетами стран, участвующих в товарообмене.

Рассмотрим товарообмен между тремя странами. Пусть структурная матрица торговли стран , имеет вид:

Найдем вектор средств, компонентами которого являются доли от общего объема торговли, должна вкладывать каждая из стран во внешней товарооборот для того, чтобы торговля была сбалансированной.

Искомый вектор средств является собственным вектором структурной матрицы, принадлежащий собственному значению . Его компоненты образуют ненулевое решение однородной СЛАУ:

Поскольку система является однородной, то расширенная матрица эквивалентна основной матрицы системы. Осуществим элементарные преобразования основной матрицы этой системы уравнений:

Находим общее решение системы, в котором – базисные переменные, – свободная переменная: 

Отсюда следует, что для сбалансированности торговли необходимо, чтобы средства, которые вкладывает в внешний товарооборот каждая страна, соотносились как

Матрицы линейных преобразований

Пусть
в n-
мерном линейном пространстве с базисом
,,…,
задано линейное преобразование А. Тогда
векторы А,А,…,А–
также векторы этого пространства и их
можно представить в виде линейной
комбинации векторов базиса:

A=
a₁₁+
a₂₁+…+
a_n1

A=
a₁₂+
a₂₂+…+
a_n2

……………………………….

A=
a_n1+
a_n2+…+
a_nn

Тогда
матрица А =

называется матрицей
линейного преобразования А.

Если
в пространстве L
взять вектор
=
x₁+
x₂+…+
x_n,
то A
L.

,
где

……………………………..

Эти
равенства можно назвать линейным
преобразованием в базисе
,,…,.

В
матричном виде:

,
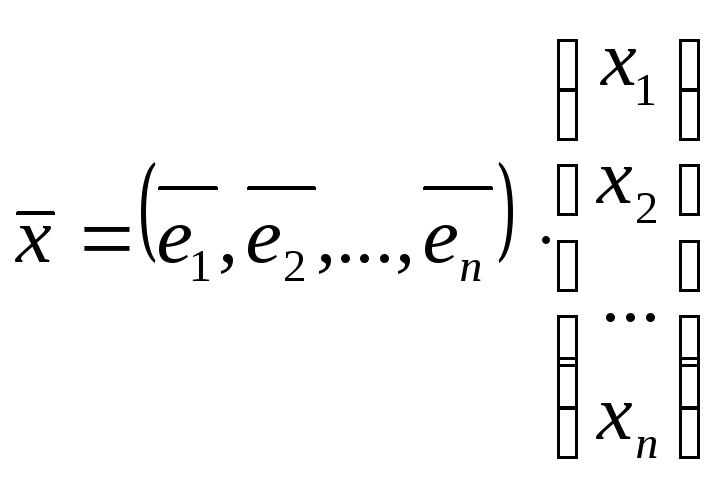
А,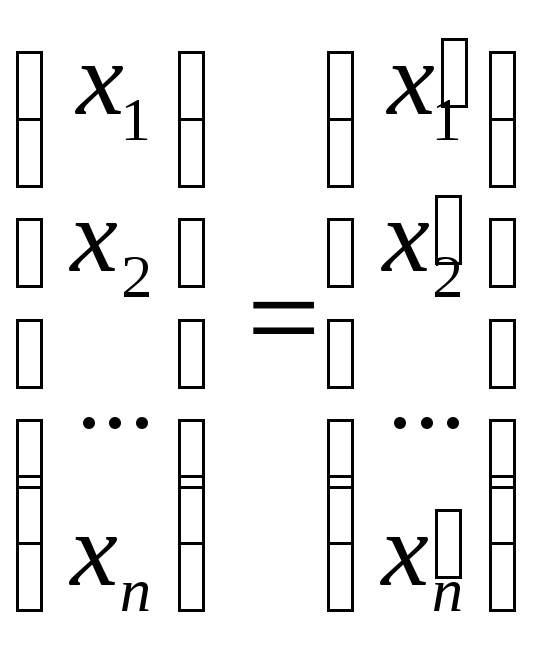

Пример.
Найти матрицу линейного преобразования,
заданного в виде:

x
= x + y

y
= y + z

z
= z + x

x
= 1x
+ 1y
+ 0z

y
= 0x
+ 1y
+ 1z

z
= 1x
+ 0y
+ 1z

A
=

На практике действия
над линейными преобразованиями сводятся
к действиям над их матрицами.

Определение:
Если вектор
переводится
в вектор

линейным преобразованием с матрицей
А, а вектор

в вектор

линейным преобразованием с матрицей
В, то последовательное применение этих
преобразований равносильно линейному
преобразованию, переводящему вектор

в вектор
(оно
называется произведением
составляющих преобразований).

С
= ВА

Пример.
Задано линейное преобразование А,
переводящее вектор
в
вектор

и линейное преобразование В, переводящее
вектор

в вектор
.
Найти матрицу линейного преобразования,
переводящего вектор

в вектор
.

С
= ВА

Т.е.

Примечание:
Если А=
0, то преобразование вырожденное, т.е.,
например, плоскость преобразуется не
в целую плоскость, а в прямую.

Собственные значения и собственные векторы линейного преобразования

Определение:
Пусть L
– заданное n-
мерное линейное пространство. Ненулевой
вектор
L
называется собственным
вектором
линейного преобразования А, если
существует такое число ,
что выполняется равенство:

A.

При
этом число 
называется собственным
значением (характеристическим числом)
линейного преобразования А, соответствующего
вектору
.

Определение:
Если линейное преобразование А в
некотором базисе
,,…,
имеет матрицу А =
,
то собственные значения линейного
преобразования А можно найти как корни
₁,
₂,
… ,_n
уравнения:

Это
уравнение называется характеристическим
уравнением,
а его левая часть- характеристическим
многочленом
линейного преобразования А.

Следует
отметить, что характеристический
многочлен линейного преобразования не
зависит от выбора базиса.

Рассмотрим
частный
случай. Пусть
А – некоторое линейное преобразование
плоскости, матрица которого равна
.
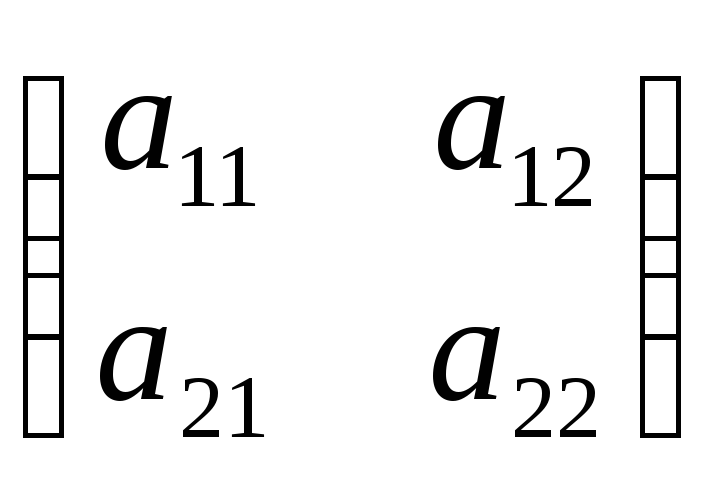
Тогда преобразование А может быть задано
формулами:

;

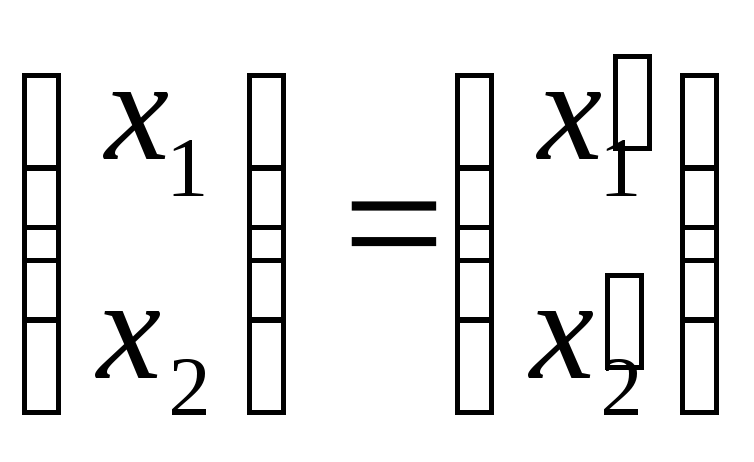
в
некотором базисе
.

Если
преобразование А имеет собственный
вектор с собственным значением ,
то А.

или

Т.к.
собственный вектор
ненулевой,
то х₁
и х₂
не равны нулю одновременно. Т.к. данная
система однородна, то для того, чтобы
она имела нетривиальное решение,
определитель системы должен быть равен
нулю. В противном случае по правилу
Крамера система имеет единственное
решение – нулевое, что невозможно.

Полученное
уравнение является характеристическим
уравнением линейного преобразования
А.

Таким
образом, можно найти собственный вектор
(х₁,
х₂)
линейного преобразования А с собственным
значением ,
где 
– корень характеристического уравнения,
а х₁
и х₂
– корни системы уравнений при подстановке
в нее значения .

Понятно,
что если характеристическое уравнение
не имеет действительных корней, то
линейное преобразование А не имеет
собственных векторов.

Следует
отметить, что если
–
собственный вектор преобразования А,
то и любой вектор ему коллинеарный –
тоже собственный с тем же самым собственным
значением .

Действительно,
.
Если учесть, что векторы имеют одно
начало, то эти векторы образуют так
называемое собственное
направление или
собственную
прямую.

Т.к.
характеристическое уравнение может
иметь два различных действительных
корня ₁
и ₂,
то в этом случае при подстановке их в
систему уравнений получим бесконечное
количество решений. (Т.к. уравнения
линейно зависимы). Это множество решений
определяет две собственные
прямые.

Если
характеристическое уравнение имеет
два равных корня ₁
= ₂
= ,
то либо имеется лишь одна собственная
прямая, либо, если при подстановке в
систему она превращается в систему
вида:
.
Эта система удовлетворяет любым значениям
х₁
и х₂.
Тогда все векторы будут собственными,
и такое преобразование называется
преобразованием
подобия.

Пример.
Найти характеристические числа и
собственные векторы линейного
преобразования с матрицей А =
.

Запишем
линейное преобразование в виде:

Составим
характеристическое уравнение:

²
– 8
+ 7 = 0;

Корни
характеристического уравнения: ₁
= 7; ₂
= 1;

Для
корня ₁
= 7:

Из
системы получается зависимость: x₁
– 2x₂
= 0. Собственные
векторы для первого корня характеристического
уравнения имеют координаты: (t;
0,5t)
где t–
параметр.

Для
корня ₂
= 1:

Из
системы получается зависимость: x₁
+ x₂
= 0. Собственные
векторы для второго корня характеристического
уравнения имеют координаты: (t;
–t)
где t–
параметр.

Полученные
собственные векторы можно записать в
виде:

Пример.
Найти характеристические числа и
собственные векторы линейного
преобразования с матрицей А =
.

Запишем
линейное преобразование в виде:

Составим
характеристическое уравнение:

²
– 4
+ 4 = 0;

Корни
характеристического уравнения: ₁
= ₂
= 2;

Получаем:

Из
системы получается зависимость: x₁
– x₂
= 0. Собственные
векторы для первого корня характеристического
уравнения имеют координаты: (t;
t)
где t–
параметр.

Собственный
вектор можно записать:
.

Рассмотрим
другой частный
случай. Если
–
собственный вектор линейного преобразования
А, заданного в трехмерном линейном
пространстве, а х₁,
х₂,
х₃
– компоненты этого вектора в некотором
базисе
,
то

,

где 
– собственное значение (характеристическое
число) преобразования А.

Если
матрица линейного преобразования А
имеет вид:

,
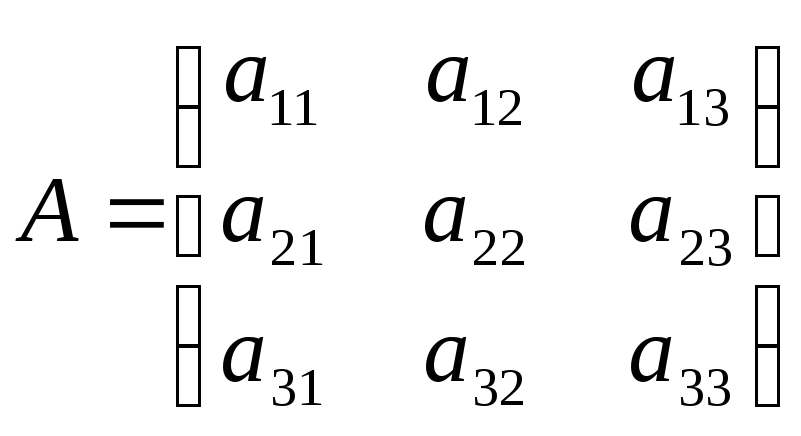
то

Характеристическое
уравнение:

Раскрыв
определитель, получим кубическое
уравнение относительно .
Любое кубическое уравнение с действительными
коэффициентами имеет либо один, либо
три действительных корня.

Тогда
любое линейное преобразование в
трехмерном пространстве имеет собственные
векторы.

Пример.
Найти характеристические числа и
собственные векторы линейного
преобразования А, матрица линейного
преобразования А =
.

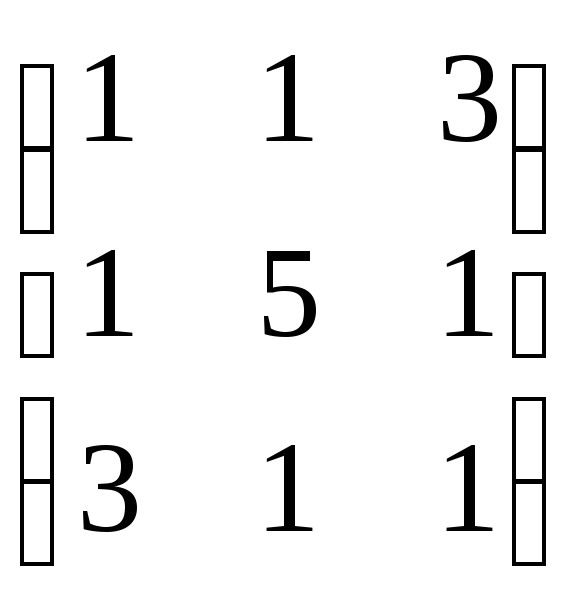
Составим
характеристическое уравнение:

(1
– )((5
– )(1
– )
– 1) – (1 – 
– 3) + 3(1 – 15 + 3)
= 0

(1
– )(5
– 5
– 
+ ²
– 1) + 2 + 
– 42 + 9
= 0

(1
– )(4
– 6
+ ²)
+ 10
– 40 = 0

4
– 6
+ ²
– 4
+ 6²
– ³
+ 10
– 40 = 0

-³
+ 7²
– 36 = 0

-³
+ 9²
– 2²
– 36 = 0

-²(
+ 2) + 9(²
– 4) = 0

(
+ 2)(-²
+ 9
– 18) = 0

Собственные
значения: ₁
= -2; ₂
= 3; ₃
= 6;

1)
Для ₁
= -2:

Если
принять х₁
= 1, то

х₂
= 0; x₃
= -1;

Собственные
векторы:

2)
Для ₂
= 3:

Если
принять х₁
= 1, то

х₂
= -1; x₃
= 1;

Собственные
векторы:

3)
Для ₃
= 6:

Если
принять х₁
= 1, то

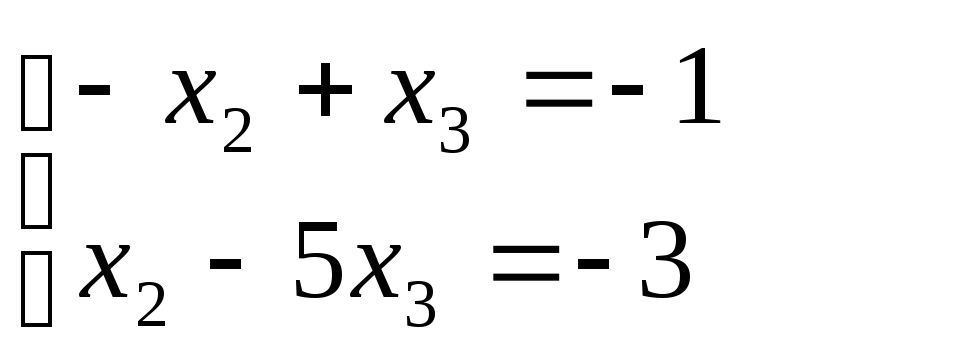
х₂
= 2; x₃
= 1;

Собственные
векторы:

Пример.
Найти характеристические числа и
собственные векторы линейного
преобразования А, матрица линейного
преобразования А =
.

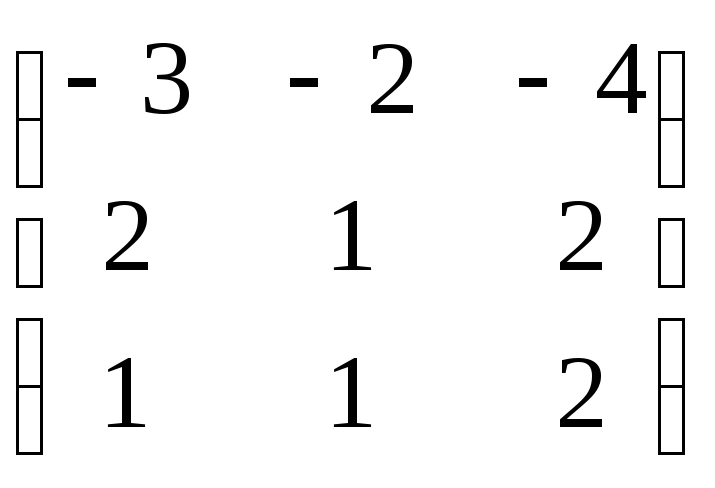
Составим
характеристическое уравнение:

-(3
+ )((1
– )(2
– )
– 2) + 2(4 – 2
– 2) – 4(2 – 1 + )
= 0

-(3
+ )(2
– 
– 2
+ ²
– 2) + 2(2 – 2)
– 4(1 + )
= 0

-(3
+ )(²
– 3)
+ 4 – 4
– 4 – 4
= 0

-3²
+ 9
– ³
+ 3²
– 8
= 0

-³
+ 
= 0

₁
= 0; ₂
= 1; ₃
= -1;

Для
₁
= 0:

Если
принять х₃
= 1, получаем х₁
= 0, х₂
= -2

Собственные
векторы
t,
где t
– параметр.

Для
самостоятельного решения:
Аналогично найти
и

для ₂
и ₃.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #