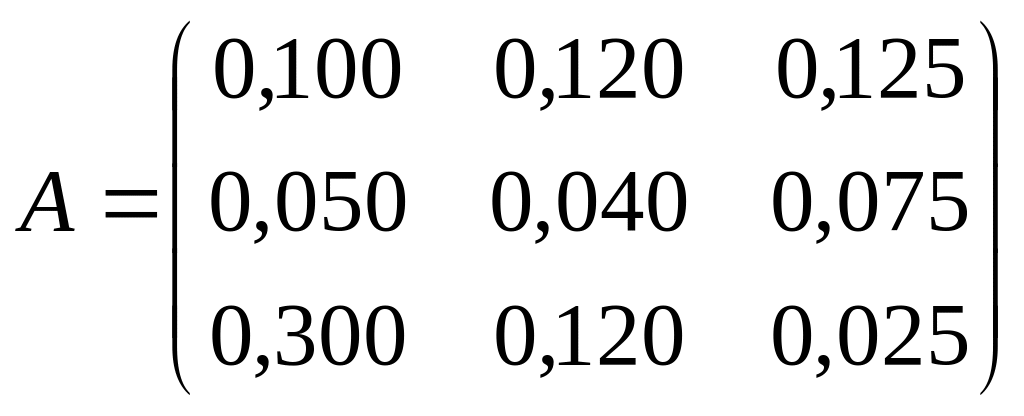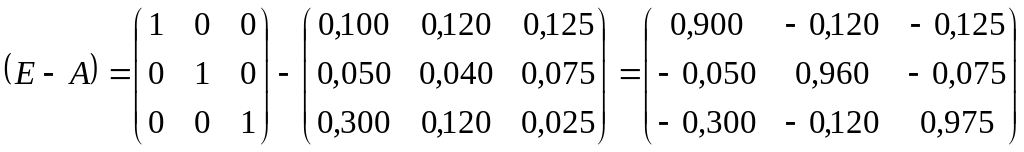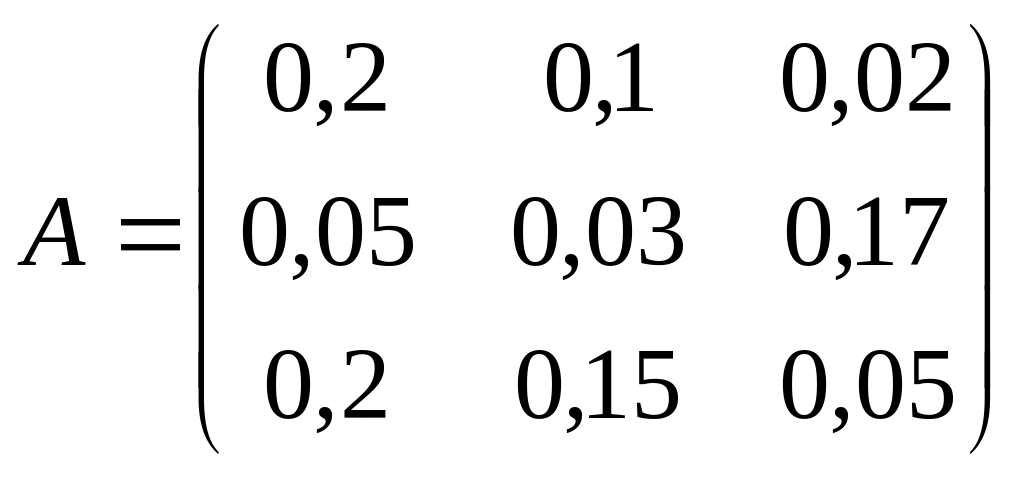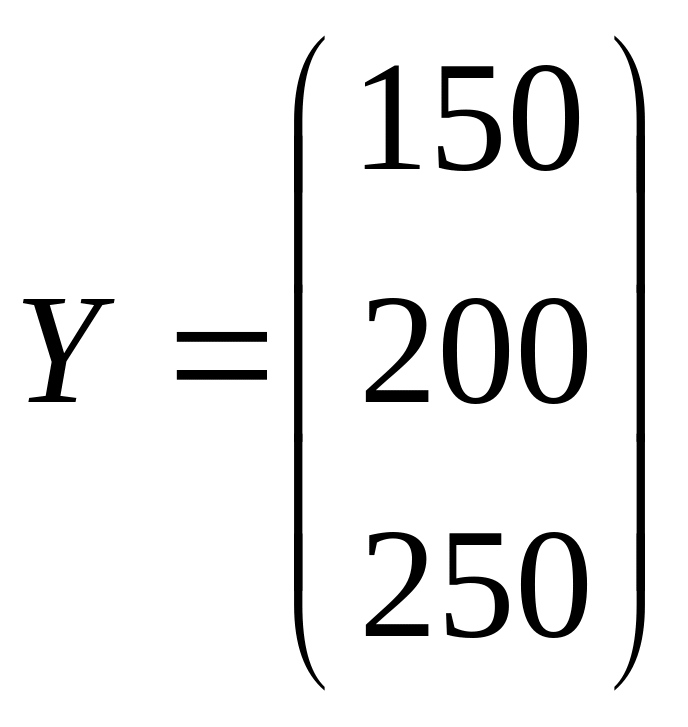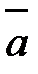Как найти матрицу прямых материальных затрат - Сайт, где вы сможете решить свои вопросы

Задача

Экономика
представлена двумя отраслями производства: промышленностью и сельским
хозяйством. За отчетный период получены следующие данные о межотраслевых
поставках

и векторе объемов конечного использования

Требуется:

Указание:
При вычислениях производить округление с точностью до тысячных.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Матрица прямых затрат

Найдем
валовые выпуски отраслей, просуммировав в каждой строке межотраслевые поставки
и координату вектора

Найдем
матрицу прямых затрат. Ее элементы можно найти по формуле:

Подставляя
числовые значения, получаем:

Матрица «Затраты – выпуск»

Найдем матрицу
«Затраты – выпуск»

Вектор конечного использования Y для валового объема выпуска X

Вектор
конечного использования Y для валового объема выпуска X определим на основе
балансового соотношения:

Для этого выполним умножение двух матриц

Матрица полных затрат

Найдем
матрицу коэффициентов полных материальных затрат

-она будет равна обратной матрице

Определитель матрицы

Алгебраические
дополнения:

Обратная матрица:

Вектор валового объема выпуска X для конечного использования Y

Вектор валового объема выпуска

для конечного продукта

определим формуле:

Приросты валовых объемов выпуска

Найдем
приросты валовых объемов выпуска, если конечное потребление должно изменяться
на

по сравнению с

Матрица полных затрат ресурсов S

Найдем
матрицу полных затрат ресурсов S для заданной матрицы ее прямых затрат M:

Суммарная потребность в ресурсах

Суммарная потребность в ресурсах для вектора Y₀:

Суммарная потребность в ресурсах для вектора Y_n:

Матрицы косвенных затрат и сумма затрат

Найдем
матрицы косвенных затрат первого, второго и третьего порядка

Сумма затрат:

Разность
матриц:

Вектор потребности в продукции

Найдем
вектор потребности в продукции всех отраслей материального производства b_ij
для получения единицы конечного продукта b_j вида. Для этого
просуммируем столбцы матрицы полных затрат:

Это значит, что для производства
единицы конечного продукта в первой отрасли во всех отраслях надо расходовать
продукции на сумму 1,913 ден.ед., для производства единицы конечного продукта
во второй отрасли -на 2,021 ден.ед.

Источник

Перейдем к построению математической модели. Для этого введем понятие коэффициентов прямых материальных затрат:

(1)

Коэффициент aij показывает, какое количество i-го продукта затрачивается на производство единицы j-го продукта.

Поскольку продукция измеряется в стоимостных единицах, коэффициенты прямых затрат являются величинами безразмерными. Кроме того, из (1) следует, что

(2)

Считая коэффициенты прямых материальных затрат постоянными, запишем систему балансовых соотношений

следующим образом:

Перенося yi в правую часть, а xi в левую и меняя знаки на противоположные, получаем

В матричной форме эта система уравнений выглядит следующим образом:

X – AX = Y или (E – A) X = Y,

где Е – единичная матрица n-го порядка;

– матрица коэффициентов прямых материальных затрат.

Итак, мы получили систему уравнений межотраслевого баланса, которую называют моделью Леонтьева. Используя эту модель, можно ответить на основной вопрос межотраслевого анализа – каким должно быть валовое производство каждой отрасли для того, чтобы экономическая система в целом произвела заданное количество конечной продукции?

Следует отметить одно важное свойство А – сумма элементов любого ее столбца меньше единицы:

(3)

Для доказательства разделим обе части балансового соотношения

на хj и, выполнив простейшие преобразования, получим

где vj / xj= – доля условно-чистой продукции в единице валового выпуска.

Очевидно, что >0, так как в процессе производства не может не создаваться новой стоимости. Из этого следует справедливость соотношения (3).

Свойства (2) и (3) матрицы А играют ключевую роль в доказательстве ее продуктивности, т. е. в доказательстве того, что при любом неотрицательном Y система

X – AX = Y или (E – A) X = Y,

имеет единственное и неотрицательное решение Х=(Е-А)-1Y. Матрицу (Е-А)-1 обозначают через В и называют матрицей коэффициентов полных материальных затрат, или обратной матрицей Леонтьева. Коэффициент bij этой матрицы показывает, каким должен быть валовой выпуск i-й отрасли для того, чтобы обеспечить производство единицы конечного продукта j-й отрасли. Используя матрицу В, можем записать

Х = ВY

или в развернутом виде

Преимущество такой формы записи балансовой модели состоит в том, что, вычислив матрицу В лишь однажды, мы можем многократно использовать ее для вычисления Х прямым счетом, т.е. умножением В на Y. Это гораздо проще, чем каждый раз решать систему линейных уравнений.

Обратную матрицу В можно вычислить, используя метод обращения с применением формулы разложения ее в матричный ряд:

В=Е+А+А2+…+Аk+… (4)

Число членов ряда, необходимое для получения достаточно точного приближения, зависит от матрицы А, но в любом случае приемлемый результат достигается при k 30.

Формула (4) имеет строгое математическое доказательство. Но мы ограничимся тем, что попытаемся осмыслить ее, рассматривая Х как результат некоторого гипотетического процесса последовательного уточнения промежуточной продукции, необходимой для создания заданного конечного продукта.

Итак, вектор конечной продукции, которую должна произвести экономическая система, равен Y. Будем считать, что это и есть первоначальное задание отраслям, т. е. Х0 =Y. Для выполнения собственного задания каждая отрасль нуждается в продукции других отраслей. Если бы все отрасли подсчитали потребности и подали заявки в некоторый центр, то оказалось бы, что суммарная потребность составляет X1 =АХ0=АY. Вектор X1 можно рассматривать как промежуточную продукцию, необходимую для производства Х0. Но под обеспечение производства X1 тоже нужна промежуточная продукция: X2 =АХ1 =А2Y. Рассуждая так и далее, мы приходим к выводу, что

Х=Х0+Х1+Х2+…+Хk+… = Y+АY+А2Y+…+AkY+… =

= (Е+А+А2+…+Аk+…)Y.

Полные затраты можно разложить на прямую и косвенную составляющие. Прямые затраты осуществляются непосредственно при производстве данного продукта, а косвенные А2+А3+…+Аk+… относятся к предшествующим стадиям производства. Они осуществляются не прямо, а через посредство других ингредиентов, входящих в данный продукт. Элементы матрицы А2 представляют собой косвенные затраты первого порядка, элементы матрицы А3 – косвенные затраты второго порядка и т. д.

Пример 1. Рассматривается трехотраслевой МОБ. Известна матрица коэффициентов прямых материальных затрат и задан вектор конечного продукта:

Определить валовое производство X, обеспечивающее заданный конечный продукт.

Для ответа на поставленный вопрос необходимо составить и решить систему линейных уравнений (Е-А)Х = Y.

Получим соответствующую систему уравнений

Решим систему методом Крамера. Если определитель системы отличен от нуля, то система имеет единственное решение, которое находится по формулам

где – определитель, который получается из заменой j-го столбца столбцом свободных членов.

Применяя формулы Крамера, получаем решение системы:

Пример 2. Вычислить изменение межотраслевых потоков, если известна матрица коэффициентов полных материальных затрат и задан вектор изменения конечного продукта:

Изменение межотраслевых потоков вычисляется по формулам

Вектор изменения валового производства определяется следующим образом:

Кроме того, нам необходимо знать матрицу А. Из формулы В=(Е-А)-1 следует, что

Теперь, отвечая на поставленный вопрос, получаем:

и т.д.

Источник: https://lms2.sseu.ru

Источник

Коэффициенты прямых и полных материальных затрат.

При исследовании
модели межотраслевого баланса сначала
нужно рассмотреть основные свойства
матрицы коэффициентов прямых материальных
затрат A.

Основные свойства
матрицы коэффициентов прямых материальных
затрат

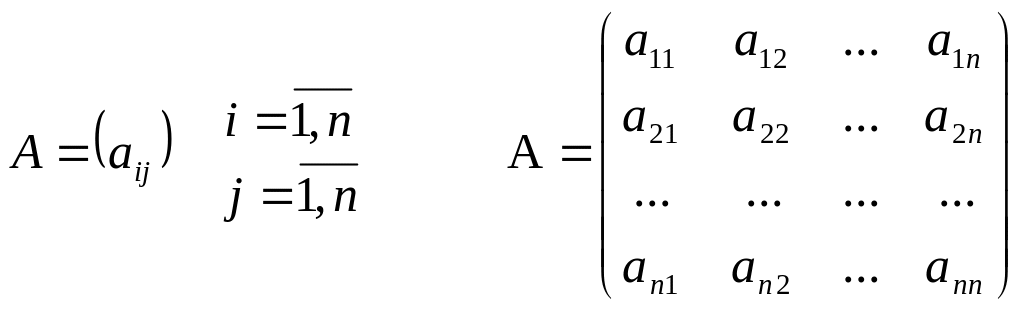
1. Коэффициенты
прямых затрат по определению являются
неотрицательными

,
поэтому матрица А
в целом может быть названа неотрицательной:

.

2. Диагональные
элементы матрицы А
меньше единицы

,
так как процесс воспроизводства нельзя
было бы осуществлять, если бы для
собственного воспроизводства в отрасли
затрачивалось больше количество
продукта, чем создавалось.

Система уравнений
межотраслевого баланса является
отражением реальных экономических
процессов, в которых содержательный
смысл могут иметь лишь неотрицательные
значения валовых выпусков. Значит,
вектор валовой продукции состоит из
неотрицательных компонентов и называется
неотрицательным, т.е.

.

Экономическая
система способна обеспечить положительный
конечный выпуск по всем отраслям, если
матрица коэффициентов прямых материальных
затрат А
является продуктивной.

Продуктивность
матрицы А.

Неотрицательную
матрицу А
называют продуктивной, если существует
такой неотрицательный вектор

,
что справедливо:

(13)

Это условие означает
существование положительного вектора
конечной продукции

для модели межотраслевого баланса

(7).

Существует несколько
способов
проверки продуктивности матрицы А.

Матрица коэффициентов
прямых материальных затрат А продуктивна,
если выполняется одно из условий:

1. Матрица

неотрицательно обратима, т.е существует
обратная матрица

.

2. Матричный ряд

сходится и его сумма равна обратной
матрице

3. Наибольшее по
модулю собственное значение

матрицы А
меньше 1.

Собственные числа
матрицы А
– корни характеристического уравнения

.

4. Все главные
миноры матрицы

,
т.е. определители матриц, образованные
элементами первых строк и первых столбцов
этой матрицы, порядка от 1 до n,
положительны.

Наиболее простым,
но только достаточным признаком
продуктивности матрицы А
является ограничение на величину ее
нормы, т.е. на величину наибольшей из
сумм элементов матрицы А
в каждом столбце. Если норма матрицы А
строго меньше единицы, то эта матрица
продуктивна.

Но эти условия
являются только достаточными, т.е.
матрица А
может быть продуктивной и в случае,
когда ее норма больше единицы.

Пример № 1.

Проверить
продуктивность матрицы

.
Найдем матрицу

Найдем определитель
матрицы

Находим элементы
присоединенной матрицы

;

Сначала найдем
транспонированную матрицу

:

обозначим ее через
D.

,
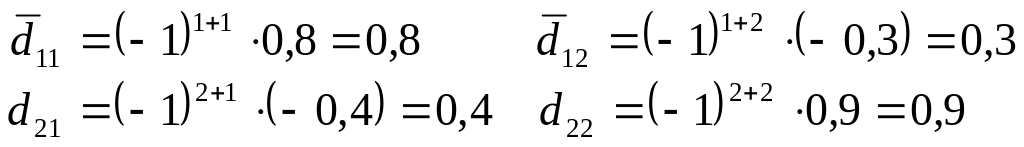
значит, матрица А
продуктивна.

Пример № 2.

Проверить
продуктивность матрицы

.

Найдем главные
миноры матрицы

;

Главный минор
I-ого
порядка: 0,900 > 0/

Главный минор
II-ого
порядка:

> 0.

Главный минор
III-его
порядка:

> 0.

Итак: все главные
миноры матрицы

положительны, значит матрица А
является продуктивной.

Анализ матрицы
коэффициентов полных материальных
затрат.

Матрица

– матрица коэффициентов полных материальных
затрат

.

Ранее было дано
определение коэффициента b_ij
полных материальных затрат, что b_ij
показывает сколько нужно произвести
продукции i-той
отрасли, чтобы с учетом прямых и косвенных
материальных затрат, получить единицу
конечной продукции отрасли j.

Дадим другое
определение коэффициента полных
материальных затрат, исходя из того,
что, кроме прямых затрат существуют
косвенные затраты той или иной продукции
при производстве продукции данной
отрасли.

Например,
при производстве автомобиля в виде
прямых затрат расходуется уголь, стальной
прокат, цветные металлы, электроэнергия
и т.д. Но на производство стального
проката также расходуется уголь. Это
будут косвенные затраты I-го
порядка при производстве автомобиля.
При производстве стального проката
расходуются цветные металлы, для
производства которых также расходуется
уголь. Но при производстве автомобиля
это будут косвенные затраты II-го
порядка и т.д.

В связи с этим
имеет место следующее определение:
коэффициентом
полных материальных затрат (с_i_j)
называется сумма прямых затрат продукции
i-той
отрасли для производства единицы
продукции j-той
отрасли через все промежуточные продукты
на всех предшествующих стадиях
производства.

Обозначим коэффициент
косвенных материальных затрат k-го
порядка через

,
тогда имеет место равенство:

(14)

Если ввести в
рассмотрение матрицу коэффициентов
полных материальных затрат

и матрицы коэффициентов материальных
затрат различных порядков:

,
то можно записать формулу:

(15)

где А
– матрица коэффициентов прямых
материальных затрат;

А⁽¹⁾
– матрица коэффициентов косвенных
материальных затрат I-го
порядка;

А⁽²⁾
– матрица коэффициентов косвенных
материальных затрат II-го
порядка и т.д.;

А⁽^k⁾
– матрица коэффициентов косвенных
материальных затрат k-го
порядка.

;

и т.д.

.

Итак:

(16)

Если матрица
коэффициентов прямых материальных
затрат А
является продуктивной, то из второго
условия продуктивности следует, что
существует матрица

,
которая является суммой сходящегося
матричного ряда:

(17)

Тогда сопоставляя
соотношения (16) и (17), можно сделать вывод
о связи между двумя матрицами коэффициентов
полных материальных затрат.

(18)

или

Экономический
смысл различия между коэффициентами
матриц В
и С:
в отличие от коэффициентов матрицы С,
которые учитывают только затраты на
производство продукции, коэффициенты
матрицы В
включают в себя кроме затрат также саму
единицу конечной продукции, которая
выходит за сферу производства.

Таким образом,
если матрица А
продуктивна, то для нахождения
матрицы В
можно использовать способы:

1. По формулам
обращения матриц:

(19)

2. Приближенный
способ по формулам разложения в матричный
ряд:

(20)

В этом случае
обычно ограничиваются косвенными
затратами до некоторого порядка
включительно.

Пример.

Дана матрица
коэффициентов прямых материальных
затрат и вектор конечной продукции:

Найти коэффициенты
полных материальных затрат, вектор
валовой продукции, заполнить схему
межотраслевого баланса.

Решение:

1. Определитель
матрицы

:

;

2. Транспонируем
матрицу

:

.

3. Находим
алгебраические дополнения для элементов
матрицы

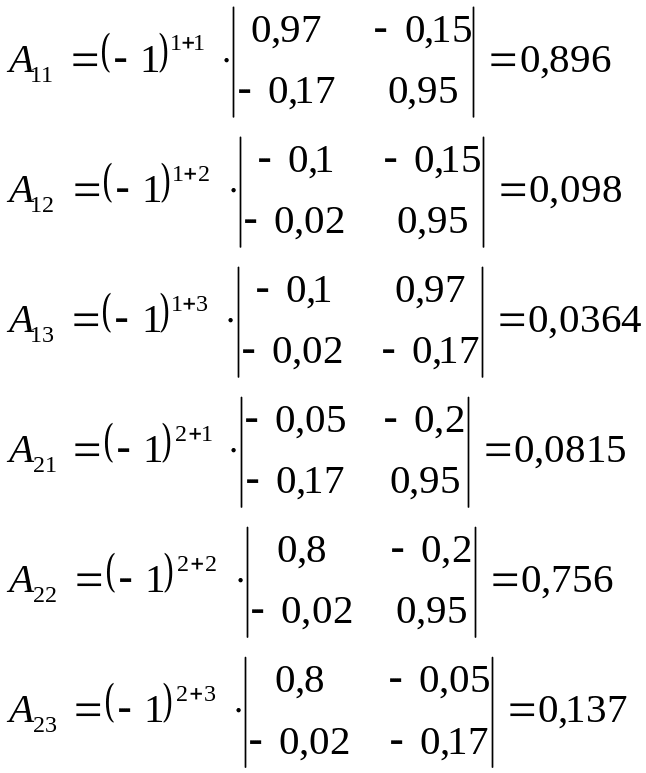
Присоединенная
матрица:

Найдем вектор
валовой продукции по формуле:

Для заполнения
схемы межотраслевого баланса, необходимо
найти:

Находим условно-чистую
продукцию отраслей:

Межотраслевой
баланс производства и распределения
продукции:

Производящие отрасли	Потребляющие отрасли	Конечная продукция	Валовая продукция
1	2	3
1 2 3	46,32 11,58 46,32	28,05 8,415 42,075	7,124 60,554 17,81	150 200 250	231,6 280,5 356,2
Условно-чистая продукция	127,38	201,96	270,712	600,0
Валовая продукция	231,6	280,5	356,2		868,3

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Балансовый анализ. Математическая модель многоотраслевой экономики (метод Леонтьева)

Цель балансового анализа – ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объём производства каждой из п отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а сдругой – как потребитель продукции и своей, и произведённой, другими отраслями.

Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. американским экономистом В.Леонтьевым

Предположим, что рассматривается п отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.

Рассмотрим процесс производства за некоторый период времени (например, год).

Введём следующие обозначения: х_i – общий (валовой) объём продукции i – й отрасли (i= 1,2. n);

x_ij – объём продукции i – й отрасли, потребляемой j-й отраслью в процессе производства (i, j = 1,2. n);

у_i – объём конечного продукта i – й отрасли для непроизводственного потребления.

Так как валовой объём продукции любой i – й отрасли равен суммарному объёму продукции, потребляемой п отраслями, и конечного продукта, то

(1.15)

Уравнения (1.15) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в (1.15), имеют стоимостное выражение.

Введём коэффициенты прямых затрат :

(1.16)

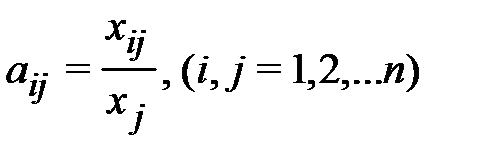
показывающие затраты продукции i-й отрасли на производство единицы продукции j-й отрасли.

Можно полагать, что в некотором промежутке времени коэффициенты a_ij будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.

(1.17)

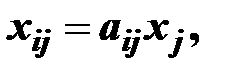
вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной. Теперь соотношения баланса (1.15) примут вид:

(1.18)

Обозначим , , ,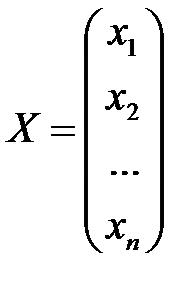

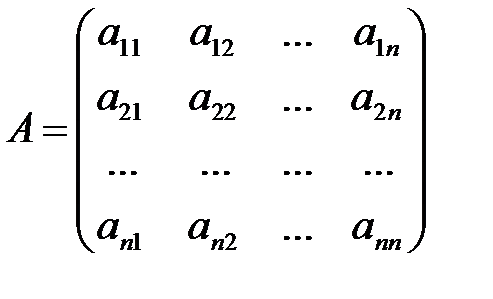
где Х – вектор валового выпуска, Y – вектор конечного продукта,А – матрица прямых затрат (технологическая или структурная матрица).

Тогда систему (1.15) можно записать в матричном виде:

Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y.

Перепишем уравнение (1.19) в виде:

Если матрица (Е – А) невырожденная, т.е. |Е – А|≠0, то

Матрица S = (Е – А) -1 называется матрицей полных затрат.

Каждый элемент s_ij матрицы S есть величина валового выпуска продукции i-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j-й отрасли (j=1,2. n).

В соответствии с экономическим смыслом задачи значения х_i должны быть неотрицательны при неотрицательных значениях

и , где i, j = 1, 2,…,n.

Определение. Матрица А ≥ 0 называется продуктивной, если для любого вектора Y ≥ 0 существует решение X ≥ 0 уравнения (Е-А)Х=Y. В этом случае и модель Леонтьева называется продуктивной.

Существует несколько критериев продуктивности матрицы А.

Первый критерий продуктивности. Матрица А продуктивна, если максимум сумм элементов её столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы, т.е. матрица А продуктивна, если для любых i, j = 1,2. n и , и существует номер j такой, что .

Второй критерий продуктивности. Матрица A ≥ 0 продуктивна тогда и только тогда, когда матрица (Е – А) – 1 существует и неотрицательна.

Пример 9. В таблице приведены данные об исполнении баланса за отчетный период, усл. ден. ед.:

Отрасль	Потребление	Конеч-ный продукт	Валовой выпуск
энергетика	машиностроение
Производство	Энергетика Машиностроение

Вычислить необходимый объём валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроение сохранится на прежнем уровне.

Решение. Имеем .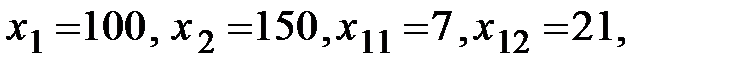

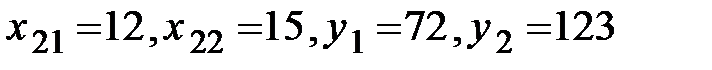
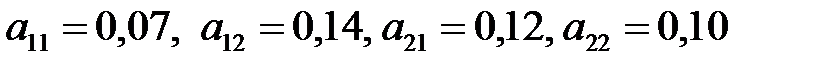
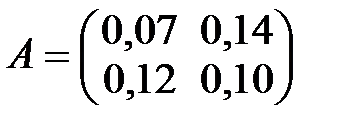
По формуле (1.16) находим коэффициенты прямых затрат: , т.е матрица прямых затрат

имеет неотрицательные элементы и удовлетворяет первому критерию продуктивности: .

Поэтому для любого вектора конечного продукта Y можно найти необходимый объём валового выпуска Х по формуле (1.21):

Найдём матрицу полных затрат S = (E – A) -1 :

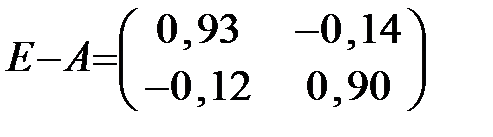
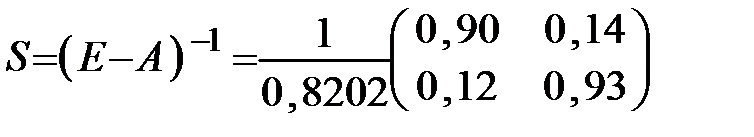
. Так как |Е – А|=0,8202 ≠ 0, то по формуле (1.14) для вычисления обратной матрицы имеем: .

По условию вектор конечного продукта должен быть равен 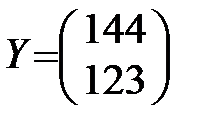. Тогда по формуле (1.21) получаем вектор валового выпуска:

, т.е. валовой выпуск в энергетической отрасли надо увеличить до 179, 0 усл. ед., а в машиностроительной – до 160,5 усл. ед.

Ответ: (усл. ед.), (усл. ед.).

Векторная алгебра

Основные понятия векторной алгебры

Определение. Вектором называется направленный отрезок АВ, в котором

точка А рассматривается как начало, а точка В – как конец.

Вектор обозначается или , и изображается следующим образом:

В Модуль (длина) вектора обозначается или .

А или

Определение. Векторы называются коллинеарными, если они расположены

на одной или на параллельных прямых, и компланарными,

если они лежат на одной или на параллельных плоскостях.

Определение. Векторы называются равными, если: а) равны их длины;

б) они коллинеарны; с) направлены в одну сторону.

Определение. Координатами 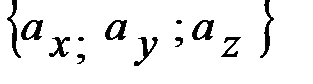вектора в системе ХОУ

называются проекции этого вектора на оси Ох, Оу, Оz.

В этом случае пишут : =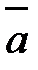

Определение. Базисными ортами называются единичные векторы 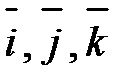, направленные соответственно по координатным осям Ох, Оу, Оz.

Координаты вектора являются коэффициентами его разложения по ортам:

= а_х · + а_у · + а_z · . (2.1)

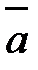
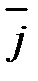
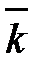
координаты вектора равны разностям соответсвующих координат его

конца В и начала А, т.е.

. (2.2)

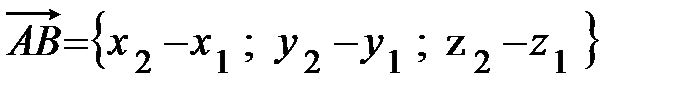
Длина вектора , заданного своими координатами = , вычисляется по формуле:

. (2.3)

При сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются), а при умножении вектора на число каждая его координата умножается на это число.

Пример 10. Вектор задан координатами начала А и конца В: А (-2;3;-5 ),

В ( 2; -3; 1 ). Найти координаты вектора и его длину.

Решение. По формуле (2.2) найдём координаты вектора : =

По формуле (2.3) определяем его длину: .

Ответ: = ; .

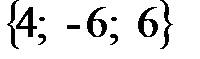
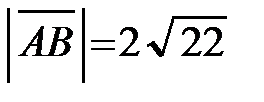
Пример 11. Даны три вектора: , , .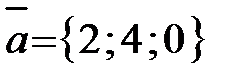

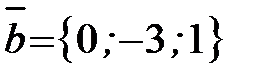
Найти координаты вектора .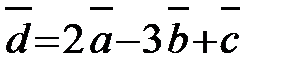

Решение. Имеем , , .

Тогда .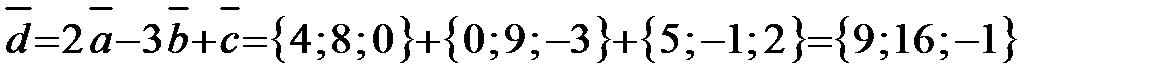

Ответ: .

Межотраслевой баланс

С помощью сервиса в онлайн режиме можно:

найти коэффициенты полных материальных затрат, определить вектор валовой продукции;
составить межотраслевой баланс, составить схему межотраслевого баланса труда;
проверить продуктивность матрицы.

Шаг №1
Шаг №2
Видеоинструкция
Оформление Word

Межотраслевой баланс отражает производство и распределение валового национального продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.

Система уравнений X = AX + Y называется экономико-математической моделью межотраслевого баланса (МОБ) или моделью «затраты – выпуск». C помощью нее можно выполнить следующие расчеты:

подставив в модель объемы валовой продукции каждой отрасли X_i, можно определить объем конечной продукции отрасли Y_j: Y = (E – A)X
задав величины конечной продукции всех отраслей Y_j, можно определить величины валовой продукции каждой отрасли X_i: X = (E – A) -1 Y
установив для ряда отраслей величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти объемы конечной продукции первых отраслей и объемы валовой продукции вторых.

Здесь A – матрица прямых затрат, коэффициенты которой, a_ij показывают затраты i-й отрасли на производство единицы продукции j-й отрасли. Введем обозначение B = (E – A) -1 . Матрица B называется матрицей полных материальных затрат, коэффициенты которой, b_ij показывают полный объем продукции i-й отрасли, используемой для производства единицы продукции j-й отрасли. С учетом линейности соотношений эффект распространения спроса ΔX, вызванный изменением конечного спроса на величину ΔY рассчитывается как: ΔX = B·ΔY
Через C=A-B обозначают матрицу косвенных затрат.

Пример №1 . Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат A и вектор конечной продукции Y .

Пример №2 . Дан межотраслевой баланс трехотраслевой модели хозяйства:

№ отрасли потребления	1	2	3	Конечный продукт	Валовый продукт	Y’
№ отрасли	1	20	20	60	100	200	150
отрасли	2	20	40	60	80	200	100
производства	3	20	0	10	70	100	100

Определить:
1) технологическую матрицу;
2) матрицу коэффициентов полных затрат;
3) дать экономический анализ каждого столбца матрицы коэффициентов полных затрат;
4) определить валовый выпуск X’ на новый ассортимент конечной продукции Y’;

Решение.
Находим валовой объем продукции x_i;
x₁ = 20 + 20 + 60 + 100 = 200
x₂ = 20 + 40 + 60 + 80 = 200
x₃ = 20 + 0 + 10 + 70 = 100

Отрасль	Потребление	Конечный продукт	Валовой выпуск
Производство	20	20	60	100	200
20	40	60	80	200
20	0	10	70	100

По формуле a_ij = x_ij / x_j находим коэффициенты прямых затрат:
a₁₁ = 20/200 = 0.1; a₁₂ = 20/200 = 0.1; a₁₃ = 60/100 = 0.6; a₂₁ = 20/200 = 0.1; a₂₂ = 40/200 = 0.2; a₂₃ = 60/100 = 0.6; a₃₁ = 20/200 = 0.1; a₃₂ = 0/200 = 0; a₃₃ = 10/100 = 0.1;

0.1	0.1	0.6
0.1	0.2	0.6
0.1	0	0.1

Определим матрицу коэффициентов полных затрат с помощью формул обращения невырожденных матриц.
а) Находим матрицу (E-A):

(E-A) =

0,9	-0,1	-0,6
-0,1	0,8	-0,6
-0,1	0	0,9

б) Вычисляем обратную матрицу (E-A) -1 :

0,9	-0,1	-0,6
-0,1	0,8	-0,6
-0,1	0	0,9

Найдем величины валовой продукции трех отраслей

X’ = (B -1 *Y’) =

1,23	0,15	0,92
0,26	1,28	1,03
0,14	0,0171	1,21

Пример №3 . В модели межотраслевого баланса

Производство	Потребление	Конечная продукция	Валовая продукция
1	2	3
1	10	5	15	70	100
2	20	…	…	…	…
3	30	…	…	…	…
Оплата труда	30	…	…	…	…
Прибыль D	D	…	…	…	…

прибыль D равна:
D = Валовая продукция – Затраты на производство – Оплата труда = 100 – (10+20+30) – 30 = 10.

Как найти вектор валового выпуска

МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ

ИНСТИТУТ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА

Кафедра «Моделирование в экономике и управлении»

МАТЕМАТИЧЕСКИЕ МОДЕЛИ В УПРАВЛЕНИИ

Методическое пособие по проведению лабораторных работ.

Тема «Балансовые экономико-математические модели и их моделирование на Excel»:

Тема 1. Экономико-математическая модель межотраслевого баланса (модель Леонтьева).

Тема 2. Экономико-математическая модель международной торговли.

Лабораторная работа №5

Курс “Математические модели в управлении” читается студентам второго курсов дневной и вечерней форм обучения факультета управления по специальностям: 061000 – “Государственное и муниципальное управление”, 061100 – “Менеджмент”. Курс читается два семестра и охватывает основные темы исследования операций, теории массового обслуживания и теории игр.

Предметом изучения дисциплины “Математические модели в управлении” являются математические модели и методы решения исследования операций, теории массового обслуживания и теории игр.

Цель курса – сформировать у студентов комплекс знаний необходимых для:

· анализа современных проблем в области производства, торговли, финансов, денежного обращения и кредитов;

· оптимальному решению тактических и стратегических задач организационного управления;

Задачи курса научить студентов:

· владеть приемами постановки задач организационного управления;

· на основе описательных задач строить математические модели;

· умению выбрать соответствующий метод решения задачи;

· проведению численных исследований математических моделей;

· умению проведения анализа результатов вычислений;

· умению выбрать наиболее эффективное управляющее решение.

Особенностью программы для студентов факультета управления является:

· рассмотрение актуальных проблем организационного управления в различных структурах – производственных, торговых, финансово – кредитных;

· применение математических методов при анализе и выработки управляющих решений.

Изучив курс, студент:

должен владеть моделями математического программирования, теории игр и массового обслуживания;

уметь использовать математические методы при решении задач организационного управления;

должен уметь использовать в своей работе средства вычислительной техники и современных информационных технологий.

Лабораторные работы призваны, на практике, помочь студентам применить знания полученные на лекциях и при самостоятельной работе. В качестве программной среды используются средства Microsoft Offis Excel (электронные таблицы MS Offis ).

Программные средства Excel – Поиск решения является мощным инструментом решения вычислительных и оптимизационных задач.

Порядок выполнения работы

На лабораторную работу каждый студент приносит тетрадь для выполнения лабораторных работ, в которой будут содержаться математические модели и результаты решения задач на Excel.

Задание . Получить вариант задачи у преподавателя. Составить математическую модель задачи. Найти решение задачи в Excel и показать результаты поиска решения преподавателю на экране компьютера.

Отчет. Отчет по лабораторной работе представляется в тетради студента и должен содержать все полученные результаты. Отчет демонстрируется преподавателю на данном лабораторном занятии.

Лабораторная работа № 5

Лабораторная работы №5 состоит из двух тем: Тема 1. Экономико-математическая модель межотраслевого баланса (модель Леонтьева), и Тема 2. Экономико-математическая модель международной торговли.

Тема 1. Экономико-математическая модель межотраслевого баланса (модель Леонтьева). Моделирование средствами Excel .

Программное обеспечение: Microsoft Excel

Рассмотрим модель межотраслевого баланса, называемую еще моделью Леонтьева или моделью «затраты-выпуск».

Предположим, что производственный сектор народного хозяйства разбит на n отраслей (энергетика, машиностроение, сельское хозяйство и т.д.).

Рассмотрим отрасль i , i = 1, 2,…, n . Она выпускает некую продукцию за данный промежуток времени (например, за год) в объеме x_i, который еще называют валовым выпуском. Часть объема продукции x_i , произведенная i-ой отраслью используется для собственного производства в объеме x_i _i , часть – поступает в остальные отрасли j = 1, 2,…, n для потребления при производстве в объемах x_ij , и некоторая часть объемом y _i – для потребления в непроизводственной сфере, так называемый объем конечного потребления. Перечисленные сферы распределения валового продукта i-ой отрасли приводят к соотношению баланса

, i = 1, 2,…, n .

Введем коэффициенты прямых затрат a _ij , которые показывают, сколько единиц продукции i-ой отрасли затрачивается на производство одной единицы продукции в отрасли j. Тогда можно записать, что количество продукции, произведенной в отрасли i в объеме x_ij и поступающей для производственных нужд в отрасль j, равно

Считаем сложившуюся технологию производства во всех отраслях неизменной (за рассматриваемый период времени), означающую, что коэффициенты прямых затрат a _ij постоянны. Тогда получаем следующее соотношение баланса, называемого моделью Леонтьева

, i = 1, 2,…, n . (1)

Введя вектор валового выпуска X, матрицу прямых затрат A и вектор конечного потребления Y

модель Леонтьева (1) можно записать в матричном виде

Матрица A ≥ 0, у которой все элементы a _ij ≥ 0 (неотрицательны), называется продуктивной матрицей, если существует такой неотрицательный вектор X ≥ 0, для которого выполняется неравенство

Это неравенство означает, что существует хотя бы один режим работы отраслей данной экономической системы, при котором продукции выпускается больше, чем затрачивается на ее производство. Другими словами, при этом режиме создается конечный (прибавочный) продукт Y = X – AX > 0.

Модель Леонтьева с продуктивной матрицей A называется продуктивной моделью.

Для проверки продуктивности матрицы A достаточно существования обратной матрицы B = ( E – A ) -1 с неотрицательными элементами, где матрица E – единичная матрица

С помощью модели Леонтьева (2) можно выполнить три вида плановых расчетов, при условии соблюдения условия продуктивности матрицы A:

1) Зная (или задавая) объемы валовой продукции всех отраслей X можно определить объемы конечной продукции всех отраслей Y

2) Задавая величины конечной продукции всех отраслей Y можно определить величины валовой продукции каждой отрасли

X = ( E – A ) -1 Y (3)

3) Задавая для ряда отраслей величины валовой продукции, а для всех остальных отраслей – объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.

называется матрицей полных материальных затрат. Ее смысл следует из матричного равенства (3), которое можно записать в виде X = BY . Элементы матрицы B показывают, сколько всего необходимо произвести продукции в i-ой отрасли, для выпуска в сферу конечного потребления единицы продукции отрасли j.

Пример с использованием технологии Excel

Задача . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

1) Матрицу коэффициентов полных материальных затрат B

2) Проверить продуктивность матрицы A

2) Вектор валового выпуска X

3) Межотраслевые поставки продукции x_ij

Математическая модель и последовательность расчетов

Модель Леонтьева имеет вид

Матрица полных материальных затрат B равна

Продуктивность матрицы A проверяется, по вычисленной матрице B. Если эта матрица существует и все ее элементы неотрицательны, то матрица A продуктивна.

Вектор валового выпуска X рассчитывается по формуле

Межотраслевые поставки продукции x_ij вычисляются по формуле

Процесс решения задачи средствами Microsoft Excel

Для решения задачи межотраслевого баланса необходимо уметь выполнять с помощью Excel следующие операции над матрицами:

– Умножение матрицы на вектор

– Умножение двух матриц

– Транспонирование матрицы или вектора

– Сложение двух матриц

1. Задание Исходных данных задачи

Вызовите Microsoft Excel.

Введите матрицу A в ячейки с адресами А2:С4 и вектор Y в ячейки с адресами Е2:Е4 (рис. 1).

Рис. 1. Задание исходных данных и последовательное выполнение плановых расчетов

2. Вычисление матрицы коэффициентов полных материальных затрат B.

2.1. Введите единичную матрицу Е в ячейки с номерами А7:С9.

2.2. Вычислите матрицу Е – А. Матрица Е – А является разностью двух матриц Е и А. Для вычисления разности двух матриц необходимо проделать следующее:

– установите курсор мыши в левый верхний угол (это ячейка с адресом А12) результирующей матрицы Е – А, которая будет расположена в ячейках с адресами А12:С14;

– введите формулу =А7-А2 для вычисления первого элемента результирующей матрицы Е – А, предварительно установив английскую раскладку клавиатуры;

– введенную формулу скопируйте во все остальные ячейки результирующей матрицы. Для этого, установите курсор мыши в ячейку А12; наведите указатель мыши на точку в правом нижнем углу ячейки, так чтобы указатель мыши принял вид крестика; при нажатой левой кнопке мыши протяните указатель до ячейки С12, а затем так же протяните указатель мыши до ячейки С14.

В результате в ячейках А12:С14 появится искомая матрица, равная разности двух исходных матриц Е и А.

2.3. Вычислите матрицу B = ( E – A ) -1 , являющейся обратной по отношению к матрице Е – А. Матрица Е – А расположена в ячейках с адресами А12:С14. Для вычисления матрицы В необходимо проделать следующее:

– выделите диапазон ячеек А17:С19 для размещения матрицы В;

– нажмите на панели инструментов кнопку Вставка, а затем кнопку Функция. В появившемся окне в поле Категория выберите Математические, а в поле Выберите функцию – имя функции МОБР. Щелкните на кнопке ОК;

– появившееся диалоговое окно МОБР мышью отодвиньте в сторону от исходной матрицы Е – А и введите диапазон матрицы Е – А (диапазон ячеек А12:С14) в рабочее поле Массив (протащив указатель мыши при нажатой левой кнопке от ячейки А12 до ячейки С14);

– нажмите комбинацию клавиш Ctrl+Shift+Enter. Обратите внимание, что нажимать надо не клавишу ОК(!), а именно комбинацию клавиш Ctrl+Shift+Enter.

В диапазоне ячеек А17:С19 появится искомая обратная матрица ( E – A ) -1 , равная матрице B.

3. Проверка продуктивности матрицы А.

Поскольку матрица В найдена, следовательно она существует. Все элементы матрицы В неотрицательны, поэтому матрица В – продуктивна.

4. Вычисление вектора валового выпуска X .

Вычисление вектора валового выпуска X находим по матричной формуле X = BY , в которой матрица В вычислена, а вектор Y задан.

Вычисление вектора X = BY производится с помощью операции умножения матриц, а в данном случае – умножения матрицы В на вектор Y. Для этого необходимо:

– выделить диапазон ячеек Е7:Е9, где будет расположен вектор Х. Обратите внимание, что по правилам умножения матриц, размерность результирующей матрицы Х должна быть равна количеству строк матрицы В на количество столбцов матрицы Y. В нашем случае, размерность вектора Х равна: три строки на один столбец;

– нажать на панели инструментов кнопку Вставка, а затем кнопку Функция. В появившемся окне в поле Категория выберите Математические, а в поле Выберите функцию – имя функции МУМНОЖ. Щелкните на кнопке ОК;

– появившееся диалоговое окно МУМНОЖ мышью отодвиньте в сторону от исходных матриц В и Y и введите диапазон матрицы В (диапазон ячеек А17:С19) в рабочее поле Массив 1 (протащив указатель мыши при нажатой левой кнопке от ячейки А17 до ячейки С19), а диапазон вектора Y (ячейки Е2:Е4) в рабочее поле Массив 2 (рис. 2);

Рис. 2. Диалоговое окно умножения матриц МУМНОЖ

В диапазоне ячеек Е7:Е9 появится искомый вектор Х.

5. Вычисление межотраслевых поставок продукции x_ij

Межотраслевые поставки продукции x_ij вычисляются по формуле

где a _ij – элементы исходной матрицы А, расположенной в ячейках А2:С4, x_j – элементы вектора Х, найденного выше в п. 4 и расположенные в ячейках Е7:Е9.

Для проведения вычислений x_ij необходимо проделать следующее.

5.1. Вычислить транспонированный вектор Х т относительно вектора Х. При этом вектор-столбец Х станет вектором-строкой Х т . Это необходимо для согласования размерностей дальнейшего умножения элементов векторов.

– выделить указателем мыши при нажатой левой кнопке ячейки Е12:G12, в которых будет располагаться транспонированный вектор Х т ;

– нажать на панели инструментов кнопку Вставка, а затем кнопку Функция. В появившемся окне в поле Категория выберите Ссылки и массивы, а в поле Выберите функцию – имя функции ТРАНСП (рис. 3). Щелкните на кнопке ОК;

– появившееся диалоговое окно ТРАНСП мышью отодвиньте в сторону от исходного вектора Х и введите диапазон вектора Х (диапазон ячеек Е7:Е9) в рабочее поле Массив (протащив указатель мыши при нажатой левой кнопке от ячейки Е7 до ячейки Е9);

– нажмите сочетание клавиш Ctrl+Shift+Enter.

Рис. 3. Диалоговое окно транспонирования матрицы

В результате в поле ячеек Е12:G12 расположится транспонированный вектор Х т .

5.2. Вычислить межотраслевые поставки продукции x_ij . Для этого проделать следующие операции:

– поставить курсор мыши в ячейку А22, в которой будет расположено значение x₁₁. В этой ячейке набрать формулу =A2*E12, которая означает, что x₁₁ = a ₁₁ x₁ .

– введенную формулу скопируйте во все остальные ячейки первой строки (в ячейки А22:С22, протащив мышью крестик в правом нижнем углу от ячейки А22 при нажатой левой кнопке мыши, до ячейки С22. При этом будут вычислены x₁₂ = a ₁₂ x₂ и x₁₃ = a ₁₃ x₃ .

Затем в ячейке А23 наберите формулу =A3*E12 и повторяя аналогичную процедуру, получите значения x₂₁ = a ₂₁ x₁ , x₂₂ = a ₂₂ x₂ и x₂₃ = a ₂₃ x₃ . Повторите аналогичные действия для ячеек А24:С24.

В результате все межотраслевые поставки продукции будут найдены и расположатся в матрице с ячейками А22:С24.

Тема 2. Экономико-математическая модель международной торговли (линейная модель обмена). Моделирование средствами Excel

Рассмотрим бюджеты n стран, которые обозначим как x₁, x₂, … , x _n .

Предположим, что национальный доход x _j страны j затрачивается на закупку товаров внутри страны и на импорт из других стран.

Обозначим через x_ij количество средств страны j расходуемое на закупку товаров из страны i, при этом x _j _j – затраты на закупку товаров внутри страны j. Тогда сумма всех затрат страны j, идущее на закупку товаров как внутри страны, так и на импорт из других стран должна равняться национальному доходу страны x _j , т.е.

, j = 1, 2,…, n . (4)

Разделив обе части равенства (4) на x _j и введя коэффициенты получим

, j = 1, 2,…, n (5)

Коэффициенты равны доли национального дохода страны j расходуемую на закупку товаров у страны i.

Матрица A коэффициентов

(6)

называется структурной матрицей торговли. Понятно, что сумма элементов каждого столбца равна единице.

С другой стороны, количество средств страны j расходуемое на закупку товаров из страны i и равное x_ij, является выручкой для страны i за свой товар, который у нее закупила страна j. Суммарная выручка i-ой страны равна

, i = 1, 2,…, n (7)

Так как , то и равенство (7) можно записать в виде

, i = 1, 2,…, n . (8)

Международная торговля называется сбалансированной, если сумма платежей (затрат) каждого государства равна его суммарной выручке от внешней и внутренней торговли.

В сбалансированной системе международной торговли не должно быть дефицита, другими словами, у каждой страны выручка от торговли должна быть не меньше ее национального дохода, т.е.

, i = 1, 2,…, n .

Одновременное выполнение этих неравенств может иметь место только в том случае, если

, i = 1, 2,…, n , (9)

т.е. у всех торгующих стран выручка от внешней и внутренней торговли должна совпадать с национальным доходом.

Равенства (9), с использованием (8), можно записать в матричном виде

где А – структурная матрица (6) международной торговли; Х – вектор национальных доходов стран

Матричное уравнение (10) соответствует задаче на собственное значение и собственный вектор матрицы А. Очевидно, что собственное значение матрицы А, согласно уравнению (10), равно 1, а собственный вектор, соответствующий этому собственному значению, равен Х.

Таким образом, баланс в международной торговле достигается тогда, когда собственное значение структурной матрицы международной торговли равно единице, а вектор национальных доходов торгующих стран является собственным вектором, соответствующим этому единичному собственному значении.

С помощью линейной модели международной торговли можно, зная структурную матрицу международной торговли А найти такие величины национальных доходов торгующих стран (вектор Х), чтобы международная торговля была сбалансированной.

Моделирование с использованием технологии Excel.

Определение собственного вектора X матрицы А с помощью средств Micro so ft Excel невозможно.

Поэтому математическую модель международной торговли сводят к задаче линейного программирования. Для этого, систему уравнений

где Е – единичная матрица

которая получается из уравнений (10) переносом правой части в левую, трактуют как ограничения-равенства.

Кроме того, вводят новое ограничение-неравенство

отражающее условие, по которому сумма бюджетов всех стран должна быть не больше заданной величины S.

В качестве целевой функции вводится сумма бюджетов всех стран, которая должна достигать максимума:

Итак, математическая модель сбалансированной международной торговли сводится к следующей оптимизационной задаче линейного программирования. Необходимо найти максимум целевой функции

Пример с использованием технологии Excel

Задача . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна

а сумма бюджетов стран не превышает 7680 млн.ден.ед.

Решение задачи средствами Excel

Методика решения задачи линейного программирования с помощью средств Поиска решения Excel подробно рассматривалась в Лабораторной работе №1 и поэтому здесь уже рассматриваться не будет.

Рис. 4. Исходные данные в Excel

Задание исходных данных на рабочем листе Excel приведено на рис.4.

В ячейки В2:Е6 занесены коэффициенты при системе ограничений, в ячейках G2:G6 содержатся ограничения в правых частях, в ячейки I2:I6 занесены формулы левых частей ограничений, ячейки В9:Е9 содержат изменяемые переменные . Например, в ячейке I2 записана формула ограничений =СУММПРОИЗВ(В2:Е2;В9:Е9). Аналогичные формулы записаны в ячейках I3:I6. Формула целевой функции =СУММ(В9:Е9) занесена в ячейку С10.

Рис. 5.Решение задачи средствами Excel

Процесс решения – занесение в окно Поиск решения ячейки с формулой целевой функции, занесение изменяемых ячеек, внесение ограничений приведено на рис. 5. В окне Параметры необходимо отметить: Линейная модель, Неотрицательные значения, Автоматическое масштабирование.

На рис. 5 приведены также результаты решения, согласно которым национальные доходы четырех стран равны соответственно 1015.359, 1458.228, 3251.308, 1955.105 млн.ден.ед. Из содержимого ячеек I2:I6 видно, что все ограничения выполнены. Значение целевой функции (ячейка С10) равно 7680 млн.ден.ед.

Индивидуальные задания по Теме 1

Задание 1 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Определить: 1) Матрицу коэффициентов полных материальных затрат B. 2) Проверить продуктивность матрицы A. 2) Вектор валового выпуска X. 3) Межотраслевые поставки продукции x_ij

Задание 2 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Задание 3 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Задание 4 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Задание 5 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Задание 6 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Задание 7 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Задание 8 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Задание 9 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Задание 10 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Задание 11 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Задание 12 . Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

Индивидуальные задания по Теме 2

Задание 1 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна

а сумма бюджетов стран не превышает 4590 млн.ден.ед.

Задание 2 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна

а сумма бюджетов стран не превышает 15055 млн.ден.ед.

Задание 3 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна

а сумма бюджетов стран не превышает 9000 млн.ден.ед.

Задание 4 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна

а сумма бюджетов стран не превышает 59550 млн.ден.ед.

Задание 5 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна

а сумма бюджетов стран не превышает 15590 млн.ден.ед.

Задание 6 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна

а сумма бюджетов стран не превышает 51503 млн.ден.ед.

Задание 7 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна

а сумма бюджетов стран не превышает 25590 млн.ден.ед.

Задание 8 . Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна

а сумма бюджетов стран не превышает 83355 млн.ден.ед.

1. Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач. – М.: Вузовский учебник, 2004

[spoiler title=”источники:”]

http://axd.semestr.ru/econ/balans.php

http://meu.rsuh.ru/madera/HTML-LR5.htm

[/spoiler]

Источник

Задача

Матрица прямых затрат

Матрица «Затраты – выпуск»

Вектор конечного использования Y для валового объема выпуска X

Матрица полных затрат

Вектор валового объема выпуска X для конечного использования Y

Приросты валовых объемов выпуска

Матрица полных затрат ресурсов S

Суммарная потребность в ресурсах

Матрицы косвенных затрат и сумма затрат

Вектор потребности в продукции

Коэффициенты прямых и полных материальных затрат.

Балансовый анализ. Математическая модель многоотраслевой экономики (метод Леонтьева)

Межотраслевой баланс

Как найти вектор валового выпуска

Вам также может понравиться

Электротехника формула как найти мощность

Как найти котангенс алгебра

Найди ботинки как на фото

Добавить комментарий Отменить ответ