-
Основные
определения
Граф
![]() – это совокупность двух множеств: вершин
– это совокупность двух множеств: вершин![]() и ребер
и ребер![]() ,
,
между которыми определено отношениеинцидентности.
Каждое ребро e
из E
инцидентно ровно двум вершинам
![]() и
и![]() ,
,
которые оно соединяет. При этом вершина![]() и реброe
и реброe
называются инцидентными
друг другу, а вершины
![]() и
и![]() называютсясмежными.
называютсясмежными.
Принято обозначение
n
для числа вершин графа (мощность множества
![]() ):
):![]() иm
иm
для числа его ребер:
![]() .
.
Говорят, что графG
есть (n,
m)
граф, где n
– порядок графа, m
– размер графа.
Если все ребра
![]() графа неориентированные, т.е. пары
графа неориентированные, т.е. пары
вершин, определяющие элементы множестваE,
неупорядочены, то такой граф называется
неориентированным графом, или неографом.
На рис. 12.1 показан пример неографа. Этот
граф имеет пять вершин и шесть ребер.

Рис. 12.1
Маршрут
– последовательность ребер, в которой
каждые два соседних ребра имеют общую
вершину. Граф связен,
если любые две вершины соединены хотя
бы одним маршрутом. Число ребер маршрута
определяет его длину.
Ребра, инцидентные
одной паре вершин, называются параллельными
или кратными.
Граф с кратными ребрами называется
мультиграфом.
Ребро
![]() называетсяпетлей
называетсяпетлей
(концевые вершины совпадают). Граф,
содержащий петли и кратные ребра,
называется псевдографом.
На рис. 12.2 показан псевдограф.

Рис. 12.2
Степень
deg(v)
вершины – это число ребер, инцидентных
v.
В неографе
сумма степеней всех вершин равна
удвоенному числу ребер
(лемма о рукопожатиях):
![]() . (12.1)
. (12.1)
Петля дает вклад,
равный 2, в степень вершины.
Степенная
последовательность
– последовательность степеней всех
вершин графа, записанная в определенном
порядке (по возрастанию или убыванию).
Пример
12.1. Степенная
последовательность неографа, изображенного
на рис. 12.1, записанная по возрастанию,
выглядит так:
![]() =1,
=1,
![]() =2,
=2,![]() =3,
=3,![]() =3,
=3,![]() =3.
=3.
Сумма степеней
всех вершин графа равна:
![]() .
.
Этот результат
не противоречит лемме о рукопожатиях,
поскольку граф имеет шесть ребер (m
= 6).
Матрица
смежности
графа – квадратная матрица A
порядка n,
где элемент
![]() равен числу ребер, соединяющих вершиныi
равен числу ребер, соединяющих вершиныi
и j.
Пример 12.2.
Граф, показанный на рис. 12.1, имеет
следующую матрицу смежности
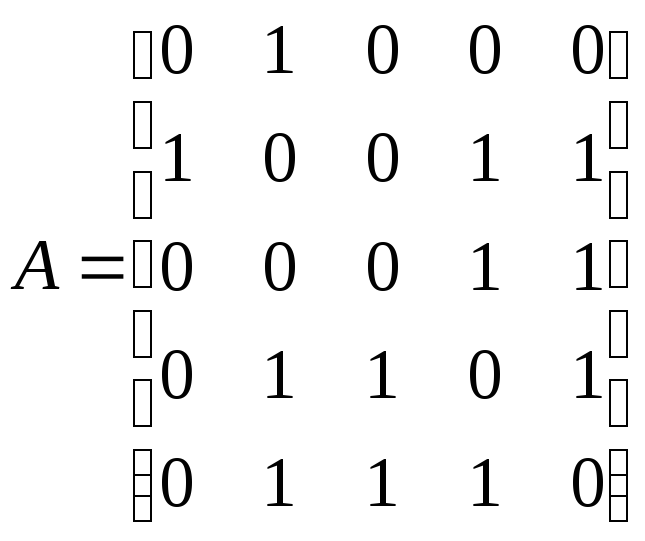 .
.
Матрица
инцидентности
I
– еще один способ описания графа. Число
строк этой матрицы равно числу вершин,
число столбцов – числу ребер;
![]() =1,
=1,
если вершинаv
инцидентна ребру e;
в противном случае
![]() =0.
=0.
В каждом столбце матрицы инцидентности
простого графа (без петель и без кратных
ребер) содержится по две единицы. Число
единиц в строке равно степени
соответствующей вершины.
Пример 12.3.
Граф, показанный на рис. 12.1, имеет
следующую матрицу инцидентности
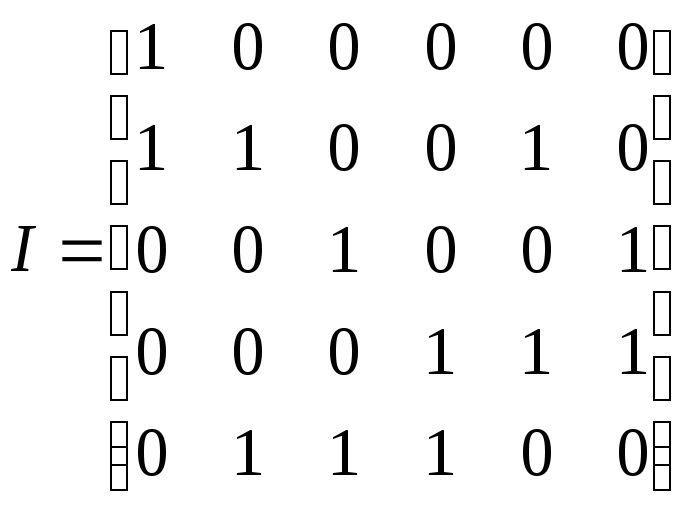 .
.
Граф
![]() называетсяподграфом
называетсяподграфом
графа
![]() ,
,
если![]() и
и![]() .
.
Если![]() ,
,
то подграф называетсяостовным.
Компонента
связности
графа – максимальный по включению
вершин и ребер связной подграф.
Ранг
графа
![]() ,
,
гдеk
– число компонент связности.
Дерево
– связной граф, содержащий n
– 1 ребро.
Пример 12.4.
На рис. 12.3 показано дерево, которое
одновременно является остовным подграфом
графа, показанного на рис. 12.1.

Рис. 12.3
-
Радиус, диаметр
и центр графа
Вычисление
расстояний и определение маршрутов в
графе являются одной из наиболее
очевидных и практичных задач, которые
возникают в теории графов. Введем
некоторые необходимые определения.
Эксцентриситет
вершины графа – расстояние до максимально
удаленной от нее вершины. Для графа, для
которого не определен вес
его ребер, расстояние определяется в
виде числа ребер.
Радиус
графа – минимальный эксцентриситет
вершин, а диаметр
графа – максимальный эксцентриситет
вершин.
Центр
графа образуют вершины, у которых
эксцентриситет равен радиусу. Центр
графа может состоять из одной, нескольких
или всех вершин графа.
Периферийные
вершины имеют эксцентриситет, равный
диаметру.
Простая цепь с
длиной, равной диаметру графа, называется
диаметральной.
Теорема 12.1.
В связном графе диаметр не больше ранга
его матрицы смежности.
Теорема 12.2.
(Жордана) Каждое дерево имеет центр,
состоящий из одной или двух смежных
вершин.
Теорема 12.3.
Если диаметр дерева четный, то дерево
имеет единственный центр, и все
диаметральные цепи проходят через него,
если диаметр нечетный, то центров два
и все диаметральные цепи содержат ребро,
их соединяющее.
Очевидно практическое
значение центра графа. Если, например,
речь идет о графе дорог с вершинами-городами,
то в математическом центре целесообразно
размещать административный центр,
складские помещения и т.п. Этот же подход
можно применять и для взвешенного графа,
где расстояния – это веса ребер. В
качестве веса можно брать евклидовое
расстояние, время или стоимость
передвижения между пунктами.
Пример 12.5.
Найти радиус, диаметр и центр графа,
изображенного на рис. 12.1.
Решение.
В данной задаче удобно использовать
матрицу
расстояний S.
Элемент этой квадратной симметричной
матрицы
![]() равен расстоянию между вершинойi
равен расстоянию между вершинойi
и вершиной j.
Для графа, показанного на рис. 12.1, матрица
расстояний имеет следующий вид:
 . (12.2)
. (12.2)
Вычислим
эксцентриситет
![]() каждой вершины. Эту величину можно
каждой вершины. Эту величину можно
определить как максимальный элемент
соответствующего столбца матрицы
расстояний (или строки – поскольку
матрицаS
симметрична).
Получаем
|
№ |
1 |
2 |
3 |
4 |
5 |
|
|
3 |
2 |
3 |
2 |
2 |
Радиус графа r
– минимальный эксцентриситет вершин.
В данном случае r
= 2. Такой эксцентриситет имеют вершины
№ 2, № 4 и № 5. Эти вершины образуют центр
графа. Диаметр графа d
– максимальный эксцентриситет вершин.
В данном случае d
= 3. Такой эксцентриситет имеют вершины
№ 1 и № 3, это периферия графа. В
исследованном графе вершины оказались
либо центральными, либо периферийными.
В графах большего порядка существуют
и другие вершины.
Эксцентриситеты
вершин небольшого графа легко вычислять
непосредственным подсчетом по рисунку.
Однако не всегда граф задан своим
рисунком. Кроме того, граф может иметь
большой размер. Поэтому необходим другой
способ решения предыдущей задачи.
Известна следующая теорема.
Теорема
12.4. Пусть
![]() – матрица смежности графаG
– матрица смежности графаG
без петель и
![]() ,
,
где![]() .
.
Тогда![]() равно числу маршрутов длиныk
равно числу маршрутов длиныk
от вершины
![]() к вершине
к вершине![]() .
.
Решение задач
теории графов с помощью различных
преобразований матрицы смежности
называют алгебраическим
методом.
Пример 12.6.
Найти матрицу расстояний графа,
изображенного на рис. 12.1, алгебраическим
методом.
Решение.
Матрица смежности данного графа равна:
 .
.
Будем заполнять
матрицу расстояний, рассматривая степени
матрицы смежности. Единицы матрицы
смежности показывают пары вершин,
расстояние между которыми равно единице
(т.е. они соединены одним ребром).
 .
.
Диагональные
элементы матрицы расстояний – нули.
Умножаем матрицу смежности на себя:
 .
.
Согласно теореме
между вершинами 2 и 3, 1 и 4 и т.д. имеется
некоторое число маршрутов длиной 2
(поскольку степень матрицы равна двум).
Число маршрутов здесь не используется,
важен сам факт наличия маршрута и его
длина, на что и указывает ненулевой
элемент степени матрицы, не совпадающий
с элементом, отмеченным при вычислении
маршрута меньшей длины. Проставляем 2
в незаполненные элементы матрицы
расстояний и получаем следующее
приближение:
 .
.
Осталось неизвестным
расстояние между вершинами 1 и 3. Будем
умножать матрицу смежности
![]()
саму на себя до тех пор, пока в матрице
![]()
не появится ненулевой элемент
![]() .
.
Тогда соответствующий элемент матрицы
расстояний равен степени матрицы
смежности:
![]() .
.
На следующем шаге получаем
 ,
,
следовательно,
![]() ,
,
и окончательно
 .
.
Полученная матрица
совпадает с матрицей расстояний S
(12.2), найденной непосредственными
вычислениями по рисунку.
-
Эйлерова цепь
Маршрут в неографе,
в котором все ребра разные, называется
цепью.
Цепь в графе называется эйлеровой,
если она содержит все ребра и все вершины
графа.
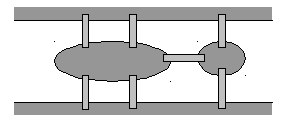
Рис. 12.4. Схема
Кенигсбергских мостов
Теория графов
многократно переоткрывалась разными
авторами при решении различных прикладных
задач. В их ряду – знаменитый математик
Леонард Эйлер (1707-1783). К созданию теории
графов его подтолкнула задача о
Кенигсберских мостах, которую он решил
в 1736 году. По условию задачи требовалось
пройти по всем семи мостам города
Кенигсберга через реку Преголь по одному
разу и вернуться к исходной точке. На
рис. 12.4 показана схема этих мостов (один
из них соединяет между собой два острова,
а остальные – острова с берегами). Этой
схеме соответствует приведенный на
следующем рисунке мультиграф с четырьмя
вершинами.

Рис. 12.5
Эйлер решил задачу
о Кенигсбергских мостах в отрицательном
смысле. Он доказал, что данная задача
не имеет решения. Для этого ему пришлось
доказать следующую теорему.
Теорема 12.5
(Эйлера).
Мультиграф обладает эйлеровой цепью
тогда и только тогда, когда он связен и
число вершин нечетной степени равно 0
или 2.
Вершины нечетной
степени в этой теореме, очевидно, являются
началом и концом цепи. Если таких вершин
нет, то эйлерова цепь становится эйлеровым
циклом.
Граф, обладающий эйлеровым циклом,
называется эйлеровым.
Если граф имеет эйлерову цепь, но не
обладает эйлеровым циклом (число вершин
нечетной степени равно 2), то он называется
полуэйлеровым
графом.
Предположим, что
граф имеет эйлеров цикл. Двигаясь по
нему, будем подсчитывать степени вершин,
полагая их до начала прохождения
нулевыми. Прохождение каждой вершины
вносит 2 в степень этой вершины. Поскольку
эйлеров цикл содержит все ребра, то
когда обход будет закончен, будут учтены
все ребра, а степени вершин – четные.
Все четыре вершины
мультиграфа, показанного на рис. 12.5,
имеют нечетные степени. Поэтому этот
граф не обладает эйлеровым циклом, а
задача о Кенигсбергских мостах не имеет
решения.
Рассмотрим для
сравнения граф, обладающий эйлеровой
цепью. В графе на рис. 12.6 только две
вершины имеют нечетную степень,
следовательно, эйлерова цепь есть.

Рис. 12.6
Цепей может быть
несколько. Например, граф на рис. 12.6
имеет две эйлеровы цепи: 1-2-3-4-1-3 и
1-2-3-1-4-3.
-
Реберный граф
Рассмотрим два
графа G
и L(G).
Граф G
имеет произвольную форму, а вершины
графа L(G)
расположены на ребрах графа G.
В этом случае граф L(G)
называется реберным
графом по
отношению к графу G.
Английское название
реберного графа – line
graph,
отсюда и обозначение графа – L(G).
На рис. 12.7 показан реберный граф (он
выделен жирными линиями), построенный
для графа с рис. 12.1.

Рис. 12.7. Реберный
граф
Теорема 12.6.
Если
![]() – степенная последовательность (n,
– степенная последовательность (n,
m)
графа G,
то L(G)
является (m,
![]() )-графом,
)-графом,
где
![]() . (12.3)
. (12.3)
Для графа G,
показанного на рис. 12.7 (и рис. 12.1), его
степенная последовательность: 1-3-2-3-3.
Поэтому
![]() .
.
-
Раскраска графа,
хроматический полином
Предположим, что
перед нами стоит задача: раскрасить
карту мира так, чтобы каждая страна
имела свой собственный цвет. Поскольку
на свете существует несколько сотен
государств, то, естественно, потребуется
достаточно много разных красок.
Упростим задачу.
Будем использовать меньшее количество
красок, но при этом не будем допускать,
чтобы соседние страны, имеющие общие
границы, были окрашены в один цвет.
Возникает вопрос: какое минимальное
количество красок требуется, чтобы
удовлетворить этому условию?
Ответить на этот
вопрос можно с помощью теории графов.
Для этого нужно представить карту мира
в виде графа, каждая вершина которого
соответствует отдельной стране, а ребро
между смежными вершинами соответствует
наличию между странами общей границы.
Произвольная
функция
![]()
на множестве вершин графа называется
раскраской
графа. Раскраска называется правильной,
если
![]()
для любых смежных вершин
![]() и
и![]() .
.
Минимальное числоk,
при котором граф G
является k-раскрашиваемым
называется хроматическим
числом
графа
![]() .
.
Граф называется
пустым,
если в нем удалены все ребра и вершины
изолированы друг от друга. Граф называется
полным,
если в нем нельзя добавить новое ребро,
не добавив при этом одновременно новую
вершину.
Теорема 12.7
(Брукса).
Для любого графа G,
не являющегося полным,
![]() ,
,
если![]() –максимальная
–максимальная
из степеней вершин графа.
Для определения
количества способов раскраски графа в
x
цветов, необходимо составить хроматический
полином
P(G,
x).
Значение полинома при некотором
конкретном
![]() равно числу правильных раскрасок графа
равно числу правильных раскрасок графа
в![]() цветов.
цветов.
Существует лемма,
утверждающая, что хроматический
полином графа имеет вид
![]() ,(12.4)
,(12.4)
где
![]() – граф, полученный изG
– граф, полученный изG
добавлением ребра (u,
v),
а граф
![]() получается изG
получается изG
отождествлением вершин u
и v.
Другой вариант
леммы:
![]() , (12.5)
, (12.5)
где
![]() – граф, полученный изG
– граф, полученный изG
удалением ребра (u,
v),
а граф
![]() получается изG
получается изG
отождествлением вершин u
и v.
Операцию
отождествления вершин u
и
v
называют также стягиванием ребра (u,
v).
Оба варианта леммы
составляют основу для хроматической
редукции графа (reduction
– «сокращение» на английском).
Хроматическая редукция графа –
представление графа в виде нескольких
пустых или полных графов, сумма
хроматических полиномов которых равна
хроматическому полиному графа. Очевидно,
что хроматический полином пустого графа
![]() равен
равен![]() (каждая вершина может быть раскрашена
(каждая вершина может быть раскрашена
независимо от других), а для полного
графа![]() .
.
Последнее выражение называютфакториальной
степенью
переменной x:
![]() .
.
Разложения по
пустым и полным графам связаны.
Факториальную степень можно представить
в виде полинома:
![]() , (12.6)
, (12.6)
где
![]() – числа Стирлинга первого рода. И
– числа Стирлинга первого рода. И
наоборот, степень![]() можно выразить через факториальные
можно выразить через факториальные
степени:
![]() , (12.7)
, (12.7)
где
![]() – числа Стирлинга второго рода, обладающие
– числа Стирлинга второго рода, обладающие
следующими свойствами:
![]() при
при
![]() , (12.8)
, (12.8)
![]() при
при
![]() ,
,![]() при
при![]() .
.
При получении
хроматического полинома могут быть
полезны следующие теоремы.
Теорема 12.8.
Коэффициенты хроматического полинома
составляют знакопеременную
последовательность.
Теорема 12.9.
Абсолютная величина второго коэффициента
хроматического полинома равна числу
ребер графа.
Теорема 12.10.
Наименьшее число i,
для которого отличен от нуля коэффициент
при
![]()
в хроматическом полиноме графа G,
равно числу компонент связности графа
G.
Кроме вершинной
раскраски, существует еще реберная
раскраска и раскраска граней.
Пример 12.7.
Найти хроматический полином графа,
показанного на рис. 12.8.

Рис. 12.8
Решение.
В зависимости от числа ребер графа можно
использовать разложение (12.4) или (12.5).
Если граф почти полный, то, добавив
несколько ребер по разложению (12.4),
получим хроматический полином в виде
суммы факториальных степеней. Если же
ребер мало и для получения пустого графа
требуется удалить только несколько
ребер, то следует использовать разложение
(12.5) с удалением ребер. Такие действия
называются хроматической редукцией.
1. Хроматическая
редукция по пустым графам.
Воспользуемся вначале леммой (12.5). Удаляя
ребра и отождествляя соответствующие
вершины (стягивая ребра), сведем исходный
граф к пустым графам. Сначала разложим
граф на два, убрав, а затем стянув ребро
1-3. Выполненное действие запишем в виде
условного равенства:

Здесь
операция вычитания относится не к самому
графу, а к его хроматическому полиному.
Таким образом, последнее равенство
означает, что
![]() .
.
Для сокращения записи обозначениеP(…)
будем опускать. Далее разложим каждый
из графов
![]()
и
![]() ,
,
пользуясь той же леммой.


Приведем подобные
члены:
![]() (12.9)
(12.9)
В итоге получим
искомый хроматический полином:
![]() . (12.10)
. (12.10)
Разложение (12.9)
называется хроматической редукцией
графа по пустым графам.
Очевидно, что
результат соответствует утверждениям
теорем 12.8-12.10. Коэффициенты в (12.10) образуют
знакопеременную последовательность,
а коэффициент при
![]() равен четырем – числу ребер. Наименьшая
равен четырем – числу ребер. Наименьшая
степеньx
в полиноме равна 1, т.е. числу компонент
связности графа.
2. Хроматическая
редукция по полным графам.
Добавив к изображенному на рис. 12.8 графу
ребро 1–4, получим граф с большим числом
ребер. Затем в исходном графе отождествим
вершины 1 и 4. В результате получим два
графа.

Отождествление
вершин приводит к уменьшению порядка
и иногда размера графа. Второй граф –
это полный граф
![]() ,
,
его преобразовывать больше не требуется.
К первому графу добавим ребро 1–2 и
отождествим вершины 1 и 2:

В итоге получим
 (12.11)
(12.11)
Хроматический
полином примет вид
![]() (12.12)
(12.12)
Разложение (12.11)
называется хроматической редукцией
графа по полным графам.
Оба способа дали
один результат, и из редукции по полным
графам легко получить редукцию по
пустым. Для этого достаточно раскрыть
скобки и привести подобные члены, как
в (12.12). Однако обратное действие не
очевидно. Для того чтобы полином
![]() ,
,
полученный из пустых графов, выразить
в виде суммы факториальных степеней,
необходимы числа Стирлинга 2-го рода.
Согласно рекуррентным формулам (12.8)
имеем следующие числа:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Пользуясь (12.7) и
найденными числами Стирлинга 2-го рода,
получим
![]() ,
,
![]() ,
,
![]() .
.
Произведем
преобразование хроматического полинома:
![]()
Хроматическое
число
![]() графа лучше всего получить, разложив
графа лучше всего получить, разложив
хроматический полином на множители:
![]() .
.
Минимальное
натуральное число x,
при котором
![]() не обращается в нуль, равно 3. Отсюда
не обращается в нуль, равно 3. Отсюда
следует![]() .
.
Так как максимальная степень вершин
графа![]() ,
,
выполняется оценка![]() .
.
-
Ранг-полином
графа
Ранг графа
определяется как
![]() ,
,
гдеn
– число вершин, k
– число компонент связности графа.
Коранг графа, или цикломатический ранг,
есть
![]() ,
,
гдеm
– число ребер.
Ранг-полином графа
G
имеет вид
![]() ,
,
где
![]() – ранг графаG
– ранг графаG
, а
![]() – корангостовного
– корангостовного
(т.е. включающего в себя все вершины
графа) подграфа H,
а
![]() – его ранг. Суммирование ведется по
– его ранг. Суммирование ведется по
всем остовным подграфам графаG.
Ранг полином
служит для анализа множества остовных
подграфов. Так, например, коэффициент
при
![]() в
в![]() есть число подграфов размераk,
есть число подграфов размераk,
а значение
![]() равно числу подграфов (включая
равно числу подграфов (включая
несобственный подграф), ранг которых
равен рангу самого графа.
Пример
12.8. Найти
ранг-полином графа, изображенного на
рис. 12.8.
Решение.
Найдем все 16 остовных подграфов графа
G
(рис. 12.9). Множество представим в виде
четырех графов размера 1 (т.е. с одним
ребром), шести графов размера 2, четырех
графов размера 3 и двух несобственных
графов (пустой граф и граф G).

Рис. 12.9
Учитывая, что ранг
![]() графа равен 3, получаем сумму:
графа равен 3, получаем сумму:

-
Циклы
Маршрут, в котором
начало и конец совпадают, – циклический.
Циклический маршрут называется циклом,
если он – цепь.
Остовом
графа G
называется граф, не содержащий циклов
и состоящий из ребер графа G
и всех его вершин. Остов графа определяется
неоднозначно.
Ребра графа, не
входящие в остов, называются хордами.
Цикл, получающийся при добавлении к
остову графа его хорды, называется
фундаментальным
относительно
этой хорды.
Теорема 12.11.
Число ребер неографа, которые необходимо
удалить для получения остова, не зависит
от последовательности их удаления и
равно цикломатическому рангу графа.
Пример 12.8.
По заданной матрице смежности:
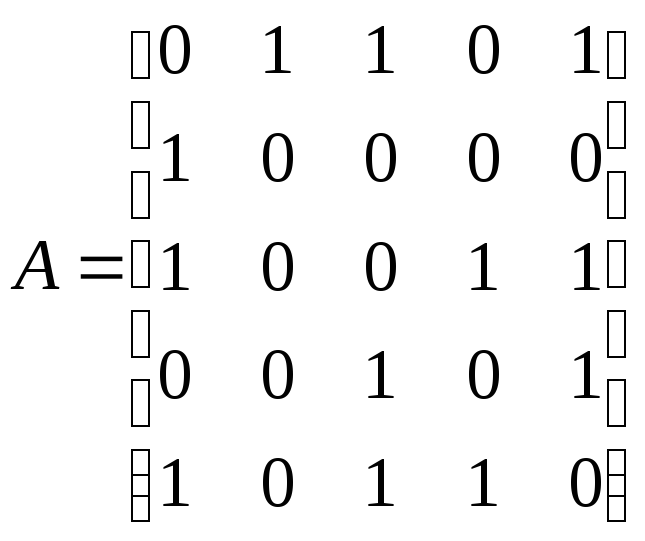 ,
,
определить число
циклов длины 3 (![]() )
)
и длины 4 (![]() ).
).
Записатьматрицу
фундаментальных циклов.
Решение.
Матрица смежности данного графа
симметричная, поэтому ей соответствует
неориентированный граф. Сумма ненулевых
элементов матрицы равна 12, следовательно,
по лемме о рукопожатиях в графе 6 ребер.
Построим этот граф (рис. 12.10). Очевидно,
в нем два цикла (3–4–5 и 1–3–5) длиной 3 и
один цикл (1–3–4–5) длиной 4. В данной
задаче решение получено прямым подсчетом
по изображению графа. Для более сложных
случаев существует алгоритм решения
задачи по матрице смежности.
Известно, что след
(trace)
матрицы смежности, возведенный в k-ю
степень, равен числу циклических
маршрутов длины k
(см. теорему 12.4). Это число включает в
себя и искомое число циклов. Цикл
отличается от циклического маршрута
тем, что в нем не повторяются ребра.
Кроме того, предполагается, что искомые
циклы не помечены, а в след матрицы
входят именно помеченные маршруты.

Рис. 12.10
Непомеченных
циклов длиной 3 в 6 раз меньше, чем
помеченных, так как каждый помеченный
цикл может отличаться началом (а их в
данном случае три) и двумя направлениями
обхода (по и против часовой стрелки).
Возведем заданную матрицу смежности в
третью степень:
 ,
,
и получим
![]() .
.
Поскольку
циклических маршрутов длиной 3, отличных
от циклов длиной 3, не существует,
найденное число и есть ответ в поставленной
задаче.
С циклами длиной
4 немного сложнее. В след четвертой
степени матрицы смежности графа
 ,
,
входят не только
циклы, но и циклические маршруты с
двойным и четырехкратным прохождением
ребер. Обозначим количество таких
маршрутов через
![]() и
и![]() соответственно. Очевидно, число маршрутов
соответственно. Очевидно, число маршрутов
с четырехкратным прохождением одного
ребра для вершины![]() равно степени этой вершины:
равно степени этой вершины:![]() .
.
Число маршрутов с двукратным прохождением
ребра складывается из числа![]() с висячей вершиной
с висячей вершиной![]() и числа
и числа![]() маршрутов с вершиной
маршрутов с вершиной![]() в центре.
в центре.
Легко заметить,
что
![]() .
.
Число![]() зависит от степеней вершин, соседних с
зависит от степеней вершин, соседних с![]() :
:
![]() ,
,
где
![]() – ребро, инцидентное вершинамi
– ребро, инцидентное вершинамi
и k.
Для графа на рис.
12.10 получим
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
С учетом того, что
непомеченных циклов длиной 4 в 8 раз
меньше, получим
![]() .
.
После преобразований
формула примет вид
 .
.
Для нахождения
матрицы фундаментальных циклов
пронумеруем ребра графа, начиная
нумерацию с хорд, как показано на рис.
12.11 (а).

Рис. 12.11
Двум хордам, 1 и 2,
соответствуют два фундаментальных
цикла: 1–4–5 и 2–4–6 (рис. 12.11 (б и в)).
Матрица фундаментальных циклов имеет
две строки (число циклов) и шесть столбцов
(число ребер).
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
2 |
0 |
1 |
0 |
1 |
0 |
1 |
В первой строке
матрицы единицами отмечены столбцы с
номерами ребер, входящих в первый цикл,
а во второй строке – номера ребер из
второго цикла.
Определение. Пусть G – связный неориентированный граф, включающий вершины u и v. Расстоянием d(u, v) между вершинами u и v называется длина самой короткой цепи, соединяющей эти вершины. По определению d(u, u) = 0.
Заметим, что введенное таким образом понятие расстояния между вершинами удовлетворяет аксиомам метрики:
1) d(u, v) больше либо равно 0;
2) d(u, v) = 0 тогда и только тогда, когда u = v;
3) d(u, v) = d(v,u);
4) справедливо неравенство треугольника:
d(u,w) меньше либо равно d(u,v) + d(v,w).
Определение. Пусть G – связный неориентированный граф со множеством вершин V, d(u, v) – расстояние между вершинами u и v. Эксцентриситетом (максимальным удалением) вершины u называется величина
Заметим, что в полном графе эксцентриситет каждой вершины равен единице, а в неориентированном графе, имеющем простые циклы длины n, эксцентриситет каждой вершины равен n2.
Определение. Пусть G – неориентированный граф. Пусть MР − матрица, строки и столбцы которой обозначены вершинами графа. Элементы, находящиеся на пересечении строки u и столбца v матрицы MР, обозначаемые dij, равны расстоянию d(u,v) между вершинами u и v. Матрица MР называется матрицей расстояний графа G.
Свойства матрицы расстояний:
1) значения расстояний всегда неотрицательны, поэтому и элементы матрицы расстояний неотрицательны;
2) если неориентированный граф G является графом без петель, то элементы главной диагонали матрицы расстояний все нулевые;
3) матрица расстояний симметрична относительно главной диагонали;
4) выполняется неравенство треугольника: dik меньше либо равно dij + djk.
Для демонстрации примеров приведём несколько примеров графов G1 – G3.
Пример 1. Определим эксцентриситет для неориентированных графов G1– G3, показанных на рис. выше.
Для неориентированного графа G1 получаем:
d(a,b) = 1, d(a,c) = 1, d(a,d) = 2, d(a,e) = 2, d(a,f) = 3,
d(b,c) = 2, d(b,d) = 1, d(b,e) = 3, d(b,f) = 2,
d(c,d) = 1, d(c,e) = 1, d(c,f) = 2,
d(d,e) = 2, d(d,f) = 1,
d(e,f) = 3,
следовательно, e(a) = e(b) = e(e) = e(f) = 3, e(c) = e(d) = 2.
Для неориентированного графа G2 получаем:
d(a,b) = 4, d(a,c) = 1, d(a,d) = 2, d(a,e) = 3, d(a,f) = 3,
d(b,c) = 3, d(b,d) = 2, d(b,e) = 1, d(b,f) = 3,
d(c,d) = 1, d(c,e) = 2, d(c,f) = 2,
d(d,e) = 1, d(d,f) = 1,
d(e,f) = 2,
следовательно, e(a) = e(b) = 4, e(c) = e(e) = e(f) = 3, e(d) = 2.
Для неориентированного графа G3 получаем d(a,a) = 0, следовательно, e(a) = 0.
Пример 2. Запишем матрицы расстояний для неориентированных графов G1– G3, показанных на рис. выше.
Неориентированный граф G1 состоит из шести вершин, поэтому его матрица расстояний имеет размерность 6 на 6:
Неориентированный граф G2 также состоит из шести вершин, поэтому его матрица расстояний также имеет размерность 6 на 6:
Неориентированный граф G3 состоит из единственной вершины, поэтому его матрица расстояний имеет размерность 1 на 1, другими словами, имеет единственный элемент, равный нулю.
Определение. Пусть G – связный неориентированный граф, e(u) – эксцентриситет (максимальное удаление) вершины u. Радиусом r(G) графа G называется минимальный эксцентриситет графа
Диаметром d(G) графа G называется максимальный эксцентриситет графа
Определение. Вершина u называется центральной, если e(u) = r(G). Множество всех центральных вершин неориентированного графа называют его центром. Вершина u называется периферийной, если e(u) = d(G).
Заметим, что для любого неориентированного графа справедливо следующее соотношение: r(G) меньше либо равно d(G).
Заметим, что в полном графе радиус графа совпадает с диаметром графа, равным единице d(Kn) = r(Kn) = 1, а в неориентированном графе, имеющем простые циклы длины n, радиус графа совпадает с диаметром графа, равным n2.
Пример 3. Определим радиус и диаметр неориентированных графов G1– G3, показанных на рис. выше. Какие вершины являются центральными, периферийными?
Для неориентированного графа G1 имеем e(a) = e(b) = e(e) = e(f) = 3, e(c) = e(d) = 2, следовательно, получаем радиус графа G1, равный 2, диаметр графа G1, равный 3. Следовательно, центральными вершинами являются вершины cи d, а периферийными вершинами – a, b, e, f.
Для неориентированного графа G2 имеем e(a) = e(b) = 4, e(c) = e(e) = e(f) = 3, e(d) = 2, следовательно, получаем радиус графа G2, равный 2, диаметр графа G1, равный 4. Следовательно, центральной вершиной является вершина d, а периферийными вершинами – a и b.
Для неориентированного графа G3 получаем: r(G3) = d(G3) = 0. Следовательно, центральной вершиной графа G3 является вершина, являющаяся также периферийной, т.е. вершина a.
В качестве Упражнения предлагается
1) определить расстояние заданного неориентированного графа (варианты ниже);
2) задать произвольным образом веса заданного неориентированного графа и записать матрицу расстояний;
3) определить радиус и диаметр.
Варианты неориентированных графов:
In mathematics, computer science and especially graph theory, a distance matrix is a square matrix (two-dimensional array) containing the distances, taken pairwise, between the elements of a set.[1] Depending upon the application involved, the distance being used to define this matrix may or may not be a metric. If there are N elements, this matrix will have size N×N. In graph-theoretic applications the elements are more often referred to as points, nodes or vertices.
Non-metric distance matrix[edit]
In general, a distance matrix is a weighted adjacency matrix of some graph. In a network, a directed graph with weights assigned to the arcs, the distance between two nodes of the network can be defined as the minimum of the sums of the weights on the shortest paths joining the two nodes.[2] This distance function, while well defined, is not a metric. There need be no restrictions on the weights other than the need to be able to combine and compare them, so negative weights are used in some applications. Since paths are directed, symmetry can not be guaranteed, and if cycles exist the distance matrix may not be hollow.
An algebraic formulation of the above can be obtained by using the min-plus algebra. Matrix multiplication in this system is defined as follows: Given two n × n matrices A = (aij) and B = (bij), their distance product C = (cij) = A ⭑ B is defined as an n × n matrix such that
Note that the off-diagonal elements that are not connected directly will need to be set to infinity or a suitable large value for the min-plus operations to work correctly. A zero in these locations will be incorrectly interpreted as an edge with no distance, cost, etc.
If W is an n × n matrix containing the edge weights of a graph, then Wk (using this distance product) gives the distances between vertices using paths of length at most k edges, and Wn is the distance matrix of the graph.
An arbitrary graph G on n vertices can be modeled as a weighted complete graph on n vertices by assigning a weight of one to each edge of the complete graph that corresponds to an edge of G and zero to all other edges. W for this complete graph is the adjacency matrix of G. The distance matrix of G can be computed from W as above, however, Wn calculated by the usual matrix multiplication only encodes the number of paths between any two vertices of length exactly n.
Metric distance matrix[edit]
The value of a distance matrix formalism in many applications is in how the distance matrix can manifestly encode the metric axioms and in how it lends itself to the use of linear algebra techniques. That is, if M = (xij) with 1 ≤ i, j ≤ N is a distance matrix for a metric distance, then
- the entries on the main diagonal are all zero (that is, the matrix is a hollow matrix), i.e. xii = 0 for all 1 ≤ i ≤ N,
- all the off-diagonal entries are positive (xij > 0 if i ≠ j), (that is, a non-negative matrix),
- the matrix is a symmetric matrix (xij = xji), and
- for any i and j, xij ≤ xik + xkj for all k (the triangle inequality). This can be stated in terms of tropical matrix multiplication
When a distance matrix satisfies the first three axioms (making it a semi-metric) it is sometimes referred to as a pre-distance matrix. A pre-distance matrix that can be embedded in a Euclidean space is called a Euclidean distance matrix.
Another common example of a metric distance matrix arises in coding theory when in a block code the elements are strings of fixed length over an alphabet and the distance between them is given by the Hamming distance metric. The smallest non-zero entry in the distance matrix measures the error correcting and error detecting capability of the code.
Additive distance matrix[edit]
An additive distance matrix is a special type of matrix used in bioinformatics to build a phylogenetic tree. Let x be the lowest common ancestor between two species i and j, we expect Mij = Mix + Mxj. This is where the additive metric comes from. A distance matrix M for a set of species S is said to be additive if and only if there exists a phylogeny T for S such that:
- Every edge (u,v) in T is associated with a positive weight duv
- For every i,j ∈ S, Mij equals the sum of the weights along the path from i to j in T
For this case, M is called an additive matrix and T is called an additive tree. Below we can see an example of an additive distance matrix and its corresponding tree:

Ultrametric distance matrix[edit]
The ultrametric distance matrix is defined as an additive matrix which models the constant molecular clock. It is used to build a phylogenetic tree. A matrix M is said to be ultrametric if there exists a tree T such that:
- Mij equals the sum of the edge weights along the path from i to j in T
- A root of the tree can be identified with the distance to all the leaves being the same
Here is an example of an ultrametric distance matrix with its corresponding tree:

Bioinformatics[edit]
The distance matrix is widely used in the bioinformatics field, and it is present in several methods, algorithms and programs. Distance matrices are used to represent protein structures in a coordinate-independent manner, as well as the pairwise distances between two sequences in sequence space. They are used in structural and sequential alignment, and for the determination of protein structures from NMR or X-ray crystallography.
Sometimes it is more convenient to express data as a similarity matrix.
It is also used to define the distance correlation.
Sequence alignment[edit]
An alignment of two sequences is formed by inserting spaces in arbitrary locations along the sequences so that they end up with the same length and there are no two spaces at the same position of the two augmented sequences.[3] One of the primary methods for sequence alignment is dynamic programming. The method is used to fill the distance matrix and then obtain the alignment. In typical usage, for sequence alignment a matrix is used to assign scores to amino-acid matches or mismatches, and a gap penalty for matching an amino-acid in one sequence with a gap in the other.
Global alignment[edit]
The Needleman-Wunsch algorithm used to calculate global alignment uses dynamic programming to obtain the distance matrix.
Local alignment[edit]
The Smith-Waterman algorithm is also dynamic programing based which consists also in obtaining the distance matrix and then obtain the local alignment.
Multiple sequence alignment[edit]
Multiple sequence alignment is an extension of pairwise alignment to align several sequences at a time. Different MSA methods are based on the same idea of the distance matrix as global and local alignments.
- Center star method. This method defines a center sequence Sc which minimizes the distance between the sequence Sc and any other sequence Si. Then it generates a multiple alignment M for the set of sequences S so that for every Si the alignment distance dM(Sc,Si) is the optimal pairwise alignment. This method has the characteristic that the computed alignment for S whose sum-of-pair distance is at most twice the optimal multiple alignment.
- Progressive alignment method. This heuristic method to create MSA first aligns the two most related sequences, and the it progressively aligns the next two most related sequences until all sequences are aligned
There are other methods that have their own program due to their popularity:
- ClustalW
- MUSCLE
- MAFFT
- MANGO
- And many more
MAFFT[edit]
Multiple alignment using fast fourier transform (MAFFT) is a program with an algorithm based on progressive alignment, and it offers various multiple alignment strategies. First, MAFFT constructs a distance matrix based on the number of shared 6-tuples. Second, it builds the guide tree based on the previous matrix. Third, it clusters the sequences with the help of the Fast Fourier Transform and starts the alignment. Based on the new alignment, it reconstructs the guide tree and align again.
Phylogenetic analysis[edit]
To perform phylogenetic analysis, the first step is to reconstruct the phylogenetic tree: given a collection of species, the problem is to reconstruct or infer the ancestral relationships among the species, i.e., the phylogenetic tree among the species. Distance matrix methods perform this activity.
Distance matrix methods[edit]
Distance matrix methods of phylogenetic analysis explicitly rely on a measure of “genetic distance” between the sequences being classified, and therefore require multiple sequences as an input. Distance methods attempt to construct an all-to-all matrix from the sequence query set describing the distance between each sequence pair. From this is constructed a phylogenetic tree that places closely related sequences under the same interior node and whose branch lengths closely reproduce the observed distances between sequences. Distance-matrix methods may produce either rooted or unrooted trees, depending on the algorithm used to calculate them.[4] Given n species, the input is an n x n distance matrix M where Mij is the mutation distance between species i and j . The aim is to output a tree of degree 3 which is consistent with the distance matrix.
They are frequently used as the basis for progressive and iterative types of multiple sequence alignment. The main disadvantage of distance-matrix methods is their inability to efficiently use information about local high-variation regions that appear across multiple subtrees.[4] Despite potential problems, distance methods are extremely fast, and they often produce a reasonable estimate of phylogeny. They also have certain benefits over the methods that use characters directly. Notably, distance methods allow use of data that may not be easily converted to character data, such as DNA-DNA hybridization assays.
The following are distance based methods for phylogeny reconstruction:
- Additive tree reconstruction
- UPGMA
- Neighbor joining
- Fitch-Margoliash
Additive tree reconstruction[edit]
Additive tree reconstruction is based on additive and ultrametric distance matrices. These matrices have a special characteristic:
Consider an additive matrix M. For any three species i, j, k, the corresponding tree is unique.[3] Every ultrametric distance matrix is an additive matrix. We can observe this property for the tree below, which consists on the species i, j, k.

The additive tree reconstruction technique starts with this tree. And then adds one more species each time, based on the distance matrix combined with the property mentioned above. If we consider for example an additive matrix M and 5 species a, b, c, d and e. First we form an additive tree for two species a and b. Then we chose a third one, let’s say c and attach it to a point x on the edge between a and b. The edge weights are computed with the property above. Next we add the fourth species d to any of the edges. If we apply the property then we identify that d should be attached to only one specific edge. Finally, we add e following the same procedure as before.
UPGMA[edit]
The basic principle of UPGMA(Unweighted Pair Group Method with Arithmetic Mean) is that similar species should be closer in the phylogenetic tree. Hence, it builds the tree by clustering similar sequences iteratively. The method works by building the phylogenetic tree bottom up from its leaves. Initially, we have n leaves (or n singleton trees), each representing a species in S. Those n leaves are referred as n clusters. Then, we perform n-1 iterations. In each iteration, we identify two clusters C1 and C2 with the smallest average distance and merge them to form a bigger cluster C. If we suppose M is ultrametric, for any cluster C created by the UPGMA algorithm, C is a valid ultrametric tree.
Neighbor joining[edit]
Neighbor is a bottom-up clustering method. It takes a distance matrix specifying the distance between each pair of sequences. The algorithm starts with a completely unresolved tree, whose topology corresponds to that of a star network, and iterates over the following steps until the tree is completely resolved and all branch lengths are known:
- Based on the current distance matrix calculate the matrix (defined below).
- Find the pair of distinct taxa i and j (i.e. with ) for which has its lowest value. These taxa are joined to a newly created node, which is connected to the central node. In the figure at right, f and g are joined to the new node u.
- Calculate the distance from each of the taxa in the pair to this new node.
- Calculate the distance from each of the taxa outside of this pair to the new node.
- Start the algorithm again, replacing the pair of joined neighbors with the new node and using the distances calculated in the previous step.[5]
Fitch-Margoliash[edit]
The Fitch–Margoliash method uses a weighted least squares method for clustering based on genetic distance. Closely related sequences are given more weight in the tree construction process to correct for the increased inaccuracy in measuring distances between distantly related sequences. The least-squares criterion applied to these distances is more accurate but less efficient than the neighbor-joining methods. An additional improvement that corrects for correlations between distances that arise from many closely related sequences in the data set can also be applied at increased computational cost.[6]
Data Mining and Machine Learning[edit]
Data Mining[edit]
A common function in data mining is applying cluster analysis on a given set of data to group data based on how similar or more similar they are when compared to other groups. Distance matrices became heavily dependent and utilized in cluster analysis since similarity can be measured with a distance metric. Thus, distance matrix became the representation of the similarity measure between all the different pairs of data in the set.
Hierarchical clustering[edit]
A distance matrix is necessary for traditional hierarchical clustering algorithms which are often heuristic methods employed in biological sciences such as phylogeny reconstruction. When implementing any of the hierarchical clustering algorithms in data mining, the distance matrix will contain all pair-wise distances between every point and then will begin to create clusters between two different points or clusters based entirely on distances from the distance matrix.
Where N is the number of points, Hierarchical clustering:
- Time Complexity is O(N^3) due to the repetitive calculations done after every cluster to update the distance matrix
- Space Complexity is O(N^2)
Machine Learning[edit]
Distance metrics are a key part of several machine learning algorithms, which are used in both supervised and unsupervised learning. They are generally used to calculate the similarity between data points: this is where the distance matrix is an essential element. The use of an effective distance matrix improves the performance of the machine learning model, whether it is for classification tasks or for clustering.[7]
K-Nearest Neighbors[edit]
A distance matrix is utilized in the k-NN algorithm which is the one of the slowest but simplest and most used instance-based machine learning algorithm that can be used in both in classification and regression tasks. It is one of the slowest machine learning algorithms since each test sample’s predicted result requires a fully computed distance matrix between the test sample and each training sample in the training set. Once the distance matrix is computed, the algorithm selects the K number of training samples that are the closest to the test sample to predict the test sample’s result based on the set’s majority(classification) or average (regression) value.
- Prediction Time Complexity O(k * n * d) to compute the distance between each test sample with every training sample to construct the distance matrix where:
- k = number of nearest neighbors selected
- n = size of the training set
- d = number of dimensions being used for the data
This classification focused model predicts the label of the target based on the distance matrix between the target and each of the training samples to determine the K-number of sample that are the closest/nearest to the target.

The distance matrix used to select K train samples for K-nn

Machine Learning model predicting target value with K-NN
Computer Vision[edit]
A distance matrix can be used in Neural Networks for 2D-to3D regression in image predicting machine learning models.
Information Retrieval[edit]
Distance Matricies Using Gaussian Mixture distance[edit]
- [1]* Gaussian mixture distance for performing accurate nearest neighbor search for information retrieval. Under an established Gaussian finite mixture model for the distribution of the data in the database, the Gaussian mixture distance is formulated based on minimizing the Kullback-Leibler divergence between the distribution of the retrieval data and the data in database. The comparison the performance of the Gaussian mixture distance with the well-known Euclidean and Mahalanobis distance based on a precision performance measurement. Experimental results demonstrate that the Gaussian mixture distance function is superior in the others for different types of testing data.
Potential basic algorithms worth noting on the topic of information retrieval is Fish School Search algorithm an information retival that partakes in the act of using distance matricies in order for gathering collective behavior of fish schools. By using a feeding operator to update their weights
Eq. A:
Eq. B:
Stepvol defines the size of the maximum volume displacement preformed with the distance matrix. Specifically using a Euclidean distance Matrix
Evaluation of the similarity or dissimilarity of Cosine similarity and Distance matrices[edit]

Conversion formula between cosine similarity and Euclidean Distance
- [2]* While the Cosine similarity measure is perhaps the most frequently applied proximity measure in information retrieval by measuring the angles between documents in the search space on the base of the cosine. Euclidean distance is invariant to mean-correction. The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean and variance. For the data which can be negative as well as positive, the null distribution for cosine similarity is the distribution of the dot product of two independent random unit vectors. This distribution has a mean of zero and a variance of 1/n. While Euclidean distance will be invariant to this correction.
Clustering Documents[edit]
The implementation of hierarchical clustering with distance-based metrics to organize and group similar documents together will require the need and utilization of a distance matrix. The distance matrix will represent the degree of association that a document has with another document that will be used to create clusters of closely associated documents that will be utilized in retrieval methods of relevant documents for a user’s query.
ISOMAP[edit]
Isomap incorporates distance matrices to utilize geodesic distances to able to compute lower-dimensional embeddings. This helps address a collection of documents that reside within a massive number of dimensions and be able perform document clustering.
Neighborhood Retrieval Visualizer (NeRV)[edit]
An algorithm used for both unsupervised and supervised visualization that uses distance matrices to find similar data based on the similarities shown on a display/screen.
The distance matrix needed for Unsupervised NeRV can be computed through fixed input pairwise distances.
The distance matrix needed for Supervised NeRV requires formulating a supervised distance metric to be able to compute the distance of the input in a supervised manner.
Chemistry[edit]
The distance matrix is a mathematical object widely used in both graphical-theoretical (topological) and geometric (topographic) versions of chemistry.[8] The distance matrix is used in chemistry in both explicit and implicit forms.
Interconversion mechanisms between two permutational isomers[edit]
Distance matrices were used as the main approach to depict and reveal the shortest path sequence needed to determine the rearrangement between the two permutational isomers.
Distance Polynomials and Distance Spectra[edit]
Explicit use of Distance matrices is required in order to construct the distance polynomials and distance spectra of molecular structures.
Structure-property model[edit]
Implicit use of Distance matrices was applied through the use of the distance based metric Weiner number/Weiner Index which was formulated to represent the distances in all chemical structures. The Weiner number is equal to half-sum of the elements of the distance matrix.
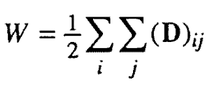
Conversion formula between Weiner Number and Distance Matrix
Graph-theoretical Distance matrix[edit]
Distance matrix in chemistry that are used for the 2-D realization of molecular graphs, which are used to illustrate the main foundational features of a molecule in a myriad of applications.
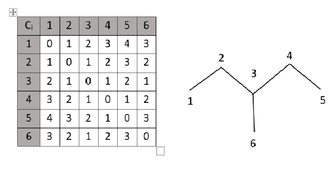
Labeled tree representation of C6H14‘s carbon skeleton based on its distance matrix
- Creating a label tree that represents the carbon skeleton of a molecule based on its distance matrix. The distance matrix is imperative in this application because similar molecules can have a myriad of label tree variants of their carbon skeleton. The labeled tree structure of hexane (C6H14) carbon skeleton that is created based on the distance matrix in the example, has different carbon skeleton variants that affect both the distance matrix and the labeled tree
- Creating a labeled graph with edge weights, used in chemical graph theory, that represent molecules with hetero-atoms.
- Le Verrier-Fadeev-Frame (LVFF) method is a computer oriented used to speed up the process of detecting the graph center in polycyclic graphs. However, LVFF requires the input to be a diagonalized distance matrix which is easily resolved by implementing the Householder tridiagonal-QL algorithm that takes in a distance matrix and returns the diagonalized distance needed for the LVFF method.
Geometric-Distance Matrix[edit]
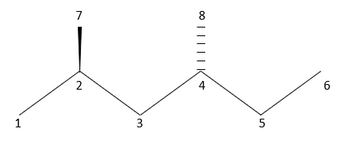
Geometric distance matrix for 2,4-dimethylhexane
While the graph-theoretical distance matrix 2-D captures the constitutional features of the molecule, its three-dimensional (3D) character is encoded in the geometric-distance matrix. The geometric-distance matrix is a different type of distance matrix that is based on the graph-theoretical distance matrix of a molecule to represent and graph the 3-D molecule structure.[8] The geometric-distance matrix of a molecular structure G is a real symmetric n x n matrix defined in the same way as a 2-D matrix. However, the matrix elements Dij will hold a collection of shortest Cartesian distances between i and j in G. Also known as topographic matrix, the geometric-distance matrix can be constructed from the known geometry of the molecule. As an example, the geometric-distance matrix of the carbon skeleton of 2,4-dimethylhexane is shown below:
Other Applications[edit]
Time Series Analysis[edit]
Dynamic Time Warping distance matrices are utilized with the clustering and classification algorithms of a collection/group of time series objects.
Examples[edit]
For example, suppose these data are to be analyzed, where pixel Euclidean distance is the distance metric.

Raw data
The distance matrix would be:
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| a | 0 | 184 | 222 | 177 | 216 | 231 |
| b | 184 | 0 | 45 | 123 | 128 | 200 |
| c | 222 | 45 | 0 | 129 | 121 | 203 |
| d | 177 | 123 | 129 | 0 | 46 | 83 |
| e | 216 | 128 | 121 | 46 | 0 | 83 |
| f | 231 | 200 | 203 | 83 | 83 | 0 |
These data can then be viewed in graphic form as a heat map. In this image, black denotes a distance of 0 and white is maximal distance.
Graphical View
See also[edit]
- Computer Vision
- Data clustering
- Distance set
- Hollow matrix
- Min-plus matrix multiplication
References[edit]
- ^ Weyenberg, G., & Yoshida, R. (2015). Reconstructing the phylogeny: Computational methods. In Algebraic and Discrete Mathematical methods for modern Biology (pp. 293–319). Academic Press.
- ^ Frank Harary, Robert Z. Norman and Dorwin Cartwright (1965) Structural Models: An Introduction to the Theory of Directed Graphs, pages 134–8, John Wiley & Sons MR0184874
- ^ a b Sung, Wing-Kin (2010). Algorithms in bioinformatics: A practical introduction. Chapman & Hall. p. 29. ISBN 978-1-4200-7033-0.
- ^ a b Felsenstein, Joseph (2003). Inferring phylogenies. Sinauer Associates. ISBN 9780878931774.
- ^ Saitou, Naruya (1987). “The neighbor-joining method: A new method for reconstructing phylogenetic trees”. Molecular Biology and Evolution. 4 (4): 406–425. doi:10.1093/oxfordjournals.molbev.a040454. PMID 3447015.
- ^ Fitch, Walter M. (1967). “Construction of Phylogenetic Trees: A method based on mutation distances as estimated from cytochrome c sequences is of general applicability”. Science. 155 (3760): 279–284. doi:10.1126/science.155.3760.279. PMID 5334057.
- ^ “4 types of distance metrics in machine learning”. February 25, 2020.
{{cite web}}: CS1 maint: url-status (link) - ^ a b Mihalic, Zlatko (1992). “The distance matrix in chemistry”. Journal of Mathematical Chemistry. 11: 223–258. doi:10.1007/BF01164206. S2CID 121181446.
Утверждение. Если для двух вершин существует маршрут, связывающий их, то обязательно найдется минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута через d(v, w).
Определение. Величину d(v, w) (конечную или бесконечную) будем называть расстоянием между вершинами v, w. Это расстояние удовлетворяет аксиомам метрики:
1) d(v, w) ![]() 0, причем d(v, w) = 0 тогда и только тогда, когда v=w;
0, причем d(v, w) = 0 тогда и только тогда, когда v=w;
2) d(v, w) = d(w, v);
3) d(v, w) ![]() d(v, u) + d(u, w).
d(v, u) + d(u, w).
Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.
Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.
Пример 82.
Для графа G, изображенного на рис. 3.16, найти радиус, диаметр и центры.
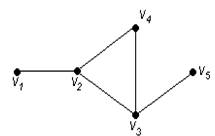
Рис. 3.16. Граф для примера 82
Решение.
Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами dij которой будут расстояния между вершинами vi и vj. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G) симметрична относительно главной диагонали. 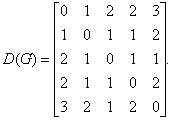
С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление из выражения: ![]() для i, j = 1, 2, …, 5. В результате получаем: r(v1) = 3, r(v2) = 2, r(v3) = 2, r(v4) = 2, r(v5) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v2, v3, v4.
для i, j = 1, 2, …, 5. В результате получаем: r(v1) = 3, r(v2) = 2, r(v3) = 2, r(v4) = 2, r(v5) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v2, v3, v4.
В математике , информатике и особенно теории графов , А матрица расстояний является квадратная матрица (двумерный массив) , содержащий расстояния , взятые попарно, между элементами набора. В зависимости от задействованного приложения расстояние , используемое для определения этой матрицы, может быть или не быть метрикой . Если есть N элементов, эта матрица будет иметь размер N × N . В теоретико-графических приложениях элементы чаще называют точками, узлами или вершинами.
Неметрические матрицы расстояний
В общем случае матрица расстояний – это взвешенная матрица смежности некоторого графа. В сети , ориентированном графе с весами, присвоенными дугам, расстояние между двумя узлами сети можно определить как минимум сумм весов на кратчайших путях, соединяющих два узла. Эта функция расстояния, хотя и хорошо определена, не является метрикой. Не требуется никаких ограничений на веса, кроме необходимости иметь возможность комбинировать и сравнивать их, поэтому в некоторых приложениях используются отрицательные веса. Поскольку пути являются направленными, симметрия не может быть гарантирована, и если существуют циклы, матрица расстояний не может быть пустой.
Алгебраическая формулировка сказанного выше может быть получена с помощью алгебры мин-плюс . Умножение матриц в этой системе определяется следующим образом: для двух матриц и их произведение расстояний определяется как матрица, такая что . Обратите внимание, что для недиагональных элементов, которые не связаны напрямую, необходимо установить бесконечность или подходящее большое значение для правильной работы операций min-plus. Ноль в этих местах будет неправильно интерпретирован как грань без расстояния, стоимости и т. Д.
Если – матрица, содержащая веса ребер графа , то (с использованием этого произведения расстояний) дает расстояния между вершинами, используя пути длины на большинстве ребер, и является матрицей расстояний графа.
Произвольный граф G на n вершинах можно смоделировать как взвешенный полный граф на n вершинах, присвоив вес, равный единице, каждому ребру полного графа, который соответствует ребру G, и нулю всем остальным ребрам. W для этого полного графа является матрица смежности из G . Матрица расстояний G может быть вычислена из W, как указано выше, однако W n, вычисленное обычным умножением матриц, кодирует только количество путей между любыми двумя вершинами длины ровно n .
Матрицы метрических расстояний
Ценность формализма матрицы расстояний во многих приложениях заключается в том, как матрица расстояний может явно кодировать аксиомы метрики и в том, как она поддается использованию методов линейной алгебры. То есть, если M = ( x ij ) с 1 ≤ i , j ≤ N – матрица расстояний для метрического расстояния, то
- все элементы на главной диагонали равны нулю (то есть матрица является пустой матрицей ), т.е. x ii = 0 для всех 1 ≤ i ≤ N ,
- все недиагональные элементы положительны ( x ij > 0, если i ≠ j ) (то есть неотрицательная матрица ),
- матрица является симметричной матрицей ( x ij = x ji ), и
- для любых i и j , x ij ≤ x ik + x kj для всех k (неравенство треугольника). Это можно сформулировать в терминах умножения тропических матриц
Когда матрица расстояний удовлетворяет первым трем аксиомам (что делает ее полуметрической), ее иногда называют матрицей предварительных расстояний. Матрица предварительных расстояний, которая может быть встроена в евклидово пространство, называется матрицей евклидовых расстояний .
Другой распространенный пример метрической матрицы расстояний возникает в теории кодирования, когда в блочном коде элементы представляют собой строки фиксированной длины по алфавиту, а расстояние между ними задается метрикой расстояния Хэмминга . Наименьший ненулевой элемент в матрице расстояний измеряет способность кода исправлять и обнаруживать ошибки.
Приложения
Иерархическая кластеризация
Матрица расстояний необходима для иерархической кластеризации .
Филогенетический анализ
Матрицы расстояний используются в филогенетическом анализе .
Другое использование
В биоинформатике матрицы расстояний используются для представления структур белков независимым от координат образом, а также попарных расстояний между двумя последовательностями в пространстве последовательностей. Они используются для структурного и последовательного выравнивания, а также для определения структур белков с помощью ЯМР или рентгеновской кристаллографии .
Иногда удобнее представить данные в виде матрицы сходства .
Он используется для определения корреляции расстояний .
Примеры
Например, предположим, что эти данные должны быть проанализированы, где евклидово расстояние пикселя является метрикой расстояния .

Необработанные данные
Матрица расстояний будет следующей:
| а | б | c | d | е | ж | |
|---|---|---|---|---|---|---|
| а | 0 | 184 | 222 | 177 | 216 | 231 |
| б | 184 | 0 | 45 | 123 | 128 | 200 |
| c | 222 | 45 | 0 | 129 | 121 | 203 |
| d | 177 | 123 | 129 | 0 | 46 | 83 |
| е | 216 | 128 | 121 | 46 | 0 | 83 |
| ж | 231 | 200 | 203 | 83 | 83 | 0 |
Затем эти данные можно просмотреть в графической форме в виде тепловой карты . На этом изображении черный цвет обозначает расстояние 0, а белый – максимальное расстояние.
Графический вид
Смотрите также
- Кластеризация данных
- Компьютерное зрение
- Умножение матриц мин-плюс












