Как найти матрицу скалярного произведения - Сайт, где вы сможете решить свои вопросы

Скалярное произведение векторов равно произведению

Скаля́рное произведе́ние (иногда называемое внутренним произведением) — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат.
Используется в определении длины векторов и угла между ними.

Обычно для скалярного произведения векторов и используется одно из следующих обозначений.

{displaystyle (mathbf {a} ,mathbf {b} )}

{displaystyle mathbf {a} cdot mathbf {b} , {vec {a}}cdot {vec {b}}}

или просто

второе обозначение применяется в квантовой механике для векторов состояния^[1].

В простейшем случае, а именно в случае конечномерного вещественного евклидового пространства, иногда используют «геометрическое» определение скалярного произведения ненулевых векторов и как произведения длин этих векторов на косинус угла между ними^[2]:

{displaystyle (mathbf {a} ,mathbf {b} )=|mathbf {a} ||mathbf {b} |cos(theta ).}

Равносильное определение: скалярное произведение есть произведение длины проекции первого вектора на второй и длины второго вектора (см. рисунок). Если хотя бы один из векторов нулевой, то произведение считается равным нулю^[3].

У понятия скалярного произведения существует также большое количество обобщений для различных векторных пространств, то есть для множеств векторов с операциями сложения и умножения на скаляры^[⇨]. Данное выше геометрическое определение скалярного произведения предполагает предварительное определение понятий длины вектора и угла между ними. В современной математике используется обратный подход: аксиоматически определяется скалярное произведение, а уже через него — длины и углы^[4]. В частности, скалярное произведение определяется для комплексных векторов, многомерных и бесконечномерных пространств, в тензорной алгебре.

Скалярное произведение и его обобщения играют чрезвычайно большую роль в векторной алгебре, теории многообразий, механике и физике. Например, работа силы при механическом перемещении равна скалярному произведению вектора силы на вектор перемещения^[5].

Определение и свойства[править | править код]

Будем говорить, что в вещественном или комплексном векторном пространстве определено скалярное произведение, если каждой паре векторов из поставлено в соответствие число из того числового поля, над которым задано удовлетворяющее следующим аксиомам.

Для любых трёх элементов ${displaystyle mathbf {a} _{1},mathbf {a} _{2},mathbf {b} }$ пространства и любых чисел справедливо равенство: ${displaystyle (alpha mathbf {a} _{1}+beta mathbf {a} _{2},mathbf {b} )=alpha (mathbf {a} _{1},mathbf {b} )+beta (mathbf {a} _{2},mathbf {b} )}$ (линейность скалярного произведения по первому аргументу).
Для любых справедливо равенство , где черта означает комплексное сопряжение.
Для любого имеем: , причём только при (положительная определённость и невырожденность скалярного произведения соответственно).

Заметим, что из аксиомы 2 следует, что — вещественное число. Поэтому аксиома 3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения. Если аксиома 3 не выполняется, то произведение называется индефинитным или неопределённым.

Если не только при , то произведение называется квазискалярным^[6].

Из данных аксиом получаются следующие свойства:

коммутативность для вещественных векторов:

Дистрибутивность скалярного произведения в случае вещественного евклидового пространства
дистрибутивность относительно сложения: и
инволюционная линейность относительно второго аргумента: ${displaystyle (mathbf {a} ,(alpha _{1}mathbf {b} _{1}+alpha _{2}mathbf {b} _{2}))={overline {alpha _{1}}}(mathbf {a} ,mathbf {b} _{1})+{overline {alpha _{2}}}(mathbf {a} ,mathbf {b} _{2});}$ (в случае вещественного — просто линейность по второму аргументу).
(что совпадает с для вещественного ).

Также есть свойства, связанные не с данными аксиомами:

неассоциативность относительно умножения на вектор^[7]‘: ;
ортогональность: два ненулевых вектора a и b ортогональны тогда и только тогда, когда (a, b) = 0 (определения ниже).

Замечание. В квантовой физике скалярное произведение (волновых функций, которые комплекснозначны) принято определять как линейное по второму аргументу (а не по первому), соответственно, по первому аргументу оно будет инволюционо линейным. Путаницы обычно не возникает, поскольку традиционное обозначение для скалярного произведения в квантовой физике также отличается: , т.е. аргументы отделяются вертикальной чертой, а не запятой, и скобки всегда угловые.

Определение и свойства в евклидовом пространстве[править | править код]

Вещественные векторы[править | править код]

В -мерном вещественном евклидовом пространстве векторы определяются своими координатами — наборами вещественных чисел в ортонормированном базисе. Определить скалярное произведение векторов ${displaystyle mathbf {a} =(a_{1},a_{2}dots a_{n}),mathbf {b} =(b_{1},b_{2}dots b_{n})}$ можно так^[4]:

${displaystyle langle mathbf {a} ,mathbf {b} rangle =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+dots +a_{n}b_{n}.}$

Проверка показывает, что все три аксиомы выполнены.

Например, скалярное произведение векторов и будет вычислено так:

${displaystyle {begin{aligned} (1,3,-5)cdot (4,-2,-1)&=1cdot 4+3cdot (-2)+(-5)cdot (-1)\&=4-6+5\&=3.end{aligned}}}$

Можно доказать^[8], что эта формула равносильна определению через проекции или через косинус:

Комплексные векторы[править | править код]

Для комплексных векторов ${displaystyle mathbf {a} =(a_{1},a_{2}dots a_{n}),mathbf {b} =(b_{1},b_{2}dots b_{n})}$ определим аналогично^[9]:

${displaystyle langle mathbf {a} ,mathbf {b} rangle =sum _{k=1}^{n}a_{k}{overline {b_{k}}}=a_{1}{overline {b_{1}}}+a_{2}{overline {b_{2}}}+cdots +a_{n}{overline {b_{n}}}.}$

Пример (для n=2 ):

Свойства[править | править код]

Помимо общих свойств скалярного произведения, для многомерных евклидовых векторов верно следующее:

в отличие от обычного умножения скаляров, где если ab = ac и a ≠ 0, то b равняется c, для скалярного умножения векторов это неверно: если a · b = a · c, то есть a · (b − c) = 0, то в общем случае a и b − c лишь ортогональны; но вектор b − c в общем случае не равен 0, то есть b ≠ c;
правило произведения: для дифференцируемых вектор-функций a(t) и b(t) верно соотношение (a(t), b(t))′ = a′(t) ⋅ b(t) + a(t) ⋅ b′(t)^[10];
оценка угла между векторами:

в формуле знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение больше 0, если угол между векторами острый, и меньше 0, если угол между векторами тупой;
проекция вектора на направление, определяемое единичным вектором :

${displaystyle a_{e}=(mathbf {a} ,mathbf {e} )=|mathbf {a} ||mathbf {e} |cos angle {(mathbf {a} ,mathbf {e} )}=|mathbf {a} |cos angle {(mathbf {a} ,mathbf {e} )}}$ , так как
площадь параллелограмма, натянутого на два вектора и , равна ${displaystyle {sqrt {(mathbf {a} ,mathbf {a} )(mathbf {b} ,mathbf {b} )-(mathbf {a} ,mathbf {b} )^{2}}}.}$

Теорема косинусов в вещественном пространстве[править | править код]

Теорема косинусов легко выводится с использованием скалярного произведения. Пусть на сторонах треугольника находятся векторы a, b и c, первые два из которых образуют угол θ, как показано в изображении справа. Тогда, следуя свойствам и определению скалярного произведения через косинус:

${displaystyle {begin{aligned}mathbf {color {orange}c} cdot mathbf {color {orange}c} &=(mathbf {color {red}a} -mathbf {color {blue}b} )cdot (mathbf {color {red}a} -mathbf {color {blue}b} )\&=mathbf {color {red}a} cdot mathbf {color {red}a} -mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {blue}b} cdot mathbf {color {red}a} +mathbf {color {blue}b} cdot mathbf {color {blue}b} \&=|mathbf {color {red}a} |^{2}-mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {red}a} cdot mathbf {color {blue}b} +|mathbf {color {blue}b} |^{2}\&=|mathbf {color {red}a} |^{2}-2mathbf {color {red}a} cdot mathbf {color {blue}b} +|mathbf {color {blue}b} |^{2}\&=|mathbf {color {red}a} |^{2}+|mathbf {color {blue}b} |^{2}-2|mathbf {color {red}a} |{cdot }|mathbf {color {blue}b} |cos mathbf {color {purple}theta } .\end{aligned}}}$

Связанные определения[править | править код]

В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия^[11]:

Длина вектора, под которой обычно понимается его евклидова норма:

{displaystyle |mathbf {a} |={sqrt {(mathbf {a} ,mathbf {a} )}}}

(термин «длина» обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).

Углом varphi между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):

${displaystyle cos varphi ={frac {(mathbf {a} ,mathbf {b} )}{|mathbf {a} ||mathbf {b} |}} (0leqslant varphi leqslant pi ).}$

Данные определения позволяют сохранить формулу: и в общем случае. Корректность формулы для косинуса гарантирует неравенство Коши — Буняковского^[12]:

Для любых элементов векторного пространства со скалярным произведением выполняется неравенство:

${displaystyle vert (mathbf {a} ,mathbf {b} )vert ^{2}leqslant (mathbf {a} ,mathbf {a} )(mathbf {b} ,mathbf {b} )}$

В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):

{displaystyle |(mathbf {a} ,mathbf {b} )|=|mathbf {a} ||mathbf {b} |operatorname {ch} varphi .}

Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.
Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.
- При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.
Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.

История[править | править код]

Скалярное произведение было введено У. Гамильтоном в 1846 году^[13] одновременно с векторным произведением в связи с кватернионами — соответственно, как скалярная и векторная часть произведения двух кватернионов, скалярная часть которых равна нулю^[14].

Вариации и обобщения[править | править код]

В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных или комплексных функций можно ввести положительно определённое скалярное произведение:

${displaystyle (mathbf {f} ,mathbf {g} )=int limits _{Omega }f(x){overline {g(x)}}dOmega }$

При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора^[15] $g_{ij}$ :

${displaystyle (mathbf {a} ,mathbf {b} )=g_{ij}a^{i}b^{j}}$

При этом сама метрика (говоря точнее, её представление в данном базисе) так связана со скалярными произведениями базисных векторов $f_{i}$ :

${displaystyle g_{ij}=(mathbf {f} _{i},mathbf {f} _{j})}$

Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:

${displaystyle (mathbf {f} ,mathbf {g} )=int limits _{(Omega _{1}times Omega _{2})}K(x_{1},x_{2})f(x_{1})g(x_{2})d(Omega _{1}times Omega _{2})}$

${displaystyle (mathbf {f} ,mathbf {g} )=int limits _{Omega }K(x)f(x)g(x)dOmega }$

где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).

Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свёртка по повторяющимся индексам.

См. также[править | править код]

Гильбертово пространство
Векторное произведение
Внешнее произведение
Псевдоскалярное произведение
Смешанное произведение

Примечания[править | править код]

↑ Hall B. C. Quantum Theory for Mathematicians. — NY: Springer Science & Business Media, 2013. — xvi + 553 p. — (Graduate Texts in Mathematics. Vol. 267). — ISBN 978-1-4614-7115-8. Архивная копия от 31 января 2016 на Wayback Machine — P. 85.
↑ Имеется в виду наименьший угол между векторами, не превосходящий
↑ Векторная алгебра // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 634.
↑ ¹ ² Гельфанд, 1971, с. 30—31.
↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193—194. — 704 с. — ISBN 5-85270-087-8.
↑ Кудрявцев Л. Д. Математический анализ. II том. — М., Высшая школа, 1970. — с. 316.
↑ Weisstein, Eric W. Dot Product Архивная копия от 29 апреля 2021 на Wayback Machine. From MathWorld — A Wolfram Web Resource.
↑ Calculus II – Dot Product. tutorial.math.lamar.edu. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.
↑ Гельфанд, 1971, с. 86.
↑ Stewart, James (2016), Calculus (8 ed.), Cengage, Section 13.2.
↑ Гельфанд, 1971, с. 34.
↑ §9.5. Линейные пространства со скалярным произведением: евклидовы и унитарные
↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101. Архивная копия от 6 марта 2019 на Wayback Machine
↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
↑ Гельфанд, 1971, с. 240.

Литература[править | править код]

Гельфанд И. М. Лекции по линейной алгебре. — 4-е изд. — М.: Наука, 1971. — 272 с.

Ссылки[править | править код]

Емелин А. Скалярное произведение векторов. Дата обращения: 14 ноября 2019.

Источник

Основные свойства скалярного произведения: 1. ( , ) = ( , );

∑ .

10	1. Элементы линейной алгебры

15> x; y; z

16[1] 1 2 3 4

17[1] 4 3 2 1

18[1] 1 3 4 2

19> a <- c(1,-2,3,-4); t <- c(1,4,2,3)

20> d <- matrix(c(x,y,z,t), nrow=length(x), byrow=TRUE)

21> if(det(d) != 0) solve(d,a) else

22+ stop(“Векторы линейно зависимы!”)

23[1] -0.3000000 -1.6333333 2.3666667 -0.6333333

Так как векторы , , уже были определены ранее 1–2 , то для постановки задачи достаточно лишь убедиться в существовании одноимённых переменных 15–18 и определить дополнительные векторы и 19 .

Для решения системы линейных алгебраических уравнений используется функция «solve()» с двумя аргументами 21 : матрицей коэффициентов «d» и вектором правых частей «a» системы уравнений. Матрица коэффициентов системы линейных алгебраических уравнений «d» образуется путём композиции функций «matrix()» и «c()» из векторов «(x,y,z,t)» с числом строк, определяемым длиной первого вектора «nrow=length(x)» 20 , а условие «if(det(d) != 0)» используется для проверки линейной независимости векторов «x,y,z,t», что является необходимым и достаточным условием для существования одноимённого базиса. Если же указанное условие не будет выполнено: «det(d) == 0», то вместо искомых координат в строке 22 будет выдано сообщение об ошибке.

Символ «+» в начале строки 22 появляется при переносе слишком длинного выражения с предыдущей строки.

Как видно из приведённого в строке 23 ответа, искомые координаты вектора ′ в базисе { , , , } будут равны (−0.3, −1.6, 2.4, −0.6).

1.3. Скалярное произведение векторов

Скалярным произведением векторов и называется число (скаляр), обозначаемое как ( , ) или просто и определяемое соотношением

( , ) = =

1.3. Скалярное произведение векторов

2.( 1 + 2, ) = ( 1, ) + ( 2, );

3.( , ) = ( , ) для любого вещественного ;

Вдополнение к свойствам 1–4 для скалярного произведения двух любых векторов и выполняется неравенство Коши–Буняков- ского: ( , )2 6 ( , ) · ( , ).

Векторы и называются коллинеарными, если = . Практически это означает, что координаты векторов и пропорциональны друг другу.

Векторы и называются ортогональными, если их скалярное произведение равно нулю: ( , ) = 0.

Вещественное линейное пространство называется евклидовым, если в нём определено скалярное произведение элементов. В евклидовом пространстве удобно использовать базис { 1, 2, . . . , }, все элементы которого взаимно ортогональны и имеют единичную длину:

( , ) = ,	= {1,	если = ;
	0,	если ̸= ,

где –– символ Кронекера. Такие базисы называются ортонормированными и существуют в любом евклидовом пространстве. В ортонормированном базисе координаты вектора можно представить в виде: = ( , ), = 1, 2, . . . , , а разложение такого вектора по

базису

= ∑( , ) .

Введение в рассмотрение скалярного произведения позволяет в дальнейшем эффективно использовать такие геометрически содержательные понятия, как ортогональность, угол и длина. Эти свойства широко используются при получении системы нормальных уравнений метода наименьших квадратов, а также для объяснения свойств МНК-оценок.

Пример 1.3. В продолжение предыдущего примера выясним ортогональность вектора с базисом ( , , , ) с помощью языка R.

24> a

25[1] 1 -2 3 -4

12	1. Элементы линейной алгебры

26> d

27[,1] [,2] [,3] [,4]

28	[1,]	1	2	3	4
29	[2,]	4	3	2	1
30	[3,]	1	3	4	2
31	[4,]	1	4	2	3
32	> as.vector(d%*%a)
33	[1]	-10	0	-1	-13

Для проверки ортогональности вектора с векторами базиса потребуется вычислить четыре скалярных произведения: ( , ), ( , ), ( , ), ( , ). Напомним, что в предыдущем примере мы сформировали вспомогательную матрицу «d» из столбцов базисных векторов 21 . Внимательные читатели наверняка обратили внимание, что компоненты матрицы «d» отображаются на экране в обычном порядке 26–31 , а компоненты вектора «a» –– в транспонированном 24–25 . Это связано с тем, что построчный вывод «длинных» векторов позволяет более эффективно использовать площадь экрана при статистической обработке выборочных данных.

Для вычисления искомых скалярных произведений перемножим матрицу «d» на вектор «a» и представим полученный результат как вектор 32–33 : «as.vector(d%*%a)», где «%*%» означает операцию матричного умножения, определённую далее в разделе 1.5 и позволяющую получить искомые скалярные произведения одной командой.

Как показывают расчёты, ортогональной является вторая пара векторов: ( , ) = 0 (4, 3, 2, 1) (1, −2, 3, −4).

1.4. Матрицы

Прямоугольная таблица чисел, содержащая строк и столбцов, называется числовой матрицей. Пара чисел и называются размером матрицы. Обозначаются матрицы следующим образом:

= ( ) =	11	12
21	22
	. . . . . .

1	2

. . . 1	.
. . .	2
. . . . . .

. . .

Числа , = 1, 2, . . . , , = 1, 2, . . . , , составляющие матрицу, называются её элементами. В случае, если = , матрица называется квадратной, а –– порядком матрицы.

Матрицу размера 1 × называют матрицей-строкой, а матрицу размера × 1 –– матрицей-столбцом. Очевидно, что последняя может рассматриваться как элемент векторного пространства .

Главной диагональю квадратной матрицы порядка называется совокупность элементов: , = = 1, 2, . . . , . Квадратная матрица называется диагональной, если все её элементы, не лежащие на главной диагонали, равны нулю. Диагональная матрица, все диагональные элементы которой равны единице, называется единичной и обозначается .

Две матрицы и называются равными, если они имеют одинаковый размер и равные соответствующие элементы.

Основные операции над матрицами:

1.Суммой матриц и одинакового размера называется матрица того же размера, определяемая равенством

+ = ( + ), = 1, 2, . . . , , = 1, 2, . . . , ;

2.Произведением матрицы на число называется матрица того же размера, определяемая равенством

= ( ), = 1, 2, . . . , , = 1, 2, . . . , .

Основные свойства операций над матрицами:

1.+ = + , = ;

2.( + ) + = + ( + ), ( ) = ( ) ;

3.( + ) = + , ( + ) = + ;

4.+ = , 0 = , где –– нулевая матрица, то есть матрица, все элементы которой равны нулю.

Пример 1.4. Проиллюстрируем вышеуказанные свойства для произвольных матриц , , с помощью R.

1 > matrix(round(runif(9, min=-9, max=9)), nrow=3) -> A; A

2[,1] [,2] [,3]

3	[1,]	-1	9	0
4	[2,]	-6	5	1
5	[3,]	2	-7	-8
6	> matrix(round(runif(9, min=-9, max=9)), nrow=3) -> B; B

7[,1] [,2] [,3]

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Выражение скалярного произведения через координаты векторов

Разумеется, что величина скалярного произведения любых векторов vec{a} и vec{b} не зависит от базиса. Однако формулы, выражающие скалярное произведение langlevec{a},vec{b}rangle через координаты множителей, зависят от базиса, относительно которого определены координаты. Рассмотрим сначала случай стандартного базиса в пространстве, а затем — произвольного.

Скалярное произведение векторов в ортонормированном базисе

Теорема 1.6 (формула вычисления скалярного произведения в ортонормированном базисе). В ортонормированном базисе скалярное произведение векторов равно сумме произведений одноименных координат векторов:

— если векторы vec{a} и vec{b} относительно ортонормированного базиса на плоскости имеют координаты x_a,y_a и x_b,y_b соответственно, то скалярное произведение этих векторов вычисляется по формуле

$langlevec{a},vec{b}rangle=x_a cdot x_b+y_a cdot y_b;$

(1.9)

— если векторы vec{a} и vec{b} относительно ортонормированного базиса в пространстве имеют координаты x_a,y_a,z_a и x_b,y_b,z_b соответственно, то скалярное произведение этих векторов вычисляется по формуле

$langlevec{a},vec{b}rangle=x_a cdot x_b+y_a cdot y_b+z_a cdot z_b,.$

(1.10)

Докажем формулу (1.10). Пусть в пространстве задан ортонормированный (стандартный) базис vec{i},vec{j},vec{k} . Скалярные произведения базисных векторов находятся по определению:

$begin{gathered} langlevec{i},vec{i}rangle=1,qquad langlevec{i},vec{j}rangle=0,qquad langlevec{i},vec{k}rangle=0,\[3pt] langlevec{j},vec{i}rangle=0,qquad langlevec{j},vec{j}rangle=1,qquad langlevec{j},vec{k}rangle=0,\[3pt] langlevec{k}, vec{i}rangle= 0,qquad langlevec{k}, vec{j}rangle=0,qquad langlevec{k}, vec{k}rangle=1. end{gathered}$

(1.11)

Используя линейность скалярного произведения по любому множителю, для векторов $vec{a}=x_a,vec{i}+y_a,vec{j}+z_a,vec{k}$ и $vec{b}=x_b,vec{i}+y_b,vec{j}+z_b,vec{k}$ получаем:

$begin{gathered}langlevec{a},vec{b}rangle=bigllangle x_a,vec{i}+y_a,vec{j}+z_a,vec{k},,x_b,vec{i}+y_b,vec{j}+z_b,vec{k}bigrrangle=\[3pt]x_ax_blanglevec{i},vec{i}rangle+x_ay_blanglevec{i},vec{j}rangle+x_az_blanglevec{i},vec{k}rangle+y_ax_blanglevec{j},vec{i}rangle+y_ay_blanglevec{j},vec{j}rangle+y_az_blanglevec{j},vec{k}rangle+z_ax_blanglevec{k},vec{i}rangle+z_ay_blanglevec{k},vec{j}rangle+z_az_blanglevec{k},vec{k}rangle. end{gathered}$

Учитывая (1.11), из девяти слагаемых только три отличны от нуля, поэтому

$bigllanglevec{a},vec{b}bigrrangle=x_a cdot x_b+y_a cdot y_b+z_a cdot z_b,$

что и требовалось доказать.

Замечания 1.10

1. Для доказательства формулы (1.9) можно использовать следующее соображение. Множество векторов на плоскости со стандартным базисом vec{i},vec{j} можно рассматривать как множество таких векторов в пространстве с базисом vec{i},vec{j},vec{k} , у которых аппликата равна нулю. Поэтому формулу вычисления скалярного произведения векторов $vec{a}=x_a,vec{i}+y_a,vec{j}$ и $vec{b}=x_b,vec{i}+y_b,vec{j}$ можно получить из (1.10), полагая z_a=z_b=0 .

2. Скалярное произведение можно записать в матричном виде: если $a=begin{pmatrix}x_a&y_a&z_aend{pmatrix}^T$ и $b=begin{pmatrix}x_b&y_b&z_bend{pmatrix}^T$ координатные столбцы векторов vec{a} и vec{b} в стандартном базисе, то их скалярное произведение находится формуле:

$langlevec{a},vec{b}rangle=a^Tcdot b=begin{pmatrix}x_a&y_a&z_aend{pmatrix}^Tcdotbegin{pmatrix}x_b\y_b\z_bend{pmatrix}.$

Для векторов на плоскости соответственно получаем

$langlevec{a},vec{b}rangle=a^Tcdot b=begin{pmatrix}x_a&y_aend{pmatrix}^Tcdotbegin{pmatrix}x_b\y_bend{pmatrix}.$

3. Координаты вектора vec{a} в ортонормированием базисе равны его скалярным произведениям на соответствующие базисные векторы:

$x_a=langlevec{a},vec{i}rangle,~~~y_a=langlevec{a},vec{j}rangle,~~~z_a=langlevec{a},vec{k}rangle.$

В самом деле, подставляя в (1.10) координаты (1;0;0) базисного вектора vec{i} , приходим к первому равенству (остальные равенства получаются аналогично).

4. Формулы (1.9) и (1.10) совместно с геометрическими свойствами скалярного произведения имеют многочисленные приложения.

Пример 1.15. Даны векторы vec{a}=vec{i}-2vec{j}+2vec{k},~vec{b}=2vec{i}+3vec{j}+2vec{k},~vec{c}=vec{j}-vec{k} . Найти скалярные произведения

langlevec{a},vec{b}rangle,quad langlevec{a},vec{c}rangle,quad langlevec{b},vec{c}rangle,quad langlevec{a},vec{i}rangle,quad langlevec{a},vec{j}rangle,quad langlevec{a},vec{k}rangle.

Решение. По формуле (1.10) вычисляем

$begin{aligned} langlevec{a},vec{b}rangle&=langle1cdotvec{i}-2cdotvec{j}+2cdotvec{k},,2cdotvec{i}+3cdotvec{j}+2cdotvec{k}rangle=1cdot2+(-2)cdot3+2cdot2=0;\[3pt] langlevec{a},vec{c}rangle&=langle1cdotvec{i}-2cdotvec{j}+2cdotvec{k},,0cdotvec{i}+1cdotvec{j}-1cdotvec{k}rangle=1cdot0+(-2)cdot1+2cdot(-1)=-4;\[3pt] langlevec{b},vec{c}rangle&=langle2cdotvec{i}+3cdotvec{j}+2cdotvec{k},,0cdotvec{i}+1cdotvec{j}-1cdotvec{k}rangle=2cdot0+3cdot1+2cdot(-1)=1;\[3pt] langlevec{a},vec{i}rangle&=langle1cdotvec{i}-2cdotvec{j}+2cdotvec{k},,1cdotvec{i}+0cdotvec{j}+0cdotvec{k}rangle=1cdot1+(-2)cdot0+2cdot0=1;\[3pt] langlevec{a},vec{j}rangle&=langle1cdotvec{i}-2cdotvec{j}+2cdotvec{k},,0cdotvec{i}+1cdotvec{j}+0cdotvec{k}rangle=1cdot0+(-2)cdot1+2cdot0=-2;\[3pt] langlevec{a},vec{k}rangle&=langle1cdotvec{i}-2cdotvec{j}+2cdotvec{k},,0cdotvec{i}+0cdotvec{j}+1cdotvec{k}rangle=1cdot0+(-2)cdot0+2cdot1=2. end{aligned}$

Сравнивая вектор vec{a}=vec{i}-2,vec{j}+2,vec{k} со скалярными произведениями langlevec{a},vec{i}rangle=1,~langlevec{a},vec{j}rangle=-2,~langlevec{a},vec{k}rangle=2 обнаруживаем, что при умножении вектора на базисный вектор получается соответствующая координата данного вектора. Этот результат иллюстрирует пункт 3 замечаний 1.10.

Для нахождения скалярного произведения можно использовать матричную запись (см. пункт 2 замечаний 1.10). Например, векторам vec{a},vec{b},,vec{i} соответствуют координатные столбцы

$a=begin{pmatrix}1\-2\2end{pmatrix}!,~~~b=begin{pmatrix}2\3\2end{pmatrix}!,quad i=begin{pmatrix}1\0\0end{pmatrix}.$

Поэтому

$begin{gathered} langlevec{a},vec{b}rangle=a^T cdot b=begin{pmatrix}1&-2&2end{pmatrix}{cdot}begin{pmatrix}2\3\2end{pmatrix}=1cdot2+(-2)cdot3+2cdot2=0;\ langlevec{a},vec{i}rangle=a^T cdot i=begin{pmatrix}1&-2&2end{pmatrix}{cdot}begin{pmatrix}2\3\2end{pmatrix}=1cdot1+(-2)cdot0+2cdot0=1, end{gathered}$

что совпадает с полученными ранее результатами.

Пример 1.16. Прямоугольный параллелепипед ABCDA_1B_1C_1D_1 построен на векторах $overrightarrow{AB}=4,vec{i},~overrightarrow{AD}=5,vec{j},~overrightarrow{AA_1}=4,vec{k}$ (см. рис. 1.38). Точка — центр грани ABB_1A_1 , точка делит ребро A_1D_1 в отношении A_1Q:QD_1=4:1 . Требуется найти:

а) величину varphi угла между векторами $overrightarrow{AC_1}$ и overrightarrow{PQ} ;

б) длину ортогональной проекции вектора overrightarrow{PQ} на прямую .

Прямоугольный параллелепипед, построенный на векторах

Решение. Находим координаты векторов в стандартном базисе vec{i},vec{j},vec{k} :

$begin{aligned}&overrightarrow{AC_1}=overrightarrow{AB}+overrightarrow{AD}+overrightarrow{AA_1}=4cdotvec{i}+5cdotvec{j}+4cdotvec{k};\[3pt]&overrightarrow{AC}=overrightarrow{AB}+overrightarrow{AD}=4cdotvec{i}+5cdotvec{j}+0cdotvec{k};\[3pt] &overrightarrow{PQ}= -2cdotvec{i}+ 4cdotvec{j}+ 2cdotvec{k}.end{aligned}$ (см. решение примера 1.12)

По формуле (1.10) находим скалярные произведения:

$bigllangleoverrightarrow{AC_1},overrightarrow{PQ}bigrrangle=4cdot(-2)+ 5cdot4+ 4cdot2=20;quad bigllangle overrightarrow{AC}, overrightarrow{PQ}bigrrangle=4cdot(-2)+5cdot4+0cdot2=12.$

а также длины векторов (см. геометрическое свойство 1 скалярного произведения):

$|AC_1|=sqrt{bigllangleoverrightarrow{AC_1},overrightarrow{AC_1}bigrrangle}=sqrt{4^2+5^2+4^2}=sqrt{57};quad bigr|ACbigr|= sqrt{bigllangle overrightarrow{AC}, overrightarrow{AC}bigrrangle}= sqrt{4^2+5^2}=sqrt{41}.$

Длина left|overrightarrow{PQ}right|=2sqrt{6} была найдена в примере 1.12.

Теперь по геометрическому свойству 2 находим косинус искомого угла

$cosvarphi=frac{bigllangleoverrightarrow{AC_1},overrightarrow{PQ}bigrrangle}{bigr|overrightarrow{AC_1}bigr|cdotbigr|overrightarrow{PQ}bigr|}=frac{20}{sqrt{57}cdot2sqrt{6}}=frac{10}{3sqrt{38}},$ т.е. $varphi=arccosfrac{10}{3sqrt{38}}.$

Алгебраическое значение длины ортогональной проекции находим по геометрическомусвойству 3:

$operatorname{pr}_{overrightarrow{AC}}overrightarrow{PQ}=frac{bigllangleoverrightarrow{PQ},overrightarrow{AC}bigrrangle}{bigr|overrightarrow{AC}bigr|}=frac{12}{sqrt{41}}.$

Скалярное произведение векторов в произвольном базисе

Пусть $vec{e}_1,vec{e}_2,vec{e}_3$ — произвольный базис в пространстве. Найдем скалярное произведение векторов $vec{a}=a_1vec{e}_1+a_2vec{e}_2+a_3vec{e}_3$ и $vec{b}=b_1vec{e}_1+b_2vec{e}_2+b_3vec{e}_3$ :

$bigllanglevec{a},vec{b}bigrrangle=bigllangle a_1vec{e}_1+a_2vec{e}_2+a_3vec{e}_3,,b_1vec{e}_1+b_2vec{e}_2+b_3vec{e}_3 bigrrangle= sum_{i=1}^3 sum_{j=1}^3 a_icdot b_jcdot bigllanglevec{e}_1,vec{e}_2bigrrangle.$

Запишем полученную формулу в матричном виде. Для этого из чисел $bigllanglevec{e}_1,vec{e}_2bigrrangle$ , называемых метрическими коэффициентами базиса, составим матрицу Грама системы векторов $vec{e}_1, vec{e}_2, vec{e}_3$ :

$Gbigl(vec{e}_1, vec{e}_2, vec{e}_3bigl)= begin{pmatrix} langlevec{e}_1, vec{e}_1 rangle & langlevec{e}_1, vec{e}_2rangle & langlevec{e}_1,vec{e}_3rangle\[2pt]langlevec{e}_2, vec{e}_1rangle& langlevec{e}_2,vec{e}_2rangle& langle vec{e}_2, vec{e}_3rangle\[2pt] langle vec{e}_3, vec{e}_1 rangle & langle vec{e}_3, vec{e}_2rangle&langlevec{e}_3,vec{e}_3rangleend{pmatrix}$

(1.12)

Координаты каждого из векторов vec{a} и vec{b} представим в виде столбцов

$a=begin{pmatrix}a_1\a_2\a_3end{pmatrix}$ и $b=begin{pmatrix}b_1\b_2\b_3end{pmatrix}$ соответственно.

Тогда для скалярного произведения получим

$bigllanglevec{a}, vec{b}bigrrangle,= sum_{i=1}^3 sum_{j=1}^3 a_ib_jbigllanglevec{e}_1, vec{e}_2bigrrangle,= begin{pmatrix}a_1&a_2&a_3end{pmatrix}!!begin{pmatrix}langlevec{e}_1,vec{e}_1rangle&langlevec{e}_1,vec{e}_2rangle&langlevec{e}_1,vec{e}_3rangle\[2pt] langlevec{e}_2, vec{e}_1rangle & langlevec{e}_2, vec{e}_2rangle & langlevec{e}_2,vec{e}_3rangle\[2pt]langlevec{e}_3, vec{e}_1rangle & langlevec{e}_3, vec{e}_2rangle & langlevec{e}_3, vec{e}_3rangle!end{pmatrix}!!!begin{pmatrix}b_1\[2pt]b_2\[2pt] b_3end{pmatrix}$

или, короче,

$bigllanglevec{a}, vec{b} bigrrangle,= a^Tcdot Gbigl(vec{e}_1,vec{e}_2,vec{e}_3bigr)cdot b,.$

(1.13)

Теорема 1.7 (формула вычисления скалярного произведения в произвольном базисе). В произвольном базисе $vec{e}_1, vec{e}_2, vec{e}_3$ скалярное произведение векторов vec{a} и vec{b} вычисляется по формуле (1.13), где vec{a},vec{b} — координатные столбцы векторов vec{a} и vec{b} соответственно, a $G(vec{e}_1,vec{e}_2,vec{e}_3)$ —матрица Грама (1.12) базиса $vec{e}_1,vec{e}_2,vec{e}_3$ .

Замечания 1.11.

1. Для ортонормированного базиса vec{i},vec{j},vec{k} матрица Грама имеет вид

$Gbigl(vec{i},vec{j},vec{k}bigl)=begin{pmatrix}langlevec{i},vec{i}rangle&langlevec{i},vec{j}rangle&langlevec{i},vec{k}rangle\[2pt]langlevec{j},vec{i}rangle&langlevec{j},vec{j}rangle&langlevec{j},vec{k}rangle\[2pt] langlevec{k}, vec{i}rangle & langlevec{k}, vec{j}rangle & langlevec{k}, vec{k}rangle end{pmatrix}= begin{pmatrix} 1&0&0\[2pt]0&1&0\[2pt]0&0&1end{pmatrix}$

т.е. является единичной. В этом случае по формуле (1.13) получаем

$begin{gathered}bigllanglevec{a},vec{b}bigrrangle=bigllangle x_acdotvec{i}+y_acdotvec{j}+z_acdotvec{k},, x_bcdotvec{i}+y_bcdotvec{j}+z_bcdotvec{k} bigrrangle=\=begin{pmatrix}x_a&y_a&z_aend{pmatrix}!!begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}=x_acdot x_b+y_acdot y_b+z_acdot z_b,end{gathered}$ что совпадает с (1.10).

2. Для произвольного базиса $vec{e}_1,vec{e}_2$ на плоскости скалярное произведение векторов $vec{a}=a_1cdotvec{e}_1+a_2cdotvec{e}_2$ и $vec{b}=b_1cdotvec{e}_1+b_2cdotvec{e}_2$ находится по формуле:

$bigllanglevec{a},vec{b}bigrrangle=a^Tcdot Gbigl(vec{e}_1,vec{e}_2bigl)cdot b,$

где $a=begin{pmatrix} a_1\a_2 end{pmatrix}!,~ b= begin{pmatrix}b_1\b_2end{pmatrix}$ — координатные столбцы векторов vec{a} и vec{b} соответственно, a $Gbigl(vec{e}_1,vec{e}_2bigl)=begin{pmatrix}langlevec{e}_1,vec{e}_1rangle&langlevec{e}_1,vec{e}_2rangle\langlevec{e}_2,vec{e}_1rangle&langlevec{e}_2,vec{e}_2rangleend{pmatrix}$ — матрица Грама базиса $vec{e}_1,vec{e}_2$ .

В частности, для ортонормированного базиса vec{i},vec{j} матрица Грама является единичной: $Gbigl(vec{i},vec{j}bigl)=begin{pmatrix}1&0\0&1end{pmatrix}$ , поэтому скалярное произведение векторов $vec{a}=x_acdotvec{i}+y_acdotvec{j}$ и $vec{b}=x_bcdotvec{i}+y_bcdotvec{j}$ находится по формуле $langlevec{a},vec{b}rangle=x_ax_b+y_ay_b$ , что совпадает с (1.9). Заметим, что эта формула также следует из полученной в пункте 1 при z_a=z_b=0 .

Треугольник и тетраэдр, построенные на векторах

Пример 1.17. Найти матрицы Грама для следующих базисов:

а) два единичных вектора $vec{e}_1=overrightarrow{OA},~vec{e}_2=overrightarrow{OB}$ , служащие сторонами правильного треугольника OAB (рис.1.39,а);

б) три единичных вектора $vec{e}_1=overrightarrow{OA},~vec{e}_2=overrightarrow{OB},~vec{e}_3=overrightarrow{OC}$ , служащие ребрами правильного тетраэдра (рис. 1.39,6).

Найти длины векторов, имеющих в данных базисах следующие разложения: $vec{a}=vec{e}_1+2vec{e}_2;~vec{b}=vec{e}_1-2vec{e}_2+3vec{e}_3$ .

Решение. а) Учитывая, что длины базисных векторов равны единице, а угол между ними равен $frac{pi}{3}$ , получаем

$langlevec{e}_1,vec{e}_1rangle=1,qquad langlevec{e}_1, vec{e}_2rangle= langlevec{e}_2,vec{e}_1rangle=frac{1}{2},qquad langlevec{e}_2,vec{e}_2rangle=1.$

Записываем матрицу Грама $Gbigl(vec{e}_1,vec{e}_2bigl)=begin{pmatrix}langlevec{e}_1,vec{e}_1rangle&langlevec{e}_1,vec{e}_2rangle\langlevec{e}_2,vec{e}_1rangle&langlevec{e}_2,vec{e}_2rangleend{pmatrix}=begin{pmatrix}1&1/2\ 1/2&1 end{pmatrix}.$

Найдем теперь длину вектора $vec{a}=vec{e}_1+2vec{e}_2$ . Составляем координатный столбец этого вектора $a=begin{pmatrix}1\2end{pmatrix}$ .

Учитывая формулу (1.13), находим скалярный квадрат: $langlevec{a},vec{a}rangle=a^TG(vec{e}_1,vec{e}_2)=begin{pmatrix}1\2end{pmatrix}!!begin{pmatrix} 1&1/2\ 1/2&1 end{pmatrix}!!begin{pmatrix}1\2end{pmatrix}=7$ . Следовательно, |vec{a}|=sqrt{langlevec{a},vec{a}rangle}=sqrt{7} .

б) Учитывая, что длины базисных векторов равны единице, а угол между любыми двумя из них равен $frac{pi}{3}$ , получаем

$langlevec{e}_1,vec{e}_1rangle=langlevec{e}_2,vec{e}_2rangle=langlevec{a},vec{b}rangle=1;qquad langlevec{e}_1,vec{e}_2rangle=langlevec{e}_2,vec{e}_1rangle=langlevec{e}_1,vec{e}_3rangle=langlevec{e}_3,vec{e}_1rangle=langlevec{e}_2,vec{e}_3rangle=langlevec{e}_3,vec{e}_2rangle=frac{1}{2}.$

Записываем матрицу Грама: $G(vec{e}_1,vec{e}_2,vec{e}_3)=begin{pmatrix}1&1/2&1/2\ 1/2& 1& 1/2\ 1/2& 1/2&1 end{pmatrix}$ . Найдем теперь длину вектора $vec{b}=vec{e}_1-2vec{e}_2+3vec{e}_3$ . Составляем координатный столбец этого вектора $b=begin{pmatrix}1&-2&3end{pmatrix}^T$ . Учитывая формулу (1.13), находим скалярный квадрат:

$bigllanglevec{b},vec{b}bigrrangle=b^Tcdot Gbigl(vec{e}_1,vec{e}_2,vec{e}_3bigl)cdot b=begin{pmatrix}1&-2&3end{pmatrix}!!begin{pmatrix}1&1/2&1/2\ 1/2&1&1/2\ 1/2&1/2&1 end{pmatrix}!cdot! begin{pmatrix}1\-2\3end{pmatrix}!!=9$

Следовательно, |vec{b}|= sqrt{langlevec{b}, vec{b}rangle}=3.

Скалярное произведение векторов во взаимных базисах

Пусть на плоскости задан базис $vec{e}_1,vec{e}_2$ . Базис $vec{e}_1,!!^*,vec{e}_2,!!^*$ называется взаимным по отношению к базису $vec{e}_1,vec{e}_2$ , если

$bigllanglevec{e}_1,vec{e}_1,!!^*bigrrangle=1,~~bigllanglevec{e}_1,vec{e}_2,!!^*bigrrangle=0,~~bigllanglevec{e}_2,vec{e}_1,!!^*bigrrangle=0,~~bigllanglevec{e}_2,vec{e}_2,!!^*bigrrangle=1.$

Пусть в пространстве задан базис $vec{e}_1,vec{e}_2,vec{e}_3$ . Базис $vec{e}_1,!!^*,vec{e}_2,!!^*,vec{e}_3,!!^*$ называется взаимным по отношению к базису $vec{e}_1,vec{e}_2,vec{e}_3$ , если

$bigllanglevec{e}_i,vec{e}_j,!!^*bigrrangle=begin{cases}1,&i=j,\0,&ine j,end{cases}i=1,2,3;~j=1,2,3.$

Взаимные базисы обладают следующими основными свойствами.

1. Свойство взаимности базисов симметричное: если второй базис взаимен по отношению к первому, то первый взаимен ко второму.

2. Для каждого базиса (на плоскости или в пространстве) существует единственный взаимный базис.

3. Пусть векторы vec{a} и vec{b} заданы своими координатами относительно взаимных базисов:

$vec{a}=a_1,!!^*cdotvec{e}_1,!!^*+a_2,!!^*cdotvec{e}_2,!!^*+a_3,!!^*cdotvec{e}_3,!!^*,~~~~vec{b}=b_1cdotvec{e}_1+b_2cdotvec{e}_2+b_3cdotvec{e}_3.$

Тогда их скалярное произведение вычисляется по формуле: $bigllanglevec{a},vec{b}bigrrangle=a_1,!!^*b_1+a_2,!!^*b_2+a_3^3b_3$ , т.е. равно сумме произведений одноименных координат векторов, как и в случае ортонормированного базиса.

4. Если $vec{e}_1,vec{e}_2,vec{e}_3$ и $vec{e}_1,!!^*,vec{e}_2,!!^*,vec{e}_3,!!^*$ взаимные базисы, то координаты a_1,a_2,a_3 любого вектора vec{a} относительно базиса $vec{e}_1,vec{e}_2,vec{e}_3$ находятся по формулам

$a_1=bigllanglevec{a},vec{e}_1,!!^*bigrrangle,~~~a_2=bigllanglevec{a},vec{e}_2,!!^*bigrrangle,~~~a_3=bigllanglevec{a},vec{e}_3,!!^*bigrrangle.$

Докажем свойство 2. Пусть на плоскости задан базис $vec{e}_1,vec{e}_2$ (рис.1.40,а). Вектор $vec{e}_1,!!^*$ взаимного базиса перпендикулярен вектору $vec{e}_2$ , так как $langlevec{e}_2,vec{e}_1,!!^*rangle$ (см. второе геометрическое свойство скалярного произведения). Из двух возможных направлений для вектора $vec{e}_1,!!^*$ выбираем то, которое образует острый угол $varphi<frac{pi}{2}$ с вектором $vec{e}_1$ , так как $langlevec{e}_1,vec{e}_1,!!^*rangle=1>0$ . Следовательно, направление вектора $vec{e}_1,!!^*$ определено однозначно. Осталось выбрать его длину, используя (1.7): $bigr|vec{e}_1,!!^*bigr|=frac{1}{bigr|vec{e}_1bigr|{cdot}cosvarphi}$ , так как $langlevec{e}_1,vec{e}_1,!!^*rangle=1$ .

Взаимный базис

Таким образом, направление и длина первого вектора взаимного базиса определяются однозначно. То же можно сказать и в отношении выбора вектора $vec{e}_2,!!^*$ . Доказательство существования и единственности взаимного базиса в пространстве (рис. 1.40,6) проводится аналогично.

Заметим, что для стандартного базиса vec{i},vec{j} на плоскости (или базиса vec{i},vec{j},vec{k} в пространстве) взаимный базис совпадает с самим базисом (соответственно )

Докажем свойство 3. Находим скалярное произведение, используя свойства коммутативности и линейности, а также определение взаимных базисов:

$begin{gathered}bigllanglevec{a},vec{b}bigrrangle=bigllanglevec{a}_1,!!^*vec{e}_1,!!^*+vec{a}_2,!!^*vec{e}_2,!!^*+vec{a}_3,!!^*vec{e}_3,!!^*,vec{b}_1vec{e}_1+vec{b}_2vec{e}_2+vec{b}_3vec{e}_3bigrrangle=sum_{i=1}^{3}sum_{j=1}^{3}a_i,!!^*b_jbigllanglevec{e}_i,!!^*,vec{e}_jbigrrangle=\[3pt]=sum_{i=1}^{3}sum_{j=1}^{3}a_i,!!^*b_jbigllanglevec{e}_j,vec{e}_i,!!^*bigrrangle=a_1,!!^*b_1+a_2,!!^*b_2+a_3,!!^*b_3,end{gathered}$

что и требовалось доказать.

Свойство 4 следует из формулы, приведенной в пункте З. В самом деле, $langlevec{a},vec{e}_1,!!^*rangle=bigllangle a_1vec{e}_1+a_2vec{e}_2+a_3vec{e}_3,,vec{e}_1,!!^*bigrrangle=a_1$ . Аналогично доказываются остальные формулы в п.4.

Пример 1.18. а) Найти базис, взаимный базису, заданному в примере 1.17,а (рис.1.39,а).

б) Внутри угла AOB величиной $frac{pi}{3}$ взята точка , удаленная от сторон и на расстояния 11 и 2 соответственно. Найти длину отрезка (рис.1.41,б).

Базис и взаимные базисы

Решение. а) Так как базисный вектор $vec{e}_1$ единичный, то, учитывая геометрический смысл скалярного произведения (см. разд. 1.4.1), вектор $vec{e}_1,!!^*$ можно построить следующим образом. Через начало вектора $vec{e}_2=overrightarrow{OB}$ (точку ) и конец вектора $vec{e}_1=overrightarrow{OA}$ (точку ) проводим прямые, перпендикулярные векторам $vec{e}_2$ и $vec{e}_1$ соответственно (штриховые линии на рис. 1.41,а). Точка пересечения этих прямых — конец вектора $vec{e}_1,!!^*$ (его начало совпадает с точкой ). Аналогично строится вектор $vec{e}_2,!!^*$ (построение изображено штрих- пунктирными линиями на рис. 1.41,а). Тогда по построению справедливо $vec{e}_1,!!^*perpvec{e}_2,~vec{e}_2,!!^*perpvec{e}_1$ , а также $operatorname{pr}_{vec{e}_1}vec{e}_1,!!^*=|vec{e}_1|=1,~operatorname{pr}_{vec{e}_2}vec{e}_2,!!^*=|vec{e}_2|=1$ . Следовательно, учитывая геометрическое свойство 2 и формулу (1.8): $langlevec{e}_1,vec{e}_2,!!^*rangle=0,~langlevec{e}_1,vec{e}_1,!!^*rangle=1,~langlevec{e}_2,vec{e}_2,!!^*rangle=1$ , т.е. выполняются условия взаимности базисов. Найдем длины векторов взаимного базиса. Поскольку угол между векторами $vec{e}_1$ и $vec{e}_1,!!^*$ равен $frac{pi}{6}$ (напомним, что $angle AOB=frac{pi}{3}$ ), то из прямоугольного треугольника с катетом $OAcolon |vec{e}_1,!!^*|=frac{|vec{e}_1|}{cosfrac{pi}{6}}=frac{2}{sqrt{3}}$ . Длина вектора $vec{e}_2,!!^*$ такая же.

б) Зададим на плоскости базис из единичных векторов $vec{e}_1=overrightarrow{OA},~vec{e}_2=overrightarrow{OB}$ , который совпадает с базисом, рассмотренным в пункте “а”. По условию задачи известны длины ортогональных проекций вектора { overrightarrow{OC}} на оси, определяемые векторами взаимного базиса: $operatorname{pr}_{vec{e}_1,!!^{ast}}overrightarrow{OC}=2,~operatorname{pr}_{vec{e}_2,!!^{ast}}overrightarrow{OC}=11$ . По третьему геометрическому свойству скалярного произведения с учетом свойства 4 взаимных базисов, получаем

$operatorname{pr}_{vec{e}_1,!!^{ast}}overrightarrow{OC}=frac{bigllangleoverrightarrow{OC},vec{e}_1,!!^{ast}bigrrangle}{bigr|vec{e}_1,!!^{ast}bigr|}=frac{x_1}{bigr|vec{e}_1,!!^{ast}bigr|}=2;qquad operatorname{pr}_{vec{e}_2,!!^{ast}}overrightarrow{OC}=frac{bigllangleoverrightarrow{OC},vec{e}_2,!!^{ast}bigrrangle}{bigr|vec{e}_2,!!^{ast}bigr|}=frac{x_2}{bigr|vec{e}_2,!!^{ast}bigr|}=11,$

где x_1,x_2 — координаты вектора { overrightarrow{OC}} в базисе $vec{e}_1,vec{e}_2$ . Так как $bigr|vec{e}_1,!!^{ast}bigr|,= bigr|vec{e}_2,!!^{ast}bigr|,= frac{2}{sqrt{3}}$ (см. пункт “а”), то $x_1=frac{4}{sqrt{3}},~x_2=frac{22}{sqrt{3}}$ . Длину вектора вычисляем по формуле, следующей из пункта 2 замечаний 1.10 при vec{a}=vec{b} , используя матрицу Грама для базиса $vec{e}_1,vec{e}_2$ , найденную в примере 1.17 пункт “а”:

$bigllangleoverrightarrow{OC}, overrightarrow{OC} bigrrangle,=begin{pmatrix}dfrac{4}{sqrt{3}}&dfrac{22}{sqrt{3}}end{pmatrix}!!begin{pmatrix}1&frac{1}{2}\frac{1}{2}&1end{pmatrix}!!begin{pmatrix}frac{4}{sqrt{3}}\frac{22}{sqrt{3}}end{pmatrix}=196.$

Следовательно, bigr|overrightarrow{OC}bigr|,= sqrt{bigl langleoverrightarrow{OC},overrightarrow{OC}bigrrangle}=sqrt{196}=14. .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

С матрицами (таблицами с числовыми элементами) могут проводиться различные вычислительные действия. Одни из них – умножение на число, вектор, другую матрицу, несколько матриц. Произведение иногда получается неверным. Ошибочный результат – итог незнания правил выполнения вычислительных действий. Давайте разберемся, как следует осуществлять умножение.

Матрица и число

Начнем с самого простого – с умножения таблицы с числами на конкретную величину. Например, мы имеем матрицу A с элементами aij (i – это номера строк, а j – это номера столбцов) и число e. Произведением матрицы на число e будет матрица B с элементами bij, которые находятся по формуле:

Вам будет интересно:Обомлеть — это что значит? Определение и синонимы

bij = e × aij.

Т. е. для получения элемента b11 нужно взять элемент a11 и умножить его на нужное число, для получения b12 требуется найти произведение элемента a12 и числа e и т. д.

Решим задачу № 1, представленную на картинке. Для получения матрицы B просто умножим элементы из A на 3:

a11 × 3 = 18. Это значение записываем в матрицу B в то место, где пересекаются столбец № 1 и строка № 1.

a21 × 3 = 15. Мы получили элемент b21.

a12 × 3 = –6. Мы получили элемент b12. Записываем его в матрицу B в место, где пересекаются столбец № 2 и строка № 1.

a22 × 3 = 9. Данный результат – это элемент b22.

a13 × 3 = 12. Данное число вносим в матрицу на место элемента b13.

a23 × 3 = –3. Последнее полученное число – это элемент b23.

Таким образом, мы получили прямоугольный массив с числовыми элементами.

Векторы и условие существования произведения матриц

Вам будет интересно:“Неожиданный” – это какой? Значение слова

В математических дисциплинах существует такое понятие, как «вектор». Под этим термином понимается упорядоченный набор величин от a1 до an. Они называются координатами векторного пространства и записываются в виде столбца. Еще есть термин «транспонированный вектор». Его компоненты располагаются в виде строки.

Векторы можно называть матрицами:

вектор-столбец – это матрица, построенная из одного столбца;
вектор-строчка – это матрица, которая включает в себя только одну строку.

При выполнении над матрицами операций умножения важно помнить о том, что есть условие существования произведения. Вычислительное действие A × B может быть выполнено только тогда, когда число столбцов в таблице A равно числу строчек в таблице B. Итоговая матрица, получаемая в результате вычисления, всегда имеет число строк таблицы A и число столбцов таблицы B.

При умножении не рекомендуется переставлять местами матрицы (множители). Их произведение обычно не соответствует коммутативному (переместительному) закону умножения, т. е. результат операции A × B не равен результату операции B × A. Такая особенность именуется некоммутативностью произведения матриц. В некоторых случаях результат умножения A × B равен результату умножения B × A, т. е. произведение коммутативно. Матрицы, при которых равенство A × B = B × A выполняется, называются перестановочными. С примерами таких таблиц можно ознакомиться ниже.

Умножение на вектор-столбец

Вам будет интересно:Инженерия знаний. Искусственный интеллект. Машинное обучение

При выполнении умножения матрицы на вектор-столбец обязательно учитываем условие существования произведения. Число столбцов (n) в таблице должно совпадать с количеством координат, из которых составлен вектор. Результат вычисления – преобразованный вектор. Его количество координат равно числу строчек (m) из таблицы.

Как вычисляются координаты вектора y, если есть матрица A и вектор x? Для расчетов созданы формулы:

y1 = a11x1 + a12x2 + … + a1nxn,

y2 = a21x1 + a22x2 + … + a2nxn,

…………………………………,

ym = am1x1 + am2x2 + … + amnxn,

где x1, …, xn – координаты из x-вектора, m – число строк в матрице и количество координат в новом y-векторе, n – число столбцов в матрице и количество координат в x-векторе, a11, a12, …, amn – элементы матрицы A.

Таким образом, для получения i-й компоненты нового вектора выполняется скалярное произведение. Из матрицы A берется i-я вектор-строка, и она умножается на имеющийся вектор x.

Решим задачу № 2. Произведение матрицы на вектор найти можно, ведь A имеет 3 столбца, и x состоит из 3 координат. В результате мы должны получить вектор-столбец с 4 координатами. Воспользуемся вышеуказанными формулами:

Вычислим y1. 1 × 4 + (–1) × 2 + 0 × (–4). Итоговое значение равно 2.

Вычислим y2. 0 × 4 + 2 × 2 + 1 × (–4). При расчете получим 0.

Вычислим y3. 1 × 4 + 1 × 2 + 0 × (–4). Сумма произведений указанных множителей равна 6.

Вычислим y4. (–1) × 4 + 0 × 2 + 1 × (–4). Координата равна –8.

Умножение вектор-строки на матрицу

Нельзя умножить матрицу, состоящую из нескольких столбцов, на вектор-строку. В таких случаях не выполняется условие существования произведения. А вот умножение вектор-строки на матрицу возможно. Эта вычислительная операция выполняется при совпадении количества координат в векторе и числа строк в таблице. Результат произведения вектора на матрицу – новая вектор-строка. Ее количество координат должно равняться числу столбцов в матрице.

Вычисление первой координаты нового вектора подразумевает умножение вектор-строки и первого вектор-столбца из таблицы. Аналогичным способом производится расчет второй координаты, но вместо первого вектор-столбца берется уже второй вектор-столбец. Вот общая формула для вычисления координат:

yk = a1kx1 + a2kx2 + … + amkxm,

где yk – координата из y-вектора, (k находится в промежутке от 1 до n), m – число строк в матрице и количество координат в x-векторе, n – число столбцов в матрице и количество координат в y-векторе, a с буквенно-цифровыми индексами – элементы матрицы A.

Произведение прямоугольных матриц

Это вычислительное действие может показаться сложным. Однако умножение легко выполняется. Начнем с определения. Произведение матрицы A с m строками и n столбцами и матрицы B с n строками и p столбцами – это матрица C с m строками и p столбцами, в которой элемент cij представляет собой сумму произведений элементов i-й строки из таблицы A и j-го столбца из таблицы B. Если говорить более простым языком, то элемент cij – это скалярное произведение i-й вектор-строчки из таблицы A и j-го вектор-столбца из таблицы B.

Теперь разберемся на практике в том, как находить произведение матриц прямоугольного вида. Решим для этого задачу № 3. Условие существования произведения выполняется. Приступим к расчету элементов cij:

Матрица C будет состоять из 2 строк и 3 столбцов.

Рассчитаем элемент c11. Для этого выполним скалярное произведение строки № 1 из матрицы A и столбца № 1 из матрицы B. c11 = 0 × 7 + 5 × 3 + 1 × 1 = 16. Далее поступаем аналогичным образом, меняя только строки, столбцы (в зависимости от индекса элемента).

c12 = 12.

c13 = 9.

c21 = 31.

c22 = 18.

c23 = 36.

Вам будет интересно:Изотоп лития: определение и применение

Элементы рассчитаны. Теперь осталось только составить прямоугольный блок из полученных чисел.

Умножение трех матриц: теоретическая часть

Можно ли найти произведение трех матриц? Эта вычислительная операция выполнима. Результат можно получить несколькими способами. Например, есть 3 квадратных таблицы (одного порядка) – A, B и C. Чтобы вычислить произведение, можно:

Умножить сначала A и B. Результат затем умножить на C.

Найти сначала произведение B и C. Далее матрицу A умножить на полученный результат.

Если требуется перемножить матрицы прямоугольного вида, то сначала нужно удостовериться в том, что данная вычислительная операция возможна. Должны существовать произведения A × B и B × C.

Поэтапное умножение не является ошибкой. Есть такое понятие, как «ассоциативность умножения матриц». Под этим термином понимается равенство (A × B) × C = A × (B × C).

Умножение трех матриц: практика

Квадратные матрицы

Начнем с умножения небольших квадратных матриц. Ниже на рисунке представлена задача № 4, которую нам предстоит решить.

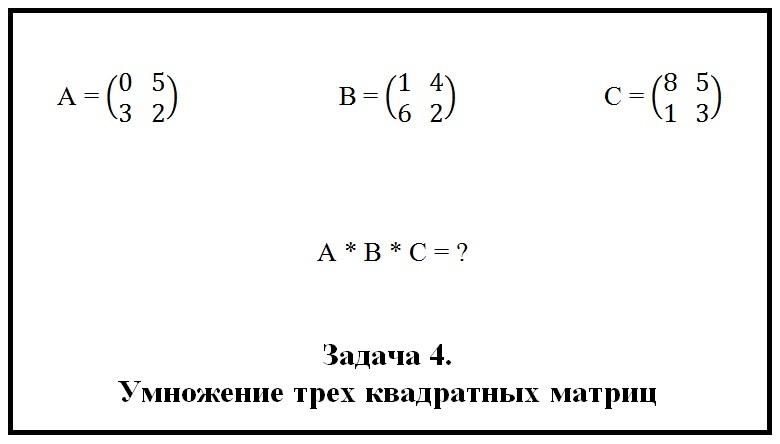
Будем пользоваться свойством ассоциативности. Перемножим сперва либо A и B, либо B и C. Помним только одно: нельзя переставлять местами множители, т. е. нельзя умножать B × A или C × B. При таком умножении мы получим ошибочный результат.

Ход решения.

Шаг первый. Для нахождения общего произведения умножим сначала A на B. При умножении двух матриц будем руководствоваться теми правилами, которые были изложены выше. Итак, результатом умножения A и B будет матрица D с 2 строчками и 2 столбцами, т. е. прямоугольный массив будет включать в себя 4 элемента. Найдем их, выполнив расчет:

d11 = 0 × 1 + 5 × 6 = 30;
d12 = 0 × 4 + 5 × 2 = 10;
d21 = 3 × 1 + 2 × 6 = 15;
d22 = 3 × 4 + 2 × 2 = 16.

Промежуточный результат готов.

Шаг второй. Теперь умножим матрицу D на матрицу C. Результатом должна быть квадратная матрица G с 2 строками и 2 столбцами. Рассчитаем элементы:

g11 = 30 × 8 + 10 × 1 = 250;
g12 = 30 × 5 + 10 × 3 = 180;
g21 = 15 × 8 + 16 × 1 = 136;
g22 = 15 × 5 + 16 × 3 = 123.

Таким образом, результатом произведения квадратных матриц является таблица G с вычисленными элементами.

Прямоугольные матрицы

Ниже на рисунке представлена задача № 5. Требуется перемножить прямоугольные матрицы и найти решение.

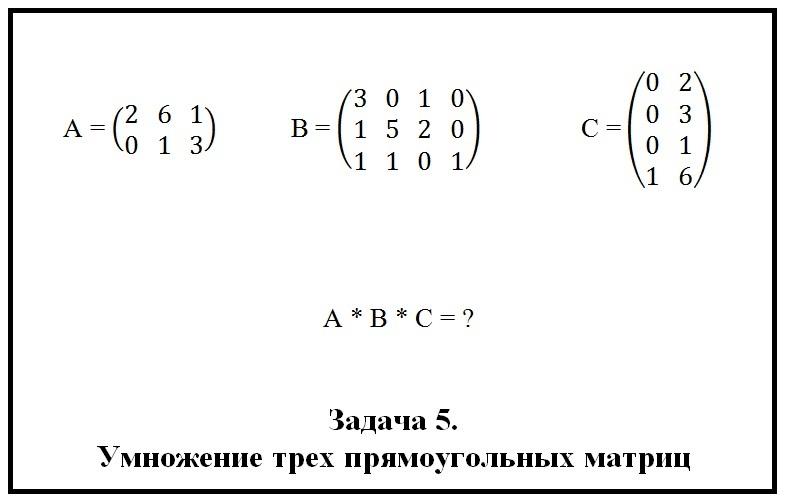
Проверим, выполняется ли условие существования произведений A × B и B × C. Порядки указанных матриц позволяют нам выполнять умножение. Приступим к решению задачи.

Ход решения.

Шаг первый. Умножим B на C для получения D. Матрица B содержит 3 строчки и 4 столбца, а матрица C – 4 строчки и 2 столбца. Это значит, что матрица D у нас получится с 3 строчками и 2 столбцами. Рассчитаем элементы. Вот 2 примера вычислений:

d11 = 3 × 0 + 0 × 0 + 1 × 0 + 0 × 1 = 0;
d12 = 3 × 2 + 0 × 3 + 1 × 1 + 0 × 6 = 7.

Продолжаем решать задачу. В результате дальнейших вычислений мы находим значения d21, d22, d31 и d32. Эти элементы равны 0, 19, 1 и 11 соответственно. Запишем найденные значения в прямоугольный массив.

Шаг второй. Умножим A на D, чтобы получить итоговую матрицу F. В ней будет 2 строчки и 2 столбца. Рассчитаем элементы:

f11 = 2 × 0 + 6 × 0 + 1 × 1 = 1;
f12 = 2 × 7 + 6 × 19 + 1 × 11 = 139;
f21 = 0 × 0 + 1 × 0 + 3 × 1 = 3;
f22 = 0 × 7 + 1 × 19 + 3 × 11 = 52.

Составим прямоугольный массив, являющийся конечным результатом умножения трех матриц.

Знакомство с прямым произведением

Достаточно сложным для понимания материалом является кронекеровское произведение матриц. У него есть еще дополнительное название – прямое произведение. Что же понимается под этим термином? Допустим, у нас есть таблица A порядка m × n и таблица B порядка p × q. Прямым произведением матрицы A на матрицу B является матрица порядка mp × nq.

У нас есть 2 квадратные матрицы A, B, которые представлены на картинке. Первая из них состоит из 2 столбцов и 2 строк, а вторая – из 3 столбцов и 3 строк. Мы видим, что матрица, полученная в результате прямого произведения, состоит из 6 строк и точно такого же количества столбцов.

Как при прямом произведении вычисляют элементы новой матрицы? Найти ответ на этот вопрос очень легко, если проанализировать рисунок. Сначала заполняют первую строку. Берут первый элемент из верхней строчки таблицы A и последовательно умножают на элементы первой строки из таблицы B. Далее берут второй элемент первой строчки таблицы A и последовательно умножают на элементы первой строки таблицы B. Для заполнения второй строки снова берут первый элемент из первой строки таблицы A и умножают его на элементы второй строки таблицы B.

Итоговую матрицу, получаемую прямым произведением, называют блочной. Если вновь проанализировать рисунок, то можно заметить, что наш результат состоит из 4 блоков. Все они включают элементы матрицы B. Дополнительно элемент каждого блока умножен на конкретный элемент матрицы A. В первом блоке все элементы умножены на a11, во втором – на a12, в третьем – на a21, в четвертом – на a22.

Определитель произведения

При рассмотрении темы, касающейся умножения матриц, стоит еще рассмотреть такой термин, как «определитель произведения матриц». Что такое определитель? Это важная характеристика квадратной матрицы, определенное значение, которое ставится в соответствие этой матрице. Буквенное обозначение определителя – det.

Для матрицы A, состоящей из двух столбцов и двух строчек, определитель легко найти. Существует небольшая формула, представляющая собой разность произведений конкретных элементов:

det A = a11 × a22 – a12 × a21.

Рассмотрим пример вычисления определителя для таблицы второго порядка. Существует матрица A, в которой a11 = 2, a12 = 3, a21 = 5 и a22 = 1. Для вычисления определителя воспользуемся формулой:

det A = 2 × 1 – 3 × 5 = 2 – 15 = –13.

У матриц 3 × 3 определитель вычисляется по более сложной формуле. Она представлена ниже для матрицы A:

det A = a11a22a33 + a12a23a31 + a13a21a32 – a13a22a31 – a11a23a32 – a12a21a33.

Для запоминания формулы придумали правило треугольника, которое проиллюстрировано на картинке. Сначала умножаются элементы главной диагонали. К полученному значению прибавляются произведения тех элементов, на которые указывают углы треугольников с красными сторонами. Далее отнимается произведение элементов побочной диагонали и отнимаются произведения тех элементов, на которые указывают углы треугольников с синими сторонами.

Вам будет интересно:Погранвойска СССР: знаки отличия, функции, структура

Теперь поговорим об определителе произведения матриц. Существует теорема, которая гласит, что данный показатель равен произведению определителей таблиц-сомножителей. Убедимся в этом на примере. У нас есть матрица A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и матрица B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Найдем определители для матриц A и B, произведение A × B и определитель этого произведения.

Ход решения.

Шаг первый. Вычислим определитель для A: det A = 2 × 1 – 3 × 1 = –1. Далее вычислим определитель для B: det B = 4 × 2 – 5 × 1 = 3.

Шаг второй. Найдем произведение A × B. Новую матрицу обозначим буквой C. Вычислим ее элементы:

c11 = 2 × 4 + 3 × 1 = 11;
c12 = 2 × 5 + 3 × 2 = 16;
c21 = 1 × 4 + 1 × 1 = 5;
c22 = 1 × 5 + 1 × 2 = 7.

Шаг третий. Вычислим определитель для C: det C = 11 × 7 – 16 × 5 = –3. Сравним со значением, которое могло бы получиться при умножении определителей исходных матриц. Числа одинаковые. Вышеуказанная теорема верна.

Ранг произведения

Ранг матрицы – это характеристика, отражающая максимальное количество линейно независимых строк или столбцов. Для вычисления ранга выполняют элементарные преобразования матрицы:

перестановку местами двух параллельно лежащих рядов;
умножение всех элементов определенного ряда из таблицы на число, не равняющееся нулю;
прибавление к элементам одного ряда элементов из другого ряда, умноженных на конкретное число.

После элементарных преобразований смотрят на количество ненулевых строк. Их число – это и есть ранг матрицы. Рассмотрим предыдущий пример. В нем было представлено 2 матрицы: A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Также будем использовать матрицу C, полученную в результате умножения. Если мы выполним элементарные преобразования, то в упрощенных матрицах нулевых строк не будет. Это значит, что и ранг таблицы A, и ранг таблицы B, и ранг таблицы C равен 2.

Теперь особое внимание уделим рангу произведения матриц. Существует теорема, которая гласит, что ранг произведения таблиц, содержащих числовые элементы, не превышает ранга любого из сомножителей. Это можно доказать. Пусть A – это матрица размера k × s, а B – это матрица размера s × m. Произведение A и B равно C.

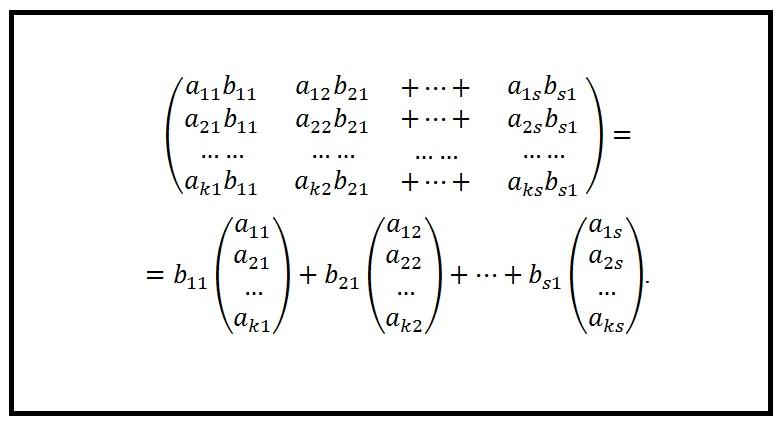
Изучим рисунок, представленный выше. На нем изображен первый столбец матрицы C и его упрощенная запись. Этот столбец – линейная комбинация столбцов, входящих в матрицу A. Аналогичным образом можно сказать о любом другом столбце из прямоугольного массива C. Таким образом, подпространство, образованное векторами-столбцами таблицы C, имеется в подпространстве, образованном векторами-столбцами таблицы A. По этой причине размерность подпространства № 1 не превосходит размерности подпространства № 2. Отсюда следует вывод, что ранг по столбцам таблицы C не превышает ранга по столбцам таблицы A, т. е. r(C) ≤ r(A). Если рассуждать аналогичным образом, то можно убедиться в том, что строчки матрицы C – это линейные комбинации строчек матрицы B. Из этого следует неравенство r(C) ≤ r(B).

Как находить произведение матриц – достаточно сложная тема. Ее можно легко освоить, но для достижения такого результата придется уделить немало времени заучиванию всех существующих правил и теорем.

Источник

Определение и свойства[править | править код]

Определение и свойства в евклидовом пространстве[править | править код]

Вещественные векторы[править | править код]

Комплексные векторы[править | править код]

Свойства[править | править код]

Теорема косинусов в вещественном пространстве[править | править код]

Связанные определения[править | править код]

История[править | править код]

Вариации и обобщения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

1.3. Скалярное произведение векторов

1.4. Матрицы

Выражение скалярного произведения через координаты векторов

Скалярное произведение векторов в ортонормированном базисе

Скалярное произведение векторов в произвольном базисе

Скалярное произведение векторов во взаимных базисах

Матрица и число

Векторы и условие существования произведения матриц

Умножение на вектор-столбец

Умножение вектор-строки на матрицу

Произведение прямоугольных матриц

Умножение трех матриц: теоретическая часть

Умножение трех матриц: практика

Знакомство с прямым произведением

Определитель произведения

Ранг произведения

Вам также может понравиться

Как составить смету на строительство двухэтажного дома

Составить план государства как политического института

Как найти гида по китаю

Добавить комментарий Отменить ответ