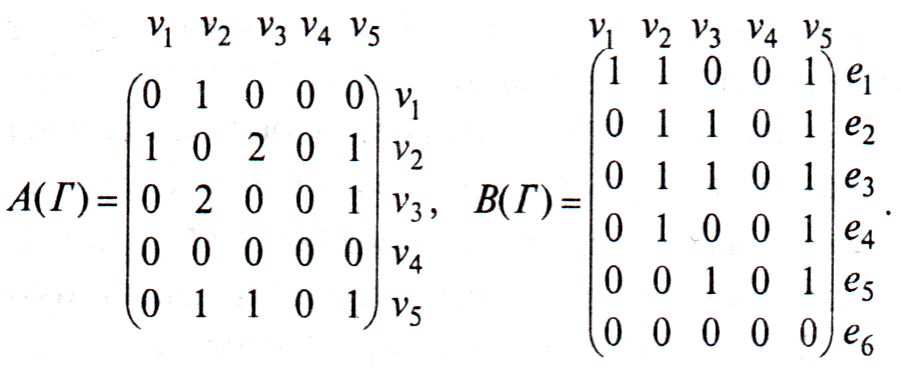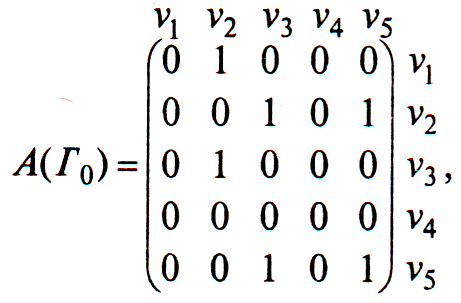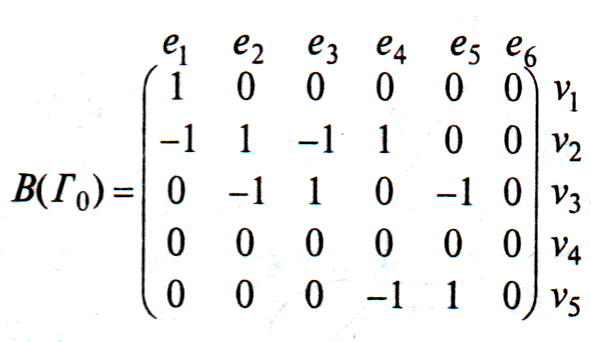Как найти матрицу смежности по матрице инцидентности

Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор

В этой статье:

Матрица смежности

Матрица инцидентности

Список смежности (инцидентности)

Взвешенный граф (коротко)

Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.

Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).

Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).

Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.

Матрица смежности

Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.

Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными. 

Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.  

Каждая ячейка матрицы равна либо 1, либо 0;

Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.

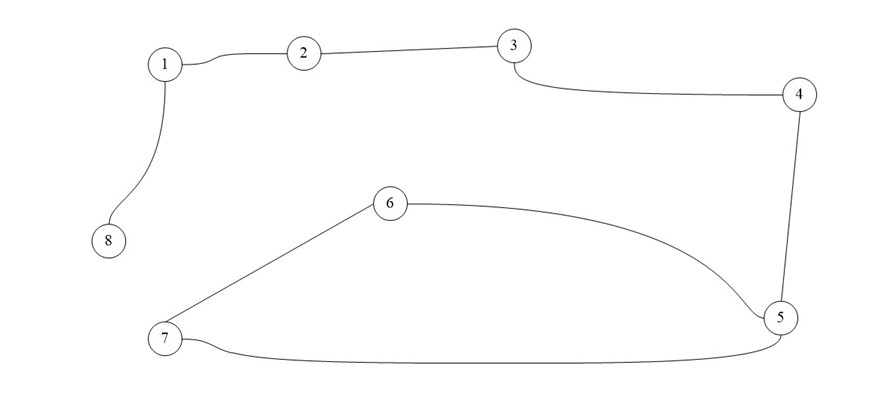
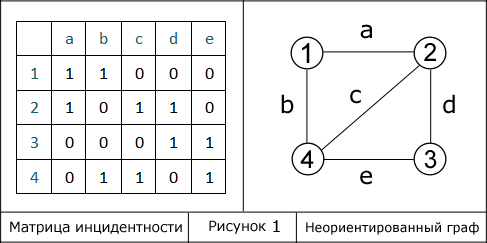
Для практического примера возьмем самый обыкновенный неориентированный граф:

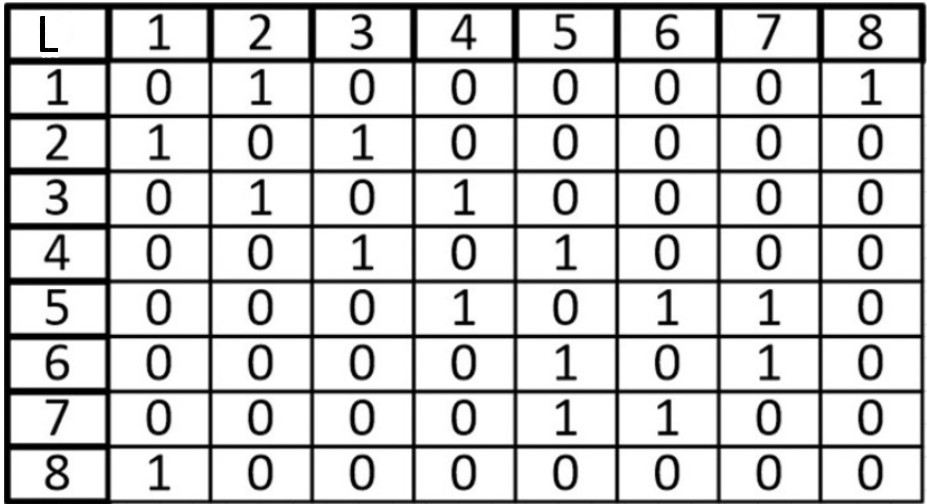
А теперь представим его в виде матрицы:

Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.

С одной стороны объем памяти будет:

Но используя вышеописанный подход получается:

Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.

Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.

Если мы используем ориентированный граф, то кое-что меняется.

Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.

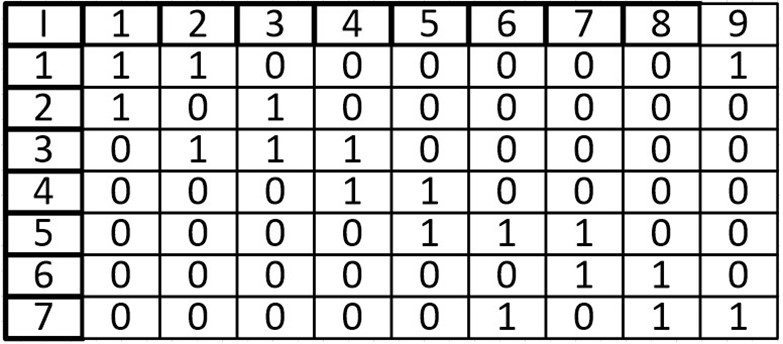
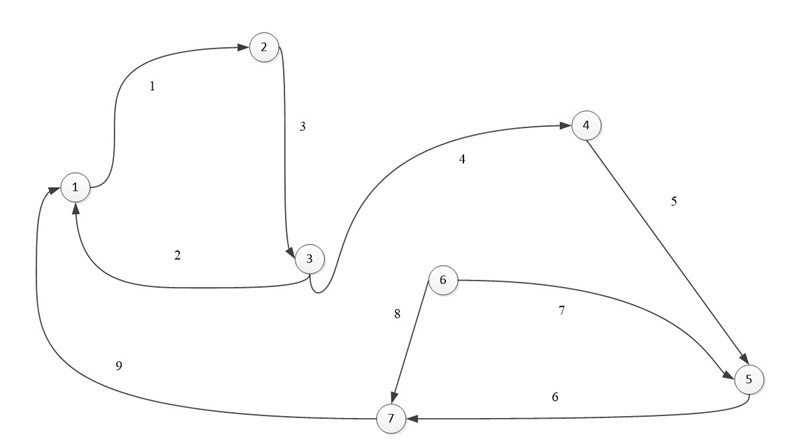
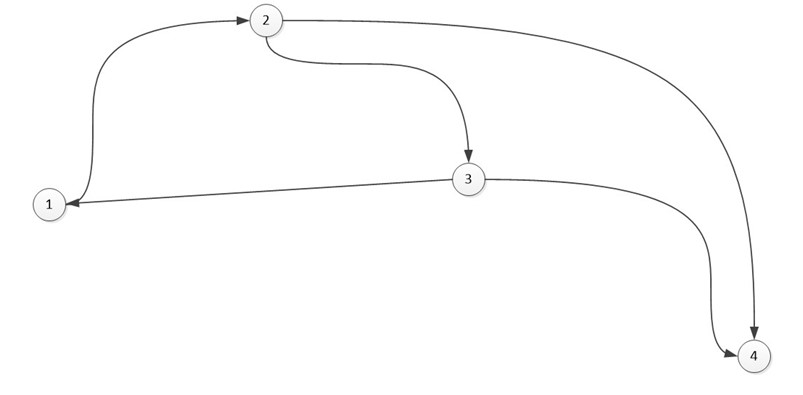
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:

В виде матрицы:

Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.

Объем памяти:

Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.

Используя петли мы должны запомнить, что в неориентированном графе петля учитывается дважды, а в ориентированном – единожды.

Матрица инцидентности

Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.

Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.

Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.

Сразу же иллюстрируем данное правило:

В виде матрицы:

Сумма элементов i-ой строки равна степени вершины.

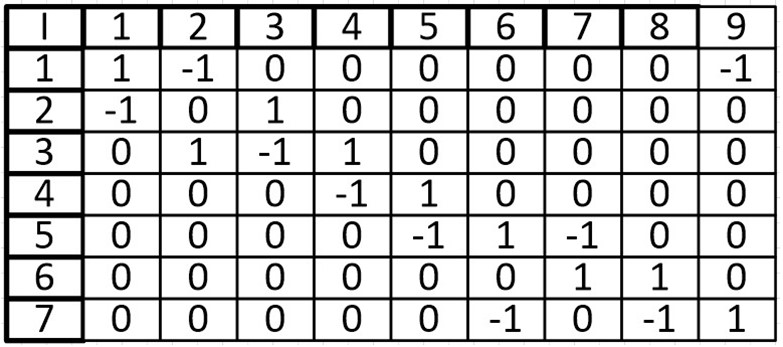
При ориентированным графе, ячейка I (i, j) равна 1, если вершина V (i) начало дуги E(j) и ячейка I (i, j) равна -1 если вершина V (i) конец дуги E (j), иначе ставится 0.

Ориентированный граф:

В виде матрицы:

Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.

При суммировании строки, ячейки со значением -1, могут складываться только с ячейками, также имеющими значение -1, то же касается и 1, мы можем узнать степень входа и степень выхода из вершины. Допустим при сложении первой вершины, мы узнаем, что из нее исходит 1 ребро и входят два других ребра. Это является еще одной особенностью (при том очень удобной) данной матрицы.

Объем памяти:

Список смежности (инцидентности)

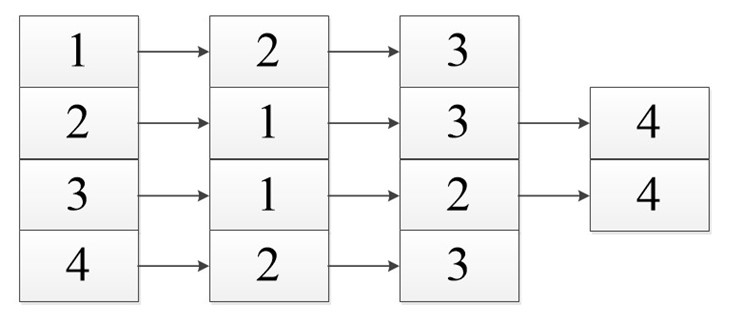
Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.

В виде списка это будет выглядеть так:

Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.

Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:

Объем памяти:

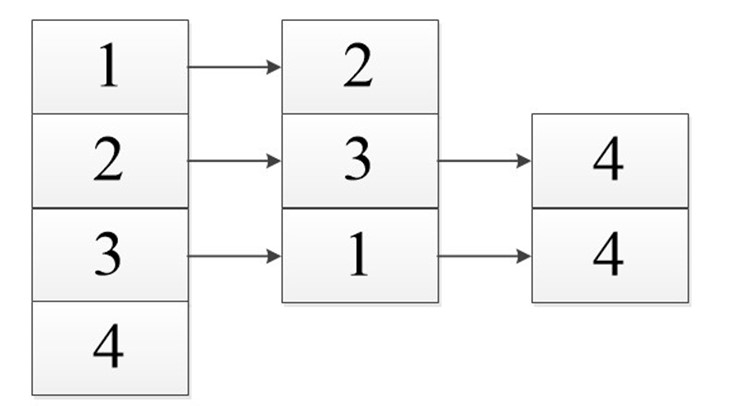
Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).

В виде списка:

Сумма длин всех списков:

Объем памяти:

Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.

К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.

Взвешенность графа

Взвешенный граф – это граф, в котором вместо 1 обозначающее наличие связи между вершинами или связи между вершиной и ребром, хранится вес ребра, то есть определённое число с которым мы будем проводить различные действия.

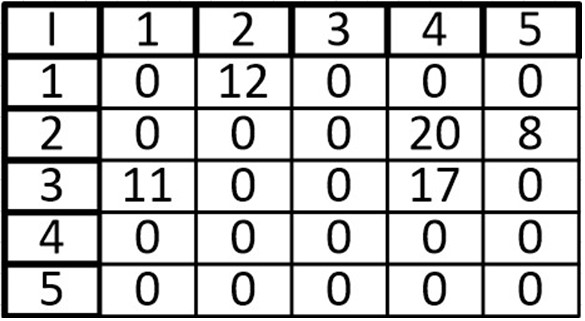
К примеру, возьмем граф с весами на ребрах:

И сделаем матрицу смежности:

В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.

Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.

Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.

Если заметили ошибку или есть предложения пишите в комментарии.

На каком языке программирования проводить операции с графами

Проголосовали 47 пользователей.

Воздержались 8 пользователей.

Немного опередил MBo 🙂 – пока я все комментарии расписывал. Ну, не пропадать же коду…

Раз у вас С++, лучше использовать векторы.

#include <vector>
#include <iostream>

using namespace std;

vector<vector<int>> rebuild(const vector<vector<int>>& G)
{
    size_t vxs = G[0].size(); // Количество столбцов

    // Здесь по-хорошему нужно убедиться, что
    // в каждой строке одно и то же число столбцов

    vector<vector<int>> R(vxs, vector<int>(vxs,0)); // Результат

    // Проход по строкам
    for(const auto& s: G)
    {
        vector<size_t> ix; // Собираем ненулевые значения
        for(size_t i = 0; i < s.size(); ++i)
            if (s[i]) ix.push_back(i);
        // Если их хотя бы 2...
        if (ix.size() > 1)
        {
            // Каждый с каждым - расставляем единицы
            for(size_t i = 0; i < ix.size()-1; ++i)
                for(size_t j = i+1; j < ix.size(); ++j)
                    R[ix[i]][ix[j]] = R[ix[j]][ix[i]] = 1;
        }
    }
    return R;
}

int main([[maybe_unused]] int argc,
         [[maybe_unused]] const char * argv[])
{
    vector<vector<int>> G = {{1,1,0,0},{1,0,1,1},{0,0,0,1},{0,1,1,0}};

    vector<vector<int>> R = rebuild(G);

    for(size_t i = 0; i < R.size(); ++i)
    {
        for(size_t j = 0; j < R[i].size(); ++j)
            cout << R[i][j] << "  ";
        cout << endl;
    }
}

Матрица инцидентности и матрица смежности

На рис. 1,2 изображено
множество точек

и
множество линий
,
соединяющих эти точки,
которые все вместе образуют граф
.Если линии имеют
стрелки, то граф называется ориентированным
или орграфом

(рис. 2).

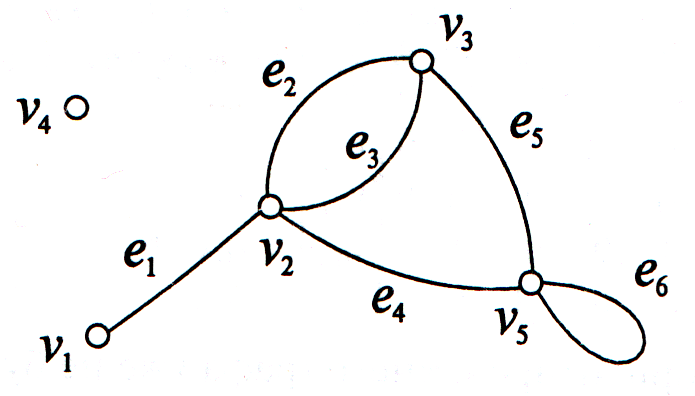
Рис. 1. Граф

.

Рис. 2.
Орграф

.

Графы
и
можно представить в
аналитической форме либо матрицей
смежности
,либо матрицей
инцидентности
.

Для нашего конкретного
неориентированного графа

матрицы
и
выглядят следующим
образом:

Матрица смежности для неориентированного
графа всегда симметрична.

Фигурирующая в ней 2 может быть в некоторых
случаях заменена на 1.

В матрице инцидентности
сумма единиц по столбцам указывает на
степень вершины v_i.
Нередко расположение вершин и ребер в
этой матрице меняют местами (транспонируют).
Так, для нашего конкретного орграфа
матрицы
и
выглядят существенно
иначе:

В общем случае матрица
смежности для ориентированного графа


уже не будет симметричной. В матрице
инцидентности ставится 1, если дуга
исходит из вершины, и —1, если дуга
заходит в нее.

Матрица
смежности и матрица инцидентности

Есть два стандартных способа представить
граф G = (V,E) 

• – как набор списков смежных вершин

• как матрицу смежности.

Первый обычно предпочтительнее, ибо
дает более компактное представление
разреженных графов– тех, у
которых |E| много меньше
|V|².

Большинство стандартных алгоритмов
используют именно это представление.
Но в некоторых ситуациях удобнее
пользоваться матрицей смежности –
например, для плотных графов, у
которых |EG| сравнимо с |VG|².

Матрица смежности позволяет быстро
определить, соединены ли две данные
вершины ребром. Алгоритмы отыскания
кратчайших путей для всех пар вершин,
используют представление графа с помощью
матрицы смежности.

• Определение Матрицей смежностиграфа G = (V, E) называется квадратная
  булева матрицаAпорядкаn,элементы которой определяются
  следующим образом:

Свойства

1. А – симметрическая матрица

2. На главной диагонали матрицы смежности
   всегда стоят 0.

3. Число единиц в строке равно степени
   соответствующей вершины.

Матрицей инцидентностиграфаGназывается булева матрица размера
|V|´|G|
вида

Свойства:

1.   В каждом столбце матрицы ровно две
   единицы

2. Равных столбцов нет.

Например, на следующем рисунке граф
задан графически, списком смежных
вершин, матрицей смежности и матрицей
инцидентности.

графически	список смежных вершин     номер вершины степень вершины 1 2 2 5 2 4 1 3 4 5 3 2 2 4 4 3 2 3 5 5 3 1 2 4
матрица смежности 1 2 3 4 5 1 0 1 0 0 1 2 1 0 1 1 1 3 0 1 0 1 0 4 0 1 1 0 1 5 1 1 0 1 0	матрица инцидентности e1 e2 e3 e4 e5 e6 e7 1 1 1 0 0 0 0 0 2 0 1 1 0 1 1 0 3 0 0 0 0 0 1 1 4 0 0 0 1 1 0 1 5 1 0 1 1 0 0 0

Рассматриваются
также графы
с нагруженными ребрами
или взвешенные –
графы, у которых каждому ребру поставлено
в соответствие некоторое вещественное
число – вес или нагрузка ребра.

Такой граф можно
задать матрицей
расстояний –
квадратной матрицей размера |V|´|V|,
где на пересечении i-ой
строки и j-го
столбца записан вес ребра (i,
j),
если ребро есть, ¥,
если ребра нет и 0, если i = j.

Соседние файлы в папке ДМ ВВО

• #
• #
• #
• #
• #
• #
• #

Говорить о том, что ребро g и каждая из вершин u и y инцидентна g, стоит лишь в том случае, если g соединяет u и y. Уяснив это, перейдем к рассмотрению данного метода. Матрица инцидентности строиться по похожему, но не по тому же принципу, что и матрица смежности. Так если последняя имеет размер n×n, где n – число вершин, то матрица инцидентности – n×m, здесь n – число вершин графа, m – число ребер. То есть теперь чтобы задать значение какой-либо ячейки, нужно сопоставить не вершину с вершиной, а вершину с ребром.

В каждой ячейки матрицы инцидентности неориентированного графа стоит 0 или 1, а в случае ориентированного графа, вносятся 1, 0 или -1. То же самое, но наиболее структурировано:

1) Неориентированный граф

a. 1 – вершина инцидентна ребру

b. 0 – вершина не инцидентна ребру

2) Ориентированный граф

a. 1 – вершина инцидентна ребру, и является его началом

b. 0 – вершина не инцидентна ребру

c. -1 – вершина инцидентна ребру, и является его концом

Построим матрицу инцидентности сначала для неориентированного графа, а затем для орграфа.

Ребра обозначены буквами от a до e, вершины – цифрами. Все ребра графа не направленны, поэтому матрица инцидентности заполнена положительными значениями.

Для орграфа графа матрица имеет немного другой вид. В каждую из ее ячеек внесено одно из трех значений. Обратите внимание, что нули в двух этих матрицах (рис. 1 и 2) занимают одинаковые позиции, ведь в обоих случаях структура графа одна. Но некоторые положительные единицы сменились на отрицательные, например, в неориентированном графе ячейка (1, b) содержит 1, а в орграфе -1. Действительно, это уместно, т. к. в первом случае ребро b не направленное, а во втором – направленное, и, причем вершиной входа для него является вершина «1».

Каждый столбец отвечает за какое-либо одно ребро, поэтому граф, описанный при помощи матрицы инцидентности, всегда будет иметь следующий признак: любой из столбцов матрицы инцидентности содержит две единицы, либо 1 и -1 когда это ориентированное ребро, все остальное в нем – нули.

В программе матрица инцидентности задается, также как и матрица смежности, а именно при помощи двумерного массива. Его элементы могут быть инициализированы при объявлении, либо по мере выполнения программы.

( 2 оценки, среднее 5 из 5 )