Как найти матрицу связности для графа - Сайт, где вы сможете решить свои вопросы

Неориентированный
граф называется связным,
если каждая пара различных вершин может
быть соединена, по крайней мере, одной
цепью.

Ориентированный
граф называется сильно
связным,
если для любых двух его вершин

существует
хотя бы один путь, соединяющий

.
Ориентированный граф называется
односторонне
связным,
если для любых двух его вершин, по крайней
мере, одна достижима из другой.

Компонентой
связности неориентированного графа
называется его связный подграф, не
являющийся собственным подграфом
никакого другого связного подграфа
данного графа (максимально связный
подграф).

Компонентой
сильной связности ориентированного
графа
называется его сильно связный подграф,
не являющийся собственным подграфом
никакого другого сильно связного
подграфа данного графа (максимально
сильно связный подграф).

Компонентой
односторонней связности ориентированного
графа называется
его односторонне связный подграф, не
являющийся собственным подграфом
никакого другого односторонне связного
подграфа данного графа (максимально
односторонне связный подграф).

Пусть

неориентированный граф с множеством
вершин

.
Квадратная матрица

порядка

,
у которой

называется
матрицей
связности графа

Для ориентированного
графа квадратная матрица

порядка

,
у которой

называется
матрицей
односторонней связности (достижимости).

Квадратная матрица

порядка

,
у которой

называется матрицей
сильной связности.

Пример. У
неориентированного графа, изображенного
на рис. 22 две компоненты связности.
Первая компонента связности включает
вершины

,
а вторая
состоит из одной вершины

Рис. 22. Компоненты
связанности неориентированного графа

Матрица связности
этого графа имеет вид:

.

Мы видим, что 1-ая,
2-ая, 4-ая и 5-ая строки матрицы

одинаковы.

Пример. У
ориентированного графа, изображенного
на рис. 23 две компоненты сильной связности.
Первая компонента связности включает
вершины

,
а вторая
состоит из одной вершины

.
Действительно, для любой пары вершин
из множества

существует
хотя бы один путь, соединяющий эти
вершины. Например, путь

соединяет все эти вершины. Из вершины

нет пути ни в одну вершину графа.

Рис. 23. Компоненты
сильной связанности ориентированного
графа

Матрица сильной
связности этого графа имеет вид:

Заметим, что 1-ая,
2-ая, 3-ая и 5-ая строки матрицы

одинаковы.

Для того, чтобы
выделить компоненты сильной связности,
необходимо сначала найти матрицу
достижимости

ориентированного графа, затем находим
матрицу сильной связности

ориентированного графа (она должна быть
симметрической).

Алгоритм выделения
компонента сильной связности:

1. Присваиваем

(

− количество компонент связности),

2. Включаем в
множество вершин

компоненты
сильной связности

вершины, соответствующие единицам
первой строки матрицы

.
В качестве матрицы смежности

возьмем подматрицу матрицы

,
состоящую из элементов матрицы

,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из

3. Вычеркиваем из

строки и столбцы, соответствующие
вершинам из

.
Если не остается ни одной строки (и
столбца), то


количество компонент сильной связности.
В противном случае обозначим оставшуюся
после вычеркивания срок и столбцов
матрицу как

,
присваиваем

и переходим к п. 2.

Пример. Выделим
компоненты связности ориентированного
графа, изображенного на рис. 25. Количество
вершин

.

Рис. 25.

Значит, для данного
ориентированного графа матрица смежности
будет иметь размерность

и будет выглядеть следующим образом

Найдем матрицу
достижимости и матрицу сильной связности
для данного ориентированного графа:

Присваиваем

и составляем множество вершин первой
компоненты сильной связности

:
это те вершины, которым соответствуют
единицы в первой строке матрицы

.
Таким образом, первая компонента сильной
связности состоит из одной вершины

.

Вычеркиваем из
матрицы

строку и столбец, соответствующие
вершине

,
чтобы получить матрицу

.

Присваиваем

.
Множество вершин второй компоненты
связности составят те вершины, которым
соответствуют единицы в первой строке
матрицы

,
то есть

.
Составляем матрицу смежности для
компоненты сильной связности

исходного графа

− в ее
качестве возьмем подматрицу матрицы

,
состоящую из элементов матрицы

,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из

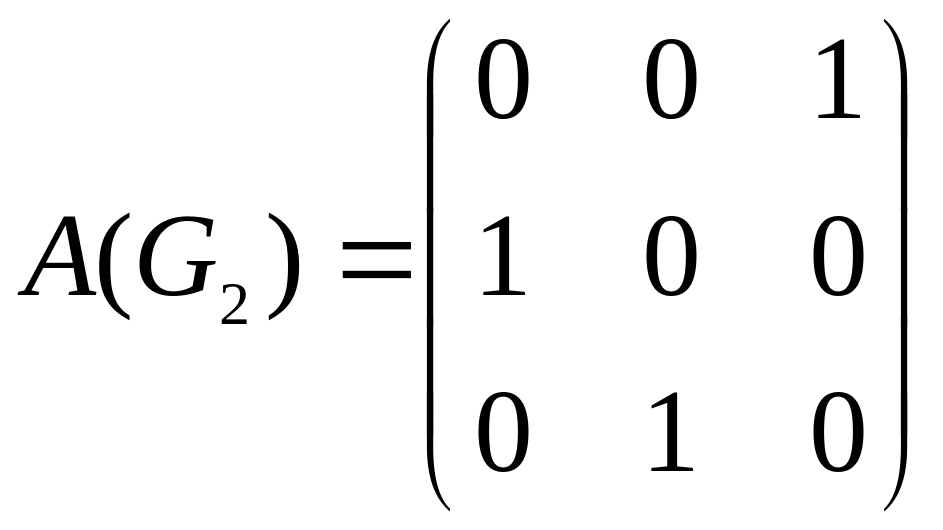
Вычеркиваем из
матрицы

строки и столбцы, соответствующие
вершинам из

,чтобы
получить матрицу

,
которая состоит из одного элемента

,
присваиваем

.
Таким образом, третья компонента сильной
связности исходного графа, как и первая,
состоит из одной вершины

.

Таким образом,
выделены 3 компоненты сильной связности
ориентированного графа

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 апреля 2020 года; проверки требуют 11 правок.

Матрица достижимости простого ориентированного графа — бинарная матрица замыкания по транзитивности отношения (оно задаётся матрицей смежности графа). Таким образом, в матрице достижимости хранится информация о существовании путей между вершинами орграфа.

Способы построения матрицы достижимости[править | править код]

Перемножение матриц[править | править код]

Пусть дан простой граф , матрица смежности которого есть ${displaystyle mathbf {A} =(a_{ij})_{ntimes n}}$ , где ${displaystyle a_{ij}=1Leftrightarrow (i,j)in A}$ . Матрица смежности даёт информацию о всех путях длины 1 (то есть дугах) в орграфе. Для поиска путей длины 2 можно найти композицию отношения с самим собой:

По определению, матрица композиции отношений есть ${displaystyle mathbf {A^{2}} =({a^{2}}_{ij})_{ntimes n}={Bigl (}sum _{k}a_{ik}a_{kj}{Bigr )}={Bigl (}(a_{i1}land a_{1j})lor (a_{i2}land a_{2j})lor ldots lor (a_{in}land a_{nj}){Bigr )}}$ , где land — конъюнкция, а lor — дизъюнкция.

После нахождения матриц ${displaystyle mathbf {A} ^{k}}$ композиций ${displaystyle underbrace {Acirc ldots circ A} _{k}}$ для всех , будет получена информация о всех путях длины от до n-1 . Таким образом, матрица ${displaystyle mathbf {R(G)} =mathbf {E} lor mathbf {A} lor mathbf {A^{2}} lor ldots lor mathbf {A^{n-1}} =({a^{*}}_{ij})_{ntimes n}=({a}_{ij}lor {a^{2}}_{ij}lor ldots lor {a^{n-1}}_{ij})}$ есть искомая матрица достижимости, где — единичная матрица.

${displaystyle mathbf {E} ={begin{pmatrix}1&0&0&0\0&1&0&0\0&0&1&0\0&0&0&1end{pmatrix}}}$

Случай нескольких путей[править | править код]

Если булевы операции дизъюнкции и конъюнкции заменить обычными алгебраическими операциями +,times сложения и умножения соответственно, нахождение матрицы достижимости сведётся к обычному пошаговому перемножению матриц с последующим сложением результатов каждого шага. Тогда получившаяся матрица будет состоять не только из 0 и 1 и будет характеризовать не только наличие путей между вершинами, но уже и количество таких путей. В таком случае можно разрешить наличие кратных рёбер в графе.

Пример[править | править код]

Граф

Рассмотрим простой связный ориентированный граф .
Он имеет матрицу смежности вида:

${displaystyle mathbf {A} ={begin{pmatrix}0&1&1&0\0&0&0&0\0&1&0&1\0&0&1&0end{pmatrix}}}$

Найдём булевы степени этой матрицы ${displaystyle mathbf {A^{2}} }$ , ${displaystyle mathbf {A^{3}} }$ :

${displaystyle mathbf {A^{2}} ={begin{pmatrix}0&1&0&1\0&0&0&0\0&0&1&0\0&1&0&1end{pmatrix}}}$ ,
${displaystyle mathbf {A^{3}} ={begin{pmatrix}0&0&1&0\0&0&0&0\0&1&0&1\0&0&1&0end{pmatrix}}}$ ,

Получим матрицу достижимости

${displaystyle mathbf {R(G)} =mathbf {Elor Alor A^{2}lor A^{3}} ={begin{pmatrix}1&1&1&1\0&1&0&0\0&1&1&1\0&1&1&1end{pmatrix}}}$

Таким образом, из вершины можно добраться в любую другую.

При использовании же алгебраических операций получится матрица

${displaystyle mathbf {R(G)} =mathbf {E+A+A^{2}+A^{3}} ={begin{pmatrix}1&2&2&1\0&1&0&0\0&2&2&2\0&1&2&2end{pmatrix}}}$

Она показывает количество путей длины от 0 до 3 между вершинами орграфа.

Алгоритм Уоршелла[править | править код]

Существует другой алгоритм, позволяющий найти матрицу достижимости в точности за $2n^{3}$ шагов — алгоритм Уоршелла.

Связанные понятия[править | править код]

Матрица сильной связности[править | править код]

Матрица сильной связности простого орграфа — бинарная матрица, содержащая информацию обо всех сильно связанных вершинах в орграфе. Матрица сильной связности симметрична. У сильно связного графа такая матрица заполнена единицами.

Построение матрицы сильной связности[править | править код]

Матрица сильной связности может быть построена из матрицы достижимости. Пусть $mathbf {E} ^{*}$ — матрица достижимости орграфа G=(V,E) . Тогда матрица сильной связности состоит из элементов $(c_{ij})=left((e_{ij})land (e_{ji})right)$ .

Пример[править | править код]

Рассмотрим тот же граф, что и ранее.

Его матрица достижимости:

${displaystyle mathbf {E^{*}} ={begin{pmatrix}1&1&1&1\0&1&0&0\0&1&1&1\0&1&1&1end{pmatrix}}}$

Из неё получаем матрицу сильной связности:

${displaystyle mathbf {C} ={begin{pmatrix}1&0&0&0\0&1&0&0\0&0&1&1\0&0&1&1end{pmatrix}}}$

Вершины 3 и 4 сильно связаны друг с другом и сами с собой.

Матрица связности графа[править | править код]

Для обычного (не ориентированного) связного графа существует понятие матрицы связности, сходное с матрицей достижимости.

Матрица контрдостижимости[править | править код]

Матрица контрдостижимости Q графа G может быть найдена из матрицы достижимости путем ее транспонирования.

Примечания[править | править код]

Источник

С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.

Cоставляем матрицу смежности A(D) размерности (N− количество вершин) для данного ориентированного графа: она состоит из нулей и единиц, номера строк – индексы вершин, из которых исходят дуги, номера столбцов – индексы вершин, в которые дуги входят (если есть дуга, исходящая из вершины Vi и входящая в Vj, то элемент матрицы смежности, стоящий на пересечении I-той строки и J-того столбца равен 1, иначе – 0.).

Для того, чтобы выделить компоненты сильной связности, необходимо сначала найти матрицу достижимости T(D) ориентированного графа по первой формуле утверждения 3, затем находим матрицу сильной связности S(D) ориентированного графа (она должна быть симметрической) по второй формуле из того же утверждения.

Алгоритм выделения компонент сильной связности

1. Присваиваем P=1 (P − количество компонент связности), .

2. Включаем в множество вершин Vp Компоненты сильной связности Dp вершины, соответствующие единицам первой строки матрицы Sp. В качестве матрицы A(Dp) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из Vp.

3. Вычеркиваем из Sp строки и столбцы, соответствующие вершинам из Vp. Если не остается ни одной строки (и столбца), то P– количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как Sp+1, присваиваем P=P+1 и переходим к п. 2.

Пример

Выделим компоненты связности ориентированного графа, изображенного на рис. 6. В данной задаче количество вершин N=5.

Рис. 6.

Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом

Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения 3:

, ,

Следовательно,

Таким образом, матрица сильной связности, полученная по формуле 2) утверждения 3, будет следующей:

Присваиваем P=1 и составляем множество вершин первой компоненты сильной связности D1: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины .

Вычеркиваем из матрицы S1(D) строку и столбец, соответствующие вершине V1, чтобы получить матрицу S2(D):

Присваиваем P=2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S2(D), то есть . Составляем матрицу смежности для компоненты сильной связности исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2:

Вычеркиваем из матрицы S2(D) строки и столбцы, соответствующие вершинам из V2 ,чтобы получить матрицу S3(D), которая состоит из одного элемента:

И присваиваем P=3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины .

Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:

< Предыдущая		Следующая >

Источник

Привет, сегодня поговорим про матрица достижимости, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
матрица достижимости , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

матрица достижимости простого ориентированого графа 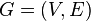— бинарная матрица замыкания по транзитивности отношения 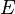(оно задается матрицей смежности графа). Таким образом, в матрице достижимости хранится информация о существовании путей между вершинами орграфа.

В теории графов , достижимость относится к способности , чтобы получить от одной вершины к другой в пределах графика. Вершина может достичь вершины (а также доступен из ), если существует последовательность смежных вершин (т.е. путь ), начинающаяся с и заканчивается .

В неориентированном графе достижимость между всеми парами вершин может быть определена путем идентификации связанных компонентов графа. Любая пара вершин в таком графе может достигать друг друга тогда и только тогда, когда они принадлежат одной компоненте связности; следовательно, в таком графе достижимость симметрична ( достигает если только достигает ). Связные компоненты неориентированного графа могут быть идентифицированы за линейное время. Остальная часть статьи посвящена более сложной проблеме определения попарной достижимости в ориентированном графе (который, кстати, не обязательно должен быть симметричным).

Матица достижимости неориентированного графа.

Утверждение. ЕслиА– матрица смежности графа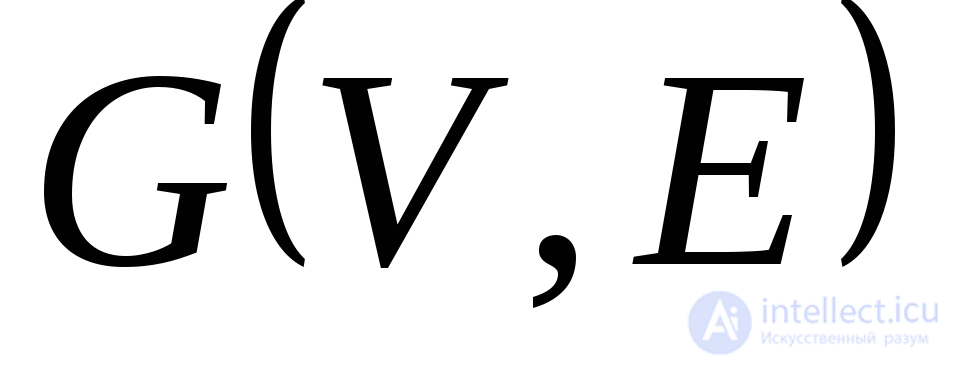, то элемент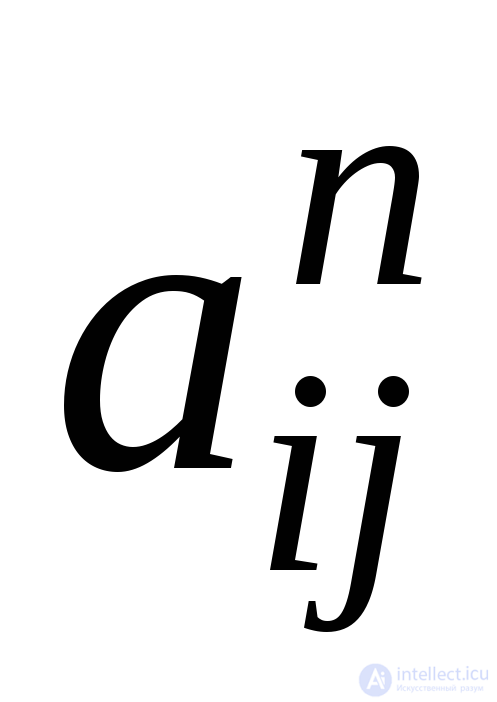матрицыА^правен числу маршрутов длинып, соединяющих вершиныv_iиv_jграфаG.

Доказательство.Методом математической индукции по числуп.

База индукции.Прип= 1 утверждение верно, так как всякое ребро графаG– это маршрут длины 1.

Индуктивное предположение.Пусть утверждение справедливо для всехnk.

Индуктивный переход.Рассмотрим матрицуА^k⁺¹. В ней.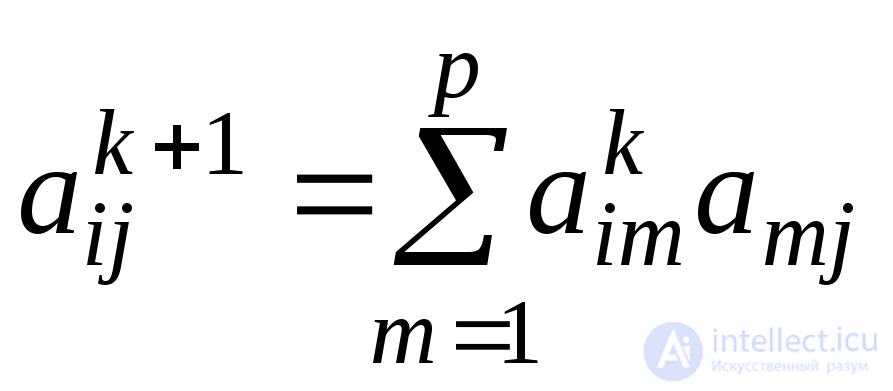

В силу индуктивного предположения произведение 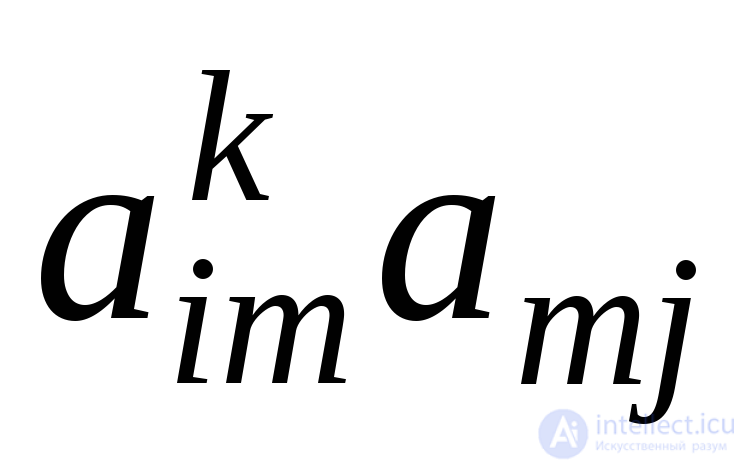есть число маршрутов длиныk+ 1, соединяющих вершинуv_iс вершинойv_jс предпоследней вершиной всех таких маршрутовv_m. Значит, сумма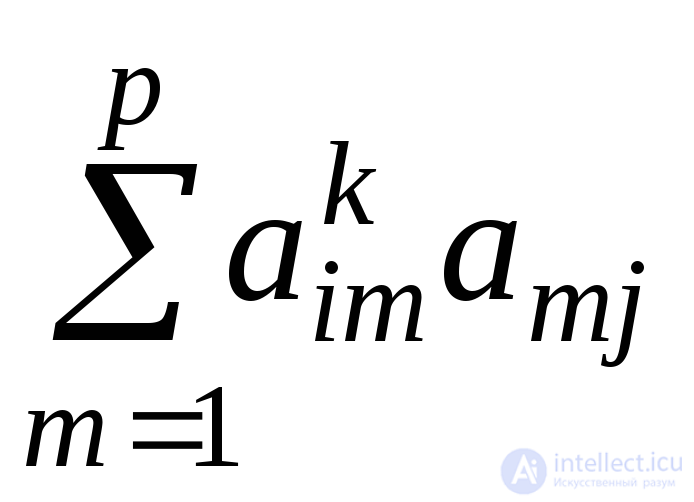действительно равна числу маршрутов длинk+ 1, соединяющих вершинуv_iс вершинойv_j.

Следствие.Пусть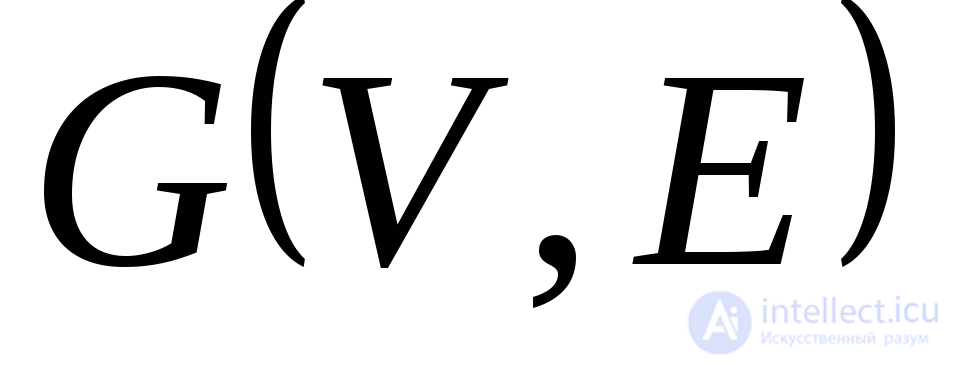– связный граф срвершинами. Тогда любые две вершины графаможно соединить простой цепью. Но в простой цепи не может быть более (р1) ребер. Следовательно, все элементы матрицы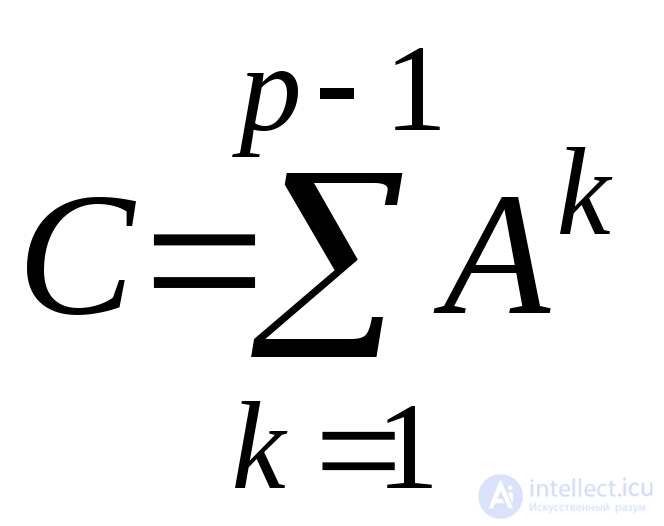отличны от нуля. Ясно, что верно и обратное утверждение.

В некоторых случаях при вычислениях степеней матрицы Аи матрицыСважно знать не число соответствующих маршрутов, а только есть ли в графе эти маршруты или нет . Об этом говорит сайт https://intellect.icu . Тогда при вычислении элементов матрицА²,А³, … ,А^р^-1вместо обычного сложения используют операцию, введенную нами при рассмотрении матриц конечных бинарных отношений. В результате матрицыА,А²,А³, …,A^p^–¹,Cсостоят только из нулей и единиц.

Полученная таким образом матрица Сназываетсяматрицей достижимостиграфаG. ГрафGсвязен тогда и только тогда, когда каждый элемент матрицы достижимости равен 1 (р3).

Матрица достижимости ориентированного графа.

Случай орграфа ничем не отличается от случая неориентированного графа. Если G– орграф ср вершинами иА– его матрица смежности, то элемент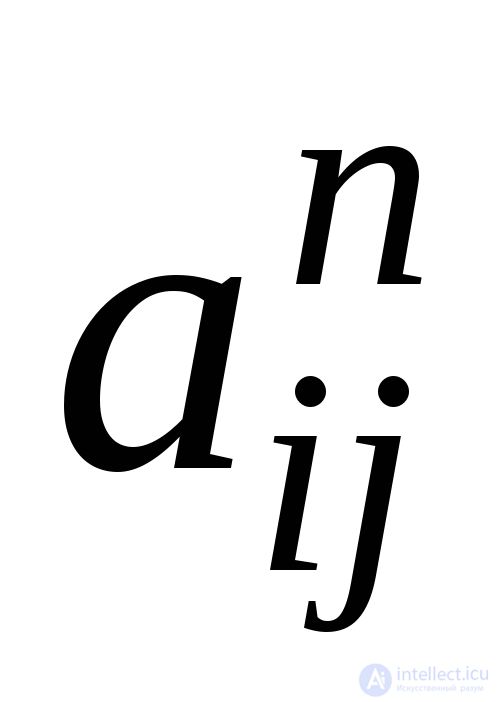матрицыА^правен числу ориентированных маршрутов длинып, соединяющих вершинуv_iс вершинойv_j.

+Граф G сильно связен тогда и только тогда, когда каждый элемент его матрицы достижимости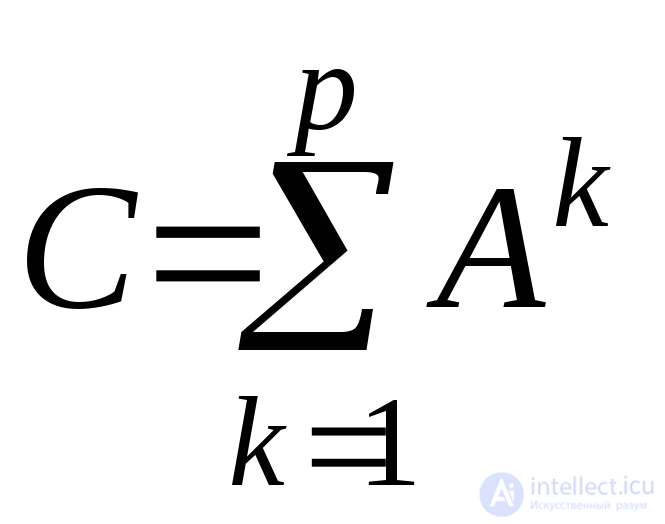равен 1.

Способы построения матрицы достижимости

Перемножение матриц

Пусть дан простой граф 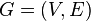, матрица смежности которого есть 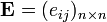, где 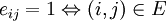. Матрица смежности дает информацию о всехпутях длины 1 (то есть, ребрах) в ографе. Для поиска путей длины 2 можно найти композицию отношения 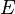с самим собой:

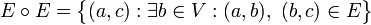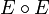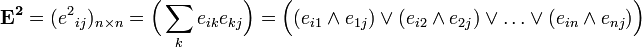По определению, матрица композиции отношений есть , где 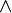— конъюнкция, а 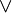— дизъюнкция.

После нахождения матриц 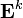композиций 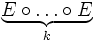для всех 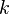, 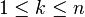будет получена информация о всех путях длины от 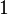до 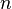. Таким образом, матрица 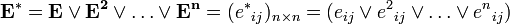есть искомая матрица достижимости.

Случай нескольких путей

Если булевы операции 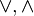дизъюнкции и конъюнкции заменить обычными алгебраическими операциями 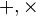сложения и умножения соответственно, нахождение матрицы достижимости 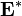сведется к обычному пошаговому перемножению матриц с последующим сложением результатов каждого шага. Тогда получившаяся матрица 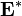будет состоять не только из 0 и 1 и будет характеризовать не только наличие путей между вершинами, но уже и количество таких путей. В таком случае можно разрешить наличие кратных ребер в графе.

Пример

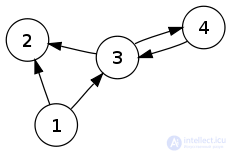
Граф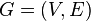

Рассмотрим простой связный ориентированный граф 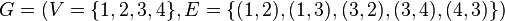. Он имеет матрицу смежности 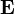вида:

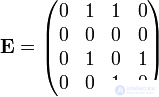
$mathbf E = begin{pmatrix} 0&1&1&0 \ 0&0&0&0 \ 0&1&0&1 \ 0&0&1&0 end{pmatrix}$

Найдем булевы степени этой матрицы , , :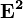

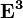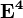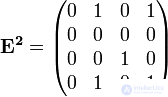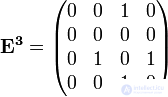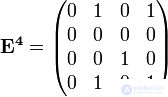$mathbf{E^2} = begin{pmatrix} 0&1&0&1 \ 0&0&0&0 \ 0&0&1&0 \ 0&1&0&1 end{pmatrix}$ , $mathbf{E^3} = begin{pmatrix} 0&0&1&0 \ 0&0&0&0 \ 0&1&0&1 \ 0&0&1&0 end{pmatrix}$ , $mathbf{E^4} = begin{pmatrix} 0&1&0&1 \ 0&0&0&0 \ 0&0&1&0 \ 0&1&0&1 end{pmatrix}$ .

Получим матрицу достижимости

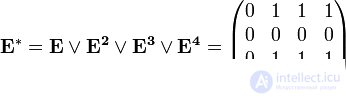
Таким образом, из вершины 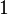можно добраться в любую другую.

При использовании же алгебраических операций получится матрица

Она показывает количество путей длины от 1 до 4 между вершинами орграфа.

Алгоритм Уоршелла

Алгоритм Уоршелла

Существует другой алгоритм, позволяющий найти матрицу достижимости в точности за 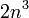шагов — алгоритм Уоршелла.

Связанные понятия

Матрица сильной связности

Построение матрицы сильной связности

Матрица сильной связности может быть построена из матрицы достижимости. Пусть 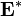— матрица достижимости орграфа 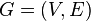. Тогда матрица сильной связности 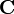состоит из элементов .

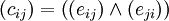Пример

Рассмотрим тот же граф, что и ранее.

Его матрица достижимости:

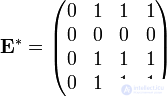
Из нее получаем матрицу сильной связности:

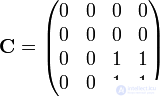
Вершины 3 и 4 сильно связаны друг с другом и сами с собой.

Матрица связности графа

Для связного графа существует понятие матрицы связности, сходное с матрицей достижимости.

Программа 1. Вычисление матрицы достижимости по заданной матрице смежностей с помощью алгоритма Уоршалла.

#include <iostream.h>
#define MaxNodes 4

class Warshall
{
  private:
    unsigned Adj[MaxNodes][MaxNodes];  //Матрица смежностей.
    unsigned Path[MaxNodes][MaxNodes]; //Матрица достижимости.
  public:
    void Vvod();
    void TransClose();
    void Vyvod();
};

void Warshall::Vvod()
{
  //Ввод матрицы смежностей заданного графа.
  cout <<"Вводите элементы матрицы смежностей по строкам:n";
  for (int i=0;i<MaxNodes;i++)
    for (int j=0;j<MaxNodes;j++)
     {
       cout <<"Введите Adj["<< (i+1) << "]["<< (j+1) << "]: ";
       cin >> Adj[i][j];
     }
}

void Warshall::TransClose()
//Вычисление матрицы достижимости.
{
  //Инициализация матрицы Path матрицей смежностей Adj.
  for (int i=0;i<MaxNodes;i++)
    for (int j=0;j<MaxNodes;j++)
      Path[i][j] = Adj[i][j];
  //Нахождение следующих значений матрицы Path.
  for (int k=0;k<MaxNodes;k++)
    for (i=0;i<MaxNodes;i++)
      if (Path[i][k]==1) 
         for (int j=0;j<MaxNodes;j++)
               Path[i][j] = (Path[i][j] || Path[k][j]);
}

void Warshall::Vyvod()
//Вывод матрицы достижимости.
{
  cout << "Матрица достижимости:n";
  for (int i=0;i<MaxNodes;i++)
  {
    for (int j=0;j<MaxNodes;j++)
      cout << Path[i][j] << " ";
    cout << endl;
  }
}

void main()
{
  Warshall A;
  A.Vvod();
  A.TransClose();
  A.Vyvod();
}

Связанные проблемы

Связанная с этим проблема – решить запросы о достижимости с некоторым числом. вершинных отказов. Например: «Может вершина все еще дойти до вершины хотя вершины потерпели неудачу и больше не могут быть использованы? »Подобная проблема может относиться к сбоям ребер, а не к сбоям вершин, или их сочетанию. Методика поиска в ширину работает так же хорошо с такими запросами, но создание эффективного оракула более важно сложно.

Другая проблема, связанная с запросами о достижимости, заключается в быстром пересчете изменений отношений достижимости при изменении какой-либо части графа. Например, это актуальная проблема для сборки мусора, которая должна сбалансировать восстановление памяти (чтобы ее можно было перераспределить) с проблемами производительности работающего приложения.

См. также

Гаммоид
st -соединение

Напиши свое отношение про матрица достижимости. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое матрица достижимости
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

Источник

Способы построения матрицы достижимости[править | править код]

Перемножение матриц[править | править код]

Случай нескольких путей[править | править код]

Пример[править | править код]

Алгоритм Уоршелла[править | править код]

Связанные понятия[править | править код]

Матрица сильной связности[править | править код]

Построение матрицы сильной связности[править | править код]

Пример[править | править код]

Матрица связности графа[править | править код]

Матрица контрдостижимости[править | править код]

Примечания[править | править код]

Матица достижимости неориентированного графа.

Матрица достижимости ориентированного графа.

Способы построения матрицы достижимости

Перемножение матриц

Случай нескольких путей

Пример

Алгоритм Уоршелла

Связанные понятия

Матрица сильной связности

Построение матрицы сильной связности

Пример

Матрица связности графа

Связанные проблемы

См. также

Вам также может понравиться

Как найти вокал для трека

Как найти отключенные звуковые устройства

Сказал сделал как исправить

Добавить комментарий Отменить ответ