Время на прочтение
7 мин
Количество просмотров 314K
Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
Введение
Это было очень давно, когда я учился классе в десятом. Среди довольно скудного в научном плане фонда районной библиотеки мне попалась книга — Угаров В. А. «Специальная теория относительности». Эта тема интересовала меня в то время, но информации школьных учебников и справочников было явно недостаточно.
Однако, книгу эту я читать не смог, по той причине, что большинство уравнений представлялись там в виде тензорных соотношений. Позже, в университете, программа подготовки по моей специальности не предусматривала изучение тензорного исчисления, хотя малопонятный термин «тензор» всплывал довольно часто в некоторых специальных курсах. Например, было жутко непонятно, почему матрица, содержащая моменты инерции твердого тела гордо именуется тензором инерции.
Погружение в специальную литературу не приносило просветления. Технарю достаточно тяжело переварить строгий абстрактный язык чистой математики. Тем не менее, от случая к случаю я возвращался к этому вопросу, и вот спустя почти шестнадцать лет наступило просветление, о чем и будет рассказано под катом. Возможно, мои рассуждения покажутся примитивными и упрощенными, но понимание любой сложной вещи принято разворачивать от процесса оперирования простыми понятиями, поэтому начнем.
1. Вектор на плоскости. Контравариантные, ковариантные координаты и связь между ними
Рассмотрим вектор, и без потери общности наших рассуждений, рассмотрим вектор заданный на плоскости. Как известно из курса ещё школьной геометрии, любой вектор можно задать на плоскости с помощью двух неколлинеарных векторов
Здесь — коэффициенты разложения, (под верхним индексом следует понимать именно номер компоненты, а не возвдение в степень), называемые контрвариантные координаты вектора
. Геометрически это можно изобразить так, как показано на рисунке ниже. Векторы
называют базисными, угол между ними, при условии
, может быть произвольным, произвольна так же ненулевая длина базисных векторов. Указанный базис задает косоугольную систему координат на плоскости, с осями
.
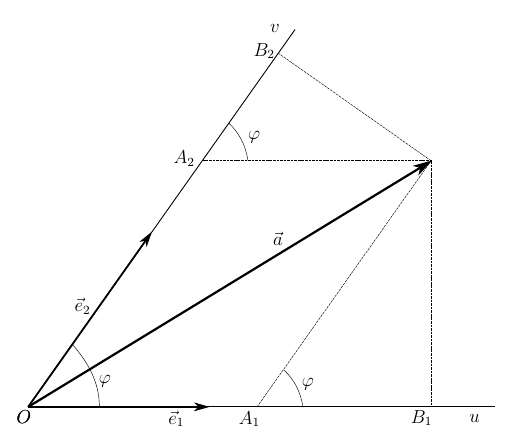
Исходя из чертежа длины отрезков и
равны
Однако, это не единственный способ определить вектор в данной системе координат. Его можно так же задать ортогональными проекциями на оси
. Нетрудно видеть, что эти проекции равны
С другой стороны, выразим длины этих проекций через длины базисных векторов таким образом
где и
— ковариантные координаты вектора
.
Сравниваем (3), (5) и (4), (6)
Умножим (7) на , а (8)
на и преобразуем их
Введем матрицу
тогда (9) и (10) можно выразить следующим соотношением
Выражение (12) дает связь между ковариантными и контрaвариантными координатами вектора, определяемую лишь видом матрицы , зависящей от длин взаимного расположения базисных векторов. Пока никак не будем интерпретировать полученный результат, а просто запомним его.
Набор контравариантных и ковариантных компонент, по сути, задают в выбранном базисе один и тот же вектор. При использовании контравариантных координат этот вектор задается матрицей-столбцом
а в ковариантной форме — матрицей-строкой
2. Скалярное произведение векторов
Перейдем к пространству более высокой размерности и рассмотрим два вектора
где базисные векторы , как и выше, ненулевые
некомпланарные векторы. Перемножим векторы скалярно.
В последнем выражении аккуратно раскроем скобки
и снова введем матрицу
и тогда скалярное произведение можно свернуть весьма компактным образом
Первое, что можно заметить, при уменьшении числа измерений пространства мы перейдем от (14) к (11) а выражение
(15) будет работать и давать склярное произведение векторов, но уже на плоскости. То есть мы получили некую обобщающую форму записи операции скалярного умножения, не зависящую ни от размерности пространства, ни от рассматриваемого базиса, все свойства которого обраны в матрице . Внимательно взглянув на (15) мы поймем ещё одну вещь
что есть ничто иное как ковариантные координаты вектора . То есть, (15) можно переписать
Но и это не предел упрощения
3. Правило Эйнштейна
Хитный и проницательный Альберт Эйнштейн придумал правило суммирования, в выражениях подобных (17), избавляющее математика от надоедливой и избыточной . В выражениях (16) и (17) можно опустить знак суммы, подразумевая суммирование по повторяющемуся индексу, который называют «немым». То есть, (16) переписываем так
здесь j — индекс, по которому происходит суммирование. По правилу, этот индекс должен чередовать свое положение — если у первого множителя он внизу, то у второго должен быть вверху и наоборот. Выражение (17) будет выглядеть так
Ну а (15) придет к виду
А теперь мы посмотрим, для чего надо было городить такой огород.
4. Анализ на простых примерах
Допустим, что наш базис — декартов, то есть ортонормированый. Тогда, матрица становится единичной
Пусть вектор задан в таком базисе. Квадрат длины вектора, как известно, это скалярное произведение этого вектора самого на себя, то есть
И мы получили… квадрат длины вектора, заданного в прямоугольной системе координат!
Ещё пример, дабы не загроможнать который, будем работать в двух измерениях. Пусть система координат подобна той, что изображена на рисунке из параграфа 1, и в ней задан вектор своими контравариантными rоординатами. Тогда
где — угол между векторами базиса. Вычислим длину вектора
Ровно такой же результат мы получим, если воспользуемся теоремой косинусов и найдем квадрат длины диагонали параллелограмма.
Что получается? Работая в разных системах координат, мы использовали одну единственную формулу (20) для вычисления скалярного произведения. И её вид совершенно не зависит ни от базиса, ни от числе измерений пространства, в котором мы работаем. Базисом определяются лишь конкретные значения компонент матрицы .
Так вот, уравнение (20) выражает скалярное произведение двух векторов в тензорной, то есть независимой от выбранного базиса форме.
Матрица задает так называемый метрический тензор. Её вид
определяет каким образом в выбранных координатах вычисляется расстояние между двумя точками.
Но почему мы называем эту матрицу тензором? Следует понимать, что математическая форма, в данном случае квадратная матрица, содержащая набор компонент, это ещё не тензор. Понятие тензора несколько шире, и прежде чем мы скажем, что такое тензор, мы рассмотрим ещё один вопрос.
5. Преобразование метрического тензора при смене базиса
Перепишем соотношение (20) в матричной форме, так нам будет легче оперировать им
где c — скалярное произведение векторов. Верхний индекс несет смысл системы координат, в которой заданы векторы и определен метрический тензор. Скажем это система координат СК0. Преобразование вектора к некоторой другой системе
координат СК1 описывается матрицей преобразования , то есть
Подставим (22) в (21)
в последнем выражении
метрический тензор, компоненты которого определяются новым базисом. То есть, в новом базисе операция имеет аналогичную форму
Тем самым мы показали ещё одно свойство тензора — его компоненты меняются синхронно с компонентами векторов того пространства, в котором определен тензор. То есть теперь мы можем сказать, что тензор — это математический объект, представленный набором компонент и правилом их преобразования при смене базиса.
Теперь, используя правило Эйнштейна, перепишем (22) и (23) в тензорной форме
где — элементы матрицы
. Проиллюстрируем (25) на трехмерном примере. Пусть матрица преобразования координат имеет вид
Распишем преобразование компонента метрического тензора, выполняя суммирование по немым индексам k и l в (25)
откуда видно что в (25) выполняется транспонирование матрицы перехода, умножение результата на метрический тензор и
умножение полученной матрицы на матрицу перехода.
Теперь рассмотрим конкретный пример, на плоскости, чтобы не писать излишне громоздких выкладок
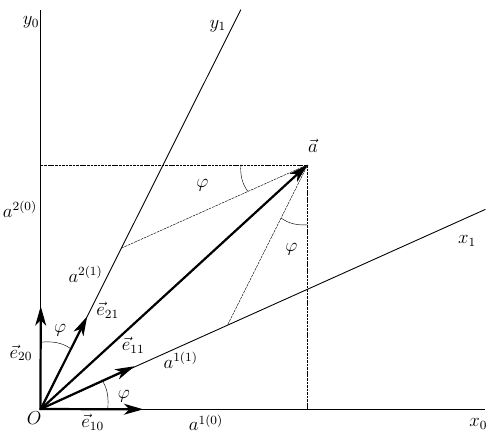
Пусть вектор задан в двух нормированных базисах: прямоугольном
и косоугольном
. Преобразование из косоугольной системы координат в прямоугольную выражается матрицей
обратное преобразование
Пусть также, в прямоугольных координатах наш вектор имеет компоненты
и совсем нетрудно увидеть, что длина его . Метрический тензор в ортонормированном базисе представляется единичной матрицей
значит
Зададим угол наклона осей и вычислим контравариантные компоненты вектора в косоугольных осях
Вместе с вектором необходимо преобразовать и метрический тензор
Ну а теперь вычислим длину вектора в новом базисе
то есть
и скалярное произведение и длина вектора инвариантны, то есть неизменны при преобразовании координат, а так и должно быть. При этом, мы использовали по сути одно и то же соотношение (20) для работы в разных базисах, предварительно преобразовав метрический тензор в соответствии с правилом преобразования векторов в рассматриваемых пространствах
(25).
Заключение и выводы
Что мы увидели в предыдущем параграфе? Если свойства пространства, в котором заданы векторы известны, то для нас не составляет труда выполнить, строго формальным образом, действия над векторами, используя соотношения, вид которых от формы пространства независим. Причем соотношения (20), (24) и (25) дают нам и алгоритм вычисления и способ преобразования компонент выражений, используемых алгоритмом. В этом — мощь и сила тензорного подхода.
Многие физические теории, например ОТО, оперируют искривленным пространством-временем, и там другой подход просто неприемлем. В искривленном пространстве-времени метрический тензор задан локально, в каждой его точке, и если попытаться обойтись без тензоров, у нас ничего не выйдет — мы получим громоздкие и неповоротливые уравнения, если получим их вообще.
В прикладных областях науки тензорная запись выражений применима там, где требуется получать уравнения, независимые от используемой системы координат.
Но это ещё не всё. Мы не поговорили о свойствах метрического тензора, не рассмотрели векторное произведение и тензор Леви-Чевиты. Не поговорили о ранге тензоров и операциях с ними, не разобрались до конца с правилами индексации компонент тензоров и о многом другом. Об этом будет написано несколько позднее, а пока — спасибо всем моим читателям за внимание.
Продолжение следует…
Вводимые
ниже операции с тензорами во всех случаях
требуют обоснования того, что результатом
каждой из них является также тензор. В
рамках данного курса эти утверждения
предлагаются в качестве упражнений.
Сложение
тензоров
|
Определение Пр.4.3.1. |
Пусть |
|
Пример 4.3.1. |
Сумма |
Умножение
тензоров на число
|
Определение Пр.4.3.2. |
Пусть |
|
Замечание: |
нетрудно |
Тензорное
произведение
|
Определение Пр.4.3.3. |
Пусть Иногда |
|
Пример Пр.4.3.2. |
Мы |
|
Заметим, |
|
Задача Пр.4.3.1. |
Определить |
|
Решение |
По
Таким
|
Свертывание
тензоров
|
Определение Пр.4.3.4. |
Пусть |
Заметим,
что в последнем равенстве правая часть
– это сумма n
слагаемых, где m
– индекс, по которому выполняется
суммирование, а само данное тензорное
равенство равносильно
![]()
скалярным равенствам.
|
Пример Пр.4.3.3. |
Свертка |
Операция
свертки часто комбинируется с операцией
умножения тензоров. Например, результатом
произведения один раз ковариантного
тензора на один раз контравариантный
с последующей сверткой является
инвариант, представляющий значение
линейного функционала в
![]() .
.
Действительно,
![]() .
.
В этом случае говорят, что тензор
![]()
свертывается
с тензором
![]() .
.
|
Задача Пр.4.3.2. |
Даны
a
b
c Найти |
|
Решение |
1.
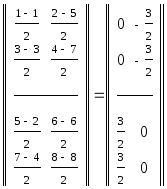
2.
|
Транспонирование
тензоров
Как
уже отмечалось ранее, перестановка
местами любой пары ковариантных (или
пары контравариантных) индексов у
тензора, то есть транспонирования
тензора, вообще говоря, приводит к его
изменению, поскольку в определении
тензора говорится об упорядоченной
системе индексов. При этом новый тензор
будет того же типа, что и исходный.
В
общем случае для группы, состоящей из
N
верхних (или нижних) индексов, существует
N!
различных способов перестановок. Это
означает, что, переставляя данные
индексы, можно построить N!
новых тензоров.
|
Задача Пр.4.3.3. |
Тензор |
|
Решение |
Данный |
Симметрирование
и альтернирование тензоров
|
Определение Пр.4.3.5. |
Тензор |
|
Определение Пр.4.3.6. |
Тензор |
Выделим
у тензора группу, состоящую из N
индексов (либо верхних, либо нижних),
построим путем перестановок индексов
данной группы N!
всевозможных новых тензоров и возьмем
их среднее арифметическое. В результате
мы получим тензор, симметричный по
выбранной группе индексов.
Данная
операция называется симметрированием
тензора по группе индексов.
Группа индексов, по которой выполняется
симметрирование тензора, выделяется
круглыми скобками.
|
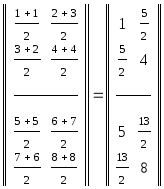
Пример Пр.4.3.4. |
N=1 |
|
|
N=2 |
|
|
|
N=3 |
|
|
|
… |
… |
Операция
симметрирования часто комбинируется
с умножением, причем имеет место следующий
порядок действий: сначала умножение, а
потом симметрирование.
|
Пример Пр.4.3.5. |
|
Выделим
у тензора группу, состоящую из N
индексов (либо верхних, либо нижних),
построим путем перестановок индексов
данной группы N!
всевозможных новых тензоров, приписав
каждому из них знак
![]() ,
,
где
![]()
– число беспорядков в перестановке чисел
![]() ,
,
и возьмем их среднее арифметическое. В
результате мы получим тензор,
антисимметричный по выбранной группе
индексов.
Данная
операция называется альтернированием
тензора по группе индексов.
Группа индексов, по которой выполняется
альтернирование тензора, выделяется
квадратными скобками.
|
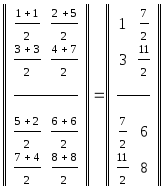
Пример Пр.4.3.6. |
N=1 |
|
|
N=2 |
|
|
|
N=3 |
|
|
|
… |
… |
Операция
альтернирования часто комбинируется
с умножением, причем имеет место следующий
порядок действий: сначала умножение, а
потом альтернирование.
|
Пример Пр.4.3.7. |
|
Заметим,
что как симметрирование кососимметричного
тензора, так и альтернирование
симметричного дает нулевой тензор.
|
Задача Пр.4.3.4. |
Тензор |
|
Решение |
1.
Тензор
2.
тензор |
|
а |
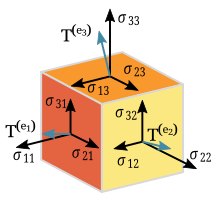
Тензор механического напряжения может быть представлен как матрица, столбцами которой являются силы, действующие на грани куба
Те́нзор (от лат. tensus, «напряжённый») — применяемый в математике и физике объект линейной алгебры, заданный на векторном пространстве 


Использование тензоров в физике позволяет глубже понять физические законы и уравнения, упростить их запись за счет сведения многих связанных физических величин в один тензор, а также записывать уравнения в форме, не зависящей от выбранной системы отсчета.
Тензоры различаются по типу, который определяется парой натуральных чисел 





Тензоры типа 









Именно полилинейная связь между 






Компоненты тензора при фиксированном базисе 


Таким образом, тензоры типа (1,0) — это векторы пространства 



Компоненты тензора типа 








В приложениях часто применяются тензорные поля, которые сопоставляют различным точкам пространства разные тензоры (например, тензор напряжений внутри объекта). Тем не менее, часто их упрощенно тоже называют тензорами.
Тензоры были популяризованы в 1900 году Туллио Леви-Чивита и Грегорио Риччи-Курбастро, которые продолжили более ранние работы Бернхарда Римана и Элвина Бруно Кристоффеля. Слово «тензор» придумал немецкий физик В. Фогт в 1898 году[1].
Предварительные сведения[править | править код]
Правило Эйнштейна[править | править код]
Здесь и далее по тексту статьи в основном будет использоваться общепринятое соглашение — так называемое правило Эйнштейна, в соответствии с которым, если в записи присутствуют верхний и нижний индексы, обозначенные одинаковой буквой (так называемый “немой” индекс), то по нему предполагается суммирование. Например, запись 



Контравариантность векторов[править | править код]
Пусть набор векторов 




Рассмотрим другой набор векторов 







Ковариантность линейных функционалов[править | править код]
Если координаты какого-либо объекта будут преобразовываться как базис, то есть с помощью матрицы преобразования базиса, то это называется ковариантность. Примером ковариантного объекта являются так называемые ковекторы – это линейные функционалы (линейные формы) на пространстве 











В новом базисе имеем: 







Замечания[править | править код]
1. В случае ортонормированных базисов обратная матрица преобразования базиса равна просто транспонированной: 

2. В пространствах с (псевдо)скалярным произведением ((псевдо)евклидовы пространства) пространство 




Примеры пересчета координат при замене базиса[править | править код]
Пример пересчета координат вектора при смене базиса[править | править код]

Изменение координат вектора 
Рассмотрим некоторый вектор 





Теперь введем новый базис 









Очевидно 







Поскольку 





Видно, что, координаты вектора в новом базисе, действительно, отличаются от координат в старом базисе (что было видно уже по рисунку), при этом сам вектор 
Пример пересчета координат линейного функционала[править | править код]
Линейные функционалы являются ковекторами (ковариантными тензорами 1 ранга), поэтому при смене базиса их координаты преобразуются также как и базис (с помощью той же матрицы). Для примера рассмотрим то же двумерное евклидово пространство с тем же первоначальным красным базисом и зеленым вектором.
Пусть в этом базисе (точнее в дуальном к нему) некоторый линейный функционал 










Значение линейного функционала не зависит от выбранного базиса, а зависит только от аргумента-вектора, который тоже от базиса не зависит, тем не менее в координатной записи и вектор и ковектор зависят от базиса.
Определения[править | править код]
Существует несколько по существу эквивалентных определений тензоров. Их эквивалентность связана с тем, что между множествами объектов (включая и тензорные операции и отношения между ними), порождаемых этими определениями, можно установить взаимно-однозначное соответствие (говорят пространства этих объектов изоморфны друг другу).
Тензор как набор компонент (многоиндексный объект)[править | править код]
Общее определение. Правило преобразования координат[править | править код]
Тензором типа 






то есть 

Число 





Соответственно, из этого определения следует, что вектор пространства 



Преобразования координат в частных случаях[править | править код]
Для вектора 





Для линейной формы 





Для билинейной формы 


Для линейного оператора 


Псевдотензоры[править | править код]
Псевдотензоры — алгебраические объекты, координаты которых преобразуются аналогично тензорам, за исключением смены ориентации базиса — в этом случае псевдотензоры меняют знак, в отличие от истинных тензоров. Формально это означает, что в законе преобразования координат необходимо добавить множитель, равный знаку определителя матрицы преобразования базиса: 
Частными случаями псевдотензоров являются псевдоскаляры и псевдовекторы. Пример псевдоскаляра — так называемый ориентированный объем. Пример псевдовектора — результат векторного произведения в трехмерном пространстве, например вектор момента импульса. Псевдотензорами являются также символы Леви-Чивиты.
Многоиндексные объекты, не являющиеся тензорами[править | править код]
Любой набор чисел (например, матрица), при отсутствии или несоответствии закона их изменения при изменении базиса пространства тензорному закону преобразования координат, тензором не является. Не являются тензорами также многоиндексные объекты, которые хотя бы в одном базисе равны нулю (все координаты в этом базисе равны нулю).
Существуют объекты, которые похожи на тензоры (к ним применимы стандартные операции с тензорами, например, свертка с векторами или другими тензорами), но закон преобразования которых при смене базиса не является тензорным. Классическим, но сложным примером таких объектов, являются символы Кристоффеля 
К тензорам не относятся также сами матрицы преобразования координат (матрицы Якоби), являющегося частным случаем диффеоморфизма между двумя многообразиями, с помощью которых и вводится классическое определение тензора, хотя по многим своим свойствам они напоминают тензор. Для них также можно ввести верхние и нижние индексы, операции умножения, сложения и свёртки. Однако, в отличие от тензора, компоненты которого зависят лишь от координат на заданном многообразии, компоненты матрицы Якоби также зависят от координат на многообразии-образе. Это различие очевидно в том случае, когда рассматриваются матрицы Якоби диффеоморфизма двух произвольных многообразий, однако при отображении многообразия в себя его можно не заметить, так как касательные пространства образа и прообраза изоморфны (не канонически). Тем не менее, оно сохраняется. Аналогию между матрицами Якоби и тензорами можно развить, если рассматривать произвольные векторные расслоения над многообразием и их произведения, а не только касательное и кокасательное расслоение.
Тензор как полилинейная функция[править | править код]
Общее определение[править | править код]
Тензором типа 







Координатами тензора в некотором базисе будут значения полилинейной функции на различных комбинациях базисных векторов: 
Полилинейные функции на V как ковариантные тензоры[править | править код]
На пространстве 

Полилинейные функции от 





где 






Классический пример тензоров типа 



Полилинейные функции на V* как контравариантные тензоры[править | править код]
Аналогично можно показать, что полилинейные функции на сопряженном пространстве 

Несколько сложнее в данном определении понять, что контравариантные тензоры типа 











Полилинейные функции как линейные отображения[править | править код]
Аналогично можно показать, что закон преобразования полилинейных функций общего вида также соответствует тензорному.
Неочевидным из этого определения является то, что линейные операторы на 












Рассуждая аналогично, можно показать, что линейные отображения 



Тензор как элемент тензорного произведения векторных пространств[править | править код]
Общее определение[править | править код]
Тензор ранга 







Пояснения по тензорному произведению[править | править код]
Данное определение считается современным, но требует предварительного пояснения непростого понятия тензорного произведения векторных пространств. Тензорное произведение векторных пространств — это векторное пространство 


Тензорное произведение векторов проще определить в координатном представлении: это вектор, координатами которого являются всевозможные произведения координат «умножаемых» векторов. Например, если «умножаются» два вектора x и y пространства 











Координатное представление тензора[править | править код]
Выберем в пространстве 





Тогда в пространстве тензоров 
.
Произвольный тензор 
Используя соглашение Эйнштейна, это разложение можно записать как
Числа 

Нижние индексы компонент тензора называются ковариантными, а верхние — контравариантными.
Например, разложение некоторого дважды ковариантного тензора 
Тензорное поле[править | править код]
Для так называемых гладких многообразий 


Классический пример тензорного поля, называемого обычно просто тензором, -метрический тензор в римановых многообразиях (пространствах) и применяемый также в общей теории относительности.
Примеры и применение тензоров[править | править код]
Примеры тензоров сгруппированных по валентности[править | править код]
| ковариантный ранг (число нижних индексов) | 0 | 1 | 2 | 3 | s |
|---|---|---|---|---|---|
| 0 | Скаляр, длина вектора, интервал (теория относительности), скалярная кривизна | Вектор (алгебра), 4-векторы в СТО, например 4-вектор энергии-импульса (4-импульс) | Тензор энергии-импульса в ОТО, бивектор, обратный метрический тензор | Спин-тензор в квантовой теории поля | Поливектор |
| 1 | Ковектор, линейная форма, градиент скалярной функции | Линейный оператор  , дельта Кронекера , дельта Кронекера
|
|||
| 2 | Билинейная форма, Скалярное произведение, Метрический тензор, Тензор Риччи, Тензор кручения, Тензор электромагнитного поля, Тензор напряжений, Тензор деформаций, Квадрупольный момент | Линейное отображение 
|
Тензор упругости (жесткости) | ||
| 3 | Тензор Леви-Чивиты | Тензор кривизны Римана | |||
| r | Полилинейная форма, Форма объема | Линейное отображение 
|
Линейное отображение 
|
Примеры тензоров в различных областях математики и физики[править | править код]
Тензоры широко применяются в различных разделах математики и физики. Многие уравнения в физике и математике, при использовании тензорной записи, становятся более короткими и удобными. Использование тензоров позволяет увидеть различные симметрии физических величин, уравнений и моделей, а также записать их в общековариантной форме (не зависящей от конкретной системы отсчета).
В математике тензоры являются предметом исследования тензорного исчисления, включающего тензорную алгебру и тензорный анализ. В дифференциальной топологи и геометрии, изучающей гладкие (в том числе римановы) многообразия, рассматриваются различные тензоры: касательный вектор, билинейная форма, метрический тензор, градиент скалярной функции, связность или ковариантная производная, тензор кручения, тензор кривизны Римана и его свертки — тензор Риччи и скалярная кривизна и т. д.
В физике термин тензор имеет тенденцию применяться только к тензорам над обычным физическим 3-мерным пространством или 4-мерным пространством-временем, или, в крайнем случае, над наиболее простыми и прямыми обобщениями этих пространств (хотя принципиальная возможность применения его в более общих случаях остаётся). Например, линейные операторы квантовой механики, могут быть интерпретированы как тензоры над некими абстрактными пространствами (пространствами состояний), но традиционно такое применение термина тензор практически не используется, как и вообще крайне редко используется для описания линейных операторов над бесконечномерными пространствами. Тензоры в физике широко используются в теориях, обладающих геометрической природой (таких, как общая теория относительности) или допускающих полную или значительную геометризацию (к таковым можно в значительной степени отнести практически все современные фундаментальные теории — электродинамика, релятивистская механика и т. д.), а также в теории анизотропных сред (которые могут быть анизотропны изначально, как кристаллы низкой симметрии, или вследствие своего движения или напряжений, как текущая жидкость или газ, или как деформированное твёрдое тело). Кроме того, тензоры широко используются в механике абсолютно твердого тела. Большинство тензоров в физике (не рассматривая скаляров и векторов) — второго ранга (с двумя индексами). Тензоры, имеющие большую валентность (такие, как тензор Римана в ОТО) встречаются, как правило, только в теориях, считающихся достаточно сложными, да и то нередко фигурируют в основном в виде своих свёрток меньшей валентности. Большинство тензоров в физике симметрично или антисимметрично.
Ниже представлена таблица применения тензоров в физике по направлениям.
| Раздел науки | Тензоры и их применение |
|---|---|
| Специальная теория относительности (СТО) | 4-векторы, в том числе 4-вектор координат в 4-мерном пространстве-времени Минковского, метрический тензор, интервал (теория относительности) («длина» в этом пространстве); 4-тензоры применяются для обозначения любого тензора над четырёхмерным пространством-временем, повороты системы отсчёта в котором включают как обычные повороты трёхмерного пространства, так и переход между системами отсчёта, которые движутся с разными скоростями одна относительно другой. Это тензор над пространством 4-векторов, тензор, каждый индекс которого принимает четыре значения: одно «временно́е» и три «пространственных». Примером, является 4-импульс (4-вектор энергии-импульса); |
| Общая теория относительности (ОТО) | метрический тензор над псевдоримановым 4-мерным многообразием, являющийся в ОТО развитием понятия ньютоновского гравитационного потенциала и получающиеся из него свертки тензора кривизны Римана — тензор Риччи и скалярная кривизна (свёртка тензора Риччи), связанные в этой же теории с энергией гравитационного поля и непосредственно входящие в основное уравнение теории (в левой части уравнения Эйнштейна они совместно образуют т. н. тензор Эйнштейна), тензор энергии-импульса материальных полей, входящие в правую часть уравнения Эйнштейна |
| Классическая электродинамика | Тензор электромагнитного поля над пространством Минковского, содержащий напряжённости электрического и магнитного поля и являющийся главным объектом классической электродинамики в 4-мерной записи. В частности, уравнения Максвелла записываются с его помощью в виде единственного 4-мерного уравнения. |
| Теория упругости и Механика сплошных сред | Тензоры второго ранга над 3-мерным физическим пространством Тензор деформаций и тензор напряжений, связанные между собой через тензор упругости 4-го ранга. Также применяются модули упругости. |
| Квантовая теория поля | В релятивистской теории поля возникают тензор энергии-импульса и Спин-тензор, которые в КТП принимают вид линейных операторов над вектором состояния |
| Кинематика твёрдого тела | Важнейшую роль играет тензор инерции, связывающий угловую скорость с моментом импульса и кинетической энергией вращения. Этот тензор отличается от большинства других тензоров в физике, представляющих собой, вообще говоря, тензорные поля, тем, что один тензор характеризует одно абсолютно твёрдое тело, полностью определяя, вместе с массой, его инерцию |
| Теория поля | Квадрупольный момент и вообще тензоры, входящие в мультипольное разложение: всего один тензор целиком представляет момент распределения зарядов соответствующего порядка в данное время. |
| другие разделы | Многие величины, являющихся скалярными характеристиками вещества в случае изотропности последнего, являются тензорами в случае анизотропного вещества. Говоря конкретнее, это относится к субстанциальным коэффициентам, связывающим векторные величины или стоящие перед произведениями (в частности, квадратами) векторов. Примерами могут быть удельная электропроводность (также и обратное ей удельное сопротивление), теплопроводность, диэлектрическая восприимчивость и диэлектрическая проницаемость, скорость звука (зависящая от направления) и т. д. Часто в физике полезен псевдотензор Леви-Чивиты, входящий, например, в координатную запись векторного и смешанного произведений векторов. Компоненты этого тензора всегда записываются практически одинаково (с точностью до скалярного множителя, зависящего от метрики), а в правом ортонормированном базисе — совершенно одинаково всегда (каждая равна 0, +1 или −1). |
Симметричные и антисимметричные тензоры[править | править код]
В различного рода приложениях часто возникают тензоры с определённым свойством симметрии.
Симметричным по двум ко-(контра-)вариантным индексам называется тензор, который не изменяется от перестановки этих индексов:
или
При рассмотрении тензора как полилинейной функции это означает, что значение функции не меняется от перестановки этих двух аргументов местами.
Кососимметичным (косая симметрия) или антисимметричным по двум ко-(контра-)вариантным индексам называется тензор, который при перестановке этих индексов меняет знак :
или
При рассмотрении тензора как полилинейной функции это означает, что значение функции меняет знак от перестановки этих двух аргументов местами.
Эти определения естественным образом обобщаются на случай более чем двух индексов. Тензор симметричен по набору индексов, если при любой перестановке индексов из этого набора тензор не изменяется. Тензор антисимметричен по набору индексов, если он меняет знак при нечетной перестановке (получаемых нечетным числом перестановок двух индексов) и не меняется при четных перестановках по этому набору индексов.
Симметрия или антисимметрия не обязательно должна охватывать только соседние индексы, она может включать в себя любые индексы, учитывая, правда, следующее: симметрия или антисимметрия может относиться только к индексам одного сорта: ко- или контравариантным. Симметрии же, смешивающие ко- и контравариантные индексы тензоров, как правило, не имеют особого смысла, так как, даже если они наблюдаются в компонентах, то разрушаются при переходе к другому базису отнесения (то есть неинвариантны). Впрочем, в присутствии метрического тензора, наличие операций поднятия или опускания индекса устраняет это неудобство, и ограничение этим по сути снимается, когда тензор представлен подходящим образом (так, например, тензор кривизны Римана 
Существуют и более сложные симметрии, например первое тождество Бьянки для тензора кривизны.
Тензорные операции[править | править код]
Стандартные линейные операции[править | править код]
Тензоры одинаковой валентности являются элементами некоторого линейного пространства и допускают операции суммирования и умножения на скаляр, аналогичные операциям на произвольном линейном пространстве. При умножении на скаляр каждый компонент тензора умножается на него (аналогично умножению вектора на скаляр). При сложении тензоров — складываются компоненты этих тензоров (тоже аналогично векторам).
Тензорное произведение[править | править код]
Между тензорами произвольной валентности определена операция тензорного произведения.
В координатном представлении компоненты тензорного произведения по существу это всевозможные произведения соответствующих компонент умножаемых тензоров, например 
При рассмотрении тензоров как полилинейных функций тензорное произведение — это полилинейная функция, равная произведению множителей-полилинейных функций. Соответственно, если один множитель содержит 



Соответственно, произведением тензора ранга 


Это еще более очевидно, если использовать определение тензора как элемента тензорного произведения, а именно, если 

Тем самым операция тензорного произведения делает из множества всех тензорных пространств на данном векторном пространстве так называемую биградуированную алгебру 
Свёртка[править | править код]
Правило подразумеваемого в записи Эйнштейна суммирования по так называемому немому индексу (когда в записи какой-то верхний и нижний индексы обозначены одной буквой) фактически определяет специфическую тензорную операцию, называемую свёрткой.
Свертка тензора[править | править код]
Свёртка тензора — операция, понижающая валентность тензора, вычисляется суммированием по паре индексов (верхнего и нижнего, если они различаются) и пробегающих, оставаясь равными друг другу, все свои значения, например:
Итоговый тензор обозначается обычно той же буквой, несмотря на то, что это уже тензор другого ранга (количества индексов) на 2 меньше ранга исходного тензора.
В случае тензора типа (1,1) свертка приводит в результате к одному числу, называемому следом тензора (по аналогии со следом След матрицы). След является инвариантной (не зависящей от базиса) величиной, скаляром (его иногда называют инвариантом тензора).
Свертка нескольких тензоров[править | править код]
Операция свёртки применяется также и к двум или нескольким тензорам (в том числе между тензором и вектором), например:
.
Эту операцию можно свести к последовательному тензорному умножению этих тензоров : 

Свёртка вектора с тензором ранга два есть действие линейного оператора, определяемого этим тензором, на вектор:
.
Свёртка (однократная) двух тензоров валентности два реализует композицию линейных операторов, определяемых этими тензорами:
.
Свёртка вектора и ковектора 

Опускание и поднятие индекса[править | править код]
В пространствах с метрическим тензором (евклидовые и псевдоевклидовые пространства, римановы и псевдоримановые многообразия) определены операции опускания и поднятия индексов посредством свертки с метрическим тензором (такие операции меняют характер валентности тензора, оставляя неизменным общий ранг тензора):



Операции опускания и поднятия индексов позволяют определить инварианты полностью ковариантных или полностью контравариантных тензоров. Например, дважды ковариантный тензор Риччи можно привести к смешанному виду 

Симметризация и антисимметризация[править | править код]
Симметризация и антисимметризация — конструирование тензора того же типа с определённым видом симметрии. Для примера, симметризация тензора 

![scriptstyle T_{[ij]} = {1over 2}left(T_{ij}-T_{ji}right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/29dd00af72830bf8d2dd8c196a3e8b48669a46fe)
В общем случае симметризация по 
а антисимметризация (альтернирование):
Здесь 



Разумеется, не обязательно симметризовать тензор по всем индексам, здесь это используется лишь для упрощения записи.
Если 


Если 

![T_{[ij]} in V wedge V.](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c09407e682021ea86ba2a19d9b8b6e91324019c)


Связанные понятия и обобщения[править | править код]
Тензоры в бесконечномерных пространствах[править | править код]
Понятие тензора формально можно обобщить на случай бесконечномерных линейных пространств. Обобщения тензоров на топологические пространства осуществляется путем введения топологического тензорного произведения.
Для корректного определения тензоров на таких пространствах необходимо выполнение свойства рефлексивности этого пространства, то есть оно должно быть канонически изоморфно своему второму сопряженному пространству (конечномерные пространства этим свойством обладают все). Тогда, например, определение в форме полилинейных функций имеет корректный смысл и приводит к тому, что векторы и линейные операторы на таких пространствах являются тензорами.
В частности тензоры определяются на гильбертовых пространствах и тогда линейные отображения в гильбертовых пространствах являются тензорами. Тем не менее, в приложениях (в физике), обычно термин «тензор» к таким объектам не применяется (например, операторы в квантовой физике, изображающие различные физические величины, являются по существу тензорами в гильбертовом пространстве, тем не менее таковыми их обычно не называют).
Девиатор и шаровая часть[править | править код]
Любой тензор второго ранга 

Здесь 


См. также[править | править код]
- Тензорное поле
- Метрический тензор
- Тензор кривизны
- Тензорные вычисления (программное обеспечение)[en]
Примечания[править | править код]
- ↑ Woldemar Voigt, Die fundamentalen physikalischen Eigenschaften der Krystalle in elementarer Darstellung [The fundamental physical properties of crystals in an elementary presentation] (Leipzig, Germany: Veit & Co., 1898), p. 20. From page 20: “Wir wollen uns deshalb nur darauf stützen, dass Zustände der geschilderten Art bei Spannungen und Dehnungen nicht starrer Körper auftreten, und sie deshalb tensorielle, die für sie charakteristischen physikalischen Grössen aber Tensoren nennen.” (We therefore want [our presentation] to be based only on [the assumption that] conditions of the type described occur during stresses and strains of non-rigid bodies, and therefore call them “tensorial” but call the characteristic physical quantities for them “tensors”.)
- ↑ Климов Д. М., Петров А. Г., Георгиевский Д. В. Вязкопластические течения: динамический хаос, устойчивость, перемешивание. — М., Наука, 2005. — с. 21 — ISBN 5-02-032945-2.
Литература[править | править код]
- Акивис М. А., Гольдберг В. В. Тензорное исчисление. — М.: Наука, 1969;
- Винберг Э. Б. Курс алгебры. 3-е изд. — М.: МЦНМО, 2017. — 592 с. — ISBN 978-5-4439-0209-8.
- Димитриенко Ю. И. Тензорное исчисление: Учеб. пособие. — М.: Высшая школа, 2001. — 576 с. — ISBN 5-06-004155-7.
- Коренев Г. В. Тензорное исчисление: Учеб. пособие. — М.: Издательство МФТИ, 2000. — 240 с. — ISBN 5-89155-047-4.
- Кострикин А. И. Введение в алгебру. 2-е изд. — М.: МЦНМО, 2012. — Ч. II: Линейная Алгебра. — 368 с. — ISBN 978-5-94057-888-8.
- Кочин Н. Е. Векторное исчисление и начала тензорного исчисления (9-е издание). — М.: Наука, 1965.
- Мак-Коннел А. Дж. Введение в тензорный анализ с приложениями к геометрии, механике и физике. — М.: Физматлит, 1963.
- Номидзу К. Группы Ли и дифференциальная геометрия. — М.: ИЛ, 1960.
- Победря Б. Е. Лекции по тензорному анализу: Учеб. пособие. (3-е изд.). — М.: Изд-во МГУ, 1986.
- Рашевский П. К. Риманова геометрия и тензорный анализ (3-е издание). — М.: Наука, 1967.
- Шарипов Р. А. Быстрое введение в тензорный анализ. — БашГУ.
В заметке Магия тензорной алгебры было дано очень неплохое введение в математику тензоров. Но, как мне кажется, этот текст все-равно несколько сложен для понимания. В нем не до конца понятно, что же это такое тензор и зачем он вообще нужен.
Сейчас я попытаюсь дать совсем простое введение в тензоры. Я не претендую на математическую строгость, поэтому некоторые термины могут употребляться не совсем корректно.
Откуда появился термин тензор
Насколько я помню, термин тензор происходит от латинского tensus или английского слова tension — напряжение. Термин возник в процессе осмысления следующей задачи. Пусть нам дано некоторое твердое тело произвольной формы в трехмерном пространстве. К разным концам тела приложены некоторые силы. Как описать возникающие напряжения в некотором сечении этого тела? Ответ на эту задачу — напряжения описываются тензорным полем. Но для понимания этого ответа давайте рассмотрим более простые задачи.
Тензор нулевого ранга
Пусть нам дан в трехмерном пространстве однородный кубик. Давайте его начнем нагревать с какой-либо стороны. Теперь зафиксируем какой-либо момент времени и попробуем описать значения температуры в каждой точке кубика.
Температура — это скаляр, нам нужно только одно число. Введем произвольную систему координат. В рамках этой системы координат температура будет описываться как скалярная функция от
(x, y, z).
А давайте теперь возьмем другую систему координат. Что изменится? А ничего! Температура в каждой точке пространства осталась таким же скаляром и при смене системы координат не поменялась.
Вот уже интересно! Мы получили некоторый математический объект, скаляр, который не изменяется при смене системы координат. Назовем его тензором нулевого ранга. Идем дальше.
(Уточнение из комментариев: координаты точек изменятся, но температура в этих точках от поворота системы координат не изменится. Именно температура и есть тензор ранга (0,0))
Тензор первого ранга
Итак, мы нагрели наш однородный кубик. Под действием температуры молекулы какого-либо вещества в нем начали как-то двигаться. Опять зафиксируем какой-либо момент времени и попробуем описать значения скоростей молекул в каждой точке кубика.
Скорость — это вектор. Введем произвольную систему координат. В рамках этой системы скорости в каждой точке пространства будут описываться как векторные функции от
(x, y, z). А давайте теперь возьмем другую систему координат? Что изменится? Давайте рассуждать.
Векторное поле скоростей в кубике не изменилось, оно осталось таким же, мы просто взяли другую линейку (другую систему координат) для измерения скоростей. Но изменились компоненты этого вектора. Зная старую и новую систему координат, закон изменения компонент вектора несложно вывести.
Таким образом, мы получили математический объект, вектор, который опять же не изменяется при смене системы координат, но изменяются его компоненты, причем по заранее определенному закону. Это тензор первого ранга. Теперь начинается самое интересное.
Тензор второго ранга
Мы нагрели наш кубик, молекулы начали двигаться. Но представим теперь, что наш кубик перестал быть однородным. Он теперь пористый, внутри состоит из разных каналов с разной ориентацией. Скорость движения молекулы вдоль канала гораздо больше, чем скорость движения поперек канала. Как нам описать такую неоднородную среду?
Зафиксируем какой-либо момент времени, возьмем одну молекулу со своим вектором скорости. Вопрос, как этот вектор скорости изменится в следующий момент времени? Если молекула попала в канал и вектор ее скорости направлен вдоль канала, то скорость не изменится, если вектор направлен поперек канала, то уменьшится в несколько раз, а если под углом, то вектор скорости вообще изменит свое направление.
Это очень похоже на то, что в каждой точке кубика задано нечто, что умеет поворачивать и масштабировать вектора. Да, да, это матрица! Но не произвольная, а специальная, которая не уничтожает вектора, а преобразовывает.
Хорошо, а что будет с нашей матрицей, если мы возьмем другую систему координат, что изменится? Конфигурация каналов в кубике осталась такой же, и эта матрица должна поворачивать вектора скоростей точно таким же образом. Да, компоненты этой матрицы изменятся, но само ее действие на вектора останется таким же.
Таким образом, мы опять же имеем математический объект, матрицу специального вида, действие которой на вектор не зависит от смены системы координат, а ее компоненты пересчитываются по определенному закону. Назовем его тензором второго ранга.
Так что же такое тензор?
Итак, тензор это математический объект, который как объект не зависит от смены системы координат, но его компоненты при смене системы координат преобразуются по определенному математическому закону. В трехмерном пространстве тензор второго ранга проще всего представить как матрицу, заданную в каждой точке пространства, которая описывает неоднородность этого пространства и действует на входящий вектор, изменяя его направление и масштаб.
Оригинал статьи на Хабре (2015 год)
К лучшим публикациям Хабра за сутки
 .
. ,
, .
. ;
; ;
;
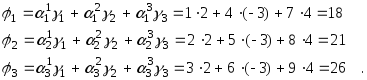
 .
. .
.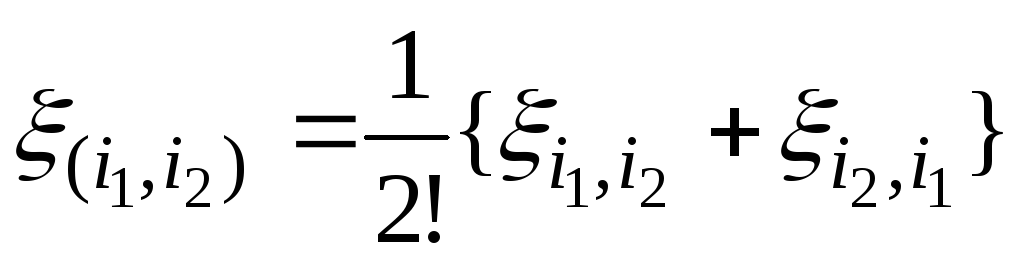



 .
.
 ,
, ,
, ,
, .
.











![T_{[i_1ldots i_n]} = {1over n!}sum_{sigma} mathrm{sign},(sigma) T_{sigma(i_1)ldots sigma(i_n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec6f1fcd3020ee0710a2852707f3d63ce44f61ca)

