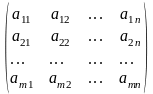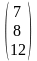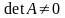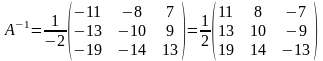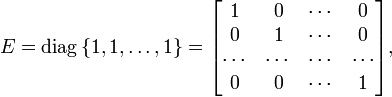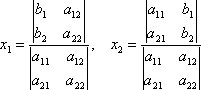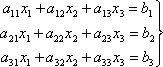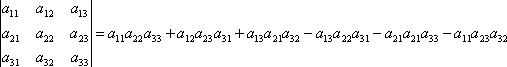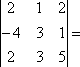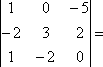Многие считают, что тема «Транспонированные матрицы» довольно сложная, но это не так. В студенческом курсе математики транспонирование выполняется легко и без каких-либо усилий. Для того чтобы понимать, как именно осуществляется операция, необходимо знать, что такое матрица.
Онлайн-калькулятор
Что такое транспонированная матрица
Матрица, полученная из данной заменой каждой ее строки столбцом с этим же номером, называется матрицей транспонированной данной. Обозначается такая матрица ATA^{T} или A′A’.
При транспонировании матрицы AA размера m×nmtimes n получаем матрицу ATA^{T} размера n×mntimes m.
В общем виде транспонированная матрица для матрицы
Am×n=(a11a12…a1na21a22…a2n…………am1am2…amn)A_{mtimes n}=begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\a_{21}&a_{22}&…&a_{2n}\…&…&…&…\a_{m1}&a_{m2}&…&a_{mn}end{pmatrix}
выглядит следующим образом:
An×mT=(a11a21…am1a12a22…am2…………a1na2n…amn)A^{T}_{ntimes m}=begin{pmatrix}a_{11}&a_{21}&…&a_{m1}\a_{12}&a_{22}&…&a_{m2}\…&…&…&…\a_{1n}&a_{2n}&…&a_{mn}end{pmatrix}.
Элементы ii строки исходной матрицы становятся элементами ii столбца транспонированной матрицы. Таким образом, транспонирование матрицы заключается в том, что строки исходной матрицы AA записывают в новую матрицу по столбцам.
Транспонировать матрицы K=(15−2314−18)K=begin{pmatrix}15&-23&14&-18end{pmatrix} и L=(25−10118)L=begin{pmatrix}25\-10\11\8end{pmatrix}.
KT=(15−2314−18)K^{T}=begin{pmatrix}15\-23\14\-18end{pmatrix},
LT=(25−10118)L^{T}=begin{pmatrix}25&-10&11&8end{pmatrix}.
Транспонировать матрицу G=(5−311820514−86537−94)G=begin{pmatrix}5&-3&11&8\2&0&5&1\4&-8&6&5\3&7&-9&4end{pmatrix}.
GT=(5243−30−871156−98154)G^{T}=begin{pmatrix}5&2&4&3\-3&0&-8&7\11&5&6&-9\8&1&5&4end{pmatrix}.
Свойства транспонированных матриц
- Дважды транспонированная матрица равна исходной матрице: ATT=(AT)T=AA^{TT}=(A^{T})^{T}=A.
- Транспонированная матрица суммы равна сумме транспонированных матриц: (A+B)T=AT+BT(A+B)^{T}=A^{T}+B^{T}.
- Транспонированная матрица произведения равна произведению транспонированных матриц: (A⋅B)T=AT⋅BT(Acdot B)^{T}=A^{T}cdot B^{T}.
- При транспонировании можно выносить скаляр (число, на которое можно разделить все элементы матрицы): (k⋅A)T=k⋅AT(kcdot A)^{T}=kcdot A^{T}.
- Определитель исходной матрицы и определитель транспонированной матрицы равны.
С понятием определителя матрицы мы познакомимся на следующем уроке.
Возникли сложности с матрицей? На нашем сервисе предусмотрена платная помощь с решением задач по алгебре от экспертов!
Тест по теме «Транспонирование матрицы»
Определение транспонированной матрицы
Содержание:
- Что такое транспонированная матрица
- Свойства транспонированной матрицы, как найти
- Как транспонировать матрицу в Excel
- Как транспонировать матрицу в Python
Что такое транспонированная матрица
Транспонированной матрицей называют такую матричную форму представления данных (A^{T}), которая образована из начальной A с помощью замещения строк столбцами.
С теоретической точки зрения, транспонированная матрица в случае с некоторой матричной формой А, обладающей размерностью (mtimes n), сформирована как матрица под названием (A^{T}) со следующими габаритами: (n times m), соответствующая такому выражению, которое можно вычислить:
(A_{{ij}}^{T}=A_{{ji}})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Пример 1
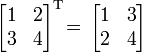
({begin{bmatrix}1&2\3&4end{bmatrix}}^{{{mathrm {T}}}}!!;!=,{begin{bmatrix}1&3\2&4end{bmatrix}} и {begin{bmatrix}1&2\3&4\5&6end{bmatrix}}^{{{mathrm {T}}}}!!;!=,{begin{bmatrix}1&3&5\2&4&6end{bmatrix}};)
Исходя из данного определения и принципа построения матричных форм, можно прийти к выводу, что при записи транспонированной матрицы из начального массива данных, выстроенных в определенном порядке, строки нужно составить как колонки в аналогичной последовательности. Тогда получится необходимая матричная форма, которую далее можно решать при необходимости.
Свойства транспонированной матрицы, как найти
Задачи с матрицами обладают разной степенью сложности. Когда предстоит в процессе решения выполнить подобного рода преобразования такие, как транспонирование строчек и колонок матричной формы, можно воспользоваться простым алгоритмом операций. Данная последовательность действий позволит исключить ошибки при формировании обозначения нужной матрицы:
- проанализировать исходную запись данных;
- определить расположение строк и столбцов;
- изменить места колонок и строчек с помощью ранее записанной формулы (A_{ij} ^T = A_{ji});
- сформулировать ответ в соответствии с заданием.
Значительно упростить расчеты при работе с матричными формами помогут справедливые закономерности. Запишем ряд полезных свойств, применимых к примерам с транспонированием матрицы:
Свойства:
- Предположим, что у некоторой матрицы АА имеются следующие размеры: (m times n). В таком случае при транспонировании этих записей с данными получится матрица (A^T) , которая обладает размерами (n times m).
- Если выполнить рассматриваемое действие два раза подряд, то конечный результат не поменяется, а матрица останется в прежней форме.
- Допустимо переносить множитель за пределы транспонированной матричной формы. При этом целесообразно воспользоваться следующим соотношением: ((lambda cdot A)^T = lambda cdot A^T).
- Если пару матриц сложить, то их также можно транспонировать. С этой целью допустимо применить следующую закономерность: ((A+B)^T = A^T + B^T).
- Транспонирование выражения, в котором умножают матрицы, подразумевает умножение данных транспонированных матричных форм, то есть: ((A times B)^T = A^T times B^T.)
Пример 2
Рассмотрим процесс транспонирования пары матриц, которые имеют следующий вид:
(A = begin{pmatrix} 1&2&3\4&5&6\7&8&9 end{pmatrix})
(B = begin{pmatrix} 1&2&3\4&5&6end{pmatrix})
В процессе решения нужно воспользоваться определением данной математической операции и закономерностями, которые перечислены выше. В результате получим, что:
(A^T = begin{pmatrix} 1&2&3\4&5&6\7&8&9 end{pmatrix}^T = begin{pmatrix} 1&4&7\2&5&8\3&6&9 end{pmatrix}^T)
(В^T = begin{pmatrix} 1&2&3\4&5&6 end{pmatrix}^T = begin{pmatrix} 1&4\2&5\3&6 end{pmatrix}^T)
Как транспонировать матрицу в Excel
Многим знаком редактор MS Excel. Это функциональный компонент пакета Microsoft Office. Программа позволяет работать с разнообразными табличными формами. В числе полезных опций возможность выполнить транспонирование матрицы. Подобное действие целесообразно реализовать по средствам особой функции ТРАНСП(). Рассмотрим наглядный пример:
Источник: my-excel.ru
Заметим, что компоненты начальной матричной формы 2 на 2 размещены в поле от А7 до В8. В таком случае, чтобы транспонировать матрицу следует последовательно выполнить ряд простых действий, а именно:
- выделить ячейки площадью 2 на 2, которые не должны иметь какие-либо пересечения с начальным диапазоном А7:В8;
- в строке для ввода формул напечатать выражение: =ТРАНСП(A7:B8);
- нажать одновременно сочетание клавиш на клавиатуре CTRL+SHIFT+ENTER, то есть выполнить ввод выражения для массива.
Источник: my-excel.ru
Как транспонировать матрицу в Python
В распространенных случаях программирование начинают осваивать с высокоуровневого языка под названием Python. На его базе создаются разнообразные приложения, в том числе, для смартфонов, планшетов и других гаджетов, разрабатывают функциональные версии программного обеспечения, обучают машины определенным командам и алгоритмам. Разработчики оценивают Python с точки зрения достойной эффективности, простоте освоения, возможностей работы на разнообразных платформах. В нем также есть опции транспонирования матричных форм. Рассмотрим основные из таких методик.
Первым способом является применение NumPy transpose(). Данная библиотека предназначена для работы с массивами данных. Соответствующий метод по вызову реализует нужное действие:
Источник: pythonist.ru
Следующий способ транспонирования матричных форм заключается в применении метода numpy.transpose(). В процессе осуществляется передача матрицы как аргумента:
Источник: pythonist.ru
Если заранее импортировать в Python библиотеку SymPy, то можно достаточно просто выполнить транспонирование матричной формы. Последовательность операций:
- вызов transpose (T) с помощью точечного оператора;
- внесение итогов в новую переменную sympy_transpose;
- печать начальной матрицы matrix в следующей строке;
- запись транспонированной матричной формы в sympy_transpose.
Источник: pythonist.ru
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Загрузить PDF
Загрузить PDF
Если вы научитесь транспонировать матрицы, то лучше поймете их структуру. Возможно, вы уже знаете о квадратных матрицах и об их симметрии, что поможет вам освоить транспонирование. Помимо прочего, транспонирование помогает переводить векторы в матричную форму и находить векторные произведения.[1]
При работе с комплексными матрицами эрмитово-сопряженные (сопряженно-транспонированные) матрицы помогают решить самые разные задачи.
-
1
Возьмите любую матрицу. Можно транспонировать любую матрицу, независимо от количества строк и столбцов. Наиболее часто приходится транспонировать квадратные матрицы, которые имеют одинаковое количество строк и столбцов, поэтому для простоты рассмотрим в качестве примера такую матрицу:[2]
- матрица A =
1 2 3
4 5 6
7 8 9
- матрица A =
-
2
Представьте первую строку прямой матрицы в виде первого столбца транспонированной матрицы. Просто запишите первую строку в виде столбца:
- транспонированная матрица = AT
- первый столбец матрицы AT:
1
2
3
-
3
Проделайте то же самое с остальными строками. Вторая строка исходной матрицы станет вторым столбцом транспонированной матрицы. Переведите все строки в столбцы:
-
AT =
1 4 7
2 5 8
3 6 9
-
AT =
-
4
Попробуйте транспонировать неквадратную матрицу. Точно таким же образом можно транспонировать любую прямоугольную матрицу. Просто запишите первую строку в виде первого столбца, вторую строку — в виде второго столбца, и так далее. В приведенном ниже примере каждая строка исходной матрицы обозначена своим цветом, чтобы было понятнее, как она преобразуется при транспонировании:
- матрица Z =
4 7 2 1
3 9 8 6 - матрица ZT =
4 3
7 9
2 8
1 6
- матрица Z =
-
5
Выразим транспонирование в виде математической записи. Хотя идея транспонирования очень проста, лучше все же записать ее в виде строгой формулы. При матричной записи не требуются какие-либо специальные термины:
- Предположим, дана матрица B, состоящая из m x n элементов (m строк и n столбцов), тогда транспонированная матрица BT представляет собой набор из n x m элементов (n строк и m столбцов).[3]
- Для каждого элемента bxy (строка x и столбец y) матрицы B в матрице BT существует эквивалентный ему элемент byx (строка y и столбец x).
Реклама
- Предположим, дана матрица B, состоящая из m x n элементов (m строк и n столбцов), тогда транспонированная матрица BT представляет собой набор из n x m элементов (n строк и m столбцов).[3]
-
1
(MT)T = M. После двойного транспонирования получается исходная матрица.[4]
Это довольно очевидно, так как при повторном транспонировании вы вновь меняете строки и столбцы, в результате чего получается первоначальная матрица. -
2
Зеркально отобразите матрицу относительно главной диагонали. Квадратные матрицы можно “переворачивать” относительно главной диагонали. При этом элементы вдоль главной диагонали (от a11 до нижнего правого угла матрицы) остаются на месте, а остальные элементы перемещаются по другую сторону этой диагонали и остаются на том же расстоянии от нее.
- Если вам сложно представить данный метод, возьмите лист бумаги и нарисуйте матрицу 4×4. Затем переставьте ее боковые элементы относительно главной диагонали. Проследите при этом за элементами a14 и a41. При транспонировании они должны поменяться местами, как и другие пары боковых элементов.
-
3
Транспонируйте симметричную матрицу. Элементы такой матрицы симметричны относительно главной диагонали. Если проделать описанную выше операцию и “перевернуть” симметричную матрицу, она не изменится. Все элементы поменяются на аналогичные.[5]
Фактически, это стандартный способ определить, симметрична ли та или иная матрица. Если выполняется равенство A = AT, значит, матрица A симметрична.Реклама
-
1
Рассмотрим комплексную матрицу. Элементы комплексной матрицы состоят из действительной и мнимой части. Такую матрицу также можно транспонировать, хотя в большинстве практических применений используют сопряженно-транспонированные, или эрмитово-сопряженные матрицы.[6]
- Пусть дана матрица C =
2+i 3-2i
0+i 5+0i
- Пусть дана матрица C =
-
2
Заменим элементы комплексно-сопряженными числами. При операции комплексного сопряжения действительная часть остается такой же, а мнимая часть меняет свой знак на обратный. Проделаем эту операцию со всеми четырьмя элементами матрицы.
- найдем комплексно-сопряженную матрицу C* =
2-i 3+2i
0-i 5-0i
- найдем комплексно-сопряженную матрицу C* =
-
3
Транспонируем полученную матрицу. Возьмем найденную комплексно-сопряженную матрицу и просто транспонируем ее. В результате у нас получится сопряженно-транспонированная (эрмитово-сопряженная) матрица.
- сопряженно-транспонированная матрица CH =
2-i 0-i
3+2i 5-0i
Реклама
- сопряженно-транспонированная матрица CH =
Советы
- В данной статье транспонированная матрица относительно матрицы А обозначается как AT. Встречается также обозначение A’ или Ã.[7]
- В данной статье эрмитово-сопряженная матрица относительно матрицы А обозначается как AH — это общепринятое обозначение в линейной алгебре. В квантовой механике часто используют обозначение A†. Иногда эрмитово-сопряженную матрицу записывают в виде A*, однако такого обозначения лучше избегать, так как оно используется также для записи комплексно-сопряженной матрицы.[8]
Реклама
Об этой статье
Эту страницу просматривали 49 820 раз.
Была ли эта статья полезной?
Транспонированная матрица — матрица 

Формально, транспонированная матрица для матрицы 




Например,
и
То есть для получения транспонированной матрицы из исходной нужно каждую строчку исходной матрицы записать в виде столбца в том же порядке.
Свойства транспонированных матриц[править | править код]
- Дважды транспонированная матрица А равна исходной матрице А.
- Транспонированная сумма матриц равна сумме транспонированных матриц.
- Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.
- При транспонировании можно выносить скаляр.
- Определитель транспонированной матрицы равен определителю исходной матрицы.
Связанные определения[править | править код]
Симметричная матрица (симметрическая матрица) — матрица,
удовлетворяющая соотношению 
Для того чтобы матрица 
Антисимметричная (кососимметричная) матрица (антисимметрическая, кососимметрическая) — матрица,
удовлетворяющая соотношению 
Для того чтобы матрица 
Отсюда следует, что элементы главной диагонали антисимметричной матрицы равняются нулю:

Для любой квадратной матрицы 

где 

См. также[править | править код]
- Сопряжённо-транспонированная матрица
Транспонирование матриц
Определение.
Матрицу АТ
называют транспонированной
матрицей А,
если элементы каждой строки матрицы А
записать в том же порядке в столбцы
матрицы АТ.(т.е.
строки матрицы А заменены на столбцы и
наоборот)
А
=
; АТ=
;
Пример: Даны матрицы
А =
,
В =
,
С =
и число
= 2. Найти АТВ+С.
AT
=
; ATB
=
=
=
;
C
=
;
АТВ+С
=
+
=
.
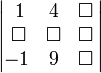
Пример: Даны матрицы
А =
и В =
.
Найти произведение матриц АВ и ВА.
АВ
=
=
.
ВА
=
= (21
+ 44
+ 13)
= (2 + 16 + 3) = (21).
Пример: Найти
произведение матриц А=
,
В =

АВ
=
=
=
.
Определение.
Элементарными
преобразованиями
матрицы назовем следующие преобразования:
1) умножение строки
на число, отличное от нуля;
2) прибавление к
элементам одной строки элементов другой
строки;
3) перестановка
строк;
4) вычеркивание
(удаление) одной из одинаковых строк
(столбцов);
5) транспонирование
Обратная матрица
Определение:
Матрица
называется обратной по отношению к
квадратной матрице
,
если
.
Обратная матрица
существует только для квадратной
матрицы, определитель которой не равен
нулю. Такая матрица называется
невырожденной.
Рассмотрим общий
подход к нахождению обратной матрицы.
Рассмотрим на
примере, как найти обратную матрицу
.
Пусть

1)Найти определитель
матрицы
.
Так как
,
то обратная матрица
существует.
2) Сформировать
матрицу из алгебраических дополнений
каждого элемента матрицы.

если
– четное число,
если
– нечетное число.

3) Транспонируем
матрицу из алгебраических дополнений.
.
4) Обратная матрица
определяется формулой
,
.
Укажем следующие
свойства
обратных матриц:
-
(A-1)-1
= A; -
(AB)-1
= B-1A-1 -
(AT)-1
= (A-1)T.
2.
Квадратная матрица
В
случае, когда число строк прямоугольной
матрицы равно числу ее столбцов, матрица
называется квадратной матрицей:

n
-порядок квадратной матрицы.
Верхнетреугольная
матрица — квадратная матрица, в которой
все элементы ниже главной диагонали
равны нулю.
Нижнетреугольная
матрица — квадратная матрица, в которой
все элементы выше главной диагонали
равны нулю.
Диагональная
матрица — квадратная матрица, все
элементы которой, стоящие вне главной
диагонали, равны нулю

Диагональная
матрица является симметричной:
DT
= D.
Ранг
диагональной матрицы равен количеству
ненулевых элементов, находящихся на
главной диагонали.
Определитель
диагональной матрицы равен произведению
диагональных элементов:
Примеры
Нулевая
матрица
единичная
матрица
Скалярная
матрица — диагональная матрица, элементы
главной диагонали которой равны. Частным
случаем скалярной матрицы является
единичная матрица

Свойства
Скалярная
матрица — это произведение скаляра и
единичной матрицы.
Множество
скалярных матриц — это ровно все те
матрицы, которые коммутируют со всеми
квадратными матрицами того же размера,
то есть для любой матрицы A и скалярной
матрицы S того же размера: AS = SA.
единичная
матрица – квадратная матрица, все
диагональные элементы которой единицы,
а остальные – нули:
Единичная
матрица размера
обычно обозначается En и имеет вид:

Свойства
Произведение
любой матрицы и единичной матрицы
подходящего размера равно самой матрице:
AE
= EA = A
Квадратная
матрица в нулевой степени дает единичную
матрицу того же размера:
A0
= E
При
умножении матрицы на обратную ей тоже
получается единичная матрица:
Единичная
матрица получается при умножении
ортогональной матрицы на ей
транспонированную:
AAT
= E
Определитель
единичной матрицы равен единице:
Примеры
Единичные
матрицы первых порядков имеют вид

3.
Транспонированная
матрица — матрица AT, полученная из
исходной матрицы A заменой строк на
столбцы.
и

Свойства
транспонированных матриц
-
Дважды
транспонированная матрица А равна
исходной матрице А.
-
Транспонированная
сумма матриц равна сумме транспонированных
матриц.
-
Транспонированное
произведение матриц равно произведению
транспонированных матриц
-
При
транспонировании можно выносить скаляр.
-
Определитель
транспонированной матрицы равен
определителю исходной матрицы
4.
Элементарные
преобразования матрицы — это такие
преобразования матрицы, в результате
которых сохраняется эквивалентность
матриц. Таким образом, элементарные
преобразования не изменяют множество
решений системы линейных алгебраических
уравнений, которую представляет эта
матрица.
Определение
Элементарными
преобразованиями строк называют:
-
перестановка
местами любых двух строк матрицы; -
умножение
любой строки матрицы на константу
,
-
прибавление
к любой строке матрицы другой строки,
умноженной на константу,
Обозначение
указывает на то, что матрица
может быть получена из
путём элементарных преобразований
(или наоборот)
Свойства
-
Инвариантность
ранга при элементарных преобразованиях
Теорема
(об инвариантности ранга при элементарных
преобразованиях)
Если
,
то
-
Эквивалентность
СЛАУ при элементарных преобразованиях
Назовём
элементарными преобразованиями над
системой линейных алгебраических
уравнений:
перестановку
уравнений;
умножение
уравнения на ненулевую константу;
сложение
одного уравнения с другим, умноженным
на некоторую константу.
Т.е.
элементарные преобразования над её
расширенной матрицей. Тогда справедливо
следующее утверждение:
Теорема
(об эквивалентности систем уравнений
при элементарных преобразованиях).
Система
линейных алгебраических уравнений,
полученная путём элементарных
преобразований над исходной системой,
эквивалентна ей
-
Нахождение
обратных матриц
Теорема
(о нахождении обратной матрицы).
Пусть
определитель матрицы
не равен нулю, пусть матрица
определяется выражением
. Тогда при элементарном преобразовании
строк матрицы
к единичной матрице
в составе
одновременно происходит преобразование
к
-
Приведение
матриц к ступенчатому виду
Введём
понятие ступенчатых матриц:
Матрица
имеет ступенчатый вид, если:
Все
нулевые строки матрицы
стоят последними;
Для
любой ненулевой строки матрицы
(пусть для определённости её номер равен
) справедливо следующее: если
— первый ненулевой элемент строки
, то
.
Тогда
справедливо следующее утверждение:
Теорема
(о приведении матриц к ступенчатому
виду).
Любую
матрицу путём элементарных преобразований
только над строками можно привести к
ступенчатому виду.
Эквивалентные
матрицы
Определение.
Матрицы, полученные в результате
элементарного преобразования, называются
эквивалентными.
Надо
отметить, что равные матрицы и эвивалентные
матрицы – понятия совершенно различные.
Теорема.
Наибольшее число линейно независимых
столбцов в матрице равно числу линейно
независимых строк.
Т.к.
элементарные преобразования не изменяют
ранг матрицы, то можно существенно
упростить процесс нахождения ранга
матрицы.
5.
Блочная
(клеточная) матрица — вид квадратной
матрицы, каждый элемент которой является
квадратной подматрицей меньшей, кратной
размерности.
Пример
записи
Матрица
размерностью 4×4
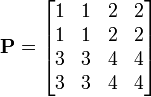
является
блочной, состоящей из четырех
подматриц-блоков размерностью 2×2
Если
каждый блок будет определен как
то,
блочная матрица может быть записана в
следующем виде
Операции
с блочными матрицами
-
При
сложении блочных матриц нужно, чтобы
подматрицы были одного размера. -
При
умножении блочной матрицы на число a
каждая подматрица умножается на a. -
При
перемножении блочных матриц необходимо
согласовать размеры подматриц. -
При
транспонировании блоки на главной
диагонали транспонируются и остаются
на месте, остальные блоки меняются
местами и транспонируются.
6.
Определители второго
и третьего порядков
Метод Гаусса,
рассмотренный выше, весьма прост, состоит
из однотипных вычислений и не требует
больших усилий при алгоритмической
реализации. Однако его существенным
недостатком является то, что он не дает
возможность сформулировать условия
совместности или определенности системы
по информации о коэффициентах и свободных
членах этой системы. С другой стороны,
даже при условии определенности системы
этот метод не позволяет построить
формулы, выражающие решение системы
через ее коэффициенты и свободные члены.
Все это, однако, оказывается необходимым
при решении различных теоретических
вопросов, в частности в геометрических
исследованиях. Поэтому теорию систем
линейных алгебраических уравнений
приходится развивать иными, более
глубокими методами.
Сначала рассмотрим
частный случай определенных систем,
имеющих равное число уравнений и
неизвестных.
Пусть дана система
двух линейных уравнений с двумя
неизвестными
(1)
коэффициенты которого
составляют квадратную матрицу второго
порядка
(2)
Применяя к системе
(1) метод уравнивания коэффициентов
(первое уравнение умножаем на a22, а второе
– на a12 и получаем выражение для x1,
аналогично – для x2) получим:
предположим, что
a11a22 – a12a21¹0. Тогда
(3)
Общий знаменатель
значений неизвестных (3) легко выражается
через элементы матрицы (2): он равен
произведению элементов главной диагонали
минус произведение элементов второй
диагонали. Это число называется
определителем или детерминантом матрицы
(2), причем, как говорят, определителем
второго порядка, т. к. матрица (2) есть
матрица второго порядка. Для обозначения
определителя матрицы (2) употребляется
следующий символ:
(4)
Произведения а11 а22 –
а12 а21 называются членами определителя
второго порядка.
Итак, матрица есть
таблица чисел, а определитель – число,
соответствующее матрице.
Примеры:
1)
2)
Числитель выражений
(3) имеет такой же вид, как и знаменатель,
т. е. это тоже знаменатель второго
порядка. Числитель выражения для x1 есть
определитель матрицы, получающейся из
матрицы (2) заменой ее первого столбца
столбцом из свободных членов системы
(1), а числитель выражения для x2 есть
определитель матрицы, получающейся из
матрицы (2) такой же заменой ее второго
столбца. Таким образом, формулы (3) в
новых обозначениях записываются в
следующем виде:
(5)
Это и есть правило
Крамера решения системы двух линейных
уравнений с двумя неизвестными:
Если определитель
(4) из коэффициентов системы уравнений
(1) отличен от нуля, то получаем решение
системы (1), беря в качестве значений для
неизвестных дроби, общим знаменателем
которых служит определитель (4) матрицы
коэффициентов системы (1), а числителем
для неизвестного хi (i=1,2) является
определитель, получающийся заменой в
определителе (4) i-го столбца (т. е. столбца
коэффициентов при неизвестном) столбцом
из свободных членов системы (1).
Пример:
Определитель из
коэффициентов есть
Он отличен от нуля, и
поэтому к системе применимо правило
Крамера. Числителями для неизвестных
будут определители
Таким образом, решением
системы служит следующая пара чисел:
Введение определителей
второго порядка не вносит существенных
упрощений в решение систем двух линейных
уравнений с двумя неизвестными, и без
того не представляющее никаких трудностей.
Однако, уже для случая трех уравнений
с тремя неизвестными аналогичные методы
становятся практически полезными.
Пусть дана система
(6)
с квадратной матрицей
из коэффициентов
(7)
Если мы умножим обе
части первого из уравнений (6) на число
а22а33 – а23а32, обе части второго – на а13а32
– а12а33, обе части третьего – на а12а23 –
а13а22, а затем сложим все три уравнения,
то, как легко проверить, коэффициенты
при х2 и х3 окажутся равными нулю, т. е.
эти неизвестные одновременно исключаются,
и мы получим равенство:
(a11a22a33+
a12a23a31+ a13a21a32- a13a22a31- a12a21a33- a11a23a32)х1=
= b1a22a33+
a12a23b3+ a13b2a32- a13a22b3- a12b2a33- b1a23a32
(8)
Коэффициенты при х1
в этом равенстве называются определителем
третьего порядка, соответствующим
матрице (7). Для его записи употребляется
такая же символика, как и в случае
определителя второго порядка:
(9)
Хотя выражение
определителя третьего порядка выглядит
весьма громоздким, закон его составления
из элементов матрицы (7) оказывается
довольно простым. В самом деле, один из
трех членов определителя, входящих со
знаком «плюс» есть произведение элементов
главной диагонали, каждый из двух других
– произведением элементов, лежащих на
параллели к этой диагонали с добавлением
третьего множителя из противоположного
угла матрицы. Члены, входящие в (9) со
знаком «минус» строятся также, но
относительно второй диагонали. На рис.
1 слева указано правило вычисления
положительных членов определителя
третьего порядка, а справа – правило
вычисления отрицательных членов. Это
правило называется правилом Саррюса.
Шесть
основных свойств определителя 3-го
порядка.
Определители
третьего порядка (как и определители
2-го порядка) обладают следующими шестью
свойствами, следующими из формулы (9)
(для определителей второго порядка –
из формулы (4)).
1.
определитель не изменится, если строки
его матрицы сделать столбцами, а столбцы
строками;
2.
при перестановке двух строк определителя
он меняет знак;
3.
если в определителе имеются две
одинаковые строки, то определитель
равен нулю;
4.
общий множитель определителя строки
можно вынести за знак определителя;
5.
если элементы одной строки определителя
пропорциональны элементам другой, то
определитель равен нулю;
6.
если к одной строке определителя
прибавить другую, умноженную на любое
число, то определитель не изменится.
Примеры:
-
2×3×5+1×1×2+2×(-4)×3-2×3×2-1×(-4)×5-2×1×3=30
+ 2 – 24 – 12 +20 – 6 =10
-
1×3×0+0×2×1+(-5)×(-2)×(-2)-(-5)×3×1-0×(-2)×0-1×2×(-3)=
=
-20 + 15 +4 = – 1
Правая
часть равенства (8) также будет определителем
третьего порядка, а именно определителем
матрицы, получающейся из матрицы (7)
заменой ее первого столбца столбцом из
свободных членов системы (6). Обозначим
определитель (9) символом D, а определитель
матрицы, получающейся заменой j-го
столбца столбцом из свободных членов
системы (6) символом D1. Тогда равенство
(8) приобретает вид D×x1=D1, откуда при D¹0
следует
(10)
Таким
же путем, умножая уравнения (6) соответственно
на числа а23а31 – а21а33, а11а33 – а13а31, а13а21
– а11а23, получим для х2 следующее выражение
(снова при d¹0):
(11)
Наконец,
умножая уравнения (6) соответственно на
а21а32 – а22а31, а12а31 – а11а32, а11а22 – а12а21,
придем к выражению для х3:
(12)
Таким
образом, если определитель из коэффициентов
системы трех линейных уравнений с тремя
неизвестными отличен от нуля, то решение
этой системы может быть найдено по
правилу Крамера, формулируемому также,
как и в случае системы двух уравнений.
Пример:
Решить систему:

Определитель
из коэффициентов системы отличен от
нуля:
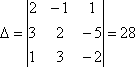
поэтому
к системе применимо правило Крамера.
Числителями для неизвестных будут
определители
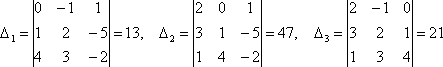
т.
е. решением системы являются следующие
значения хi:
7.
Минор
матрицы A ― определитель квадратной
матрицы порядка k (который называется
также порядком этого минора), элементы
которой стоят в матрице A на пересечении
строк с номерами
и столбцов с номерами
.
Если номера отмеченных
строк совпадают с номерами отмеченных
столбцов, то минор называется главным,
а если отмечены первые k строк и первые
k столбцов ― угловым или ведущим главным.
Дополнительный минор
элемента матрицы n-го порядка есть
определитель порядка (n-1), соответствующий
той матрице, которая получается из
матрицы путем вычеркивания i-ой строки
и j-го столбца.
Базисным минором
матрицы называется любой её ненулевой
минор максимального порядка. Для того
чтобы минор был базисным, необходимо и
достаточно, чтобы все окаймляющие его
миноры (то есть содержащие его миноры
на единицу большего порядка) были равны
нулю. Система строк (столбцов) матрицы,
связанных с базисным минором, является
максимальной линейно независимой
подсистемой системы всех строк (столбцов)
матрицы.
Пример
Например, есть матрица:
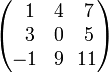
Предположим, надо
найти дополнительный минор . Этот минор
— определитель матрицы, получающейся
путем вычеркивания строки 2 и столбца
3:
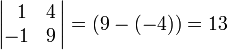
Получаем
8.
Алгебраические
дополнения:
Алгебраическим
дополнением элемента аij называется его
минор, взятый со знаком “+”, если
сумма (i + j) четное число, и со знаком “-“,
если эта сумма нечетное число. Обозначается
Аij.
Аij = (-1)i+j × Мij.
Тогда можно
переформулировать изложенное выше
свойство. Определитель матрицы равен
сумме произведение элементов некторого
ряда (строки или столбца) матрицы на
соответствующие им алгебраические
дополнения. Пример:
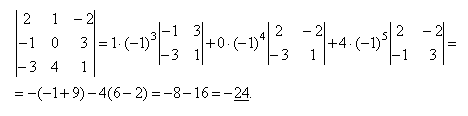
9.
Определение через
разложение по первой строке
Схема расчета
определителя матрицы .
Для матрицы первого
порядка детерминантом является сам
единственный элемент этой матрицы:
Для матрицы
детерминант определяется как
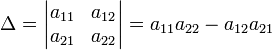
Для матрицы
определитель задаётся рекурсивно:
, где
— дополнительный минор к элементу a1j.
Эта формула называется разложением по
строке.
В частности, формула
вычисления определителя матрицы
такова:
=
a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 −
a13a22a31
Легко доказать, что
при транспонировании определитель
матрицы не изменяется (иными словами,
аналогичное разложение по первому
столбцу также справедливо, то есть даёт
такой же результат, как и разложение по
первой строке):
10.
Основные
свойства определителей
Прежде
всего отметим, что det[A] = det[A]t, т. е.
определитель матрицы не изменяет своего
значения при взаимной замене ее строк
и столбцов. Поэтому все свойства
определителя, сформулированные для
столбцов, справедливы и для строк, и
обратно.
Ниже
приводятся основные свойства определителей,
которые легко доказываются на основе
общего выражения (1).
1.
При перестановке двух столбцов
определитель меняет знак на противоположный
(свойство антисимметрии).
2.
Определитель равен нулю, если все
элементы какого-нибудь столбца равны
нулю или если один из столбцов является
линейной комбинацией любых его других
столбцов (в частности, определитель, у
которого хотя бы два столбца одинаковы,
равен нулю).
3.
Умножение всех элементов какого-нибудь
столбца на скаляр k равнозначно умножению
определителя на k (общий множитель
элементов строки или столбца можно
вынести за знак определителя).
4.
Умножение матрицы n-го порядка на скаляр
k соответствует умножению ее определителя
на kn, т.е.
det(k[A])
= kndet[A].
5.
Значение определителя не изменится,
если к какому-нибудь столбцу прибавить
другой столбец, умноженный на скаляр
k.
6.
Если два определителя одинаковых
порядков различаются между собой только
элементами j-го столбца, то их сумма
равна определителю, элементы j-го столбца
которого равны суммам соответствующих
элементов j-х столбцов исходных
определителей, а остальные элементы те
же, что у исходных (свойство линейности).
11.
Невырожденные матрицы
Пусть А – квадратная
матрица n – ого порядка.

Квадратная матрица
А называется невырожденной, если
определитель матрицы (Δ = det A) не равен
нулю (Δ = det A ≠ 0). В противном случае (Δ =
0) матрица А называется вырожденной.
Матрицей, союзной к
матрице А, называется матрица

, где Аij
– алгебраическое дополнение элемента
аij данной матрицы (оно определяется
так же, как и алгебраическое дополнение
элемента определителя матрицы).
Матрица А-1
называется обратной матрице А, если
выполняется условие:
А × А-1 = А-1
× А = Е
, где Е – единичная
матрица того же порядка, что и матрица
А. Матрица А-1 имеет те же размеры,
что и матрица А.
12.
Обра́тная ма́трица
— такая матрица A−1, при умножении
на которую исходная матрица A даёт в
результате единичную матрицу E:
Квадратная матрица
обратима тогда и только тогда, когда
она невырожденная, то есть её определитель
не равен нулю. Для неквадратных матриц
и вырожденных матриц обратных матриц
не существует. Однако возможно обобщить
это понятие и ввести псевдообратные
матрицы, похожие на обратные по многим
свойствам.
Способы нахождения
обратной матрицы
Если матрица обратима,
то для нахождения обратной матрицы
можно воспользоваться одним из следующих
способов:
Точные (прямые)
методы
Метод Гаусса—Жордана
Возьмём две матрицы:
саму A и единичную E. Приведём матрицу A
к единичной матрице методом Гаусса—Жордана.
После применения каждой операции к
первой матрице применим ту же операцию
ко второй. Когда приведение первой
матрицы к единичному виду будет завершено,
вторая матрица окажется равной A−1.
При использовании
метода Гаусса первая матрица будет
умножаться слева на одну из элементарных
матриц Λi (трансвекцию или диагональную
матрицу с единицами на главной диагонали,
кроме одной позиции):
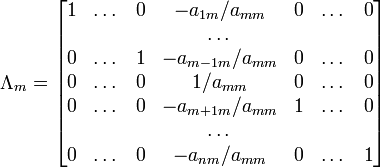
Вторая матрица после
применения всех операций станет равна
Λ, то есть будет искомой. Сложность
алгоритма — O(n3).
С помощью матрицы
алгебраических дополнений
,
где CT — транспонированная матрица
алгебраических дополнений;
Полученная матрица
A−1 и будет обратной. Сложность
алгоритма зависит от сложности алгоритма
расчета определителя Odet и равна
O(n²)·Odet.
Иначе говоря, обратная
матрица равна единице, делённой на
определитель исходной матрицы и
умноженной на транспонированную матрицу
алгебраических дополнений элементов
исходной матрицы.
13.
Обратная матрица
вычисляется по формуле
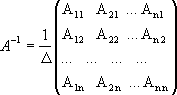
14.
Свойства обратной
матрицы
,
где
обозначает определитель.
для любых двух обратимых матриц A и B.
где * T обозначает транспонированную
матрицу.
для любого коэффициента
.
Если необходимо решить
систему линейных уравнений Ax = b, (b —
ненулевой вектор) где x — искомый вектор,
и если A − 1 существует, то x = A −
1b. В противном случае либо размерность
пространства решений больше нуля, либо
их нет вовсе.
15.
Рангом системы строк
(столбцов) матрицы A с m строк и n столбцов
называется максимальное число линейно
независимых строк (столбцов). Несколько
строк (столбцов) называются линейно
независимыми, если ни одна из них не
выражается линейно через другие. Ранг
системы строк всегда равен рангу системы
столбцов, и это число называется рангом
матрицы.
Пусть
— прямоугольная матрица.
Тогда по определению
рангом матрицы A является:
-
ноль,
если A — нулевая матрица; -
число
, где Mr — минор матрицы A порядка r, а Mr
+ 1 — окаймляющий к нему минор порядка
(r + 1), если они существуют.
Теорема (о корректности
определения рангов). Пусть все миноры
матрицы
порядка k равны нулю (Mk = 0). Тогда
, если они существую
16.
Строчнопсевдотреугольная
– если в каждой нулевой строке найдется
хотябы один нулевой элемент, в столбце
которого все нижележащие елементы (если
они есть) = 0
Строчнопсевдодиагональная
– если в каждой нулевой строке найдется
хотябы один нулевой елемент, в столбце
которого строго все елементы лежащие
выше (если они есть) = 0
17.
Линейное пространство.
Основные понятия
Пусть
множество элементов произвольной
природы, для которых определены операции
сложения и умножения на действительное
число:
паре элементов
множества
,
отвечает элемент
, называемый суммой
и
;
паре
,
отвечает элемент
, называемый произведением числа
и элемента
.
Будем называть
множество
линейным пространством, если для всех
его элементов определены операции
сложения и умножения на действительное
число и для любых элементов
и произвольных чисел
справедливо:
,
сложение коммутативно;
,
сложение ассоциативно;
существует единственный
нулевой элемент
такой, что
,
;
для каждого элемента
существует единственный противоположный
элемент
такой, что
,
,
умножение на число ассоциативно;
;
,
;
,
умножение на число дистрибутивно
относительно сложения элементов;
,
умножение вектора на число дистрибутивно
относительно сложения чисел.
Равенства 1–8 называют
аксиомами линейного пространства.
Линейное пространство
часто называют векторным пространством,
а его элементы – векторам
18.
РАЗМЕРНОСТЬ ЛИЕЙНОГО
ПРОСТРАНСТВА
Число k называется
размерностью линейного пространства
L, если в L существует система из k линейно
независимых векторов, а любая система
из k+1 вектора — линейно зависима.
Обозначается dimL = k.
Пространство L называется k- мерным.
Иногда обозначается Lk.
Векторы i и j — линейно
независимая система векторов линейного
пространства геометрических
радиусов-векторов плоскости R2 .
Рассмотрим произвольную
систему из трёх векторов x, y, z .

На рисунке показано,
что вектор z линейно выражается через
векторы x и y: z = α1·x + α2·y.
Итак, в пространстве
R2 существует система из двух
линейно независимых векторов ( i , j), а
любые три вектора образуют линейно
зависимую систему. То есть размерность
пространства R2 равна 2, dim R2
= 2.
19.
Изоморфи́зм — это
очень общее понятие, которое употребляется
в различных разделах математики. В общих
чертах его можно описать так: Пусть даны
два множества с определённой структурой
(группы, кольца, линейные пространства
и т. п.). Биекция между ними называется
изоморфизмом, если она сохраняет эту
структуру. Если между такими множествами
существует изоморфизм, то они называются
изоморфными. Изоморфизм всегда задаёт
отношение эквивалентности на классе
таких множеств со структурой.
Объекты, между которыми
существует изоморфизм, являются в
определённом смысле «одинаково
устроенными», они называются изоморфными.
Классическим примером изоморфных систем
могут служить множество
всех вещественных чисел с определённой
на нём операцией сложения и множество
положительных вещественных чисел с
заданной на нём операцией умножения.
Отображение
в этом случае является изоморфизмом.
20.
Определение: W
называется подпространством пространства
V, если оно само является векторным
пространством над полем P.
Теорема 1: Критерий
подпространства. Непустое множество
является подпространством пространства
V тогда и только тогда, когда W замкнуто
относительно сложения векторов и
умножения их на скаляры. Иными словами,
выполняются следующие два условия:
Теорема 2:
Пересечение любого семейства подпространств
данного пространства V вновь является
подпространством постранства V.
Линейная оболочка
системы векторов
Пусть
– система векторов из векторного
пространства V над полем P.
Определение 2:
Линейной оболочкой L системы A называется
множество всех линейных комбинаций
векторов системы A. Обозначение L(A).
21.
СУММА И ПЕРЕСЕЧЕНИЕ
ПОДПРОСТРАНСТВ
Пусть L1..Lk – линейные
подпространства пространства V. Суммой
подпространств L1..Lk называется множество
всевозможных векторов x, представимых
в виде x = x1 + … + xk, где xi из Li для любых i
от 1 до k. Обозначается как L1 + L2 +.. + Lk
Представление вектора
в виде такой суммы называется разложением
вектора x по подпространствам L1.. Lk
Пересечением
подпространств L1..Lk называется множество,
в котором содержаться только те вектора,
которые содержатся в каждом из
подпространств L1..Lk
Пересечение пустым
не бывает, как минимум это нулевой
вектор.
Теорема. Сумма и
пересечение подпространств линейного
пространства V также является
подпространством V.
Доказательство следует
из определения подпространства.
Теорема. Сумма линейных
подпространств есть линейная оболочка
совокупности базисов слагаемых
подпространств.
Доказательство –
просто проверяем двустороннее вложение.
Следствие. Размерность
суммы подпространств равна рангу
мовокупности базисов слагаемых
подпространств.
Теорема. Для любых
двух подпространств выполняется
равенство dim(L1+L2) = dimL1 + dim L2 – dim(L1^L2)
Доказательство.
Если пересечение
ненулевое, то смотрим его базис – f1..fn
– так как пересечение является
подпространством каждого из исходных
подпространств, этот базис можно
дополнить до базиса каждого из
подпространств. Дополним, получим два
базиса. В каждом из них будет n векторов
из базиса пересечения. А если дополнить
до базиса совокупности сразу, получим
n векторов из базиса пересечения и еще
m и s дополняющих векторов до базиса
первого и второго подпространства. То
есть, m+s+n = m+n + s +n – s – верно, доказано.
22.
Теоре́ма Кро́некера
— Капе́лли — критерий совместности
системы линейных алгебраических
уравнений:
Система линейных
алгебраических уравнений совместна
тогда и только тогда, когда ранг её
основной матрицы равен рангу её
расширенной матрицы, причём система
имеет единственное решение, если ранг
равен числу неизвестных, и бесконечное
множество решений, если ранг меньше
числа неизвестных.
Необходимость
Пусть система совместна.
Тогда существуют числа
такие, что
. Следовательно, столбец b является
линейной комбинацией столбцов
матрицы A. Из того, что ранг матрицы не
изменится, если из системы его строк
(столбцов) вычеркнуть или приписать
строку (столбец), которая является
линейной комбинацией других строк
(столбцов) следует, что
Достаточность
Пусть
. Возьмем в матрице A какой-нибудь базисный
минор. Так как
, то он же и будет базисным минором и
матрицы B. Тогда согласно теореме о
базисном миноре последний столбец
матрицы B будет линейной комбинацией
базисных столбцов, то есть столбцов
матрицы A. Следовательно, столбец
свободных членов системы является
линейной комбинацией столбцов матрицы
A.
24.