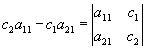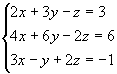Решение матричных уравнений
Финальная глава саги.
Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».
Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.
Краткое содержание прошлых частей:
- Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
- Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
- Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
- Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
- Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
- Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.
И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.
❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.
Что такое матричное уравнение
Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.
Шаг 1. Упрощаем уравнение
Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.
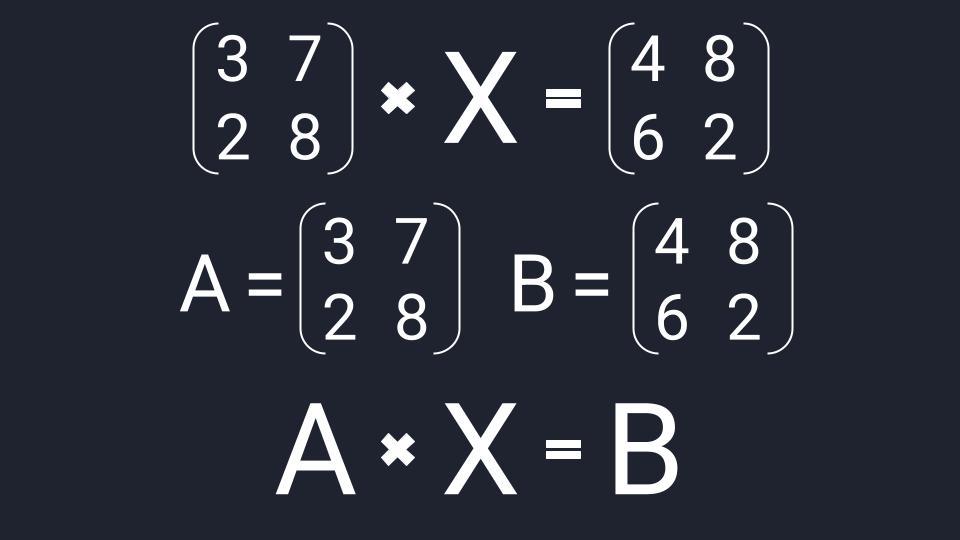
Шаг 2. Вводим единичную матрицу
В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.
Можно представить, что есть число 100 — это «сто в первой степени», 100 1
И есть число 0,01 — это «сто в минус первой степени», 100 -1
При перемножении этих двух чисел получится единица:
100 1 × 100 -1 = 100 × 0,01 = 1.
Вот такое, только в мире матриц.
Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А -1 . Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:
А -1 × А × Х = А -1 × В
Добавляем единичную матрицу и упрощаем запись:
А -1 × А = E — единичная матрица
E × Х = А -1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем
Х = А -1 × В — новая запись уравнения
После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.
💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A -1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.
Шаг 3. Находим обратную матрицу
Вспоминаем формулу и порядок расчёта обратной матрицы:
- Делим единицу на определитель матрицы A.
- Считаем транспонированную матрицу алгебраических дополнений.
- Перемножаем значения и получаем нужную матрицу.
Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Шаг 4. Вычисляем неизвестную матрицу
Нам остаётся посчитать матрицу X: умножаем обратную матрицу А -1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Шаг 5. Проверяем уравнение
Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.
👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Ну и что
Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:
Решение задач с матрицами.
Матричный калькулятор
| Очистить | Размер × |
| Транспонировать | Умножить на |
| Найти определитель | Возвести в степень |
| Найти ранг | Найти обратную |
| Очистить | Размер × |
| Транспонировать | Умножить на |
| Найти определитель | Возвести в степень |
| Найти ранг | Найти обратную |
Ввод данных в матричный калькулятор
В матричный калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности матричного калькулятора
- Между полями для ввода можно перемещаться нажимая клавиши , , и на клавиатуре.
Теория. Матрицы
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Матричный калькулятор онлайн
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Инструкция матричного онлайн калькулятора
С помощью матричного онлайн калькулятора вы можете сложить, вычитать, умножить, транспонировать матрицы, вычислить обратную матрицу, псевдообратную матрицу, ранг матрицы, определитель матрицы, m-норму и l-норму матрицы, возвести матрицу в степень , умножить матрицу на число , сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы, проводить исключение Гаусса, решить матричное уравнение AX=B, сделать LU разложение матрицы, вычислить ядро (нуль пространство) матрицы, сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта.
Матричный онлайн калькулятор работает не только с десятичными числами, но и с дробями. Для ввода дроби нужно в исходные матрицы 
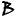
Кнопка 



При вычислениях пустая ячейка воспринимается как нуль.
Для операций с одной матрицей (т.е. транспонирование, обратное, псевдообратное, скелетное разложение и т.д.) сначала выбирается конкретная матрица с помощью радиокнопки .
Кнопки Fn1, Fn2 и Fn3 переключают разные группы функциий.
Нажимая на вычисленных матрицах открывается меню (Рис.2), что позволяет записать данную матрицу в исходные матрицы 
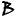
Вычисление суммы, разности, произведения матриц онлайн
Матричным онлайн калькулятором можно вычислить сумму, разность или произведение матриц. Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.
Для вычисления суммы, разности или произведения матриц:
- Введите размерности матриц
и
.
- Введите элементы матриц.
- Нажмите на кнопку «A+B «,»A-B» или «A×B».
Вычисление обратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить обратную матрицу. Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления обратной матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «обратное «.
Для подробного вычисления обратной матрицы по шагам, пользуйтесь этим калькулятором для вычисления обратной матрицы. Теорию вычисления обратной матрицы смотрите здесь.
Вычисление определителя матрицы онлайн
Матричным онлайн калькулятором можно вычислить определитель матрицы. Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления определителя матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «определитель «.
Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы. Теорию вычисления определителя матрицы смотрите здесь.
Вычисление ранга матрицы онлайн
Матричным онлайн калькулятором можно вычислить ранг матрицы.
Для вычисления ранга матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «ранг «.
Для подробного вычисления ранга матрицы по шагам, пользуйтесь этим калькулятором для вычисления ранга матрицы. Теорию вычисления ранга матрицы смотрите здесь.
Вычисление псевдообратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить псевдообратную матрицу. Псевдообратная к данной матрице всегда существует.
Для вычисления псевдообратной матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «псевдообратное «.
Удаление линейно зависимых строк или столбцов матрицы онлайн
Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.
Для удаления линейно зависимых строк или столбцов матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «полный ранг строк » или «полный ранг столбцов».
Скелетное разложение матрицы онлайн
Для проведения скелетного разложения матрицы онлайн
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «скелетное разложение «.
Решение матричного уравнения или системы линейных уравнений AX=B онлайн
Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.
Для решения матричного уравнения:
- Введите размерности матриц
и
.
- Введите элементы матриц.
- Нажмите на кнопку «решение AX=B».
Учтите, что матрицы 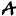
Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.
Для исключения Гаусса или приведения матрицы к треугольному виду
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «Треугольный вид».
LU-разложение или LUP-разложение матрицы онлайн
Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU), где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение , при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «LU-разложение».
Построение ядра (нуль-пространства) матрицы онлайн
С помощью матричного калькулятора можно построить нуль-пространство (ядро) матрицы.
Для построения нуль-пространства (ядра) матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «ядро (·)».
Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн
С помощью матричного калькулятора можно сделать ортогонализацию и ортонормализацию Грамма-Шмидта матрицы онлайн.
Для ортогонализации или ортонормализации матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «Ортогонализация Г.-Ш. (·)» или «Ортонормализация Г.-Ш. (·)».
источники:
http://ru.onlinemschool.com/math/assistance/matrix/
http://matworld.ru/calculator/matrix-calculator-1.php
Рассмотрим
матричное уравнение вида
|
(4.5) |
где и
—
данные матрицы, имеющие одинаковое
количество строк, причем матрица квадратная.
Требуется найти матрицу ,
удовлетворяющую уравнению (4.5).
Теорема
4.2 о существовании и единственности
решения матричного уравнения (4.5). Если
определитель матрицы отличен
от нуля, то матричное уравнение (4.5) имеет
единственное решение.
В
самом деле, подставляя в
левую часть равенства (4.5), получаем,
т.е. правую часть этого равенства.
Заметим,
что решением матричного уравнения служит
обратная матрица.
Рассмотрим
также матричное уравнение вида
|
(4.6) |
где и
—
данные матрицы, имеющие одинаковое
количество столбцов, причем
матрица квадратная.
Требуется найти матрицу ,
удовлетворяющую уравнению (4.6).
Теорема
4.3 о существовании и единственности
решения матричного уравнения (4.6). Если
определитель матрицы отличен
от нуля, то уравнение (4.6) имеет единственное
решение.
Заметим,
что матрица является
как бы “левым” частным от “деления”
матрицына
матрицу,
поскольку матрицав
(4.5) умножается наслева,
а матрица—
“правым” частным, так как матрицав
(4.6) умножается насправа.
Пример
4.5. Даны
матрицы
Решить
уравнения: а) ;
б);
в).
Решение. Обратная
матрица была
найдена в примере 4.2.
а)
Решение уравнения находим,
умножая обе его части слева на
б)
Уравнение не имеет решений, так как
матрицы и
имеют
разное количество столбцов.
в)
Решение уравнения находим,
умножая обе его части справа на
Пример
4.6. Решить
уравнение: ,
где.
Решение. Преобразуя
левую часть уравнения:
приведем
его к виду (4.1)
где
Следовательно, .
Обратная матрица найдена в примере 4.2:
Значит,
Пример
4.7. Решить
уравнение ,
где
Решение. Обратные
матрицы
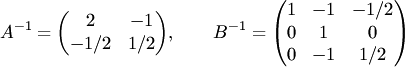
найдены в примерах 4.2, 4.3 соответственно.
Решение уравнения находим по формуле
Пример
4.8. Решить
уравнение ,
где
Решение. Определитель
матрицы равен
нулю, следовательно, обратная матрица
не существует. Поэтому нельзя использовать
формулу.
Будем искать элементы матрицы.
Подставляя в уравнение, получаем
Находим
произведение, а затем приравниваем
соответствующие элементы матриц в левой
и правой частях уравнения:
Здесь,
учитывая пропорциональность уравнений,
в системе оставлены только два уравнения
из четырех. Выразим неизвестные и
Следовательно,
решение матричного уравнения имеет вид
где
параметры и
могут
принимать любые значения. Таким образом,
данное матричное уравнение имеет
бесконечное множество решений.
22. Решение системы линейных уравнений матричным методом. Правило Крамера.
|
Рассмотрим |
|
|
|
|
|
|
|
Очевидно, |
|
тогда
Такое
Если
Умножим
А-1(АХ)=А-1С
(А-1А) Например, |
|
|
|
|
|
Не
А =1·[-1·4
Определитель
А11 =
А12 =
А13 =
А21 =
А22 =
А23 =
А31 =
А32 = А33 = |
|
|
|
|
|
|
Можно
Действительно |
|
Решение Применим |
|
|
или |
|
система
Решим
Умножим
(а11а22 – аналогично (а11а22 – |
|
1) |
|
2) определитель, |
|
3) |
|
|
Видим, |
|
Как |
|
Эти
Возможны
1.
2. =0 ,
3. =0 Пример: |
|
|
|
|
|
Так |
|
|
|
Так получим |
|
|
|
Решив
То Если |
Теорема
(правило Крамера). Если
определитель системы Δ ≠ 0, то
рассматриваемая система имеет одно и
только одно решение, причём
Доказательство.
Итак, рассмотрим систему 3-х уравнений
с тремя неизвестными. Умножим 1-ое
уравнение системы на алгебраическое
дополнение A11 элемента a11,
2-ое уравнение – наA21 и
3-е – на A31:
Сложим
эти уравнения:
Рассмотрим
каждую из скобок и правую часть этого
уравнения. По теореме о разложении
определителя по элементам 1-го столбца
.
Далее
рассмотрим коэффициенты при x2:
Аналогично
можно показать, что и .
Наконец
несложно заметить, что
Таким
образом, получаем равенство: .
Следовательно, .
Аналогично
выводятся равенства и
,
откуда и следует утверждение теоремы.
Таким
образом, заметим, что если определитель
системы Δ ≠ 0, то система имеет единственное
решение и обратно. Если же определитель
системы равен нулю, то система либо
имеет бесконечное множество решений,
либо не имеет решений, т.е. несовместна.
Матричные уравнения
Рассмотрим матричное уравнение вида
(4.5)
где и
— данные матрицы, имеющие одинаковое количество строк, причем матрица
квадратная. Требуется найти матрицу
, удовлетворяющую уравнению (4.5).
Теорема 4.2 о существовании и единственности решения матричного уравнения (4.5). Если определитель матрицы отличен от нуля, то матричное уравнение (4.5) имеет единственное решение
.
В самом деле, подставляя в левую часть равенства (4.5), получаем
, т.е. правую часть этого равенства.
Заметим, что решением матричного уравнения служит обратная матрица
.
Рассмотрим также матричное уравнение вида
(4.6)
где и
— данные матрицы, имеющие одинаковое количество столбцов, причем матрица
квадратная. Требуется найти матрицу
, удовлетворяющую уравнению (4.6).
Теорема 4.3 о существовании и единственности решения матричного уравнения (4.6). Если определитель матрицы отличен от нуля, то уравнение (4.6) имеет единственное решение
.
Заметим, что матрица является как бы “левым” частным от “деления” матрицы
на матрицу
, поскольку матрица
в (4.5) умножается на
слева, а матрица
— “правым” частным, так как матрица
в (4.6) умножается на
справа.
Пример 4.5. Даны матрицы
Решить уравнения: а) ; б)
; в)
.
Решение. Обратная матрица была найдена в примере 4.2.
а) Решение уравнения находим, умножая обе его части слева на
б) Уравнение не имеет решений, так как матрицы и
имеют разное количество столбцов
.
в) Решение уравнения находим, умножая обе его части справа на
Пример 4.6. Решить уравнение: , где
.
Решение. Преобразуя левую часть уравнения:
приведем его к виду (4.1)
где
Следовательно, . Обратная матрица найдена в примере 4.2:
Значит,
Пример 4.7. Решить уравнение , где
Решение. Обратные матрицы
были найдены в примерах 4.2, 4.3 соответственно. Решение уравнения находим по формуле
Пример 4.8. Решить уравнение , где
Решение. Определитель матрицы равен нулю, следовательно, обратная матрица не существует. Поэтому нельзя использовать формулу
. Будем искать элементы матрицы
. Подставляя в уравнение, получаем
Находим произведение, а затем приравниваем соответствующие элементы матриц в левой и правой частях уравнения:
Здесь, учитывая пропорциональность уравнений, в системе оставлены только два уравнения из четырех. Выразим неизвестные и
Следовательно, решение матричного уравнения имеет вид
где параметры и
могут принимать любые значения. Таким образом, данное матричное уравнение имеет бесконечное множество решений.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
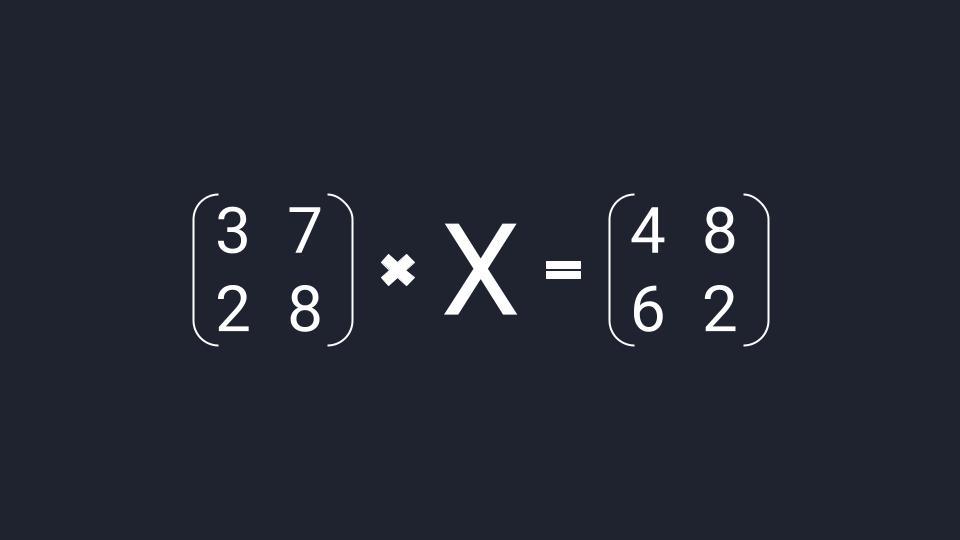




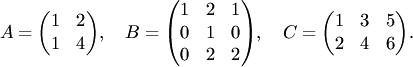




 – матрица
– матрица –
– ,
,
 матрица
матрица
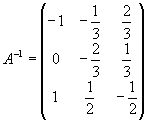



 или
или –
–