- Что такое MD5?
- Проблемы надежности MD5
- Обзор средств для декодирования хеш-кода MD5
- Основы безопасности при использовании MD5
MD5 является одним из алгоритмов хеширования на 128-битной основе. Под хешированием понимают преобразование входных данных по определенному алгоритму в битовую строку определенной длины. При этом полученный в ходе вычислений результат представлен в шестнадцатеричной системе исчисления. Она называется хешем, хеш-суммой или хеш-кодом.
Процесс хеширования широко применяется в программировании и веб-индустрии. В основном для создания уникальных значений в ассоциативных массивах, идентификаторов.
Область применения хеш-кодов:
- Создание электронных подписей;
- Хранение паролей в базах данных систем безопасности;
- В рамках современной криптографии для создания уникальных ключей онлайн;
- Проверка подлинности и целостности элементов файловой системы ПК.
MD5 как стандарт хеширования был разработан в 1991 году для создания уникального хеш-кода от заданного значения с последующей проверкой его подлинности.
Утилита md5sum, предназначенная для хеширования данных заданного файла по алгоритму MD5, возвращает строку. Она состоит из 32 чисел в шестнадцатеричной системе исчисления (016f8e458c8f89ef75fa7a78265a0025).
То есть хеш, полученный от функции, работа которой основана на этом алгоритме, выдает строку в 16 байт (128) бит. И эта строка включает в себя 16 шестнадцатеричных чисел. При этом изменение хотя бы одного ее символа приведет к последующему бесповоротному изменению значений всех остальных битов строки:
Казалось бы, такая характеристика MD5 должна обеспечивать 100% гарантии неуязвимости и сохранения данных. Но даже этого оказалось мало. В ходе проводимых исследований учеными был выявлен целый ряд прорех и уязвимостей в этом уже распространенном на тот момент алгоритме. Основной причиной слабой защищенности MD5 является относительно легкое нахождение коллизий при шифровании.
Под коллизией понимают возможность получения одинакового результата вычислений хеш-функции при разных входных значениях.
Проще говоря, чем больше вероятность нахождения коллизий, тем надежность используемого алгоритма ниже. Вероятность нахождения коллизий при шифровании более надежными хеш-функциями практически сводится к 0.
То есть большая вероятность расшифровки паролей MD5 является основной причиной отказа от использования этого алгоритма. Многие криптологи (специалисты по шифрованию данных) связывают низкую надежность MD5 с малой длиной получаемого хеш-кода.
Область применения алгоритма хеширования:
- Проверка целостности файлов, полученных через интернет – многие инсталляционные пакеты программ снабжены хеш-кодом. Во время активации приложения его значение сравнивается со значением, расположенным в базе данных разработчика;
- Поиск в файловой системе продублированных файлов – каждый из файлов снабжен своим хеш-кодом. Специальное приложение сканирует файловую систему компьютера, сравнивая между собой хеши всех элементов. При обнаружении совпадения утилита оповещает об этом пользователя или удаляет дубликат. Одной из подобных программ является Duplifinder:
- Для хеширования паролей – в семействе операционных систем UNIX каждый пользователь системы имеет свой уникальный пароль, для защиты которого используется хеширование на основе MD5. Некоторые системы на основе Linux также пользуются этим методом шифрования паролей.
Иногда при работе с компьютером или поврежденными базами данных требуется декодировать зашифрованное с помощью MD5 значение хеша.
Удобнее всего использовать специализированные ресурсы, предоставляющие возможность сделать это online:
- md5.web-max.ca – данный сервис обладает простым и понятным интерфейсом. Для получения декодированного значения нужно ввести хеш и заполнить поле проверочной капчи:
- md5decrypter.com – аналогичный сервис;
- msurf.ru – данный ресурс имеет простой русскоязычный интерфейс. Его функционал позволяет не только расшифровывать значения хеш-кодов, но и создавать их:
Если происмотреться к значениям декодинга, отображенных на показонном выше рисунке, то становится понятно, что процесс расшифровки почти не дает результатов. Эти ресурсы представляют собой одну или несколько объединенных между собой баз данных, в которые занесены расшифровки самых простых слов.
При этом данные декодирования хеша MD5 даже такой распространенной части пароля как «админ» нашлись лишь в одной базе. Поэтому хеши паролей, состоящих из более сложных и длинных комбинаций символов, практически невозможно расшифровать.
Создание хеша MD5 является односторонним процессом. Поэтому не подразумевает обратного декодирования первоначального значения.
Этот стандарт кодирования является одним из самых распространенных методов защиты данных не только в прикладном, но и в веб-программировании. Поэтому не будет лишним обезопасить свой md5 hash от намеренного взлома.
Основным способом, гарантирующим безопасность хеша вашего пароля, является использование «соли». Он основан на добавлении к паролю нескольких случайных символов и последующем хешировании результата.
Во многих языках программирования для этого используются специальные классы и функции. Не являются исключением из правил и серверные языки программирования.
Создать хеш-код MD5 в php можно с помощью нескольких функций:
- md5() – в качестве одного из параметров принимает значение «соли»;
- crypt() – в отличие от предыдущей эта функция полностью автоматизирует весь процесс, в том числе и генерирование значения соли.
Ее синтаксис:
string crypt ( string $str [, string $salt ] )
Пример использования:
$hash = crypt('password')
При использовании функции md5() в PHP для задания значения соли используют методы генерации случайных чисел. Например, rand():
<?php
$pass = 'admin';
function salt() {
$s = '';
$length = rand(7,12); // длина соли
for($i=0; $i<$length; $i++) {
$s .= chr(rand(33,126));//случайный символ из таблицы ASCII
}
return $s;
}
echo md5(md5($pass).salt());
?>
Кроме применения «соли» было разработано еще несколько методов защиты хеша MD5:
- MD5 (Unix) – заданное первоначальное значение проходит цикл хеширования около 1000 раз;
- MD5 (HMAC) – данный метод основан на использовании в хешировании специального ключа;
- MD5 (Base64) – полученный хеш еще раз кодируются с помощью алгоритма Base64.
В статье приведены лишь начальные сведения об обеспечении безопасности хеша, полученного с помощью этого алгоритма. Самым простым и эффективным из них является использование уникального значения «соли», которая позволяет существенно «насолить» злоумышленнику и «подсластить» жизнь владельцу взламываемого пароля.
There are many examples to do this, but some of them are not equivalent because some of them explicitly or implicitly include the newline, and some others do not.
I would like to clearly specify which of the popular methods includes the newline and which are not.
Here are some examples along to calculating the md5 hash WITHOUT trailing newline (CORRECT):
Using a file with text:
$ echo -n "test" > test.txt
$ wc test.txt
0 1 4 test.txt
$ md5sum test.txt
098f6bcd4621d373cade4e832627b4f6 test.txt
Note: -n in echo means: “do not output the trailing newline”.
Using echo with -n inline:
$ echo -n "test" | md5sum
098f6bcd4621d373cade4e832627b4f6 -
Using printf:
$ printf "%s" "test" | md5sum
098f6bcd4621d373cade4e832627b4f6 -
Using only md5sum command:
(Let’s write md5sum, press Enter then write string test and then press double combination Ctrl+d)
$ md5sum
test098f6bcd4621d373cade4e832627b4f6 -
Using md5sum - command:
(Let’s write md5sum -, press Enter then write string test and then press double combination Ctrl+d)
$ md5sum -
test098f6bcd4621d373cade4e832627b4f6 -
Here are some examples along to calculating the md5 hash WITH trailing newline (SO NOT CORRECT):
Using a file with text:
$ echo "test" > test_n.txt
$ wc test_n.txt
1 1 5 test_n.txt
$ md5sum test_n.txt
d8e8fca2dc0f896fd7cb4cb0031ba249 test_n.txt
Using echo WITHOUT -n inline:
echo "test" | md5sum
d8e8fca2dc0f896fd7cb4cb0031ba249 -
Using here strings:
$ md5sum <<< "test"
d8e8fca2dc0f896fd7cb4cb0031ba249 -
Using only md5sum command but with Enter key after writing the text:
(Let’s write md5sum, press Enter then write string test and then press agaien Enter and once combination Ctrl+d)
$ md5sum
test
d8e8fca2dc0f896fd7cb4cb0031ba249 -
Using md5sum - command but with Enter key after writing the text:
(Let’s write md5sum -, press Enter then write string test and then press agaien Enter and once combination Ctrl+d)
$ md5sum -
test
d8e8fca2dc0f896fd7cb4cb0031ba249 -
Много на просторах интернета, в том числе на хабре, написано о различный хэш-функциях, однако, в данном топике я дам свой взгляд на алгоритм и реализацию MD5.
Что такое хэш-функция и чем её едят?
Хэш-функция предназначена для свертки входного массива любого размера в битовую строку, для MD5 длина выходной строки равна 128 битам. Для чего это нужно? К примеру у вас есть два массива, а вам необходимо быстро сравнить их на равенство, то хэш-функция может сделать это за вас, если у двух массивов хэши разные, то массивы гарантировано разные, а в случае равенства хэшей — массивы скорее всего равны.
Однако чаще всего хэш-функции используются для проверки уникальности пароля, файла, строки и тд. К примеру, скачивая файл из интернета, вы часто видите рядом с ним строку вида b10a8db164e0754105b7a99be72e3fe5 — это и есть хэш, прогнав этот файл через алгоритм MD5 вы получите такую строку, и, если хэши равны, можно с большой вероятностью утверждать что этот файл действительно подлинный (конечно с некоторыми оговорками, о которых расскажу далее).
Конкретнее о MD5
Не буду углубляться в историю создания, об этом можно почитать в википедии, однако отмечу что алгоритм был создан профессором Р. Риверстом в 1991 году на основе алгоритма md4. Описан этот алгоритм в RFC 1321
Алгоритм состоит из пяти шагов:
1)Append Padding Bits
В исходную строку дописывают единичный байт 0х80, а затем дописывают нулевые биты, до тех пор, пока длина сообщения не будет сравнима с 448 по модулю 512. То есть дописываем нули до тех пор, пока длина нового сообщения не будет равна [длина] = (512*N+448),
где N — любое натуральное число, такое, что это выражение будет наиболее близко к длине блока.
2)Append Length
Далее в сообщение дописывается 64-битное представление длины исходного сообщения.
3)Initialize MD Buffer
На этом шаге инициализируется буффер
word A: 01 23 45 67
word B: 89 ab cd ef
word C: fe dc ba 98
word D: 76 54 32 10
Как можно заметить буффер состоит из четырех констант, предназначенный для сбора хэша.
4)Process Message in 16-Word Blocks
На четвертом шаге в первую очередь определяется 4 вспомогательные логические функции, которые преобразуют входные 32-битные слова, в, как ни странно, в 32-битные выходные.
F(X,Y,Z) = XY v not(X) Z
G(X,Y,Z) = XZ v Y not(Z)
H(X,Y,Z) = X xor Y xor Z
I(X,Y,Z) = Y xor (X v not(Z))
Также на этом шаге реализуется так называемый «белый шум» — усиление алгоритма, состоящее 64 элементного массива, содержащего псевдослучайные числа, зависимые от синуса числа i:
T[i]=4,294,967,296*abs(sin(i))
Далее начинается «магия». Копируем каждый 16-битный блок в массив X[16] и производим манипуляции:
AA = A
BB = B
CC = C
DD = D
Затем происходят «чудесные» преобразования-раунды, которых всего будет 4. Каждый раунд состоит из 16 элементарных преобразований, которые в общем виде можно представить в виде [abcd k s i], которое, в свою очередь, можно представить как A = B + ((A + F(B,C,D) + X[k] + T[i]) <<< s), где
A, B, C, D — регистры
F(B,C,D) — одна из логических функций
X[k] — k-тый элемент 16-битного блока.
T[i] — i-тый элемент таблицы «белого шума»
<<< s — операция циклического сдвига на s позиций влево.
Приводить все раунды не имеет смысла, все их можно посмотреть тут
Ну и в конце суммируем результаты вычислений:
A = A + AA
B = B + BB
C = C + CC
D = D + DD
5) Output
Выводя побайтово буффер ABCD начиная с A и заканчивая D получим наш хэш.
Надежность
Существует мнение что взломать хэш MD5 невозможно, однако это неправда, существует множество программ подбирающих исходное слово на основе хэша. Абсолютное большинство из них осуществляет перебор по словарю, однако существуют такие методы как RainbowCrack, он основан на генерировании множества хэшей из набора символов, чтобы по получившейся базе производить поиск хэша.
Также у MD5, как у любой хэш-функции, существует такое понятие как коллизии — это получение одинаковых хэшей для разных исходных строк. В 1996 году Ганс Доббертин нашёл псевдоколлизии в MD5, используя определённый инициализирующий буффер (ABCD). Также в 2004 году китайские исследователи Ван Сяоюнь, Фен Дэнгуо, Лай Сюэцзя и Юй Хунбо объявили об обнаруженной ими уязвимости в алгоритме, позволяющей за небольшое время (1 час на кластере IBM p690) находить коллизии. Однако в 2006 году чешский исследователь Властимил Клима опубликовал алгоритм, позволяющий находить коллизии на обычном компьютере с любым начальным вектором (A,B,C,D) при помощи метода, названного им «туннелирование».
Прилагаю собственный пример реализации функции на C#:
md5.rar
Содержание
- Вычисление хэша от строки
- Вычисление хэша от файла
MD5 хэш (Message Digest 5) – это 128 битный алгоритм вычисления хэша от сообщения произвольной длины. Чаще всего хэш вычисляется от строки (для проверки паролей) и от файла (для контроля его целостности).
Следует сразу же заметить, что хранение паролей в виде md5-хэшей в настоящее время считается небезопасным, т.к. md5-хэш довольно сильно подвержен коллизиям. Коллизией называется ситуация, когда у двух исходных сообщений хэши равны. То есть для успешного прохождения проверки пароля, сохраняемого в виде md5-хэша, вам даже не обязательно знать именно этот пароль. Достаточно знать пароль, имеющий такой же хэш. Более того, хэши от простых паролей можно напрямую искать в Google.
Алгоритм хэширования MD5 является частью стандартной библиотеки Java, поэтому вычислить хэш от строки (например, от пароля) достаточно легко.
public String getMd5Hash(String source) {
try {
var md = MessageDigest.getInstance(“MD5”);
md.update(source.getBytes());
byte[] digest = md.digest();
return bytesToHex(digest);
} catch (NoSuchAlgorithmException e) {
throw new RuntimeException(e);
}
}
Тут мы используем стандартный класс MessageDigest, который по имени алгоритма возвращает его реализацию. Если алгоритм по имени не найден, то метод getInstance() кидает исключение NoSuchAlgorithmException. Поскольку мы передаём в него константу «MD5», то точно знаем, что такой ошибки не возникнет. Поэтому обрачиваем это проверяемое исключение в RuntimeException, которое является непроверяемым, чтобы не «портить» сигнатуру метода.
Затем преобразуем исходную строку, от которой требуется посчитать хэш, в массив байт. Затем передаём этот массив в метод update(). В результате он возвращает хэш также в виде массива байт. Для удобства отображения массива байт в виде строки, напишем вспомогательный метод bytesToHex().
private String bytesToHex(byte[] bytes) {
var builder = new StringBuilder();
for (var b : bytes) {
builder.append(String.format(“%02x”, b & 0xff));
}
return builder.toString();
}
Тут мы каждый байт преобразуем в строку, выполняя побитовое объединение этого байта с байтом 0xff. Во избежания создания лишних экземпляров строк, конкатенацию результата делаем с помощью StringBuilder, который в конце преобразуем в строку.
Байты в виде строки представляются в шестнадцатеричной (hexadecimal) системе счисления, поэтому содержат цифры от 0 до 9 и буквы от a до f.
Теперь вычислим хэш:
public static void main(String[] args) {
var example = new PasswordExample();
var hash = example.getMd5Hash(“P@$$w0rd”);
System.out.println(hash); // c53e479b03b3220d3d56da88c4cace20
}
Если вы используете Spring, то всё то же самое можно сделать в одну строчку с помощью метода DigestUtils.md5DigestAsHex().
Для контроля целостности файла можно вычислить его хэш, а затем сравнить с заранее известным. Вычислить хэш можно следующим образом:
public String getMd5HashForFile(String filename) throws IOException {
try {
var md = MessageDigest.getInstance(“MD5”);
var buffer = new byte[8192];
try (var is = Files.newInputStream(Paths.get(filename))) {
int read;
while ((read = is.read(buffer)) > 0) {
md.update(buffer, 0, read);
}
}
byte[] digest = md.digest();
return bytesToHex(digest);
} catch (NoSuchAlgorithmException e) {
throw new RuntimeException(e);
}
}
Для чтения файла создаём InputStream в конструкции try-with-resources, которая автоматически закроет этот поток по завершению работы с ним. Сам поток получаем с помощью метода Files.newInputStream(). Затем в цикле считываем данные в созданный нами буфер – массив байт фиксированного размера. На каждой итерации вызываем метод update() для вычисления нового хэша на основе данных из буфера и прошлого значения хэша. Затем аналогично предыдущему примеру получаем значение хэша в виде массива байт и выводим его в виде строки.
Теперь передав в метод полный путь до проверяемого файла вы можете быстро вычислить его хэш. Если у вас Linux, то для проверки значения хэша можете использовать утилиту md5sum.
| MD5 | |
|---|---|
| Создан | 1991 г. |
| Опубликован | апрель 1992 г. |
| Предшественник | MD4 |
| Преемник | SHA-2 |
| Стандарты | RFC 1321 |
| Размер хеша | 128 бит |
| Число раундов | 64 |
| Тип | хеш-функция |
MD5 (англ. Message Digest 5) — 128-битный алгоритм хеширования, разработанный профессором Рональдом Л. Ривестом из Массачусетского технологического института (Massachusetts Institute of Technology, MIT) в 1991 году. Предназначен для создания «отпечатков» или дайджестов сообщения произвольной длины и последующей проверки их подлинности. Широко применялся для проверки целостности информации и хранения хешей паролей.
История[править | править код]
MD5 — один из серии алгоритмов по построению дайджеста сообщения, разработанный профессором Рональдом Л. Ривестом из Массачусетского технологического института. Был разработан в 1991 году как более надёжный вариант предыдущего алгоритма MD4[1]. Описан в RFC 1321[2]. Позже Гансом Доббертином были найдены недостатки алгоритма MD4.
В 1993 году Берт ден Бур (Bert den Boer) и Антон Босселарс (Antoon Bosselaers) показали, что в алгоритме возможны псевдоколлизии, когда разным инициализирующим векторам соответствуют одинаковые дайджесты для входного сообщения[3].
В 1996 году Ганс Доббертин (Hans Dobbertin) объявил о коллизии в алгоритме[4], и уже в то время было предложено использовать другие алгоритмы хеширования, такие как Whirlpool, SHA-1 или RIPEMD-160.
Из-за небольшого размера хеша в 128 бит можно рассматривать birthday-атаки. В марте 2004 года был запущен проект MD5CRK с целью обнаружения уязвимостей алгоритма, при помощи birthday-атаки. Проект MD5CRK закончился 17 августа 2004 года, когда Ван Сяоюнь (Wang Xiaoyun), Фэн Дэнго (Feng Dengguo), Лай Сюэцзя (Lai Xuejia) и Юй Хунбо (Yu Hongbo) обнаружили уязвимости в алгоритме[5].
1 марта 2005 года Арьен Ленстра, Ван Сяоюнь и Бенне де Вегер продемонстрировали построение двух документов X.509 с различными открытыми ключами и одинаковым хешем MD5[6].
18 марта 2006 года исследователь Властимил Клима (Vlastimil Klima) опубликовал алгоритм, который может найти коллизии за одну минуту на обычном компьютере, метод получил название «туннелирование»[7].
В конце 2008 года US-CERT призвал разработчиков программного обеспечения, владельцев веб-сайтов и пользователей прекратить использовать MD5 в любых целях, так как исследования продемонстрировали ненадёжность этого алгоритма[8].
24 декабря 2010 года Тао Се (Tao Xie) и Фэн Дэнго (Feng Dengguo) впервые представили коллизию сообщений длиной в один блок (512 бит)[9].
Ранее коллизии были найдены для сообщений длиной в два блока и более. Позднее Марк Стивенс (Marc Stevens) повторил успех, опубликовав блоки с одинаковым хешем MD5, а также алгоритм для получения таких коллизий[10].
В 2011 году был опубликован информационный документ RFC 6151. Он признаёт алгоритм хеширования MD5[2] небезопасным для некоторых целей и рекомендует отказаться от его использования в пользу SHA-2.
Алгоритм MD5[править | править код]
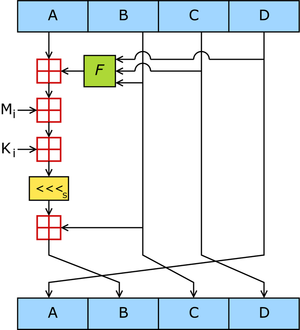
Схема работы алгоритма MD5. F — нелинейная функция. Mi обозначает 32-битный блок входного сообщения, а Ki — 32-битную константу. <<<s обозначает циклический сдвиг влево на s бит. 
На вход алгоритма поступает входной поток данных, хеш которого необходимо найти. Длина сообщения измеряется в битах и может быть любой (в том числе нулевой). Запишем длину сообщения в L. Это число целое и неотрицательное. Кратность каким-либо числам необязательна. После поступления данных идёт процесс подготовки потока к вычислениям.
Ниже приведены 5 шагов алгоритма[2]:
Шаг 1. Выравнивание потока[править | править код]
Сначала к концу потока дописывают единичный бит.
Затем добавляют некоторое число нулевых бит такое, чтобы новая длина потока 

Выравнивание происходит в любом случае, даже если длина исходного потока уже сравнима с 448.
Шаг 2. Добавление длины сообщения[править | править код]
В конец сообщения дописывают 64-битное представление длины данных (количество бит в сообщении) до выравнивания. Сначала записывают младшие 4 байта, затем старшие. Если длина превосходит 

Шаг 3. Инициализация буфера[править | править код]
Для вычислений инициализируются четыре переменные размером по 32 бита, начальные значения которых задаются шестнадцатеричными числами (порядок байтов little-endian):
А = 01 23 45 67; // 67452301h В = 89 AB CD EF; // EFCDAB89h С = FE DC BA 98; // 98BADCFEh D = 76 54 32 10. // 10325476h
В этих переменных будут храниться результаты промежуточных вычислений. Начальное состояние ABCD называется инициализирующим вектором.
Шаг 4. Вычисление в цикле[править | править код]
Определим функции и константы, которые понадобятся нам для вычислений.
- Для каждого раунда потребуется своя функция. Введём функции от трёх параметров — слов, результатом также будет слово:
- 1-й этап:
,
- 2-й этап:
,
- 3-й этап:
,
- 4-й этап:
,
- где
побитовые логические операции XOR, AND, OR и NOT соответственно.
Заносим в блок данных элемент n из массива 512-битных блоков. Сохраняются значения A, B, C и D, оставшиеся после операций над предыдущими блоками (или их начальные значения, если блок первый).
- AA = A
- BB = B
- CC = C
- DD = D
Этап 1
/* [abcd k s i] a = b + ((a + F(b,c,d) + X[k] + T[i]) <<< s). */ [ABCD 0 7 1][DABC 1 12 2][CDAB 2 17 3][BCDA 3 22 4] [ABCD 4 7 5][DABC 5 12 6][CDAB 6 17 7][BCDA 7 22 8] [ABCD 8 7 9][DABC 9 12 10][CDAB 10 17 11][BCDA 11 22 12] [ABCD 12 7 13][DABC 13 12 14][CDAB 14 17 15][BCDA 15 22 16]
Этап 2
/* [abcd k s i] a = b + ((a + G(b,c,d) + X[k] + T[i]) <<< s). */ [ABCD 1 5 17][DABC 6 9 18][CDAB 11 14 19][BCDA 0 20 20] [ABCD 5 5 21][DABC 10 9 22][CDAB 15 14 23][BCDA 4 20 24] [ABCD 9 5 25][DABC 14 9 26][CDAB 3 14 27][BCDA 8 20 28] [ABCD 13 5 29][DABC 2 9 30][CDAB 7 14 31][BCDA 12 20 32]
Этап 3
/* [abcd k s i] a = b + ((a + H(b,c,d) + X[k] + T[i]) <<< s). */ [ABCD 5 4 33][DABC 8 11 34][CDAB 11 16 35][BCDA 14 23 36] [ABCD 1 4 37][DABC 4 11 38][CDAB 7 16 39][BCDA 10 23 40] [ABCD 13 4 41][DABC 0 11 42][CDAB 3 16 43][BCDA 6 23 44] [ABCD 9 4 45][DABC 12 11 46][CDAB 15 16 47][BCDA 2 23 48]
Этап 4
/* [abcd k s i] a = b + ((a + I(b,c,d) + X[k] + T[i]) <<< s). */ [ABCD 0 6 49][DABC 7 10 50][CDAB 14 15 51][BCDA 5 21 52] [ABCD 12 6 53][DABC 3 10 54][CDAB 10 15 55][BCDA 1 21 56] [ABCD 8 6 57][DABC 15 10 58][CDAB 6 15 59][BCDA 13 21 60] [ABCD 4 6 61][DABC 11 10 62][CDAB 2 15 63][BCDA 9 21 64]
Суммируем с результатом предыдущего цикла:
A = AA + A B = BB + B C = CC + C D = DD + D
После окончания цикла необходимо проверить, есть ли ещё блоки для вычислений. Если да, то переходим к следующему элементу массива (n + 1) и повторяем цикл.
Шаг 5. Результат вычислений[править | править код]
Результат вычислений находится в буфере ABCD, это и есть хеш. Если выводить побайтово, начиная с младшего байта A и заканчивая старшим байтом D, то мы получим MD5-хеш.
1, 0, 15, 34, 17, 18…
Псевдокод[править | править код]
// Все переменные — 32-битные беззнаковые целые. Все сложения выполняются по модулю 2^32. var int s[64], K[64] var int i // s обозначает величины сдвигов для каждой операции: s[ 0..15] := { 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22 } s[16..31] := { 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20 } s[32..47] := { 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23 } s[48..63] := { 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21 } // Определяем таблицу констант следующим образом for i from 0 to 63 do K[i] := floor(2^32 × abs (sin(i + 1))) end for // (Или просто используем заранее подсчитанные значения): K[ 0.. 3] := { 0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee } K[ 4.. 7] := { 0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501 } K[ 8..11] := { 0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be } K[12..15] := { 0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821 } K[16..19] := { 0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa } K[20..23] := { 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8 } K[24..27] := { 0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed } K[28..31] := { 0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a } K[32..35] := { 0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c } K[36..39] := { 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70 } K[40..43] := { 0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05 } K[44..47] := { 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665 } K[48..51] := { 0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039 } K[52..55] := { 0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1 } K[56..59] := { 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1 } K[60..63] := { 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391 } // Инициализация переменных: var int a0 := 0x67452301 // A var int b0 := 0xefcdab89 // B var int c0 := 0x98badcfe // C var int d0 := 0x10325476 // D // Подготовка: добавляем бит "1" в конец сообщения. append "1" bit to message // Заметка: входные байты представлены строкой из бит, // причем первый бит — старший (big-endian). // Подготовка: дописываем нулевые биты, пока длина сообщения не станет сравнима с 448 по модулю 512 append "0" bit until message length in bits ≡ 448 (mod 512) // Дописываем остаток от деления изначальной длины сообщения на 2^64 append original length in bits mod 2^64 to message // Разбиваем подготовленное сообщение на 512-битные "куски": for each 512-bit chunk of padded message do // и работаем с каждым по отдельности break chunk into sixteen 32-bit words M[j], 0 ≤ j ≤ 15 // разбиваем "кусок" на 16 блоков по 32 бита // Инициализируем переменные для текущего куска: var int A := a0 var int B := b0 var int C := c0 var int D := d0 // Основные операции: for i from 0 to 63 do var int F, g if 0 ≤ i ≤ 15 then F := (B and C) or ((not B) and D) g := i else if 16 ≤ i ≤ 31 then F := (D and B) or ((not D) and C) g := (5×i + 1) mod 16 else if 32 ≤ i ≤ 47 then F := B xor C xor D g := (3×i + 5) mod 16 else if 48 ≤ i ≤ 63 then F := C xor (B or (not D)) g := (7×i) mod 16 F := F + A + K[i] + M[g] // M[g] — 32 битный блок A := D D := C C := B B := B + (F <<< s[i]) // Выполняем битовый сдвиг end for // Прибавляем результат текущего "куска" к общему результату a0 := a0 + A b0 := b0 + B c0 := c0 + C d0 := d0 + D end for var char digest[16] := a0 append b0 append c0 append d0 // (Результат в формате little-endian)
Сравнение MD5 и MD4[править | править код]
Алгоритм MD5 происходит от MD4. В новый алгоритм добавили ещё один раунд, теперь их стало 4 вместо 3 в MD4. Добавили новую константу для того, чтобы свести к минимуму влияние входного сообщения, в каждом раунде на каждом шаге и каждый раз константа разная, она суммируется с результатом F и блоком данных. Изменилась функция 

Примеры MD5-хешей[править | править код]
Хеш содержит 128 бит (16 байт) и обычно представляется как последовательность из 32 шестнадцатеричных цифр[12].
Несколько примеров хеша:
MD5("md5") = 1BC29B36F623BA82AAF6724FD3B16718
Даже небольшое изменение входного сообщения (в нашем случае на один бит: ASCII символ «5» с кодом 3516 = 0001101012 заменяется на символ «4» с кодом 3416 = 0001101002) приводит к полному изменению хеша. Такое свойство алгоритма называется лавинным эффектом.
MD5("md4") = C93D3BF7A7C4AFE94B64E30C2CE39F4F
Пример MD5-хеша для «нулевой» строки:
MD5("") = D41D8CD98F00B204E9800998ECF8427E
Криптоанализ[править | править код]
На данный момент существуют несколько видов «взлома» хешей MD5 — подбора сообщения с заданным хешем[13][14]:
- Перебор по словарю
- Brute-force
- RainbowCrack
- Коллизия хеш-функции
При этом методы перебора по словарю и brute-force могут использоваться для взлома хеша других хеш-функций (с небольшими изменениями алгоритма). В отличие от них, RainbowCrack требует предварительной подготовки радужных таблиц, которые создаются для заранее определённой хеш-функции. Поиск коллизий специфичен для каждого алгоритма.
Атаки переборного типа[править | править код]
Для полного перебора или перебора по словарю можно использовать программы PasswordsPro[15], MD5BFCPF[16], John the Ripper. Для перебора по словарю существуют готовые словари[17]. Основным недостатком такого типа атак является высокая вычислительная сложность.
RainbowCrack — ещё один метод нахождения прообраза хеша из заданного множества. Он основан на генерации цепочек хешей, чтобы по получившейся базе вести поиск заданного хеша. Хотя создание радужных таблиц занимает много времени и памяти, последующий взлом производится очень быстро. Основная идея данного метода — достижение компромисса между временем поиска по таблице и занимаемой памятью.
Коллизии MD5[править | править код]
Коллизия хеш-функции — это получение одинакового значения функции для разных сообщений и идентичного начального буфера. В отличие от коллизий, псевдоколлизии определяются как равные значения хеша для разных значений начального буфера, причём сами сообщения могут совпадать или различаться. В MD5 вопрос коллизий не решается[14].
В 1996 году Ганс Доббертин нашёл псевдоколлизии в MD5, используя определённые инициализирующие векторы, отличные от стандартных. Оказалось, что можно для известного сообщения построить второе, такое, что оно будет иметь такой же хеш, как и исходное. C точки зрения математики это означает: MD5(IV,L1) = MD5(IV,L2), где IV — начальное значение буфера, а L1 и L2 — различные сообщения. Например, если взять начальное значение буфера[4]:
A = 0x12AC2375 В = 0x3B341042 C = 0x5F62B97C D = 0x4BA763E
и задать входное сообщение
| AA1DDABE | D97ABFF5 | BBF0E1C1 | 32774244 |
| 1006363E | 7218209D | E01C136D | 9DA64D0E |
| 98A1FB19 | 1FAE44B0 | 236BB992 | 6B7A779B |
| 1326ED65 | D93E0972 | D458C868 | 6B72746A |
то, добавляя число 
Тогда MD5(IV, L1) = MD5(IV, L2) = BF90E670752AF92B9CE4E3E1B12CF8DE.
В 2004 году китайские исследователи Ван Сяоюнь (Wang Xiaoyun), Фэн Дэнго (Feng Dengguo), Лай Сюэцзя (Lai Xuejia) и Юй Хунбо (Yu Hongbo) объявили об обнаруженной ими уязвимости в алгоритме, позволяющей за небольшое время (1 час на кластере IBM p690) находить коллизии[5][18].
В 2005 году Ван Сяоюнь и Юй Хунбо из университета Шаньдуна в Китае опубликовали алгоритм, который может найти две различные последовательности в 128 байт, которые дают одинаковый MD5-хеш. Одна из таких пар (различающиеся разряды выделены):
| d131dd02c5e6eec4693d9a0698aff95c | 2fcab58712467eab4004583eb8fb7f89 |
| 55ad340609f4b30283e488832571415a | 085125e8f7cdc99fd91dbdf280373c5b |
| d8823e3156348f5bae6dacd436c919c6 | dd53e2b487da03fd02396306d248cda0 |
| e99f33420f577ee8ce54b67080a80d1e | c69821bcb6a8839396f9652b6ff72a70 |
и
| d131dd02c5e6eec4693d9a0698aff95c | 2fcab50712467eab4004583eb8fb7f89 |
| 55ad340609f4b30283e4888325f1415a | 085125e8f7cdc99fd91dbd7280373c5b |
| d8823e3156348f5bae6dacd436c919c6 | dd53e23487da03fd02396306d248cda0 |
| e99f33420f577ee8ce54b67080280d1e | c69821bcb6a8839396f965ab6ff72a70 |
Каждый из этих блоков даёт MD5-хеш, равный 79054025255fb1a26e4bc422aef54eb4[19].
В 2006 году чешский исследователь Властимил Клима опубликовал алгоритм, позволяющий находить коллизии на обычном компьютере с любым начальным вектором (A,B,C,D) при помощи метода, названного им «туннелирование»[7][20].
Алгоритм MD5 использует итерационный метод Меркла — Дамгора, поэтому становится возможным построение коллизий с одинаковым, заранее выбранным префиксом. Аналогично, коллизии получаются при добавлении одинакового суффикса к двум различным префиксам, имеющим одинаковый хеш. В 2009 году было показано, что для любых двух заранее выбранных префиксов можно найти специальные суффиксы, с которыми сообщения будут иметь одинаковое значение хеша. Сложность такой атаки составляет всего 239 операций подсчёта хеша[21].
Метод Ван Сяоюня и Юй Хунбо[править | править код]
Метод Ван Сяоюня[en] и Юй Хунбо использует тот факт, что MD5 построен на итерационном методе Меркла — Дамгора. Поданный на вход файл сначала дополняется, так чтобы его длина была кратна 64 байтам, после этого он делится на блоки по 64 байта каждый 









Метод позволяет для заданного инициализирующего вектора найти две пары 


Эта атака является разновидностью дифференциальной атаки, которая, в отличие от других атак этого типа, использует целочисленное вычитание, а не XOR в качестве меры разности. При поиске коллизий используется метод модификации сообщений: сначала выбирается произвольное сообщение 












Применение этой атаки к MD4 позволяет найти коллизию меньше чем за секунду. Она также применима к другим хеш-функциям, таким как RIPEMD и HAVAL[5].
Примеры использования[править | править код]
Ранее считалось, что MD5 позволяет получать относительно надёжный идентификатор для блока данных. На данный момент данная хеш-функция не рекомендуется к использованию, так как существуют способы нахождения коллизий с приемлемой вычислительной сложностью[14][22].
Свойство уникальности хеша широко применяется в разных областях[23]. Приведенные примеры относятся и к другим криптографическим хеш-функциям.
С помощью MD5 проверяли целостность и подлинность скачанных файлов — так, некоторые программы поставляются вместе со значением контрольной суммы. Например, пакеты для инсталляции свободного ПО[24].
MD5 использовался для хеширования паролей. В системе UNIX каждый пользователь имеет свой пароль и его знает только пользователь. Для защиты паролей используется хеширование. Предполагалось, что получить настоящий пароль можно только полным перебором. При появлении UNIX единственным способом хеширования был DES (Data Encryption Standard), но им могли пользоваться только жители США, потому что исходные коды DES нельзя было вывозить из страны. Во FreeBSD решили эту проблему. Пользователи США могли использовать библиотеку DES, а остальные пользователи имеют метод, разрешённый для экспорта. Поэтому в FreeBSD стали использовать MD5 по умолчанию.[25]. Некоторые Linux-системы также используют MD5 для хранения паролей[26].
Многие системы используют базы данных для аутентификации пользователей и существует несколько способов хранения паролей[27]:
- Пароли хранятся как есть. При взломе такой базы все пароли станут известны.
- Хранятся только хеши паролей. Найти пароли можно, используя заранее подготовленные таблицы хешей. Такие таблицы составляются из хешей простых или популярных паролей.
- К каждому паролю добавляется несколько случайных символов (их называют «соль») и результат хешируется. Полученный хеш вместе с «солью» сохраняются в открытом виде. Найти пароль с помощью таблиц таким методом не получится.
Существует несколько надстроек над MD5.
- MD5 (HMAC) — Keyed-Hashing for Message Authentication (хеширование с ключом для аутентификации сообщения) — алгоритм позволяет хешировать входное сообщение L с некоторым ключом K, такое хеширование позволяет аутентифицировать подпись[28].
- MD5 (Base64) — здесь полученный MD5-хеш кодируется алгоритмом Base64.
- MD5 (Unix) — алгоритм вызывает тысячу раз стандартный MD5 для усложнения процесса. Также известен как MD5crypt[29].
Примечания[править | править код]
- ↑ What are MD2, MD4, and MD5? (англ.) (недоступная ссылка — история). RSA Laboratories (2000). Дата обращения: 11 июля 2009. Архивировано 23 августа 2011 года.
- ↑ 1 2 3 4 Rivest, 1992.
- ↑ Boer, Bosselaers, 1993.
- ↑ 1 2 Hans Dobbertin. The Status of MD5 After a Recent Attack. Дата обращения: 22 октября 2015.
- ↑ 1 2 3 Xiaoyun Wang, Dengguo Feng, Xuejia Lai, Hongbo Yu. Collisions for Hash Functions MD4, MD5, HAVAL-128 and RIPEMD (англ.) (недоступная ссылка — история) (17 августа 2004). Дата обращения: 19 ноября 2008. Архивировано 23 августа 2011 года.
- ↑ Arjen Lenstra, Xiaoyun Wang and Benne de Weger. Colliding X.509 Certificates. eprint.iacr.org (1 марта 2005). Дата обращения: 4 декабря 2015. Архивировано 4 марта 2016 года.
- ↑ 1 2 Vlastimil Kli’ma. Tunnels in Hash Functions: MD5 Collisions Within a Minute (англ.) (недоступная ссылка — история) (17 апреля 2006). Дата обращения: 19 ноября 2008. Архивировано 23 августа 2011 года.
- ↑ CERT Vulnerability Note VU#836068 (англ.). kb.cert.org (30 декабря 2008). Дата обращения: 10 октября 2015. Архивировано 26 июля 2011 года.
- ↑ Tao Xie, Dengguo Feng. Construct MD5 Collisions Using Just A Single Block Of Message (PDF) (16 декабря 2010). Дата обращения: 16 октября 2015. Архивировано 14 мая 2017 года.
- ↑ Marc Stevens – Research – Single-block collision attack on MD5. Marc-stevens.nl (2012). Дата обращения: 16 октября 2015. Архивировано 15 мая 2017 года.
- ↑ Иными словами, в таблице представлены по 32 бита после десятичной запятой от значений функции sin, где аргумент n в радианах.
- ↑ Detection Of Phishing Websites And Secure Transactions. Anna University (2012). Дата обращения: 20 октября 2015. Архивировано из оригинала 4 марта 2016 года.
- ↑ Ah Kioon, Wang, Deb Das, 2013.
- ↑ 1 2 3 Updated Security Considerations for the MD5 Message-Digest and the HMAC-MD5 Algorithms. Internet Engineering Task Force (март 2011). Дата обращения: 23 октября 2015. Архивировано 15 июня 2017 года.
- ↑ PasswordsPro. InsidePro Software. — Программа для восстановления паролей к хешам различных типов. Дата обращения: 19 ноября 2008. Архивировано из оригинала 27 августа 2011 года.
- ↑ Проект MD5 на сайте SourceForge.net
- ↑ CERIAS — Security Archive. Center for Education and Research in Information Assurance and Security (июнь 2000). Дата обращения: 19 ноября 2008. Архивировано 7 декабря 2008 года.
- ↑ Philip Hawkes, Michael Paddon, Gregory G. Rose. Musings on the Wang et al. MD5 Collision (англ.) (недоступная ссылка — история) (13 октября 2004). Дата обращения: 19 ноября 2008. Архивировано 23 августа 2011 года.
- ↑ 1 2 Wang, Yu, 2005.
- ↑ Vlastimil Klima. MD5 collisions (англ.) (недоступная ссылка — история). Дата обращения: 19 ноября 2008. Архивировано 23 августа 2011 года.
- ↑ Stevens, Lenstra, Weger, 2012.
- ↑ Marc Stevens, Arjen Lenstra and Benne de Weger. Vulnerability of software integrity and code signing applications to chosen-prefix collisions for MD5 (30 ноября 2007). Дата обращения: 25 октября 2015. Архивировано 13 декабря 2007 года.
- ↑ Ilya Mironov. Hash functions: Theory, attacks, and applications. Microsoft Research (14 ноября 2005). Дата обращения: 13 ноября 2015. Архивировано 4 марта 2016 года.
- ↑ Turnbull J. [ ] // // [ Hardening Linux] (англ.) — 1 — Apress, 2005. — . — P. 57—58.
- ↑ Bill Swingle. Руководство FreeBSD (DES, MD5 и шифрование) (2006). Дата обращения: 20 ноября 2008. Архивировано из оригинала 17 сентября 2009 года.
- ↑ Vicki Stanfield, Roderick W. Smith. Linux System Administration (Craig Hunt Linux Library). — 2. — Sybex, 2002. — С. 479—483. — 656 с. — ISBN 978-0782141382.
- ↑ Hossein Bidgoli. The Internet Encyclopedia, Volume 3. — 1. — Wiley, 2003. — С. 3—4. — 908 с. — ISBN 978-0471222019.
- ↑ Krawczyk, Hugo, Canetti, Ran, Bellare, Mihir. HMAC: Keyed-Hashing for Message Authentication. tools.ietf.org. Дата обращения: 5 декабря 2015. Архивировано 15 апреля 2021 года.
- ↑ Steven Alexander. password protection for modern operating systems. USENIX 2004 (июнь 2004). Дата обращения: 5 декабря 2015. Архивировано 8 декабря 2015 года.
Литература[править | править код]
- Rivest R. [ ] // // [ The MD5 Message-Digest Algorithm] (англ.) — IETF, 1992. — . — P. . — 21 p. — doi:10.17487/RFC1321
- Boer B. d., Bosselaers A. [ ] // // [ Collisions for the compression function of MD5] (англ.) // Advances in Cryptology — EUROCRYPT ’93: Workshop on the Theory and Application of Cryptographic Techniques Lofthus, Norway, May 23–27, 1993 Proceedings / T. Helleseth — 1 — Berlin: Springer Berlin Heidelberg, 1993. — . — P. . — 465 p. — ISBN 978-3-540-57600-6 — doi:10.1007/3-540-48285-7_26
- Xiaoyun W., Yu H. [ ] // // [ How to Break MD5 and Other Hash Functions] (англ.) // Advances in Cryptology — EUROCRYPT 2005: 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, May 22-26, 2005. Proceedings / R. Cramer — Springer Science+Business Media, 2005. — . — P. . — 578 p. — ISBN 978-3-540-25910-7 — doi:10.1007/11426639_2
- Stevens M., Lenstra A. K., Weger B. d. [ ] // // [ Chosen-prefix collisions for MD5 and applications] (англ.) // International Journal of Applied Cryptography — Inderscience Publishers, 2012. — . — P. . — ISSN 1753-0563; 1753-0571 — doi:10.1504/IJACT.2012.048084
- Ah Kioon, Mary Cindy, Wang Z., Deb Das S. [ ] // // [ Security Analysis of MD5 Algorithm in Password Storage] (англ.) // Applied Mechanics and Materials — 2013. — . — P. . — ISSN 1660-9336; 1662-7482; 2297-8941 — doi:10.4028/WWW.SCIENTIFIC.NET/AMM.347-350.2706