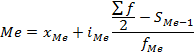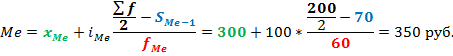У этого термина существуют и другие значения, см. Медиана.
Медиа́на (от лат. mediāna «середина») или набора чисел — число, которое находится в середине этого набора, если его упорядочить по возрастанию, то есть такое число, что половина из элементов набора не меньше него, а другая половина не больше. Другое равносильное определение[1]: медиана набора чисел — это число, сумма расстояний (или, если более строго, модулей) от которого до всех чисел из набора минимальна. Это определение естественным образом обобщается на многомерные наборы данных и называется 1-медианой.
Например, медианой набора {11, 9, 3, 5, 5} является число 5, так как оно стоит в середине этого набора после его упорядочивания: {3, 5, 5, 9, 11}. Если в выборке чётное число элементов, медиана может быть не определена однозначно: тогда для числовых данных чаще всего используют полусумму двух соседних значений (то есть медиану набора {1, 3, 5, 7} принимают равной 4), подробнее см. ниже.
В математической статистике медиана может использоваться как одна из характеристик выборки или совокупности чисел.
Также определяется медиана случайной величины: в этом случае оно определяется как число, которое делит пополам распределение. Грубо говоря, медианой случайной величины является такое число, что вероятность получить значение случайной величины справа от него равна вероятности получить значение слева от него (и они обе равны 1/2), — более точное определение дано ниже.
Можно также сказать, что медиана является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.
Свойства медианы для случайных величин[править | править код]
Если распределение непрерывно, то медиана является одним из решений уравнения
,
где 
— функция распределения случайной величины 
, связанная с плотностью распределения 
как
- .
Если распределение является непрерывной строго возрастающей функцией, то решение уравнения однозначно. Если распределение имеет разрывы, то медиана может совпадать с минимальным или максимальным (крайним) возможным значением случайной величины, что противоречит «геометрическому» пониманию этого термина.
Медиана является важной характеристикой распределения случайной величины и, так же как математическое ожидание, может быть использована для центрирования распределения. Поскольку оценки медианы более робастны, её оценивание может быть более предпочтительным для распределений с т. н. тяжёлыми хвостами. Однако о преимуществах оценивания медианы по сравнению с математическим ожиданием можно говорить только в случае, если эти характеристики у распределения совпадают, в частности, для симметричных функций плотности распределения вероятностей.
Медиана определяется для всех распределений, а в случае неоднозначности, естественным образом доопределяется, в то время как математическое ожидание может быть не определено (например, у распределения Коши).
Пример использования[править | править код]
Рассмотрим финансовое состояние 19 малоимущих, у каждого из каких есть только 5 ₽, и одного миллионера, у которого буквально 1 млн ₽. Тогда в сумме у них получается 1 000 095 ₽. Если деньги равными долями разделить на 20 человек, получится 50 004,75 ₽. Это будет среднее арифметическое значение суммы денег, которая была у всех 20 человек в этой комнате.
Медиана же будет равна 5 ₽ (сумма «расстояния» от этой величины до состояния каждого из рассматриваемых людей минимальна). Это можно интерпретировать следующим образом: «разделив» всех рассматриваемых людей на две равные группы по 10 человек, мы получаем, что в первой группе у каждого не больше 5 ₽, во второй же — не меньше 5 ₽.
Из этого примера получается, что в качестве «серединного» состояния, грубо говоря, корректнее всего использовать именно медиану, а вот среднее арифметическое, наоборот, значительно превышает сумму наличных, имеющуюся у случайного человека из выборки.
Различны изменения в динамике и у средней арифметической с медианой, например в вышеприведённом примере, если у миллионера станет 1,5 млн. ₽ (+50 %), а у остальных станет 6 ₽ (+20 %), то средняя арифметическая выборки станет равна 75 005,70 ₽, то есть как бы у всех повысились равномерно на 50 %, при этом медиана станет равной 6 ₽ (+20 %).
Неуникальность значения[править | править код]
Если имеется чётное количество случаев и два средних значения различаются, то медианой, по определению, может служить любое число между ними (например, в выборке {1, 3, 5, 7} медианой может служить любое число из интервала (3,5)). На практике в этом случае чаще всего используют среднее арифметическое двух средних значений (в примере выше это число (3+5)/2=4). Для выборок с чётным числом элементов можно также ввести понятие «нижней медианы» (элемент с номером n/2 в упорядоченном ряду из 
элементов; в примере выше это число 3) и «верхней медианы» (элемент с номером (n+2)/2; в примере выше это число 5)[2]. Эти понятия определены не только для числовых данных, но и для любой порядковой шкалы.
См. также[править | править код]
- Мода — значение во множестве наблюдений, которое встречается наиболее часто.
- Среднее арифметическое набора чисел — число, сумма квадратов расстояний от которого до всех чисел из набора минимальна[3].
Примечания[править | править код]
- ↑ Сущность медианы. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.
- ↑ Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест Рональ Л., Штайн, Клиффорд. Алгоритмы. Построение и анализ. — 2-е издание. — М.: Издательский дом «Вильямс», 2005. — С. 240. — 1296 с.
- ↑ Почему это равносильные определения среднего арифметического.
Литература[править | править код]
- Медиана // Маниковский — Меотида. — М. : Большая российская энциклопедия, 2012. — С. 479—480. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 19). — ISBN 978-5-85270-353-8.
- Медиана // Большая российская энциклопедия [Электронный ресурс]. — 2017.
В статистических исследованиях довольно широко применяются средние величины. Их нахождение позволяет выявить типичное значение признака исследуемой совокупности. Например, типичный уровень доходов покупателей или возраст большинства клиентов компании. При этом вычисление, к примеру, среднего арифметического не всегда уместно.
Представим такую ситуацию: мы опросили 10 человек на предмет их уровня доходов. У 9-х доходы оказались примерно одинаковыми и составили 10 тыс. руб. Что касается 10-ого опрошенного, то оказалось, что его доход равняется 410 тыс. руб. в месяц. Если мы вычислим простое среднее арифметическое, то типичный доход будет равняться 50 тыс. руб.! Но это явно не так. В таких ситуациях более объективную и правдоподобную картину дает вычисление моды или медианы, которые относятся к структурным средним показателям.
Понятие медианы
Медиана (Me) — значение признака в исследуемом ряду величин, которое делит этот ряд на две равные части.
То есть половина (50%) всех значений в исследуемом ряду будет меньше медианы, а другая половина — больше ее. Поэтому медиану еще называют 50-й перцентиль или квантиль 0,5.
Формула для расчета медианы
Если значений немного, то медиану можно определить «на глазок». Для этого достаточно расположить все значения в порядке возрастания и найти середину.
Если число случаев четное и в центре ряда находятся два разных числа, то медианой будет среднее между ними (даже если такого значения нет в самом ряду исследуемых случаев). Например, в ряду 1 2 3 4 5 6, медианой будет 3,5.
Для нахождения медианы в более сложных случаях (по интервальным рядам) используется специальная формула:
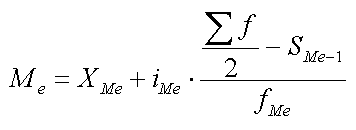
где: Me — медиана;
Xme — нижняя граница медианного интервала (того интервала, накопленная частота которого превышает полусумму всех частот);
ime — величина медианного интервала;
f — частота (сколько раз в ряду встречается то или иное значение);
Sme-1 — сумма частот интервалов предшествующих медианному интервалу;
fme — число значений в медианном интервале (его частота).
Пример вычисления медианы
Был проведен опрос среди покупателей с целью выяснить их типичный возраст. По результатам опроса было установлено, что: 25 покупателей имеют возраст до 20 лет; 32 покупателя — 20-40 лет; 18 покупателей — 40-60 лет; 15 покупателей — свыше 60 лет. Найдем медиану.
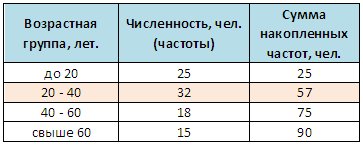
Сначала находим медианный интервал. Для этого вычисляем сумму частот: 25 + 32 + 18 + 15 = 90. Половина этой суммы — 45. Это соответствует возрастной группе 20-40 лет (т. к. полученная полусумма частот — 45, и накопленная частота 1-й группы меньше ее, а 3-ей — больше). Тогда нижняя граница медианного интервала — 20 (лет), а величина медианного интервала — 20 (40 лет за вычетом 20). Сумма частот интервалов предшествующих медианному интервалу — 25. Число значений в медианном интервале — 32 (количество покупателей в возрасте 20-40 лет).
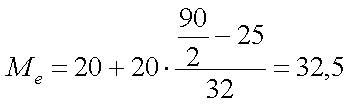
Расчетное значение медианы — 32,5. Округив его, получим средний возраст покупателя — 33 года.
Область применения медианы
При вычислении типичного признака неоднородных рядов, имеющих «выбросы» — значения во много раз отличающиеся от других значений ряда.
Особенности медианы
- Медиана обладает высокой робастностью, то есть нечувствительностью к неоднородностям и ошибкам выборки;
- Сумма разностей между членами ряда выборки и медианой меньше, чем сумма этих разностей с любой другой величиной. В том числе с арифметическим средним.
Источники
- Медиана // Википедия. URL: http://ru.wikipedia.org/wiki/Медиана_(статистика) (дата обращения: 23.10.2013)
- Минашкин В. Г. и др. Курс лекций по теории статистики. – М.: МЭСИ, 2001.
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.
Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.Р. Медиана // Сайт преподавателя экономики. [2013]. URL: https://galyautdinov.ru/post/mediana (дата обращения: 18.05.2023).
Загрузить PDF
Загрузить PDF
Среднее значение, медиана и мода — значения, которые часто используются в статистике и математике. Эти значения найти довольно легко, но их легко и перепутать. Мы расскажем, что они из себя представляют и как их найти.
-
1
Сложите все числа, которые вам даны. Допустим, вам даны числа 2, 3 и 4. Сложим их: 2 + 3 + 4 = 9.
-
2
Сосчитайте количество чисел. У нас есть три цифры.
-
3
Разделите сумму чисел на их количество. Берем 9, делим на 3. 9/3 = 3. Среднее значение в данном случае равно 3. Помните, что не всегда получается целое число.
Реклама
-
1
Запишите все числа, которые вам даны, в порядке возрастания. Например, нам даны числа: 4, 2, 8, 1, 15. Запишите их от меньшего к большему, вот так: 1, 2, 4, 8, 15.
-
2
Найдите два средних числа. Мы расскажем, как это сделать, если у вас имеется четное количество чисел, и как это сделать, если количество чисел нечетное:
- Если у вас нечетное количество чисел, вычеркните левое крайнее число, затем правое крайнее число и так далее. Один оставшийся номер и будет искомой медианой. Если вам дан ряд чисел 4, 7, 8, 11, 21, тогда 8 — медиана, так как 8 стоит посередине.
- Если у вас четное количество чисел, вычеркните по одному числу с каждой стороны, пока у вас не останется два числа посередине. Сложите их и разделите на два. Это и есть значение медианы. Если вам дан ряд чисел 1, 2, 5, 3, 7, 10, то два средних числа — это 5 и 3. Сложим 5 и 3, получим 8, разделим на два, получим 4. Это и есть медиана.
Реклама
-
1
Запишите все числа в ряд. Например, вам даны числа 2, 4, 5, 5, 4 и 5. Запишите их в порядке возрастания.
-
2
Найдите число, которое чаще всего встречается. В данном случае это 5. Если два числа встречаются одинаково часто, то этот ряд двухвершинный или бимодальный, а если больше — то мультимодальный.
Реклама
Советы
- Вам будет легче найти моду и медиану, если вы запишете числа в порядке возрастания.
Реклама
Об этой статье
Эту страницу просматривали 353 377 раз.
Была ли эта статья полезной?
Центральную тенденцию данных можно рассматривать не только, как значение с нулевым суммарным отклонением (среднее арифметическое) или максимальную частоту (мода), но и как некоторую отметку (значение в совокупности), делящую ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Половина исходных данных меньше этой отметки, а половина – больше. Это и есть медиана.
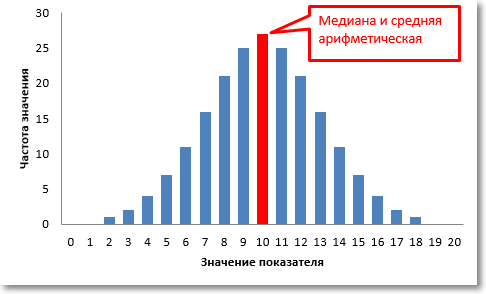
Итак, медиана в статистике – это уровень показателя, который делит набор данных на две равные половины. Значения в одной половине меньше, а в другой больше медианы. В качестве примера обратимся к набору нормально распределенных случайных чисел.
Очевидно, что при симметричном распределении середина, делящая совокупность пополам, будет находиться в самом центре – там же, где средняя арифметическая (и мода). Это, так сказать, идеальная ситуация, когда мода, медиана и средняя арифметическая совпадают и все их свойства приходятся на одну точку – максимальная частота, деление пополам, нулевая сумма отклонений – все в одном месте. Однако, жизнь не так симметрична, как нормальное распределение.
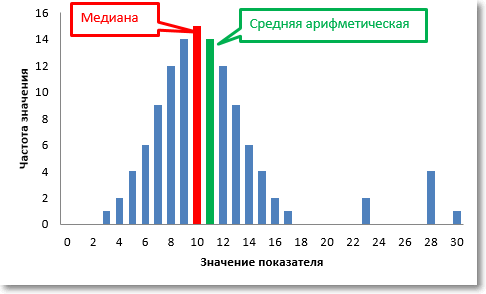
Допустим, мы имеем дело с техническими замерами отклонений от ожидаемой величины чего-нибудь (содержания элементов, расстояния, уровня, массы и т.д. и т.п.). Если все ОК, то отклонения, скорее всего, будут распределены по закону, близкому к нормальному, примерно, как на рисунке выше. Но если в процессе присутствует важный и неконтролируемый фактор, то могут появиться аномальные значения, которые в значительной мере повлияют на среднюю арифметическую, но при этом почти не затронут медиану.
Медиана выборки – это альтернатива средней арифметической, т.к. она устойчива к аномальным отклонениям (выбросам).
Математическим свойством медианы является то, что сумма абсолютных (по модулю) отклонений от медианного значения дает минимально возможное значение, если сравнивать с отклонениями от любой другой величины. Даже меньше, чем от средней арифметической, о как! Данный факт находит свое применение, например, при решении транспортных задач, когда нужно рассчитать место строительства объектов около дороги таким образом, чтобы суммарная длина рейсов до него из разных мест была минимальной (остановки, заправки, склады и т.д. и т.п.).
Формула медианы
Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.
Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:
где
№Me – номер значения, соответствующего медиане,
N – количество значений в совокупности данных.
Тогда медиана обозначается, как
Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:
В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу.
Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.
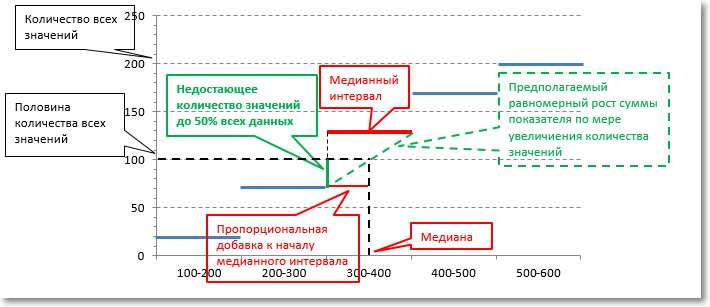
Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.
Обратимся к наглядной схеме.
Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:
где xMe — нижняя граница медианного интервала;
iMe — ширина медианного интервала;
∑f/2 — количество всех значений, деленное на 2 (два);
S(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;
fMe — число наблюдений в медианном интервале.
Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%.
Для примера рассчитаем медиану по следующим данным.
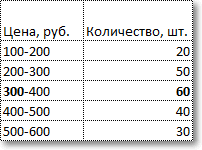
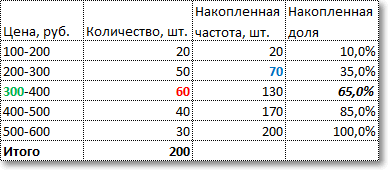
Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.
По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.
То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.
Расчет медианы в Excel
Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.
Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:
а) 11;
б) 5;
в) 10;
г) 5, 10, 11.
Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.
Ниже видеоролик о том, как рассчитать медиану в Excel.
Поделиться в социальных сетях:
План урока:
Понятие выборки и генеральной совокупности
Среднее арифметическое выборки
Упорядоченный ряд и таблица частот
Размах выборки
Мода выборки
Медиана выборки
Ошибки в статистике
Понятие выборки и генеральной совокупности
Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.
В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:
Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.
В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.
В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.
Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.
Среднее арифметическое выборки
Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.
Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=
= 349:20 = 17,45.
Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.
Упорядоченный ряд и таблица частот
В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Такую запись называют упорядоченным рядом данных.
Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:
При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,
2+3+1+1+2+2+1+2+2+1+1+2 = 20.
С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:
(12•2+13•3+14•1+15•1+16•2+17•2+18•1+19•2+20•2+21•1+24•1+25•2):20 =
(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.
Размах выборки
Следующий важная характеристика ряда данных – это размах выборки.
Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:
25 – 12 = 13,
так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.
Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:
(8+9+9+8+9):5 = 43:5 = 8,6;
(7+10+10+6+10):5 = 43:5 = 8,6.
Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен
9 – 8 = 1,
в то время как размах выборки второго спортсмена равен
10 – 6 = 4.
Размах выборки может быть очень важен в метеорологии. Например, в Алма-Ате и Амстердаме средняя температура в течение года почти одинакова и составляет 10°С. Однако в Алма-Ате в январе и феврале иногда фиксируются температуры ниже -30°С, в то время как в Амстердаме за всю историю наблюдений она никогда не падала ниже -20°С.
Мода выборки
Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.
В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде
1, 2, 3, 3, 3, 4, 5, 5, 5
варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:
6, 6, 7, 7, 8, 8.
Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.
Медиана выборки
Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:
Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:
Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна
(17+17):2 = 34:2 = 17.
Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.
Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):
39, 41, 67, 36, 60, 58, 46, 44, 39, 69.
Найдем среднее арифметическое, размах, моду и медиану для этого ряда.
Решение. Сначала перепишем ряд в упорядоченном виде:
36, 39, 39, 41, 44, 46, 58, 60, 67, 69.
Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):
(36+39+39+41+44+46+58+60+67+69):10 =
= 499:10 = 49,9 кг.
Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен
69 – 36 = 33 кг.
В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.
В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно
(44+46):2 = 90:2 = 45 кг.
Поэтому и медиана ряда будет равна 45 кг.
Ошибки в статистике
Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?
Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.
В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.
Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.
При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.
Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.
