Мода и медиана функции плотности распределения f(x)
Задача 5. Плотность распределения вероятностей случайной величины Х имеет вид

1. Найти:
а) параметр распределения С (в виде дроби);
а) математическое ожидание M(X);
б) дисперсию D(X) и среднее квадратическое отклонение σ(Х);
в) функцию распределения F(x) случайной величины X;
г) моду M0;
д) медиану Me;
е) вероятность осуществления неравенств ![]() и
и ![]() .
.
2. Построить графики функций f(x) и F(x). Изобразить на графике функции f(x) найденные характеристики и вероятности.
Решение находим с помощью калькулятора.
Случайная величина Х задана плотностью распределения f(x):
0, x ≤ 0
2•A(8/5-x), 0 < x < 8/5
0, x ≥ 8/5
Найдем параметр A из условия:


или
64/25*A-1 = 0
Откуда,
A = 25/64
Поскольку находили квадрат A, то ![]()
а) Математическое ожидание.


б) Дисперсия.


= -25/128•(8/5)4+5/12•(8/5)3 – (-25/128•04+5/12•03) – (8/15)2 = 32/225
Среднеквадратическое отклонение.
![]()
в) Функция распределения F(x) случайной величины X.



г) Мода M0.
Модой M0(X) называют то возможное значение X, при котором плотность распределения имеет максимум.
Построим график функции плотности распределения.

Как видим, максимум функции соответствует x = 0.
Mo( 0) = 2•25/64(8/5-0) = 5/4
д) Медиана Me.
Медианой Me(X) называют то возможное значение X, при котором ордината f(x) делит пополам площадь, ограниченную кривой распределения.
Необходимо найти такое x, при котором функция распределения равна ½.


Решая уравнение:
![]()
получаем:
![]()
![]()
Поскольку функция ограничена на интервале (0; 1,6), то искомое значение x = 0,46.
![]()
Построим график функции распределения.

е) Вероятность осуществления неравенств ![]() и
и ![]() .
.
![]()
![]()
Перейти к онлайн решению своей задачи
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике – мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
Мода и медиана случайных величин
Основными числовыми
характеристиками случайных величин
являются математическое ожидание,
дисперсия и среднее квадратическое
отклонение. Однако часто возникает
потребность и в некоторых других числовых
характеристиках. Две из них, обозначенные
в заголовке, и будут далее определены.
Пусть Х
– дискретная случайная величина. Модой
этой с.в. (обозначается d(X)
) называется такое ее возможное значение,
которое имеет наибольшую вероятность.
Пример.
Пусть дискретная
с.в. Х
задана законом распределения
|
Х |
1 |
2 |
3 |
4 |
5 |
6 |
|
Р |
0.1 |
0.1 |
0.3 |
0.1 |
0.3 |
0.1 |
Тогда ее мода
принимает 2 значения: d(Х)=3
и d(Х)=5.
Пусть Х
– непрерывная
случайная величина с плотностью
вероятности f(х).
Модой
этой с.в. называется точка максимума ее
плотности вероятности. Эта точка
максимума функции f(x)
находится обычными методами с
использованием производной.
Пример.
Дана плотность вероятности н.с.в. :
 .
.
Найти значение
параметра а
и моду этой случайной величины.
Пусть Х
– непрерывная случайная величина.
Медианой
с.в. Х
(обозначается h(X)
) называется такое число h,
которое делит всю числовую прямую на 2
промежутка (−∞,
h)
и
[h,+∞),
в которые с.в. Х
попадает с равной вероятностью. Таким
образом, если медиана h(X)=h,
то выполняется
равенство
P(X
< h)=P(X
≥ h)
=![]() .
.
Вспоминая, что
вероятность P(X
< h)
по определению функции распределения
есть значение этой функции в точке h,
получаем, что значение h
медианы h(X)
удовлетворяет уравнению
![]() .
.
Если же у н.с.в.
задана не функция распределения F(x),
а плотность вероятности f(x),
то вспоминая выражение функции
распределения через плотность вероятности
![]()
, получим, что значение h
медианы удовлетворяет уравнению
![]() .
.
Медиана h(X)
непрерывной с.в. Х
ищется из одного из выписанных выше
уравнений (в зависимости от того, что
задано: F(x)
или f(x)
). Для дискретных случайных величин
медиана не определяется.
Пример.
Найти медиану н.с.в. Х,
заданной своей функцией распределения
 .
.
Ответ: h(X)=1.5
.
Некоторые важные законы распределения случайных величин
Среди различных
законов распределения случайных величин
некоторые встречаются в приложениях
наиболее часто. Поэтому для них получены
формулы расчета их числовых характеристик:
математического ожидания, дисперсии,
моды, медианы и ряда других. Рассмотрим
некоторые из таких законов распределения.
Биномиальный закон распределения
Среди законов
распределения дискретных
случайных величин наиболее распространенным
является биномиальное распределение,
с которым мы уже встречались при
рассмотрении так называемой схемы
Бернулли (число появлений некоторого
события в серии независимых испытаний).
Дискретная случайная
величина Х
распределена по биномиальному
закону, если
она принимает значения 0,
1, 2, … , n
с вероятностями р0
, р1
, … ,
рn,
которые вычисляются по формуле
![]() ,
,
где параметр
распределения р
заключен между нулем и единицей 0
≤ р ≤ 1 , а
q=1−p
. Таким образом, д.с.в Х,
распределенная по биномиальному закону,
имеет следующий закон распределения:
|
Х |
0 |
1 |
2 |
… |
n |
|
Р |
|
|
|
… |
|
Как уже говорилось,
по биномиальному закону распределено
число успехов в схеме Бернулли. Пусть
производится n
независимых
испытаний, в каждом из которых некоторое
событие А
может появиться с одной и той же
вероятностью р.
Рассмотрим с.в. Х
– число появлений события А
во всех n
испытаниях (то, что ранее называли число
успехов). Тогда с.в. Х
распределена по биномиальному закону.
Мы уже находили формулы для математического
ожидания этой случайной величины,
которые и являются формулами математического
ожидания и дисперсии произвольной
случайной величины, распределенной по
схеме Бернулли:
![]() ,
,
![]() .
.
Найдем моду d(X)
биномиально распределенной случайной
величины Х,
т.е. наивероятнейшее
число успехов в схеме Бернулли.
По определению моды d(X)=k,
если вероятность
![]()
наибольшая среди всех вероятностей р0
, р1
, … , рn
. Найдем
такое число k
(это целое
неотрицательное число). При таком k
вероятность pk
должна быть не меньше соседних с ней
вероятностей: pk−1
≤ pk
≤ pk+1
. Подставив вместо каждой вероятности
соответствующую формулу, получим, что
число k
должно удовлетворять двойному неравенству:
![]() .
.
Если расписать
формулы для числа сочетаний и провести
простые преобразования, можно получить,
что левое неравенство дает k
≤ (n+1)∙p,
а правое k
≥ (n+1)∙p
−1. Таким
образом, число k
удовлетворяет двойному неравенству
(n+1)∙p
−1 ≤ k
≤ (n+1)∙p
, т.е. принадлежит отрезку
[(n+1)∙p
−1, (n+1)∙p]
. Поскольку длина этого отрезка, очевидно,
равна 1,
то в него может попасть либо одно, либо
2 целых числа. Если число (n+1)∙p
целое, то в
отрезке [(n+1)∙p
−1, (n+1)∙p]
имеется 2 целых числа, лежащих на концах
отрезка. Если же число (n+1)∙p
не целое, то
в этом отрезке есть только одно целое
число.
Таким образом,
если число (n+1)∙p
целое, то
мода биномиально распределенной
случайной величины Х
принимает 2 соседних значения : d(X)=(n+1)∙p
−1 и
d(X)=(n+1)∙p
. Если же число (n+1)∙p
не целое,
то мода биномиально распределенной
случайной величины Х
одно значение
d(X)=k,
где k
есть
единственное целое число, удовлетворяющее
неравенству
(n+1)∙p
−1 ≤ k
≤ (n+1)∙p
. Если вспомнить, что запись [a]
означает взятие целой части от числа
а,
то в этом случае можно записать
d(X)=[(n+1)∙p]
.
Пример.
Кубик подбрасывается 100 раз. Каково
наивероятнейшее число выпадений
шестерки?
Пример.
Вероятность попадания стрелком в цель
равна 0.7 . Найти наивероятнейшее число
попаданий в цель при 30 выстрелах.
Пример.
Вероятность изготовления бракованной
детали на станке равна 0.06 . Каково
наивероятнейшее число бракованных
деталей в партии из 200 деталей, выточенных
на этом станке?
Пример.
Банк выдал 7 кредитов. Известно, что в
среднем не возвращается 2 кредита из
10. Найти среднее число невозвращенных
кредитов.
Соседние файлы в папке методичка
- #
- #
- #
Для нахождения моды и медианы случайной величины необходимы хорошие умения интегрировать и знания следующего теоретического материала. Модой 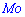 дискретной случайной величины
дискретной случайной величины 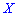 называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины
называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины 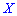 , которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
, которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
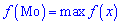
В зависимости от вида функции 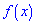 случайная величина
случайная величина 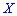 может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой  случайной величины
случайной величины 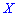 называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
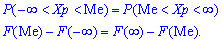
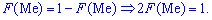
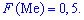
Графически мода и медиана изображенные на рисунке
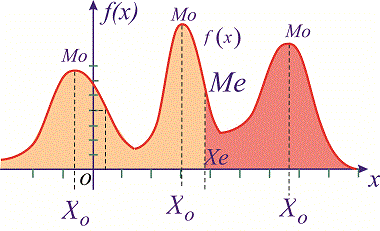
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью. Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин 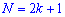 то медиана равна средней величине
то медиана равна средней величине
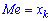
в случае четного количества 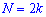 полусумме средних величин
полусумме средних величин
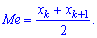
Рассмотрим примеры определения моды и медианы.
Пример 1. В развлекательном центре работник обслуживает четыре дорожки для боулинга. Вероятность того, что какая-то дорожка нуждается в уборке в течение смены является постоянной величиной с вероятностью 85%.
Построить закон распределения вероятностей дискретной случайной величины 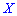 — количество дорожек, которые требуют уборки. Найти моду
— количество дорожек, которые требуют уборки. Найти моду 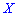 .
.
Решение. Случайной величина может принимать значения
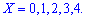
Вероятности появления значений определяем по образующей функцией
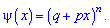
Для заданной задачи входные величины принимают значения
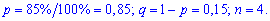
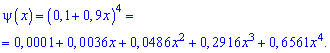
Искомые вероятности входят множителями при степенях аргумента
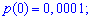
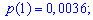
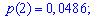
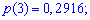
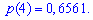
Закон распределения вероятностей запишем в виде таблицы
С таблице определяем моду 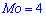 , как значение при максимальной вероятности. Получили одномодальное распределение
, как значение при максимальной вероятности. Получили одномодальное распределение
Пример 2. По заданной плотностью вероятностей
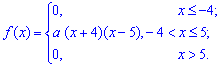
найти параметр  , плотность вероятностей
, плотность вероятностей 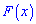 , моду
, моду 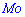 .
.
Решение. Применяя условие нормирования выполняем интегрирование
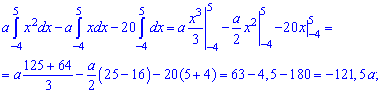
после того определяем параметр
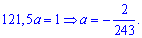
Плотность вероятностей, учитывая найденное значение будет иметь вид
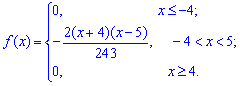
а ее график изображен на рисунке ниже
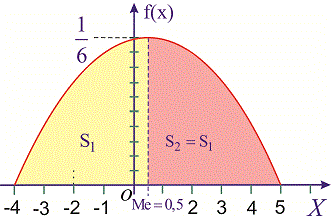
Из графика плотности вероятностей видим, что мода принимает значение 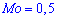 . Определим медиану
. Определим медиану  с помощью функции распределения вероятностей. Ее значение на промежутке
с помощью функции распределения вероятностей. Ее значение на промежутке 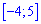 находим интегрированием
находим интегрированием
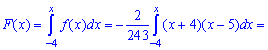
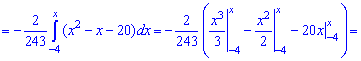
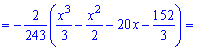
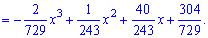
Функция распределения иметь следующий вид
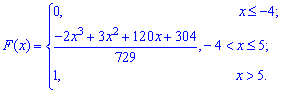
а ее график будет иметь вид
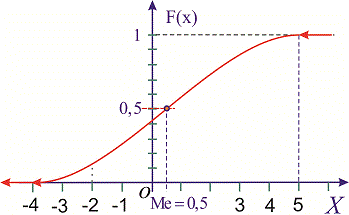
Для определения медианы случайной величины  применяем формулу
применяем формулу
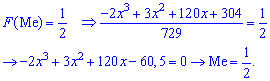
Медиану  можно найти с помощью плотности вероятностей
можно найти с помощью плотности вероятностей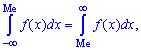
для дискретной случайной величины из промежутка 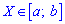
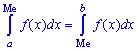
Таким образом медиану  — возможное значение случайной величины
— возможное значение случайной величины 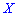 , при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости
, при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости 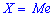 , делит площадь фигуры, ограниченной функцией плотности вероятностей
, делит площадь фигуры, ограниченной функцией плотности вероятностей 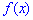 на две равные части.
на две равные части.
——————————-
Задача на определение моды и медианы случайной величины встречаются на практике не так часто, как плотности распределения вероятностей, однако вышеприведенный теоретический материал и решения распространенных примеров помогут Вам находить эти величины без больших затрат времени. При необходимости Вы всегда можете заказать решение задач по теории вероятностей в нас.
$begingroup$
Find the median of the random variable with the probability density function given below. (Round your answer to four decimal places.)
f(x) = 1/x on [1, e]
I do know that I am going to somehow use 1/2 but that is about it.
So for this problem I am not exactly sure where to start. We have had examples in our notes of finding the median but not with an equation like this one. I previously worked out a problem involving this on this website but I cannot figure out how to do this one. If someone could explain to me how to get to the answer it would be greatly appreciated. I know that I have to take the integral at some point but that is about it.
asked Nov 22, 2016 at 1:50
$endgroup$
2
$begingroup$
Solve: $$int_1^x frac1t~dt=frac12$$
answered Nov 22, 2016 at 1:52
$endgroup$
6
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
