Как найти медиану массива java

Sorting the array is unnecessary and inefficient. There’s a variation of the QuickSort (QuickSelect) algorithm which has an average run time of O(n); if you sort first, you’re down to O(n log n). It actually finds the nth smallest item in a list; for a median, you just use n = half the list length. Let’s call it quickNth (list, n).

The concept is that to find the nth smallest, choose a ‘pivot’ value. (Exactly how you choose it isn’t critical; if you know the data will be thoroughly random, you can take the first item on the list.)

Split the original list into three smaller lists:

• One with values smaller than the pivot.
• One with values equal to the pivot.
• And one with values greater than the pivot.

You then have three cases:

1. The “smaller” list has >= n items. In that case, you know that the nth smallest is in that list. Return quickNth(smaller, n).
2. The smaller list has < n items, but the sum of the lengths of the smaller and equal lists have >= n items. In this case, the nth is equal to any item in the “equal” list; you’re done.
3. n is greater than the sum of the lengths of the smaller and equal lists. In that case, you can essentially skip over those two, and adjust n accordingly. Return quickNth(greater, n – length(smaller) – length(equal)).

Done.

If you’re not sure that the data is thoroughly random, you need to be more sophisticated about choosing the pivot. Taking the median of the first value in the list, the last value in the list, and the one midway between the two works pretty well.

If you’re very unlucky with your choice of pivots, and you always choose the smallest or highest value as your pivot, this takes O(n^2) time; that’s bad. But, it’s also very unlikely if you choose your pivot with a decent algorithm.

Sample code:

import java.util.*;

public class Utility {
   /****************
   * @param coll an ArrayList of Comparable objects
   * @return the median of coll
   *****************/
   
   public static <T extends Number> double median(ArrayList<T> coll, Comparator<T> comp) {
      double result;
      int n = coll.size()/2;
      
      if (coll.size() % 2 == 0)  // even number of items; find the middle two and average them
         result = (nth(coll, n-1, comp).doubleValue() + nth(coll, n, comp).doubleValue()) / 2.0;
      else                      // odd number of items; return the one in the middle
         result = nth(coll, n, comp).doubleValue();
         
      return result;
   } // median(coll)
   
   

   /*****************
   * @param coll a collection of Comparable objects
   * @param n  the position of the desired object, using the ordering defined on the list elements
   * @return the nth smallest object
   *******************/
   
   public static <T> T nth(ArrayList<T> coll, int n, Comparator<T> comp) {
      T result, pivot;
      ArrayList<T> underPivot = new ArrayList<>(), overPivot = new ArrayList<>(), equalPivot = new ArrayList<>();
      
      // choosing a pivot is a whole topic in itself.
      // this implementation uses the simple strategy of grabbing something from the middle of the ArrayList.
      
      pivot = coll.get(n/2);
      
      // split coll into 3 lists based on comparison with the pivot
      
      for (T obj : coll) {
         int order = comp.compare(obj, pivot);
         
         if (order < 0)        // obj < pivot
            underPivot.add(obj);
         else if (order > 0)   // obj > pivot
            overPivot.add(obj);
         else                  // obj = pivot
            equalPivot.add(obj);
      } // for each obj in coll
      
      // recurse on the appropriate list
      
      if (n < underPivot.size())
         result = nth(underPivot, n, comp);
      else if (n < underPivot.size() + equalPivot.size()) // equal to pivot; just return it
         result = pivot;
      else  // everything in underPivot and equalPivot is too small.  Adjust n accordingly in the recursion.
         result = nth(overPivot, n - underPivot.size() - equalPivot.size(), comp);
         
      return result;
   } // nth(coll, n)
   
   
   
   public static void main (String[] args) {
      Comparator<Integer> comp = Comparator.naturalOrder();
      Random rnd = new Random();
      
      for (int size = 1; size <= 10; size++) {
         ArrayList<Integer> coll = new ArrayList<>(size);
         for (int i = 0; i < size; i++)
            coll.add(rnd.nextInt(100));
      
         System.out.println("Median of " + coll.toString() + " is " + median(coll, comp));
      } // for a range of possible input sizes
   } // main(args)
} // Utility

Java code To Calculate Median – In this article, we will brief in on the mentioned means to  Finding the middle element in array. The following median code has been written in 4 different ways. If you have any doubts you can leave a comment here.

The source code has written in:

• Using Standard Method
• Using Static Method
• Using Scanner Class
• Using Command Line Arguments
• Using Separate Class

The median of a given group of data is the value which falls in between of the given values. The only difference between Median and Mean is that Mean gives a rough average of the whole data.

Whereas the median will give the exact value which falls in between of the smallest and highest values.

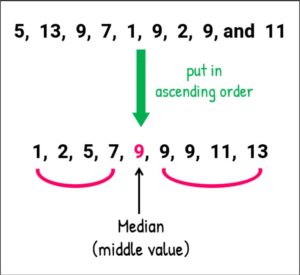
As you can see, in the given order of values, firstly, it has to be arranged in an ascending or descending order. Then, the middle value is noted down.

9 is the middle value of the given set of numbers. Thus, 9 is the median of the group.

Calculate Median Array – Standard Method

For this problem, we first taken the inputs. The inputs are the number of elements or the size of array and the data values which are to be stored in the array (a).

One important thing to be kept in mind is that the data values are to be entered in a sorted order. This is necessary because we need to find the middle element.

After taking the inputs, we need to first check whether the number of elements is odd or even.

• if(n%2==1)
• If the number of elements is odd then, the center-most element is the median.
• m=a[(n+1)/2-1];
• Else, the average of the two middle elements.
• m=(a[n/2-1]+a[n/2])/2;

Output:

Using Static Method

In the case of making use of static method, we split up the code into two parts.

The inputs i.e., the size of array and data values of array in a sorted order, is read using the scanner class.

After reading the inputs, another static method is called to which the inputs are passed as arguments.

This method consists of set of statements to return the mean based on the same logic as discussed above. T

In this, both the main method as well as the static method are written within the same class.

Output1:

Using Scanner Class

In the above example, we had mentioned that, the inputs are taken making use of the scanner class.

Scanner class in Java is that class which reads input at runtime given by the tester/user for any primitive datatype.

So here, we make use of the scanner class to first read an integer number which is considered as the size of array (total number of data values) followed by which we take the data values which could either be integers or decimal value and therefore, we choose double type. It is essential to make sure that, these data values must be taken in sorted order only.

After gathering the inputs, we will find the median of the given data values with the same logic as explained above.

Output:

Using Command Line Arguments

Apart from making use of scanner class to take inputs at runtime, we can also give values along with the run command itself separated by space between each argument.

This method is called the using of command line arguments.

Here, we first give the number of elements (arg[0]) followed by which we give as many arguments having data values as mentioned. These variables are first converted to their respective datatypes using parsing and then stored in the variable.

After acquiring all the inputs the same steps as mentioned in the beginning are followed.

Using Separate Class

To enhance the readability and make things smoother to find any part of the code if we ever require to make modifications in the future, we split the code into different classes.

Here, the class containing main method has all the necessary input operations using the scanner class. This is followed by creating of an object referencing another class (MedianCal).

This separate class (MedianCal) has a constructor which is responsible for performing set of instructions as mentioned above to find the median and store it in a variable of the separate class (MedianCal).

This variable is called in the main method with the help of the object created and printed as output.

Output:

In the code you’ve provided it looks like you’re trying to find the mean not the median. I’ve provided some code below that should help with finding the mean. To find the median you’d need to sort the array, which is a little more complicated.

The short answer is to remove the input=0 line. Assuming that data is a public variable and that sum is a function that sums that public variable your code should work.

The implementation should depend on the context, but I would recommend a static function that takes an array of doubles as the single argument.

public class Median{
   public static void main(String[] args){
      double numbers[] ={1.0, 2.0, 3.0};
      System.out.println(median(numbers));
   }
   public static double median(double[]x){
      double sum = 0;
      for(int i=0;i<x.length;i++){
         sum += x[i];
      }
      return sum/x.length;
   }
}

How to Calculate median in Java? | With Array and List | Programming Blog

Find median of Java Array and List values using 2 ways

What is Median?

Median is mid value of particular data set. This data set must be sorted. 

In simple word, Median is mid value of sorted data.

Median will be middle, if total number of elements is odd or average of middle elements when total number of elements is even.

Example :

So the formula become for our code :

So lets jump on code. We will take elements form user.

Method 1 : Using code logic

In this approach, we does not use any library function for find median.

Example 1 : Find median from Java array

Output :

Example 2 : Find median from Java List

Output :

Method 2 : Using Apache commons library

This problem can also solve by Apache commons Math library. 

org.apache.commons.math3.stat.descriptive.rank.Median package provides solution for evaluate median of array.

We must have to use double array for use this library. lets see how ii works.

Output :

Other articles :

• Java program to check given alphabet is an uppercase or lowercase vowel or not  
• Sort custom object property with null values using Java 8 lambda expression
• Divide and compute Modulo of large number | Print modulo of BigInteger in Java | Convert large String to BigInteger in Java