Задания
Версия для печати и копирования в MS Word
Тип 12 № 4008 

i
На клетчатой бумаге с размером клетки 1 × 1 изображён треугольник ABC. Найдите длину его медианы, выходящей из вершины B.
Спрятать решение
Решение.
Медиана, проведенная из вершины B, будет делить основание AC пополам. Построим медиану BK. Из прямоугольного треугольника по теореме Пифагора находим длину медианы:
Ответ: 10.
Аналоги к заданию № 3929: 4008 4370 5424 … Все
Источники:
ВПР по математике 8 класс 2020 года. Вариант 15;
ВПР по математике 8 класса 2021 года. Вариант 1.
Спрятать решение
·
Прототип задания
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Рассмотрим задачи, в которых требуется по рисунку на клетчатой бумаге найти длину медианы треугольника.
Задачи.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его медианы, проведённой из вершины C.
Решение:
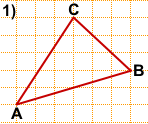 Медиана, проведённая из вершины C, соединяет точку C с серединой противолежащей стороны AB.
Медиана, проведённая из вершины C, соединяет точку C с серединой противолежащей стороны AB.
Следовательно, задачу начинаем с нахождения середины AB.
Как правило, сторона AB в таких задачах изображается не горизонтальным или вертикальным отрезком.
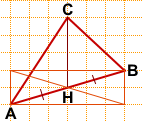 Чтобы найти середину AB, можно построить по клеточкам прямоугольник с диагональю AB и провести его вторую диагональ. По свойству прямоугольника, точка H пересечения диагоналей — середина AB.
Чтобы найти середину AB, можно построить по клеточкам прямоугольник с диагональю AB и провести его вторую диагональ. По свойству прямоугольника, точка H пересечения диагоналей — середина AB.
Длину медианы CH считаем по клеточкам — CH=4.
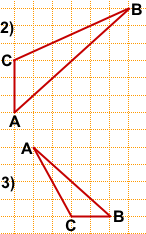
2) Аналогично предыдущей задаче, сначала найдём середину отрезка AB.
Можно достроить прямоугольник с диагональю AB, провести вторую диагональ и отметить точку H пересечения диагоналей.
Длину медианы CH находим по клеточкам:
CH=3.
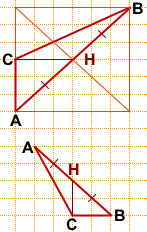
3) Можно найти середину отрезка AB и без дополнительных построений.
Например, можно рассуждать так:
AH=BH как диагонали равных квадратов (со стороной 2 клетки), следовательно, точка H — середина AB, CH — медиана треугольника ABC.
CH=2.
Если медиана треугольника расположена не горизонтально либо вертикально, посчитать её длину по клеточкам не удастся.
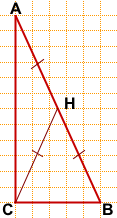 4) В прямоугольном треугольнике длину медианы, проведённой к гипотенузе, можно найти, опираясь на соответствующее свойство.
4) В прямоугольном треугольнике длину медианы, проведённой к гипотенузе, можно найти, опираясь на соответствующее свойство.
То есть для нахождения длины медианы нужно знать гипотенузу.
Длины катетов определяем по клеточкам: AC=12, BC=5.
По теореме Пифагора: AB²=AC²+BC²,
AB²=12²+5²=169, AB=13,
CH= 1/2 AB=6,5.
5) 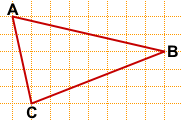 Середину отрезка AB — точку H — найдём как точку пересечения диагоналей прямоугольника с диагональю AB
Середину отрезка AB — точку H — найдём как точку пересечения диагоналей прямоугольника с диагональю AB
(достаточно провести вторую диагональ, прямоугольник можно не строить).
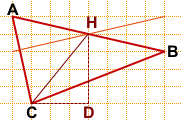 Длину диагонали по клеточкам определить не получится.
Длину диагонали по клеточкам определить не получится.
Достроим прямоугольный треугольник CHD с гипотенузой CH.
CD=3, HD=4.
CH находим по теореме Пифагора (можно также заметить, что CHD — египетский треугольник): CH=5.
На клетчатой бумаге с размером клетки 1 x 1 изображён треугольник АВС. Найдите длину его медианы, проведённой из вершины С.
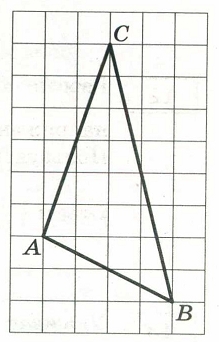
Источник задания: ОГЭ 2021 Математика, И.В. Ященко. 36 вариантов.
Решение:
Медиана из вершины С будет делить противолежащую сторону АВ на две равные части:
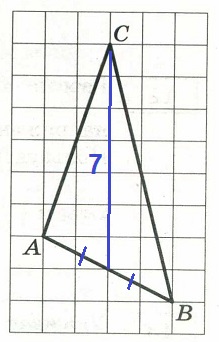
Длинна её равна 7 клеток.
Ответ: 7.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.6 / 5. Количество оценок: 16
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Рубрика Задание 3, Решаем ЕГЭ по математике Комментарии (0)
Задание. На клетчатой бумаге с размером клетки 1 × 1 изображен треугольник АВС. Найдите длину его медианы, проведенной из вершины С.
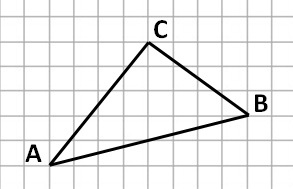
Решение:
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
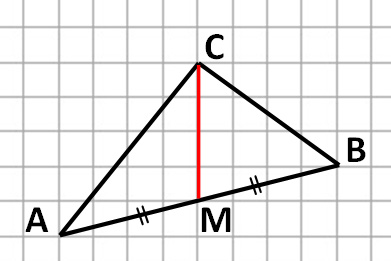
Найдем середину стороны АВ и проведем отрезок СМ. Отрезок СМ – медиана треугольника АВС.
По клеточкам легко найти, что СМ = 4.
Ответ: 4
Понравилось? Нажмите
Чтобы найти длину медианы, выходящей из вершины B, нужно провести медиану из вершины B до середины стороны AC. Обозначим точку середины стороны AC как M. Тогда медиана, выходящая из вершины B, будет проходить через точку M и делить сторону AC пополам.
Чтобы найти координаты точки M, нужно найти среднее арифметическое координат точек A и C по каждой оси. Пусть координаты точки A равны (x₁, y₁), а координаты точки C равны (x₃, y₃). Тогда координаты точки M будут равны ((x₁+x₃)/2, (y₁+y₃)/2).
Зная координаты точки M, можно найти длину медианы, выходящей из вершины B, используя теорему Пифагора. Обозначим длину медианы, выходящей из вершины B, как MB, а длины отрезков AM и MC, как a и b соответственно. Тогда:
MB² = a² + b²
Таким образом, чтобы найти длину медианы, выходящей из вершины B, нужно найти длины отрезков AM и MC, используя формулы расстояния между точками, а затем подставить их в формулу для длины медианы.
Приведу пример нахождения длины медианы на конкретном треугольнике: пусть вершины треугольника АВС имеют координаты (0,0), (4,0) и (2,3) соответственно. Тогда середина стороны AC будет иметь координаты ((0+2)/2, (0+3)/2) = (1,5). Длина отрезка AM будет равна расстоянию между точками (0,0) и (1,5), которое можно найти с помощью формулы расстояния между точками:
a = √((1-0)² + (5-0)²) = √26/2
Аналогично, длина отрезка MC будет равна расстоянию между точками (2,3) и (1,5), которое можно найти также с помощью формулы расстояния между точками:
b = √((2-1)² + (3-5)²) = √5/2
Итак, мы нашли длины сторон треугольника: AB = 6, AC = 8 и BC = 10. Чтобы найти медиану, выходящую из вершины B, нужно найти середину стороны AC (точку M) и соединить её с вершиной B. Так как стороны треугольника параллельны осям координат на клетчатой бумаге, то точка M будет иметь координаты (5, 1). Также заметим, что точка B имеет координаты (3, 3).
Теперь мы можем найти длину медианы BM, используя теорему Пифагора для прямоугольного треугольника MBP, где P – точка пересечения медиан:
BM^2 = MP^2 + BP^2
Найдём длину MP, используя координаты точек M и B:
MP = sqrt((5-3)^2 + (1-3)^2) = sqrt(8)
Найдём длину BP, используя координаты точек B и середины стороны AC:
BP = sqrt((5-3)^2 + (3-1)^2) = sqrt(8)
Таким образом, получаем:
BM^2 = 8 + 8 = 16
BM = 4
Ответ: длина медианы, выходящей из вершины B, равна 4 клеткам.
