Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике – мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
Мода и медиана случайных величин
Основными числовыми
характеристиками случайных величин
являются математическое ожидание,
дисперсия и среднее квадратическое
отклонение. Однако часто возникает
потребность и в некоторых других числовых
характеристиках. Две из них, обозначенные
в заголовке, и будут далее определены.
Пусть Х
– дискретная случайная величина. Модой
этой с.в. (обозначается d(X)
) называется такое ее возможное значение,
которое имеет наибольшую вероятность.
Пример.
Пусть дискретная
с.в. Х
задана законом распределения
|
Х |
1 |
2 |
3 |
4 |
5 |
6 |
|
Р |
0.1 |
0.1 |
0.3 |
0.1 |
0.3 |
0.1 |
Тогда ее мода
принимает 2 значения: d(Х)=3
и d(Х)=5.
Пусть Х
– непрерывная
случайная величина с плотностью
вероятности f(х).
Модой
этой с.в. называется точка максимума ее
плотности вероятности. Эта точка
максимума функции f(x)
находится обычными методами с
использованием производной.
Пример.
Дана плотность вероятности н.с.в. :
 .
.
Найти значение
параметра а
и моду этой случайной величины.
Пусть Х
– непрерывная случайная величина.
Медианой
с.в. Х
(обозначается h(X)
) называется такое число h,
которое делит всю числовую прямую на 2
промежутка (−∞,
h)
и
[h,+∞),
в которые с.в. Х
попадает с равной вероятностью. Таким
образом, если медиана h(X)=h,
то выполняется
равенство
P(X
< h)=P(X
≥ h)
=![]() .
.
Вспоминая, что
вероятность P(X
< h)
по определению функции распределения
есть значение этой функции в точке h,
получаем, что значение h
медианы h(X)
удовлетворяет уравнению
![]() .
.
Если же у н.с.в.
задана не функция распределения F(x),
а плотность вероятности f(x),
то вспоминая выражение функции
распределения через плотность вероятности
![]()
, получим, что значение h
медианы удовлетворяет уравнению
![]() .
.
Медиана h(X)
непрерывной с.в. Х
ищется из одного из выписанных выше
уравнений (в зависимости от того, что
задано: F(x)
или f(x)
). Для дискретных случайных величин
медиана не определяется.
Пример.
Найти медиану н.с.в. Х,
заданной своей функцией распределения
 .
.
Ответ: h(X)=1.5
.
Некоторые важные законы распределения случайных величин
Среди различных
законов распределения случайных величин
некоторые встречаются в приложениях
наиболее часто. Поэтому для них получены
формулы расчета их числовых характеристик:
математического ожидания, дисперсии,
моды, медианы и ряда других. Рассмотрим
некоторые из таких законов распределения.
Биномиальный закон распределения
Среди законов
распределения дискретных
случайных величин наиболее распространенным
является биномиальное распределение,
с которым мы уже встречались при
рассмотрении так называемой схемы
Бернулли (число появлений некоторого
события в серии независимых испытаний).
Дискретная случайная
величина Х
распределена по биномиальному
закону, если
она принимает значения 0,
1, 2, … , n
с вероятностями р0
, р1
, … ,
рn,
которые вычисляются по формуле
![]() ,
,
где параметр
распределения р
заключен между нулем и единицей 0
≤ р ≤ 1 , а
q=1−p
. Таким образом, д.с.в Х,
распределенная по биномиальному закону,
имеет следующий закон распределения:
|
Х |
0 |
1 |
2 |
… |
n |
|
Р |
|
|
|
… |
|
Как уже говорилось,
по биномиальному закону распределено
число успехов в схеме Бернулли. Пусть
производится n
независимых
испытаний, в каждом из которых некоторое
событие А
может появиться с одной и той же
вероятностью р.
Рассмотрим с.в. Х
– число появлений события А
во всех n
испытаниях (то, что ранее называли число
успехов). Тогда с.в. Х
распределена по биномиальному закону.
Мы уже находили формулы для математического
ожидания этой случайной величины,
которые и являются формулами математического
ожидания и дисперсии произвольной
случайной величины, распределенной по
схеме Бернулли:
![]() ,
,
![]() .
.
Найдем моду d(X)
биномиально распределенной случайной
величины Х,
т.е. наивероятнейшее
число успехов в схеме Бернулли.
По определению моды d(X)=k,
если вероятность
![]()
наибольшая среди всех вероятностей р0
, р1
, … , рn
. Найдем
такое число k
(это целое
неотрицательное число). При таком k
вероятность pk
должна быть не меньше соседних с ней
вероятностей: pk−1
≤ pk
≤ pk+1
. Подставив вместо каждой вероятности
соответствующую формулу, получим, что
число k
должно удовлетворять двойному неравенству:
![]() .
.
Если расписать
формулы для числа сочетаний и провести
простые преобразования, можно получить,
что левое неравенство дает k
≤ (n+1)∙p,
а правое k
≥ (n+1)∙p
−1. Таким
образом, число k
удовлетворяет двойному неравенству
(n+1)∙p
−1 ≤ k
≤ (n+1)∙p
, т.е. принадлежит отрезку
[(n+1)∙p
−1, (n+1)∙p]
. Поскольку длина этого отрезка, очевидно,
равна 1,
то в него может попасть либо одно, либо
2 целых числа. Если число (n+1)∙p
целое, то в
отрезке [(n+1)∙p
−1, (n+1)∙p]
имеется 2 целых числа, лежащих на концах
отрезка. Если же число (n+1)∙p
не целое, то
в этом отрезке есть только одно целое
число.
Таким образом,
если число (n+1)∙p
целое, то
мода биномиально распределенной
случайной величины Х
принимает 2 соседних значения : d(X)=(n+1)∙p
−1 и
d(X)=(n+1)∙p
. Если же число (n+1)∙p
не целое,
то мода биномиально распределенной
случайной величины Х
одно значение
d(X)=k,
где k
есть
единственное целое число, удовлетворяющее
неравенству
(n+1)∙p
−1 ≤ k
≤ (n+1)∙p
. Если вспомнить, что запись [a]
означает взятие целой части от числа
а,
то в этом случае можно записать
d(X)=[(n+1)∙p]
.
Пример.
Кубик подбрасывается 100 раз. Каково
наивероятнейшее число выпадений
шестерки?
Пример.
Вероятность попадания стрелком в цель
равна 0.7 . Найти наивероятнейшее число
попаданий в цель при 30 выстрелах.
Пример.
Вероятность изготовления бракованной
детали на станке равна 0.06 . Каково
наивероятнейшее число бракованных
деталей в партии из 200 деталей, выточенных
на этом станке?
Пример.
Банк выдал 7 кредитов. Известно, что в
среднем не возвращается 2 кредита из
10. Найти среднее число невозвращенных
кредитов.
Соседние файлы в папке методичка
- #
- #
- #
Для нахождения моды и медианы случайной величины необходимы хорошие умения интегрировать и знания следующего теоретического материала. Модой 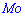 дискретной случайной величины
дискретной случайной величины 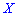 называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины
называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины 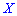 , которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
, которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
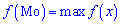
В зависимости от вида функции 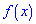 случайная величина
случайная величина 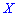 может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой  случайной величины
случайной величины 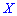 называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
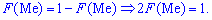
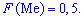
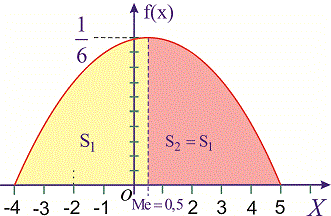
Графически мода и медиана изображенные на рисунке
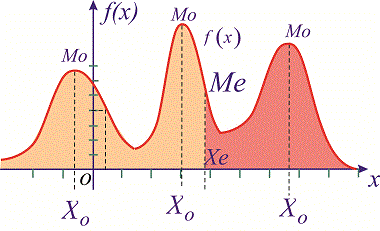
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью. Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин 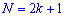 то медиана равна средней величине
то медиана равна средней величине
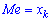
в случае четного количества 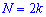 полусумме средних величин
полусумме средних величин
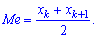
Рассмотрим примеры определения моды и медианы.
Пример 1. В развлекательном центре работник обслуживает четыре дорожки для боулинга. Вероятность того, что какая-то дорожка нуждается в уборке в течение смены является постоянной величиной с вероятностью 85%.
Построить закон распределения вероятностей дискретной случайной величины 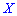 — количество дорожек, которые требуют уборки. Найти моду
— количество дорожек, которые требуют уборки. Найти моду 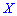 .
.
Решение. Случайной величина может принимать значения
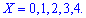
Вероятности появления значений определяем по образующей функцией
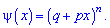
Для заданной задачи входные величины принимают значения
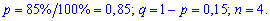
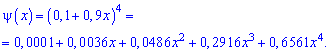
Искомые вероятности входят множителями при степенях аргумента
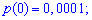
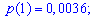
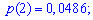
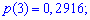
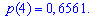
Закон распределения вероятностей запишем в виде таблицы
С таблице определяем моду 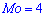 , как значение при максимальной вероятности. Получили одномодальное распределение
, как значение при максимальной вероятности. Получили одномодальное распределение
Пример 2. По заданной плотностью вероятностей
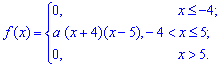
найти параметр  , плотность вероятностей
, плотность вероятностей 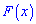 , моду
, моду 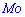 .
.
Решение. Применяя условие нормирования выполняем интегрирование
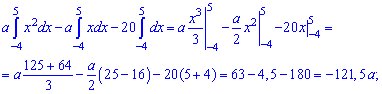
после того определяем параметр
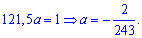
Плотность вероятностей, учитывая найденное значение будет иметь вид
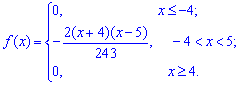
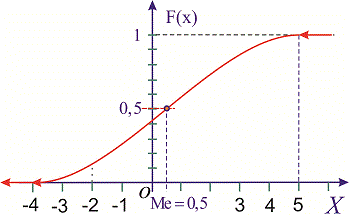
а ее график изображен на рисунке ниже
Из графика плотности вероятностей видим, что мода принимает значение 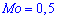 . Определим медиану
. Определим медиану  с помощью функции распределения вероятностей. Ее значение на промежутке
с помощью функции распределения вероятностей. Ее значение на промежутке 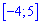 находим интегрированием
находим интегрированием
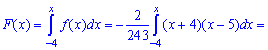
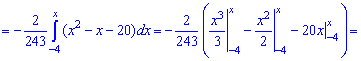
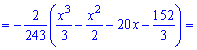
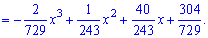
Функция распределения иметь следующий вид
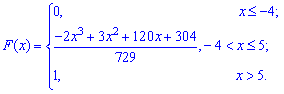
а ее график будет иметь вид
Для определения медианы случайной величины  применяем формулу
применяем формулу
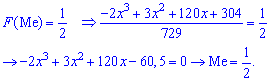
Медиану  можно найти с помощью плотности вероятностей
можно найти с помощью плотности вероятностей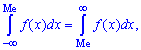
для дискретной случайной величины из промежутка 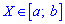
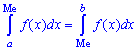
Таким образом медиану  — возможное значение случайной величины
— возможное значение случайной величины 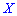 , при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости
, при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости 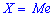 , делит площадь фигуры, ограниченной функцией плотности вероятностей
, делит площадь фигуры, ограниченной функцией плотности вероятностей 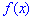 на две равные части.
на две равные части.
——————————-
Задача на определение моды и медианы случайной величины встречаются на практике не так часто, как плотности распределения вероятностей, однако вышеприведенный теоретический материал и решения распространенных примеров помогут Вам находить эти величины без больших затрат времени. При необходимости Вы всегда можете заказать решение задач по теории вероятностей в нас.
У этого термина существуют и другие значения, см. Медиана.
Медиа́на (от лат. mediāna «середина») или набора чисел — число, которое находится в середине этого набора, если его упорядочить по возрастанию, то есть такое число, что половина из элементов набора не меньше него, а другая половина не больше. Другое равносильное определение[1]: медиана набора чисел — это число, сумма расстояний (или, если более строго, модулей) от которого до всех чисел из набора минимальна. Это определение естественным образом обобщается на многомерные наборы данных и называется 1-медианой.
Например, медианой набора {11, 9, 3, 5, 5} является число 5, так как оно стоит в середине этого набора после его упорядочивания: {3, 5, 5, 9, 11}. Если в выборке чётное число элементов, медиана может быть не определена однозначно: тогда для числовых данных чаще всего используют полусумму двух соседних значений (то есть медиану набора {1, 3, 5, 7} принимают равной 4), подробнее см. ниже.
В математической статистике медиана может использоваться как одна из характеристик выборки или совокупности чисел.
Также определяется медиана случайной величины: в этом случае оно определяется как число, которое делит пополам распределение. Грубо говоря, медианой случайной величины является такое число, что вероятность получить значение случайной величины справа от него равна вероятности получить значение слева от него (и они обе равны 1/2), — более точное определение дано ниже.
Можно также сказать, что медиана является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.
Свойства медианы для случайных величин[править | править код]
Если распределение непрерывно, то медиана является одним из решений уравнения
,
где 


.
Если распределение является непрерывной строго возрастающей функцией, то решение уравнения однозначно. Если распределение имеет разрывы, то медиана может совпадать с минимальным или максимальным (крайним) возможным значением случайной величины, что противоречит «геометрическому» пониманию этого термина.
Медиана является важной характеристикой распределения случайной величины и, так же как математическое ожидание, может быть использована для центрирования распределения. Поскольку оценки медианы более робастны, её оценивание может быть более предпочтительным для распределений с т. н. тяжёлыми хвостами. Однако о преимуществах оценивания медианы по сравнению с математическим ожиданием можно говорить только в случае, если эти характеристики у распределения совпадают, в частности, для симметричных функций плотности распределения вероятностей.
Медиана определяется для всех распределений, а в случае неоднозначности, естественным образом доопределяется, в то время как математическое ожидание может быть не определено (например, у распределения Коши).
Пример использования[править | править код]
Рассмотрим финансовое состояние 19 малоимущих, у каждого из каких есть только 5 ₽, и одного миллионера, у которого буквально 1 млн ₽. Тогда в сумме у них получается 1 000 095 ₽. Если деньги равными долями разделить на 20 человек, получится 50 004,75 ₽. Это будет среднее арифметическое значение суммы денег, которая была у всех 20 человек в этой комнате.
Медиана же будет равна 5 ₽ (сумма «расстояния» от этой величины до состояния каждого из рассматриваемых людей минимальна). Это можно интерпретировать следующим образом: «разделив» всех рассматриваемых людей на две равные группы по 10 человек, мы получаем, что в первой группе у каждого не больше 5 ₽, во второй же — не меньше 5 ₽.
Из этого примера получается, что в качестве «серединного» состояния, грубо говоря, корректнее всего использовать именно медиану, а вот среднее арифметическое, наоборот, значительно превышает сумму наличных, имеющуюся у случайного человека из выборки.
Различны изменения в динамике и у средней арифметической с медианой, например в вышеприведённом примере, если у миллионера станет 1,5 млн. ₽ (+50 %), а у остальных станет 6 ₽ (+20 %), то средняя арифметическая выборки станет равна 75 005,70 ₽, то есть как бы у всех повысились равномерно на 50 %, при этом медиана станет равной 6 ₽ (+20 %).
Неуникальность значения[править | править код]
Если имеется чётное количество случаев и два средних значения различаются, то медианой, по определению, может служить любое число между ними (например, в выборке {1, 3, 5, 7} медианой может служить любое число из интервала (3,5)). На практике в этом случае чаще всего используют среднее арифметическое двух средних значений (в примере выше это число (3+5)/2=4). Для выборок с чётным числом элементов можно также ввести понятие «нижней медианы» (элемент с номером n/2 в упорядоченном ряду из 
См. также[править | править код]
- Мода — значение во множестве наблюдений, которое встречается наиболее часто.
- Среднее арифметическое набора чисел — число, сумма квадратов расстояний от которого до всех чисел из набора минимальна[3].
Примечания[править | править код]
- ↑ Сущность медианы. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.
- ↑ Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест Рональ Л., Штайн, Клиффорд. Алгоритмы. Построение и анализ. — 2-е издание. — М.: Издательский дом «Вильямс», 2005. — С. 240. — 1296 с.
- ↑ Почему это равносильные определения среднего арифметического.
Литература[править | править код]
- Медиана // Маниковский — Меотида. — М. : Большая российская энциклопедия, 2012. — С. 479—480. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 19). — ISBN 978-5-85270-353-8.
- Медиана // Большая российская энциклопедия [Электронный ресурс]. — 2017.
Лекция 8. Тема: Случайные величины (продолжение). Медианой распределения
случайной величины 𝑋 называется такое число m, что
1
1
𝑃(𝑋 ≤ 𝑚) ≥ 2 , 𝑃(𝑋 ≥ 𝑚) ≥ 2.
Число m существует. Пусть 𝐹(𝑥) – функция распределения случайной величины 𝑋. Тогда
1
1
𝑃(𝑋 ≤ 𝑚) ≥ ⟺ 𝐹(𝑚 + 0) ≥ ,
2
2
1
1
1
𝑃(𝑋 ≥ 𝑚) ≥ 2 ⟺ 1 − 𝐹(𝑚) ≥ 2 ⟺ 𝐹(𝑚) ≤ 2.
Так как 𝑙𝑖𝑚 𝐹(𝑥) = 0, 𝑙𝑖𝑚 𝐹(𝑥) = 1 и функции 𝐹(𝑥) является неубывающей (см. лекцию
𝑥→−∞
𝑥→+∞
6), то существует такая точка m, в которой
1
1
𝐹(𝑚) ≤ 2, 𝐹(𝑚 + 0) ≥ 2.
Если уравнение 𝐹(𝑥) = 0,5 имеет решение, то любое его решение является медианой.
F
1
0,5
x
x
𝑥 – точка непрерывности функции 𝐹(𝑥).
F
1
0,5
x
x
𝑥 – точка разрыва функции 𝐹(𝑥).
F
1
0,5
x
b
a
Любая точка 𝑥 ∈ [𝑎, 𝑏] является медианой
Если у уравнения 𝐹(𝑥) = 0,5 нет решений, медианой является наибольшее решение
неравенства 𝐹(𝑥) < 0,5 (легко доказать, что оно существует).
F
1
0,5
x
x
𝑥 – медиана распределения.
1
В общем случае медиана определяется неоднозначно. Но если случайная величина
является абсолютно непрерывной и имеет строго возрастающую функцию распределения
𝐹(𝑥), то медиана равна единственному корню уравнения 𝐹(𝑥) = 0,5.
F
1
0,5
x
x
Модой абсолютно непрерывного распределения называют любую точку локального
максимума плотности распределения. Для дискретных распределений модой называют то
значение случайной величины, вероятность которого больше вероятностей соседних
значений. Рассмотрим только абсолютно непрерывный тип распределения с некоторой
плотностью 𝑓(𝑥). Распределения с одной, двумя или большим числом мод называются
соответственно унимодальными, бимодальными и мультимодальными.
f
f
x
x
b
a
Бимодальное распределение.
a
Унимодальное распределение.
Если математическое ожидание абсолютно непрерывной случайной величины
существует, то можно доказать, что в случае унимодального и симметричного
относительно некоторой точки a распределения математическое ожидание, мода и медиана
равны a.
Пример 1. Случайная величина 𝑋 в интервале (3, 5) задана плотностью распределения
− 3⁄4𝑥 2 + 6𝑥 − 45⁄4 при 𝑥 ∈ (3, 5),
𝑓(𝑥) = {
0 при 𝑥 ∉ (3, 5).
Найдите моду, математическое ожидание и медиану 𝑋.
+∞
5
Решение. Ясно, что 𝑀(𝑋) = ∫−∞ 𝑥𝑓(𝑥)𝑑𝑥 = ∫3 𝑥𝑓(𝑥)𝑑𝑥 существует. График квадратного
трехчлена 𝑓(𝑥) = − 3⁄4𝑥 2 + 6𝑥 − 45⁄4 симметричен относительно прямой 𝑥 = 𝑥в , где
𝑏
6
абсцисса вершины 𝑥в = − 2𝑎 = − 2(−3⁄4) = 4. Эта точка является единственной точкой
локального максимума плотности. Интервал (3, 5) симметричен относительно
вертикальной прямой 𝑥 = 4. Следовательно, мы имеем симметричное относительно точки
𝑥 = 4 унимодальное распределение.
f
3⁄4
x
3
5
4
Мода, математическое ожидание и медиана 𝑋 равны 4.
2
Из оставшихся числовых характеристик распределений нам понадобятся квантили. Они
нам понадобятся только в случае абсолютно непрерывных распределений со строго
возрастающей функцией распределения 𝐹(𝑥). Квантилью уровня 𝛾, где 𝛾 – любое число из
интервала (0, 1), называется решение уравнения (оно существует и является единственным)
𝐹(𝑥) = 𝛾.
F
1
𝛾
x
𝑥𝛾
Квантиль уровня 𝛾 обозначается через 𝑥𝛾 . Таким образом, медиана является квантилью
1
уровня 2. Квантили делятся на разные группы. Например, квантили 𝑥1⁄4 , 𝑥1⁄2 , 𝑥3⁄4
называются квартилями (ясно, что 𝑥1⁄2 – медиана).
Перейдем к рассмотрению пар случайных величин. Пусть случайные величины 𝑋 и 𝑌
определены на одном и том же вероятностном пространстве и имеют конечные абсолютные
моменты второго порядка 𝑀(𝑋 2 ) и 𝑀(𝑌 2 ). Ковариацией случайных величин 𝑋 и 𝑌
называется число
𝑐𝑜𝑣( 𝑋, 𝑌) = 𝑀[(𝑋 − 𝑀(𝑋))(𝑌 − 𝑀(𝑌))].
Заметим, что
𝑐𝑜𝑣( 𝑋, 𝑌) = 𝑀[(𝑋 − 𝑀(𝑋))(𝑌 − 𝑀(𝑌))] = 𝑀(𝑋𝑌 − 𝑌𝑀(𝑋) − 𝑋𝑀(𝑌) + 𝑀(𝑋)𝑀(𝑌)) =
= 𝑀(𝑋𝑌) − 𝑀(𝑋)𝑀(𝑌).
Если случайные величины 𝑋 и 𝑌 независимы, то 𝑀(𝑋𝑌) = 𝑀(𝑋)𝑀(𝑌), следовательно,
𝑐𝑜𝑣( 𝑋, 𝑌) = 0. Таким образом, если ковариация 𝑐𝑜𝑣( 𝑋, 𝑌) отлична от нуля, то случайные
величины 𝑋 и 𝑌 не является независимыми. Как известно, если случайные величины 𝑋 и 𝑌
независимы, то 𝐷(𝑋 + 𝑌) = 𝐷(𝑋)+ 𝐷(𝑌). В общем случае
2
𝐷(𝑋 + 𝑌) = 𝑀 ((𝑋 + 𝑌 − 𝑀(𝑋 + 𝑌)) ) = 𝑀{[(𝑋 − 𝑀(𝑋)) + (𝑌 − 𝑀(𝑌))]2 } =
𝑀[(𝑋 − 𝑀(𝑋))2 + (𝑌 − 𝑀(𝑌))2 + 2(𝑋 − 𝑀(𝑋))(𝑌 − 𝑀(𝑌))] = 𝐷(𝑋) + 𝐷(𝑌) + 2 𝑐𝑜𝑣( 𝑋, 𝑌).
Ковариация имеет ряд недостатков. Эта величина имеет размерность. Если случайные
величины 𝑋 и 𝑌 измеряются, например, в метрах, то их ковариация будет измеряться в м2 .
Если мы перейдем к другой системе измерения величин 𝑋, 𝑌, то их ковариация изменится,
так как легко проверить, что
𝑐𝑜𝑣( 𝑎𝑋 + 𝑏, 𝑐𝑌 + 𝑑) = 𝑎𝑐 𝑐𝑜𝑣( 𝑋, 𝑌).
Коэффициентом корреляции случайных величин 𝑋 и 𝑌 называется число
𝑐𝑜𝑣(𝑋,𝑌)
𝑀[(𝑋−𝑀(𝑋))(𝑌−𝑀(𝑌))]
𝑟(𝑋, 𝑌) =
=
.
2
2
√𝐷(𝑋)√𝐷(𝑌)
√𝑀([𝑋−𝑀(𝑋)] )√𝑀([𝑌−𝑀(𝑌)] )
Коэффициент корреляции является безразмерной величиной и не меняется при переходе к
другой системе измерения величин 𝑋, 𝑌. Легко проверить, что при 𝑎 > 0 и 𝑐 > 0
𝑟(𝑎𝑋 + 𝑏, 𝑐𝑌 + 𝑑) = 𝑟(𝑋, 𝑌).
Легко доказать следующие свойства коэффициента корреляции:
1. |𝑟(𝑋, 𝑌)| ≤ 1.
2. |𝑟(𝑋, 𝑌)| = 1 тогда и только тогда, когда существуют такие постоянные 𝑎 и 𝑏, что
𝑌 = 𝑎𝑋 + 𝑏.
3. Если случайные величины 𝑋 и 𝑌 независимы, то 𝑟(𝑋, 𝑌) = 0.
Из свойства 3 следует, что отличный от нуля коэффициент корреляции 𝑟(𝑋, 𝑌) является
признаком отсутствия независимости случайных величин 𝑋 и 𝑌. Если коэффициент
3
корреляции случайных величин 𝑋 и 𝑌 равен нулю, то такие величины называются
некоррелированными. В противном случае случайные величины 𝑋 и 𝑌 называются
коррелированными. Коррелированные случайные величины не являются независимыми.
Если коэффициент корреляции 𝑟(𝑋, 𝑌) > 0, то случайные величины 𝑋 и 𝑌 называются
положительно коррелированными. Если коэффициент корреляции 𝑟(𝑋, 𝑌) < 0, то
случайные величины 𝑋 и 𝑌 называются отрицательно коррелированными. Из
некоррелированности случайных величин не следует их независимость.
𝜋
Пример 2. Пусть Ω = {0, 2 , 𝜋} и все исходы равновозможны. Пусть 𝑋 = 𝑠𝑖𝑛𝜔, 𝑌 = 𝑐𝑜𝑠𝜔.
Эти случайные величины имеют следующие распределения:
-1
1
𝑋
1
𝑌
2/3
1/3
1/3
1/3
1/3
P
P
1
Ясно, что 𝑀(𝑋) = 1/3, 𝑀(𝑌) = 0. Заметим, что 𝑋𝑌 = 2 𝑠𝑖𝑛2𝜔 = 0 ∀𝜔𝜖Ω. Следовательно,
𝑀(𝑋𝑌) = 0, 𝑀(𝑋)𝑀(𝑌) = 0, 𝑐𝑜𝑣( 𝑋, 𝑌) = 0, 𝑟(𝑋, 𝑌) = 0. Таким образом, случайные
величины 𝑋 и 𝑌 некоррелированы. Но эти величины не являются независимыми.
Действительно, 𝑃(𝑋 = 0) = 2/3, 𝑃(𝑌 = −1) = 1/3. Благоприятным для события {𝑋 =
0, 𝑌 = −1} является единственный исход 𝜔 = 𝜋, так как 𝑠𝑖𝑛𝜔=0 и 𝑐𝑜𝑠𝜔 = −1 только при
𝜔 = 𝜋. Следовательно, по классической схеме, 𝑃(𝑋 = 0, 𝑌 = −1) = 1/3. В случае
независимых случайных 𝑋 и 𝑌 должно выполняться равенство
𝑃(𝑋 = 0, 𝑌 = −1) = 𝑃(𝑋 = 0)𝑃(𝑌 = −1).
Но в нашем случае,
1
2
𝑃(𝑋 = 0, 𝑌 = −1) = 3 ≠ 9 = 𝑃(𝑋 = 0)𝑃(𝑌 = −1).
Следовательно, некоррелированные случайные величины 𝑋 и 𝑌 не являются независимыми.
Пусть случайные величины 𝑋 и 𝑌 коррелированы, т.е. 𝑟(𝑋, 𝑌) ≠ 0. Тогда случайные
величины 𝑋 и 𝑌 не являются независимыми. Естественно ожидать, что знание значения
случайной величины 𝑋 позволяет вынести некоторые суждения и о значении случайной
величины 𝑌. Пусть 𝑓(𝑥) – борелевская функция одной переменной (напомним, что все
непрерывные функции являются борелевскими). Случайную величину 𝑓(𝑋) будем
называть оценкой для 𝑌. Меняя функцию 𝑓(𝑥), мы можем получить разные оценки.
Выделим из них одну оценку. Оценку 𝑓 ∗ (𝑋) для 𝑌 назовем оптимальной в
среднеквадратическом смысле, если
𝑀(𝑌 − 𝑓 ∗ (𝑋))2 ≤ 𝑀(𝑌 − 𝑓(𝑋))2 для любой оценки 𝑓(𝑋) для 𝑌.
Перед общим методом построения оптимальной оценки, рассмотрим один простой
приближенный метод. Ясно, что удобно работать с оценками, имеющими простой вид.
Самыми удобными для использования являются линейные функции. Для нахождения
оптимальной оценки для 𝑌 в классе линейных функций вида 𝑓(𝑋) = 𝑎 + 𝑏𝑋, рассмотрим
функцию двух переменных 𝑎 и 𝑏
𝑔(𝑎, 𝑏) = 𝑀(𝑌 − (𝑎 + 𝑏𝑋))2.
Легко найти методами математического анализа точку минимума (𝑎 ∗ , 𝑏 ∗ ) этой функции:
𝑎 ∗ = 𝑀(𝑌) − 𝑟(𝑋, 𝑌)
𝑏 ∗ = 𝑟(𝑋, 𝑌)
√𝐷(𝑌)
√𝐷(𝑋)
√𝐷(𝑌)
𝑀(𝑋),
.
√𝐷(𝑋)
Следовательно, оптимальной в среднеквадратическом смысле линейной оценкой для
значения случайной величины 𝑌 по значению случайной величины 𝑋 является
𝑓 ∗ (𝑋) = 𝑀(𝑌) + 𝑟(𝑋, 𝑌)
√𝐷(𝑌)
√𝐷(𝑋)
(𝑋 − 𝑀(𝑋)).
(1)
Полученная линейная аппроксимация оптимальной оценки позволяет лучше понять
значение коэффициента корреляции 𝑟(𝑋, 𝑌) при изучении пары случайных величин. Из
уравнения (1) видно, почему при 𝑟(𝑋, 𝑌) > 0 случайные величины 𝑋 и 𝑌 называются
4
положительно коррелированными, а при 𝑟(𝑋, 𝑌) < 0 – отрицательно коррелированными. Из
уравнения (1) следует, что
𝑀(𝑌 − 𝑓 ∗ (𝑋))2 = [1 − 𝑟 2 (𝑋, 𝑌)]𝐷(𝑌).
(2)
Эта величина характеризует качество нашей оценки 𝑓 ∗ (𝑋) для 𝑌 (расхождение нашего
прогноза 𝑓 ∗ (𝑋) для 𝑌 от реальной ситуации с 𝑌). Из формулы (2) следует, что чем больше
по модулю коэффициент корреляции, тем сильнее линейная зависимость между 𝑋 и 𝑌. Если
𝑟(𝑋, 𝑌) = ±1, то из формулы (2) следует, что 𝑀(𝑌 − 𝑓 ∗ (𝑋))2 = 0. Но это равенство
возможно тогда и только тогда, когда 𝑌 − 𝑓 ∗ (𝑋) = 0 с вероятностью 1, т.е. мы можем
считать, что 𝑌 = 𝑎∗ + 𝑏 ∗ 𝑋. В этом случае мы имеем линейную зависимость 𝑌 от 𝑋. Заметим,
что если 𝑟(𝑋, 𝑌) = 0, т.е. случайные величины некоррелированы, то 𝑓 ∗ (𝑋) = 𝑀(𝑌).
Мы рассмотрели приближенный метод для построения оптимальной оценки. Вернемся
к общему методу для решения этой задачи. Для этого введем так называемые условные
распределения. Сначала рассмотрим дискретный тип совместного распределения пары 𝑋 и
𝑌. Пусть дан совместный закон их распределения.
𝑋
𝑌
…
𝑦1
𝑦𝑛
…
𝑥1
𝑝11
𝑝1𝑛
…
…
….
…
….
𝑥𝑚
𝑝𝑚1
𝑝𝑚𝑛
Ясно, что ∑𝑛𝑗=1 𝑝𝑖𝑗 = 𝑝𝑖 = 𝑃(𝑋 = 𝑥𝑖 ), ∑𝑚
𝑖=1 𝑝𝑖𝑗 = 𝑞𝑗 = 𝑃(𝑌 = 𝑦𝑗 ). Из совместного закона
распределения можно найти частные распределения 𝑋 и 𝑌.
…
…
𝑋
𝑥1
𝑥2
𝑥𝑚
𝑌
𝑦1
𝑦2
𝑦𝑛
…
…
𝑝1
𝑝2
𝑝𝑚
𝑞1
𝑞2
𝑞𝑛
P
P
Зафиксируем значение случайной величины 𝑋: пусть 𝑋 = 𝑥𝑖 . Построим новый закон
распределения:
…
𝑌
𝑦1
𝑦2
𝑦𝑛
|𝑥
|𝑥
…
𝑝(𝑦|𝑥𝑖 ) 𝑝(𝑦1 𝑖 ) 𝑝(𝑦2 𝑖 )
𝑝(𝑦𝑛 |𝑥𝑖 )
где
𝑝(𝑦𝑗 |𝑥𝑖 ) = 𝑃(𝑌 = 𝑦𝑗 |𝑋 = 𝑥𝑖 ) =
𝑃(𝑋=𝑥𝑖 ,𝑌=𝑦𝑗 )
𝑃(𝑋=𝑥𝑖 )
=
𝑝𝑖𝑗
𝑝𝑖
.
Этот закон распределения называют условным распределением 𝑌 при условии 𝑋 = 𝑥𝑖 .
Условным математическим ожиданием дискретной случайной величины 𝑌 при условии
𝑋 = 𝑥𝑖 называется число
𝑀(𝑌|𝑋 = 𝑥𝑖 ) = ∑𝑛𝑗=1 𝑦𝑗 𝑝(𝑦𝑗 |𝑥𝑖 ).
Аналогично, зафиксируем значение случайной величины 𝑌: пусть 𝑌 = 𝑦𝑗 . Построим
новый закон распределения:
𝑋
𝑥1
𝑥2
𝑝(𝑥|𝑦𝑗 ) 𝑝(𝑥1 |𝑦𝑗 ) 𝑝(𝑥2 |𝑦𝑗 )
где
…
…
𝑥𝑚
𝑝(𝑥𝑛 |𝑦𝑗 )
𝑝(𝑥𝑖 |𝑦𝑗 ) = 𝑃(𝑋 = 𝑥𝑖 |𝑌 = 𝑦𝑗 ) =
𝑃(𝑋=𝑥𝑖 ,𝑌=𝑦𝑗 )
𝑃(𝑌=𝑦𝑗 )
=
𝑝𝑖𝑗
𝑞𝑗
.
Этот закон распределения называют условным распределением 𝑋 при условии 𝑌 = 𝑦𝑗 .
Условным математическим ожиданием дискретной случайной величины 𝑋 при условии
𝑌 = 𝑦𝑗 называется число
𝑀(𝑋|𝑌 = 𝑦𝑗 ) = ∑𝑚
𝑖=1 𝑥𝑖 𝑝(𝑥𝑖 |𝑦𝑗 ).
Рассмотрим теперь абсолютно непрерывный тип совместного распределения пары 𝑋 и
𝑌. Пусть дана их совместная плотность распределения 𝑓(𝑥, 𝑦). Как мы знаем, из совместной
плотности распределения случайных величин 𝑋, 𝑌 можно найти плотности распределения
случайных величин 𝑋, 𝑌:
5
+∞
𝑓𝑋 (𝑥) = ∫−∞ 𝑓(𝑥, 𝑦)𝑑𝑦,
+∞
𝑓𝑌 (𝑦) = ∫−∞ 𝑓(𝑥, 𝑦)𝑑𝑥.
Зафиксируем значение случайной величины 𝑋: пусть 𝑋 = 𝑥. Условной плотностью
распределения 𝑌 при 𝑋 = 𝑥 называется функция
𝜙(𝑦|𝑥) = 𝑓(𝑥, 𝑦)⁄𝑓𝑋 (𝑥).
Условным математическим ожиданием 𝑌 при 𝑋 = 𝑥 называется функция
+∞
𝑀𝑥 (𝑌) = ∫−∞ 𝑦𝜙(𝑦|𝑥) 𝑑𝑦.
Аналогично, зафиксируем значение случайной величины 𝑌: пусть 𝑌 = 𝑦. Условной
плотностью распределения 𝑋 при 𝑌 = 𝑦 называется функция
𝜙(𝑥|𝑦) = 𝑓(𝑥, 𝑦)⁄𝑓𝑌 (𝑦).
Условным математическим ожиданием 𝑋 при 𝑌 = 𝑦 называется функция
+∞
𝑀𝑦 (𝑋) = ∫−∞ 𝑥𝜙(𝑥|𝑦) 𝑑𝑥.
Введенные условные математические ожидания используются при построении
оптимальных оценок. Пусть дана пара случайных величин 𝑋 и 𝑌 с конечными моментами
второго порядка 𝑀(𝑋 2 ) и 𝑀(𝑌 2 ). Пусть одна из них, например 𝑋, наблюдаема, а другая, в
данном случае 𝑌, наблюдению не подлежит. Вернемся к вопросу об оптимальной оценке
для ненаблюдаемой случайной величины 𝑌 по наблюдениям над значениями 𝑋. Так как
𝑀(𝑌 2 ) < +∞, то естественно искать оценки 𝑓(𝑋) для 𝑌 только среди случайных величин с
конечными вторыми моментами, т.е. будем считать, что 𝑀(𝑓 2 (𝑋)) < +∞. Ясно, что в этом
классе находятся и линейные оценки 𝑓(𝑋) = 𝑎 + 𝑏𝑋, так как 𝑀(𝑋 2 ) < +∞. Можно
доказать, что оптимальную в среднеквадратическом смысле оценку 𝑓 ∗ (𝑋) для 𝑌 можно
получить, если в качестве функции 𝑓 ∗ (𝑥) взять функцию 𝑀𝑥 (𝑌). Эта функция 𝑀𝑥 (𝑌)
называется функцией регрессии 𝑌 на 𝑋. Аналогично можно ввести определение функции
регрессии 𝑋 на 𝑌.
На следующей лекции мы рассмотрим один частный случай, в котором можно получить
точное выражение для функции 𝑀𝑥 (𝑌). На практике в общем случае используются
различные аппроксимации для этой зависимости. Например, если использовать линейную
аппроксимацию для функции регрессии 𝑀𝑥 (𝑌), то мы опять придем к результату, что
наилучшей линейной аппроксимацией для функции регрессии 𝑀𝑥 (𝑌)является функция
𝑓 ∗ (𝑥) = 𝑀(𝑌) + 𝑟(𝑋, 𝑌)
√𝐷(𝑌)
√𝐷(𝑋)
(𝑥 − 𝑀(𝑋)).
Эту функцию называют линейной средней квадратической регрессией 𝑌 на 𝑋.
Перейдем к рассмотрению основных видов распределений случайных величин. Начнем
с нормального распределения. Говорят, что абсолютно непрерывная случайная величина X
имеет нормальное (гауссовское) распределение с параметрами a и 𝜎 2 , если ее плотность
распределения 𝑓𝑋 (𝑥) имеет вид
1
𝑓𝑋 (𝑥) = 𝜎√2𝜋 𝑒
−
(𝑥−𝑎)2
2𝜎2
,
(3)
где 𝑎 – произвольная постоянная, а 𝜎 – произвольная положительная постоянная. Название
этого распределения связано с тем, что многие случайные величины имеют плотность
такого вида. Это название не говорит о «ненормальности» других распределений, а
выделяет это распределение из других, отводит для него особое место. Подробнее об этом
будет сказано при рассмотрении центральной предельной теоремы. Запись 𝑋 ∼ 𝒩(𝑎, 𝜎 2 )
означает, что случайная величина X имеет нормальное распределение с параметрами a и 𝜎 2 .
1
В правой части формулы (3) присутствуют множитель 𝜎√2𝜋. Для объяснения
1
происхождения этого множителя, представим плотность 𝑓𝑋 (𝑥) = 𝜎√2𝜋 𝑒
𝑓𝑋 (𝑥) = 𝐶𝑒
(𝑥−𝑎)2
−
2𝜎2
+∞
−
(𝑥−𝑎)2
2𝜎2
в виде
и найдем постоянную 𝐶 из свойства плотности ∫−∞ 𝑓𝑋 (𝑥)𝑑𝑥 = 1. Итак,
6
𝑡=
+∞
1 = ∫−∞ 𝐶𝑒
+∞
∫−∞ 𝑒 −𝑡
Интеграл
2
+∞
∫−∞ 𝑒 −𝑡 /2 𝑑𝑡
2 /2
(𝑥−𝑎)2
−
2𝜎2
𝑥−𝑎
𝑑𝑡 =
𝑑𝑥 =
𝜎
𝑑𝑥
𝜎
,
+∞
,
= 𝐶𝜎 ∫−∞ 𝑒 −𝑡
2 /2
𝑑𝑡.
𝜎𝑑𝑡 = 𝑑𝑥,
[−∞ < 𝑡 < +∞.]
называется интегралом Пуассона. Можно
𝑑𝑡
доказать, что
1
= √2𝜋. Таким образом, 1 = 𝐶𝜎√2𝜋. Отсюда 𝐶 = 𝜎√2𝜋.
0,25
f
0,2
0,15
0,1
0,05
x
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
11
График плотности нормального распределения с параметрами a=3 и 𝜎 2 = 4.
Можно доказать, что если 𝑋 ∼ 𝒩(𝑎, 𝜎 2 ), то 𝑀(𝑋) = 𝑎, 𝐷(𝑋) = 𝜎 2 . Нормальное
распределение с параметрами a=0 и 𝜎 2 = 1 называется стандартным нормальным
распределением. Плотность стандартного нормального распределения имеет вид 𝜑(𝑥) =
1
√2𝜋
𝑒
−
𝑥2
2
. Эту функцию мы ввели при рассмотрении локальной теоремы Муавра-Лапласа и
назвали функцией Гаусса.
0,45
0,4
0,35
0,3
0,25
0,2
0,15
0,1
0,05
-5
-4
-3
+∞
Ясно, что ∫−∞ 𝜑(𝑥)𝑑𝑥
=
-2
-1
1
2
3
4
5
График функции 𝜑(𝑥).
+∞
= ∫0 𝜑(𝑥)𝑑𝑥 = 0,5. По определению, функция
1, ∫−∞ 𝜑(𝑥)𝑑𝑥
𝑥
стандартного нормального распределения имеет вид 𝑁(𝑥) = ∫−∞ 𝜑(𝑡)𝑑𝑡. Эту функцию
7
𝑥
𝑥
можно выразить через функцию Лапласа: 𝑁(𝑥) = ∫−∞ 𝜑(𝑡)𝑑𝑡 = ∫−∞ 𝜑(𝑡)𝑑𝑡 + ∫0 𝜑(𝑡)𝑑𝑡 =
𝑥
0,5 + 𝛷(𝑥), где 𝛷(𝑥) = ∫0 𝜑(𝑡)𝑑𝑡 =
1
𝑥
∫ 𝑒 −𝑡
√2𝜋 0
1,1
2 ⁄2
𝑑𝑡 – функция Лапласа.
N
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
-5
-4
-3
-2
-1
1
2
3
4
x
5
График функции стандартного нормального распределения.
Пусть 𝑋 ∼ 𝒩(𝑎, 𝜎 2 ). Тогда для функции распределения 𝐹𝑋 (𝑥) случайной величины 𝑋
справедлива формула:
𝑡−𝑎
𝑑𝑡
𝑥−𝑎
𝑥
(𝑡−𝑎)2
𝑦=
, 𝑑𝑦 =
𝜎
1
1 −𝑦 2
−
𝜎
𝜎
2
2
𝐹𝑋 (𝑥) = ∫
𝑒 2𝜎 𝑑𝑡 = [
𝑥 − 𝑎 ] = ∫−∞ √2𝜋 𝑒 𝑑𝑦 =
−∞ 𝜎√2𝜋
𝜎𝑑𝑦 = 𝑑𝑡, −∞ < 𝑡 <
.
𝜎
𝑥−𝑎
𝑥−𝑎
=𝑁( 𝜎 )= 0,5 + Φ( 𝜎 ).
Отсюда следует, что если 𝑋 ∼ 𝒩(𝑎, 𝜎 2 ), то
𝑥−𝑎
𝑥−𝑎
𝑃(𝑋 ≤ 𝑥) = 𝑃(𝑋 < 𝑥)= 0,5 + Φ( 𝜎 ), 𝑃(𝑋 ≥ 𝑥) = 𝑃(𝑋 > 𝑥) = 0,5 − Φ( 𝜎 ),
𝑃(𝑥1 ≤ 𝑋 ≤ 𝑥2 ) = 𝑃(𝑥1 < 𝑋 ≤ 𝑥2 ) =
𝑥 −𝑎
𝑥 −𝑎
= 𝑃(𝑥1 ≤ 𝑋 < 𝑥2 ) = 𝑃(𝑥1 < 𝑋 < 𝑥2 ) = Φ ( 2𝜎 ) − Φ( 1𝜎 ). (4)
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
-4
-3
-2
-1
𝐹𝑋 (𝑥)
x
1
2
3
4
5
6
7
8
9
График функции нормального распределения с параметрами a=3 и 𝜎 2 = 4.
Из формулы (4) следует «правило трех сигм»: если 𝑋 ∼ 𝒩(𝑎, 𝜎 2 ), то практически
достоверно, что значения случайной величины 𝑋 заключены в интервале (𝑎 − 3𝜎, 𝑎 + 3𝜎).
Действительно,
𝑎+3𝜎−𝑎
𝑎−3𝜎−𝑎
𝑃(𝑎 − 3𝜎 < 𝑋 < 𝑎 + 3𝜎) = Φ ( 𝜎 ) − Φ ( 𝜎 ) = Φ(3) − Φ(−3) = 2Φ(3) ≈ 0,9973.
8
