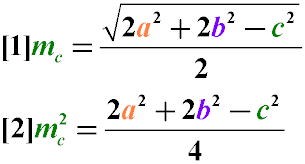Как найти медиану по двум сторонам треугольника - Сайт, где вы сможете решить свои вопросы

Рассмотрим задачу, в которой требуется по сторонам треугольника найти его медиану.

Задача.

Даны стороны треугольника. Найти длину медианы, проведенной к наибольшей стороне.

Дано: ∆ ABC,

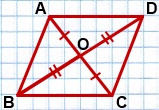
BC=a, AC=b, AB=c,

сторона AC — наибольшая,

BO- медиана.

Найти: BO.

Решение:

1) На луче BO отложим отрезок OD, OD=BO.

2) Проведем отрезки AD и CD.

3) Рассмотрим четырехугольник ABCD.

AO=CO (так как BO — медиана треугольника ABC по условию);

BO=DO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

4) По свойству диагоналей параллелограмма,

$[A{C^2} + B{D^2} = 2(A{B^2} + A{D^2})]$

$[{b^2} + B{D^2} = 2({a^2} + {c^2})]$

$[B{D^2} = 2({a^2} + {c^2}) - {b^2}]$

$[BD = sqrt {2({a^2} + {c^2}) - {b^2}} ]$

так как BO=1/2 BD (по построению),

$[underline {BO = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} .} ]$

Если ввести обозначение

$[BO = {m_b},]$

формула для нахождения медианы треугольника по его сторонам примет вид:

$[{{m_b} = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} }]$

Запоминать эту формулу не обязательно. При решении конкретной задачи следует привести все рассуждения.

Если медиана проведена не к наибольшей, а к наименьшей либо средней по величине стороне, решение задачи аналогично.

Соответственно, формулы для нахождения длины медианы в этих случаях:

$[{m_a} = frac{1}{2}sqrt {2({b^2} + {c^2}) - {a^2}} ]$

$[{m_c} = frac{1}{2}sqrt {2({a^2} + {b^2}) - {c^2}} ]$

Приём, который применили для решения задачи — метод удвоения медианы.

Источник

Все формулы медианы треугольника

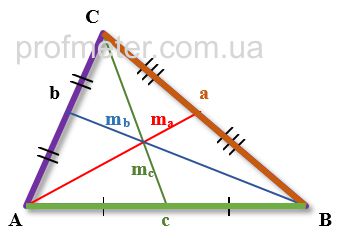
Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.

Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M – медиана, отрезок |AO|

c – сторона на которую ложится медиана

a, b – стороны треугольника

γ – угол CAB

Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

Подробности

Автор: Administrator

Опубликовано: 08 октября 2011

Обновлено: 13 августа 2021

Источник

Чтобы по сторонам треугольника найти медиану, не обязательно запоминать дополнительную формулу. Достаточно знать алгоритм решения.

Для начала рассмотрим задачу в общем виде.

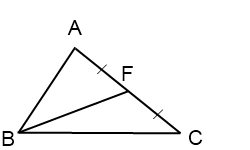
Дан треугольник со сторонами a, b, c. Найти длину медианы, проведенной к стороне b.

AB=a, AC=b, BC=c.

Решение.

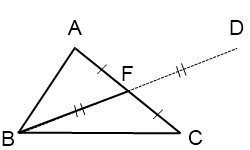
На луче BF отложим отрезок FD, FD=BF.

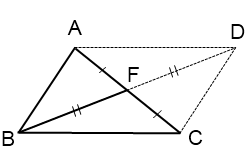
Соединим точку D с точками A и C.

Четырехугольник ABCD — параллелограмм (по признаку), так как у него диагонали в точке пересечения делятся пополам.

Свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Отсюда: AC²+BD²=2(AB²+BC²), значит, b²+BD²=2(a²+c²),

BD²=2(a²+c²)-b². По построению, BF — половина BD, следовательно,

$[BD = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} ]$

Это — формула нахождения медианы треугольника по его сторонам. Обычно ее записывают так:

$[{m_b} = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} ]$

Переходим к рассмотрению конкретной задачи.

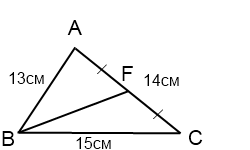
Стороны треугольника равны 13 см, 14 см и 15 см. Найти медиану треугольника, проведенную к его средней по длине стороне.

Решение:

Применяя аналогичные рассуждения, получаем:

AC²+BD²=2(AB²+BC²).

Отсюда

14²+BD²=2(13²+15²)

BD²=2(169+225)-196=592

$[BF = frac{1}{2}DD = frac{1}{2} cdot 4sqrt {37} = 2sqrt {37} (cm)]$

Ответ:

Источник

Как найти медиану треугольника по его сторонам

Медиана – это отрезок, соединяющий вершину треугольника и середину противолежащей стороны. Зная длины всех трех сторон треугольника, можно найти его медианы. В частных случаях равнобедренного и равностороннего треугольника, очевидно, достаточно знания, соответственно, двух (не равных друг другу) и одной стороны треугольника.

Инструкция

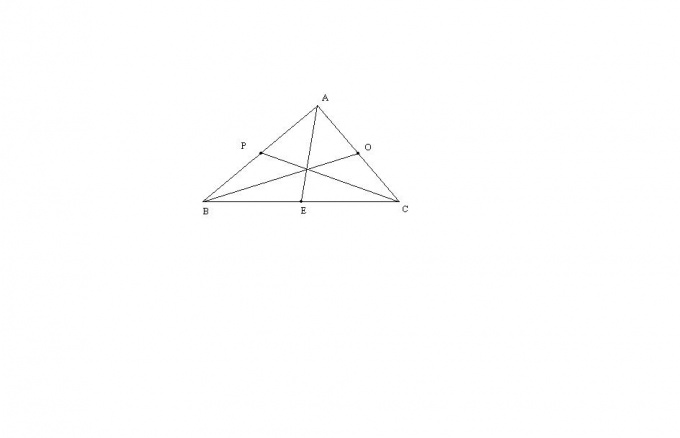
Рассмотрим самый общий случай треугольника ABC с тремя не равными друг другу сторонами. Длину медианы AE этого треугольника можно вычислить по формуле: AE = sqrt(2*(AB^2)+2*(AC^2)-(BC^2))/2. Остальные медианы находятся абсолютно аналогично. Эта формула выводится через теорему Стюарта, либо через достроение треугольника до параллелограмма.

Если треугольник ABC – равнобедренный и AB = AC, то медиана AE будет являться одновременно и высотой этого треугольника. Следовательно, треугольник BEA будет прямоугольным. По теореме Пифагора, АЕ = sqrt((AB^2)-(BC^2)/4). Из общей формулы длины медианы треугольника, для медиан BO и СP справедливо: BO = CP = sqrt(2*(BC^2)+(AB^2))/2.

Если треугольник ABC – равносторонний, то, очевидно, что все его медианы равны друг другу. Так как угол при вершине равностороннего треугольника равен 60 градусам, то AE = BO = CP = a*sqrt(3)/2, где a = AB = AC = BC – длина стороны равностороннего треугольника.

Источники:

Медианы и бессектрисы треугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Примечание. В данном уроке изложены задачи по геометрии о медиане треугольника. Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. Почти наверняка курс будет дополнен.

Задача. Найти длину медианы треугольника через его стороны

Стороны треугольника равны 8, 9 и 13 сантиметров. К наибольшей стороне треугольника проведена медиана. Определите медиану треугольника исходя из размеров его сторон.

Решение.

Задача имеет два способа решения. Первый, который не нравится учителям средней школы, но является наиболее универсальным.

Способ 1.

Применим Теорему Стюарта, согласно которой квадрат медианы равен одной четвертой от суммы удвоенных квадратов сторон из которой вычли квадрат стороны, к которой проведена медиана.

m_c² = ( 2a² + 2b² – c² ) / 4

Соответственно

m_c² = ( 2 * 8² + 2 * 9² – 13²) / 4
m_c² = 30,25
m_c = 5,5 см

Способ 2.

Второй способ решения, который преподаватели в школе любят – это дополнительные построения треугольника до параллелограмма и решение через теорему о диагоналях параллелограмма.

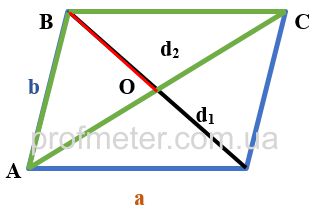
Продлим стороны треугольника и медиану достроив их до параллелограмма. В этом случае медиана BO треугольника ABC будет равна половине диагонали получившегося параллелограмма, а две стороны треугольника AB, BC – его боковым сторонам. Третья сторона треугольника AC, к которой была проведена медиана, является второй диагональю получившегося параллелограмма.

Согласно теореме, сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.

2(a²+b²)=d₁²+d₂²

Обозначим диагональ параллелограмма, которая образована продолжением медианы исходного треугольника как х, получим:

2( 8² + 9² ) = 13² + x²
290 = 169 + x²
x² = 290 – 169
x² = 121
х = 11

Поскольку искомая медиана равна половине диагонали параллелограмма, то величина медианы треугольника составит 11 / 2 = 5,5 см

Ответ: 5,5 см

Медиана треугольника |

Описание курса

| Нахождение площади через медианы

Источник

Все формулы медианы треугольника

Как найти медиану треугольника по его сторонам

Задача. Найти длину медианы треугольника через его стороны

Вам также может понравиться

Как найти имущество по фамилии владельца

Как найти титаниум в террарии

Как найти повара в хабаровске

Добавить комментарий Отменить ответ