Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике – мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
Мода и медиана функции плотности распределения f(x)
Задача 5. Плотность распределения вероятностей случайной величины Х имеет вид

1. Найти:
а) параметр распределения С (в виде дроби);
а) математическое ожидание M(X);
б) дисперсию D(X) и среднее квадратическое отклонение σ(Х);
в) функцию распределения F(x) случайной величины X;
г) моду M0;
д) медиану Me;
е) вероятность осуществления неравенств ![]() и
и ![]() .
.
2. Построить графики функций f(x) и F(x). Изобразить на графике функции f(x) найденные характеристики и вероятности.
Решение находим с помощью калькулятора.
Случайная величина Х задана плотностью распределения f(x):
0, x ≤ 0
2•A(8/5-x), 0 < x < 8/5
0, x ≥ 8/5
Найдем параметр A из условия:


или
64/25*A-1 = 0
Откуда,
A = 25/64
Поскольку находили квадрат A, то ![]()
а) Математическое ожидание.


б) Дисперсия.


= -25/128•(8/5)4+5/12•(8/5)3 – (-25/128•04+5/12•03) – (8/15)2 = 32/225
Среднеквадратическое отклонение.
![]()
в) Функция распределения F(x) случайной величины X.



г) Мода M0.
Модой M0(X) называют то возможное значение X, при котором плотность распределения имеет максимум.
Построим график функции плотности распределения.

Как видим, максимум функции соответствует x = 0.
Mo( 0) = 2•25/64(8/5-0) = 5/4
д) Медиана Me.
Медианой Me(X) называют то возможное значение X, при котором ордината f(x) делит пополам площадь, ограниченную кривой распределения.
Необходимо найти такое x, при котором функция распределения равна ½.


Решая уравнение:
![]()
получаем:
![]()
![]()
Поскольку функция ограничена на интервале (0; 1,6), то искомое значение x = 0,46.
![]()
Построим график функции распределения.

е) Вероятность осуществления неравенств ![]() и
и ![]() .
.
![]()
![]()
Перейти к онлайн решению своей задачи
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Мода и медиана случайных величин
Основными числовыми
характеристиками случайных величин
являются математическое ожидание,
дисперсия и среднее квадратическое
отклонение. Однако часто возникает
потребность и в некоторых других числовых
характеристиках. Две из них, обозначенные
в заголовке, и будут далее определены.
Пусть Х
– дискретная случайная величина. Модой
этой с.в. (обозначается d(X)
) называется такое ее возможное значение,
которое имеет наибольшую вероятность.
Пример.
Пусть дискретная
с.в. Х
задана законом распределения
|
Х |
1 |
2 |
3 |
4 |
5 |
6 |
|
Р |
0.1 |
0.1 |
0.3 |
0.1 |
0.3 |
0.1 |
Тогда ее мода
принимает 2 значения: d(Х)=3
и d(Х)=5.
Пусть Х
– непрерывная
случайная величина с плотностью
вероятности f(х).
Модой
этой с.в. называется точка максимума ее
плотности вероятности. Эта точка
максимума функции f(x)
находится обычными методами с
использованием производной.
Пример.
Дана плотность вероятности н.с.в. :
 .
.
Найти значение
параметра а
и моду этой случайной величины.
Пусть Х
– непрерывная случайная величина.
Медианой
с.в. Х
(обозначается h(X)
) называется такое число h,
которое делит всю числовую прямую на 2
промежутка (−∞,
h)
и
[h,+∞),
в которые с.в. Х
попадает с равной вероятностью. Таким
образом, если медиана h(X)=h,
то выполняется
равенство
P(X
< h)=P(X
≥ h)
=![]() .
.
Вспоминая, что
вероятность P(X
< h)
по определению функции распределения
есть значение этой функции в точке h,
получаем, что значение h
медианы h(X)
удовлетворяет уравнению
![]() .
.
Если же у н.с.в.
задана не функция распределения F(x),
а плотность вероятности f(x),
то вспоминая выражение функции
распределения через плотность вероятности
![]()
, получим, что значение h
медианы удовлетворяет уравнению
![]() .
.
Медиана h(X)
непрерывной с.в. Х
ищется из одного из выписанных выше
уравнений (в зависимости от того, что
задано: F(x)
или f(x)
). Для дискретных случайных величин
медиана не определяется.
Пример.
Найти медиану н.с.в. Х,
заданной своей функцией распределения
 .
.
Ответ: h(X)=1.5
.
Некоторые важные законы распределения случайных величин
Среди различных
законов распределения случайных величин
некоторые встречаются в приложениях
наиболее часто. Поэтому для них получены
формулы расчета их числовых характеристик:
математического ожидания, дисперсии,
моды, медианы и ряда других. Рассмотрим
некоторые из таких законов распределения.
Биномиальный закон распределения
Среди законов
распределения дискретных
случайных величин наиболее распространенным
является биномиальное распределение,
с которым мы уже встречались при
рассмотрении так называемой схемы
Бернулли (число появлений некоторого
события в серии независимых испытаний).
Дискретная случайная
величина Х
распределена по биномиальному
закону, если
она принимает значения 0,
1, 2, … , n
с вероятностями р0
, р1
, … ,
рn,
которые вычисляются по формуле
![]() ,
,
где параметр
распределения р
заключен между нулем и единицей 0
≤ р ≤ 1 , а
q=1−p
. Таким образом, д.с.в Х,
распределенная по биномиальному закону,
имеет следующий закон распределения:
|
Х |
0 |
1 |
2 |
… |
n |
|
Р |
|
|
|
… |
|
Как уже говорилось,
по биномиальному закону распределено
число успехов в схеме Бернулли. Пусть
производится n
независимых
испытаний, в каждом из которых некоторое
событие А
может появиться с одной и той же
вероятностью р.
Рассмотрим с.в. Х
– число появлений события А
во всех n
испытаниях (то, что ранее называли число
успехов). Тогда с.в. Х
распределена по биномиальному закону.
Мы уже находили формулы для математического
ожидания этой случайной величины,
которые и являются формулами математического
ожидания и дисперсии произвольной
случайной величины, распределенной по
схеме Бернулли:
![]() ,
,
![]() .
.
Найдем моду d(X)
биномиально распределенной случайной
величины Х,
т.е. наивероятнейшее
число успехов в схеме Бернулли.
По определению моды d(X)=k,
если вероятность
![]()
наибольшая среди всех вероятностей р0
, р1
, … , рn
. Найдем
такое число k
(это целое
неотрицательное число). При таком k
вероятность pk
должна быть не меньше соседних с ней
вероятностей: pk−1
≤ pk
≤ pk+1
. Подставив вместо каждой вероятности
соответствующую формулу, получим, что
число k
должно удовлетворять двойному неравенству:
![]() .
.
Если расписать
формулы для числа сочетаний и провести
простые преобразования, можно получить,
что левое неравенство дает k
≤ (n+1)∙p,
а правое k
≥ (n+1)∙p
−1. Таким
образом, число k
удовлетворяет двойному неравенству
(n+1)∙p
−1 ≤ k
≤ (n+1)∙p
, т.е. принадлежит отрезку
[(n+1)∙p
−1, (n+1)∙p]
. Поскольку длина этого отрезка, очевидно,
равна 1,
то в него может попасть либо одно, либо
2 целых числа. Если число (n+1)∙p
целое, то в
отрезке [(n+1)∙p
−1, (n+1)∙p]
имеется 2 целых числа, лежащих на концах
отрезка. Если же число (n+1)∙p
не целое, то
в этом отрезке есть только одно целое
число.
Таким образом,
если число (n+1)∙p
целое, то
мода биномиально распределенной
случайной величины Х
принимает 2 соседних значения : d(X)=(n+1)∙p
−1 и
d(X)=(n+1)∙p
. Если же число (n+1)∙p
не целое,
то мода биномиально распределенной
случайной величины Х
одно значение
d(X)=k,
где k
есть
единственное целое число, удовлетворяющее
неравенству
(n+1)∙p
−1 ≤ k
≤ (n+1)∙p
. Если вспомнить, что запись [a]
означает взятие целой части от числа
а,
то в этом случае можно записать
d(X)=[(n+1)∙p]
.
Пример.
Кубик подбрасывается 100 раз. Каково
наивероятнейшее число выпадений
шестерки?
Пример.
Вероятность попадания стрелком в цель
равна 0.7 . Найти наивероятнейшее число
попаданий в цель при 30 выстрелах.
Пример.
Вероятность изготовления бракованной
детали на станке равна 0.06 . Каково
наивероятнейшее число бракованных
деталей в партии из 200 деталей, выточенных
на этом станке?
Пример.
Банк выдал 7 кредитов. Известно, что в
среднем не возвращается 2 кредита из
10. Найти среднее число невозвращенных
кредитов.
Соседние файлы в папке методичка
- #
- #
- #
Центральную тенденцию данных можно рассматривать не только, как значение с нулевым суммарным отклонением (среднее арифметическое) или максимальную частоту (мода), но и как некоторую отметку (значение в совокупности), делящую ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Половина исходных данных меньше этой отметки, а половина – больше. Это и есть медиана.
Итак, медиана в статистике – это уровень показателя, который делит набор данных на две равные половины. Значения в одной половине меньше, а в другой больше медианы. В качестве примера обратимся к набору нормально распределенных случайных чисел.
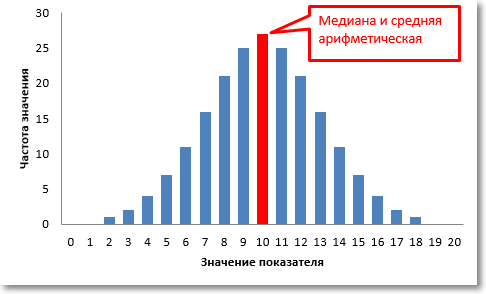
Очевидно, что при симметричном распределении середина, делящая совокупность пополам, будет находиться в самом центре – там же, где средняя арифметическая (и мода). Это, так сказать, идеальная ситуация, когда мода, медиана и средняя арифметическая совпадают и все их свойства приходятся на одну точку – максимальная частота, деление пополам, нулевая сумма отклонений – все в одном месте. Однако, жизнь не так симметрична, как нормальное распределение.
Допустим, мы имеем дело с техническими замерами отклонений от ожидаемой величины чего-нибудь (содержания элементов, расстояния, уровня, массы и т.д. и т.п.). Если все ОК, то отклонения, скорее всего, будут распределены по закону, близкому к нормальному, примерно, как на рисунке выше. Но если в процессе присутствует важный и неконтролируемый фактор, то могут появиться аномальные значения, которые в значительной мере повлияют на среднюю арифметическую, но при этом почти не затронут медиану.
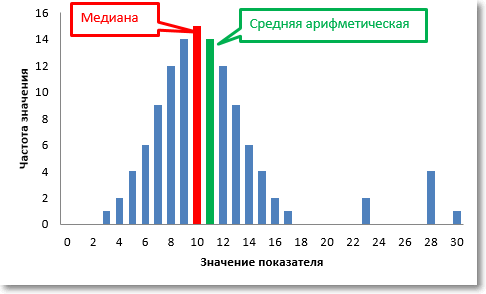
Медиана выборки – это альтернатива средней арифметической, т.к. она устойчива к аномальным отклонениям (выбросам).
Математическим свойством медианы является то, что сумма абсолютных (по модулю) отклонений от медианного значения дает минимально возможное значение, если сравнивать с отклонениями от любой другой величины. Даже меньше, чем от средней арифметической, о как! Данный факт находит свое применение, например, при решении транспортных задач, когда нужно рассчитать место строительства объектов около дороги таким образом, чтобы суммарная длина рейсов до него из разных мест была минимальной (остановки, заправки, склады и т.д. и т.п.).
Формула медианы
Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.
Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:
![]()
где
№Me – номер значения, соответствующего медиане,
N – количество значений в совокупности данных.
Тогда медиана обозначается, как
![]()
Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:
![]()
В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу.
Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.
Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.
Обратимся к наглядной схеме.
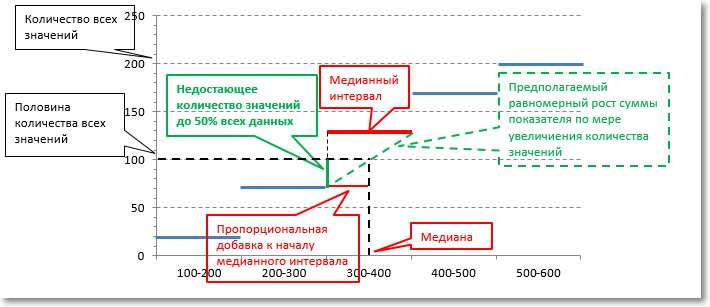
Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:
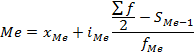
где xMe — нижняя граница медианного интервала;
iMe — ширина медианного интервала;
∑f/2 — количество всех значений, деленное на 2 (два);
S(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;
fMe — число наблюдений в медианном интервале.
Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%.
Для примера рассчитаем медиану по следующим данным.
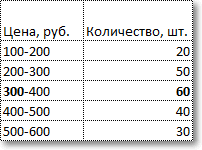
Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.
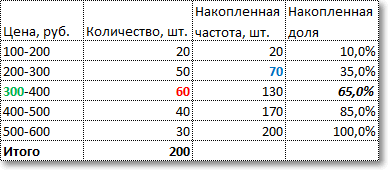
По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.
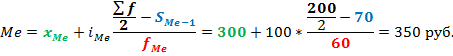
То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.
Расчет медианы в Excel
Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.
Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:
а) 11;
б) 5;
в) 10;
г) 5, 10, 11.
Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.
Ниже видеоролик о том, как рассчитать медиану в Excel.
Поделиться в социальных сетях:
У этого термина существуют и другие значения, см. Медиана.
Медиа́на (от лат. mediāna «середина») или набора чисел — число, которое находится в середине этого набора, если его упорядочить по возрастанию, то есть такое число, что половина из элементов набора не меньше него, а другая половина не больше. Другое равносильное определение[1]: медиана набора чисел — это число, сумма расстояний (или, если более строго, модулей) от которого до всех чисел из набора минимальна. Это определение естественным образом обобщается на многомерные наборы данных и называется 1-медианой.
Например, медианой набора {11, 9, 3, 5, 5} является число 5, так как оно стоит в середине этого набора после его упорядочивания: {3, 5, 5, 9, 11}. Если в выборке чётное число элементов, медиана может быть не определена однозначно: тогда для числовых данных чаще всего используют полусумму двух соседних значений (то есть медиану набора {1, 3, 5, 7} принимают равной 4), подробнее см. ниже.
В математической статистике медиана может использоваться как одна из характеристик выборки или совокупности чисел.
Также определяется медиана случайной величины: в этом случае оно определяется как число, которое делит пополам распределение. Грубо говоря, медианой случайной величины является такое число, что вероятность получить значение случайной величины справа от него равна вероятности получить значение слева от него (и они обе равны 1/2), — более точное определение дано ниже.
Можно также сказать, что медиана является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.
Свойства медианы для случайных величин[править | править код]
Если распределение непрерывно, то медиана является одним из решений уравнения
,
где 


.
Если распределение является непрерывной строго возрастающей функцией, то решение уравнения однозначно. Если распределение имеет разрывы, то медиана может совпадать с минимальным или максимальным (крайним) возможным значением случайной величины, что противоречит «геометрическому» пониманию этого термина.
Медиана является важной характеристикой распределения случайной величины и, так же как математическое ожидание, может быть использована для центрирования распределения. Поскольку оценки медианы более робастны, её оценивание может быть более предпочтительным для распределений с т. н. тяжёлыми хвостами. Однако о преимуществах оценивания медианы по сравнению с математическим ожиданием можно говорить только в случае, если эти характеристики у распределения совпадают, в частности, для симметричных функций плотности распределения вероятностей.
Медиана определяется для всех распределений, а в случае неоднозначности, естественным образом доопределяется, в то время как математическое ожидание может быть не определено (например, у распределения Коши).
Пример использования[править | править код]
Рассмотрим финансовое состояние 19 малоимущих, у каждого из каких есть только 5 ₽, и одного миллионера, у которого буквально 1 млн ₽. Тогда в сумме у них получается 1 000 095 ₽. Если деньги равными долями разделить на 20 человек, получится 50 004,75 ₽. Это будет среднее арифметическое значение суммы денег, которая была у всех 20 человек в этой комнате.
Медиана же будет равна 5 ₽ (сумма «расстояния» от этой величины до состояния каждого из рассматриваемых людей минимальна). Это можно интерпретировать следующим образом: «разделив» всех рассматриваемых людей на две равные группы по 10 человек, мы получаем, что в первой группе у каждого не больше 5 ₽, во второй же — не меньше 5 ₽.
Из этого примера получается, что в качестве «серединного» состояния, грубо говоря, корректнее всего использовать именно медиану, а вот среднее арифметическое, наоборот, значительно превышает сумму наличных, имеющуюся у случайного человека из выборки.
Различны изменения в динамике и у средней арифметической с медианой, например в вышеприведённом примере, если у миллионера станет 1,5 млн. ₽ (+50 %), а у остальных станет 6 ₽ (+20 %), то средняя арифметическая выборки станет равна 75 005,70 ₽, то есть как бы у всех повысились равномерно на 50 %, при этом медиана станет равной 6 ₽ (+20 %).
Неуникальность значения[править | править код]
Если имеется чётное количество случаев и два средних значения различаются, то медианой, по определению, может служить любое число между ними (например, в выборке {1, 3, 5, 7} медианой может служить любое число из интервала (3,5)). На практике в этом случае чаще всего используют среднее арифметическое двух средних значений (в примере выше это число (3+5)/2=4). Для выборок с чётным числом элементов можно также ввести понятие «нижней медианы» (элемент с номером n/2 в упорядоченном ряду из 
См. также[править | править код]
- Мода — значение во множестве наблюдений, которое встречается наиболее часто.
- Среднее арифметическое набора чисел — число, сумма квадратов расстояний от которого до всех чисел из набора минимальна[3].
Примечания[править | править код]
- ↑ Сущность медианы. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.
- ↑ Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест Рональ Л., Штайн, Клиффорд. Алгоритмы. Построение и анализ. — 2-е издание. — М.: Издательский дом «Вильямс», 2005. — С. 240. — 1296 с.
- ↑ Почему это равносильные определения среднего арифметического.
Литература[править | править код]
- Медиана // Маниковский — Меотида. — М. : Большая российская энциклопедия, 2012. — С. 479—480. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 19). — ISBN 978-5-85270-353-8.
- Медиана // Большая российская энциклопедия [Электронный ресурс]. — 2017.
