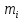Как найти медиану ранжированного ряда

1. Медиана

Медианой
(Me)
называется значение признака, которое
лежит в середине ранжированного ряда.
Ранжированный
ряд
– ряд, расположенный в порядке возрастания
или убывания значений признака.

В
дискретном ряду медиана находится на
основе накопленных частот. Номер медианы
равен половине суммы всех частот. Частоты
накапливаются до тех пор, пока не будет
превзойдён номер медианы. Медиана
равняется частоте, соответствующей
номеру медианы.

В
интервальном ряду сначала находится
медианный интервал. Номер медианы равен

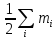или.
По номеру определяется интервал, которому
этот номер принадлежит. Затем медиана
определяется по формуле:

где

x_k-1
– нижняя граница медианного интервала;

h_k
– длина медианного интервала;

F_k-1
–
накопленная частота интервала,
предшествующему медианному;

m_k
–
частота медианного интервала;

P_k-1
– накопленная частость интервала,
предшествующему медианному.

Если
требуется найти медиану в ранжированном
ряду без частот, то номер медианы можно
определить по формуле (N+1)/2,
если ряд содержит нечётное число
элементов. Затем по номеру медианы
выбирается медиана из значений признака.
Если ряд содержит четное число элементов,
то медиана вычисляется по формуле:

где

N
– число элементов в ряду.

В
интервальном ряду медиана определяется
по кумуляте. Для этого из точки на шкале
накопленных частот (частостей),
соответствующей
,
проводится прямая, параллельная оси
абсцисс до пересечения с кумулятой.
Затем на ось абсцисс опускается
перпендикуляр. Абсцисса точки пересечения
является медианой.

Пример 15.
Вычисление
медианы для дискретного вариационного
ряда

Найти
медиану для распределения сотрудников
по тарифным разрядам.

Тарифный разряд	Число сотрудников, чел	Накопленная частота
2	11	11
3	18	29
4	22	51
5	20	71
6	14	85
Итого	85

Ряд
является дискретным. Номер медианы
равен 42 или 43 (85/2). Накапливать частоты
нужно до тех пор, пока не будет превзойдён
номер медианы: 11 сотрудников имеют не
более, чем 2 разряд; 29 сотрудников имею
не более, 3 разряд; 51 сотрудник имеет не
более, чем 4 разряд. Т.е. число сотрудников
42 и 43 приходится на 4 разряд. Следовательно,
Me=4.

Пример 16.
Вычисление
медианы для интервального вариационного
ряда с равной длиной интервалов

Найти
медиану для распределения сотрудников
по возрастам.

Возрастные группы сотрудников, лет	Число сотрудников, чел	Накоплен- ные частоты	Частости	Накопленные частости
в долях	в %	в долях	в %
20 – 30	11	11	0,1294	12,94	0,1294	12,94
30 – 40	33	44	0,3882	38,82	0,5176	51,76
40 – 50	22	66	0,2588	25,88	0,7764	77,64
50 – 60	15	81	0,1765	17,65	0,9529	95,29
60 – 70	4	85	0,0471	4,71	1	100
Итого	85		1	100

Ряд
является интервальным. Номер медианы,
рассчитанный на основе накопленных
частот, равен 42 или 43 (85/2), а накопленный
на основе частостей равен 50 (100/2). На
основе накопленных частот определяется,
что числу сотрудников 42 и 43 соответствует
возрастной интервал 30 – 40. Далее находится
медиана:

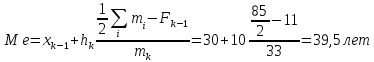
Графическое
определение медианы:

Пример 17.
Вычисление
медианы ранжированного ряда с нечетным
числом интервалов

Найти
медиану для ранжированного ряда, в
котором представлены набранные баллы
участников конкурса.

Место	Фамилия	Баллы
1	Иванов	135
2	Смирнов	117
3	Петров	98
4	Сидоров	89
5	Фёдоров	64
6	Макаров	57
7	Казаков	53

В
таблице нечётное число элементов. Номер
медианы равен ((7+1)/2)=4. Этому номеру
соответствует медиана M_e
= 89 баллов.

Пример 18.
Вычисление
медианы ранжированного ряда с нечетным
числом интервалов

Найти
медиану для ранжированного ряда, в
котором представлены набранные баллы
участников конкурса.

Место	Фамилия	Баллы
1	Иванов	135
2	Смирнов	117
3	Петров	98
4	Сидоров	89
5	Фёдоров	64
6	Макаров	7

В
таблице чётное число элементов. Медиана
вычисляется по формуле:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

8.4. МОДА и МЕДИАНА (структурные средние)

 Мода и медиана наиболее часто используемые в экономической практике структурные средние.

---

Мода – это величина признака (варианта), который наиболее часто встречается  в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.

---

В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.

---

Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:

(8.16 – формула Моды)

---

где х_о – начальная (нижняя) граница модального интервала;

h – величина интервала;

f_Мо – частота модального интервала;

f_Мо-1 – частота интервала, предшествующая модальному;

f_Мо+1– частота интервала следующая за модальным.

---

---

Медианой  называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.

В дискретном ряду медиана находится  непосредственно по накопленной частоте, соответствующей номеру медианы.

В случае интервального вариационного ряда медиану определяют по формуле:

                                           (8.17 – формула Медианы)

---

где х_о – нижняя граница медианного интервала;

N_Ме– порядковый номер медианы (Σf/2);

S _Me-1 – накопленная частота до медианного интервала;

f_Ме –  частота медианного интервала.

---

Пример вычисления Моды.

Рассчитаем моду и медиану по данным табл. 8.4.

Таблица 8.4 – Распределение семей города N  по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)

Группы семей по размеру дохода, руб.	Число семей	Накоп- ленные частоты	в % к итогу
До 5000	600	600	6
5000-6000	700	1300 (600+700)	13
6000-7000	1700 (fМо-1)	3000 (S Me-1 ) (1300+1700)	30
7000-8000  (хо)	2500 (fМо) (fМе)	5500 (S Me)	55
8000-9000	2200 (fМо+1)	7700	77
9000-10000	1500	9200	92
Свыше 10000	800	10000	100
Итого	10000	–	–

Пример вычисления Моды. Найдем моду по формуле (8.16) см. обозначения в таблице, а h = 8000-7000=1000, т.е. получаем:

Пример вычисления Моды

---

Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):

1) сначала находим  порядковый  номер медианы: N_Ме = Σf_i/2= 5000.

2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее  значение медианы  определим по формуле (8.17):

Пример вычисления Медианы

---

Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.

---

Пример .СРЕДНИЙ, МЕДИАННЫЙ И МОДАЛЬНЫЙ УРОВЕНЬ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ  ЦЕЛОМ ПО РОССИИ И ПО СУБЪЕКТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ЗА 2013 год см. по ссылке. Источник: оценка на основании данных ^{выборочного обследования бюджетов домашних хозяйств и макроэкономического показателя денежных доходов населения}

---

Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.

Если Мо<М_е<Х – имеет место правосторонняя асимметрия.

При Х<М_е<Мо следует сделать вы­вод о левосторонней асимметрии ряда.

---

Средние величины (арифметическая, гармоническая, геометрическая, квадратическая) см. по ссылке

Оценка статьи:

Загрузка…

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4.

Расчёт структурных характеристик
вариационного ряда распределения.

Студент
должен:

знать:

–   область применения и методику расчёта структурных
средних величин;

уметь:

–   исчислять структурные средние величины;

–   формулировать вывод по полученным результатам.

Методические указания

В
статистике исчисляются мода и медиана, которые относятся к структурным средним,
так как  их величина зависит от строения статистической совокупности.

Расчёт моды

Модой называется значение признака
(варианта), чаще всеговстречающееся в изучаемой
совокупности. В дискретном ряду распределения модой будет варианта с наибольшей
частотой.

Например: Распределение проданной женской обуви по размерам характеризуется
следующим образом:

Размер обуви	34	35	36	37	38	39	40	41
Количество проданных пар	8	19	34	108	72	51	6	2

В этом ряду
распределения  модой является 37 размер,
т.е. Мо=37 размер.

Для
интервального ряда распределения мода определяется по формуле:

где Х_Mo –
нижняя граница модального интервала;

h_Mo  – величина модального интервала;

f_Mo –
частота модального интервала;

f_{Mo–1  и} 
f_Mo+1 – частота интервала соответственно

предшествующего модальному и следующего за ним.

Например:
Распределение рабочих по стажу работы характеризуется следующими данными.

Стаж работы, лет	до 2	2-4	4-6	6-8	8-10	10 и более
Число рабочих, чел.	4	23	20	35	11	7

Определить моду
интервального ряда распределения.

Мода интервального ряда составляет

Мода всегда бывает
несколько неопределённой, т.к. она зависит от величины групп и точного
положения границ групп. Мода широко применяется в коммерческой практике при
изучении покупательского спроса, при регистрации цен и т.п.

Расчёт медианы

Медианой в статистике называется варианта,
расположенная в середине упорядоченного ряда данных, и которая делит
статистическую совокупность на две равные части так, что у одной половины
значения меньше медианы, а у другой половины – больше её. Для определения
медианы необходимо построить ранжированный ряд, т.е. ряд в порядке возрастания
или убывания индивидуальных значений признака.

В дискретном
упорядоченном ряду с нечётным числом членов медианой будет варианта,
расположенная в центре ряда.

Например: Стаж пяти рабочих составил 2, 4, 7, 9 и 10 лет. В таком ряду медиана-7
лет, т.е. Ме=7 лет

Если дискретный
упорядоченный ряд состоит из чётного числа членов, то медианой будет средняя
арифметическая из двух смежных вариант, стоящих в центре ряда.

Например: Стаж работы шести рабочих составил 1, 3, 4, 5, 10 и 11лет. В этом ряду
имеются две варианты, стоящие в центре ряда. Это варианты 4 и 5. Средняя
арифметическая из этих значений и будет медианой ряда

 

Чтобы определить медиану для
сгруппированных данных, необходимо считать накопленные частоты.

Например: По имеющимся данным определим медиану размера обуви

Размер обуви	Количество проданных пар	Сумма накопленных частот
34	8	8
35	19	8+19=27
36	34	27+34=61
37	108	61+108=169
38	72	–
39	51	–
40	6	–
41	2	–
Итого	300

Для
определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание
итога продолжается до получения накопленной суммы  частот, превышающей половину суммы частот
ряда. В нашем примере сумма частот составила 300, её половина – 150. Накопленная
сумма частот получилась равной 169. Варианта, соответствующая этой сумме, т.е.
37 и есть медиана ряда.

Если
же сумма накопленных частот против одной из вариант равна точно половине суммы
частот ряда, то медиана определяется как средняя арифметическая этой варианты и
последующей.

Например: По имеющимся данным определим медиану заработной платы рабочих

Месячная заработная плата, тыс.руб.	Число рабочих, чел.	Сумма накопленных частот
14,0	2	2
14,2	6	2+6=8
16,0	12	8+12=20
16,8	16	–
18,0	4	–
Итого:	40	–

Медиана будет равна:

Медиана
интервального вариационного ряда распределения определяется по формуле:

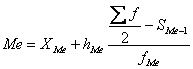
Где  Х_Ме – нижняя граница медианного интервала;

h_Me –
величина медианного интервала;

∑f 
– сумма частот ряда;

f_Ме – частота медианного интервала;

Например: По имеющимся данным о распределении предприятий по численности
промышленно – производственного персонала рассчитать медиану в интервальном
вариационном ряду

Группы предприятий по численности ППП, чел.	Число предприятий	Сумма накопленных частот
100-200	1	1
200-300	3	1+3=4
300-400	7	4+7=11
400-500	30	11+30=41
500-600	19	–
600-700	15	–
700-800	5
Итого:	80

Определим, прежде всего,
медианный интервал. В данном примере сумма накопленных частот, превышающих половину
суммы всех значений ряда, соответствует интервалу 400-500.Это и есть медианный
интервал, т.е. интервал, в котором находится медиана ряда. Определим её
значение

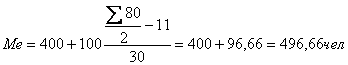
Если же сумма накопленных частот
против одного из интервалов равна точно половине суммы частот ряда, то медиана
определяется по формуле:

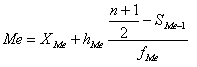
где n – число
единиц в совокупности.

Например: По имеющимся данным о распределении предприятий по
численности промышленно – производственного персонала рассчитать медиану в
интервальном вариационном ряду

Группы предприятий по численности ППП, чел.	Число предприятий	Сумма накопленных частот
100-200	1	1
200-300	3	1+3=4
300-400	6	4+6=10
400-500	30	10+30=40
500-600	20	40+20=60
600-700	15	–
700-800	5
Итого:	80

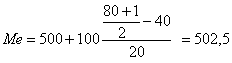чел

Моду и медиану в
интервальном ряду можно определить
графически:

моду
в дискретных рядах – по полигону распределения, моду в интервальных рядах – по
гистограмме распределения, а медиану – по кумуляте.

Мода интервального ряда распределения
определяется по гистограмме распределения определяют
следующим образом. Для этого выбирается самый высокий прямоугольник, который
является в данном случае модальным. Затем правую вершину модального
прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения.

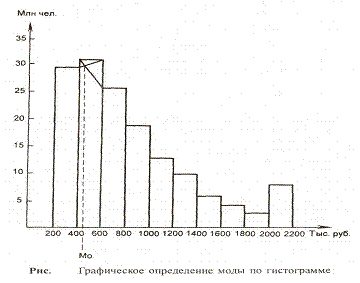
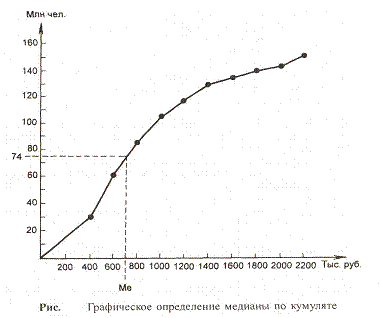
Медиана рассчитывается по
кумуляте. Для её определения из точки на шкале
накопленных частот (частостей), соответствующей 50%,
проводится прямая, параллельная оси абсцисс, до
пересечения с кумулятой. Затем из точки пересечения
указанной прямой с кумулятой опускается перпендикуляр
на ось абсцисс. Абсцисса точки пересечения является медианой.

Кроме моды и медианы в вариантных рядах могут быть
определены и другие структурные характеристики – квантили. Квантили
предназначены для более глубокого изучения структуры ряда распределения.

Квантиль – это значение
признака, занимающее определенное место в упорядоченной по данному признаку
совокупности. Различают следующие виды квантилей:

–      квартили  – значения признака, делящие упорядоченную
совокупность на четыре
равные части;

–      децили
– значения признака, делящие упорядоченную совокупность на десять
равных частей;

–      перцентели –
значения признака, делящие упорядоченную совокупность на сто равных частей.

Таким образом, для характеристики положения центра ряда распределения
можно использовать 3 показателя: среднее значение признака, мода, медиана. При выборе вида и формы конкретного показателя
центра распределения необходимо исходить из следующих рекомендаций:

–                
для устойчивых социально-экономических
процессов в качестве показателя центра используют среднюю
арифметическую. Такие процессы характеризуются симметричными распределениями, в
которых ;

–                
для неустойчивых процессов положение
центра распределения характеризуется с помощью Mo
или Me. Для асимметричных процессов предпочтительной
характеристикой центра распределения является медиана, поскольку занимает
положение между средней арифметической и модой.



3.1.3. Медиана

Медиана  вариационного ряда* – это значение, которая делит его на две

равные части (по количеству вариант).

* не важно, дискретного или интервального, генеральной совокупности или выборочной.

Медиану можно отыскать несколькими способами. Если даны первичные данные, то сортируем их по возрастанию либо

убыванию и находим середину ранжированного ряда: .

Почему именно 13-я варианта? Потому что перед ней находится 12 чисел и после неё тоже 12 чисел, таким образом, значение  разделило ряд на две равные части, а значит, является

медианой. Этот номер можно найти аналитически:

– если совокупность содержит нечётное количество вариант (наш случай), то делим её объём пополам:  и округляем полученное значение в бОльшую сторону: 13

– получая тем самым номер искомой варианты;

– если совокупность содержит чётное количество вариант, например 20, то делаем то же самое:  и медианное значение рассчитываем как среднее

арифметическое 10-й и следующей варианты: .
Подчёркиваю, что изложенная выше инструкция работает для упорядоченного (по возрастанию либо убыванию) ряда. Но есть и

более быстрый путь, где ничего не нужно сортировать. Это использование стандартной функции Экселя:

– забиваем в любую свободную ячейку =МЕДИАНА(, выделяем мышью все варианты, закрываем скобку ) и жмём Enter. Попробуйте самостоятельно. Этот способ удобен, когда вам дано много чисел.

Следует отметить, что в Экселе существуют и отдельные функции для вычисления средней (=СРЗНАЧ), моды

(=МОДА) и ещё много чего, но я против использования этих функций в учебном курсе, за исключением случаев, где это

действительно целесообразно. …Почему против? Потому что они не помогают понять суть показателей. Так, среднюю гораздо

вразумительнее рассчитывать следующим образом:

=СУММ(выделяем мышью диапазон) / объем совокупности. Вычисления рекомендую опробовать лично (ссылка выше).

Ситуация вторая. Когда составлен либо изначально дан готовый дискретный ряд. Тут

можно поступить «по любительски» – начать отсчитывать примерно равное количество вариант по краям ряда:

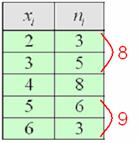
после чего мысленно либо на черновике их отбрасывать, в данном случае отбросим по 8 штук сверху и снизу:

откуда становится ясно, что медианное значение:

Или в более солидном стиле, находим относительные накопленные

частоты:

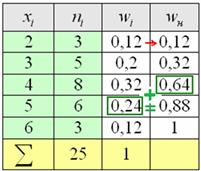
и ту варианту, у которой  «перевалила» за

отметку 0,5 (50% упорядоченной совокупности). Для варианты  успело накопиться  (32% совокупности), а вот для  – уже  (64%). Таким образом, отметка в 50% пройдена именно здесь, и, стало быть, .

Запишем красивый ответ:

И тут возникает следующий закономерный вопрос: а зачем вообще нужна мода с медианой? –

ведь есть средняя. А дело в том, что в ряде случаев среднее значение неудовлетворительно характеризует центральную

тенденцию совокупности:

Пример 9

Известны результаты продаж пиджаков в универмаге города:

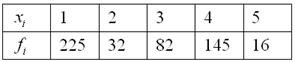
где  – количество пуговиц на пиджаке,  – число продаж.

Обратите внимание, что в условии задачи ничего не сказано о том, генеральная ли это совокупность или

выборочная, и в подобной ситуации я не рекомендую ничего додумывать – среднюю просто

обозначаем через , без подстрочного индекса.

Задание: вычислить среднюю. В экселевском файле уже забиты исходные

данные и приведена краткая инструкция. Если под пальцами нет Экселя, считаем на калькуляторе. Ну а если вам не нравятся

пиджаки, то представьте какие-нибудь шляпки с цветочками:)

….Есть? Какие мысли на счёт полученного значения ? …С такой статистикой магазин разорится.

Ещё хуже в этом смысле ситуация с медианой, продолжаем решать задачу в Экселе либо в тетради. Особо зоркие читатели, медиану углядят устно.

И, конечно, важнейший показатель здесь мода: . Потому что такая мода 🙂 Более того, в прикладных исследованиях рассматривают

несколько модальных значений, в частности, ещё одной модой можно считать варианту . Но это уже «попсовая» статистика, которую я не буду развивать в настоящем курсе.

Теперь надеваем пиджаки / шляпы и возвращаемся на фабрику, где бухгалтер Петрова вычислила генеральную среднюю заработную плату рабочих:  денежных единиц. Здесь мы плавно переходим к интервальному ряду, который целесообразно составлять для «денежных» показателей.

Что будет, если к совокупности добавить руководящий персонал и директора Петрова? Средняя зарплата немного увеличится: , и это уже будет несколько искажённая картина.

А вот если сюда добавить олигарха Петровского, то полученная средняя  вообще вызовет широкое возмущение общественности.

Поэтому если в статистической совокупности есть «аномальные» отклонения в ту или иную сторону, то в качестве оценки

центрального значения как нельзя лучше подходит медиана, которая в нашем условном примере будет равна,

скажем, . Ниже этой планки зарабатывает ровно

половина сотрудников фабрики и выше – другая половина, включая Петрова и Петровского. …Главное только, чтобы они наняли

правильного статистика 🙂

3.1.4. Как вычислить среднюю, моду и медиану интервального ряда?

3.1.2. Мода

| Оглавление |



Структурные средние – мода, медиана, квантиль, дециль

Краткая теория

---

Наиболее широкое применение в статистике имеют структурные
средние, к числу которых относятся мода и медиана (непараметрические средние).

Мода  – величина признака (варианта), которая
встречается в ряду распределения с наибольшей частотой (весом). К моде (Мо)
прибегают для выявления величины признака, имеющей наибольшее распространение
(цена на рынке, по которой было совершено наибольшее число продаж данного
товара, номер обуви, который пользуется наибольшим спросом у покупателей и т.
д.). Мода используется только в совокупностях большой численности. В дискретном
ряду мода находится как варианта, имеющая наибольшую частоту. В интервальном
ряду сначала находится модальный интервал, то есть  интервал, обладающий наибольшей частотой, а
затем – приближенное значение модальной величины признака по формуле:

 – нижняя граница модального интервала

  – величина модального интервала

 – частота интервала, предшествующего
модальному

 – частота модального интервала

 

 – частота интервала, следующего за модальным

Квантили –
величины, разделяющие совокупность на определенной количество равных по
численности элементов частей. Самый известный квантиль – медиана,  делящая совокупность на две равные части.  Кроме медианы часто используются квартили,  делящие ранжированный ряд на 4 равные части,  децили -10 частей и перцентили – на 100
частей.

Медиана –
величина признака у единицы, находящейся в середине ранжированного
(упорядоченного) ряда. Если ряд распределения представлен конкретными
значениями признака, то медиана (Me) находится как
серединное значение признака.

Если ряд распределения дискретный, то медиана находится как
серединное значение признака (например, если число значений нечетное – 45, то

 соответствует 23 значению признака в ряду
значений, расположенных в порядке возрастания, если число значений четное – 44,
то медиана соответствует полусумме 22 и 23 значений
признака).

Если ряд распределения интервальный, то первоначально
находят медианный интервал, который содержит единицу, находящуюся в середине
ранжированного ряда. Для определения этого интервала сумму частот

 делят пополам и на основании  последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:

  – нижняя граница медианного интервала

   – величина медианного интервала

  – сумма
частот ряда

 – сумма накопленных частот в интервалах,
предшествующих медианному

 – частота медианного интервала

Квартили – это значения
признака в ранжированном ряду, выбранные таким образом, что 25% единиц
совокупности будут меньше величины

,  25% единиц будут заключены между 

 и

 ; 25%  –
между  

  и

,
остальные 25% превосходят

.  Квартили определяются по формулам,
аналогичным формуле для расчета медианы. Для интервального ряда:

Децилем
называется структурная переменная, делящая распределение на 10 равных частей по
числу единиц в совокупности. Децилей 9, а децильных
групп 10. Децили определяются по формулам, аналогичным формуле для расчета
медианы и квартилей.

В целом общая формула для расчета квантилей в интервальном
ряду такова:

 – порядковый номер квантиля

 – размерность квантиля (на сколько частей эти
квартили делят совокупность)

 – нижняя граница квантильного
интервала

 – ширина квантильного
интервала

 – накопленная частота предквантильного
интервала

Для дискретного ряда номер квантиля можно
найти по формуле:

Примеры решения задач

---

Задача 1

(дискретный ранжированный ряд)

В
результате исследований установлен среднемесячный доход жильцов одного
подъезда:

1.5	1.8	2	2.5	2.8	2.8	2.8	3.0	3.6	3.8
3.9	4	5.8	5.9	6	6	6	6.8	7	7

Определите:

Модальный
и медианный доход, квартили и децили дохода.

Решение

Имеем уже ранжированный ряд – значения дохода жильцов распределены по возрастанию.

Мода
– наиболее часто встречающееся значение. В данном случае имеем ряд с двумя
модами.

 и

Медиана
– такое значение признака, которое делит упорядоченное множество данных
пополам.

Квартили
– значения признака в ранжированном ряду, выбранные таким образом, что 25%
единиц совокупности будут меньше величины

; 25% единиц будут
заключены между

 и

;  25% – между

 и

; остальные 25%
превосходят

.

Дицили делят ряд на 10 равных частей:

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

---

Задача 2

(интервальный ряд)

Для
определения среднего размера вклада в кредитном учреждении были получены
следующие данные:

Размер вклада, тыс.р.	до 10.0	10.0-16.0	16.0-22.0	22.0-28.0	28.0-34.0	Свыше 34.0
Удельный вес вкладов, %	5.0	8.0	15.0	22.0	30.0	20.0

Рассчитайте
 структурные средние (моду, медиану,
квартили).

Решение

Вычислим моду размера вклада:

Мода – варианта, которой соответствует наибольшая частота.

Мода вычисляется по формуле:

   –
начало модального интервала

    –
величина интервала

   –
частота модального интервала

   –
частота интервала, предшествующего модальному

   –
частота интервала, следующего за модальным

Таким образом,  наибольшее
количество вкладов имеют размер 30,7 тыс.р.

Медиана – варианта, находящаяся в середине ряда распределения.

Расчет медианы производится по формуле:

   -начало
(нижняя граница) медианного интервала

   
-величина интервала

 
-сумма всех частот ряда

  
-частота медианного интервала

-сумма накопленных частот вариантов до
медианного

Таким образом, половина вкладов имеет размер до 28 тыс.р.,
другая половина – более 28 тыс.р.

Вычислим квартили:

Таким
образом 25% вкладов меньше 20,8 тыс.р., 25% вкладов
лежат в интервале от 20,8 тыс.р. до 28 тыс.р., 25% лежат в интервале от 28 тыс.р.
до 33 тыс.р., 25% больше величины в 33 тыс.р.

---

Задача 3

Постройте
графики для вариационного ряда. На графике покажите моду, медиану, среднюю, квартили.

Возраст детей (лет)	Число детей (доли)
0-3	0.15
3-6	0.2
6-9	0.4
9-12	0.2
12-15	0.05

Решение

Вычислим
среднюю

: Для этого просуммируем
произведения середин интервалов и соответствующих частот, и полученную сумму
разделим на сумму частот.

Вычисление моды интервального ряда на графике

Построим
гистограмму.

Мода определяется по

гистограмме распределения. Для этого выбирается самый высокий прямоугольник,
который в данном случае является модальным. Затем правую вершину модального
прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс.

Абсцисса точки пересечения
этих прямых и будет модой распределения

Гистограмма

По
гистограмме получаем, что

Вычисление медианы и квартилей интервального ряда на графике

Построим
кумулятивную кривую частот (график накопленных частот)

Кумулятивная кривая частот

На получившимся графике
накопленных частот из последней получившейся точки (в нашем примере) проведем
линию перпендикулярную к оси

 она так же
является максимальной высотой. Поделим ее на 4 части. Через полученные точки
строим параллельную оси

 линии которая должна пересекать высоту к оси

 и кумуляту. От
места пересечения кумуляты опускаем перпендикуляры. Получившиеся точки есть квартили
и медиана (квартиль при

).

Вывод к задаче

Таким образом
средний возраст детей 6,9 лет. Наибольшее количество детей имеют возраст 7,5
лет. Четверть детей младше 4,5 лет, а самая старшая четверть детей старше 9,1
лет. Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.