Определение и свойства медианы равностороннего треугольника
В данной статье мы рассмотрим определение и свойства медианы равностороннего треугольника, а также разберем примеры решения задач для закрепления изложенного материала.
Определение медианы
Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.

Треугольник называется равносторонним, если все его стороны равны (AB = BC = AC).
Свойства медианы равностороннего треугольника
Свойство 1
Любая медиана в равностороннем треугольнике одновременно является и высотой, и серединным перпендикуляром, и биссектрисой угла, из которого проведена.

-
BD – медиана, высота и серединный перпендикуляр к стороне AC, а также биссектриса угла ABC;
Свойство 2
Все три медианы в равностороннем треугольнике равны между собой. Т.е. AF = BD = CE.

Свойство 3
Медианы в равностороннем треугольнике пресекаются в одной точке, которая делит их в отношении 2:1.

Свойство 4
Любая медиана равностороннего треугольника делит его на два равных по площади (равновеликих) прямоугольных треугольника. Т.е. S1 = S2.

Свойство 5
Равносторонний треугольник делится тремя медианами на шесть равновеликих прямоугольных треугольников. Т.е. S1 = S2 = S3 = S4 = S5 = S6.

Свойство 6
Точка пересечения медиан в равностороннем треугольнике является центром описанной вокруг и вписанной окружностей.

- r – радиус вписанной окружности;
- R – радиус описанной окружности;
- R = 2r (следует из Свойства 3).
Свойство 7
Длину медианы равностороннего треугольника можно вычислить по формуле:

a – сторона треугольника.
Примеры задач
Задача 1
Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.
Решение
Для нахождения требуемого значения применим формулу выше:

Задача 2
Самая большая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равняется 8 см. Найдите длину стороны данного треугольника.
Решение
Нарисуем чертеж согласно условиям задачи.

Из Свойства 5 мы знаем, что в результате пересечения всех медиан образуются 6 прямоугольных треугольников.
- BG = 8 см (самая большая сторона, является гипотенузой △BFG);
- FG = 4 см (катет △BFG, в 2 раза меньше гипотенузы BG – следует из Свойства 3).
Применяем теорему Пифагора, чтобы найти длину второго катета BF:
BF 2 = BG 2 – FG 2 = 8 2 – 4 2 = 48 см 2 .
Следовательно, BF ≈ 6,93 см.
BF равняется половине стороны BC (т.к. медиана делит сторону треугольника пополам), следовательно, BC ≈ 13,86 см.
Медиана равностороннего треугольника
Какими свойствами обладает медиана равностороннего треугольника? Как выразить длину медианы через сторону треугольника? Через радиус вписанной и описанной окружностей?
(свойство медианы равностороннего треугольника)
В равностороннем треугольнике медиана, проведённая к любой стороне, является также его биссектрисой и высотой.
Пусть в треугольнике ABC AB=BC=AC.
Проведём медиану BF.
Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.
По свойству медианы равнобедренного треугольника, BF является также его биссектрисой и высотой.
Аналогично, так как AB=AC, треугольник ABC — равнобедренный с основанием BC, AK — его медиана, биссектриса и высота;
так как AC=BC, треугольник ABC — равнобедренный с основанием AB, CD — его медиана, биссектриса и высота.
Что и требовалось доказать .
(свойство медиан равностороннего треугольника)
Все три медианы равностороннего треугольника равны между собой.
Пусть в треугольнике ABC AB=BC=AC,
AK, BF, CD — его медианы.
Следовательно, треугольники ABK, BCF и CAK равны (по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон:
Что и требовалось доказать .
Из 1 и 2 теоремы следует, что все медианы, биссектрисы и высоты равностороннего треугольника равны между собой.
1) Выразим длину медианы равностороннего треугольника через его сторону.
Так как медиана равностороннего треугольника является также его высотой, треугольник ABF- прямоугольный.
Обозначим AB=a, BF=m, тогда AF=a/2.
Таким образом, формула медианы равностороннего треугольника по его стороне:
2) Выразим медиану равностороннего треугольника через радиусы вписанной и описанной окружностей.
Центр правильного треугольника является центром его вписанной и описанной окружностей.
Так как центр вписанной окружности лежит в точке пересечения биссектрис треугольника, а медианы равностороннего треугольника являются также его биссектрисами, в равностороннем треугольнике ABC OF — радиус вписанной, BO — радиус описанной окружностей:
Так как медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то BO:OF=2:1. Таким образом,
Отсюда медиана равностороннего треугольника через радиус вписанной окружности равна
Формула и свойства медианы в равностороннем треугольнике
Пожалуй, каждый хоть раз сталкивался с геометрическими вычислениями. Одной из самых распространённых фигур является многоугольник. Его особенность заключается в свойствах, благодаря которым можно легко и быстро определить нужные параметры. Часто при расчётах приходится использовать медиану. В равностороннем треугольнике она разбивает фигуру на две равные площади. При этом она и центр тяжести, чем зачастую и пользуются при решении задач.
Свойства и виды треугольников
Многоугольник с тремя углами называют треугольником. Образуется он тремя отрезками, соединяющими 3 точки, располагающиеся на разных прямых. Эти точки называются вершинами, а замкнутые линии — сторонами. Площадь, заключённую сторонами, называют внутренней.
Вершины фигуры принято обозначать большими латинскими буквами A, B, C. Углы же греческими символами α, β, γ. Треугольники принято различать по видам. Они бывают:
- остроугольными — все углы в фигуре имеют разворот меньше 90 градусов;
- тупоугольными — один из углов треугольника больше 90 градусов;
- прямоугольными — 2 стороны фигуры образуют прямой угол.
Кроме этого, их разделяют по числу равных сторон на разносторонние, равнобедренные и равносторонние (правильные). В треугольнике можно построить так называемые замечательные прямые. Отрезок, проведённый из середины вершины к противолежащей стороне, является медианой. В любом виде фигуры может быть построено 3 таких прямых. Они будут пересекаться в центре внутренней площади треугольника, а их общая точка являться центром массы.
Кроме медианы, может быть отложена высота и биссектриса. Первая это перпендикуляр, опущенный из угла на противоположное основание, а вторая — линия, проходящая из угла и делящая противоположную сторону пополам.
Зная высоту или биссектрису, найти медиану равностороннего треугольника очень просто. Всё дело в том, что для него все 3 линии полностью совпадают. Это и есть одно из замечательных свойств равносторонней фигуры,поэтому знание этого параметра позволяет находить много различных размеров многоугольника.
В треугольник можно вписать окружность и описать её вокруг него. Радиус вписанной фигуры находится из отношения площади фигуры к полупериметру, а описанной — как произведение сторон, делённое на 4 площади. Внутреннее пространство для равносторонней фигуры можно определить по формуле: S = (a2 √3) / 4. При этом углы любого равностороннего треугольника будут равны 60 градусам.
Особенности медианы
С латинского «медиана» переводится как «средняя», поэтому так называют отрезок, соединяющий вершину с серединой противоположного углу отрезка. Точку, в которой она соприкасается с прямой, называют основанием медианы. Существуют свойства, характерные только для рассматриваемой прямой. Так, можно, зная медиану, найти сторону треугольника, его площадь или угол вершины.
К свойствам отрезков, делящих сторону пополам в произвольном треугольнике, относят:
- деление медиан в точке их пересечения в отношении 2:1;
- разделение фигуры на 2 треугольника с равными площадями, то есть являющимися равновеликими;
- если построить 3 медианы, то треугольник окажется разделённым на 6 одинаковых фигур;
- зная значения сторон, длину параметров можно вычислить по следующей формуле: m = √(2b 2 + 2c 2 — a 2 ) / 2.
Для доказательства равенства площадей нужно построить треугольник и провести медиану, например, из вершины B. Точку пересечения с противоположной стороной можно обозначить буквой D. Площадь новых фигур будет равняться: S1 = (AD * BE) / 2 и S2 = (DC * BE) / 2. Так как ограниченная прямая — это медиана, то AD = DC. Отсюда следует, что фигура делится на 2 равные части. Значит, S1 = S2, что и нужно было доказать.
Доказательство равенства 6 фигур при построении трёх медиан: пусть одна из полученных фигур будет иметь вершины A, O, F. Если из угла опустить перпендикуляр на линию BF, будет верным равенство: S = (OF * AK) / 2 = (BF * AK) / 6 = S / 3. Беря во внимание свойства, что линия рассекает фигуру на 2 равные части, можно утверждать о справедливости записи: Sabf = Sabc / 2 → Saof = Sabf / 3 = Sabc / 6. Свойство доказано.
В равнобедренном треугольнике медиана совпадает с высотой. Доказать это утверждение просто. Пусть есть многоугольник ABC. Из вершины B опущена высота BD. Полученные 2 фигуры равны: ABD = CDB, значит, их сторона BD – общая и является катетом. Следовательно, AD = CD. Так как гипотенузы треугольников равны, AB = BC. Замечательное свойство доказано.
Существуют 2 следствия из свойств:
- если вокруг прямоугольного треугольника описать круг, его центр совпадёт с серединой гипотенузы;
- треугольник, где медиана равна половине длины стороны, к которой её построили, будет прямоугольным.
Эти свойства и следствия очень важны. Зная их и формулы нахождения площади, решить большинство задач не составит труда. Но при этом часто приходится использовать формулу нахождения длины медианы.
Решение задачи
Для закрепления теоретического материала преподаватель учащимся предлагает решить ряд задач. Самостоятельное вычисление ответа позволяет не только научиться применять знания на практике, но и разобраться в различных тонкостях. Вот одна из таких задач, рассчитанная на школьников среднего уровня подготовки.
Дан равносторонний треугольник ABC. Длина медианы BH, проведённой на основание AC, составляет 9 * √3. Определить, чему равны стороны фигуры. Перед тем как непосредственно перейти к решению, нужно обратить внимание, что все стороны у фигуры будут одинаковые, при этом углы также равны. По сути, равносторонний многоугольник является равнобедренным, поэтому медиана является и высотой, а значит, угол H будет составлять 90 градусов. При этом все остальные углы равны 60 градусам.
Решить задачу можно двумя способами:
- Первый предполагает решение через тригонометрические функции. Так как известен острый угол в прямоугольном треугольнике ABH, используя синус (значение противолежащего катета к гипотенузе) можно записать: sin BAH = BH / AB. Отсюда AB = BH / sin BAH = (9 * √3) / (√3 / 2) = 9 * 2 = 18.
- В основе второго способа лежит теорема Пифагора. Сторона AB — это гипотенуза. Для удобства её можно обозначить как х. Так как медиана делит сторону пополам, то AH = x / 2. По теореме: AB2 = AH2 + BH2. Подставив известные значения в формулу, можно получить выражение: x2 = (x/2) 2 + (9 * √3) 2 = (x 2 / 4) + 81 * 3 = 81 * 4. Отсюда x = √ 81 * √ 4 = 9 * 2 = 18.
Это классические методы, с помощью которых можно найти сторону треугольника, если известна медиана. Какой из них выбрать, зависит от предпочтения решающего задачу. Конечно же, первый занимает меньше времени, но требует знаний хотя бы основ тригонометрии.
Следует отметить, что формула: m = a √3 / 2 называется выражением медианы через высоту. И находится она как раз по теореме Пифагора. Это позволяет, зная лишь высоту или биссектрису, находить не только величину сторон, но и площадь фигуры, радиусы вписанной и описанной окружностей. При этом эта формула работает и в обратном направлении. Так, сторона будет равна: а = m / (√3 / 2).
Онлайн-расчёты на калькуляторе
Найти медиану в треугольнике при известных размерах сторон или площади фигуры довольно просто. В школьных задачах обычно подбираются исходные данные так, что при решении не нужно пользоваться калькулятором или делать сложные расчёты. Ответ часто получается в удобной форме в виде десятичных чисел.
Но на практике начальные данные, используемые для нахождения медианы, могут представлять коренные, степенные, дробные выражения, поэтому приходится выполнять громоздкие вычисления, которые могут занять много времени. При этом существует риск допустить оплошность, приводящую к неправильному ответу.
В интернете существуют математические онлайн-калькуляторы. Это сервисы, предлагающие услуги по автоматическому нахождению ответа в различных заданиях. Чтобы воспользоваться сайтом, пользователю даже не нужно знать формулы. Всё что от него требуется, это просто указать значения сторон в предложенной форме и нажать кнопку «Рассчитать» или «Вычислить». При этом эти сервисы бесплатны и не требуют даже регистрации.
Из онлайн-калькуляторов, существующих в русском сегменте интернета, можно отметить следующие:
- Allcalc. Настоящий комбайн вычислений. Сайт содержит несколько сотен математических калькуляторов и конвертеров. Пользователь также может скачать бесплатное приложение для системы Android.
- Planetcalc. Отличается удобной навигацией и интуитивно понятным интерфейсом. Работу того или иного калькулятора можно оценить в комментариях.
- Geleot. Позиционируется не только как онлайн-расчётчик, но и как справочник.
Кроме быстрого и правильного расчёта, сайты могут предложить пользователю различный теоретический материал, касающийся вычислений. На их страницах приведены не только формулы, используемые для нахождения ответа, но и их объяснения. При этом расчёт сопровождается комментариями и подробными действиями.
Использовать онлайн-калькулятор для вычисления медианы не зазорно, особенно в процессе обучения. Благодаря ему можно не только проверить ответ, но и в случае ошибки быстро её найти и разобраться в причинах появления, поэтому ими часто пользуются не только школьники, но и инженеры, выполняющие сложные геометрические расчёты.
[spoiler title=”источники:”]
http://prostudenta.ru/article-2296.html
[/spoiler]
В равностороннем треугольнике медианы, также как в равнобедренном медиана основания, равны друг другу и совпадают с биссектрисами и высотами. Воспользуясь этим свойством, найдем медиану равностороннего треугольника как высоту. Для этого обратимся к прямоугольному треугольнику, в котором медиана является катетом, а сторона треугольника – гипотенузой. Поскольку все углы в равностороннем треугольнике равны 60°, то медиана равностороннего треугольника будет выглядеть следующим образом:

В данной статье мы рассмотрим определение и свойства медианы равностороннего треугольника, а также разберем примеры решения задач для закрепления изложенного материала.
- Определение медианы
-
Свойства медианы равностороннего треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
-
Свойство 7
- Примеры задач
Определение медианы
Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.

- BD – медиана, проведенная к стороне AC;
- AD = DC.
Треугольник называется равносторонним, если все его стороны равны (AB = BC = AC).
Свойства медианы равностороннего треугольника
Свойство 1
Любая медиана в равностороннем треугольнике одновременно является и высотой, и серединным перпендикуляром, и биссектрисой угла, из которого проведена.

- BD – медиана, высота и серединный перпендикуляр к стороне AC, а также биссектриса угла ABC;
- ∠ABD = ∠CBD.
Свойство 2
Все три медианы в равностороннем треугольнике равны между собой. Т.е. AF = BD = CE.

Свойство 3
Медианы в равностороннем треугольнике пресекаются в одной точке, которая делит их в отношении 2:1.

- G – центр тяжести (центроид) треугольника;
- AG = 2GF;
- BG = 2GD;
- CG = 2GE.
Свойство 4
Любая медиана равностороннего треугольника делит его на два равных по площади (равновеликих) прямоугольных треугольника. Т.е. S1 = S2.

Свойство 5
Равносторонний треугольник делится тремя медианами на шесть равновеликих прямоугольных треугольников. Т.е. S1 = S2 = S3 = S4 = S5 = S6.

Свойство 6
Точка пересечения медиан в равностороннем треугольнике является центром описанной вокруг и вписанной окружностей.

- r – радиус вписанной окружности;
- R – радиус описанной окружности;
- R = 2r (следует из Свойства 3).
Свойство 7
Длину медианы равностороннего треугольника можно вычислить по формуле:
![]()
a – сторона треугольника.
Примеры задач
Задача 1
Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.
Решение
Для нахождения требуемого значения применим формулу выше:
![]()
Задача 2
Самая большая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равняется 8 см. Найдите длину стороны данного треугольника.
Решение
Нарисуем чертеж согласно условиям задачи.

Из Свойства 5 мы знаем, что в результате пересечения всех медиан образуются 6 прямоугольных треугольников.
- BG = 8 см (самая большая сторона, является гипотенузой △BFG);
- FG = 4 см (катет △BFG, в 2 раза меньше гипотенузы BG – следует из Свойства 3).
Применяем теорему Пифагора, чтобы найти длину второго катета BF:
BF2 = BG2 – FG2 = 82 – 42 = 48 см2.
Следовательно, BF ≈ 6,93 см.
BF равняется половине стороны BC (т.к. медиана делит сторону треугольника пополам), следовательно, BC ≈ 13,86 см.
Медиана равностороннего треугольника


4.6
Средняя оценка: 4.6
Всего получено оценок: 140.
4.6
Средняя оценка: 4.6
Всего получено оценок: 140.
Равносторонний треугольник стоит особняком среди всех фигур: в нем легко можно найти значение всех сторон и углов, так как все углы известны заранее, а найдя одну сторону, можно найти сразу все три. Но именно из-за этих свойств, составители задач любят писать каверзные условия, в которых не всегда можно разобраться с первого раза, например, не всегда можно понять, что такое медиана, потому что человеку проще воспринимать понятие высоты, нежели медианы. Рассмотрим же понятие медианы в равностороннем треугольнике подробно.
Определения
Равносторонний треугольник – это треугольник, все стороны которого равны, а углы по 60 градусов.
Равносторонний треугольник это частный случай равнобедренного, но в равностороннем любую сторону можно считать основанием.
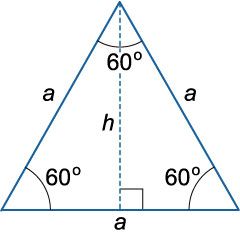
Из этого следует, что любая высота равностороннего треугольника является медианой и биссектрисой, так как любая высота проводится к стороне, которую можно считать основанием.
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположно стороны. Медиана также имеет ряд свойств, которые можно использовать в решении задач.
Медианы в треугольнике пересекаются в одной точке и делят эту точку в отношении 2:3, считая от вершины. При этом медианы разбивают треугольник на 6 разновеликих треугольников. Если посмотреть на рисунок, то можно увидеть, что в равностороннем треугольнике каждый из 6 этих треугольников будет прямоугольным.
Формула медианы равностороннего треугольника
Выведем формулу медианы равностороннего треугольника. В равностороннем треугольнике АВС проведем высоту АН. Она же будет являться медианой и высотой. Медиана разобьет треугольник на два прямоугольных: АНС и АНВ. Рассмотрим треугольник АНС.
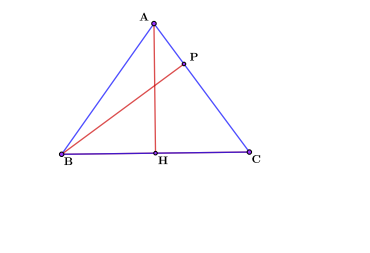
В нем применим теорему Пифагора:
$$АС^2=AH^2+HC^2$$
$$AH=sqrt{AB^2-BH^2}$$
Каждую из сторон обозначим буквой а. Тогда АВ=а; $$ВН={аover2}$$
$$АН=sqrt{a^2-{aover2}^2}=sqrt{a^2-{a^2over4}}$$
Это и есть формула медианы равностороннего треугольника. С другой стороны, можно воспользоваться тригонометрическими тождествами и вывести еще одну формулу:
$$sin(ACH)={AHover AC}$$
При этом угол АСН равен 60 градусам. Значит, можно определить синус угла: $$sin(ACH)={sqrt{3}over 2}$$
Выразим значение медианы АН
$$АН=sin(ACH)*AC={sqrt{3}over2}*AC={sqrt{3}over2}*a$$
Вот еще одна формула, характерная для равностороннего треугольника.
Задача
Для закрепления темы решим простую задачу на обратное использование формулы медианы.
В равностороннем треугольнике медиана равна $$20over{sqrt{3}}$$. Найти площадь треугольника.
Для нахождения площади воспользуемся классической формулой.
Классическую формулу можно использовать для нахождения площади любого треугольника.
Для нее нам нужно значение стороны и высоты. Высота в равностороннем треугольнике совпадает с медианой, поэтому нужно найти только сторону. Выразим ее через формулу медианы равностороннего треугольника.
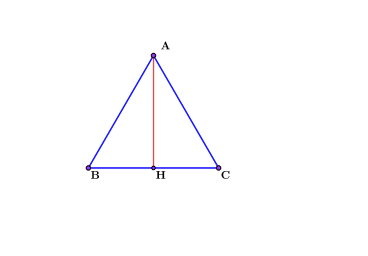
$$m={sqrt{3}over2}*a$$
$$a={mover{sqrt{3}over2}}=m*{2oversqrt{3}}$$
Подставим в формулу значение медианы:
$$a={20oversqrt{3}}*{2oversqrt{3}}={40over3}$$
Посчитаем площадь:
$$S={1over2}*a*m={1over2}*{40over3}*{20 oversqrt{3}}={400over{3sqrt{3}}}$$

Что мы узнали?
Мы вывели две формулы медианы равностороннего треугольника, дали определения, необходимые для решения задач и решили небольшую задачу для закрепления знаний.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Александр Рудаков
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 140.
А какая ваша оценка?
Пожалуй, каждый хоть раз сталкивался с геометрическими вычислениями. Одной из самых распространённых фигур является многоугольник. Его особенность заключается в свойствах, благодаря которым можно легко и быстро определить нужные параметры. Часто при расчётах приходится использовать медиану. В равностороннем треугольнике она разбивает фигуру на две равные площади. При этом она и центр тяжести, чем зачастую и пользуются при решении задач.
Оглавление:
- Свойства и виды треугольников
- Особенности медианы
- Решение задачи
- Онлайн-расчёты на калькуляторе
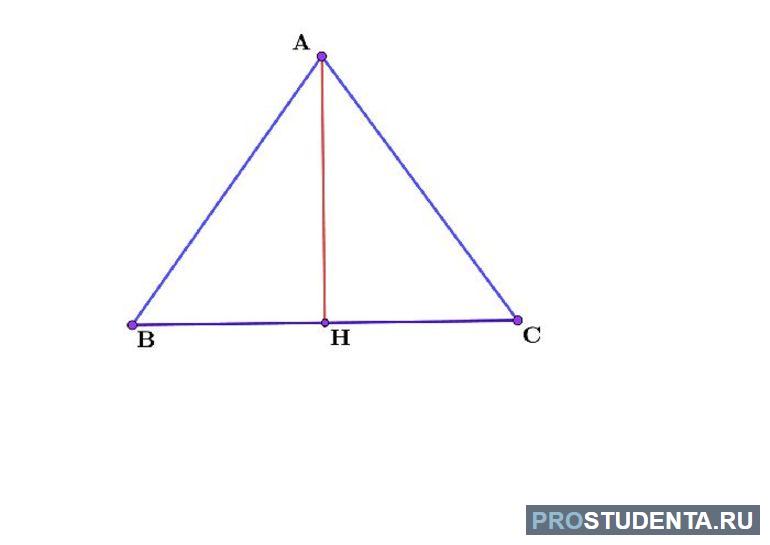
Свойства и виды треугольников
Многоугольник с тремя углами называют треугольником. Образуется он тремя отрезками, соединяющими 3 точки, располагающиеся на разных прямых. Эти точки называются вершинами, а замкнутые линии — сторонами. Площадь, заключённую сторонами, называют внутренней.
Вершины фигуры принято обозначать большими латинскими буквами A, B, C. Углы же греческими символами α, β, γ. Треугольники принято различать по видам. Они бывают:
- остроугольными — все углы в фигуре имеют разворот меньше 90 градусов;
- тупоугольными — один из углов треугольника больше 90 градусов;
- прямоугольными — 2 стороны фигуры образуют прямой угол.
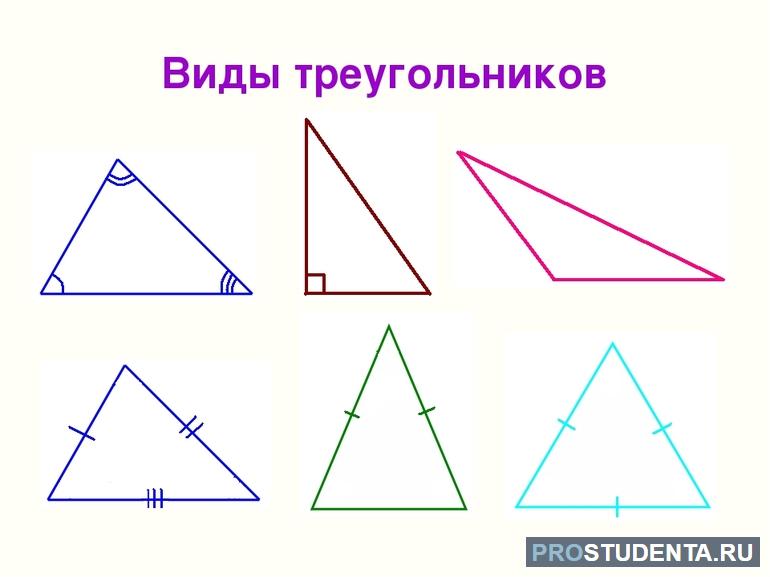
Кроме этого, их разделяют по числу равных сторон на разносторонние, равнобедренные и равносторонние (правильные). В треугольнике можно построить так называемые замечательные прямые. Отрезок, проведённый из середины вершины к противолежащей стороне, является медианой. В любом виде фигуры может быть построено 3 таких прямых. Они будут пересекаться в центре внутренней площади треугольника, а их общая точка являться центром массы.
Кроме медианы, может быть отложена высота и биссектриса. Первая это перпендикуляр, опущенный из угла на противоположное основание, а вторая — линия, проходящая из угла и делящая противоположную сторону пополам.
Зная высоту или биссектрису, найти медиану равностороннего треугольника очень просто. Всё дело в том, что для него все 3 линии полностью совпадают. Это и есть одно из замечательных свойств равносторонней фигуры,поэтому знание этого параметра позволяет находить много различных размеров многоугольника.
В треугольник можно вписать окружность и описать её вокруг него. Радиус вписанной фигуры находится из отношения площади фигуры к полупериметру, а описанной — как произведение сторон, делённое на 4 площади. Внутреннее пространство для равносторонней фигуры можно определить по формуле: S = (a2 √3) / 4. При этом углы любого равностороннего треугольника будут равны 60 градусам.
С латинского «медиана» переводится как «средняя», поэтому так называют отрезок, соединяющий вершину с серединой противоположного углу отрезка. Точку, в которой она соприкасается с прямой, называют основанием медианы. Существуют свойства, характерные только для рассматриваемой прямой. Так, можно, зная медиану, найти сторону треугольника, его площадь или угол вершины.
К свойствам отрезков, делящих сторону пополам в произвольном треугольнике, относят:
- деление медиан в точке их пересечения в отношении 2:1;
- разделение фигуры на 2 треугольника с равными площадями, то есть являющимися равновеликими;
- если построить 3 медианы, то треугольник окажется разделённым на 6 одинаковых фигур;
- зная значения сторон, длину параметров можно вычислить по следующей формуле: m = √(2b2 + 2c2 — a2) / 2.

Для доказательства равенства площадей нужно построить треугольник и провести медиану, например, из вершины B. Точку пересечения с противоположной стороной можно обозначить буквой D. Площадь новых фигур будет равняться: S1 = (AD * BE) / 2 и S2 = (DC * BE) / 2. Так как ограниченная прямая — это медиана, то AD = DC. Отсюда следует, что фигура делится на 2 равные части. Значит, S1 = S2, что и нужно было доказать.
Доказательство равенства 6 фигур при построении трёх медиан: пусть одна из полученных фигур будет иметь вершины A, O, F. Если из угла опустить перпендикуляр на линию BF, будет верным равенство: S = (OF * AK) / 2 = (BF * AK) / 6 = S / 3. Беря во внимание свойства, что линия рассекает фигуру на 2 равные части, можно утверждать о справедливости записи: Sabf = Sabc / 2 → Saof = Sabf / 3 = Sabc / 6. Свойство доказано.
В равнобедренном треугольнике медиана совпадает с высотой. Доказать это утверждение просто. Пусть есть многоугольник ABC. Из вершины B опущена высота BD. Полученные 2 фигуры равны: ABD = CDB, значит, их сторона BD – общая и является катетом. Следовательно, AD = CD. Так как гипотенузы треугольников равны, AB = BC. Замечательное свойство доказано.
Существуют 2 следствия из свойств:
- если вокруг прямоугольного треугольника описать круг, его центр совпадёт с серединой гипотенузы;
- треугольник, где медиана равна половине длины стороны, к которой её построили, будет прямоугольным.
Эти свойства и следствия очень важны. Зная их и формулы нахождения площади, решить большинство задач не составит труда. Но при этом часто приходится использовать формулу нахождения длины медианы.
Решение задачи
Для закрепления теоретического материала преподаватель учащимся предлагает решить ряд задач. Самостоятельное вычисление ответа позволяет не только научиться применять знания на практике, но и разобраться в различных тонкостях. Вот одна из таких задач, рассчитанная на школьников среднего уровня подготовки.
Дан равносторонний треугольник ABC. Длина медианы BH, проведённой на основание AC, составляет 9 * √3. Определить, чему равны стороны фигуры. Перед тем как непосредственно перейти к решению, нужно обратить внимание, что все стороны у фигуры будут одинаковые, при этом углы также равны. По сути, равносторонний многоугольник является равнобедренным, поэтому медиана является и высотой, а значит, угол H будет составлять 90 градусов. При этом все остальные углы равны 60 градусам.
Решить задачу можно двумя способами:

- Первый предполагает решение через тригонометрические функции. Так как известен острый угол в прямоугольном треугольнике ABH, используя синус (значение противолежащего катета к гипотенузе) можно записать: sin BAH = BH / AB. Отсюда AB = BH / sin BAH = (9 * √3) / (√3 / 2) = 9 * 2 = 18.
- В основе второго способа лежит теорема Пифагора. Сторона AB — это гипотенуза. Для удобства её можно обозначить как х. Так как медиана делит сторону пополам, то AH = x / 2. По теореме: AB2 = AH2 + BH2. Подставив известные значения в формулу, можно получить выражение: x2 = (x/2)2 + (9 * √3)2 = (x2 / 4) + 81 * 3 = 81 * 4. Отсюда x = √ 81 * √ 4 = 9 * 2 = 18.
Это классические методы, с помощью которых можно найти сторону треугольника, если известна медиана. Какой из них выбрать, зависит от предпочтения решающего задачу. Конечно же, первый занимает меньше времени, но требует знаний хотя бы основ тригонометрии.
Следует отметить, что формула: m = a √3 / 2 называется выражением медианы через высоту. И находится она как раз по теореме Пифагора. Это позволяет, зная лишь высоту или биссектрису, находить не только величину сторон, но и площадь фигуры, радиусы вписанной и описанной окружностей. При этом эта формула работает и в обратном направлении. Так, сторона будет равна: а = m / (√3 / 2).
Онлайн-расчёты на калькуляторе
Найти медиану в треугольнике при известных размерах сторон или площади фигуры довольно просто. В школьных задачах обычно подбираются исходные данные так, что при решении не нужно пользоваться калькулятором или делать сложные расчёты. Ответ часто получается в удобной форме в виде десятичных чисел.
Но на практике начальные данные, используемые для нахождения медианы, могут представлять коренные, степенные, дробные выражения, поэтому приходится выполнять громоздкие вычисления, которые могут занять много времени. При этом существует риск допустить оплошность, приводящую к неправильному ответу.

В интернете существуют математические онлайн-калькуляторы. Это сервисы, предлагающие услуги по автоматическому нахождению ответа в различных заданиях. Чтобы воспользоваться сайтом, пользователю даже не нужно знать формулы. Всё что от него требуется, это просто указать значения сторон в предложенной форме и нажать кнопку «Рассчитать» или «Вычислить». При этом эти сервисы бесплатны и не требуют даже регистрации.
Из онлайн-калькуляторов, существующих в русском сегменте интернета, можно отметить следующие:

- Allcalc. Настоящий комбайн вычислений. Сайт содержит несколько сотен математических калькуляторов и конвертеров. Пользователь также может скачать бесплатное приложение для системы Android.
- Planetcalc. Отличается удобной навигацией и интуитивно понятным интерфейсом. Работу того или иного калькулятора можно оценить в комментариях.
- Geleot. Позиционируется не только как онлайн-расчётчик, но и как справочник.
Кроме быстрого и правильного расчёта, сайты могут предложить пользователю различный теоретический материал, касающийся вычислений. На их страницах приведены не только формулы, используемые для нахождения ответа, но и их объяснения. При этом расчёт сопровождается комментариями и подробными действиями.
Использовать онлайн-калькулятор для вычисления медианы не зазорно, особенно в процессе обучения. Благодаря ему можно не только проверить ответ, но и в случае ошибки быстро её найти и разобраться в причинах появления, поэтому ими часто пользуются не только школьники, но и инженеры, выполняющие сложные геометрические расчёты.
