Загрузить PDF
Загрузить PDF
Среднее значение, медиана и мода — значения, которые часто используются в статистике и математике. Эти значения найти довольно легко, но их легко и перепутать. Мы расскажем, что они из себя представляют и как их найти.
-

1
Сложите все числа, которые вам даны. Допустим, вам даны числа 2, 3 и 4. Сложим их: 2 + 3 + 4 = 9.
-

2
Сосчитайте количество чисел. У нас есть три цифры.
-

3
Разделите сумму чисел на их количество. Берем 9, делим на 3. 9/3 = 3. Среднее значение в данном случае равно 3. Помните, что не всегда получается целое число.
Реклама
-

1
Запишите все числа, которые вам даны, в порядке возрастания. Например, нам даны числа: 4, 2, 8, 1, 15. Запишите их от меньшего к большему, вот так: 1, 2, 4, 8, 15.
-

2
Найдите два средних числа. Мы расскажем, как это сделать, если у вас имеется четное количество чисел, и как это сделать, если количество чисел нечетное:
- Если у вас нечетное количество чисел, вычеркните левое крайнее число, затем правое крайнее число и так далее. Один оставшийся номер и будет искомой медианой. Если вам дан ряд чисел 4, 7, 8, 11, 21, тогда 8 — медиана, так как 8 стоит посередине.
- Если у вас четное количество чисел, вычеркните по одному числу с каждой стороны, пока у вас не останется два числа посередине. Сложите их и разделите на два. Это и есть значение медианы. Если вам дан ряд чисел 1, 2, 5, 3, 7, 10, то два средних числа — это 5 и 3. Сложим 5 и 3, получим 8, разделим на два, получим 4. Это и есть медиана.
Реклама
-

1
Запишите все числа в ряд. Например, вам даны числа 2, 4, 5, 5, 4 и 5. Запишите их в порядке возрастания.
-

2
Найдите число, которое чаще всего встречается. В данном случае это 5. Если два числа встречаются одинаково часто, то этот ряд двухвершинный или бимодальный, а если больше — то мультимодальный.
Реклама
Советы
- Вам будет легче найти моду и медиану, если вы запишете числа в порядке возрастания.
Реклама
Об этой статье
Эту страницу просматривали 355 010 раз.
Была ли эта статья полезной?
В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

Иногда при работе с данными нужно описать множество значений каким-то одним числом. Например, при исследовании эффективности сотрудников, уровня вовлеченности в аккаунте, KPI или времени ответа на сообщения клиентов. В таких случаях используют меры центральной тенденции. Их можно называть проще — средние значения.
Но в зависимости от вводных данных, находить среднее значение нужно по-разному. Основной набор задач закрывается с использованием среднего арифметического, медианы и моды. Но если выбрать неверный способ — выводы будут необъективны, а результаты исследования нельзя будет признать действительными. Чтобы не допустить ошибку, нужно понимать особенности разных способов нахождения средних значений.

Cтратег, аналитик и контент-продюсер. Работает с агентством «Палиндром».

Как считать среднее арифметическое
Использовать среднее арифметическое стоит тогда, когда множество значений распределяются нормально ― это значит, что значения расположены симметрично относительно центра. Как выглядит нормальное распределение на графике и в таблице, можно посмотреть на примере:


Если данные распределяются как в примерах — вам повезло. Можно без лишних заморочек считать среднее арифметическое и быть уверенным, что выводы будут объективны. Однако, нормальное распределение на практике встречается крайне редко, поэтому среднее арифметическое в большинстве случаев лучше не использовать.
Как рассчитать
Сумму значений нужно поделить на их количество. Например, вы хотите узнать средний ER за 4 дня при нормальном распределении значений и без аномальных выбросов. Для этого считаем среднее арифметическое: складываем ER всех дней и делим полученное число на количество дней.

Если хотите автоматизировать вычисления и узнать среднее арифметическое для большого числа показателей — используйте Google Таблицы:
- Заполните таблицу данными.
- Щелкните по пустой ячейке, в которую хотите записать среднее арифметическое.
- Введите «=AVERAGE(» и выделите ряд чисел, для которых нужно вычислить среднее арифметическое. Нажмите «Enter» после ввода формулы.

Когда можно не использовать
Если данные распределены ненормально, то наши расчеты не будут отражать реальную картину. На ненормальность распределения указывают:
- Отсутствие симметрии в расположении значений.
- Наличие ярко выраженных выбросов.
Как пример ненормального распределения (с выбросами) можно рассматривать среднее время ответа на комментарии по неделям:

Если посчитать среднее значение для такого набора данных с помощью среднего арифметического, то получится завышенное число. В итоге наши выводы будут более позитивными, чем реальное положение дел. Еще стоит учитывать, что выбросы могут не только завышать среднее значение, но и занижать его. В таком случае вы получите более скромный показатель, который не будет соответствовать реальности.
Например, в группе «Золотое Яблоко» во ВКонтакте иногда публикуют конкурсные посты. Они набирают более высокие показатели вовлеченности чем обычные публикации. Если посчитать средний ER с учетом конкурсов, мы получим 0,37%, а без учета конкурсов — только 0,29%. Аналогичная ситуация с числом комментариев. С конкурсами в среднем получаем 917 комментариев, а без конкурсов — всего лишь 503. Очевидно, что из-за розыгрышей средние показатели вовлеченности завышаются. В этом случае конкурсные посты следует исключить из анализа, чтобы объективно оценить эффективность контента в группе.

Еще часто бывает так, что данных очень много, заметны явные выбросы, но на их обработку и исключение аномальных значений не хватит ни времени, ни терпения. Тем более нет гарантий, что исключив выбросы, вы получите нормальное распределение. В таком случае лучше подсчитать средние значения, используя медиану.
Как найти медиану и когда ее применять
Если вы имеете дело с ненормальным распределением или замечаете значительные выбросы — используйте медиану. Так можно получить более адекватное среднее значение, чем при использовании среднего арифметического. Чтобы понять, как работать с медианой, рассмотрим аналогичный пример с ненормальным распределением времени ответов на комментарии.

Ниже в таблице уже введены данные из графика и рассчитано среднее время ответа с помощью среднего арифметического и медианы. Из расчетов видна наглядная разница между средним арифметическим и медианой ― она составляет 17 минут. Такое различие появляется из-за низкого темпа работы на выходных и в нестандартных ситуациях, когда к ответу на сообщения нужно относиться с особой ответственностью (события конца февраля). Подобные выбросы сильно завышают среднее арифметическое, а вот на медиану они практически не влияют. Поэтому если хотите посчитать среднее значение избегая влияния выбросов, — используйте медиану. Такие данные будут без искажений.

Как рассчитать
Разберем на примере. В аккаунте опубликовали семь постов и они набрали разное количество комментариев: 35, 105, 2, 15, 2, 31, 1. Чтобы вычислить медиану, нужно пройти два этапа:
- Расположите числа в порядке возрастания. Итоговый ряд будет выглядеть так: 1, 2, 2, 15, 31, 35, 105.
- Найдите середину сформированного ряда. В центре стоит число 15 — его и нужно считать медианой.
Немного сложнее найти медиану, если вы работаете с четным количеством чисел. Например, вы собрали количество лайков на последних шести постах: 32, 48, 36, 201, 52, 12. Чтобы найти медиану, выполните три действия:
- Расставьте числа по возрастанию: 12, 32, 36, 48, 52, 201.
- Возьмите два из них, наиболее близких к центру. В нашем случае — это 36 и 48.
- Сложите два этих числа и разделите на два: (36 + 48) / 2 = 42. Результат и есть медиана.
Чтобы вычислять медиану быстрее и обрабатывать большие объемы данных — используйте Google Таблицы:
- Внесите данные в таблицу.
- Щелкните по свободной ячейке, в которую хотите записать медиану.
- Введите формулу «=MEDIAN(» и выделите ряд чисел, для которых нужно рассчитать медиану. Нажмите «Enter», чтобы все посчиталось.

Когда можно не использовать
Если данные распределены нормально и вы не видите заметных выбросов — медиану можно не использовать. В этом случае значение среднего арифметического будет очень близким к медиане. Можете выбрать любой способ нахождения среднего, с которым вам работать проще. Результат от этого сильно не изменится.
Что такое мода и где ее использовать
Мода ― это самое популярное/часто встречающееся значение. Например, стоит задача узнать, сколько комментариев чаще всего набирают посты в аккаунте. В этом случае можно не высчитывать среднее арифметическое или медиану ― лучше и проще использовать моду.
Еще пример. Нужно узнать, в какое время аудитория чаще всего взаимодействует с публикациями. Для этого можно посчитать данные вручную или использовать готовую таблицу из LiveDune (вкладка «Вовлеченность» ― таблица «Лучшее время для поста»). По ее данным ― больше всего реакций пользователи оставляют в среду в 16 часов. Это время и есть мода. Таким образом, если вам нужно найти самое популярное значение, а не классическое среднее — проще использовать моду.

Как рассчитать
Чтобы найти наиболее часто встречающееся значение в наборе данных, нужно посмотреть, какое число встречается в ряду чаще всех. Например, для ряда 5, 4, 2, 4, 7 ― модой будет число 4.
Иногда в ряде значений встречается несколько мод. Например, ряду 7, 7, 21, 2, 5, 5 свойственны две моды — 7 и 5. В этом случае совокупность чисел называется мультимодальной. Также поиск моды можно упростить с помощью Google Таблиц:
- Внесите значения в таблицу.
- Щелкните по ячейке, в которую хотите записать моду.
- Введите формулу «=MODE(» и выделите ряд чисел, для которых нужно вычислить моду. Нажмите «Enter».

Однако важно иметь в виду, что табличная функция выдает только самую меньшую моду. Поэтому будьте внимательны — можно упустить из виду несколько мод.
Когда использовать не стоит
Моду нет смысла использовать, если вас не просят найти самое популярное значение. Там, где надо найти классическое среднее значение, про моду лучше забыть.
Памятка по использованию
Среднее арифметическое
Как находим: сумма чисел / количество чисел.
Используем: если данные распределены нормально и нет ярких выбросов.
Не используем: если видим явные выбросы или ненормальное распределение.
Медиана
Как находим: располагаем числа в порядке возрастания и находим середину сформированного ряда.
Используем: если работаем с ненормальным распределением или видим выбросы.
Не используем: если выбросов нет и распределение нормальное.
Мода
Как находим: определяем значение, которое чаще всего встречается в ряду чисел.
Используем: если нужно найти не среднее, а самое популярное значение.
Не используем: если нужно найти классическое среднее значение.
Только важные новости в ежемесячной рассылке
Нажимая на кнопку, вы даете согласие на обработку персональных данных.

Подписывайся сейчас и получи гайд аудита Instagram аккаунта
Маркетинговые продукты LiveDune — 7 дней бесплатно
Наши продукты помогают оптимизировать работу в соцсетях и улучшать аккаунты с помощью глубокой аналитики

Анализ своих и чужих аккаунтов по 50+ метрикам в 6 соцсетях.
Оптимизация обработки сообщений: операторы, статистика, теги и др.
Автоматические отчеты по 6 соцсетям. Выгрузка в PDF, Excel, Google Slides.
Контроль за прогрессом выполнения KPI для аккаунтов Инстаграм.
Аудит Инстаграм аккаунтов с понятными выводами и советами.
Поможем отобрать «чистых» блогеров для эффективного сотрудничества.
Знание того, как найти среднее, медиану и моду, может помочь вам интерпретировать данные, собранные в ходе психологических исследований. Эти величины позволяют лучше понять, что можно считать “нормальным” или “ненормальным” для определенной группы людей, например, с точки зрения когнитивных процессов или поведения.
Поскольку все они являются показателями центральной тенденции, студенты-психологи часто легко путают эти три показателя. Тем не менее, существуют различия в том, что представляет собой каждый из них и как его находят. Вот несколько полезных советов, которые помогут вам различать эти показатели, а также как рассчитать среднее значение, медиану и модальность.
Определение среднего, медианы и моды
Чтобы понять разницу между средним, медианой и модой, давайте начнем с определения этих трех терминов.
- Среднее значение – это среднее арифметическое набора заданных чисел. Поэтому в математике среднее часто называют просто “средним”.
- Медиана – это средний балл в наборе заданных чисел. Как и медиана, половина оценок выше этого числа, а половина – ниже.
- Мода – это наиболее часто встречающаяся оценка в наборе заданных чисел. Другими словами, это оценка, которая встречается наибольшее количество раз.
Как найти среднее значение
Для расчета среднего значения выполните следующие два шага:
- Шаг 1: Сложите все оценки вместе
- Шаг 2: Разделите сумму на количество использованных оценок
В качестве примера представьте, что ваш психологический эксперимент дал следующий набор чисел: 3, 11, 4, 6, 8, 9, 6. Чтобы вычислить среднее значение, сначала сложите все числа вместе (3 + 11 + 4 + 6 + 8 + 9 + 6 = 47). Затем вы делите общую сумму на количество использованных оценок (47 / 7 = 6,7). В данном примере среднее или среднее значение набора чисел равно 6,7.
Обзор способа нахождения среднего значения
Среднее значение вычисляется путем сложения всех оценок вместе, а затем деления на количество оценок, которые вы добавили.
Как найти медиану
Медиана – это средний балл в наборе. Чтобы найти медиану, начните с расположения всех точек данных от наименьшей к наибольшей. В наборе с нечетным числом точек медианой будет число, находящееся в самой середине списка. В случае четного набора необходимо вычислить среднее значение двух средних чисел. Для этого:
- Шаг 1: Возьмите два средних числа из четного набора
- Шаг 2: Сложите эти два числа вместе
- Шаг 3: Разделите полученное число на 2
В качестве примера рассмотрим такой набор чисел: 5, 9, 11, 9, 7. Сначала вы расположите их в числовом порядке (5, 7, 9, 9, 11). Поскольку у вас нечетное количество оценок, число в третьей позиции набора данных является медианой, которая в данном случае равна 9 (5, 7, 9, 9, 11).
Чтобы рассчитать медиану для четного количества оценок, представьте, что ваше исследование выявило такой набор данных: 2, 5, 1, 4, 2, 7. Ваш первый шаг – расположить их в числовом порядке (1, 2, 2, 4, 5, 7). Два средних балла – 2 и 4, поэтому их нужно сложить (2+4=6), а затем разделить 6 на 2, что равно 3. В этом наборе данных медианный балл равен 3.
Обзор способа нахождения медианы
Медиана рассчитывается путем расположения оценок в числовом порядке, деления общего количества оценок на два, затем округления этого числа в большую сторону, если используется нечетное количество оценок, чтобы получить положение медианы или, если используется четное количество оценок, путем усреднения числа в данной позиции и следующей позиции.
Как найти медиану
Из всех показателей нахождение медианы требует наименьшего количества математических вычислений. Поскольку мода – это просто наиболее часто встречающийся показатель в распределении, достаточно просмотреть все показатели и выбрать наиболее часто встречающийся.
- Шаг 1: Просмотрите все оценки данных
- Шаг 2: Определите оценку данных, которая встречается наиболее часто
В качестве примера рассмотрим следующее распределение чисел: 2, 3, 6, 3, 7, 5, 1, 2, 3, 9. Модой этих чисел будет 3, поскольку это наиболее часто встречающееся число (2, 3, 6, 3, 7, 5, 1, 2, 3, 9).
Если ни одно число в наборе не встречается более одного раза, то для этого набора данных не существует моды. Также возможно, что набор данных имеет две моды. Это известно как бимодальное распределение.
Бимодальное распределение возникает, когда есть два числа, которые равны по частоте. Например, рассмотрим следующий набор чисел: 13, 17, 20, 20, 21, 23, 23, 26, 29, 30. В этом наборе и 20, и 23 встречаются дважды (13, 17, 20, 20, 21, 23, 23, 26, 29, 30). Следовательно, они оба являются модами.
Обзор того, как найти режим
Чтобы найти режим, необходимо определить показатель, который встречается чаще всего в наборе данных. В случаях, когда у вас есть большое количество оценок, создание частотного распределения может помочь в определении моды.
Плюсы и минусы среднего, медианы и моды
У каждого показателя центральной тенденции есть свои достоинства и недостатки. Вот несколько из них, которые следует рассмотреть.
- Среднее значение использует все числа в наборе для выражения меры центральной тенденции. Однако выбросы – или данные, которые находятся далеко за пределами набора данных – могут исказить общий показатель. Например, несколько чрезвычайно высоких оценок могут исказить среднее значение, так что средний балл будет казаться намного выше, чем большинство оценок на самом деле.
- Медиана позволяет избавиться от выбросов или непропорционально высоких или низких оценок. В то же время, это может стать проблемой, поскольку она может неадекватно представлять весь набор чисел.
- Мода также может быть менее подвержена влиянию выбросов и хорошо представляет то, что является “типичным” для данной группы чисел. Но она также может быть менее полезной в случаях, когда ни одно число не встречается более одного раза.
Хотя среднее значение в математике теоретически нейтрально, некоторые утверждают, что использование среднего значения в психологии может привести к неправильным выводам, если не соблюдать осторожность при его применении. Отчасти это объясняется тем, что поведение и познание являются сложными и изменчивыми по своей природе.
Когда использовать среднее, медиану и моду
Как определить, что использовать – среднее, медиану или моду при анализе психологических исследований? Выбор зависит от самих оценок данных.
Если в наборе данных нет выбросов, среднее значение может быть лучшим выбором с точки зрения точности, поскольку оно учитывает каждый отдельный балл и находит среднее значение. И наоборот, если выбросы есть, медиана или мода могут быть более точными, поскольку результаты не будут перекошены.
Также подумайте о том, что вы пытаетесь измерить. Ищете ли вы среднее значение (среднее), хотите ли определить средний балл (медиана), или вы ищете балл, который встречается чаще всего (мода)? Хотя все они являются мерами центральной тенденции, каждый из них рассматривает эту тенденцию с несколько иной точки зрения.
Пример среднего, медианы и моды в психологии
Представьте себе исследование, в котором психологи заинтересованы в выяснении типичного возраста, в котором у человека может быть диагностирована шизофрения. Чтобы собрать эти данные, они рассылают вопросник врачам, оказывающим психиатрические услуги, с просьбой сообщить возраст своих пациентов при постановке официального диагноза.
Согласно полученным ответам, пациенты врачей были следующих возрастов:
- 20
- 25
- 35
- 27
- 29
- 27
- 23
- 31
Используя приведенные выше расчеты, вы обнаружите, что среднее, медиана и мода для этого набора данных составляют около 27 лет (27.1 год, 27 лет и 27 лет соответственно). В этом случае любой из этих показателей может быть использован для определения типичного возраста начала заболевания.
Но что если у вас есть дополнительный показатель, равный 13? В этом случае среднее значение будет равно 25,6, а медиана и мода – 27. Поскольку среднее значение включает выброс, медиана и мода будут более точными, поскольку они не перекошены этим числом.
Если вам интересно, Национальный альянс по психическому здоровью сообщает, что средний возраст начала шизофрении у мужчин – конец 20-х – начало 20-х годов, в то время как у женщин это заболевание диагностируется в конце 20-х – начале 30-х годов.
Слово от Verywell
Среднее значение, медиана и мода служат ценной целью при анализе психологических данных. Все они также имеют свои плюсы и минусы. Знание того, как найти среднее, медиану и моду, а также их достоинств и недостатков поможет вам лучше интерпретировать данные, полученные в ходе психологических исследований.
2 Источники Мы используем только высококачественные источники, включая рецензируемые исследования, для подтверждения фактов в наших статьях. Ознакомьтесь с нашим редакционным процессом, чтобы узнать больше о том, как мы проверяем факты и обеспечиваем точность, надежность и достоверность нашего контента.
-
Speelman CP, McGann M. How mean is the mean? Front Psychol. 2013-4:451. doi:10.3389/fpsyg.2013.00451
-
Национальный альянс по психическим заболеваниям. Schizophrenia.
Дополнительное чтение
-
Hogg RV, McKean JW, Craig AT. Introduction to Mathematical Statistics. Boston: Pearson 2013.
-
Laerd Statistics. Measures of Central Tendency.

Кендра Черри
Кендра Черри, МС, автор и консультант по вопросам образования, помогающая студентам изучать психологию.
Как рассчитать медиану из таблицы частот (с примерами)
17 авг. 2022 г.
читать 2 мин
Вы можете найти медианное значение таблицы частот, выполнив следующие действия:
Шаг 1: Расположите все отдельные значения от наименьшего к наибольшему.
Шаг 2: Определите значение прямо в середине упорядоченного списка.
- Если имеется нечетное количество значений, медианой является значение, находящееся непосредственно посередине.
- Если имеется четное количество значений, медиана является средним значением двух средних значений.
В следующих примерах показано, как на практике найти медианное значение таблицы частот.
Пример 1: Медиана из таблицы частот (нечетное количество значений)
В следующей таблице частоты показано общее количество побед 17 футбольных команд в определенной лиге:
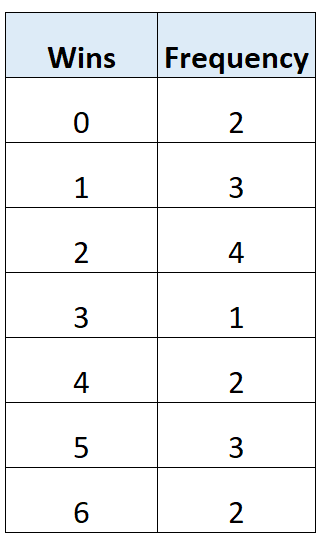
Мы можем использовать следующие шаги, чтобы найти медианное значение в этой таблице частот:
Шаг 1: Расположите все отдельные значения от наименьшего к наибольшему.
Значения: 0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 4, 4, 5, 5, 5, 6, 6
Шаг 2: Определите значение прямо в середине упорядоченного списка.
Значения: 0, 0, 1, 1, 1, 2, 2, 2, 2 , 3, 4, 4, 5, 5, 5, 6, 6
Среднее значение равно 2 .
Пример 2: Медиана из таблицы частот (четное число значений)
В следующей таблице частот показан размер домохозяйства 20 различных домохозяйств в определенном районе:
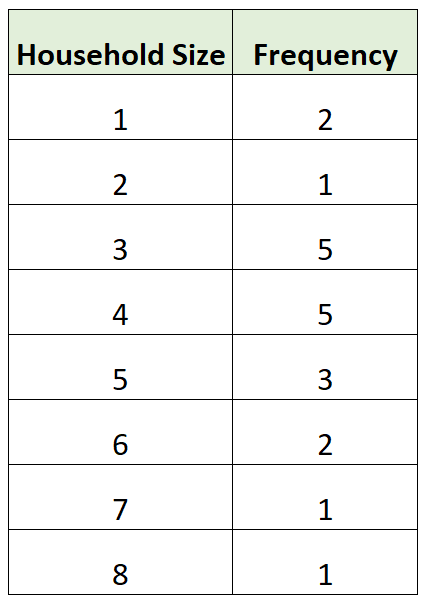
Мы можем использовать следующие шаги, чтобы найти медианное значение в этой таблице частот:
Шаг 1: Расположите все отдельные значения от наименьшего к наибольшему.
Значения: 1, 1, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8
Шаг 2: Определите значение прямо в середине упорядоченного списка.
Значения: 1, 1, 2, 3, 3, 3, 3, 3, 4, 4 , 4 , 4, 4, 5, 5, 5, 6, 6, 7, 8
Прямо посередине расположены два значения: 4 и 4.
Таким образом, медианное значение является средним из этих двух значений: (4 + 4)/2 = 4 .
Дополнительные ресурсы
Как рассчитать среднее значение из таблицы частот
Как рассчитать моду из таблицы частот
Как оценить среднее значение и медиану гистограмм
Когда использовать среднее значение против медианы
Онлайн калькулятор для нахождения медианы ряда чисел. Медианой (серединой) набора чисел называется число стоящее посередине упорядоченного по возрастанию ряда чисел. Если количество чисел в ряду чётное, то медианой ряда является полусумма двух стоящих посередине чисел.
Применяется в математической статистике — число, характеризующее выборку (например, набор чисел), также используется для вычисления медианной зарплаты.
Формула медианы числового набора, пример вычисления медианы числового ряда: 3, 7, 1, 6, 9
Решение: упорядочиваем список чисел в порядке возрастания: 1, 3, 6, 7, 9. Поскольку количество чисел в ряду нечётное, то число 6 стоящее по середине и будет являться медианой данного ряда.
Пример нахождения медианы ряда чисел: 1, 5, 8, 4, 3, 9
Решение: записываем все числа ряда в порядке возрастания: 1, 3, 4 ,5, 8, 9. Поскольку чисел в ряду чётное, то медиана этого ряда будет равна полусумме двух средних чисел: (4+5)/2 = 4.5

