Как найти медиану треугольника по теореме косинусов - Сайт, где вы сможете решить свои вопросы

Учебник

Геометрия, 9 класс

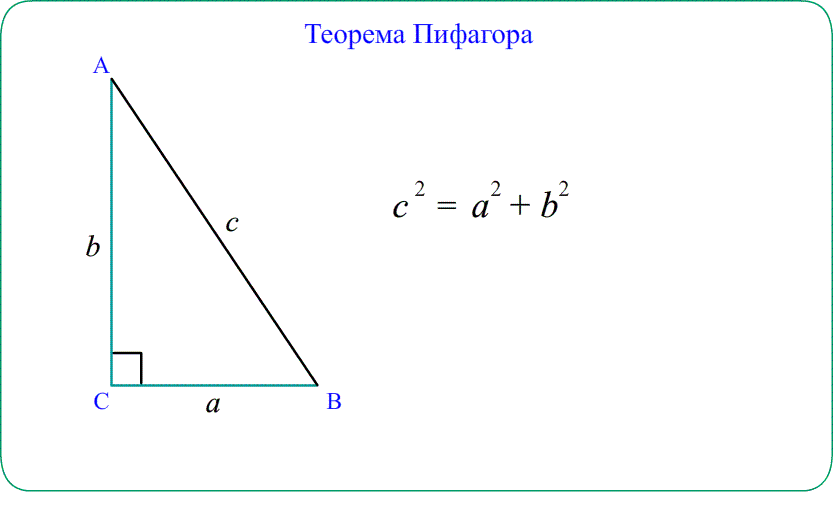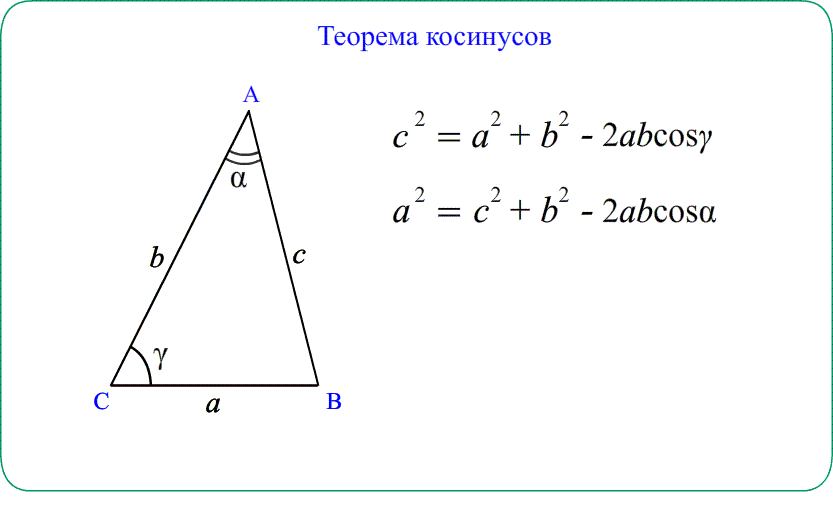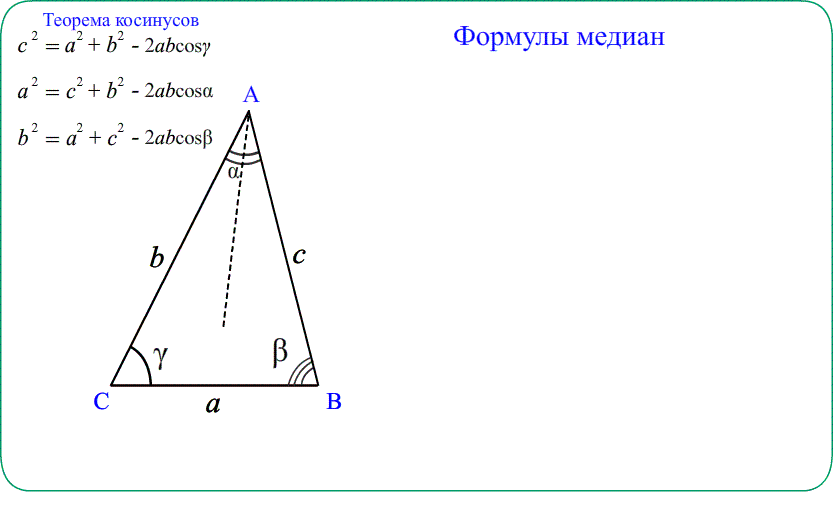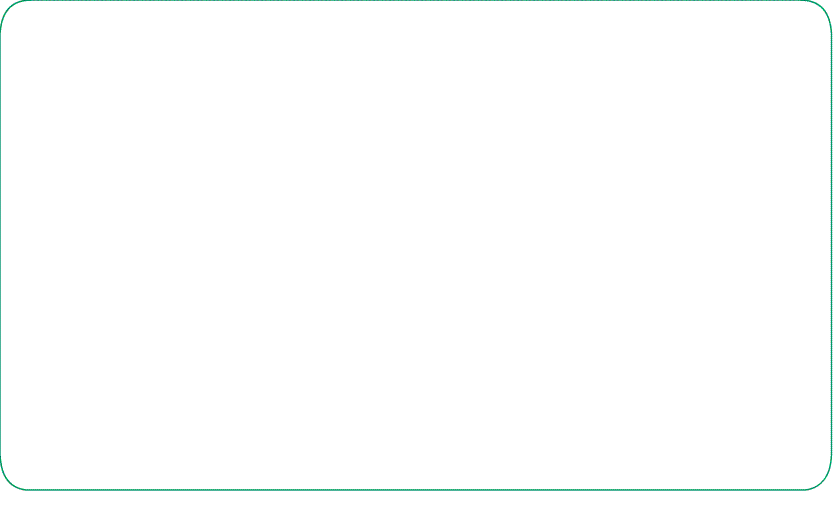
Теорема косинусов

Теорема косинусов

Если в треугольнике даны две стороны и угол между ними, то такой треугольник один, единственный. Т.е. любой другой треугольник с такими данными будет в точности равен ему, по 2-му признаку равенства треугольников. Ну, раз единственный и неповторимый, то его третья сторона должна быть однозначно определяема.

_____________________________________________________________________________________

Теорема косинусов    Квадрат стороны треугольника      равен     сумме квадратов двух

других сторон минус     удвоенное произведение этих сторон   на    косинус угла между ними.

$AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos ACB$

_____________________________________________________________________________________

Факты:

Теорема косинусов позволяет найти косинус любого угла по трем известным сторонам, а значит, и сам угол.
Если из трех сторон и одного угла известны три величины, то четвертое неизвестное можно всегда вычислить.
Теорема косинусов дает возможность вычислять медианы треугольника, применяя теорему к малым треугольникам.
Для прямоугольного треугольника теорема косинусов “упрощается” до теоремы Пифагора $AB^2=AC^2+BC^2$.

А если угол тупой? Что означает тригонометрия больших углов?

$cos130=-cos50$, $sin115=sin65$ , $tg135=-tg45$.

Связь тригонометрии тупых углов $90 < alpha < 180$ с тригонометрией острых выражается формулами:
$sinalpha=sinleft(180-alpharight)$ $cosalpha=-cosleft(180-alpharight)$ $tgalpha=-tgleft(180-alpharight)$ $ctgalpha=-ctgleft(180-alpharight)$

Если $b^2+c^2-a^2>0$, то $alpha$ – острый; если $b^2+c^2-a^2=0$, то $alpha$ – прямой; если $b^2+c^2-a^2<0$ , то угол $alpha$ – тупой.

Расчет треугольников по теореме косинусов

Задача 1: В треугольнике $ABC$ сторона $AC$ равна $7sqrt{3}$ см, сторона $BC$ равна $1$ см , угол $C$ = $150^o$ . Найти длину стороны $AB$.

Решение: Применим теорему косинусов $AB^2=left(7sqrt{3}right)^2+1-14sqrt{3}cos150$ .
Тупой угол в $150^o$ выразим через острый : $cos150=cosleft(180-30right)=-cos30=-frac{sqrt{3}}{2}$. $Rightarrow$
$AB^2=147+1-28sqrt{3}left(-frac{sqrt{3}}{2}right)$ , $AB^2= 148 + 21 = 169$ $Rightarrow$ Ответ: $AB = 13$

Задача 2: В треугольнике $ABC$ сторона $AC$ равна $17$ см, сторона $BC$ равна $14$ см , угол $ACB$ = $60^o$ .
Найти длину третьей стороны .

Решение: Из теоремы косинусов для угла $angle ACB$ : $Rightarrow$ $AB^2=17^2+14^2-2cdot17cdot14cdotcos60$ $Rightarrow$
квадрат стороны $AB^2= 289+196-238 = 247$ $Rightarrow$ Ответ: $AB = sqrt{247}$

Задача 3: В $bigtriangleup ABC$ известны $AC=3$ , $BC=5$ см, $AB=6$ .
Найти косинус угла $C$ и медиану $BM$ .

Решение: Из теоремы косинусов для стороны $AB$ выразим косинус требуемого угла $ACB$:
$cos ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}=frac{9+25-36}{30}=-frac{1}{15}$ . Отрицательное значение косинуса говорит о том, что это тупой угол $>90^o$
Для нахождения медианы $ВМ$ распишем еще раз теорему косинусов, но уже для треугольника $ВМС$ от угла $С$:
$BM^2=BC^2+MC^2-2cdot BCcdot MCcdotcos C$ учтем, что медиана делит сторону пополам $MC=frac{AC}{2}=1,5$
Подставим $BM^2=25+2,25-2cdot5cdot1.5cdotleft(-frac{1}{15}right)=27,25+1=28,25$, получим $BM=sqrt{28,25}=0,5sqrt{113}$
Ответ: $cos ACB=-frac{1}{15}$ , $BM=0,5sqrt{113}$ .

Задача 4: В прямоугольном $bigtriangleup ABC$ известны $AB=9$ , $BC=3$ см ; $M$ делит $AB$ : $frac{AM}{MB}=frac{1}{2}$.
Найти $CM$ .

Решение: По свойству аддитивности отрезка $AM + MB = 9$ , по условию $frac{AM}{MB}=frac{1}{2}$ $Rightarrow$ $AM = 3$ , $MB = 6$
Из прямоугольного $bigtriangleup ABC$ по определению косинуса угла: $cos B=frac{BC}{AB}=frac{3}{9}=frac{1}{3}$ .
Из $bigtriangleup CMB$ по теореме косинусов найдем $CM$ : $CM^2=CB^2+MB^2-2cdot CBcdot MBcdotcos B$ , подставим числа
$CM^2=3^2+6^2-2cdot3cdot6cdotfrac{1}{3}=33$ $Rightarrow$ требуемый отрезок $CM=sqrt{33}$ . Ответ: $CM=sqrt{33}$

Задача 5: Одна из сторон треугольника больше другой на $8$ см, а угол между ними $120^o$ .
Найдите периметр треугольника, если длина третьей стороны $28$ см .

Решение: Метод введения неизвестного: Обозначим одну из сторон треугольника как $x$ ,
выразим нужные величины через х и составим уравнение: величина другой стороны будет равна $x+8$ см.
По теореме косинусов: $28^2=x^2+left(x+8right)^2-2xcdotleft(x+8right)cdotcos120$ , где $cos120=cosleft(180-60right)=-cosleft(60right)=-0,5$,
Итак, составили уравнение $784=x^2+x^2+16x+64-2xleft(x+8right)left(-0,5right)$ $Rightarrow$ $3x^2+24x+720=0$
решим квадратное уравнение : один корень отрицательный – не нужен , другой $x=frac{-24+96}{6}=12$
Периметр $P=12+left(12+8right)+28=60$. Ответ: $60$.

Задача 6: В $bigtriangleup ABC$ известны стороны $a=15$ , $b=18$, $c=25$ . Найти: углы $α$, $β$, $γ$ (приближённо) .

Решение: Углы $α$ и $β$ найдём по теореме косинусов для соответствующих углов.
$cosalpha=frac{b^2+c^2-a^2}{2bc}$ , вычисляем $cosalpha=frac{18^2+25^2-15^2}{2cdot18cdot25}approx0,8$ , привлекаем калькулятор: $alphaapprox36,4^o$ ;
$cosbeta=frac{a^2+c^2-b^2}{2ac}$ , вычисляем $cosbeta=frac{15^2+25^2-18^2}{2cdot15cdot25}approx0,7$ , …. калькулятор: $betaapprox45,3^o$ .
Найдём $γ$ по теореме о 180 = сумма углов: $gamma=180-left(alpha+betaright)$ и $gammaapprox180-left(36,4+45,3right)approx98,3$ .
Ответ: $alphaapprox36,4^o$ , $betaapprox45,3^o$ , $gammaapprox98,3$

Задача 7: В $bigtriangleup ABC$ $AB=c=3$ м, $AC = b = 6$ м. , $alpha=60$ . Найти: сторону $a = BC$ , углы $β$, $γ$ .

Решение: Треугольник задан двумя сторонами и углом между ними, следовательно, он задан полностью.
По теореме косинусов $a^2=b^2+c^2-2bccdotcosalpha$ найдём сторону $a$:
$a^2=6^2+3^2-2cdot6cdot3cdotcos60=36+9-36cdotfrac{1}{2}=27$ $Rightarrow$ $a=3sqrt{3}$ .
По теореме косинусов найдем и угол $β$ : $cosbeta=frac{a^2+c^2-b^2}{2ac}$ , $cosbeta=frac{27+9-36}{18sqrt{3}}=0$ $Rightarrow$ $β=90$ .
Значит $bigtriangleup ABC$ – прямоугольный , тогда угол $γ=90-α$ . Ответ: $a=3sqrt{3}$ , $β = 90$ , $γ=30$ .

Задача 8: Стороны треугольника равны $11$ , $12$ и $13$ . Найти биссектрису, проведенную к стороне, равной 12.

дано: $AB=11$ , $BC=12$ , $AC=13$ Найти биссектрису $AK=?$ .
Решение: Найдем косинус угла из теоремы косинусов : $AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos angle ACB$
Выразим косинус $cos angle ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}$ , $cos angle ACB=frac{13^2+12^2-11^2}{2cdot 13cdot 12}=frac{19}{39}$
Найдем отрезки $BK$ , $KC$ на которые биссектриса делит сторону … по теореме биссектрис $frac{BK}{KC}=frac{AB}{AC}$
Система уравнений: $frac{BK}{KC}=frac{11}{13}$ и аддитивность $BK+KC=BC=12$. Получаем $BK=5,5$ , $BK=6,5$
Теперь, для нахождения биссектрисы $AK$ еще раз используем теорему косинусов для треугольника $bigtriangleup AKC$
$AK^2=AC^2+KC^2-2cdot ACcdot KCcdotcos angle ACB$ подставим значения $AK^2=13^2+6,5^2-2cdot 13cdot 6,5cdot frac{11}{13}=frac{429}{4}$.
Ответ: $AK=frac{sqrt429}{2}$.

Задача 9: Стороны треугольника равны $11$ , $12$ и $13$ . Найти медиану, проведенную к большей стороне.

Решение: Воспользуемся формулой для длины медианы: $m_c=frac{1}{2}sqrt{2a^2+2b^2-c^2}$
Подставим значения $m_c=frac{1}{2}sqrt{2cdot11^2+2cdot12^2-13^2}=frac{1}{2}sqrt{242+288-169}=frac{1}{2}sqrt{361}=frac{19}{2}=9,5$ Ответ: $m_c=9,5$

Задача 10: В треугольнике $ABC$ $AB=11$ , $AC=23$ , медиана $AK=10$ . Найти $BC$ .

Решение: Воспользуемся формулой для длины медианы и подставим в неё данные из условия:
$AK=frac{1}{2}sqrt{2cdot11^2+2cdot23^2-BC}$ $Rightarrow$ $100=frac{1}{4}left(242+1058-BC^2right)$ $Rightarrow$ $BC^2=900$ Ответ: $BC=30$ .

Упражнения:

Источник

Как вывести формулу медианы треугольника

Медиана в треугольнике – это отрезок, который проводят из вершины угла к середине противоположной стороны. Чтобы найти длину медианы, необходимо воспользоваться формулой выражения ее через все стороны треугольника, которую нетрудно вывести.

Инструкция

Чтобы вывести формулу для медианы в произвольном треугольнике, необходимо обратиться к следствию из теоремы косинусов для параллелограмма, получающегося путем достраивания треугольника. Формулу можно доказать на этом основании, она очень удобна при решении задач, если известны все длины сторон или их легко можно найти из других начальных данных задачи.

Фактически теорема косинусов представляет собой обобщение теоремы Пифагора. Она звучит так: для двумерного треугольника с длинами сторон a, b и c и углом α, противолежащим стороне a, справедливо следующее равенство:a² = b² + c² – 2•b•c•cos α.

Обобщающее следствие из теоремы косинусов определяет одно из важнейших свойств четырехугольника: сумма квадратов диагоналей равна сумме квадратов всех его сторон: d1² + d2² = a² + b² + c² + d².

Решите задачу: пусть в произвольном треугольнике ABC известны все стороны, найдите его медиану BM.

Достройте треугольник до параллелограмма ABCD добавлением линий, параллельных a и c. таким образом, сформировалась фигура со сторонами a и c и диагональю b. Удобнее всего строить так: отложите на продолжении прямой, которой принадлежит медиана, отрезок MD той же длины, соедините его вершину с вершинами оставшихся двух сторон A и C.

По свойству параллелограмма диагонали делятся точкой пересечения на равные части. Примените следствие из теоремы косинусов, согласно которому сумма квадратов диагоналей параллелограмма равна сумме удвоенных квадратов его сторон:BK² + AC² = 2•AB² + 2•BC².

Поскольку BK = 2•BM, а BM – это медиана m, то:(2•m) ² + b² = 2•c² + 2•a², откуда:m = 1/2•√(2•c² + 2•a² – b²).

Вы вывели формулу одной из медиан треугольника для стороны b: mb = m. Аналогично находятся медианы двух других его сторон:ma = 1/2•√(2•c² + 2•b² – a²);mc = 1/2•√(2•a² + 2•b² – c²).

Источники:

формула медианы
Формулы для медианы треугольника [видео]

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Тип урока: Урок – семинар.

Вид урока: Урок формирования умений и навыков, применения теоремы
косинусов, ее следствий при решении задач и доказательства теорем.

Цели урока:

Образовательные:
1. Совершенствовать навыки решения задач с использованием теоремы косинусов
и ее следствий.
2. Вывести формулу о медиане треугольника и показать применение этой формулы
при решении задач.
3. Ознакомить учащихся с методом дополнительных построений при выводе формул
и при решении задач.
Развивающая:
1. Формирование и совершенствование умений обобщать путем сравнения,
постановка и решение проблем, рассуждение по аналогии, оперирование уже
знакомыми геометрическими понятиями и фактами.
2. Развивать психологические характеристики личности учащихся: выдвижению
гипотез, формированию проблем.
3. Развивать психические свойства: память, воображение.
Воспитательные:
1. Отрабатывать навыки устной речи.
2. Воспитывать умение слушать друг друга и учителя.

Ход урока

1. Организационный момент.

Приветствие.
Сегодня мы с вами продолжим работу по теме : “Теорема косинусов и ее
следствия”. Используя метод дополнительного построения, выведем формулы для
вычисления медиан треугольника и применим ее при решении задач.

2. Проверка домашнего задания.

Устно формулируем теорему косинусов, ее следствия.
Анализируем ответы и этапы решения домашних задач.

№ 1.

Определите вид треугольника заданного своими сторонами 17, 8,15.

Решение:

Наибольший угол лежит против стороны, равной 17, то по следствию из теоремы
косинусов:

Треугольник прямоугольный.

Ответ: треугольник прямоугольный.

№ 2.

Найдите сторону АВ в треугольнике АВС,

№3

Найдите сторону АС равнобедренного треугольника АВС , если АВ=ВС=4 и медиана
АД равна 3.

3. Вывод формулы для вычисления медианы треугольника, если известны все
стороны треугольника.

Найдите медиану треугольника АВС с известными сторонами а,в,с.

Отложим отрезок ДК на продолжении медианы ВД, равный ВД. Соединим точки
А, К и С,К. Получившийся четырехугольник параллелограмм по признаку(
диагонали четырехугольника пересекаются и точкой пересечения делятся
пополам).

Применим следствие из теоремы косинусов для параллелограмма:

ВК²+ АС²= 2АВ²+ 2ВС²

Значит, (2m_в)²+ в²= 2с²
+ 2а² или 4m_в²= 2с²+ 2а²– в²

Запишем аналогичные формулы, для медиан проведенные к другим сторонам:

Решим домашнюю задачу с использованием этой формулы.

Делаем вывод о том, какое решение рациональней.

4. Вопрос: Можно ли найти сторону треугольника, если известны все ее медианы?
Выведем формулу для вычисления стороны треугольника по ее медианам. Для этого
воспользуемся опять дополнительным построением.

Учащийся у доски выводит формулу.

– Какое дополнительное построение будем проводить?

– Какую фигуру получили и почему?

– Какую теорему будем применять?

– Вывод?

Применим следствие из теоремы косинусов для параллелограмма АОСО₁:

Аналогично для других сторон :

Зная метод вывода формулы, всегда можно ее получить.
Применим эту формулу для решения задач. Учащиеся самостоятельно решают, затем
проверка на доске.

№ 1 В треугольнике АВС сторона АС равна 20, а медианы , проведенные к другим
сторонам равны 18 и 24 соответственно. Найдите третью медиану треугольника.

Метод дополнительного построения используется и при решении задач.

№ 2 Найдите площадь остроугольного треугольника АВС,

5. Подведение итогов урока:

Какие новые формулы изучили на уроке?
Какой метод применяли для доказательства теорем и решения задач?

6. Домашнее задание:

1. Найдите площадь треугольника, если две стороны его соответственно
равны 27 и 29, а медиана проведенная к третьей стороне равна 26.
2. Найдите площадь остроугольного треугольника АВС,

Математика, правильно понятая, обладает не только истинной, но так же
величайшей красотой.
Бертран Рёссель

Источник

Введение

Наверняка за то время, что вы изучаете геометрию, вы решили множество задач, в условии которых встречались медианы или биссектрисы. Обычно наличие таких слов предполагало лишь формальное использование определения медианы или биссектрисы, то есть то, что какая-то сторона либо какой-то угол разделены пополам.

Чуть реже мы использовали специфические свойства медиан и биссектрис. Но что делать, если нужно найти длину самой медианы или биссектрисы? Сейчас мы об этом и поговорим.

[00:0:54/Теорема о сторонах и диагоналях параллелограмма]

Докажем сначала полезную вспомогательную теорему о параллелограмме.

Теорема

В параллелограмме сумма квадратов диагоналей равна сумме квадратов сторон: .

Доказательство

Рассмотрим треугольники и (Рис. 1).

Рис. 1. Иллюстрация к доказательству теоремы

По теореме косинусов для треугольника имеем .

Теперь заметим, что и – секущая, то есть углы и – внутренние односторонние, а значит, их сумма равна . Следовательно, их косинусы равны по модулю и противоположны по знаку: . Учитывая это, сложим два равенства, получаем: .

Теорема доказана.

Длина медианы

Эта теорема и сама по себе довольно полезна, потому что с ее помощью можно быстро найти недостающую сторону или диагональ параллелограмма. Но для нас сейчас особенно важно, что именно с помощью этой теоремы мы получим формулу для вычисления длины медианы треугольника. Для этого воспользуемся одним полезным стандартным приёмом при решении геометрических задач – удвоением медианы.

Теорема

Длину медианы треугольника можно вычислить по формуле: (Рис. 2).

Рис. 2. Иллюстрация к теореме о длине медианы треугольника

Доказательство

Продлим медиану на ее длину за точку – получим точку . Заметим, что – параллелограмм по признаку: диагонали делятся точкой пересечения пополам (Рис. 3).

Рис. 3. Удвоение медианы

Значит, к нему можно применить доказанную нами теорему о сторонах и диагоналях параллелограмма:

Теорема доказана.

Итак, теперь мы умеем находить медиану треугольника, зная длины трёх его сторон. Воспользуемся этим для решения различных задач.

Примеры

Пример 1

Стороны треугольника равны и . Найти медиану, проведенную к большей стороне.

Решение

Воспользуемся формулой для длины медианы: .

Подставляем в неё известные из условия длины сторон:

Ответ: .

Пример 2

В треугольнике : , , медиана . Найти .

Решение

Воспользуемся формулой для длины медианы и подставим в неё данные из условия:

Ответ: .

Формула длины медианы применяется и для доказательства теорем.

Доказательство теоремы

Теорема

Если в треугольнике две медианы равны, то он равнобедренный.

Доказательство

Пусть (Рис. 1).

Рис. 1. Иллюстрация к теореме

Выразим длины обеих медиан через длины сторон треугольника и приравняем полученные формулы:

Получаем, что треугольник равнобедренный. Что и требовалось доказать.

Длина биссектрисы

Длину биссектрисы ищут гораздо реже. Однако формула для вычисления её длины может быть полезна для решения некоторых задач.

Теорема

Длину биссектрисы треугольника можно вычислить по формуле: (Рис. 4).

Рис. 4. Иллюстрация к теореме

Доказательство

Воспользуемся методом площадей. Запишем формулы для вычисления площади некоторых треугольников:

С другой стороны, площадь треугольника равна сумме площадей двух непересекающихся треугольников, из которых он состоит: . Тогда

Теорема доказана.

Пример

Рассмотрим задачу, которую можно решить, используя полученную формулу.

Задача

Пусть в треугольнике , , . Требуется найти биссектрису (Рис. 5).

Рис. 5. Иллюстрация к задаче

Решение

Воспользуемся полученной формулой для длины биссектрисы:

Нахождение биссектрисы по трём сторонам

Можно ли найти длину биссектрисы, если известны только длины трёх сторон треугольника? Конечно, можно по теореме косинусов найти косинус соответствующего угла треугольника, а затем по формуле косинуса двойного угла найти косинус половины угла и применить доказанную нами формулу длины биссектрисы. Но есть и другой алгоритм.

Пример

Пусть в треугольнике : и . Найти биссектрису (Рис. 1).

Рис. 1. Иллюстрация к условию задачи

Решение

1. Первым делом найдем . Заметим, что по свойству биссектрисы , значит, .

2. Далее по теореме косинусов для треугольника находим косинус угла :

3. Теперь применим теорему косинусов к треугольнику :

Если этот метод вам понравился больше, то можно использовать для нахождения длины биссектрисы и его. Впрочем, в формулу подставлять гораздо проще.

Кстати, если даны три стороны, то есть еще одна формула, позволяющая найти длину биссектрисы: где и – отрезки, на которые сторона делится биссектрисой (Рис. 6).

Рис. 6. Нахождение биссектрисы по трем сторонам

Доказательство

Пусть – точка пересечения продолжения биссектрисы и окружности, описанной около (Рис. 1).

Рис. 1. Иллюстрация к доказательству

Тогда треугольники и подобны (одна пара углов равна по определению биссектрисы, а углы и – вписанные и опираются на одну дугу).

Значит, , то есть .

Осталось заметить, что по теореме о пересекающихся хордах: , подставив это в полученное равенство, получим требуемое:

Заключение

На этом уроке мы познакомились с формулами для вычисления длины медианы и биссектрисы в треугольнике. Помимо этого, доказали важную теорему о сторонах и диагоналях параллелограмма и решили несколько задач на применение выведенных формул.

Список рекомендованной литературы

Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009.
Геометрия 11 класс, А.В. Погорелов. М.: Просвещение, 2002.
Геометрия. 11 класс. Рабочая тетрадь. Бутузов В.Ф., Глазков Ю.А., Юдина И.И. 8-е изд. – М.: Просвещение, 2013.

Рекомендованные ссылки на ресурсы сети Интернет

Интернет-портал «syl.ru» (Источник)
Интернет-портал «www-formula.ru» (Источник)
Интернет-портал «zdesformula.ru» (Источник)

Домашнее задание

Вычислите длину биссектрисы треугольника , проведённую из вершины , если .
Длины катетов прямоугольного треугольника равны и . Найдите длину биссектрисы прямого угла треугольника.
В равнобедренном треугольнике длина боковой стороны равна . Медиана, проведённая к боковой стороне, равна . Найдите длину основания треугольника.