Как найти медиану треугольника зная все стороны

Как найти медиану треугольника зная все стороны

Рассмотрим задачу, в которой требуется по сторонам треугольника найти его медиану.

Задача.

Даны стороны треугольника. Найти длину медианы, проведенной к наибольшей стороне.

po storonam treugolnika nayti ego medianuДано: ∆ ABC,

BC=a, AC=b, AB=c,

сторона AC — наибольшая,

BO- медиана.

Найти: BO.

Решение:

po storonam treugolnika nayti medianu

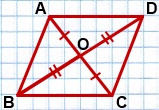
1) На луче BO отложим отрезок OD, OD=BO.

nayti medianu treugolnika po ego storonam

2) Проведем отрезки AD и CD.

3) Рассмотрим четырехугольник ABCD.

AO=CO (так как BO — медиана треугольника ABC по условию);

BO=DO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

4) По свойству диагоналей параллелограмма,

    [A{C^2} + B{D^2} = 2(A{B^2} + A{D^2})]

    [{b^2} + B{D^2} = 2({a^2} + {c^2})]

    [B{D^2} = 2({a^2} + {c^2}) - {b^2}]

    [BD = sqrt {2({a^2} + {c^2}) - {b^2}} ]

так как BO=1/2 BD (по построению),

    [underline {BO = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} .} ]

Если ввести обозначение

    [BO = {m_b},]

формула для нахождения медианы треугольника по его сторонам примет вид:

    [{{m_b} = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} }]

Запоминать эту формулу не обязательно. При решении конкретной задачи следует привести все рассуждения.

Если медиана проведена не к наибольшей, а к наименьшей либо средней по величине стороне, решение задачи аналогично.

Соответственно, формулы для нахождения длины медианы в этих случаях:

    [{m_a} = frac{1}{2}sqrt {2({b^2} + {c^2}) - {a^2}} ]

    [{m_c} = frac{1}{2}sqrt {2({a^2} + {b^2}) - {c^2}} ]

Приём, который применили для решения задачи — метод удвоения медианы.

Источник

Чтобы по сторонам треугольника найти медиану, не обязательно запоминать дополнительную формулу. Достаточно знать алгоритм решения.

Для начала рассмотрим задачу в общем виде.

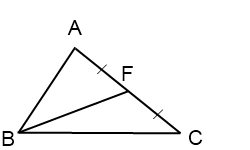
Дан треугольник со сторонами a, b, c. Найти длину медианы, проведенной к стороне b.

AB=a, AC=b, BC=c.

найти медиану треугольника по его сторонам

Решение.

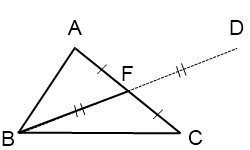
На луче BF отложим отрезок FD, FD=BF.

найти длину медианы треугольника по его сторонам

Соединим точку D с точками A и C.

нахождение медианы треугольника по его сторонам

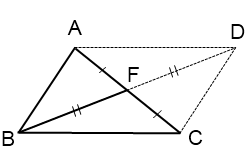
Четырехугольник ABCD — параллелограмм (по признаку), так как у него диагонали в точке пересечения делятся пополам.

Свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Отсюда: AC²+BD²=2(AB²+BC²), значит, b²+BD²=2(a²+c²),

BD²=2(a²+c²)-b². По построению, BF — половина BD, следовательно,

    [BD = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} ]

Это — формула нахождения медианы треугольника по его сторонам. Обычно ее записывают так:

    [{m_b} = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} ]

Переходим к рассмотрению конкретной задачи.

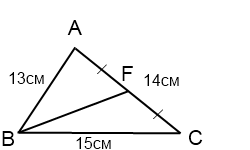
Стороны треугольника равны 13 см, 14 см и 15 см. Найти медиану треугольника, проведенную к его средней по длине стороне.

Решение:

Даны стороны треугольника. Найти медиану

Применяя аналогичные рассуждения, получаем:

AC²+BD²=2(AB²+BC²).

Отсюда

14²+BD²=2(13²+15²)

BD²=2(169+225)-196=592

    [BD = sqrt {592} = sqrt {16 cdot 37} = 4sqrt {37} (cm)]

    [BF = frac{1}{2}DD = frac{1}{2} cdot 4sqrt {37} = 2sqrt {37} (cm)]

Ответ:

    [2sqrt {37} cm]

Источник

Из какой вершины треугольника опустить медиану:

Из вершины A

Из вершины B

Из вершины C

Укажите размеры:

AB
AC
BC

A
B
C

Сторона AB

Сторона AC

Сторона BC

Результат:

Решение:

Скопировать

Ссылка на страницу с результатом:

# Теория

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Так как каждая вершина треугольника имеет свою медиану, то всего в треугольнике может быть три медианы.

Длину медианы треугольника ABC если известны все стороны треугольника можно расчитать по одной из нижепреведённых формуле:

Формула медианы

m
a
b
c

A
B
C

m_a = sqrt{ dfrac{2b^2 + 2c^2 -a^2}{4} }

  • A, B, C – вершины треугольники
  • a, b, c – стороны треугольника
  • ma – медиана треугольника опущенная из вершины A

a
b
c

A
B
C

m_b = sqrt{ dfrac{2a^2 + 2c^2 -b^2}{4} }

  • mb – медиана из вершины B

a
b
c

A
B
C

m_c = sqrt{ dfrac{2a^2 + 2b^2 -c^2}{4} }

  • mc – медиана из вершины C

Так же данные формулы можно встретить в такой записи, что по сути является тем же самым что формулы выше:

m_a = 0.5 cdot sqrt{ 2b^2 + 2c^2 – a^2 }

m_b = 0.5 cdot sqrt{ 2a^2 + 2c^2 – b^2 }

m_c = 0.5 cdot sqrt{ 2a^2 + 2b^2 – c^2 }

Похожие калькуляторы:

Войдите чтобы писать комментарии

Источник

Добавить комментарий