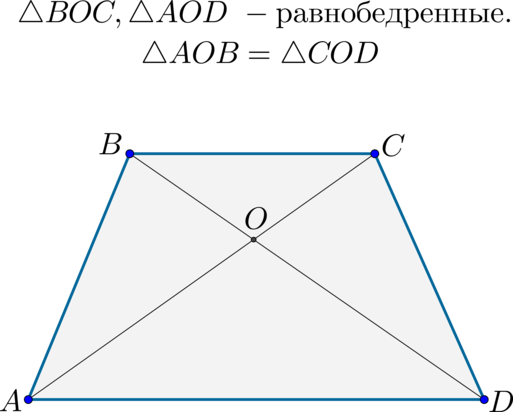
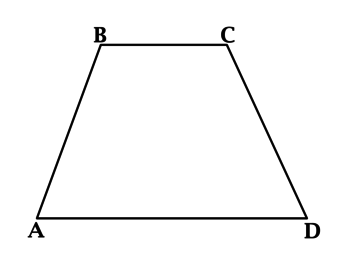
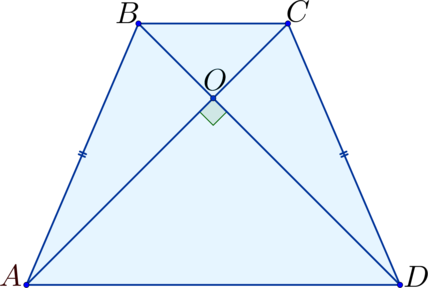
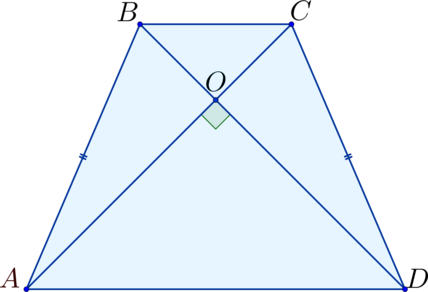
В данной публикации мы рассмотрим определение и основные свойства равнобедренной трапеции.
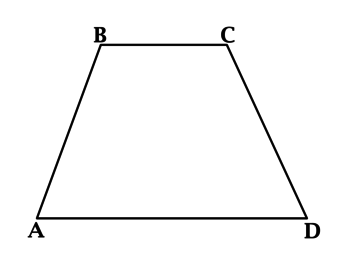
Напомним, трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны, т.е. AB = CD.
- Свойство 1
-
Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Свойство 7
Свойство 1
Углы при любом из оснований равнобедренной трапеции равны.
- ∠DAB = ∠ADC = α
- ∠ABC = ∠DCB = β
Свойство 2
Сумма противоположных углов трапеции равняется 180°.
Для рисунка выше: α + β = 180°.
Свойство 3
Диагонали равнобедренной трапеции имеют одинаковую длину.
AC = BD = d
Свойство 4
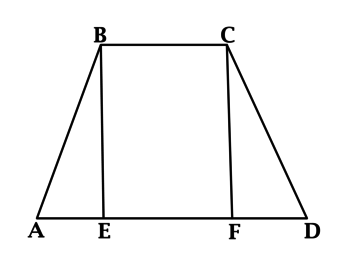
Высота равнобедренной трапеции BE, опущенная на основание большей длины AD, делит его на два отрезка: первый равняется половине суммы оснований, второй – половине их разности.
Свойство 5
Отрезок MN, соединяющий середины оснований равнобокой трапеции, перпендикулярен этим основаниям.
Прямая, проходящая через середины оснований равнобедренной трапеции, называется ее осью симметрии.
Свойство 6
Вокруг любой равнобедренной трапеции можно описать окружность.
Свойство 7
Если сумма оснований равнобокой трапеции равно удвоенной длине ее боковой стороны, в нее можно вписать окружность.
Радиус такой окружности равняется половине высоты трапеции, т.е. R = h/2.
Примечание: остальные свойства, которые применимы ко всем видам трапеций, приведены в нашей публикации – “Что такое трапеция: определение, виды, свойства”.
25
Июл 2013
Категория: Справочные материалы
Трапеция. Свойства трапеции
2013-07-25
2016-06-15
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Автор: egeMax |
комментарий 431
Печать страницы
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Признаки и свойства равнобедренной трапеции
(blacktriangleright) Равнобедренная трапеция – трапеция, у которой боковые стороны равны.
Свойства равнобедренной трапеции:
(blacktriangleright) Углы при каждом основании равны;
(blacktriangleright) Диагонали равны;
(blacktriangleright) Два треугольника, образованные диагоналями и одним из оснований, являются равнобедренными;
(blacktriangleright) Два треугольника, образованные диагоналями и боковой стороной, равны.
Задание
1
#296
Уровень задания: Равен ЕГЭ
В трапеции (ABCD): (AB = CD), (angle C – angle A = 80^{circ}). Найдите (angle D + angle B – angle C). Ответ дайте в градусах.
У равнобедренной трапеции углы при одном основании равны, тогда (angle B = angle C) и, следовательно, (angle D + angle B – angle C = angle D = angle A).
У равнобедренной трапеции сумма противоположных углов равна (180^{circ}) (так как (angle C = angle B), а (angle A + angle B = 180^{circ}), как сумма односторонних при параллельных прямых и секущей).
(angle A + angle C = 180^{circ}),
(angle C – angle A = 80^{circ})
тогда, вычитая из верхнего равенства нижнее, получаем (2cdot angle A = 100^{circ}). В итоге имеем: (angle D + angle B – angle C = angle A = 50^{circ}).
Ответ: 50
Задание
2
#1699
Уровень задания: Равен ЕГЭ
Диагонали в равнобедренной трапеции (ABCD) перпендикулярны. Найдите площадь трапеции, если диагональ (AC) равна (2).
В равнобедренной трапеции диагонали равны, поэтому (AC = BD = 2). Пускай (O) – точка пересечения диагоналей.
[begin{gathered}
S_{ABCD} = S_{triangle ABC} + S_{triangle CDA} = frac{1}{2}cdot AC cdot BO + frac{1}{2}cdot AC cdot OD =\ =frac{1}{2}cdot AC cdot(BO + OD) = frac{1}{2}cdot AC cdot BD = frac{1}{2} cdot 2 cdot 2 = 2end{gathered}]
Ответ: 2
Задание
3
#1789
Уровень задания: Равен ЕГЭ
Найдите диагонали равнобедренной трапеции, если они перпендикулярны, а площадь трапеции равна (8).
Пусть (ABCD) — трапеция с диагоналями (AC) и (BD), (O) – точка их пересечения, тогда
(S_{ABCD} = S_{triangle ABC} + S_{triangle CDA} = frac{1}{2}cdot AC cdot BO + frac{1}{2}cdot AC cdot OD = )
(frac{1}{2}cdot AC cdot(BO + OD) = frac{1}{2}cdot AC cdot BD =
frac{1}{2}cdot AC^2 = 8) (Rightarrow) (AC = 4).
Ответ: 4
Задание
4
#1704
Уровень задания: Равен ЕГЭ
В равнобедренной трапеции (ABCD) основание (AD) вдвое длиннее основания (BC) и боковой стороны. Найдите острый угол трапеции.
Если опустить высоты (BH) и (CK) на основание (AD), то они отсекут равные отрезки (AH) и (KD), причем (AB = BC = HK) (Rightarrow) (AH = frac{AD – HK}{2} = frac{HK}{2} = frac{AB}{2}) (Rightarrow) (angle ABH = 30^circ), как угол в прямоугольном треугольнике, противолежащий катету, равному половине гипотенузы (Rightarrow) (angle BAK = 90^circ – 30^circ = 60^circ).
Ответ: 60
Задание
5
#295
Уровень задания: Равен ЕГЭ
(ABCD) – трапеция с основаниями (AD) и (BC). При этом (AB = CD = 6), (BC = 4), один из углов трапеции (ABCD) равен (60^{circ}). Найдите (AD).
Пусть (angle A = 60^{circ}), (BE) – высота в треугольнике (ABD). (angle ABE = 90^{circ} – 60^{circ} = 30^{circ}). Катет, лежащий против угла в (30^{circ}), равен половине гипотенузы, тогда (AE = 0,5cdot 6 = 3).
У равнобедренной трапеции углы при одном основании равны, тогда (angle D = 60^{circ}). Пусть (CF) – высота в треугольнике (ACD), тогда аналогично тому, как находили (AE), находим, что (FD = 3). (EF = BC), так как (BCFE) – прямоугольник. Тогда (AD = AE + EF + FD = 3 + 4 + 3 = 10).
Ответ: 10
Задание
6
#1700
Уровень задания: Равен ЕГЭ
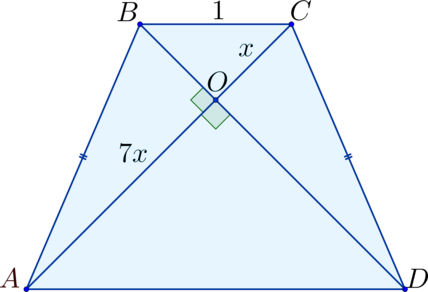
Диагонали в равнобедренной трапеции (ABCD) перпендикулярны. (O) – точка пересечения диагоналей, причем (AO:OC = 7:1). Найдите периметр трапеции, если меньшее основание равно (1).
(BC) – меньшее основание, треугольники (triangle BOC) и (triangle AOD) подобны и их стороны относятся как (1:7) (Rightarrow) (BC:AD = 1:7) (Rightarrow) (AD = 7); (OB = OC), (OB^2 + OC^2 = 1^2) (Rightarrow) (OB = OC = frac{1}{sqrt2}) (Rightarrow) (AO = frac{7}{sqrt2}). В (triangle ABO): (AO^2 + OB^2 = AB^2) (Rightarrow) (AB = 5). Тогда (P_{ABCD} = AB + BC + CD + AD = 1 + 7 + 5 + 5 = 18).
Ответ: 18
Задание
7
#1702
Уровень задания: Равен ЕГЭ
В равнобедренной трапеции (ABCD) биссектриса (angle ABC) параллельна боковой стороне (CD) и пересекает основание (AD) в точке (K), которая делит (AD) в отношении (AK:KD = 1:2). Найдите периметр трапеции, если меньшее основание равно (4).
(BCDK) – параллелограмм, т.к. противоположные стороны попарно параллельны; (angle AKB = angle KBC), т.к. накрест лежащие при параллельных (BC) и (AD); (angle BAK = angle CDK = angle KBC) (Rightarrow) (triangle ABK) – равносторонний треугольник. (BC = KD = 4) (Rightarrow) (AK = 2 = AB = CD) (Rightarrow) (P_{ABCD} = AB + BC + CD + KD + AK = 2 + 4 + 2 + 4 + 2 = 14).
Ответ: 14
Учащимся старших классов, которые готовятся сдавать ЕГЭ по математике, в обязательном порядке стоит повторить тему «Равнобедренная трапеция» и освежить в памяти ее основные свойства и признаки. Многолетняя практика показывает, что подобные задания ежегодно встречаются в программе аттестационного испытания. Поэтому, если вы хотите успешно решить задачи ЕГЭ на применение основных свойств диагоналей или углов равнобедренной трапеции, вам непременно стоит разобраться в этой теме.
Образовательный портал «Школково» предлагает новый подход к подготовке к аттестационному испытанию. Наш ресурс позволяет учащимся определить наиболее сложные темы и ликвидировать имеющиеся пробелы в знаниях. Специалисты «Школково» подготовили и изложили весь материал в максимально доступной форме.
Чтобы выпускники могли успешно справляться с геометрическими задачами, мы рекомендуем вспомнить определение равнобедренной трапеции, свойства ее сторон, углов и диагоналей, а также формулу для вычисления площади. Эта информация представлена в разделе «Теоретическая справка».
Вспомнив основные свойства углов, диагоналей и сторон равнобедренной трапеции, учащиеся имеют возможность закрепить усвоенный материал, выполнив практические задания. Упражнения различного уровня сложности представлены в разделе «Каталог». В каждом из них вы найдете подробный алгоритм решения и правильный ответ.
Практиковаться в выполнении заданий по теме «Трапеция» при подготовке к ЕГЭ выпускники могут в режиме онлайн, находясь не только в Москве, но и в любом другом городе России. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

УСТАЛ? Просто отдохни
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 5
МУНИЦИПАЛЬНОГО
ОБРАЗОВАНИЯ
город – курорт АНАПА
Рассмотрено и
рекомендовано к использованию
на заседании МО от _______________
Протокол №______
Подготовка
к ОГЭ и ЕГЭ.
«Формулы
и свойства трапеции»
Методическая разработка
учителя
математики
Снегуровой Амины Мугиновны
2018 год.
Оглавление
Введение 3
1.
Определения 4
2.
Частные случаи трапеции 5
3.
Свойства произвольной трапеции 6-7
4.
Свойства равнобедренной трапеции 8-10
5. Свойства
биссектрисы угла трапеции 10-12
6.
Свойства треугольников, образованных диагоналями трапеции 12-13
7.
Формулы нахождения диагоналей трапеции 13-14
8.
Трапеция и окружность 14-17
9.
Дополнительные построения в трапеции 17-23
10. Для
тех, кому интересно. Теоремы. 23-27
11.
Задачи с решениями.27-35
12. Список используемой литературы .
Введение
Дорогой ученик!
В материалах различных контрольных работ и экзаменов очень часто встречаются
задачи на трапецию, решение которых требует от учащихся знаний
«непрограммных» свойств трапеции. (Программными считаются свойство средней
линии трапеции, свойства диагоналей и углов
равнобедренной
трапеции.) Свойства, необходимые для решения задач, отсутствуют в
учебниках или перенесены в задачи и не воспринимаются как теоретические
положения.
Какими же замечательными свойствами обладает трапеция?
Как решать геометрические задачи, требующие глубоких знаний? Трапеция
обладает рядом интересных и полезных для решения задач свойствами. Если
овладеть ими и рассмотреть дополнительные построения в трапеции, то возникает
объективная возможность для решения задач повышенной сложности.
В планиметрии существует целый класс таких задач,
к которым традиционные методы (метод цепочек равных треугольников, метод
геометрических преобразований, векторный метод и др.) либо вовсе не применимы,
либо дают сложные и громоздкие решения. Во многих случаях решать такого рода
задачи помогает введение в чертеж дополнительных линий – так называемое
дополнительное построение. В одних случаях эти построения напрашиваются сами
собой, в других они не так очевидны и требуют от решающего достаточно большого
опыта, изобретательности, геометрической интуиции.
Так, чертеж данной в задаче фигуры можно
достраивать до фигуры другого типа, можно с многоугольной фигурой связывать
окружность, а можно целью дополнительного построения ставить выделение на
чертеже равных, равновеликих или подобных фигур.
Знание метода дополнительных построений в
большинстве случаев позволяет решать, казалось бы, сложные геометрические
задачи просто, понятно и красиво.
В этой
разработке собраны формулы, свойства и подсказки для решения задач связанных с
трапецией. Надеюсь, что ты здесь найдешь для себя много полезной информации.
1.Определения.
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
Параллельные
стороны
называются её основаниями, а две другие стороны – боковыми
сторонами.
Высотой трапеции называется расстояние между основаниями.

Kаждый
из этих отрезков EF, BM, DK, PQ является высотой трапеции ABCD.
В
формулах используются следующие обозначения:
a,
b – основания трапеции
c,
d – боковые стороны трапеции
d1
d2 – диагонали трапеции
α
β – углы при большем основании трапеции
h–
высота.
2.Частные
случаи трапеции.
Прямоугольной
трапецией называется трапециия, в которой одна из боковых сторон перпендикулярна
основаниям.
У
нее два прямых угла при меньшей боковой стороне.
Эта
сторона одновременно является и высотой трапеции.
произвольная
Трапецией
называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
У
равнобедренной трапеции так же, как и у равнобедренного треугольника, углы при
основании равны.
Трапеция,
у которой боковые стороны равны, называется равнобедренной
(равнобокой,
равнобочной).
3.Свойства произвольной
трапеции.
1. Во всякой трапеции сумма углов , прилежащих к
одной ее боковой стороне, равна 1800.


основаниям, равна полусумме этих оснований и делит диагонали трапеции пополам.

MК =
3.Четыре замечательные
точки трапеции:
Во всякой трапеции середины
оснований, точка пересечения диагоналей и точка пересечения продолжений боковых
сторон лежат на одной прямой.

4. Во всякой трапеции если
сумма углов при большем основании равна 900, то боковые стороны
лежат на перпендикулярных прямых. Длина отрезка, соединяющего середины
оснований, равна полуразности оснований.
5.
Свойства отрезка, соединяющего основания трапеции

соединяющий основания всякой трапеции, и проходящий через точку пересечения
диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований
трапеции.
Если провести отрезок, концы которого лежат на основаниях
трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то
соотношение составляющих его отрезков от стороны основания до точки пересечения
диагоналей ( KO/ON ) будет равно соотношению оснований трапеции:
6.Свойства отрезка, параллельного основаниям всякой трапеции.

провести отрезок, параллельный основаниям трапеции и проходящий через точку
пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
*Заданный отрезок (KM) делится точкой пересечения диагоналей
трапеции пополам, то есть КО=ОМ
*Длина отрезка,
проходящего через точку пересечения диагоналей трапеции и параллельного
основаниям, равна
KM = .
 |
|||
7.Во всякой трапеции с основаниями a и b отрезок, параллельный
основаниям, концы которого лежат на боковых сторонах, равен среднему
геометрическому оснований, если он делит трапецию на две трапеции, подобные
между собой.
8. Во всякой трапеции с основаниями a и b отрезок, параллельный
основаниям, концы которого лежат на боковых сторонах, равен среднему
квадратичному оснований, если он делит трапецию на две трапеции равной площади
(равновеликие).

9.Сумма
квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс
удвоенное произведение ее оснований.
d12
+ d22
= c2 + d2+
2ab, d– боковая сторона. d1 и
d2 –
диагонали.
Свойства
равнобедренной трапеции.
Трапеция является равнобедренной
тогда и только тогда, когда
*углы, прилежащие к одному
основанию, равны
*сумма противолежащих углов 1800;
*диагонали равны;

AC = BD
*отрезки диагоналей, соединяющих точку пересечения
с концами одного основания, равны; BO = OC, AO = OD.

описать окружность.
BC // AD, AB = CD. ABCD – вписанная трапеция.

большее основание на отрезки, один из которых равен полуразности оснований, а
другой полусумме оснований трапеции, т. е. средней линии трапеции.
*если в равнобедренной трапеции диагонали перпендикулярны,
то
1)квадрат ее диагонали равен половине квадрата суммы
оснований, а также удвоенному квадрату высоты и удвоенному квадрату
средней линии.
2)высота трапеции равна полусумме оснований.
3)ее высота равна средней линии.
4)
площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны,
равна квадрату её высоты.
(или квадрату полусуммы оснований, или квадрату средней линии).


диагонали трапеции взаимно перпендикулярны.
BH = HD = h =.
*высота, проведённая через
точку пересечения диагоналей, в
равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две
равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
*в равнобедренной трапеции прямая, проходящая через середины
оснований, перпендикулярна им и является осью симметрии трапеции.


*отрезки, последовательно соединяющие середины смежных сторон
равнобедренной трапеции, образуют ромб.

MNKE – ромб,
то есть
MN=NK=KE=
ME.
*в равнобедренной трапеции квадрат диагонали равен квадрату его
боковой стороны плюс произведение оснований: d2
= c2 + a b

равнобедренной трапеции с радиусом вписанной окружности равным r и углом при
основании α:
S =
Свойства
биссектрисы угла трапеции.
*биссектриса угла отсекает
от трапеции равнобедренный треугольник.



*точка пересечения биссектрис
тупых углов при основании трапеции принадлежит другому основанию.
*если диагональ трапеции является биссектрисой ее острого угла, то
меньшее основание равно боковой стороне трапеции, прилежащей к этому углу.
*биссектриса угла трапеции, пересекающая основание, отсекает от
трапеции равнобедренный треугольник.
*биссектрисы углов при боковой стороне трапеции пересекаются под
прямым углом.
* точка пересечения биссектрис трапеции, прилежащих к боковой
стороне, лежит на средней линии трапеции.
*если биссектриса тупого угла трапеции является диагональю, то
боковая сторона равна большему основанию трапеции.
*если меньшее основание трапеции равно ее
боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой
боковой стороне острого угла.
Если в условии задачи сказано, что основание трапеции равно ее боковой
стороне, то отсюда следует, что диагональ трапеции является биссектрисой ее
угла.
*если меньшее основание трапеции равно ее
боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой
боковой стороне острого угла.

трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой
прилежащего к этой боковой стороне тупого угла.
*если большее основание прямоугольной трапеции
равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла,
прилежащего к меньшему основанию.
* если меньшее основание прямоугольной трапеции
равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла,
прилежащего к большему основанию.
* если меньшее основание прямоугольной трапеции равно ее
большей боковой стороне, диагональ является биссектрисой прилежащего к этой
боковой стороне острого угла.
* если большее основание прямоугольной трапеции
равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к
этой боковой стороне тупого угла.
*если меньшее основание равнобедренной трапеции
равно ее боковой стороне, то диагональ является биссектрисой острого угла
трапеции.
* если большее основание равнобедренной трапеции
равно ее боковой стороне, то диагональ является биссектрисой тупого угла
трапеции.
Свойства
треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой
пересечения диагоналей трапеции – являются подобными.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются
вертикальными – они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD
и BC (основания трапеции параллельны между собой) и секущей прямой AC,
следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим
углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для
решения задач по геометрии подобие треугольников используется следующим
образом.
*Если
нам известны значения длин двух соответствующих элементов подобных
треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда
длины всех остальных элементов соотносятся между собой точно таким же
значением.
*В подобных треугольниках
длины всех линейных элементов пропорциональны, а именно:
отношения периметров, радиусы
вписанных окружностей, радиусы описанных окружностей, соответствующих высот, биссектрис,
медиан (проведенных из равных углов) подобных треугольников равны отношению
соответствующих сторон (лежащих против равных углов) или равны коэффициенту
подобия.
*Площади подобных
треугольников относятся как квадраты соответствующих сторон или равно квадрату
коэффициента подобия.

образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.
S12= S2 S3
S3: S2 = 2
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции
AB и CD. Это – треугольники AOB и COD. Несмотря на то, что размеры отдельных
сторон у данных треугольников могут быть совершенно различны, но площади
треугольников, образованных боковыми сторонами и точкой пересечения диагоналей
трапеции равны, то есть треугольники являются равновеликими.
Если продлить боковые стороны трапеции в сторону меньшего
основания, то они пересекутся в одной точке с прямой, соединяющей середины
оснований
Формулы для нахождения диагоналей трапеции
Далее приведены формулы, отображающие зависимость между сторонами,
углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения
задач по геометрии на тему “диагонали трапеции”

Далее, в формулах используются следующие обозначения:
a, b –
основания трапеции
c, d –
боковые стороны трапеции
d1 d2 –
диагонали трапеции
α β –
углы при большем основании трапеции
h– высота
Формулы нахождения диагоналей трапеции
через основания, боковые стороны и углы при основании

Эта группа формул отражает одно из основных свойств диагоналей
трапеции:
*Сумма квадратов диагоналей трапеции равна
сумме квадратов боковых сторон плюс удвоенное произведение ее оснований.
Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Используем
теорему косинусов.
*Данная
формула получена путем преобразования предыдущей формулы. Квадрат второй
диагонали переброшен через знак равенства, после чего из левой и правой части
выражения извлечен квадратный корень.
*Эта формула
нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что
в левой части выражения оставлена другая диагональ
4.В прямоугольной трапеции разность квадратов диагоналей равна
разности квадратов оснований
d12
– d22
= a2 –
b2
*Если
диагонали трапеции взаимно перпендикулярны, то длина отрезка, соединяющего
середины оснований трапеции равна полусумме оснований.
MH =
BDCE и FAOD прямоугольники, а диагонали
прямоугольника равны.
Трапеция и окружность.
1) Если в равнобокую трапецию можно вписать окружность, то средняя
линия трапеции равна боковой стороне.
Высота равнобедренной трапеции, в которую можно вписать окружность,
является средним геометрическим её оснований
h2
= a ∙ b
2)
Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна
средней линии. Площадь трапеции определяется произведением средней линии на
высоту трапеции.
3. Высота трапеции равна длине диаметра вписанной
окружности или двум ее радиусам.
MK —
высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности.
4. Центр вписанной
окружности является точкой пересечения биссектрис углов трапеции.
. CF =m,
FD =n, OF = r.

как сумма
внутренних односторонних углов при параллельных прямых AD и BC и секущей CD
равна 1800.
Отсюда
радиус вписанной в трапецию окружности выражается через длины отрезков, как
которые боковая сторона делится точкой касания, как r = .
А так как
высота трапеции равна ее диаметру, то и высоту трапеции можно выразить через
длины этих отрезков: h = 2 .
5.Если в трапецию можно вписать окружность и около трапеции можно
описать окружность, то проекция диагонали на большее основание, равна боковой
стороне и равна средней линии трапеции.
Если в трапецию вписана окружность, в задаче появляется несколько
путей, по которым можно повести рассуждение.
1.В четырехугольник можно вписать окружность тогда и только тогда,
когда суммы длин его противолежащих сторон равны. Отсюда следует, что если в трапецию вписана окружность, то сумма
ее оснований равна сумме боковых сторон.
AB+CD=AD+BC

проведенных из одной точки, равны. Отсюда следует, что
AL=AK BL=BM
CM=CF DF=DK
Описанная окружность.
Когда трапецию можно вписать в
окружность? Четырехугольник можно вписать в окружность тогда и только тогда,
когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать
в окружность можно только равнобокую трапецию.
Радиус окружности, описанной около трапеции, можно найти как
радиус окружности, описанной около из одного из двух треугольников, на которые
трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это
зависит от угла между диагональю трапеции и ее боковой стороной.

перпендикулярна ее боковой стороне, то центр окружности, описанной около
трапеции, лежит на середине ее большего основания. Радиус описанной около
трапеции окружности в этом случае равен половине ее большего основания:

боковой стороной острый угол, центр окружности, описанной около трапеции, лежит
внутри трапеции.
3) Если
диагональ трапеции образует с боковой стороной тупой угол, центр описанной
около трапеции окружности лежит вне трапеции, за большим основанием.
4)Радиус описанной около трапеции окружности можно найти по
следствию из теоремы синусов. Из треугольника ACD

Из треугольника ABC
Другой вариант найти радиус описанной окружности —

угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и
ACF:
При решении задач на трапецию, вписанную в окружность, можно
также использовать то, что вписанный угол равен половине соответствующего ему
центрального угла. Например,

Использовать углы COD и CAD можно и для нахождения площади
трапеции. По формуле нахождения площади четырехугольника через его диагонали
5)Если диагонали вписанной в окружность трапеции
(четырехугольника) взаимно перпендикулярны, то сумма квадратов его
противоположных сторон равна квадрату диаметра описанной окружности или
удвоенному квадрату боковой стороны:
a2
+ b2
= 4R2
= 2c2.

вписанной в нее окружности и основание перпендикуляра, опущенного из другой
вершины на основание, лежат на одной прямой.
Дополнительные построения
как прием при решении задач
Дополнительные
построения являются эффективным методом решения геометрических задач. Наиболее
часто используются при решении задач:
1.
Опускание высот из концов одного основания на другое основание
2.
Проведение через вершины трапеции прямой, параллельной боковой стороне, не
содержащей эту вершину
3.
Проведение через середину меньшего основания прямых, параллельных боковым
сторонам
4.
Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей
эту вершину .
5.
Продолжение боковых сторон до пересечения.
Рассмотрим
каждое их них.
При
решении задач на отыскание площади дополнительным построением считается
построение ее высоты или высот. Если построение высоты не помогает решить
задачу, то нужно построить прямую, параллельную одной из ее диагоналей. Потом
найти площадь полученного треугольника, который будет равновеликим исходной
трапеции.
1.
Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей
эту вершину.
При
дополнительном построении, когда переносится диагональ, образуется треугольник,
площадь которого равна площади трапеции.
S1 = S2
Задача.
Найдите
площадь трапеции, дмагонали которой равны 8 и 15, а средняя линия равна 8,5.
Решение.
Построим
CF // BD и
получим SACF = SABCD.
Почему?
ABC
= CDF, так как DF = BC и эти треугольники имеют одинаковую высоту.
Значит,
для того, чтобы найти площадь трапеции нам достаточно найти площадь ACF.
АF
= АD + ВС – сумма оснований трапеции. По условию задачи средняя линия
трапеции 8,5. Значит сумма оснований АF = 8,52=17.
Рассмотрим ACF.
Проверим, является ли он прямоугольным? В этом нам поможет теорема Пифагора:
172
= 82 + 152
289
= 64 + 225.
289
= 289.
ACF
– прямоугольный. SACF = AC*CF
= 8*15 = 60. SABCD=
60.
Если ACF
разносторонний, то его площадь вычислим по формуле Герона.
Ответ:60.
2.
Продолжение боковых сторон до пересечения.
Свойства трапеции,
достроенной до треугольника

Если продлить стороны трапеции в сторону меньшего основания, то
точка пересечения сторон будет совпадать с прямой линией, которая
проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до
треугольника. При этом:
*Треугольники, образованные основаниями трапеции с общей вершиной
в точке пересечения продленных боковых сторон являются подобными
*Прямая, соединяющая середины оснований трапеции, является,
одновременно, медианой построенного треугольника.
*Если ABCD равнобедренная трапеция, то KL
является биссектрисой, медианой и высотой одновременно.
Это
дополнительное построение позволяет перейти от трапеции к треугольнику. Если
сумма углов при большем основании равна 900, топродолжив боковые
стороны мы получим прямоугольный треугольник.
Задача.
В
трапеции ABCD основания АD и ВС равны соответственно 72 и 18, а сумма углов при основании АD равна
900. Найдите радиус окружности, проходящей через точки А и В и
касающейся прямой CD, если АВ = 18.
Решение.
Центром
О данной окружности будет точка пересечения серединного
перпендикуляра к АВ и перпендикуляра, возведенного к стороне CD
из точки касания окружности. АВО равнобедренный: АО = ВО. Продлим боковые
стороны трапеции и получим прямоугольный треугольник АМD.
KMNO – прямоугольник, где KM = MN
= NO =КО = R.
BMC
AMD.
=
, то есть
и x
= 6. Тогда R = КВ + 6 = 9 + 6 = 15.
Ответ:15.
3. Опускание высот из концов одного основания на другое основание.
Дополнительное
построение 1,2 позволяет разбить трапецию на прямоугольник (стороны которого –
одно из оснований и высота трапеции) и два прямоугольных треугольника (в
которых один из катетов – высота трапеции, а гипотенузы – боковые стороны
трапеции)
Построение
1 Построение 2

Задача. Найдите площадь трапеции с основаниями 8 и 13 и
боковыми сторонами 3 и 4.

Решение.
Проведем ВН и СM – высоты и получим ABD (египетский
треугольник) со сторонами 3,4,5, так как АD – ВС=13 – 8=5.
S= АВ* BD= 6.
Найдем высоту
трапеции: h= 2S:5 = 2*6:5=
2,4.
SABCD= 6+2,4*8=25,2. Ответ:25,2.
4. Проведение
через середину меньшего основания прямых, параллельных боковым сторонам.
Дополнительное построение 4
делит трапецию на параллелограммы и треугольник. Боковые стороны соединяются в
треугольник.


5. Проведение через вершины трапеции прямой, параллельной боковой
стороне, не содержащей эту вершину.
Задача. Основания трапеции равны 30см и 15см, а боковые стороны равны 9 см
и 12 см. Найдите высоту трапеции.
Решение.
Пусть АВСД трапеция, заданная в условии.
Проведем
через вершину С прямую, которая параллельна АВ. Пусть эта прямая пересекает АД
в точке М.
Тогда
АВСМ – параллелограмм и СМ=9, АМ=ДМ=15.
Так
как 92+122=152, то, применив обратную теорему
Пифагора, приходим к выводу, что СМ перпендикулярна СД.
Заметим,
что высота трапеции и треугольника МСД, проведенная из вершины С, совпадают.
Для определения искомой высоты применим метод площадей. Пусть искомая высота
равна х. Тогда для определения х составим уравнение, дважды вычислив площадь
треугольника МСД:
.
Решив
это уравнение находим: х=7,2. Ответ: 7,2.
Задача.
Боковые стороны AB и CD трапеции ABCD равны 15 и 12
соответственно. Найдите градусную величину угла D, если одно из оснований
трапеции на 9 больше другого.
Решение.
Из вершины угла проведем
прямую линию, параллельную стороне. Трапеция разделена данной прямой линией на
параллелограмм и треугольник. Противоположные стороны параллелограмма равны,
значит, длина стороны треугольника равна разности длин оснований трапеции. Данный
треугольник определен по трем сторонам. По теореме косинусов определим искомый
угол. Вычисления показывают, что боковая сторона перпендикулярна к основанию,
искомый угол прямой.

Для
тех, кому интересно.



Теорема.
Задачи с решениями.
Пример
1.Найдите площадь равнобедренной трапеции, описанной около окружности с
радиусом 4, если известно, что боковая сторона трапеции равна 10.
Решение.
Дано: ABCD —
равнобедренная трапеция, r = 4, AB = 10
Найти: SABCD
1.
AB = CD = 10 по условию.
2.
AB + CD = AD + BC по свойству вписанной
окружности.
3.
AD + BC = 10 + 10 = 20.
4.
FE = 2r = 2 · 4 = 8.
5.
SABCD=1/2(BC + AD)·FE, SABCD = 1/2 · 20
· 8 = 20/2 · 8 = 10 · 8 = 80.
Пример
2.Основания трапеции
равны 10 м и 31 м, а
боковые стороны —
20 м и 13 м. Найдите
высоту трапеции.
Решение.
Пусть HK
= BC = 10 м, BH
= CK = x, AH
= y, тогда KD
= 21 – y
По
теореме Пифагора:x2 +
y2 =
132x2 +
(21 – y)2 =
202x2 +
y2 =
169 (1)
x2 +
441 – 42y + y2 =
400 (2)
Вычтем
из (2) уравнения (1):441 – 42y =
23142y = 210y
= 5AH = 5 м
По
теореме Пифагора:BH2 =
AB2 –
AH2BH2 =
132 – 52BH2 =
169 – 25BH2 =
144
BH
= 12
Пример
3.Большее основание трапеции равно 24. Найдите длину меньшего основания, если
расстояние между серединами диагоналей равно 4.
Решение.

Пример
4.Диагонали AC и BD трапеции ABCD пересекаются в точке O.
Найдите
площадь трапеции, если BC < AD и площади треугольников BOC и ABO равны
соответственно равны 2 и 8.
Анализ.
Рассмотреть подобие
треугольников.
Квадраты соответствующих
сторон относятся как площади треугольников.
Введем параметры
треугольников: стороны оснований и высоты треугольников.
Площади трапеции и
треугольников определим по известным формулам.
Решение.

Пример
5.В трапеции большее основание равно 10. Диагонали трапеции, равные 8, перпендикулярны
боковым сторонам. Найдите площадь трапеции.
Анализ.
Длины диагоналей равны и
перпендикулярны боковым сторонам. Имеем равенство прямоугольных треугольников
по катету и гипотенузе: ABD
= ACD,
поэтому трапеция равнобедренная, т.е. АВ = СD.
Применим теорему Пифагора для
определения боковой стороны трапеции.
Высоту трапеции определим из
равенства площадей.
Проекцию боковой стороны на
большее основание легче определить из подобия треугольников, чем по теореме
Пифагора.
Длину средней линии в равнобокой
трапеции можно определять как разность большего основания и проекции боковой
стороны на основание.
Площадь трапеции находим как
площадь прямоугольника АМСК, который получим, если достроим трапецию.

Пример
6.Диагонали трапеции взаимно перпендикулярны, а длина ее средней линии равна 9.
Найдите длину отрезка, соединяющего середины оснований трапеции.

Задача решается построением.
Достроим прямоугольники и
используем свойство прямоугольника: диагонали прямоугольника равны и в точке
пересечения делятся пополам.
Длина средней линии равна
полусумме длин оснований.
Длина отрезка, соединяющая
середины оснований, равна полусумме длин диагоналей двух построенных
треугольников.
Пример
7.Длины оснований трапеции равны 1 и 7. Найдите длину отрезка, параллельного
основаниям и заключенного между боковыми сторонами, который делит трапецию на
две равновеликие части.
Анализ.
Провести из вершины тупого
угла трапеции прямую линию, параллельную боковой стороне.
Рассмотреть отношение площадей
трапеций.
Определить отношение при
подобии треугольников.
Рациональные алгебраические
преобразования приведут к результату.
Решение.
Пример
11.Равнобедренная трапеция ABCD описана около окружности. Боковая сторона
трапеции равна 10, а основания относятся как 1: 4. Найдите площадь трапеции.
Анализ.
Сумма противоположных сторон
трапеции равна между собой — свойство описанного четырехугольника.
Трапеция равнобедренная.
Боковая сторона равна длине
средней линии.
Применяем теорему Пифагора для
нахождения высоты трапеции.
Площадь трапеции определяем по
доступной формуле.

Пример
8.Длины боковых сторон трапеции равны 6 и 10. Известно, что в трапецию можно
вписать окружность, а средняя линия делит ее на части, площади которых
относятся как 5: 11. Найдите длину большего основания трапеции.

Трапеция является описанной.
Сумма длин оснований равна
сумме боковых сторон.
Средняя линия делит трапецию
на две трапеции, высоты которых равны.
Задача сводится к системе
уравнений.
Длина средней линии равна
половине суммы длин боковых сторон.
Пример
9.Площадь равнобедренной трапеции, описанной около окружности равна 15. Найдите
среднюю линию трапеции, если косинус острого угла при ее основании равен 4/5.

Трапеция равнобедренная.
Длина средней линии равна
боковой стороне.
Площадь трапеции определяется
произведением средней линии на высоту трапеции.
Опустим высоту трапеции из
тупого угла. Через заданный косинус угла определим синус угла.
По синусу угла выразим высоту
трапеции через боковую сторону.

Пример
10.В прямоугольной трапеции, описанной около окружности, большая боковая
сторона равна 13, а средняя линия равна 12,5. Найдите меньшее основание
трапеции.
Анализ.
Необходимо использовать
свойство сторон четырехугольника, описанной около окружности: сумма длин
противоположных сторон равна между собой.
Кроме того, длина средней
линии равна полусумме длин сторон оснований.
Проведем из вершины тупого
угла высоту трапеции.
Воспользуемся теоремой
Пифагора и определим проекцию наклонной боковой стороны на основание.
Пример
11.В равнобедренную трапецию, один из углов которой равен 60°, а площадь
равна ,
вписана окружность. Найдите радиус этой окружности.

Анализ.
Важное положение, что трапеция
является равнобедренной и имеет ось симметрии. Тогда длина боковой стороны
равна длине средней линии.
Введем параметр боковой
стороны, из прямоугольного треугольника по заданному углу определим высоту
трапеции, которая является диаметром вписанной окружности. Площадь трапеции
определяется как произведение средней линии на высоту трапеции.
.
Пример
12.Найдите площадь равнобедренной трапеции, у которой большее основание равно
13, средняя линия равна 8, а биссектриса тупого угла является диагональю
трапеции.
Анализ.
При проведении биссектрисы
тупого угла боковая сторона равна большему основанию трапеции. Проекция боковой
стороны равнобедренной трапеции равна полуразности длин оснований.
По теореме Пифагора найдем
высоту трапеции.
Площадь трапеции находим по
формул.
Список используемой литературы
1.
2.
3.
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
Определение.
Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.
На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.
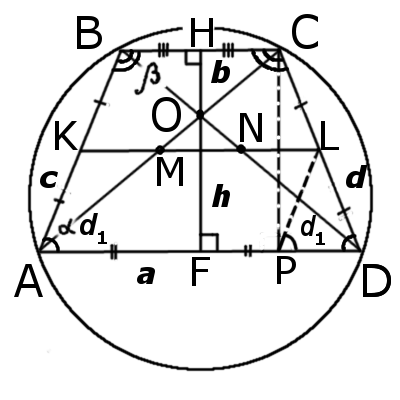 |
| Рис.1 |
Признаки равнобедренной трапеции
Трапеция будет равнобедренной если выполняется одно из этих условий:
1. Углы при основе равны:
∠ABC = ∠BCD и ∠BAD = ∠ADC
2. Диагонали равны:
AC = BD
3. Одинаковые углы между диагоналями и основаниями:
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
4. Сумма противоположных углов равна 180°:
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
5. Вокруг трапеции можно описати окружность
Основные свойства равнобедренной трапеции
1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:
AB = CD = m
3. Вокруг равнобедренной трапеции можно описать окружность
4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):
h = m
5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:
SABCD = h2
6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:
h2 = BC · AD
7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:
AC2 + BD2 = AB2 + CD2 + 2BC · AD
8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:
HF ┴ BC, HF ┴ AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
1. Формулы длины сторон через другие стороны, высоту и угол:
a = b + 2h ctg α = b + 2c cos α
b = a – 2h ctg α = a – 2c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d12 – c2 | b = | d12 – c2 | c = √d12 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
1. Формула определения длины средней линии через основания, высоту и угол при основании:
m = a – h ctg α = b + h ctg α = a – √c2 – h2 = b + √c2 – h2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Диагонали равнобедренной трапеции равны:
d1 = d2
Формулы длины диагоналей равнобедренной трапеции:
1. Формула длины диагонали через стороны:
d1 = √с2 + ab
2. Формулы длины диагонали по теореме косинусов:
d1 = √a2 + c2 – 2ac cos α
d1 = √b2 + c2 – 2bc cos β
3. Формула длины диагонали через высоту и среднюю линию:
d1 = √h2 + m2
4. Формула длины диагонали через высоту и основания:
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √4c2 – (a – b)2 |
| 4 |
2. Формула площади через стороны и угол:
S = (b + c cos α) c sin α = (a – c cos α) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = (a + b) · r = √ab·c = √ab·m
6. Формула площади через диагонали и угол между ними:
| S = | d12 | · sin γ | = | d12 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p – a)(p – c)(p – d1) |
где
a – большее основание