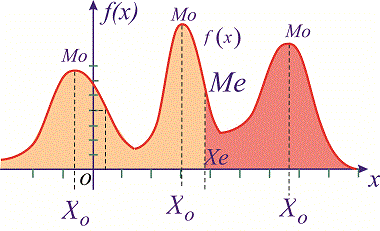
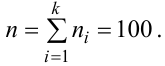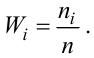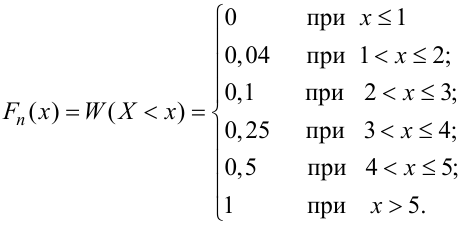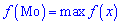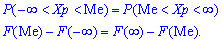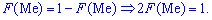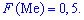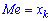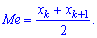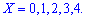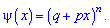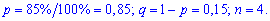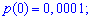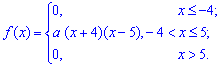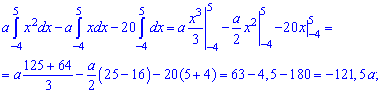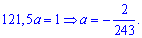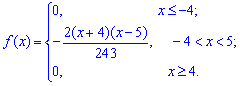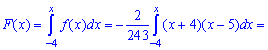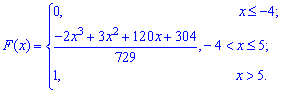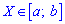У этого термина существуют и другие значения, см. Медиана.
Медиа́на (от лат. mediāna «середина») или набора чисел — число, которое находится в середине этого набора, если его упорядочить по возрастанию, то есть такое число, что половина из элементов набора не меньше него, а другая половина не больше. Другое равносильное определение[1]: медиана набора чисел — это число, сумма расстояний (или, если более строго, модулей) от которого до всех чисел из набора минимальна. Это определение естественным образом обобщается на многомерные наборы данных и называется 1-медианой.
Например, медианой набора {11, 9, 3, 5, 5} является число 5, так как оно стоит в середине этого набора после его упорядочивания: {3, 5, 5, 9, 11}. Если в выборке чётное число элементов, медиана может быть не определена однозначно: тогда для числовых данных чаще всего используют полусумму двух соседних значений (то есть медиану набора {1, 3, 5, 7} принимают равной 4), подробнее см. ниже.
В математической статистике медиана может использоваться как одна из характеристик выборки или совокупности чисел.
Также определяется медиана случайной величины: в этом случае оно определяется как число, которое делит пополам распределение. Грубо говоря, медианой случайной величины является такое число, что вероятность получить значение случайной величины справа от него равна вероятности получить значение слева от него (и они обе равны 1/2), — более точное определение дано ниже.
Можно также сказать, что медиана является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.
Свойства медианы для случайных величин[править | править код]
Если распределение непрерывно, то медиана является одним из решений уравнения
,
где 


.
Если распределение является непрерывной строго возрастающей функцией, то решение уравнения однозначно. Если распределение имеет разрывы, то медиана может совпадать с минимальным или максимальным (крайним) возможным значением случайной величины, что противоречит «геометрическому» пониманию этого термина.
Медиана является важной характеристикой распределения случайной величины и, так же как математическое ожидание, может быть использована для центрирования распределения. Поскольку оценки медианы более робастны, её оценивание может быть более предпочтительным для распределений с т. н. тяжёлыми хвостами. Однако о преимуществах оценивания медианы по сравнению с математическим ожиданием можно говорить только в случае, если эти характеристики у распределения совпадают, в частности, для симметричных функций плотности распределения вероятностей.
Медиана определяется для всех распределений, а в случае неоднозначности, естественным образом доопределяется, в то время как математическое ожидание может быть не определено (например, у распределения Коши).
Пример использования[править | править код]
Рассмотрим финансовое состояние 19 малоимущих, у каждого из каких есть только 5 ₽, и одного миллионера, у которого буквально 1 млн ₽. Тогда в сумме у них получается 1 000 095 ₽. Если деньги равными долями разделить на 20 человек, получится 50 004,75 ₽. Это будет среднее арифметическое значение суммы денег, которая была у всех 20 человек в этой комнате.
Медиана же будет равна 5 ₽ (сумма «расстояния» от этой величины до состояния каждого из рассматриваемых людей минимальна). Это можно интерпретировать следующим образом: «разделив» всех рассматриваемых людей на две равные группы по 10 человек, мы получаем, что в первой группе у каждого не больше 5 ₽, во второй же — не меньше 5 ₽.
Из этого примера получается, что в качестве «серединного» состояния, грубо говоря, корректнее всего использовать именно медиану, а вот среднее арифметическое, наоборот, значительно превышает сумму наличных, имеющуюся у случайного человека из выборки.
Различны изменения в динамике и у средней арифметической с медианой, например в вышеприведённом примере, если у миллионера станет 1,5 млн. ₽ (+50 %), а у остальных станет 6 ₽ (+20 %), то средняя арифметическая выборки станет равна 75 005,70 ₽, то есть как бы у всех повысились равномерно на 50 %, при этом медиана станет равной 6 ₽ (+20 %).
Неуникальность значения[править | править код]
Если имеется чётное количество случаев и два средних значения различаются, то медианой, по определению, может служить любое число между ними (например, в выборке {1, 3, 5, 7} медианой может служить любое число из интервала (3,5)). На практике в этом случае чаще всего используют среднее арифметическое двух средних значений (в примере выше это число (3+5)/2=4). Для выборок с чётным числом элементов можно также ввести понятие «нижней медианы» (элемент с номером n/2 в упорядоченном ряду из 
См. также[править | править код]
- Мода — значение во множестве наблюдений, которое встречается наиболее часто.
- Среднее арифметическое набора чисел — число, сумма квадратов расстояний от которого до всех чисел из набора минимальна[3].
Примечания[править | править код]
- ↑ Сущность медианы. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.
- ↑ Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест Рональ Л., Штайн, Клиффорд. Алгоритмы. Построение и анализ. — 2-е издание. — М.: Издательский дом «Вильямс», 2005. — С. 240. — 1296 с.
- ↑ Почему это равносильные определения среднего арифметического.
Литература[править | править код]
- Медиана // Маниковский — Меотида. — М. : Большая российская энциклопедия, 2012. — С. 479—480. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 19). — ISBN 978-5-85270-353-8.
- Медиана // Большая российская энциклопедия [Электронный ресурс]. — 2017.
Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
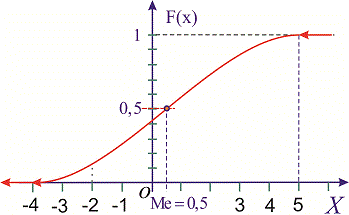
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
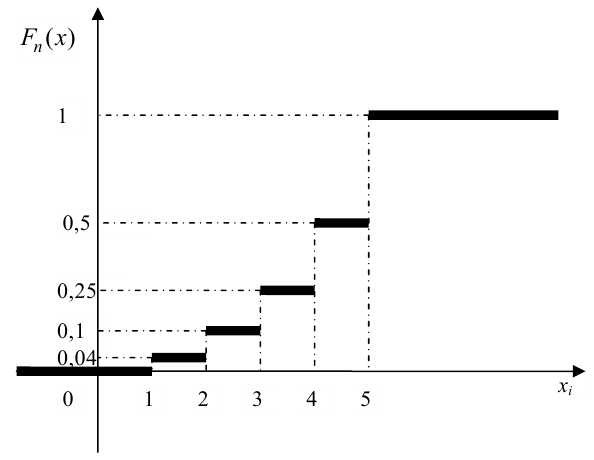
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике – мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
Значение случайной
величины
,
принимаемое с наибольшей вероятностью,
называетсямодойи обозначается
Мода называется
еще наивероятнейшим значениемслучайной величины.
Если эксперимент
описывается случайной величиной, то в
результате проведенной серии этого
эксперимента чаще всего встречается
мода случайной величины.
Медианаявляется значением случайной величины
.
Вероятность того, что случайная величина
принимает значение меньше медианы,
равна 0,5:
Не все дискретные
случайные величины имеют медиану.
Пример 1. Задан
закон распределения случайной величины
|
|
|
3 |
5 |
6 |
|
0,2 |
0,3 |
0,4 |
0,1 |
Найти моду и медиану
случайной величины
.
Найдем моду:
.
Тогда
.
Для нахождения
медианы нужно рассмотреть
,
гдезначения
случайной величины.
.
Заметим, что
.
Из данных закона
распределения случайной величины
.
Тогда
.
Нет необходимости находить.
Пример 2. Задан
закон распределения случайной величины
|
|
0 |
1 |
|
0,9 |
0,1 |
Найти моду и медиану
случайной величины
.
Значение 0 принимается с наибольшей
вероятностью
.
Тогда
.
Найдем медиану
.
Нет значения
случайной величины
,
при котором.
Поэтому случайная величинамедианы не имеет.
3.6. Корреляционный момент. Коэффициент корреляции
Вводится величина,
характеризующая зависимость между
двумя случайными величинами. Задано
совместное распределение случайных
величин
и
.
Корреляционным
моментомслучайных величини
(иликовариациеймежду
и
)
называется число
Для дискретных
случайных величин
и
имеем
.
Непосредственно
из свойств математического ожидания
вытекают свойства ковариации:
-
;
-
;
Для дискретных
случайных величин имеем
.
-
;
-
;
-
Если случайные
величины независимы, то их ковариация
равна нулю.
Обратное не верно.
Если
,
то случайные величиныи
могут быть как зависимыми, так и
независимыми.
Коэффициентом
корреляциимежду случайными величинамии
называются число
.
Приведем некоторые
свойства коэффициента корреляции.
Пусть
и введем случайную величину
.
Знакоположительная
случайная величина
имеет не отрицательное математическое
ожидание:
при любом
.
Распишем
.
Получаем квадратичное
неравенство
,
где
,
.
Неравенство
выполняется при любом
,
если дискриминант неположительный.
Тогда
,
откуда
.
Таким образом,
.
-
Если
и
независимы, то
,
что следует из свойства 5 ковариации. -
Коэффициент
корреляции равен
тогда и только тогда, когда случайные
величины линейно зависимы
Пусть
.
Тогдаи
,
.
Тогда
.
Пусть
.
Рассмотрим случайную
величину
.
Найдем
,
.
Из свойства
математического ожидания
.
Тогда
и
.
Получим линейное
выражение
через
.
Случай
разбирается аналогично. Вводится
случайная величина.
Пример 1. Задано
совместное распределение случайных
величини
|
|
2 |
4 |
|
|
||
|
0 |
0,1 |
0,3 |
|
1 |
0,2 |
0,4 |
Найти
.
Запишем распределения
случайных величин
и
-
0
1
;
0,4
0,6
-
2
4
.
0,3
0,7
Найдем основные
характеристики случайных величин
и
:
;
;
.
Используем формулу
.
Найдем
:
.
Тогда
и
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
Для дискретной случайной величины X эта формула принимает вид:
Для непрерывной случайной величины: 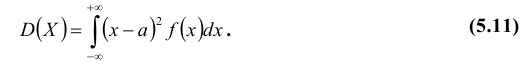
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 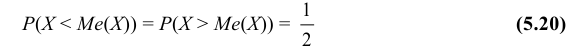
Пример №2
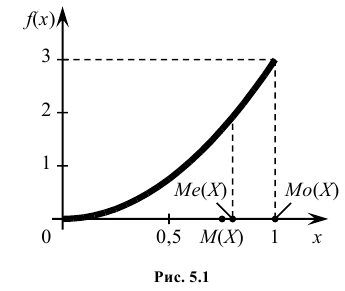
Найти моду, медиану случайной величины Х с плотностью вероятности
Решение:
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 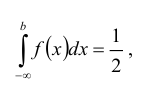
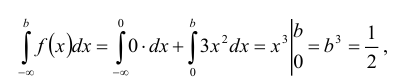
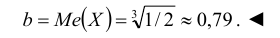
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
Пример №3
По данным примера 5.3 найти квантиль
Решение:
Находим функцию распределения 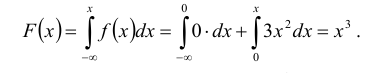
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
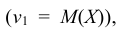
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 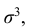
Полученная величина А называется коэффициентом асимметрии случайной величины: 
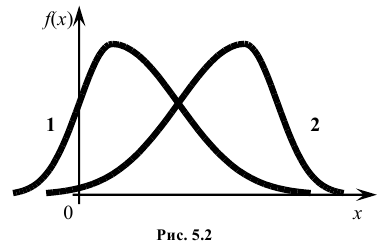
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число 
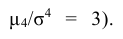
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 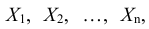
Обозначим среднее арифметическое n взаимно независимых случайных величин через
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 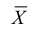
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
раз меньше дисперсии D каждой из величин:
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:
Пример:
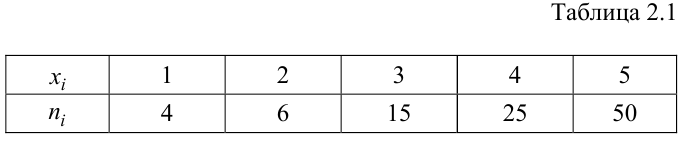
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
Решение. Определяем объем выборки:
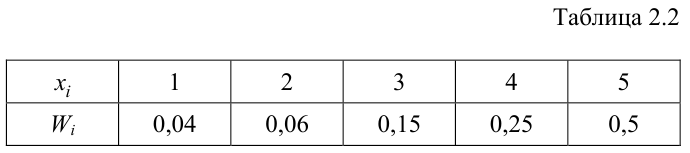
Определяем относительные частоты вариант (табл. 2.2):
Так как значение 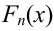
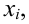
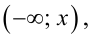
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
Для нахождения моды и медианы случайной величины необходимы хорошие умения интегрировать и знания следующего теоретического материала. Модой 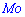
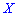
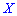
В зависимости от вида функции 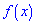
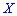
Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой 
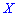
Графически мода и медиана изображенные на рисунке
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью. Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин 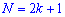
в случае четного количества 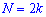
Рассмотрим примеры определения моды и медианы.
Пример 1. В развлекательном центре работник обслуживает четыре дорожки для боулинга. Вероятность того, что какая-то дорожка нуждается в уборке в течение смены является постоянной величиной с вероятностью 85%.
Построить закон распределения вероятностей дискретной случайной величины 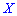
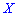
Решение. Случайной величина может принимать значения
Вероятности появления значений определяем по образующей функцией
Для заданной задачи входные величины принимают значения
Искомые вероятности входят множителями при степенях аргумента
Закон распределения вероятностей запишем в виде таблицы
С таблице определяем моду 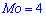
Пример 2. По заданной плотностью вероятностей
найти параметр 
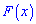
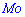
Решение. Применяя условие нормирования выполняем интегрирование
после того определяем параметр
Плотность вероятностей, учитывая найденное значение будет иметь вид
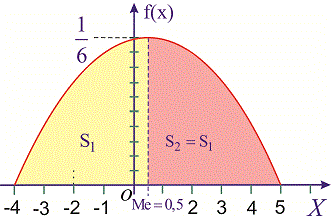
а ее график изображен на рисунке ниже
Из графика плотности вероятностей видим, что мода принимает значение 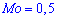

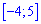
Функция распределения иметь следующий вид
а ее график будет иметь вид
Для определения медианы случайной величины 
Медиану 
для дискретной случайной величины из промежутка
Таким образом медиану 
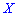
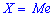
——————————-
Задача на определение моды и медианы случайной величины встречаются на практике не так часто, как плотности распределения вероятностей, однако вышеприведенный теоретический материал и решения распространенных примеров помогут Вам находить эти величины без больших затрат времени. При необходимости Вы всегда можете заказать решение задач по теории вероятностей в нас.



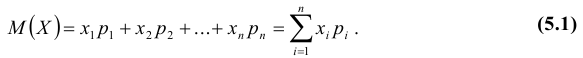
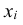
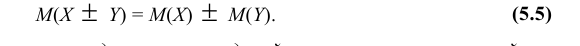


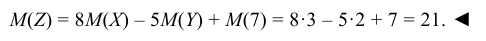







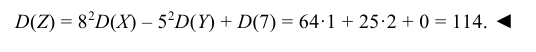
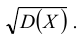

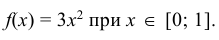

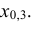
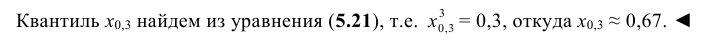



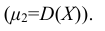
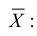
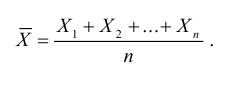

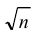 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: