Загрузить PDF
Загрузить PDF
Среднее значение, медиана и мода — значения, которые часто используются в статистике и математике. Эти значения найти довольно легко, но их легко и перепутать. Мы расскажем, что они из себя представляют и как их найти.
-

1
Сложите все числа, которые вам даны. Допустим, вам даны числа 2, 3 и 4. Сложим их: 2 + 3 + 4 = 9.
-

2
Сосчитайте количество чисел. У нас есть три цифры.
-

3
Разделите сумму чисел на их количество. Берем 9, делим на 3. 9/3 = 3. Среднее значение в данном случае равно 3. Помните, что не всегда получается целое число.
Реклама
-

1
Запишите все числа, которые вам даны, в порядке возрастания. Например, нам даны числа: 4, 2, 8, 1, 15. Запишите их от меньшего к большему, вот так: 1, 2, 4, 8, 15.
-

2
Найдите два средних числа. Мы расскажем, как это сделать, если у вас имеется четное количество чисел, и как это сделать, если количество чисел нечетное:
- Если у вас нечетное количество чисел, вычеркните левое крайнее число, затем правое крайнее число и так далее. Один оставшийся номер и будет искомой медианой. Если вам дан ряд чисел 4, 7, 8, 11, 21, тогда 8 — медиана, так как 8 стоит посередине.
- Если у вас четное количество чисел, вычеркните по одному числу с каждой стороны, пока у вас не останется два числа посередине. Сложите их и разделите на два. Это и есть значение медианы. Если вам дан ряд чисел 1, 2, 5, 3, 7, 10, то два средних числа — это 5 и 3. Сложим 5 и 3, получим 8, разделим на два, получим 4. Это и есть медиана.
Реклама
-

1
Запишите все числа в ряд. Например, вам даны числа 2, 4, 5, 5, 4 и 5. Запишите их в порядке возрастания.
-

2
Найдите число, которое чаще всего встречается. В данном случае это 5. Если два числа встречаются одинаково часто, то этот ряд двухвершинный или бимодальный, а если больше — то мультимодальный.
Реклама
Советы
- Вам будет легче найти моду и медиану, если вы запишете числа в порядке возрастания.
Реклама
Об этой статье
Эту страницу просматривали 354 465 раз.
Была ли эта статья полезной?
Как найти медиану сгруппированных данных (с примерами)
17 авг. 2022 г.
читать 2 мин
Часто нам может понадобиться вычислить медиану данных, которые каким-то образом сгруппированы.
Напомним, что медиана представляет собой значение, которое находится непосредственно в середине набора данных, когда все значения расположены от наименьшего к наибольшему.
Например, предположим, что у нас есть следующие сгруппированные данные:
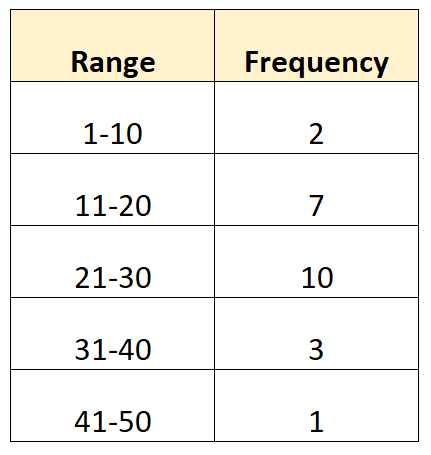
Хотя невозможно рассчитать точную медиану, поскольку мы не знаем исходных значений данных , можно оценить медиану, используя следующую формулу:
Медиана сгруппированных данных = L + W[(N/2 – C)/F]
куда:
- L : Нижний предел среднего класса
- W : Ширина среднего класса
- N : Общая частота
- C : Суммарная частота до медианного класса
- F : Частота среднего класса
Примечание.Медианный класс — это класс, содержащий значение, расположенное в N/2. В приведенном выше примере всего N = 23 значения. Таким образом, медианное значение — это значение на позиции 23/2 = 11,5, которое располагалось бы в классе 21-30.
В следующих примерах показано, как вычислить медиану сгруппированных данных в различных сценариях.
Пример 1. Вычисление медианы сгруппированных данных
Предположим, у нас есть следующее частотное распределение, показывающее, что экзамен сдан 40 учащимся в определенном классе:
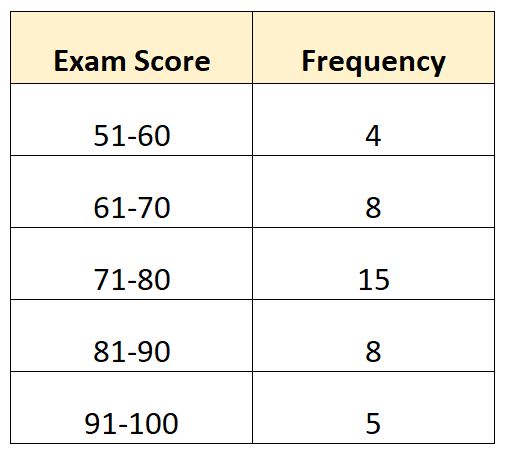
В этом примере всего N = 40 значений. Таким образом, медианное значение лежит в классе, где находится 40/2 = 20. 20-е место по величине будет находиться в классе 71-80 .
Зная это, мы можем рассчитать следующие значения:
- L : Нижний предел среднего класса: 71
- W : Ширина среднего класса: 9
- N : Общая частота: 40
- C : Суммарная частота до среднего класса: 12
- F : Частота среднего класса: 15
Мы можем подставить эти значения в формулу для расчета медианы распределения:
- Медиана = L + W[(N/2 – C) / F]
- Медиана = 71 + 9 [(40/2 – 12) / 15]
- Медиана = 75,8
По нашим оценкам, средний балл за экзамен составляет 75,8 .
Пример 2. Вычисление медианы сгруппированных данных
Предположим, у нас есть следующее распределение частот, которое показывает количество очков, набранных за игру 60 баскетболистами:
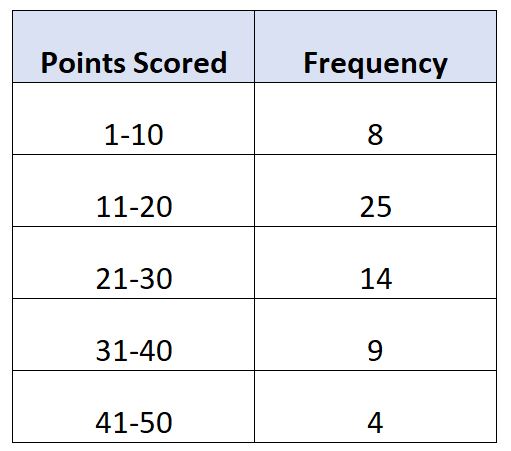
В этом примере всего N = 60 значений. Таким образом, медианное значение лежит в классе, где находится 60/2 = 30. 30-е место по величине будет находиться в классе 11-20 .
Зная это, мы можем рассчитать следующие значения:
- L : Нижний предел среднего класса: 11
- W : Ширина среднего класса: 9
- N : Общая частота: 60
- C : Суммарная частота до среднего класса: 8
- F : Частота среднего класса: 25
Мы можем подставить эти значения в формулу для расчета медианы распределения:
- Медиана = L + W[(N/2 – C) / F]
- Медиана = 11 + 9 [(60/2 – 8) / 25]
- Медиана = 18,92
По нашим оценкам, средний балл за экзамен составляет 18,92 .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные операции с сгруппированными данными:
Как найти среднее и стандартное отклонение сгруппированных данных
Как найти режим сгруппированных данных
Как рассчитать процентильный ранг для сгруппированных данных
8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:

(8.16 – формула Моды)
где хо – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1– частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:
 (8.17 – формула Медианы)
(8.17 – формула Медианы)
где хо – нижняя граница медианного интервала;
NМе– порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число
семей |
Накоп-
ленные частоты |
в % к итогу |
| До 5000 | 600 | 600 | 6 |
| 5000-6000 | 700 | 1300
(600+700) |
13 |
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 )
(1300+1700) |
30 |
| 7000-8000
(хо) |
2500
(fМо) (fМе) |
5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 |
| 9000-10000 | 1500 | 9200 | 92 |
| Свыше 10000 | 800 | 10000 | 100 |
| Итого | 10000 | – | – |
Пример вычисления Моды. Найдем моду по формуле (8.16) см. обозначения в таблице, а h = 8000-7000=1000, т.е. получаем:

Пример вычисления Моды
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):

Пример вычисления Медианы
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Пример .СРЕДНИЙ, МЕДИАННЫЙ И МОДАЛЬНЫЙ УРОВЕНЬ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ ЦЕЛОМ ПО РОССИИ И ПО СУБЪЕКТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ЗА 2013 год см. по ссылке. Источник: оценка на основании данных выборочного обследования бюджетов домашних хозяйств и макроэкономического показателя денежных доходов населения
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если Мо<Ме<Х – имеет место правосторонняя асимметрия.
При Х<Ме<Мо следует сделать вывод о левосторонней асимметрии ряда.
Средние величины (арифметическая, гармоническая, геометрическая, квадратическая) см. по ссылке
Оценка статьи:
![]() Загрузка…
Загрузка…
Онлайн калькулятор для нахождения медианы ряда чисел. Медианой (серединой) набора чисел называется число стоящее посередине упорядоченного по возрастанию ряда чисел. Если количество чисел в ряду чётное, то медианой ряда является полусумма двух стоящих посередине чисел.
Применяется в математической статистике — число, характеризующее выборку (например, набор чисел), также используется для вычисления медианной зарплаты.
Формула медианы числового набора, пример вычисления медианы числового ряда: 3, 7, 1, 6, 9
Решение: упорядочиваем список чисел в порядке возрастания: 1, 3, 6, 7, 9. Поскольку количество чисел в ряду нечётное, то число 6 стоящее по середине и будет являться медианой данного ряда.
Пример нахождения медианы ряда чисел: 1, 5, 8, 4, 3, 9
Решение: записываем все числа ряда в порядке возрастания: 1, 3, 4 ,5, 8, 9. Поскольку чисел в ряду чётное, то медиана этого ряда будет равна полусумме двух средних чисел: (4+5)/2 = 4.5
Медиана (x̃, M; Мера центральной тенденции) – это центральное значение Выборки (Sample).
В математике медиана также представляет собой тип Среднего значения (Average), который используется для нахождения “центра”. Поэтому ее еще называют мерой центральной тенденции.
Нечетное количество элементов ряда
Если в ряду нечетное количество элементов, то мы сортируем значения в возрастающем или убывающем порядке, а затем выбираем центральное.
Пример. Найдем медиану следующего ряда:
4, 17, 77, 25, 22, 23, 92, 82, 40, 24, 14, 12, 67, 23, 29
Расставив эти числа по порядку, мы получим:
4, 12, 14, 17, 22, 23, 23, 24, 25, 29, 40, 67, 77, 82, 92
Всего пятнадцать элементов, то есть 8-й будет центральным. Медианное значение этого набора чисел – 24.
Четное количество элементов ряда
Если в ряду четное количество элементов, медиана рассчитывается с помощью формулы:
$$M = frac{n + 1}{2}, где$$
$$Mspace{–}space{медиана,}$$
$$nspace{–}space{количество}space{элементов}space{в}space{выборке}$$
Пример. Найдем медиану следующего ряда:
1.79, 1.61, 2.09, 1.84, 1.96, 2.11
Выполнив подстановку, мы получим:
$$M = frac{6 + 1}{2} = 3.5$$
Центральная тенденция
Помимо медианы, выделяют еще две другие меры центральной тенденции – Среднее значение (Mean) и Мода (Mode). Среднее – это частное от суммы всех Наблюдений (Observation) к их количеству. Мода – это наиболее часто повторяющееся значение выборки.
В Науке о данных (Data Science) медиана иногда используется вместо среднего значения, когда в последовательности есть выбросы, которые могут исказить среднее. Выбросы меньше влияют на медианное значение, чем на среднее. Медиана отделяет верхнюю половину выборки, генеральной совокупности или Распределения вероятностей (Probability Distribution) от нижней.

Медиана и NumPy
Медиану можно вычислить с помощью NumPy. Для начала импортируем все необходимые библиотеки:
import numpy as npСоздадим массив из 6 элементов и вызовем встроенный метод median():
a = [10, 7, 4, 3, 2, 1]
np.median(a)NumPy определяет четность числа элементов массива (6) и применяет тот или иной метод расчета (согласно формуле):
3.5Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Фото: @garciasaldana_

