Как найти механический момент действующий на рамку

Эффект Холла

Американский
ученый Э.
Холл
обнаружил, что в проводнике, поме­щенном
в магнитное поле, возникает разность
потенциалов (поперечная) в направлении,
перпендикулярном вектору магнитной
индукции В и току I,
вследствие
действия силы Лоренца на заряды,
движущиеся в этом про­воднике (рис.
3.62).

Опыт
показывает, что поперечная
разность потенциалов пропорцио­нальна
плотности тока
j,
магнитной
индукции и расстоянию d
между электродами:

U=RdjB
(15.39)

[R
— постоянная Холла, зависящая от рода
вещества].

Допустим,
что электроны движутся с упорядоченной
средней скоро­стью υ и на каждый
электрон действует сила Лоренца, равнаяеВυ.
Под ее действием электроны смещаются
так, что одна из граней
образца заря­дится отрицательно,
другая – положительно и внутри образца
возникнет электрическое поле, т. е. е
υ
В
= еЕ.

Следовательно,
поперечная разность потенциалов равна

U=Ed=υBd

Среднюю
скорость υ
электронов можно выразить через плотность
тока j,
так как j=neυ,
поэтому

(15.40)

Приравнивая
это выражение формуле (15.39), получаем
.

Постоян­ная
Холла зависит от концентрации электронов.

По
измеренному значению постоянной Холла
можно: 1) определить концентрацию
носителей тока в проводнике (при известных
характере проводимости и заряде
носителей); 2) судить о природе проводимости
полупроводников, так как знак постоянной
Холла совпадает со знаком заряда
носителей тока. Применяется для умножения
постоянных токов в аналоговых
вычислительных машинах, в измерительной
технике (датчик Холла

Примеры решения задач

Пример.
Прямоугольная
рамка со сторонами а= 5см и b=10см,
состоящая из N=20
витков, помещена во внешнее однородное
магнитное поле с индукцией В=0,2 Тл.
Нормаль к рамке составляет с направлением
магнитного поля угол
.
Определите вращающий момент сил,
действующий на рамку, если по ней течёт
токI=2А.

Дано:
а= 5см=0,05м; b=10см=0,1м;
N=20;
В=0,2 Тл;
.
;I=2А.

Найти:
М.

Решение.
Механический
момент, действующий на рамку с током,
помещённую в однородное магнитное поле,

,

–
магнитный момент рамки с током. Модуль
M=p_mBsinα.

Поскольку
рамка состоит
N
из витков, то M=Np_mBsinα
(1)

где
магнитный момент рамки с током

p_m=IS=Iab.

(2)

Подставив
формулу (2) в выражение (1), найдём искомый
вращающий момент

M=NIBabsinα.

Ответ:
М=0,02 Н∙м

Пример.
По
тонкому проволочному кольцу течёт ток.
Определите, во сколько раз изменится
индукция в центре контура, если проводнику
придать форму квадрата, не изменяя силы
тока в проводнике.

Решение.
Вектор
в центре кругового тока направлен при
выбранном направлении тока (см.рисунок),
согласно правилу правого винта,
перпендикулярно чертежу к нам (на рисунке
это обозначено точкой в кружочке). Его
модуль

,
(1)

где
I–
сила тока; R-
радиус кольца; μ₀–
магнитная постоянная; μ – магнитная
проницаемость среды.

Сторона
квадрата, вписанная в кольцо, равна(длина окружности кольца 2πR
). Вектор
в центре квадрата направлен также
перпендикулярно чертежу к нам. Магнитная
индукция в центре квадрата равна сумме
магнитных индукций, создаваемых каждой
стороной квадрата. Тогда модуль,
согласно закону Био-Савара-Лапласа,

.
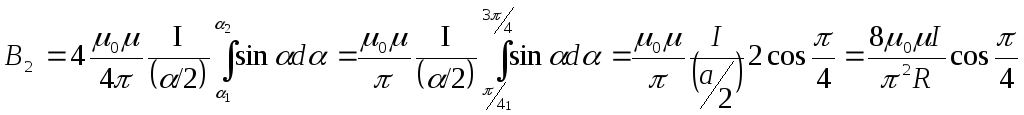(2)

Из
формул (1) и (2) получим отношение

Ответ:

Пример.
По
двум бесконечно длинным прямым
параллельным проводникам, находящимся
в вакууме на расстоянии R=30см,
текут одинаковые токи одного направления.
Определите магнитную индукцию В поля,
создаваемого токами в точке А, лежащей
на прямой, соединяющей проводники и
лежащей на расстоянии r=20см
правее правого провода (см.рисунок).
Сила тока в проводниках равна 20А.

Дано:μ=1;
R=30см=0,3м;
r=20см=0,2м;
I₁=
I₂=I=20
А.

Найти:
B.

Решение.
Пусть
токи направлены перпендикулярно
плоскости чертежа от н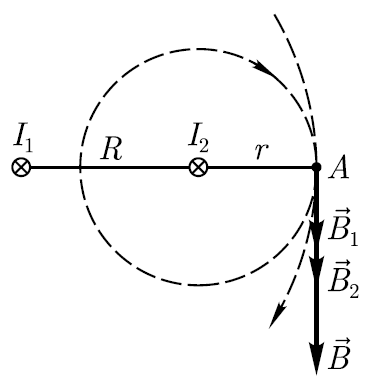ам,
что обозначено на рисунке крестиками.
Линии магнитной индукции замкнуты и
охватывают проводники с токами. Их
направление задаётся правилом правого
винта. Вектор в каждой точке направлен
по касательной к линии магнитной индукции
(см. рисунок).

Согласно
принципу суперпозиции, магнитная
индукция результирующего поля в точке
А

где
и– магнитная индукция полей в этой точке,
создаваемые первым и вторым проводниками.
Векторыии сонаправлены, поэтому сложение
векторов можно заменить сложением их
модулей

В=В₁+В₂.
(1)

Магнитная
индукция полей, создаваемых бесконечно
длинными прямыми проводниками с током
I₁
и I₂,

,

(2)

где
μ₀
– магнитная постоянная; μ- магнитная
проницаемость среды.

Подставив
выражение (2) в формулу (1) и учитывая, что
I₁=I₂=I
и μ=1 (для вакуума), получим искомое
выражение для магнитной индукции в
точке А:

Ответ:
В=28 мкТл.

Пример.
По
двум бесконечно длинным прямым
параллельным проводникам находящимся
в вакууме, расстояние между которыми
d=15см,
текут токи I₁=70A
и I₂=50A
в одном направлении. Определите магнитную
индукцию В поля, в точке А, лежащей
удалённой на r₁=10см
от первого и r₁=20см
от второго проводников.

Дано:μ=1;
d=15см=0,15
м;
I₁=70A;
I₂=50A;
r₁=10см=0,1м;
r₂=20см=0,2м.

Найти:
B.

Решение.
Пусть
токи направлены перпендикулярно
плоскости чертежа к нам. Векторы магнитной
индукции направлены по касательной к
линиям магнитной индукции.

Согласно
принципу суперпозиции, магнитная
индукция в точке А (см.рисунок)

где
и– соответственно магнитные индукции
полей, создаваемые проводниками с токомI₁
и
I₂

(направления векторов
ии токовI₁
и
I₂
показаны
на рисунке). Модуль вектора
по теореме косинусов,

(1)

где

;

;

.

Подставив
эти выражения в формулу (1), найдём искомое
В:

.

Ответ:
В=178 мкТл.

Пример.
В
одной плоскости с бесконечно прямым
проводником с током

I=10
A
расположена прямоугольная проволочная
рамка (сторона а=25см, b=10см),
по которой протекает ток I₁=2А.
Длинные стороны рамки параллельны
прямому току, причём ближайшая из них
находится от прямого тока на расстоянии
с=10см и ток в ней сонаправлен току I.
Определите силы, действующие на каждую
из сторон рамки.

Дано:I=10A;
а=25см=0.25м; b=10
см=0.10 м;; I₁=2
A;
с=10см=0,1м.

Найти:
F₁;
F₂;
F₃;
F₄;

Р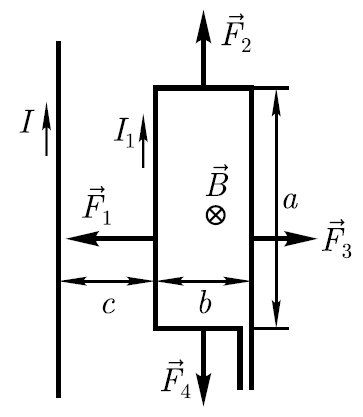ешение.Прямоугольная
рамка находится в неоднородном поле
прямого тока с индукцией

(1)

(рассматриваем
случай вакуумa),
где r
– расстояние от прямого тока до
рассматриваемой точки.

Сила,
с которой действует поле прямого тока,
может быть найдена суммированием
элементарных сил, определяемых законом
Ампера,

.

Вектор
в пределах рамки направлен перпендикулярно
её плоскости за чертёж, и в пределах
каждой стороны угол.
Это означает, что в пределах одной
стороны элементарные силы параллельны
друг другу и сложение векторов

Можно
заменить сложением их модулей:

(2)

где
интегрирование ведётся по соответствующей
стороне рамки

Короткие
стороны рамки расположены одинаково
относительно провода, а потому действующие
на них силы численно равны, но направлены
противоположно. Их направление, впрочем
как и направление других сил (см.рисунок),
определяется по правилу левой руки.
Вдоль каждой из коротких сторон
прямоугольника магнитная индукция
изменяется [см. формулу (1)]. Тогда,
произведя интегрирование [с учётом
(2)],

.

Длинные
стороны рамки параллельны прямому току,
находясь от него соответственно на
расстояниях с и с+b.
Тогда

;

,

где

и
.

Ответ
: F₁=10
мкН; F₂=2,77
мкН; F₃=5
мкН; F₄=2,77
мкН.

Пример.
Электрон,
прошедший ускоряющую разность потенциалов
U=1
кВ, влетает в однородное магнитное поле
с индукцией В=3мТл перпендикулярно
линиям магнитной индукции. Определите:
1) силу, действующую на электрон; 2) радиус
окружности, по которой электрон движется;
3) период обращения электрона.

Дано:
m=9,11∙10^-31
кг; е=1,6∙10^-19
Кл; U=1кВ=1∙10³В;
В=3мТл=3∙10^-3
Тл; α=90º.

Найти:
1)F;
2) R;
3)
T.

Решение.
При
движении электрона в магнитном поле со
скоростью υ на него действует сила
Лоренца

F_л=eυBsinα,

где
α – угол между векторами
и(в
нашем случае α=90º). Тогда

F_л=eυB.
(1)

При
прохождении ускоряющей разности
потенциалов работа сил электростатического
поля идёт на сообщение электрону
кинетической энергии
,

откуда

.
(2)

Подставив
выражение (2) в формулу (1), найдём искомую
силу, действующую на электрон,

Из
механики известно, что постоянная сила,
перпендикулярна скорости, а ею и является
сила Лоренца (1), вызывает движение по
окружности. Она сообщает электрону
нормальное ускорение
,
где R
– радиус окружности. По второму закону
Ньютона F=ma,
где F=eυB.
Тогда

,

откуда
искомый радиус окружности с учётом (2)

(3)

Период
обращения электрона

.
(4)

Подставив
выражение (3) и (2) в формулу (4), найдём
искомый период обращения электрона

.

Ответ:
1)F=9∙10^-15
Н; 2) R=3,56
см; 3) T=11,9
нс.

Пример.
Протон,
обладая скоростью υ=10⁴
м/с, влетает в однородное магнитное
поле с индукцией В=10мТл под углом α=60º
к направлению линий магнитной индукции.
Определите радиус R
и шаг h
винтовой линии, по которой будет двигаться
протон..

Дано:
υ=10⁴
м/с; е=1,6∙10^-19
Кл; m=1,67∙10^-27
кг; В=10мТл=10∙10^-3
Тл; α=60º.

Найти:R;
h.

Решение.
Движение
протона в однородном магнитном поле со
скоростью
,
направленной под углом α к вектору,
происходит по винтовой линии (см.
рисунок). Для доказательства этого
разложим вектор скорости на составляющие,
параллельную (υ_х=υcosα)
и перпендикулярную (υ_у=υsinα)
вектору индукции.

Движение
в направлении поля происходит с
равномерной скоростью υ_х,
а в направлении, перпендикулярном
вектору
,
под действием силы Лоренца – по окружности
(=const,
υ_х=const).
В результате сложения двух движений
траектория результирующего движения
протона – винтовая линия (спираль).

Сила
Лоренца сообщает протону нормальное
ускорение

(R-
радиус окружности). По второму закону
Ньютона, F=ma_n,
где F_л=eυ_yB–
сила Лоренца. Тогда

,

Откуда
искомый радиус винтовой линии, по которой
будет двигаться протон,

Шаг
винтовой линии равен расстоянию,
пройденному протоном вдоль оси ох за
время одного полного оборота, т.е.

h=υ_xT=
υTcosα,
(1)

где
период вращения

(2)

Подставив
формулу (2) в выражение (1), найдём искомый
шаг винтовой линии

h=2πRctgα.

Ответ:
R=9.04мм;
h=3,28
см.

Пример.
Между
пластинами плоского конденсатора,
находящегося в вакууме, создано однородное
магнитное поле напряжённостью Н=2кА/м.
Электрон движется в конденсаторе
параллельно пластинам конденсатора и
перпендикулярно направлению магнитного
поля со скоростью υ=2 Мм/с. Определите
напряжение U,
приложенное к конденсатору, если
расстояние d
между его пластинами составляет 1,99 см..

Дано:
μ=1; Н=2кА/м=2∙10³
А/м; υ=2Мм/с=2∙10⁶
м/с; d=1,99
см=1.99∙10^-2м).

Найти:U.

Решение.Предположим,
что магнитное поле направлено
перпендикулярно чертежу от нас. Что
указано на рисунке крестиками. Электрон
может двигаться перпендикулярно
направлению магнитного поля и параллельно
пластинам конденсатора (при выбранных
направлении магнитного поля и зарядах
на пластинах) только так, как указано
на рисунке. При этом кулоновская сила

(У- напряжённость электрического поля)
уравновешивается силой Лоренца F_л=eυB
(её направление определяется по правилу
левой руки). Тогда

откуда

U=υBd.
(1)

Формула,
выражающая связь между магнитной
индукцией
и напряжённостьмагнитного поля

,

Для
случая вакуума (μ=1) имеет вид В=μ₀Н,
Подставив эту формулу в выражение (1),
найдём искомое напряжение на пластинах
конденсатора

Ответ:
U=100
B.

Пример.
Через
сечение медной пластинки (плотность
меди ρ=8,93 г/см³)
толщиной d=0,1
мм пропускается ток I
=5 А. Пластинка с током помещается в
однородное магнитное поле с индукцией
В=0,5 Тл, перпендикулярное направлению
тока и ребру пластинки. Определите
возникающую в пластинке поперечную
(холловскую) разность потенциалов, если
концентрация n
свободных электронов равна концентрации
n‘
атомов проводника.

Дано:
ρ=8,93
г/см³=8,93∙10³
кг/м³;
d=0,1мм=1∙10^-4
м; I=5A;
В=0,5 Тл; n
= n‘
; М=63,5∙10^-3
кг/моль.

Найти:Δφ..

Решение.
На рисунке показана металлическая
пластинка с током плотностью
в
магнитном поле,
перпендикулярном(как в условии задачи). При данном
направлениискорость носителей тока в металлах –
электронов – направлена справа налево.
Электроны испытывают действие силы
Лоренца, которая в данном случае
направлена вверх. У верхнего края
пластинки возникает повышенная
концентрация электронов (он зарядится
отрицательно), а у нижнего – их недостаток
(зарядится положительно). Поэтому между
краями пластинки возникает дополнительное
поперечное электрическое поле,
направленное снизу вверх.

В
случае стационарного распределения
зарядов в поперечном направлении
(напряженность Е_В
поперечного поля достигнет такой
величины, что его действие на заряды
уравновесит силу Лоренца)

или
Δφ=υВα (1)

где
а
– ширина пластинки; Δφ – поперечная
(холловская) разность потенциалов.

Сила
тока

I=jS=neυS=neυad,
(2)

где
S
–площадь поперечного сечения пластинки
толщиной d;
n-
концентрация электронов; υ – средняя
скорость упорядоченного движения
электронов.

Подставив
(2) в (1), получим

.
(3)

Согласно
условию задачи, концентрация свободных
электронов равна концентрации атомов
проводника. Следовательно,

,
(4)

где
N_A=6,02∙10²³
моль^-1
– постоянная Авогадро; V_m–
молярный объём меди; М – молярная масса
меди; ρ- её плотность.

Подставив
формулу (4) в выражение (3), найдём искомую

Пример.
Магнитная
индукция В на оси тороида без сердечника
(внешний диаметр тороида d₁=60
см, внутренний – d₂=40см),
содержащего N=200
витков, составляет 0,16 мТл. Пользуясь
теоремой о циркуляции вектора
,
определите силу тока в обмотке тороида..

Дано:
d₁=60
см
=0,6 м; d₂=40
см
=0,4 м; N=200;
B=0,16
мТл=0,16∙10^-3
Тл.

Найти:
I.

Решение.
Циркуляция вектора

,
(1)

т.е.
равна алгебраической сумме токов,
охватываемых контуром, вдоль которого
вычисляется циркуляция, умноженной на
магнитную постоянную. В качестве контура
выберем окружность, расположенную так
же, как и линия магнитной индукции, т.е.
окружность некоторым радиусом r,
центр которой лежит на оси

тороида.
Из условия симметрии следует, что модуль
вектора

во всех точках линии магнитной индукции
одинаков, а поэтому выражение (1) можно
записать в виде

(2)

(учли,
что сила тока во всех витках одинакова,
а контур охватывает число токов, равное
числу витков тороида). Для средней линии
тороида ). Для средней линии тороида
.
Подставив r
в (2), получим искомую силу тока:

.

Ответ:
I=1
A

Пример.
В
одной плоскости с бесконечным прямолинейным
проводом, по которому течёт ток I=10А,
расположена квадратная рамка со стороной
а=15 см. Определите магнитный поток Ф,
пронизывающий рамку, если две стороны
рамки параллельны проводу, а расстояние
d
от провода до ближайшей стороны рамки
составляет 2 см.

Дано:
I=10А;
а=15
см
=0,15 м; d=2
см=0,02м.

Найти:
Ф.

Р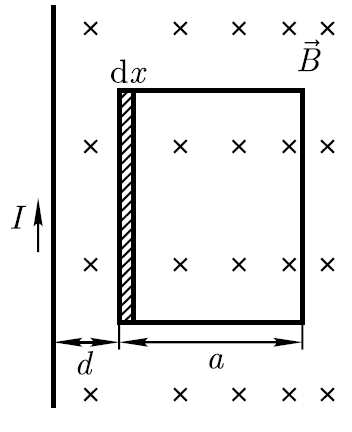ешение.
Магнитный поток Ф сквозь поверхность
площадью вычисляется по формуле:

Квадратная
рамка находится в неоднородном поле
прямого тока с индукцией

(
рассматриваем случай вакуума), где х –
расстояние от провода до рассматриваемой
точки.

Магнитное
поле создаётся прямым током (направление
показано на рисунке), и вектор
перпендикулярен плоскости рамки
(направлен перпендикулярно чертежу от
нас, что на рисунке изображено крестиками),
поэтому для всех точек рамки В_n=В.

Площадь
рамки разобьём на узкие элементарные
площадки шириной dx
и площадью adx
(см. рисунок), в пределах которых магнитную
индукцию можно считать постоянной.
Тогда поток сквозь элементарную площадку

.
(1)

Проинтегрировав
выражение (1) в пределах от до , найдём
искомый магнитный поток

.

Ответ:
Ф=0,25 мкВб

Пример.
Круговой
проводящий контур радиусом r=6см
и током I=2А
установился в магнитном поле так, что
плоскость контура перпендикулярна
направлению однородного магнитного
поля с индукцией В=10мТл. Определите
работу, которую следует совершить, чтобы
медленно повернуть контур на угол
относительно
ос, совпадающий с диаметром контура..

Дано:
r=6
см
=0,06 м; I=2
А;
B=10
мТл=10∙10^-3
Тл;
.

Найти:
А_вн.

Решение.
Работа
сил поля по перемещению замкнутого
проводника с током I

A=I(Ф₂-Ф₁),
(1)

где
Ф₁
и Ф₂–
потоки магнитной индукции, пронизывающие
контуры в начальном и конечном положениях.
Ток в контуре считаем постоянным, так
как при медленном повороте контура в
магнитном поле индукционными токами
можно пренебречь.

Поток
магнитной индукции сквозь плоский
контур площадью S
в однородном магнитном поле с индукцией
В

Ф=BScosα,

где
α– угол между вектором нормали
к поверхности контура и вектором
магнитной индукции.

В
начальном положении, рис. a,
контура (контур установился свободно)
поток магнитной индукции максимален
(α=0; cosα=1)
и Ф₁=BS
( S-
площадь контура), а в конечном положении,
рис. б (;cosα=0),
Ф₂=0.

Тогда,
подставив эти выражения в формулу (1),
найдём, что

A=-IBS=-πIBr²

(учли,
что площадь кругового контура S=πr²).

Работа
внешних сил направлена против сил поля
(равна ей по модулю, но противоположна
по знаку), поэтому искомая работа

A_вн=πIBr².

Ответ:
А_вн=226
мкДж.

32

0 Пользователей и 1 Гость просматривают эту тему.

---

---

 Готовое решение: Заказ №8367

 Тип работы: Задача

Статус:  Выполнен (Зачтена преподавателем ВУЗа)

 Предмет: Физика

 Дата выполнения: 18.08.2020

 Цена: 227 руб.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Найти механический момент, действующий на рамку с током, помещённую в магнитное поле с индукцией 0,1 Тл, если по рамке течёт ток 1 мА, и рамка содержит 200 витков тонкого провода и имеет длину 4 см и ширину 1,5 см.

Решение.

Площадь прямоугольной рамки: , где – размеры рамки. Магнитный момент одного витка: , где – сила тока в рамке. Поскольку рамка содержит витков, то её магнитный момент: . Вращающий (механический) момент, действующий на рамку с током: