Расчет на механическую прочность проводов и тросов
1. Определение исходного режима
Исходным режимом называется такой режим, при котором известны три параметра: механическое напряжение в проводе или тросе, температура и удельная нагрузка. При механическом расчёте проводов и троса в качестве исходного режима принято принимать наиболее тяжёлый режим, при котором напряжение в проводе достигает допустимого значения. Для выбора исходного режима используется понятие критических пролётов. Критическим называется граничный пролёт, при котором влияние температуры и нагрузки на напряжения в проводе оказывается равноопасным. Определяются три критических пролёта.
Первый критический пролет — это пролёт, при котором напряжение в проводе в режиме среднегодовой температуры равно допустимому при среднегодовой температуре, а в режиме низшей температуры — допустимому напряжению при низшей температуре. Первый критический пролет определяется по формуле:
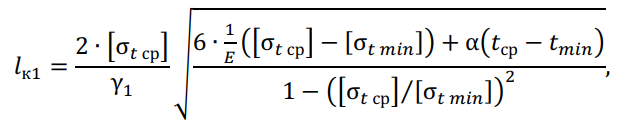
где Е — модуль упругости, ×10 4 Н/мм 2 ;
α — температурный коэффициент линейного удлинения, град -1 ;
?ср — среднегодовая температура, ℃;
[σ? ср]- допустимое напряжение при среднегодовой температуре, Н/мм 2 ;
[σ? . ]- допустимое напряжение при низшей температуре, Н/мм 2 ;
Второй критический пролет — это пролет такой длины, при котором напряжение в проводе при наибольшей нагрузке равно допустимому при наибольшей нагрузке, а в режиме низшей температуры равно допустимому напряжению при низшей температуре, находится по формуле, м:
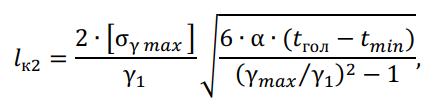
где ?гол — температура гололеда, ℃; [σγ . ]- допустимое напряжение при наибольшей нагрузке, Н/мм 2 .
Третий критический пролет — это пролет такой длины, при котором напряжение равно допустимому при среднегодовой температуре, а в режиме наибольшей нагрузки равно допустимому напряжению в режиме наибольшей нагрузки, определяется по формуле, м:
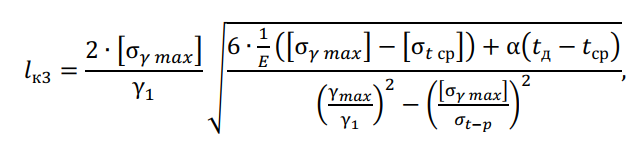
Из соотношения длин пролетов ?к1, ?к2 ?к3, ?р выбирается исходный режим при выполнении условий по соотношению длин:
Из этих условий следует принять за исходный режим — режим наибольшей нагрузки с параметрами:
- наибольшей удельной нагрузкой ?и = ?. = 82,48 ∙ 10 −3 Н/мм 2 ;
- температурой гололеда ?и = ?гол = −5℃,
- допустимым напряжением при наибольшей нагрузке:
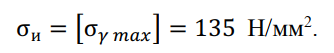
2. Расчет провода на механическую прочность
Для определения напряжений в материале провода при разных климатических условиях используют уравнение состояния провода, которое имеет следующий вид:
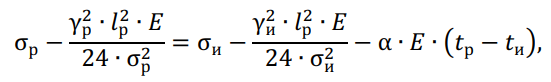
где σи, ?и, ?и — напряжение в проводе, удельная нагрузка и температура в исходном режиме; σр, ?р, ?р — то же в рассчитываемом режиме; l — рассчетная длина пролета, м; E, α — модуль упругости и температурный коэффициент линейного удлинения материала провода.
В уравнение состояния провода подставляются параметры исходного режима — режима наибольшей нагрузки и значения температуры и нагрузки, отвечающие каждому из режимов, указанных здесь в п. 2.1. Затем выполняется расчет напряжений в режимах низшей температуры, среднегодовой температуры и максимальной нагрузки. Обычно расчет производится итерационным методом касательных.
После подстановки значений в уравнение состояния провода получается кубическое уравнение, которое решается по следующему алгоритму:
1. Задаемся нулевым приближением напряжения в проводе σ0;
2. Определяем поправку путем деления самой функции на ее первую производную:
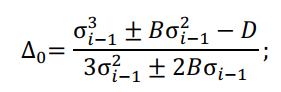
3. Находим новое значение напряжения:
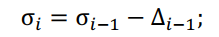
4. Выполняем проверку окончания итерационного процесса по условию |∆| ≤ ε. Если условие выполняется, то расчет необходимо прекратить, если нет, то значение σ? принимается в качестве нового приближения и расчеты повторяются.
Далее выполняем расчеты для перечисленных ниже режимов с указанием выбора значения расчетного напряжения в проводе:
- Режим низшей температуры: σр = σ? . .
- Режим среднегодовой температуры: σр = σ? ср
- Режим наибольшей нагрузки: σр = σγ . .
Проверка условий прочности провода для режимов низшей и среднегодовой температур и режима наибольшей нагрузки:
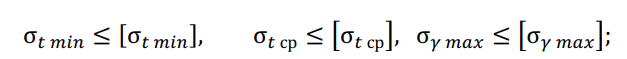
Выполнение расчетных условий свидетельствует о том, что механическая прочность проводов будет достаточной для условий проектируемой линии.
В заключение рассмотрим расчет напряжений и стрел провеса в режимах гололеда без ветра, высшей температуры и грозового режима итерационным методом касательных. При этом для перечисленных ниже режимов выбораем значения расчетного напряжения в проводе:
Расчет стрелы провеса провода проводим по формуле:
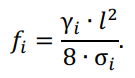
Проверку соблюдения требуемых расстояний от низшей точки провисания провода до земли выполняем по условиям:
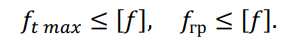
Если условия выполняются — значит, расстояние от провода до земли будет менее допустимого.
Таблица 1. Параметры провода для различных климатических режимов работы
| Режим | t, | γ×10 -3 , | σ, | f, | [σ], | [f], |
| ℃ | Н/м·мм 2 | Н/мм 2 | м | Н/мм 2 | м | |
| низшей температуры | -25 | 34,67 | 107,79 | — | 135 | — |
| среднегодовой
температуры |
0 | 34,67 | 83,36 | — | 90 | — |
| наибольшей нагрузки | 5 | 82,48 | 135 | — | 135 | — |
| режим гололёда | -5 | 79,04 | 131,9 | 4,76 | — | 6,6 |
| высшей температуры | 30 | 34,67 | 63,39 | 4,34 | — | 6,6 |
| грозовой режим | 15 | 34,67 | 72, 19 | 3,81 | — | — |
3. Расчёт грозозащитного троса на механическую прочность
Стрела провеса троса в грозовом режиме определяется по выражению, м,
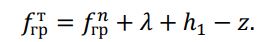
где ?гр т — стрела провеса троса в грозовом режиме; ? — длина гирлянды изоляторов; ℎ1 — расстояние от точки подвеса гирлянды верхнего провода до точки подвеса троса.
С учетом приведенных выше данных получим:
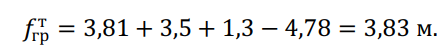
Напряжение в тросе при грозовом режиме определяется по соотношению, Н/мм 2 ,
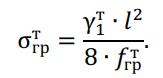
Выполняется расчет напряжений в режимах низшей температуры, среднегодовой температуры и наибольшей нагрузки.
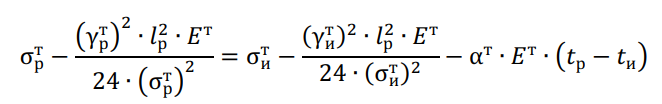
где 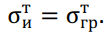
Режим наибольшей нагрузки:
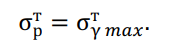
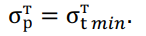
Режим среднегодовой температуры:
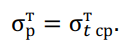
Проверка условий прочности троса для режимов низшей и среднегодовой температур и режима наибольшей нагрузки:
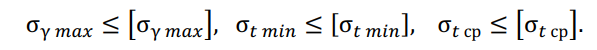
Когда условия выполняются — значит, механическая прочность тросов будет достаточной для условий проектируемой линии.
Источник
Проверка механической прочности грозозащитного троса
После определения значения fт.гпmax стрелы провеса грозозащитного троса в максимальном пролёте необходимо проверить поперечное сечение выбранного троса по условию механической прочности. Аналогично алгоритму расчёта по установлению интервалов длин пролётов с НСКУ, определяющих механическую прочность провода (см. раздел 2), определим НСКУ, определяющие механическую прочность грозозащитного троса. Физико-механические характеристики грозозащитного троса приведены в Табл. 4 и Табл. 5 исходных данных.
1. исходные условия – наибольшая механическая нагрузка, искомые условия – среднеэксплуатационные (СЭ).
Уравнение состояния троса в данном случае запишется аналогичным образом, как для провода по формуле (2.2). Найдём решение вырожденного уравнения состояния троса при l → 0
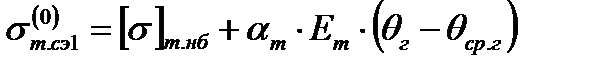
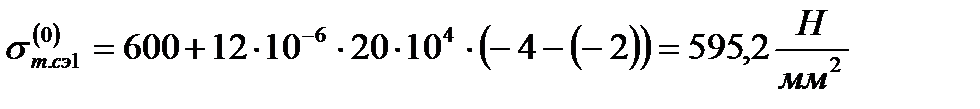
Выразим расчётные коэффициенты Aт.нб и Bт.нб как функции от длины l по формулам (2.3) и (2.4), получим
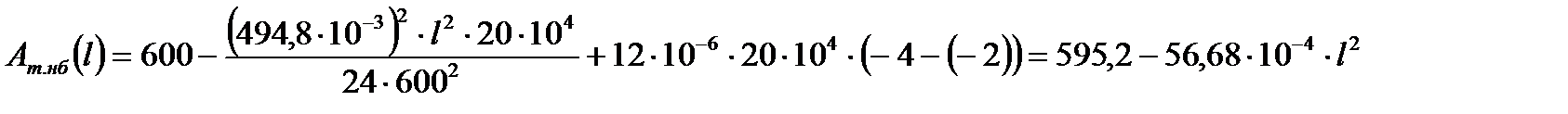
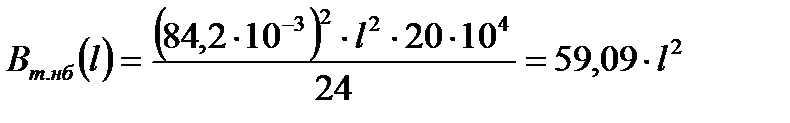
С помощью формулы (2.5) метода Ньютона находим значения механического напряжения σт.сэ1 при изменении длины пролёта в диапазоне l = (100 ÷ 600) м, результаты расчёта сведём в табл. 5.1.
Табл. 5.1 – Результаты расчёта методом Ньютона среднеэксплуатационного напряжения σт.сэ1, Н/мм 2 в низшей точке провода анкерного пролёта при НСКУ, соответствующем наибольшим механическим нагрузкам (НБ)
| l , м | Aт.нб | Bт.нб | σт.сэ1,1 | σт.сэ1,2 | σт.сэ1,3 | σт.сэ1,4 | σт.сэ1,5 |
| 538,52 | 590879,52 | 548,99 | 540,79 | 540,54 | — | — | |
| 368,48 | 2363518,06 | 440,35 | 395,36 | 385,01 | 384,47 | 384,47 | |
| 85,09 | 5317915,64 | 281,47 | 227,51 | 209,89 | 208,02 | 208,00 | |
| -311,67 | 9454072,25 | 157,78 | 144,88 | 144,04 | 144,04 | — | |
| -821,78 | 14771987,89 | 126,42 | 124,93 | 124,91 | — | — | |
| -1445,25 | 21271662,56 | 116,99 | 116,699 | 116,698 | — | — |
Рассмотрим другой предельный переход уравнения состояния троса (2.2) при l → ∞, тогда получится следующее вырожденное уравнение
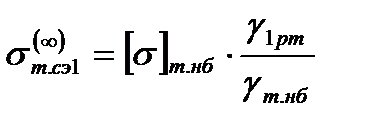
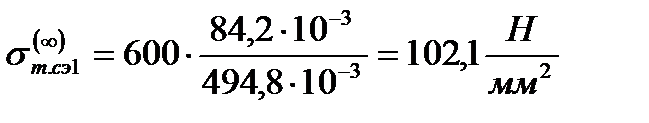
2. исходные условия – низшая температура, искомые условия – СЭ.
Уравнение состояния троса в данном случае запишется аналогичным образом, как для провода по формуле (2.7). Решение вырожденного уравнения состояния троса при l → 0
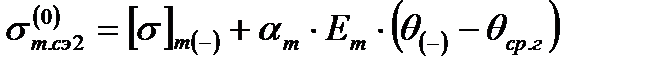
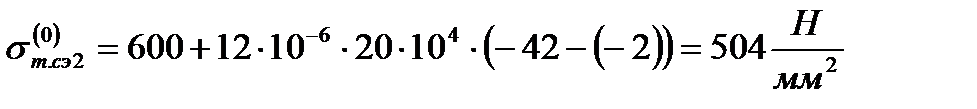
Выразим расчётные коэффициенты Aт (–) и Bт (–) как функции от длины l по формулам (2.8) и (2.9), получим
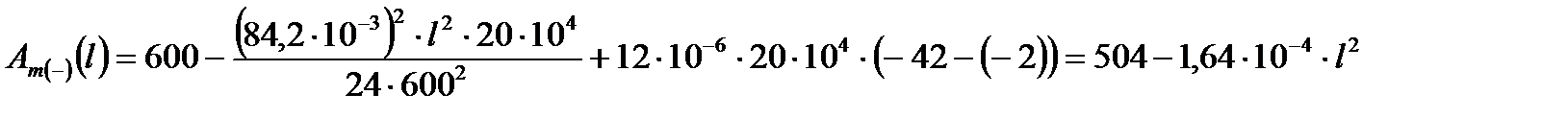
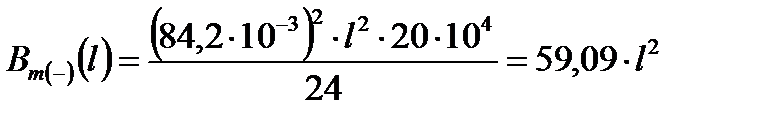
С помощью метода Ньютона находим значения механического напряжения σт.сэ2 при изменении длины пролёта в диапазоне l = (100 ÷ 600) м, результаты расчёта сведём в табл. 5.2.
Табл. 5.2 – Результаты расчёта методом Ньютона среднеэксплуатационного напряжения σт.сэ2, Н/мм 2 в низшей точке провода анкерного пролёта при НСКУ, соответствующем низшей температуре окружающей среды (НТ)
| l , м | Aт(–) | Bт(–) | σт.сэ2,1 | σт.сэ2,2 |
| 502,36 | 590879,52 | 504,68 | 504,678 | |
| 497,43 | 2363518,06 | 506,658 | 506,643 | |
| 489,23 | 5317915,64 | 509,73 | 509,698 | |
| 477,74 | 9454072,25 | 513,64 | 513,58 | |
| 462,97 | 14771987,89 | 518,08 | 518,02 | |
| 444,91 | 21271662,56 | 522,83 | 522,75 |
При l → ∞ уравнение состояния троса (2.7) преобразуется в вырожденное уравнение
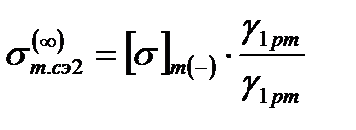
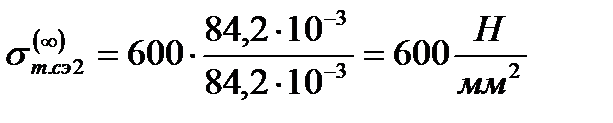
3. исходные и искомые условия – СЭ, поэтому σсэ = [σ]т.сэ = 420 Н/мм 2 .
На основании результатов расчёта в табл. 5.1 и табл. 5.2 построим семейство графиков зависимости среднеэксплуатационных напряжений σт.сэ от длины анкерного пролёта l, изображённые на Рис. 5.1.
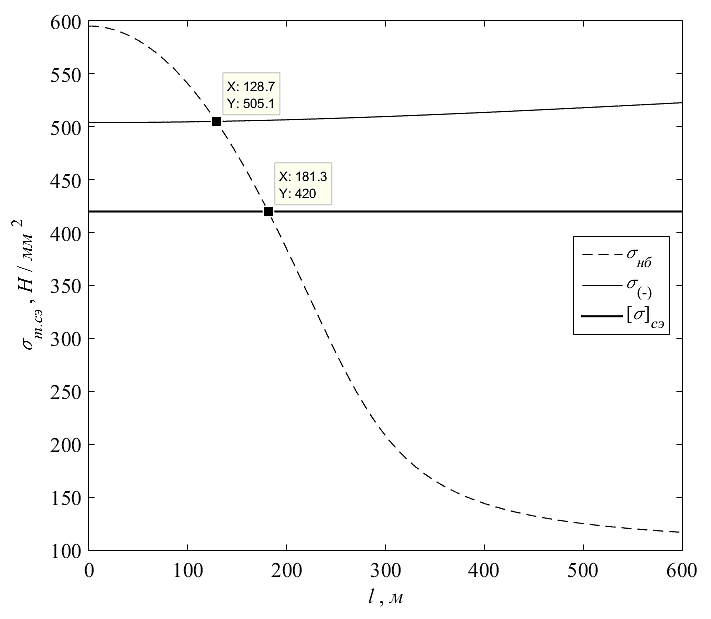 |
| Рис. 5.1 – Семейство графиков зависимости среднеэксплуатационного напряжения грозозащитного троса σт.сэ от длины анкерного пролёта l |
Из семейства графиков зависимости σт.сэ = f (l) видно, что область значений длин пролёта разбивается на два интервала:
— первый интервал при 0 181,3 м, на котором определяющим механическую прочность грозозащитного троса НСКУ являются условия, соответствующие наибольшей механической нагрузке σнб = f (l).
Далее установим НСКУ, определяющее механическую прочность грозозащитного троса и соответствующие ему интервалы значений анкерного пролёта.
Сначала выполним проверку существования lт.кр.1 первого критического пролёта для грозозащитного троса. Для этого воспользуемся следующим неравенством
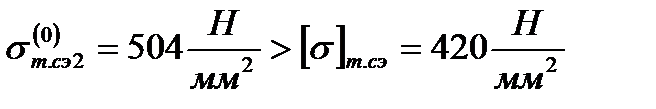 ,
,
отсюда следует, что первого критического пролёта не существует.
Далее проверим существование lт.кр.3 третьего критического пролёта
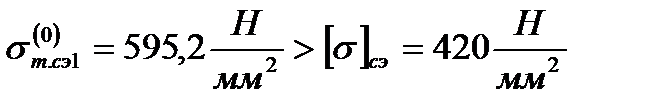 ,
,
следовательно, третий критический пролёт существует, рассчитаем его значение по формуле (2.11)
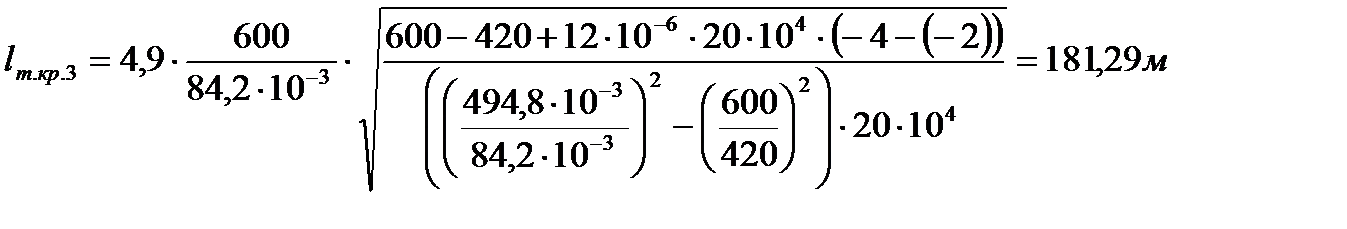
Рассчитывать значение lт.кр.2 второго критического пролёта необязательно, но для проверки правильности построения графиков зависимости определим значение lт.кр.2 по формуле (2.12)
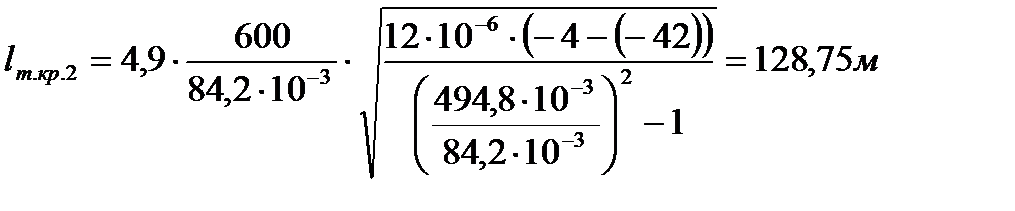
Так как подвеска грозозащитного троса изолированная и значение приведённого пролёта lприв = 330 м > lт.кр.3 = 181,29 м, то НСКУ, определяющее механическую прочность троса, является наибольшая механическая нагрузка (НБ).
Найдём с помощью уравнения состояния троса значение механического напряжения в его поперечном сечении при условии НБ: исходные условия – ГП, искомые условия – НБ, получим
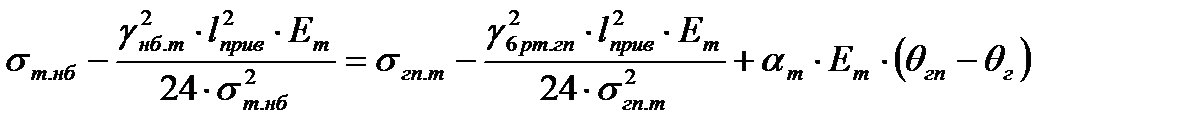
или перепишем последнее выражение в виде неполного кубического уравнения
 ,
,
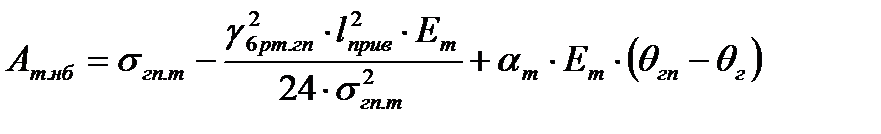
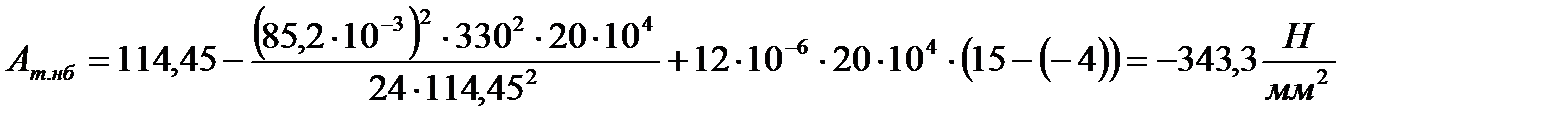
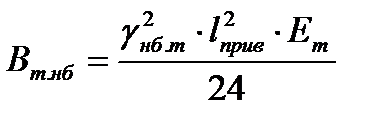
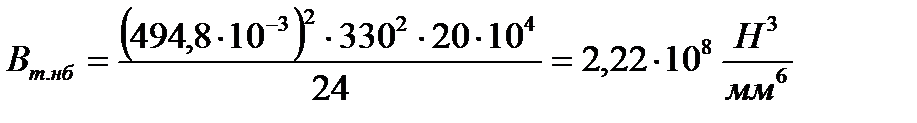
Определим значение механического напряжения нулевой итерации σт.нб(0) по эмпирическим формулам (4.9) или (4.10). В данном случае Aт.нб 2 достигнута на 3-ей итерации i = 3.
Полученное значение σт.нб = 510,21 Н / мм 2 сравниваем с допустимым значением механического напряжения в поперечном сечении грозозащитного троса при условии НБ
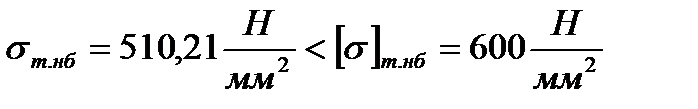 ,
,
следовательно, поперечного сечения выбранного грозозащитного троса марки ТК-11 достаточно по условию механической прочности.
ВЫВОДЫ ПО РАЗДЕЛУ 5
При выполнении раздела 5 получены следующие результаты:
— обеспечены требуемые углы защиты проводов ВЛЭП на промежуточной опоре П220-3, скорректировано значение разности высот опоры и её верхней траверсы, равное Δhтр. = 4,11 м;
— установлено, что разница значений вертикальных проекций стрел провеса провода и грозозащитного троса в середине пролёта больше нуля Δfпр-т > 0, поэтому углы защиты проводов ВЛЭП в середине пролёта меньше, чем на промежуточной опоре;
— стрела провеса грозозащитного троса при условии ГП составляет fт.гпmax = 19,56 м и соответствующее ей напряжение в низшей точке провеса троса σгп.т = 114,45 Н / мм 2 ;
— построены графики зависимости σт.сэ = f (l) (Рис. 5.1), по которым установлено, что для приведённого пролёта lприв = 330 м НСКУ, определяющим механическую прочность грозозащитного троса, является наибольшая механическая нагрузка (НБ);
— показано, что поперечного сечения выбранного грозозащитного троса марки ТК-11 достаточно по условию механической прочности.
Источник
Условие
A9. Найдите механическое напряжение, возникающее в стальном тросе при его относительном удлинении 0,001.
Решение
| Трос стальной; деформация; |
| ε = 0,001; |
|
Е ≈ 210 ГПа = 210∙109 Па;
|
| σ – ? |
Механическое напряжение и относительное удлинение связаны соотношением (~sigma = E cdot varepsilon), где Е ≈ 210 ГПа = 210∙109 Па – модуль упругости стали. Тогда
σ ≈ 210∙109 Па ∙ 0,001 = 210∙106 Па = 2,10∙108 Па.
Какой должна быть площадь поперечного сечения стального троса лифта, если лифт массой m = 500 кг может двигаться с ускорением до а = 1,2 м/с2? Запас прочности троса n = 10. Предел прочности для стали равен 500 МПа.
Спрятать решение
Решение.
Механическое напряжение, которое может быть в тросе, равно По определению
Найдем силу упругости, возникающую в тросе. По второму закону Ньютона
В проекции на вертикальную ось:
Таким образом, площадь поперечного сечения троса при максимальной нагрузке
Ответ: Не менее 1,1 см2.
Источник: Гельфгат И. М. Сборник задач по физике для 10 класса, Х.: «Гимназия», 2001 (№ 5.23)
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
![]()
7
1 ответ:
![]()
0
0
<span>Механическое напряжение </span>σ<span> – это модуль Юнга, умноженный на относительное удлинение </span>
Дано:
– модуль Юнга для стали Е = 210 ГПа = 2,1*10¹¹ Па,
<span>- относительное удлинение </span>ε = 0,001 = 10⁻³.
Тогда σ = 2,1*10¹¹*0,001 = 2,1*10⁸ Па.
Читайте также
![]()
S=s1=s2=s3
s1=(v1+v2)t1
s2=(v1-v2)t2
s3=v1t3
v1-собственная скорость катера
t1-время по течению
t2-время против течения
v2- скорость реки
(v1+v2)t1=(v1-v2)t2
v1t1+v2t1=v1t2-v2t2
v2t1+v2t2=v1t2-v1t1
v2(t1+t2)=v1(t2-t1)
v1=v2(t1+t2)/t2-t1;(подставив и посчитав получаем)
v1=5v2
v2=v1/5
s1=(5v2+v2)t1=3600v2=720v1
s1=s3
720v1=v1t3
t3=720
__________
вроде так
![]()
Выталкивающая сила действует на любое тело погруженное в жидкость.
Просто в этом примере выталкивающая сила равна силе тяжести.
================
![]()
одинаковый.так как объем воды взят одинаково.независимо от плотности вещества
![]()
<span><span>Дано:
t=20 С
k=</span></span><span>1,38*10^(-23) Дж/К
_______________
</span><span>Ек – ?
Решение:
Ek = 3/2*kT
T=273+20=293 К
Ek=1.5*</span><span><span>1,38*10^(-23)</span>*293=2.07*293*10^(-23)=606.5*10^(-23)≈6.07*10^(-21) Дж
Ответ: </span><span>6.07*10^(-21) Дж</span>
![]()
Аххаха аня приевт это твой однокланик неожидал наткнуться на тебя здесь ясно теперь как ты дз делаеш хех
Механическое напряжение и закон гука
Для решения
задач данного раздела необходимо знать
обозначения и единицы измерения для
следующих физических величин:
|
ε σ F S E |
ЗАДАЧА-ОБРАЗЕЦ:
Чему равно относительное удлинение и
механическое напряжение в стальной
струне, сечение которой равно 1 мм2,
под нагрузкой 500 Н?
Внимательно
ознакомьтесь с условием и решением этой
задачи, обязательно найдите в учебнике
указанную формулу. В справочной таблице
разыщите значение модуля упругости для
стали. Перепишите решение этой задачи
себе в рабочую тетрадь, соблюдая правила
оформления. Переписывать нужно только
текст, выделенный курсивом, а пояснения,
сделанные обычным шрифтом переписывать
не нужно.
|
Дано: |
СИ: |
Решение: |
|
S=1мм2 F= E=21011Па |
=10-6 |
|
|
ε=? |
||
|
Откройте учебник,
Кроме =E Преобразуйте
Сделайте
Не
Запишите Ответ: |
Вслед
за первой, попробуйте решить самостоятельно
следующие задачи, соблюдая все правила
их оформления:
-
Определите
относительное удлинение и механическое
напряжение в медном проводе с площадью
поперечного сечения 0,1 мм2
под нагрузкой 200Н.
(Отв:=2109Па;ε=0,02.) -
Относительное
удлинение алюминиевого стержня
составляет 0,001, диаметр равен 3 мм.
Определить величину напряжения в
проводе и значение силы, которая к нему
приложена ? (Отв:=7107Па;F=495
Н.)
Закон кулона
Для решения
задач данного раздела необходимо знать
обозначения и единицы измерения для
следующих физических величин:
|
F – сила k R q |
Обязательно
разыщите в учебнике и выучите закон
Кулона для взаимодействия наэлектризованных
тел, познакомьтесь с устройством
крутильных весов, выясните, в каком
случае заряды можно считать точечными
и неподвижными. Не забудьте, что значок
модуля в формуле закона Кулона указывает
на положительную величину силы, независимо
от знака зарядов.
ЗАДАЧА-ОБРАЗЕЦ:
Выясните, на каком расстоянии
два точечных заряженных тела в вакууме
взаимодействуют с силой 3Н. Величина
первого заряда составляет 1мкКл, а
второго 3мКл.
|
Дано: |
СИ: |
Решение: |
|
F=3Н q1=2мкКл q2=3мКл |
=1·10-6 =3·10-3 |
|
|
r=? |
||
|
По закону Кулона,
Переносом
Чтобы
В
По
Проверьте,
Запишите Ответ: |
Попробуйте
решить самостоятельно следующие задачи:
-
С
какой силой два точечных заряда
величинами 2мКл и 0,5 мкКл взаимодействуют
на расстоянии 3м? (Отв:
1Н) -
Определить
величину точечного заряда, если он
взаимодействует с другим зарядом
величиной 2мКл силой 10 Н на расстоянии
3м? (Отв:
5мкКл) -
Определите
расстояние, на котором два точечных
заряженных тела с зарядами 2мкКл, а
второго 0,6мкКл. в вакууме взаимодействуют
с силой 12Н. (Отв:
1см)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

