Как найти механическое напряжение задачи

Механическое напряжение и закон гука

Для решения
задач данного раздела необходимо знать
обозначения и единицы измерения для
следующих физических величин:

ε («эпсилон») – относительное удлинение [1] σ («сигма») – механическое напряжение [Н/м2] F – величина деформирующей силы [Н] S – площадь поперечного сечения [м2] E – модуль упругости (модуль Юнга) [Па]

ЗАДАЧА-ОБРАЗЕЦ:
Чему равно относительное удлинение и
механическое напряжение в стальной
струне, сечение которой равно 1 мм²,
под нагрузкой 500 Н?

Внимательно
ознакомьтесь с условием и решением этой
задачи, обязательно найдите в учебнике
указанную формулу. В справочной таблице
разыщите значение модуля упругости для
стали. Перепишите решение этой задачи
себе в рабочую тетрадь, соблюдая правила
оформления. Переписывать нужно только
текст, выделенный курсивом, а пояснения,
сделанные обычным шрифтом переписывать
не нужно.

Дано:	СИ:	Решение:
S=1мм2 F= 500 Н E=21011Па	=10-6 м2
ε=? =?
Откройте учебник, разыщите там формулу для вычислений механического напряжения: Кроме того, разыщите закона Гука: =E Преобразуйте эту формулу так, чтобы можно было вычислить относительное удлинение: Сделайте вычисления по первой и последней формулам, используя данные из колонки «СИ», из дано, а так же результаты вычислений:   Не забудьте проверить размерность по каждой из формул: ; Запишите ответ. Ответ: относительно удлинение составляет 0,0025; механическое напряжение равно 500 МПа.

Вслед
за первой, попробуйте решить самостоятельно
следующие задачи, соблюдая все правила
их оформления:

1. Определите
   относительное удлинение и механическое
   напряжение в медном проводе с площадью
   поперечного сечения 0,1 мм²
   под нагрузкой 200Н.
   (Отв:=210⁹Па;ε=0,02.)

2. Относительное
   удлинение алюминиевого стержня
   составляет 0,001, диаметр равен 3 мм.
   Определить величину напряжения в
   проводе и значение силы, которая к нему
   приложена ? (Отв:=710⁷Па;F=495
   Н.)

Закон кулона

Для решения
задач данного раздела необходимо знать
обозначения и единицы измерения для
следующих физических величин:

F – сила взаимодействия зарядов Н k – электрическая постоянная[9·109 ] (см. справочную табл.) R или r – расстояние между зарядами м q – величина заряда Кл

Обязательно
разыщите в учебнике и выучите закон
Кулона для взаимодействия наэлектризованных
тел, познакомьтесь с устройством
крутильных весов, выясните, в каком
случае заряды можно считать точечными
и неподвижными. Не забудьте, что значок
модуля в формуле закона Кулона указывает
на положительную величину силы, независимо
от знака зарядов.

ЗАДАЧА-ОБРАЗЕЦ:
Выясните, на каком расстоянии
два точечных заряженных тела в вакууме
взаимодействуют с силой 3Н. Величина
первого заряда составляет 1мкКл, а
второго 3мКл.

Дано:	СИ:	Решение:
F=3Н q1=2мкКл q2=3мКл	=1·10-6 =3·10-3
r=?
По закону Кулона, сила взаимодействия наэлектризованных тел определяется по формуле: Переносом сомножителей преобразуйте эту формулу: Чтобы избавится от второй степени при вычислении расстояния, извлеките квадратный корень. Для сохранения равенства, корень должен быть извлечен из обеих частей выражения: В левой части равенства квадратный корень и возведение расстояния во вторую степень взаимно сокращаются: По этой формуле вычислите расстояние между зарядами: Проверьте, какая размерность у результата: Запишите ответ. Ответ: Расстояние между зарядами 3 метра.

Попробуйте
решить самостоятельно следующие задачи:

1. С
   какой силой два точечных заряда
   величинами 2мКл и 0,5 мкКл взаимодействуют
   на расстоянии 3м? (Отв:
   1Н)

2. Определить
   величину точечного заряда, если он
   взаимодействует с другим зарядом
   величиной 2мКл силой 10 Н на расстоянии
   3м? (Отв:
   5мкКл)

3. Определите
   расстояние, на котором два точечных
   заряженных тела с зарядами 2мкКл, а
   второго 0,6мкКл. в вакууме взаимодействуют
   с силой 12Н. (Отв:
   1см)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уровень А

1. Какого вида деформации испытывают при нагрузке:

а) ножка скамейки;

б) сиденье скамейки;

в) натянутая струна гитары;

г) винт мясорубки;

д) сверло;

е) зубья пилы?

Решение

2. С какой деформацией (упругой или пластической) имеют дело при лепки фигур с глины, пластилина?

Решение

3. Проволока длиной 5,40 м под действием нагрузки удлинилась до 5,42 м. Определите абсолютное удлинение проволоки.

Решение

4. При абсолютном удлинении на 3 см длина пружины стала равной 27 см. Определите ее начальную длину, если пружину:

а) растянули;

б) сжали.

Решение

5. Абсолютное удлинение проволоки длиной 40 см равно 2,0 мм. Определите относительное удлинение проволоки.

Решение

6. Абсолютное и относительное удлинение стержня равны 1 мм и 0,1% соответственно. Определите длину недеформированного стержня?

Решение

7. При деформации стержня сечением 4,0 см² сила упругости равна 20 кН. Определите механическое напряжение материала.

Решение

8. Определите модуль силы упругости в деформированном стержне площадью 4,0 см², если при этом возникает механическое напряжение 1,5·10⁸ Па.

Решение

9. Найдите механическое напряжение, возникающее в стальном тросе при его относительном удлинении 0,001.

Решение

10. При растяжении алюминиевой проволоки в ней возникло механическое напряжение 35 МПа. Найдите относительное удлинение.

Решение

11. Чему равен коэффициент жесткость пружины, которая удлиняется на 10 см при силе упругости 5,0 H?

Решение

12. На сколько удлинилась пружина жесткостью 100 Н/м, если сила упругости при этом равна 20 Н?

Решение

13. Определите максимальную силу, которую может выдержать стальная проволока, площадь поперечного сечения которой 5,0 мм².

Решение

14. Берцовая кость человека выдерживает силу сжатия 50 кН. Считая предел прочности кости человека равным 170 МПа, оцените среднюю площадь поперечного сечения берцовой кости.

Решение

Уровень B

1. Какая колба выдержит большее давление снаружи – круглая или плоскодонная?

Решение

2. Для чего рама велосипеда делается из полых трубок, а не сплошных стержней?

Решение

3. При штамповке детали иногда предварительно нагревают (горячая штамповка). Для чего это делают?

Решение

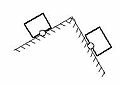
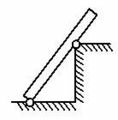
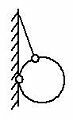
4. Укажите направление сил упругости, действующих на тела в указанных точках (рис. 1).

• 

  а

• 

  б

• 

  в

• 

  г

• 

  д

Рис. 1

Решение

5. Почему нет таблиц для коэффициента жесткости тела k, вроде таблиц для плотности вещества?

Решение

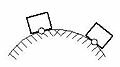
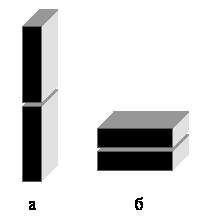
6. При какой кладке кирпичей (рис. 2) нижний из кирпичей окажется под большим напряжением?

Решение

7. Сила упругости – сила переменная: она изменяется от точки к точке по мере удлинения. А как ведет себя ускорение, вызванное этой силой?

Решение

8. К закрепленной одним концом проволоке диаметром 2,0 мм подвешен груз массой 10 кг. Найдите механическое напряжение в проволоке.

Решение

9. На две вертикальные проволоки, диаметры которых отличаются в 3 раза, прикрепили одинаковые грузики. Сравните возникающие в них напряжения.

Решение

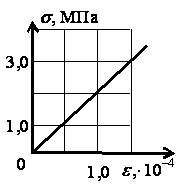
10. На рис. 3 дан график зависимости напряжения, возникающего в бетонной свае, от ее относительного сжатия. Найдите модуль упругости бетона.

Решение

11. Проволока длиной 10 м с площадью сечения 0,75 мм² при растяжении силой 100 Н удлинилась на 1,0 см. Определите модуль Юнга для материала проволоки.

Решение

12. С какой силой нужно растягивать закрепленную стальную проволоку длиной 1 м с площадью сечения 0,5 мм², чтобы удлинить ее на 3 мм?

Решение

13. Определите диаметр стальной проволоки длиной 4,2 м, чтобы при действии продольной растягивающей силы, равной 10 кН, ее абсолютное удлинение было равно 0,6 см?

Решение

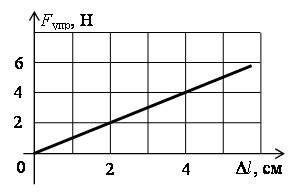
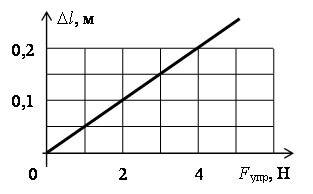
14. Определите по графику (рис. 4) коэффициент жесткости тела.

Решение

15. По графику зависимости изменения длины резинового жгута от приложенной к нему силы найдите жесткость жгута (рис. 5).

Решение

16. Постройте график зависимости силы упругости, возникающей в деформированной пружине F_упр = f(Δl), от ее удлинения, если жесткость пружины 200 Н/м.

Решение

17. Постройте график зависимости удлинения пружины от приложенной силы Δl = f(F), если коэффициент жесткости пружины 400 Н/м.

Решение

18. Закон Гука для проекции силы упругости пружины имеет вид F_x = –200 х. Чему равна проекция силы упругости, если при удлинении пружины из недеформированного состояния проекция перемещения конца пружины на ось Х составляет 10 см?

Решение

19. Два мальчика растягивают резиновый жгут, прикрепив к его концам динамометры. Когда жгут удлинился на 2 см, динамометры показывали силы по 20 Н каждый. Что показывают динамометры при растяжении жгута на 6 см?

Решение

20. Две пружины равной длины, соединенные последовательно, растягивают за свободные концы руками. Пружина жесткостью 100 Н/м удлинилась на 5 см. Какова жесткость второй пружины, если ее удлинение равно 1 см?

Решение

21. Пружина изменила свою длину на 6 см, когда к ней подвесили груз массой 4 кг. На сколько бы она изменила свою длину под действием груза массой 6 кг?

Решение

22. На двух проволоках, одинаковой жесткости, длиной 1 и 2 м подвешены одинаковые грузы. Сравните абсолютные удлинения проволок.

Решение

23. Диаметр капроновой рыболовной лески 0,12 мм, а разрывная нагрузка 7,5 Н. Найдите предел прочности на разрыв данного сорта капрона.

Решение

24. При каком наибольшем диаметре поперечного сечения стальная проволока под действием силы в 7850 Н разорвется?

Решение

25. Люстру массой 10 кг нужно подвесить на проволоке сечением не более 5,0 мм². Из какого материала следует взять проволоку, если необходимо обеспечить пятикратный запас прочности?

Решение

Уровень С

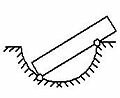
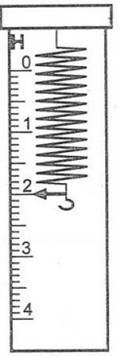
1. Если к вертикально расположенному динамометру прикрепить деревянный брусок массой 200 г, то показание динамометра окажется таким, как показано на рисунке 1. Определите ускорение, с которым начнет двигаться тот же брусок, если его оттянуть так, что пружина удлинится еще на 2 см, а затем брусок отпустить.

Решение

Задачи по теме Механические свойства твердых тел
из учебника Рымкевич (глава Молекулярная физика и термодинамика. Основы молекулярно-кинетической теории)

№ 592. Кубик, вырезанный из монокристалла, нагреваясь, может превратиться в параллелепипед. Почему это возможно?

593. Вблизи поверхности кристалла в процессе его роста
наблюдаются так называемые концентрационные потоки раствора, поднимающиеся вверх. Объяснить явление.

Задача № 594. Из задачника Рымкевича 2001 года (5-е издание)

№ 595. Какого вида деформации испытывают: а) ножка скамейки; б) сиденье скамейки; в) натянутая струна гитары; г) винт мясорубки; д) сверло; е) зубья пилы?

№ 596. Какого вида деформации возникают в стержне, на котором крепятся дверные петли?

№ 597. Какого вида деформации возникают в перекладине, когда гимнаст делает полный оборот (солнце)?

№ 598(н). Если тело обладает анизотропией, означает ли это, что оно является кристаллическим?

№ 598. Для чего рама велосипеда делается из полых трубок, а не из сплошных стержней?

№ 599(н). Почему предел упругости при сжатии больше предела упругости при растяжении?

№ 599. К закрепленной одним концом проволоке диаметром 2 мм подвешен груз массой 10 кг. Найти механическое напряжение в проволоке.

№ 600. Две проволоки, диаметры которых отличаются в 3 раза, подвержены действию одинаковых растягивающих сил. Сравнить возникающие в них напряжения.

№ 601. Балка длиной 5 м с площадью поперечного сечения 100 см2 под действием сил по 10 кН, приложенных к ее концам, сжалась на 1 см. Найти относительное сжатие и механическое напряжение.

№ 602. При растяжении алюминиевой проволоки длиной 2 м в ней возникло механическое напряжение 35 МПа. Найти относительное и абсолютное удлинения.

№ 603. Найти механическое напряжение, возникающее в стальном тросе при его относительном удлинении 0,001.

№ 604. Во сколько раз абсолютное удлинение латунной проволоки больше, чем стальной (такой же длины и такого же поперечного сечения), при действии на них одинаковых растягивающих сил?

№ 605. К концам стальной проволоки длиной 3 м и сечением 1 мм2 приложены растягивающие силы по 210 Н каждая. Найти абсолютное и относительное удлинения.

№ 606. На рисунке 68 представлен график зависимости упругого напряжения, возникающего в бетонной свае, от ее относительного сжатия. Найти модуль упругости бетона.

№ 607. Какие силы надо приложить к концам стальной проволоки длиной 4 м и сечением 0,5 мм2 для удлинения ее на 2 мм?

№ 608. Во сколько раз относительное удлинение рыболовной лесы диаметром 0,2 мм больше, чем лесы диаметром 0,4 мм, если к их концам приложены одинаковые силы?

№ 609. К проволоке был подвешен груз. Затем согнули пополам и подвесили тот же груз. Сравнить абсолютное и относительное удлинения проволоки в обоих случаях.

№ 610. Во сколько раз изменится абсолютное удлинение проволоки, если, не меняя нагрузку, заменить проволоку другой — из того же материала, но имеющей вдвое большую длину и в 2 раза больший диаметр?

№ 611. Диаметр капроновой рыболовной лесы 0,12 мм, а разрывная нагрузка 7,5 Н. Найти предел прочности на разрыв данного сорта капрона.

№ 612. Из скольких стальных проволок диаметром 2 мм должен состоять трос, рассчитанный на подъем груза массой 2т?

№ 613. При какой наименьшей длине h свинцовая проволока, подвешенная за один конец, разорвется от собственного веса?

№ 614. Проволока с висящим на ней грузом массой m1 имеет длину l1 а при увеличении массы груза до m2 длина становится l2. Найти длину проволоки l0 без нагрузки.

Физика. Рымкевич А.П. Механические свойства твердых тел.

В данной главе представлены задачи по физике из раздела Механические свойства твердых тел задачника Рымкевича А.П.

Муниципальное
общеобразовательное учреждение «Гимназия №1 городского округа Стрежевой»

Механическое
напряжение. Модуль Юнга.

Методическая
разработка учебного занятия по урочной деятельности

Автор-составитель:

Попович
Марина Александровна

2021
год

Технологическая карта

Название УМК:  Физика. Базовый
и углублённый уровни. 10 класс: учебник/ А.В. Грачёв, В.А. Погожев, А.М.
Стрелецкий и др. – М.: Вентана-Граф, 2019.

Предмет: 
физика

Класс:
10

Тема урока:
Механическое напряжение. Модуль Юнга

Место и роль урока в изучаемой теме: Восьмой
урок при изучении темы «Динамика». Урок для углубленного изучения

Тип урока:
открытие
нового знания.

Цель урока:
открытие, систематизация и расширение знаний
обучающихся

Задачи:

Обучающие: Дать
представление о механическом напряжении, относительном растяжении.

Развивающие: Развивать
умение анализировать, сопоставлять, сравнивать, выделять главное, принимать самостоятельное
решение, доказывать свою точку зрения и принимать чужую.

Воспитательные: Создать условия для
положительной мотивации при изучении физики, используя разнообразные приемы
деятельности, сообщая интересные сведения; воспитывать чувство уважения к
собеседнику, индивидуальной культуры общения.

Планируемые результаты:

личностные:

•        
формирование
осознанного, уважительного и доброжелательного отношения к другому человеку,
его мнению;

•        
формирование
коммуникативной компетентности в общении и сотрудничестве со сверстниками и
взрослыми в процессе учебной деятельности.

метапредметные:

•        
умение
определять понятия, создавать обобщения, классифицировать, строить 
рассуждение, умозаключение и делать выводы;

•        
умение
создавать, применять различные продукты для решения учебной задачи;

•        
умение
оценивать правильность выполнения учебной задачи, собственные возможности её
решения;

предметные:

•        
знать:
определение механического напряжения, относительного растяжения; формулу относительного
растяжения; закон Гука для деформации растяжения.

•        
уметь:
решать задачи на применение изученных формул.

Используемая литература:

1. Физика. Базовый и
углублённый уровни. 10 класс: учебник/ А.В. Грачёв, В.А. Погожев, А.М.
Стрелецкий и др. – М.: Вентана-Граф, 2019.

2. Демонстрационный
эксперимент по физике в школах и классах с углубленным изучением предмета:
Механика. Молекулярная физика/ С.А. Хорошавин – М.: Просвещение, 1994.

3. Физика. Задачник. 10 – 11
кл.: пособие для общеобразовательных учреждений/ А.П. Рымкевич – М.: Дрофа,
2013

Деятельность учителя	Деятельность учащихся	Формируемые УУД	Время (в мин.)
I. Организационный этап Цель : психологически настроить учащихся на учебную деятельность	2
Здравствуйте, ребята. Надеюсь вы сегодня настроены на работу. Хочу пожелать вам успешной работы на уроке. Эпиграфом нашего урока будут слова Виктора Гюго «Дерзайте! Ценой дерзаний достигается прогресс.»	Приветствие учителя;  проверяют готовность к уроку.	Саморегуляция (Р). Планирование учебного сотрудничества с учителем и сверстниками (К).
II.  Постановка цели урока. Мотивация    Цель: Включение в учебную деятельность на личностно-значимом уровне, осознание потребности к построению нового способа действий	10
Сегодня на уроке мы продолжим изучать упругие свойства твердых тел. Узнаем, какие свойства твердых тел говорят об их прочности и износостойкости. Тема урока «Механическое напряжение. Модуль Юнга» На прошлом уроке мы познакомились с деформациями тел и силой упругости. Вспомним: 1. Что такое деформация? 2. Приведите примеры известных вам видов деформаций. 3. Какие деформации называют упругими? Приведите примеры. 4. Сформулируйте закон Гука. 5. Приведите примеры сил упругости. Какова их природа?	Записывают тему урока Ученики отвечают на вопрос учителя. 1. Изменение формы или объема тела. 2. Растяжение, сжатие, сдвиг, изгиб, кручение. 3. Если после исчезновения сил, вызвавших деформации тела, оно возвращается в исходное состояние, то такие деформации называют упругими. 4. Для любого тела при упругих деформациях величины деформаций прямо пропорциональны вызвавшим их силам. 5. Сила реакции опоры, сила натяжения нити, вес тела. Эти силы имеют электромагнитную природу	Умение выражать мысли (К). Планирование (Р). Построение логической цепи (П).
III. Объяснение нового материала Цель этапа: обеспечение восприятия, осмысления и первичного закрепления	17
Для лучшего понимания нового материала проведем опыты Опыт 1. Возьмем два резиновых жгута одинаковой длины и разного поперечного сечения, штатив с лапкой, 2 грузика, динамометр, линейка. Прикрепим резиновый жгут меньшего поперечного сечения к штативу. Измерим длину жгута. Подвесим на него 2 грузика, измерим получившуюся длину жгут, вычислим удлинение (l – l0). С помощью динамометра измерим вес грузиков. Вычислим коэффициент жесткости. Аналогично проведем опыт со жгутом большего поперечного сечения. Сравним полученные коэффициенты жесткости Опыт 2. Возьмем два резиновых жгута разной длины и одинакового поперечного сечения, штатив с лапкой, 2 грузика, динамометр, линейка. 1. Прикрепим резиновый жгут меньшей длины к штативу. Измерим длину жгута. Подвесим на него 2 грузика, измерим получившуюся длину жгут, вычислим удлинение (l – l0). С помощью динамометра измерим вес грузиков. Вычислим коэффициент жесткости. 2. Прикрепим резиновый жгут большей длины к штативу. Измерим длину жгута. Подвесим на него 2 грузика, измерим получившуюся длину жгут, вычислим удлинение (l – l0). С помощью динамометра измерим вес грузиков. Вычислим коэффициент жесткости. Сравним полученные коэффициенты жесткости Для характеристики упругих свойств тела вводится механическое напряжение. Механическое напряжение — физическая величина, равная отношению силы упругости к площади поперечного сечения тела: σ = Напряжение измеряется в паскалях (Па). Даная формула напоминает формулу для расчета давления. Но, в отличие от давления, механическое напряжение – векторная величина. Из проведенных опытов мы сделали вывод, что k ~ Коэффициент пропорциональности в полученном выражении является характеристикой материала, из которого изготовлен жгут. Этот коэффициент называют модулем Юнга и обозначают буквой E. k = Е·  (1) Подставим формулу (1) в закон Гука и поделим левую и правую части на S, получим:  = E· Величину, равную отношению растяжения жгута к его первоначальной длине, называют относительным растяжением жгута: ɛ = С учетом введенных понятий, согласно закону Гука, модуль нормального механического напряжения можно вычислить по формуле: σ = E· ɛ Полученное соотношение называют законом Гука для деформации растяжения (сжатия)	Ученики проводят собственные опыты, выдвигают гипотезы, проводят их обсуждение, формулируют выводы,  проводят коррекцию Вывод 1: чем больше площадь поперечного сечения жгута, тем больше коэффициент жесткости Вывод 2: чем больше длина жгута, тем меньше коэффициент жесткости Вывод: коэффициент жесткости тела зависит от его геометрических характеристик Ученики: записывают определение механического напряжения, формулу для расчета механического напряжения записывают единицы работы l0 Ученики: записывают определение относительного растяжения, формулу для расчёта относительного растяжения Ученики: записывают закон Гука для деформации растяжения (сжатия)	Способность видеть закономерность изучаемого явления (Л) Планирование эксперимента; прогнозирование; алгоритмизация; производить сборку установки; рациональное использование времени (Р) Математическая обработка результата; использование математических символов (П) Обсуждение результатов и формулировка вывода (К)
IV. Первичное закрепление Цель этапа: проговаривание и закрепление нового знания; выявление пробелов первичного осмысления изученного материала, неверных представлений учащихся; проведение коррекции.	5
Задача К закрепленной одним концом проволоке диаметром 2мм подвешен груз массой 10кг. Найти механическое напряжение в проволоке.	Самостоятельно решают задачу, повторяя, систематизируя изученный материал. Записывают в тетрадь	Выбор наиболее эффективных способов решения задач в зависимости от конкретных условий (П).
V. Итог урока Цель этапа: осознание учащихсяся своей учебной деятельности, самооценка результатов деятельности своей и всего класса	6
– Какие физические величины мы изучили сегодня на уроке? – Что называют механическим напряжением? – Что называют модулем Юнга? – Что называют относительным растяжением? Домашнее задание. § 19, упражнение 1 с.122 Учитель:  Ребята! Спасибо за урок. Вы сегодня очень хорошо поработали.	Учащиеся дают ответы на вопросы. – Механическое напряжение, модуль Юнга, относительное растяжение – физическая величина, равная отношению силы упругости к площади поперечного сечения тела – характеристика материала, из которого изготовлен жгут – Величина, равная отношению растяжения жгута к его первоначальной длине Анализирую свою деятельность, оценивают степень освоения материала. Записывают домашнее задание.	Рефлексия способов и условий действия; (П). Самооценка; следование в поведении моральным нормам и этическим требованиям (Л). Выражение своих мыслей полно и точно; формулирование и аргументация своего мнения, учет разных мнений (К).