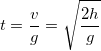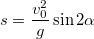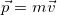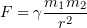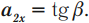Как найти механическую скорость формула

Механика Основные формулы

1. Кинематика

1.1 Скорость тела

1.2 Средняя скорость тела на участке пути

1.3 Средняя скорость при неравномерном движении

1.4 Ускорение тела

1.5 Скорость равномерно-ускоренного движения

1.6 Падение тела без начальной скорости

1.7 Тело, брошенное под углом к горизонту

1.8 Центростремительное ускорение

2. Динамика

2.1 Второй закон Ньютона

2.2 Импульс тела

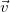
2.3 Закон изменения импульса

2.4 Закон сохранения импульса

2.5 Закон всемирного тяготения

Определения

Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.

Основная задача механики — определение положение тела в пространстве в любой момент времени.

Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение и его виды

По характеру движения точек тела выделяют три вида механического движения:

• Поступательное. Это движение, при котором все точки тела движутся одинаково. Если через тело мысленно провести прямую, то после изменения положения этого тела в пространстве данная прямая останется параллельной самой себе.
• Вращательное. Это движение, при котором все точки тела движутся, описывая окружности.
• Колебательное. Это движение тела, которое повторяется точно или приблизительно через определенные интервалы времени. От вращательного движения его отличает то, что при колебаниях тело перемещается в двух взаимно противоположных направлениях.

По типу линии, вдоль которой движется тело, выделяют два вида движения:

• Прямолинейное — тело движется по прямой линии.
• Криволинейное — тело движется по кривой линии, в том числе замкнутой.

По скорости выделяют два вида движения:

• Равномерное — скорость движущегося тела остается неизменной.
• Неравномерное — скорость движущегося тела с течением времени меняется.

По ускорению выделяют три вида движения:

• Равноускоренное — тело движется неравномерно с постоянным ускорением (положительным). Скорость увеличивается.
• Равнозамедленное — тело движется неравномерно с постоянным замедлением (отрицательным ускорением). Скорость уменьшается.
• Ускоренное — тело движется неравномерно с меняющимся ускорением. Скорость может, как увеличиваться, так и уменьшаться.

Что нужно для описания механического движения?

Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.

Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.

Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.

Тело отсчета — тело, относительно которого рассматривается движение.

Часы — прибор для отсчета времени. Время измеряется в секундах (с).

При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.

Виды систем координат

В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:

• Одномерную. Используется, когда положение материальной точки можно задать только одной координатой x — M(x) . В этом случае тело движется прямолинейно.
• Двумерную. Используется, когда положение материальной точки можно задать двумя координатами x и y — M(x,y). Тело в этом случае движения по плоскости.
• Трехмерную. Используется, когда положение материальной точки можно задать тремя координатами x, y и z — M(x,y,z). Тело в этом случае изменяет положение в трехмерном пространстве.

Способы описания механического движения

Описать механическое движение можно двумя способами:

1. координатным
2. векторным

Координатный способ

Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:

Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.

Векторный способ

Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.

Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:

Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.

Характеристики механического движения

Движение материальной точки характеризуют три физические величины:

1. перемещение
2. скорость
3. ускорение

Перемещение

Определение

Перемещение (вектор перемещения) — направленный отрезок, начало которого совпадает с начальным положением точки, а конец — с его конечным положением. Обозначается как S.

Перемещение точки определяется как изменение радиус-вектора. Это изменение обозначается как Δr. С точки зрения геометрии вектор перемещения равен разности радиус-векторов, задающих конечное и начальное положение точки:

Траектория — линия, которую описывает тело во время движения.

Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).

Путь есть функция времени:

Модуль перемещения — длина вектора перемещения. Обозначается как |Δr|. Единица измерения — метры (м).

Внимание!

Модуль перемещения необязательно должен совпадать с длиной пути.

Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.

Путь равен длине окружности. Поэтому:

Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.

Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?

Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:

Скорость

Определение

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.

В физике скорость обозначается V. Математически скорость определяется формулой:

Скорость характеризуется не только направлением вектора скорости, но и его модулем.

Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).

Математическое определение модуля скорости:

Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:

Ускорение

Определение

Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.

В физике ускорение обозначается a. Математически оно определяется формулой:

Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с²).

Математическое определение модуля скорости:

v — скорость тела в данный момент времени, v₀— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:

Проекция вектора перемещения на ось координат

Определение

Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.

Проекция вектора на ось OX:

Проекция вектора на ось OY:

Знаки проекций перемещения

• Проекция является положительной, если движение от начала проекции вектора к проекции конца происходит сонаправленно оси координат.
• Проекция является отрицательной, если движение от начала проекции вектора к проекции конца направлено в сторону, противоположную направлению координатной оси.

Внимание!

Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.

Модуль перемещения — длина вектора перемещения:

Модуль перемещения измеряется в метрах (м).

Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:

Выразив проекции вектора перемещения через координаты, эта формула примет вид:

Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:

Общий вид уравнений координат:

Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.

Определяем координаты начальной точки вектора:

Определяем координаты конечной точки вектора:

Проекция вектора перемещения на ось OX:

Проекция вектора перемещения на ось OY:

Применяем формулу для вычисления модуля вектора перемещения:

Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.

Извлекаем известные данные:

Для определения координаты точки В понадобятся формулы:

Выразим из них координаты конечного положения точки:

 

Точка В имеет координаты (5; 10).

Алиса Никитина | Просмотров: 38.6k

В прошлой статье мы немножко разобрались с тем, что такое механика  и зачем она нужна. Мы уже знаем, что такое система отсчета,  относительность движения и материальная точка. Что ж, пора двигаться дальше!  Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики  и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад  в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат  (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной  от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Здесь  – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно! 
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

3. по скорости

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( S )​ — перемещение тела относительно неподвижной системы отсчета;
​( S_1 )​ — перемещение тела относительно подвижной системы отсчета;
​( S_2 )​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( v )​ — скорость тела относительно неподвижной системы отсчета;
​( v_1 )​ — скорость тела относительно подвижной системы отсчета;
​( v_2 )​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):

Определим скорость второго тела относительно первого ( v_{21} ):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​( alpha )​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​( v )​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​( a )​, единица измерения — м/с².
В векторном виде:

где ​( v )​ – конечная скорость; ​( v_0 )​ – начальная скорость;
​( t )​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​( a_n )​ – нормальное ускорение, ​( a_{tau} )​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ​( v )​ ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​( t )​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​( t )​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

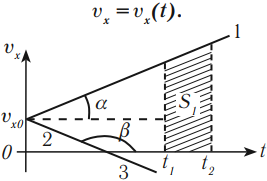
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​( x=x(t) )​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​( a_x )​ > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ​( v_{0x} )​ > 0, ​( a_x )​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,

График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ​( t_2-t_1 )​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​( n )​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​( g )​, единицы измерения – м/с².

Важно! ( g ) = 9,8 м/с², но при решении задач считается, что ( g ) = 10 м/с².

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​( v_0 )​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​( v )​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​( v_0=v_{0x} )​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​( g )​ и без начальной скорости ​( v_{0y}=0 )​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​( v_0 )​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​( alpha )​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​( a_{цс} )​, единицы измерения – ​м/с^2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​( T )​, единицы измерения – с.

где ​( N )​ – количество оборотов, ​( t )​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​( nu )​, единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​( v )​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​( omega )​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​( v_1 )​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​( (m) )​ равна нулю, мгновенная скорость в верхней точке ​( (n) )​ равна удвоенной скорости ​( v_1 )​, мгновенная скорость точки ​( (p) )​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​( (c) )​ – по теореме косинусов.

Основные формулы по теме «Кинематика»

Когда лодка движется по течению, течение помогает лодке двигаться, и лодка начинает двигаться быстрее. Таким образом, скорость самой лодки и скорость течения объединяются.

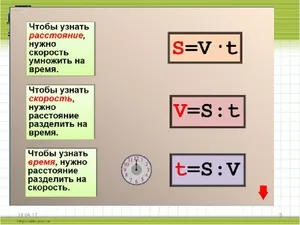
Как рассчитать скорость формула

Скорость 90 км/ч означает, что объект проходит 90 км за один час.

Запишите тип скорости.

Формулы приводятся в математической нотации, а значения выражаются общими буквами (переменными).

V — скорость, V — расстояние, S — время, t — время.

Исходя из этого, уравнение скорости приобретает вид

Примените эту формулу для решения следующей задачи.

Автомобиль, движущийся с постоянной скоростью, проезжает 120 км за 2 часа. С какой скоростью двигался автомобиль?

Пройденное расстояние (дистанция) и время, затраченное на путь, были заменены формулой для нахождения скорости. V = 60 км/ч.

Теперь, исходя из формулы скорости, напишем формулу пути.

Поезд двигался со скоростью 50 км/ч в течение 3 часов равномерно. Какое расстояние было пройдено поездом за этот период?

Используя тип маршрута, мы нашли ответ. Поезд проехал 150 км за 3 часа.

Скорость — это физическая величина, определяющая расстояние, которое проходит объект за единицу времени. Поэтому уравнение для определения скорости (равномерного движения) может быть выражено как.

V, значение скорости — S, значение пройденного расстояния — T, время движения.

Скорость почти всегда выражается в м/с или км/ч, расстояние — в метрах (м) или километрах (км), а время — в секундах, минутах или часах.

Из перечисленных выше типов скоростей можно экспортировать определенные типы маршрутов.

Пройденное расстояние — это произведение скорости на время. Если известны расстояние и скорость, то время можно найти по следующей формуле

Разделите расстояние на скорость, чтобы найти время.

Вы можете использовать онлайн-калькуляторы для быстрого и точного расчета времени, скорости и расстояния в различных единицах измерения.

С древних времен людей волновала идея достижения сверхскорости, и никогда не волновала высота, летающих машин. На самом деле, это два очень тесно связанных понятия. То, насколько быстро вы сможете добраться из одной точки в другую на современном самолете, зависит исключительно от скорости. Рассматриваются методы и виды расчетов, а также время и расстояние.

Как же рассчитать скорость?

На самом деле, существует несколько методов расчета.

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье описан самый простой метод, в котором используется самое простое уравнение. Он заключается в нахождении значения этого параметра из расстояния и времени. Кстати, формула разности также содержит эти значения. Формула выглядит следующим образом.

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, нет ничего сложного в том, чтобы быть первокурсником. Вы можете рассчитать скорость, с которой движется объект, подставив значения, соответствующие позициям букв. Например, давайте найдем значение скорости, с которой автомобиль проезжает 100 км за 1 час 30 минут. В большинстве случаев единицей измерения являются километры в час (км/ч), поэтому сначала нужно перевести 1 час 30 минут в часы. Это означает, что 1 час 30 минут равен 1,5 часа. Это потому, что 30 минут — это половина или 1/2 или 0,5 часа. Сумма 1 часа и 0,5 часа равна 1,5 часа.

Затем замените буквы алфавита на доступные значения.

Здесь v = 66,66 км/ч. Это значение очень приблизительное (неосведомленным лучше почитать о нем в специальной литературе), S = 100 км и t = 1,5ч.

С помощью этого простого метода скорость можно найти из времени и расстояния.

Что произойдет, если я захочу найти среднюю цену? Как правило, приведенный выше расчет приводит к среднему значению искомого параметра. Однако, если мы знаем, что скорость объекта не постоянна в определенном сечении по сравнению с другими сечениями, мы можем экспортировать более точные значения. В этом случае используйте тип.

V1, V2, V3 и VN — величины объектов на конкретном участке, n — количество этих участков, а VCR — средняя скорость на всех расстояниях.

Один и тот же тип можно записать по-разному, используя маршрут и время, которое объект прошел по этому маршруту.

• vср=(S1+S2+. +Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно также написать его, используя вычисления такого типа.

• vср=S/(t1+t2+. +tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Однако тот же тип можно записать и в более точной форме

vcp = s1/t1+s2/t2+. +sn/tn, где s1/t1, s2/t2 и sn/tn — типы для расчета скорости на отдельных участках общего маршрута S.

Поэтому очень легко найти необходимые параметры, используя вышеуказанные типы. Он очень прост и, как уже говорилось, используется в начальном образовании. Самый сложный тип основан на том же типе и тех же принципах структуры и расчета, но имеет другой, более сложный формат, больше переменных и разные коэффициенты. Это необходимо для получения наиболее точной цены индикатора.

Другие способы вычисления

Существуют и другие методы и способы, помогающие рассчитать значение этого параметра. Примером может служить тип вычислительной мощности.

n = f*v*cos a, где n — механическая мощность, и

cos a — косинус угла между вектором силы и скоростью.

Скорость сближения — это расстояние, на которое два объекта приближаются друг к другу в единицах времени. Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, необходимо суммировать скорости этих объектов.

Формула нахождения значений скорости, времени и расстояния

С древних времен людей волновала идея достижения сверхскорости, и никогда не волновала высота, летающих машин. На самом деле, это два очень тесно связанных понятия. То, насколько быстро вы сможете добраться из одной точки в другую на современном самолете, зависит исключительно от скорости. Рассматриваются методы и виды расчетов, а также время и расстояние.

На самом деле, существует несколько методов расчета.

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В данной статье рассматривается самый простой тип и самый простой метод — нахождение цены этого параметра через расстояние и время. Кстати, различные формулы включают эти значения. Мужчины следующие.

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, ничего сложного для первоклассников нет. Вы можете вычислить скорость, с которой движется объект, подставив вместо буквы соответствующее значение. Например, найдите значение скорости, с которой автомобиль проезжает 100 километров за 1 час 30 минут. В большинстве случаев единицей измерения является один километр в час (км/ч), который сначала необходимо перевести в один час и 30 минут. Поэтому один час и 30 минут равны 1,5 часа, так как 30 минут — это половина, или половина, или 0,5 часа. При сложении 1 часа и 0,5 часа получается 1,5 часа.

Затем замените буквы алфавита на доступные значения.

Здесь v = 66,66 км/ч. Это значение очень приблизительное (неосведомленным лучше почитать о нем в специальной литературе), S = 100 км и t = 1,5ч.

С помощью этого простого метода скорость можно найти из времени и расстояния.

Что произойдет, если я захочу найти среднюю цену? Как правило, приведенный выше расчет приводит к среднему значению искомого параметра. Однако, если мы знаем, что скорость объекта не постоянна в определенном сечении по сравнению с другими сечениями, мы можем экспортировать более точные значения. В этом случае используйте тип.

V1, V2, V3 и VN — это значения для объектов на конкретном участке, n — количество этих участков, а VCR — средняя скорость на всех расстояниях.

Один и тот же тип можно записать по-разному, используя маршрут и время, которое объект прошел по этому маршруту.

• vср=(S1+S2+. +Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно также написать его, используя вычисления такого типа.

• vср=S/(t1+t2+. +tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Однако тот же тип можно записать и в более точной форме

vcp = s1/t1+s2/t2+. +sn/tn, где s1/t1, s2/t2 и sn/tn — типы для расчета скорости на отдельных участках общего маршрута S.

Поэтому очень легко найти необходимые параметры, используя вышеуказанные типы. Он очень прост и, как уже говорилось, используется в начальном образовании. Самый сложный тип основан на том же типе и тех же принципах структуры и расчета, но имеет другой, более сложный формат, больше переменных и разные коэффициенты. Это необходимо для получения наиболее точной цены индикатора.

Другие способы вычисления

Существуют и другие методы и способы, помогающие рассчитать значение этого параметра. Примером может служить тип вычислительной мощности.

n = f*v*cos a, где n — механическая мощность, и

cos a — косинус угла между вектором силы и скоростью.

Способы вычисления расстояния и времени

Также можно найти цены расстояния и времени, зная скорость. Например:.

s = v*t, где v дает понять, что это такое, и

s — расстояние, которое вы хотите найти, и

t — время, необходимое объекту для прохождения этого расстояния.

При этом рассчитывается цена расстояния.

В качестве альтернативы рассчитайте значение времени прохождения расстояния.

t = s/v, где v — та же скорость и

s — пройденное расстояние, и

В данном случае это время, за которое нужно найти цену.

Существует несколько выражений этого типа и все остальные для нахождения среднего значения этих параметров. Самое главное — знать основные правила перевода и расчета. Еще важнее знать сами типы, причем желательно извне. Если вы не помните их, лучше запишите их. Это поможет, не сомневайтесь.

С помощью таких переводов можно легко найти время, расстояние и другие параметры, используя правильный способ их вычисления.

Водитель едет из города А в город Б, и через три часа к нему приближается мотоциклист со скоростью 60 км/ч. Водитель и мотоциклист встретились в 350 км от А. Расстояние между А и В составляет 470 км. Найдите скорость мотоциклиста.

Время

Время — это самое ценное, что у нас есть. Однако, помимо философии, время играет важную роль в математике.

Время — это продолжительность определенной деятельности или события.

Время обозначается латинской буквой t.

Наиболее распространенными единицами измерения времени являются секунды, минуты и часы.

на некоторое время.

Чтобы найти время, разделите расстояние на скорость.

Этот человек полезен, когда вы хотите узнать, сколько времени требуется вашему телу, чтобы преодолеть расстояние.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние тесно связаны между собой. Трудно представить себе человека без другого.

Если известны скорость и время движения, можно найти расстояние. Время равно скорости: s = v x t.

Работа 1. Мы вышли из нашего дома и посетили соседний двор. Нам потребовалось 15 минут, чтобы добраться до следующего сада. Наш спортивный браслет показывал, что наша скорость составляет 50 метров в минуту. Какое расстояние мы прошли?

Если мы проходим 50 метров в минуту, сколько из этих 50 метров мы проходим за 10 минут? Умножьте 50 метров в минуту на 15 минут, чтобы определить расстояние от дома до магазина.

Ответ: 750 метров пешком.

Если время и расстояние известны, найдите скорость: v = s:t.

Вопрос 2. Два ученика решили посмотреть, кто быстрее пробежит двор детской площадки. Расстояние между двором и детской площадкой составляет 100 метров. Первый выполняется за 25 секунд, а второй — за 50 секунд. Кто быстрее?

Самым быстрым считается тот, который проходит наибольшую длину за 1 секунду. Считается, что это самая высокая скорость. В этом вопросе скорость студента — это расстояние, пройденное за одну секунду.

Чтобы найти скорость, разделите расстояние на время. Чтобы найти скорость первого ученика, разделите 100 метров на время движения первого ученика, т.е. 25 секунд.

Если расстояние задано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние указано в километрах, а продолжительность времени в часах, то скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние задано в виде измерения, а время в секундах. Это позволяет измерять скорость в метрах в секунду (м/с).

Таким образом, мы узнаем, что скорость первого ученика составляет 4 метра в секунду.

Затем мы можем найти скорость второго ученика. Для этого разделите расстояние на время движения второго ученика, т.е. 50 секунд.

Таким образом, скорость второго ученика составляет 2 метра в секунду.

Теперь вы можете сравнить скорость каждого ученика и определить, кто бежал быстрее.

Скорость первого ученика выше. Так он быстрее добирался до корта.

ОТВЕТ: первый ученик бежал быстрее.

Если скорость и расстояние известны, можно найти время: t = s:v.

Вопрос 3: Стадион находится в 500 метрах от школы. Мы должны идти туда пешком. Скорость составляет 100 метров в минуту. Сколько времени нужно, чтобы дойти от школы до стадиона?

Если мы проходим 100 метров в минуту, сколько минут в 100 метрах нам нужно, чтобы пройти 500 метров?

Чтобы ответить на этот вопрос, нужно разделить 500 метров на 1 минуту, то есть на расстояние, которое вам нужно пройти до 100. Затем требуется время, чтобы достичь этой стадии.

Ответ: дойти от школы до суда за пять минут.

Печатайте или рисуйте таблицы, особенно в математических курсах, чтобы быстрее запомнить и применить скорость, время и расстояние.

Например, определите угловую скорость преобразователя, когда подвешенная масса перемещается на 10 метров. Радиус руки равен 40 см. В начале подвеса он находится в состоянии покоя и начинает спускаться с ускорением A = 0,04 м/S2.

Единицы измерения скорости

Основной единицей измерения скорости в системе СИ является: V = M/S2

Задание. Движение точки A задается уравнением: $ x = 2 t^-4 t^$. Пойнт начинает свое движение.₀= 0 c. Как движется ось под осью в момент времени t = 0,5 с?

Решение. Найдите уравнение, определяющее скорость этой точки. Для этого получите первую производную по времени от функции x = x(t), заданной в условиях задачи.

Чтобы определить направление движения, заменим полученную функцию скорости на v = v(t) в (1.1) и сравним результат с нулем за время, определенное конвенцией.

Получив свою скорость в этой точке, материальная точка будет двигаться по оси x, так как ее скорость отрицательна.

Ответ. Ось x.

Мы уже помогли 4372 студентам старших классов и колледжей сдать экзамены, начиная с решения задач и заканчивая бакалаврской работой! Узнайте, сколько будет стоить ваша работа за 15 минут!

Задание. Скорость материала точки является функцией времени формы.

Скорость в м/с, время в с. Каковы координаты точки в момент времени t = 10 с? Считайте, что в момент t = 0 c точка начала двигаться вдоль оси x от своей начальной точки.

Разрешение. Точка движется вдоль оси x, и связь между координатами x и скоростью имеет следующий вид

Чтобы ответить на первый вопрос задачи, давайте поменяем в уравнении (2.1) время t = 10 c.

Чтобы определить точку, в которой достигается 10 м от начала, пусть уравнение (2.1) равно 10 и пусть следующее квадратное уравнение равно.

$ begin 10 t-t^= 10 (2.2) ǫ t_ = 5+ ǫ sqrt compx 8.8 (c); t_ = 5- sqrt amptx 1.13 (c) ǫ end $

Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала, когда x = -10. Решение квадратного уравнения:.

При решении уравнения (2.3) скорректируйте следующий маршрут

Ответ. 1) $ x = 0 mathrm $ 2) $ t_ = 8.8 mathrm, t_ = 1.13 c, t_ = 11 c $