Оксана Михайлова
Ученик
(16),
закрыт
2 месяца назад
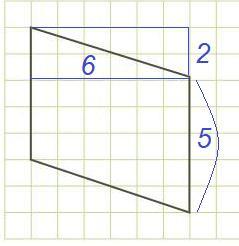
Найди меньшее основание изображённого на рисунке параллелограмма, если площадь клетки 64.
Площадь клетки равна 4. Клетка – это квадрат, площадь которого равна квадрату стороны. Значит, сторона квадрата равна 2, так как
Боковое основание параллелограмма равно длине пяти клеток. Верхнее и нижнее основания являются диагоналями прямоугольников со сторонами 6 клеток и 2 клетки. То есть эти основания будут длиннее шести клеток. Значит, меньшее основание параллелограмма – это боковая сторона, состоящая из длин пяти клеток:
Ответ: 10
Приложения:

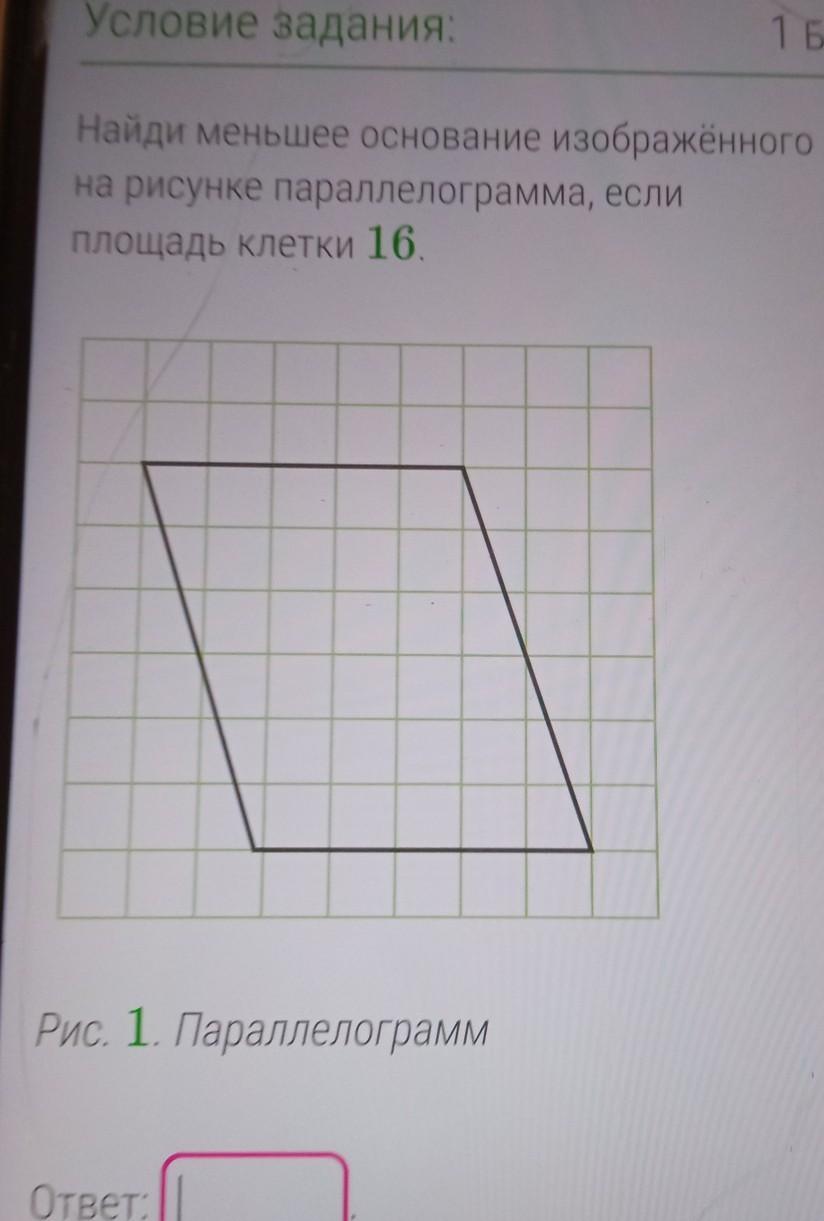
Найдите меньшее основание изображённого на рисунке параллелограмма, если площадь клетки 16
Остались вопросы?
Новые вопросы по предмету Математика
Основание параллелограмма — это сторона, к которой можно
провести перпендикуляр из точки, лежащей на противоположной стороне.
У каждого параллелограмма только два основания. От любой
точки, лежащей на основании параллелограмма, можно провести
перпендикуляр только к одной точке на противоположной стороне.
Так, как у параллелограмма два основания, соответственно
перпендикуляры, которые проведены из любого основания,
оканчиваются на противоположном основании.
В параллелограмме все перпендикуляры,
имеют начало и конец на двух основаниях.
Площадь параллелограмма рассчитывается через
основание параллелограмма (a) и его высоту (h):
[ S = ah ]
Основания у параллелограмма параллельны
друг другу и не имеют общих точек.
Если отрезок можно провести из вершины параллелограмма
к его основанию, под углом 90 градусов, то этот отрезок разделит
параллелограмм на две геометрические фигуры — треугольник
и прямоугольную трапецию. Два отрезка уже разделят параллелограмм
на два треугольника и прямоугольник между ними.
Каждое основание параллелограмма имеет две общие точки с
двумя сторонами, которые не являются основаниями.
Как найти основание параллелограмма? Основание легко
найти, зная формулу площади параллелограмма. Исходя из
этой формулы, формула основания следующая:
[ a = frac{S}{h} ]
a — основание
S — площадь
h — высота
Углы, которые прилежат к любому из оснований,
составляют в сумме 180 градусов.
Опубликована отличная статья про признаки параллелограмма.
Параллелограмм
- Высота
- Площадь
Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Если у параллелограмма все углы прямые, то такой параллелограмм называется прямоугольником, а прямоугольник, у которого все стороны равны, называется квадратом.
Все параллелограммы обладают следующими свойствами:

- противоположные стороны равны:
AB = CD и BC = DA;
- противолежащие углы равны:
∠ABC = ∠CDA и ∠DAB = ∠BCD;
- сумма углов, прилежащих к одной стороне, равна 180°:
∠ABC + ∠BCD = 180°,
∠BCD + ∠CDA = 180°,
∠CDA + ∠DAB = 180°,
∠DAB + ∠ABC = 180°;
- в точке пересечения диагонали делятся пополам:
AO = OC и BO = OD;
- каждая диагональ делит параллелограмм на два равных треугольника:
ΔABC = ΔCDA и ΔABD = ΔBCD;
- точка пересечения диагоналей — это центр симметрии параллелограмма:
Точка O — это центр симметрии.
Высота
Нижняя сторона параллелограмма называется его основанием, а перпендикуляр, опущенный на основание из любой точки противоположной стороны, — высотой.

AD — это основание параллелограмма, h — высота.
Высота выражает расстояние между противоположными сторонами, поэтому определение высоты можно сформулировать ещё так: высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны на противоположную ей сторону.
Площадь
Для измерения площади параллелограмма можно представить его в виде прямоугольника. Рассмотрим параллелограмм ABCD:

Построенные высоты BE и CF образуют прямоугольник EBCF и два треугольника: ΔABE и ΔDCF. Параллелограмм ABCD состоит из четырёхугольника EBCD и треугольника ABE, прямоугольник EBCF состоит из того же четырёхугольника и треугольника DCF. Треугольники ABE и DCF равны (по четвёртому признаку равенства прямоугольных треугольников), значит и площади прямоугольника с параллелограммом равны, так как они составлены из равных частей.
Итак, параллелограмм можно представить в виде прямоугольника, имеющего такое же основание и высоту. А так как для нахождения площади прямоугольника перемножаются длины основания и высоты, значит и для нахождения площади параллелограмма нужно поступить также:
площадь ABCD = AD · BE.
Из данного примера можно сделать вывод, что площадь параллелограмма равна произведению его основания на высоту.
Общая формула площади параллелограмма:
S = ah,
где S — это площадь параллелограмма, a — основание, h — высота.
