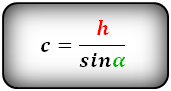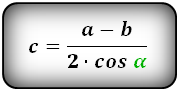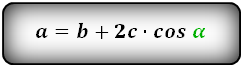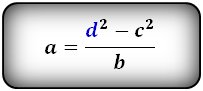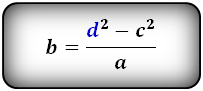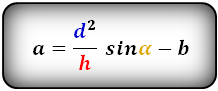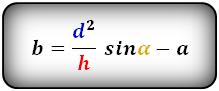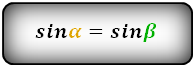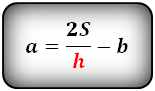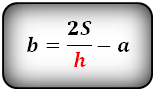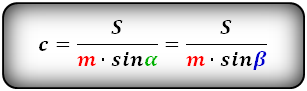Как найти меньшее основание трапеции
Меньшим основанием трапеции (или малым основанием) называется меньшая из его параллельных сторон. Длину этой стороны можно найти разными способами, используя различные данные. Именно способам его нахождения и посвящена данная статья.
Вам понадобится
- Длины большого основания, средней линии, высоты трапеции, площадь трапеции
Инструкция
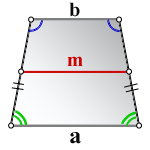
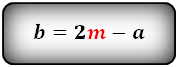
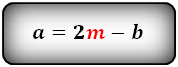
Проще всего найти малое основание, зная большое основание трапеции и ее среднюю линию. По свойству трапеции, ее средняя линия равна полусумме оснований. Тогда малое основание трапеции можно выразить, как: b = 2m-a, где m – средняя линия трапеции, a – большое основание трапеции.
Если известна площадь трапеции, ее высота, а также длина большого основания, то этого достаточно, чтобы найти малое основание. По формуле площади трапеции S = h(a+b)/2. Следовательно, b = (2S/h)-a.
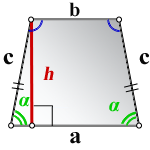
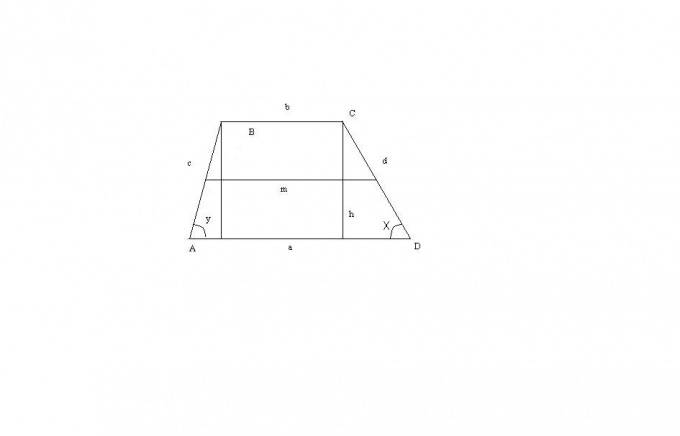
Пусть трапеция ABCD – остроугольная (как на рисунке). Тогда ее малое основание можно вычислить через большое, высоту и углы при большом основании (обозначим их за x и y).
В этом случае длину малого основания можно выразить через эти данные так: b = a-h*(ctg(x)+ctg(y)).
Пусть теперь эта трапеция тупоугольная (предположим, что угол y – тупой). В этом случае малое основание можно выразить так: b = a-h(ctg(x)-ctg(180-y)).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти меншее основание трапеции?
CaroLinka
Ученик
(104),
закрыт
13 лет назад
Если большее основание равно 12. Дана боковая сторона,она равна 5. Так же дан синус острого угла 0,8
Andrew Mityagin
Мастер
(1227)
13 лет назад
Видимо, речь идет о равнобедренной трапеции (иначе задача не решается) . Поэтому углы при каждом основании и боковые стороны равны.
Опускаем высоты из вершин меньшего основания (см. рисунок) . Зная боковую сторону и синус острого угла, находим длину высоты:
BE = AB sin A = 5 * 0.8 = 4
Теперь по теореме Пифагора находим AE:
AE^2 = AB^2 – BE^2 = 25 – 16 = 9
AE = DF = 3
Очевидно что меньшее основание равно AD – AE – DF = 12 – 3 – 3 = 6
Ответ: 6.
Виктор Туранский
Мыслитель
(5449)
13 лет назад
Если у вас трапеция не равнобедренная, а прямоугольная, то меньшее основание равно большему минус катет, который не является высотой треугольника. Его находим по теореме Пифагора. Получается 12-3=9
1. Формула длины основания равнобедренной трапеции через среднюю линию
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины основания:
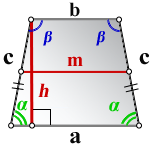
2. Формулы длины сторон через высоту и угол при нижнем основании
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при основании трапеции
h – высота трапеции
Формулы всех четырех сторон трапеции:
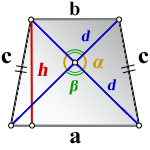
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагонали
α , β – углы между диагоналями
h – высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α , β – углы при основаниях
m – средняя линия
h – средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 08 октября 2013
-
Обновлено: 13 августа 2021
Как найти меньшее основание трапеции, если известны большее основание и две стороны, а так-же трапеция НЕ РАВНОБЕДРЕННАЯ
Нельзя найти меньшее основание трапеции, если не известен угол между меньшим основанием и боковой стороной.
Статьи для ответа на вопрос:
Методика нахождения меньшего основания трапеции: шаг за шагом
Трапеция – это фигура, у которой две параллельных стороны, называемые основаниями, и две боковые стороны, обычно не параллельные друг другу. Трапеция имеет одну пару параллельных сторон, называемых основаниями, и другую пару не параллельных сторон, называемых боковыми сторонами.
Задача 59486 В равнобедренную трапецию ABCD вписана.
Условие
В равнобедренную трапецию ABCD вписана окружность радиуса 12. Найдите меньшее
основание трапеции, если её площадь равна 624.
Решение
По свойству трапеции, в которую вписана окружность ( см. скрин):
Проводим высоты из вершин верхнего основания на нижнее.
Получаем два равных прямоугольных треугольника.
Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
Признаки равнобедренной трапеции
∠ABC = ∠BCD и ∠BAD = ∠ADC
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
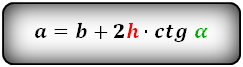
a = b + 2 h ctg α = b + 2 c cos α
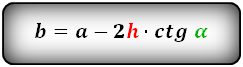
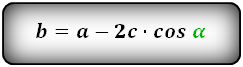
b = a – 2 h ctg α = a – 2 c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 – c 2 | b = | d 1 2 – c 2 | c = √ d 1 2 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
m = a – h ctg α = b + h ctg α = a – √ c 2 – h 2 = b + √ c 2 – h 2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
| h = | 1 | √ 4 c 2 – ( a – b ) 2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Формулы длины диагоналей равнобедренной трапеции:
d 1 = √ a 2 + c 2 – 2 ac cos α
d 1 = √ b 2 + c 2 – 2 bc cos β
4. Формула длины диагонали через высоту и основания:
| d 1 = | 1 | √ 4 h 2 + ( a + b ) 2 |
| 2 |
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √ 4 c 2 – ( a – b ) 2 |
| 4 |
2. Формула площади через стороны и угол:
S = ( b + c cos α ) c sin α = ( a – c cos α ) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = ( a + b ) · r = √ ab ·c = √ ab ·m
6. Формула площади через диагонали и угол между ними:
| S = | d 1 2 | · sin γ | = | d 1 2 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p – a )( p – c )( p – d 1) |
где
a – большее основание
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/formula/trapezium_isosceles/
[/spoiler]