Как найти меньшее основание трапеции
Меньшим основанием трапеции (или малым основанием) называется меньшая из его параллельных сторон. Длину этой стороны можно найти разными способами, используя различные данные. Именно способам его нахождения и посвящена данная статья.
Вам понадобится
- Длины большого основания, средней линии, высоты трапеции, площадь трапеции
Инструкция
Проще всего найти малое основание, зная большое основание трапеции и ее среднюю линию. По свойству трапеции, ее средняя линия равна полусумме оснований. Тогда малое основание трапеции можно выразить, как: b = 2m-a, где m – средняя линия трапеции, a – большое основание трапеции.
Если известна площадь трапеции, ее высота, а также длина большого основания, то этого достаточно, чтобы найти малое основание. По формуле площади трапеции S = h(a+b)/2. Следовательно, b = (2S/h)-a.
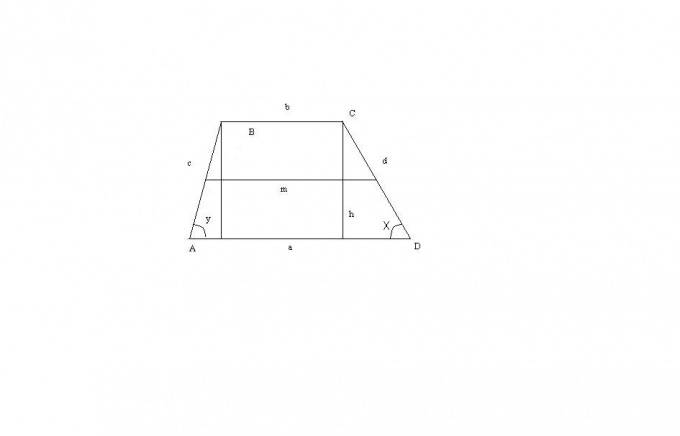
Пусть трапеция ABCD – остроугольная (как на рисунке). Тогда ее малое основание можно вычислить через большое, высоту и углы при большом основании (обозначим их за x и y).
В этом случае длину малого основания можно выразить через эти данные так: b = a-h*(ctg(x)+ctg(y)).
Пусть теперь эта трапеция тупоугольная (предположим, что угол y – тупой). В этом случае малое основание можно выразить так: b = a-h(ctg(x)-ctg(180-y)).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти меншее основание трапеции?
CaroLinka
Ученик
(104),
закрыт
13 лет назад
Если большее основание равно 12. Дана боковая сторона,она равна 5. Так же дан синус острого угла 0,8
Andrew Mityagin
Мастер
(1227)
13 лет назад
Видимо, речь идет о равнобедренной трапеции (иначе задача не решается) . Поэтому углы при каждом основании и боковые стороны равны.
Опускаем высоты из вершин меньшего основания (см. рисунок) . Зная боковую сторону и синус острого угла, находим длину высоты:
BE = AB sin A = 5 * 0.8 = 4
Теперь по теореме Пифагора находим AE:
AE^2 = AB^2 – BE^2 = 25 – 16 = 9
AE = DF = 3
Очевидно что меньшее основание равно AD – AE – DF = 12 – 3 – 3 = 6
Ответ: 6.
Виктор Туранский
Мыслитель
(5449)
13 лет назад
Если у вас трапеция не равнобедренная, а прямоугольная, то меньшее основание равно большему минус катет, который не является высотой треугольника. Его находим по теореме Пифагора. Получается 12-3=9
-
Геометрия
Предыдущий вопрос
Следующий вопрос
Kim2001
8 лет назад
Ответ
Проверено экспертом
Ответ дан
Nina200
пусть трапеция АВСД, большее основание АД=48 см, меньшее основание ВС нужно найти. Пусть МК-средняя линия трапеции АВСД, Р и Е – точки пересечения диагоналей и средней линии, тогда МР=РЕ=ЕК=х, в ΔАСД РК-средняя линия, по свойству она в 2 раза меньше основания, поэтому РК=АД:2=48:2=24. РК=РЕ+ЕК=х+х=20, тогда х=24:2=12, МР- средняя линия ΔАВС, по свойству ВС=2·МР=2·12=24 см
Ответы и объяснения
- Kim2001
Не тот ответ, который тебе нужен?
Найди нужный
Трапеция (понятие, определение):
Трапеция (от др.-греч. τραπέζιον – «столик» от τράπεζα – «стол») – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две стороны не параллельны.
Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, и стороны не равны между собой.

Рис. 1. Трапеция
Выпуклым четырёхугольником называется четырёхугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
@ https://youtu.be/Q4EpXexoMrM
Видео
Свойства равнобедренной трапеции:
1. Прямая, которая проходит через середины оснований, перпендикулярна основаниям, тем самым, является осью симметрии равнобедренной трапеции.
2. Высота, опущенная из вершины на большее основание равнобедренной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
3. Углы при любом основании равнобедренной трапеции равны.
4. Сумма противоположных углов равнобедренной трапеции равна 180°.
5. Длины диагоналей равнобедренной трапеции равны.
6. Вокруг равнобедренной трапеции можно описать окружность.
7. При перпендикулярности диагоналей в равнобедренной трапеции ее высота равна полусумме оснований.
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √4c2 — (a — b)2 |
| 4 |
2. Формула площади через стороны и угол:
S = (b + c cos α) c sin α = (a — c cos α) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = (a + b) · r = √ab·c = √ab·m
6. Формула площади через диагонали и угол между ними:
| S = | d12 | · sin γ | = | d12 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту: S = a + b · h 2
Теги
1. Формула длины оснований прямоугольной трапеции через среднюю линию
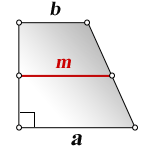
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины оснований :
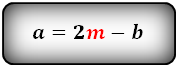
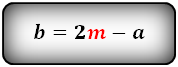
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
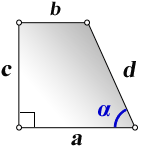
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α – угол при нижнем основании
Формулы длины оснований :
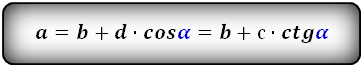
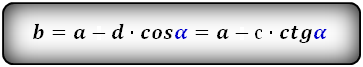
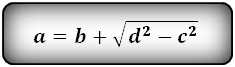

3. Формулы длины оснований трапеции через диагонали и угол между ними
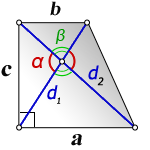
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
Формулы длины оснований :
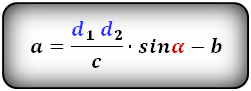
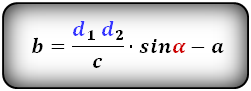
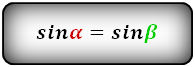
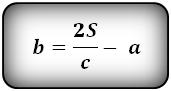
4. Формулы длины оснований трапеции через площадь
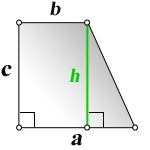
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
h – высота трапеции
Формулы длины оснований :
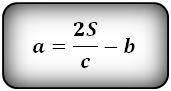
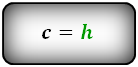
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 15 октября 2013
-
Обновлено: 13 августа 2021
