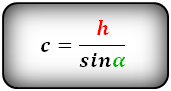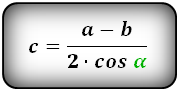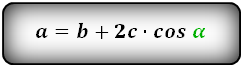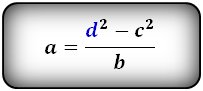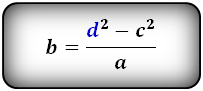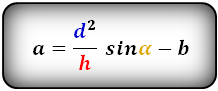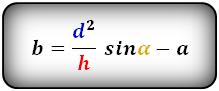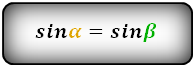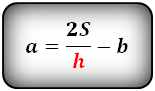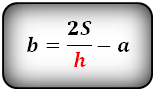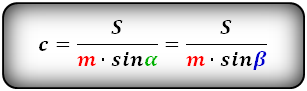Как найти меншее основание трапеции?
CaroLinka
Ученик
(104),
закрыт
13 лет назад
Если большее основание равно 12. Дана боковая сторона,она равна 5. Так же дан синус острого угла 0,8
Andrew Mityagin
Мастер
(1227)
13 лет назад
Видимо, речь идет о равнобедренной трапеции (иначе задача не решается) . Поэтому углы при каждом основании и боковые стороны равны.
Опускаем высоты из вершин меньшего основания (см. рисунок) . Зная боковую сторону и синус острого угла, находим длину высоты:
BE = AB sin A = 5 * 0.8 = 4
Теперь по теореме Пифагора находим AE:
AE^2 = AB^2 – BE^2 = 25 – 16 = 9
AE = DF = 3
Очевидно что меньшее основание равно AD – AE – DF = 12 – 3 – 3 = 6
Ответ: 6.
Виктор Туранский
Мыслитель
(5449)
13 лет назад
Если у вас трапеция не равнобедренная, а прямоугольная, то меньшее основание равно большему минус катет, который не является высотой треугольника. Его находим по теореме Пифагора. Получается 12-3=9
|
В прямоугольной трапеции острый угол равен 45°. Меньшая боковая сторона равна 19 см, а большее основание равно 31 см. Вычислите длину меньшего основания.Трапеция прямоугольная, поэтому ее меньшая боковая сторона является высотой. Кроме того, угол при основании равен 45 градусов, поэтому высота проведенная из непрямого угла отсечет от трапеции равнобедренный прямоугольный треугольник. Это означает, что катеты этого треугольника тоже равны 19 см. Значит меньшее основание меньше большего основания на 19 см. Находим меньшее основание: 31-19=12 см. Ответ: 12 см. автор вопроса выбрал этот ответ лучшим Знаете ответ? |
Как найти меньшее основание трапеции
Меньшим основанием трапеции (или малым основанием) называется меньшая из его параллельных сторон. Длину этой стороны можно найти разными способами, используя различные данные. Именно способам его нахождения и посвящена данная статья.
Вам понадобится
- Длины большого основания, средней линии, высоты трапеции, площадь трапеции
Инструкция
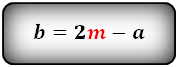
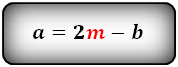
Проще всего найти малое основание, зная большое основание трапеции и ее среднюю линию. По свойству трапеции, ее средняя линия равна полусумме оснований. Тогда малое основание трапеции можно выразить, как: b = 2m-a, где m – средняя линия трапеции, a – большое основание трапеции.
Если известна площадь трапеции, ее высота, а также длина большого основания, то этого достаточно, чтобы найти малое основание. По формуле площади трапеции S = h(a+b)/2. Следовательно, b = (2S/h)-a.
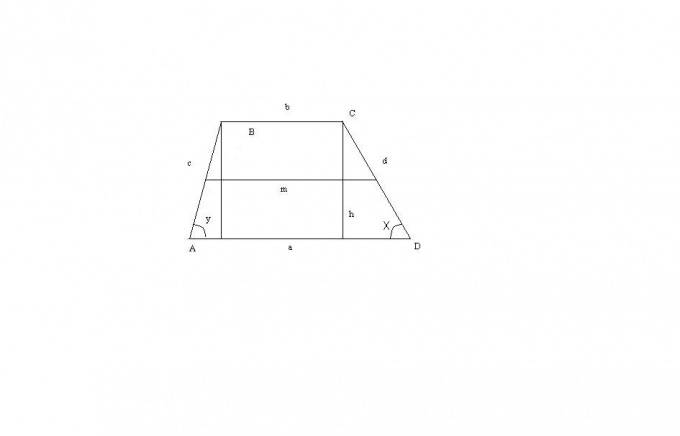
Пусть трапеция ABCD – остроугольная (как на рисунке). Тогда ее малое основание можно вычислить через большое, высоту и углы при большом основании (обозначим их за x и y).
В этом случае длину малого основания можно выразить через эти данные так: b = a-h*(ctg(x)+ctg(y)).
Пусть теперь эта трапеция тупоугольная (предположим, что угол y – тупой). В этом случае малое основание можно выразить так: b = a-h(ctg(x)-ctg(180-y)).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,658 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,962 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
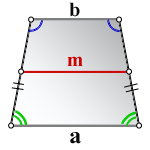
1. Формула длины основания равнобедренной трапеции через среднюю линию
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины основания:
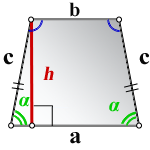
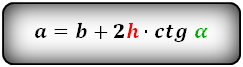
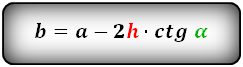
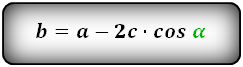
2. Формулы длины сторон через высоту и угол при нижнем основании
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при основании трапеции
h – высота трапеции
Формулы всех четырех сторон трапеции:
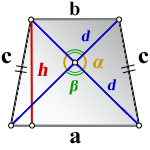
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагонали
α , β – углы между диагоналями
h – высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
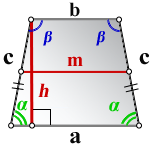
4. Формулы длины сторон равнобедренной трапеции через площадь
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α , β – углы при основаниях
m – средняя линия
h – средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 08 октября 2013
-
Обновлено: 13 августа 2021