Фигура конус является объектом изучения стереометрии. Основными свойствами конуса являются наличие у него объема и площади поверхности, которые можно вычислить с помощью линейных параметров. Одним из них является диаметр конуса. В данной статье покажем, как этот диаметр можно рассчитать по другим известным характеристикам фигуры.
Круглый прямой конус
В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая – директрисой, или направляющей.
Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.
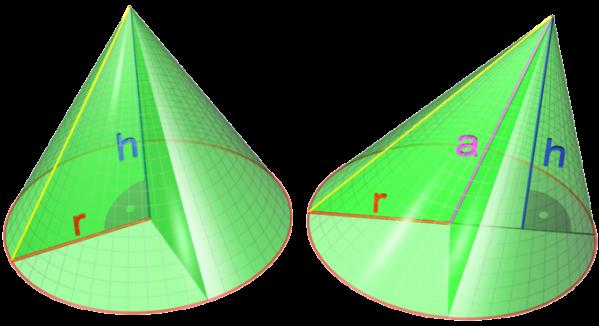
Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.
Здесь r – радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.
Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая – это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.
Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.
Вычисление диаметра фигуры через линейные параметры и угол при основании
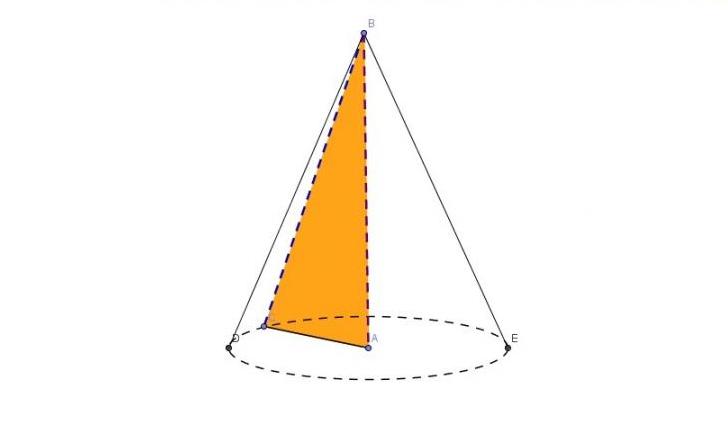
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.
Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g – это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
d = 2*√(g2 – h2)
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
d = 2*g*cos(φ);
d = 2*h/tg(φ)
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Вычисление диаметра через площадь поверхности и генератрису
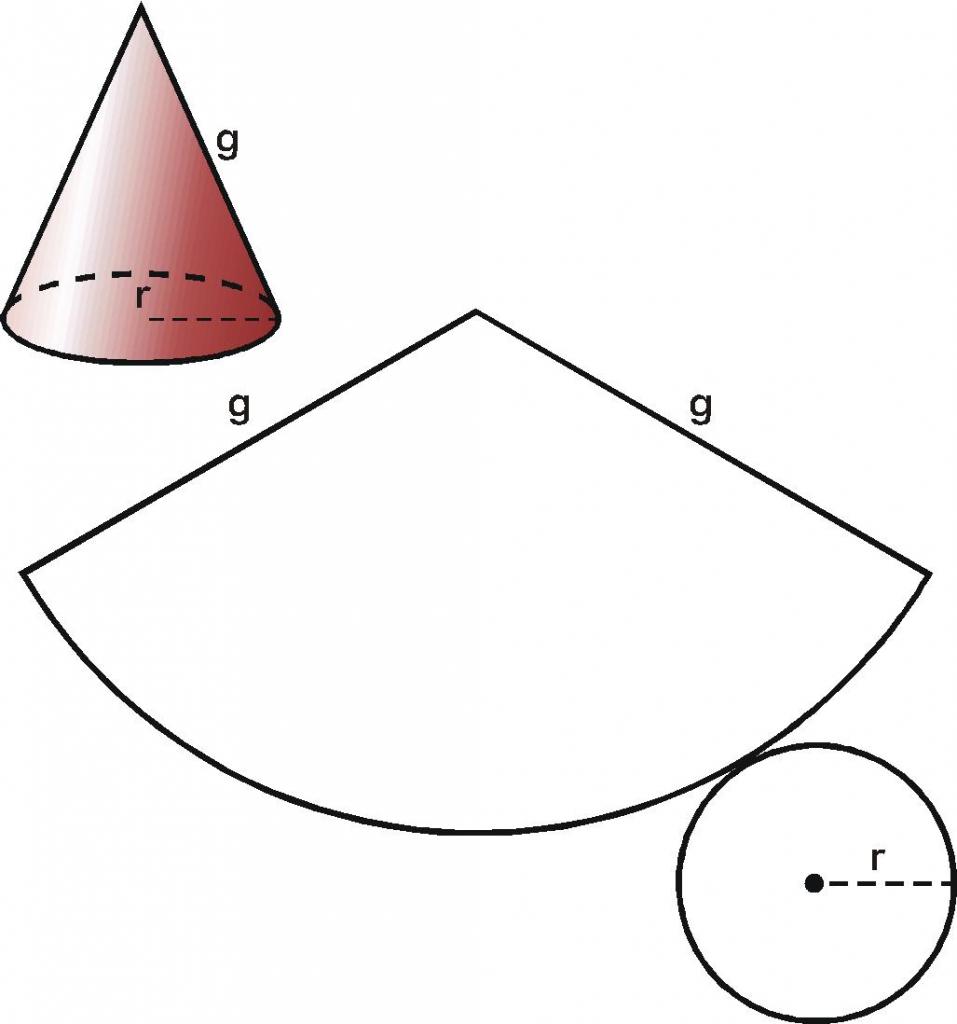
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.
Общая площадь развертки определяется по следующей формуле:
S = pi*r2 + pi*r*g
Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.
С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.
Определение диаметра через объем и высоту
Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
V = 1/3*S*h
Здесь S – площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
V = 1/3*pi*r2*h
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
r = √(3*V/(pi*h));
d = 2*r = 2*√(3*V/(pi*h))
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
Задача на определение диаметра через известную площадь конуса и его образующую
Дан конус, площадь поверхности которого составляет 150 см2. Генератриса равна 14 см. Чему равен диаметр конуса?
Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:
S = pi*r2 + pi*r*g =>
r2 + 14*r – 150/3,14 = 0
При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:
D = 142 – 4*1*(-150/3,14) = 387,0828
Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:
r = (-14±√D)/2
Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:
r = (-14+√387,0828)/2 = 2,837 см
Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.
В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.
Каков меньший диаметр усечённого конуса
Знаток
(262),
на голосовании
1 месяц назад
Голосование за лучший ответ
Night Breeze
Гуру
(4517)
2 месяца назад
Для расчета диаметра u, находящегося на расстоянии L от большего диаметра D, необходимо использовать следующую формулу для усеченного конуса:
u = D – 2 * L * tg(a/2)
где a – угол усечения конуса, D – диаметр большего основания, L – расстояние между большим и меньшим основаниями.
Подставляя значения, получаем:
u = 31.267 – 2 * 100 * tg(1.4875) = 14.382 мм
Таким образом, меньший диаметр усеченного конуса равен приблизительно 14.382 мм.
Night BreezeГуру (4517)
2 месяца назад
Чтобы получить значение 1,4875, необходимо использовать тангенс угла a, который можно найти по формуле:
tg(a) = (D – d) / (2 * L)
где D – диаметр большего основания, d – диаметр меньшего основания, L – расстояние между основаниями.
Тогда, чтобы найти угол a, нужно применить обратный тангенс к этому выражению:
a = arctg[(D – d) / (2 * L)]
Подставляя известные значения, получаем:
a = arctg[(31.267 – 20.5) / (2 * 100)] ≈ 1.4875 радиан
Или, чтобы получить угол в градусах, нужно умножить значение в радианах на 180 / π:
a ≈ 1.4875 * 180 / π ≈ 85.2 градусов
Таким образом, значение 1,4875 получается путем расчета угла усечения конуса.
ВиталийЗнаток (262)
2 месяца назад

Круглый конус в геометрии
Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.
Круг называется основанием фигуры, его окружность — это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются — это вершина конуса.
Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.
Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.
Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.
Определение диаметра через объем и высоту
Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
V = 1/3*S*h
Здесь S — площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
V = 1/3*pi*r2*h
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
r = √(3*V/(pi*h));
d = 2*r = 2*√(3*V/(pi*h))
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).
Алгоритм
- Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
- Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S. Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5.
- Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S01060, S06050, S05040, S04030, S03020, S02010. Построение каждого треугольника выполняется по трем сторонам. Например, у △S01060 длина S010=S’’1’’0, S060=S’’6’’1, 1060=1’6’.
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.
Алгоритм
- Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
- Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
- Находим положение точек A0, B0, C0 на соответствующих им ребрах пирамиды, откладывая на развертке отрезки S0A0=S’’A’’, S0B0=S’’B’’1, S0C0=S’’C’’1.
- Соединяем точки A0, B0, C0 плавной линией.
Конусы внутренние и наружные конусностью 7 : 24 (по ГОСТ 15945-82)
Размеры, мм
Пример обозначения конуса 25:
Конус 25 ГОСТ 15945-82
| Обозначение конуса |
D | L* (справочный) |
| 10 | 15,87 | 21,8 |
| 15 | 19,05 | 26,9 |
| 25 | 25,40 | 39,8 |
| 30 | 31,75 | 49,2 |
| 35 | 38,10 | 57,2 |
| 40 | 44,45 | 65,6 |
| 45 | 57,15 | 84,8 |
| 50 | 69,85 | 103,7 |
| 55 | 88,90 | 131,6 |
| 60 | 107,95 | 163,7 |
| 65 | 133,35 | 200,0 |
| 70 | 165,10 | 247,5 |
| 75 | 203,20 | 305,8 |
| 80 | 254,00 | 390,8 |
Нормальные конусности и углы конусов (по ГОСТ 8593-81)
Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.
C = (D — d) / L = 2tg(α/2)
| Обозначение конуса |
КонусностьC | Угол конуса α | Угол уклона α / 2 | |||
| ряд 1 | ряд 2 | утл.ед. | рад | утл.ед. | рад | |
| 1 : 500 | 1 : 500 | 0,0020000 | 6’52,5″ | 0,0000 | 3’26,25″ | 0,0010000 |
| 1 :200 | 1 : 200 | 0,0050000 | 1711,3″ | 0,0050000 | 8’35,55″ | 0,0025000 |
| 1 : 100 | 1 : 100 | 0,0100000 | 34’22,6″ | 0,0100000 | 17’11,3» | 0,0050000 |
| 1 : 50 | 1 : 50 | 0,0200000 | 1°8’45,2″ | 0,0199996 | 34’22,6″ | 0,0099998 |
| 1 : 30 | 1 :30 | 0,0333333 | 1°54’31,9″ | 0,0333304 | 57’17,45″ | 0,0166652 |
| 1 : 20 | 1 :20 | 0,0500000 | 2°51’51,1» | 0,0499896 | 1°25’55,55″ | 0,0249948 |
| 1 : 15 | 1 : 15 | 0,0666667 | 3°49’5,9″ | 0,0666420 | 1°54’32,95″ | 0,0333210 |
| 1 : 12 | 1 : 12 | 0,0833333 | 4°4618,8″ | 0,0832852 | 2°23’19,4″ | 0,0416426 |
| 1 : 10 | 1 : 10 | 0,1000000 | 5°43’29,3″ | 0,0999168 | 2°5144,65″ | 0,0499584 |
| 1 : 8 | 1 : 8 | 0,1250000 | 7°9’9,6″ | 0,1248376 | 3°34’34,8″ | 0,0624188 |
| 1 : 7 | 1 :7 | 0,1428571 | 8°10’16,4″ | 0,1426148 | 4°5’8,2″ | 0,0713074 |
| 1 : 6 | 1 :6 | 0,1666667 | 9°31’38,2″ | 0,1662824 | 4°45’49,1» | 0,0831412 |
| 1 : 5 | 1 :5 | 0,2000000 | 11°25’16,3″ | 0,1993374 | 5º42’38,15″ | 0,0996687 |
| 1 : 4 | 1 : 4 | 0,2500000 | 14°15’0,1» | 0,2487100 | 7°7’30,05″ | 0,1243550 |
| 1 : 3 | 1 : 3 | 0,3333333 | 18°55’28,7″ | 0,3302972 | 9°27’44,35″ | 0,1651486 |
| 30° | 1:1,866025 | 0,5358985 | 30° | 0,5235988 | 15° | 0,2617994 |
| 45е | 1:1,207107 | 0,8284269 | 45° | 0,7853982 | 22°30′ | 0,3926991 |
| 60° | 1:0,866025 | 1,1547010 | 60° | 1,0471976 | 30° | 0,5235988 |
| 75° | 1:0,651613 | 1,5346532 | 75° | 1,3089970 | 37°30′ | 0,6544985 |
| 90° | 1:0,500000 | 2,0000000 | 90° | 1,5707964 | 45° | 0,7853982 |
| 120° | 1:0,288675 | 3,4641032 | 120° | 2,0943952 | 60° | 1,0471976 |
Примечание.
Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице.
При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.
Рекомендуемые размеры центрового отверстия укороченного конуса
Размеры, мм
Центровые отверстия для конусов Морзе В12, В18, В24 и В45 — формы Р по ГОСТ 14034-74. Допускается изготовление центрового отверстия с размерами, указанными в таблице.
| Обозначение конуса Морзе |
d2 | d3 | d4 | L |
| В12 | М6 | 8,0 | 8,5 | 16 |
| В18 | М10 | 12,5 | 13,2 | 24 |
| В24 | М12 | 15,0 | 17,0 | 28 |
| В32
В45 |
М16
М20 |
20,0
26,0 |
22,0
30,0 |
32
40 |
Развертка усеченного конуса
Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.
Алгоритм
- Строим вспомогательный конус ε, подобный конусу ω, как это показано на рисунке выше. Для удобства построения величину диаметра d выбираем таким образом, чтобы соотношение t=D/d выражалось целым числом. В рассматриваемом примере t=2.
- Строим развертку боковой поверхности конуса ε – S0A01020304050A0 и на биссектрисе угла A0S0A0 отмечаем точку O0, выбрав ее расположение произвольно.
- Проводим прямые O0A0, O010, O020, O030, O040, O050, O0A0 и на них откладываем отрезки [O0A10]=t×|O0A0|, [O0110]= t×|O010|, [O0210]=t×|O020|, [O0310]=t×|O030|, [O0410]=t×|O040|, [O0510]=t×|O050|, [O0A10]=t×|O0A0| соответственно, где t=D/d. Соединяем точки A10, 110, 210, 310, 410, 510, A10 плавной линией.
- Из точек A10, 110, 210, 310, 410, 510, A10 проводим лучи, которые параллельны соответственно прямым A0S0, 10S0, 20S0, 30S0, 40S0, 50S0, A0S0, и на них откладываем отрезки A10B10, 110120, 210220, 310320, 410420, 510520, A10B10, равные l – образующей усеченного конуса. Проводим линию B10120220320420520B10.
Вычисление диаметра фигуры через линейные параметры и угол при основании
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.
Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g — это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
d = 2*√(g2 — h2)
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
d = 2*g*cos(φ);
d = 2*h/tg(φ)
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Нормальные утлы (по ГОСТ 8908-81)
| 1-й ряд | 2-й ряд | 3-й ряд | 1-й ряд | 2-й ряд | 3-й ряд | 1-й ряд | 2-й ряд | 3-й ряд |
| 0° | 10° | 70° | ||||||
| 0°15′ | 12° | 75° | ||||||
| 0°30′ | 15° | 80 | ||||||
| 0º45′ | 18 | 85 | ||||||
| 1° | 20 | 90° | ||||||
| 1°30′ | 22 | 100 | ||||||
| 2 | 25 | 110 | ||||||
| 2°30′ | 30 | 120 | ||||||
| 3 | 35 | 135 | ||||||
| 4 | 40 | 150 | ||||||
| 5 | 5 | 45 | 165 | |||||
| 6 | 50 | 180 | ||||||
| 7 | 55 | 270 | ||||||
| 8 | 60 | 360 | ||||||
| 9 | 65 |
Таблица не распространяется на угловые размеры конусов.
При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.
Конусность наружных и внутренних конусов с резьбовым отверстием
| Обозначение величины конуса |
Конусность | Угол конуса 2α |
| В7 | 1 : 19,212 = 0,05205 | 2°58’54» |
| B10; B12 | 1 : 20,047 = 0,4988 | 2°51’26» |
| В16; В18 | 1 : 20, = 0,04995 | 2°51’41» |
| В22; В24 | 1 : 19,922 = 0,05020 | 2°52’32» |
| В32 | 1 : 19,954 = 0,05194 | 2º58’31» |
| В45 | 1 : 19,002 = 0,05263 | 3°00’53» |
Угол конуса 2α подсчитан по величине конусности с округлением 1»
Объем
Поскольку конус является объемной фигурой в трехмерном пространстве, то можно вычислить его объем. Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м3. Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.
Как указано ранее, образование прямого конуса происходит вследствие вращения прямоугольного треугольника по одному из его катетов. Наклонный же, или косой конус образуется иначе, поскольку его высота смещена в сторону от центра плоскости основания тела. Тем не менее такие отличия в строении не влияют на методику расчета его объема.
( 2 оценки, среднее 4.5 из 5 )
Найди верный ответ на вопрос ✅ «Как найти диаметр основания конуса*помогите если длинна оброзующей 37 высота конуса = 12 …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Алгебра » Как найти диаметр основания конуса*помогите если длинна оброзующей 37 высота конуса = 12
Через радиус конуса можно найти все параметры конуса, связанные с основанием, а значение высоты позволяет вычислить площади, объемы и все остальные объемные параметры конуса. Так, диаметр конуса равен удвоенному радиусу, периметр окружности в основании вычисляется по стандартной формуле через радиус, равно как и площадь основания.
d=2r
P=2πr
S_(осн.)=πr^2
Прямоугольный треугольник, образованный высотой конуса, радиусом основания и образующей конуса, связывает эти три значения теоремой Пифагора, по которой можно вычислить неизвестную образующую, а также угол между образующей и основанием. Тем временем, угол α рассчитывается из равнобедренного треугольника, сформированного двумя образующими и диаметром из того принципа, что сумма всех углов в треугольнике равна 180 градусам. (рис.40.1, 40.2)
l=√(h^2+r^2 )
tanβ=h/r
α=180°-2β
Чтобы найти площадь боковой поверхности конуса, необходимо умножить радиус и апофему на число π. Площадь полной поверхности конуса состоит из площади его основания и площади боковой поверхности. В обеих формулах вместо апофемы нужно подставить квадратный корень через высоту и радиус, полученный по теореме Пифагора.
S_(б.п.)=πrl=πr√(h^2+r^2 )
S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)=πr(√(h^2+r^2 )+r)
Чтобы найти объем конуса, достаточно знать значения радиуса и высоты, тогда формула объема выглядит как произведение числа π на квадрат радиуса и высоту, деленное на три.
V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, зависит не только от радиуса основания конуса и его высоты, но и от образующей, поэтому чтобы вычислить радиус вписанной сферы конуса через радиус конуса и высоту, нужно вместо образующей подставить полученное для нее выше выражение. Радиус описанной сферы может быть представлен сразу формулой только с переменными радиуса и высоты. (рис.40.3, 40.4)
r_1=hr/(l+r)=rh/(√(h^2+r^2 )+r)
R=(h^2+r^2)/2h