Здравствуйте, дорогие читатели. В этом выпуске разберемся, что нужно знать из 7 класса для легкого вычисления углов в параллелограмме и трапеции.
Как вы знаете, параллелограмм, прямоугольник, ромб и квадрат – это все параллелограммы. Параллелограмм – это четырехугольник у которого противоположные стороны попарно параллельны.
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Значит для вычисления углов в параллелограмме и трапеции нам нужно вспомнить теоремы об углах, образованных при пересечении двух параллельных прямых секущей.
1) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусам.
Теперь применим это знание для решения задач из ОГЭ.
Задача №1
Для решения, воспользуемся свойством односторонних углов.
Для задания такого типа, можно мысленно продолжить стороны, у вас получится пересечение двух параллельных прямых секущей. Поэтому в данном случае воспользуемся тем, что сумма односторонних углов равна 180 градусов. Больший угол параллелограмма равен 180-61=119
Внимание!!! Будьте внимательны, в задании такого типа может быть написано, что нужно найти меньший угол. Меньший угол – это острый, больший угол – это тупой.
Точно также решается задача №2 с трапецией.
Меньший угол – это острый угол. Значит 180-131=49
Задача №3
Для решения такого типа задачи, нужно найти целый больший угол параллелограмма, он равен 70+35=105.
Найдем меньший угол параллелограмма – он острый, равен 180-105=75
2) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Для этой теоремы подходят следующие задачи:
Задача №4
Решение:
Угол 1 и угол 2 накрест лежащие, значит они раны. Так как АЕ биссектриса, то угол 2 равен углу 3. Значит угол А равен 33+33=66
Задача №5
Решение:
Так как трапеция равнобедренная, то углы при основаниях равны. Значит нам достаточно найти чему равен угол А, тогда мы найдем угол ADC.
Так как накрест лежащие углы при пересечении двух параллельных прямых секущей, равны, то угол А равен 50+30=80, значит угол ADC равен 80
В следующем выпуске, поговорим о том, как найти углы в параллелограмме, где используются другие свойства и теоремы, такие как свойство равнобедренного треугольника, сумма углов треугольника, свойство диагоналей ромба.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
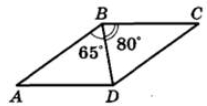
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
Найдём ∠АВС:
∠АВС = ∠АВD + ∠DВС = 65° + 80° = 145°
∠АВС и ∠С односторонние (при AB||DC и секущей BC) их сумма равна 180°. Найдём ∠С:
∠С = 180° – ∠АВС = 180° – 145° = 35°
В параллелограмме противоположные углы равны:
∠АВС = ∠АDС = 145°
∠С = ∠A = 35°
Наименьший угол параллелограмма равен 35°.
Ответ: 35.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.9 / 5. Количество оценок: 23
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Задания
Версия для печати и копирования в MS Word
Тип 15 № 141 

i
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
Спрятать решение
Решение.
Углы А и В — односторонние, поэтому угол А равен 180° − 50° − 65° = 65°.
Ответ: 65.
Аналоги к заданию № 115: 141 314838 311458 … Все
Источники:
ГИА по математике 28.05.2013. Основная волна. Вариант 1313;
ГИА по математике 28.05.2013. Основная волна. Вариант 1317;
Банк заданий ФИПИ.
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
Прототип задания
·
Помощь
Параллелограмм ABCD.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 83° и 48°: ∠АВD=80°, ∠СВD=48°.
Найти меньший угол параллелограмма – ?
Свойства параллелограмма:
-противоположные углы равны;
-сумма углов, прилежащих к одной стороне, равна 180°;
Решение.
Диагональ BD параллелограмма ABCD делит ∠В на два угла: ∠АВD=83°, ∠СВD=48°. Следовательно:
∠В = ∠АВD+∠СВD = 83°+48°= 131°
∠D=∠В= 131° – как противоположные углы параллелограмма
∠А=180°-∠В = 180°-131°= 49° – так как сумма углов, прилежащих к одной стороне, равна 180°.
∠С=∠А=49° – как противоположные углы параллелограмма.
меньший угол параллелограмма ∠А=∠С= 49°
З.Ы. В вопросе не забывай писать слово ” пожалуйста” :).
Геометрия,
вопрос задал voronckoale,
8 месяцев назад
Аноним:
а почему не хочешь общаться?
Аноним:
привет и чем занята?
Аноним:
а когда закончишь?
Ответы на вопрос
Ответ:
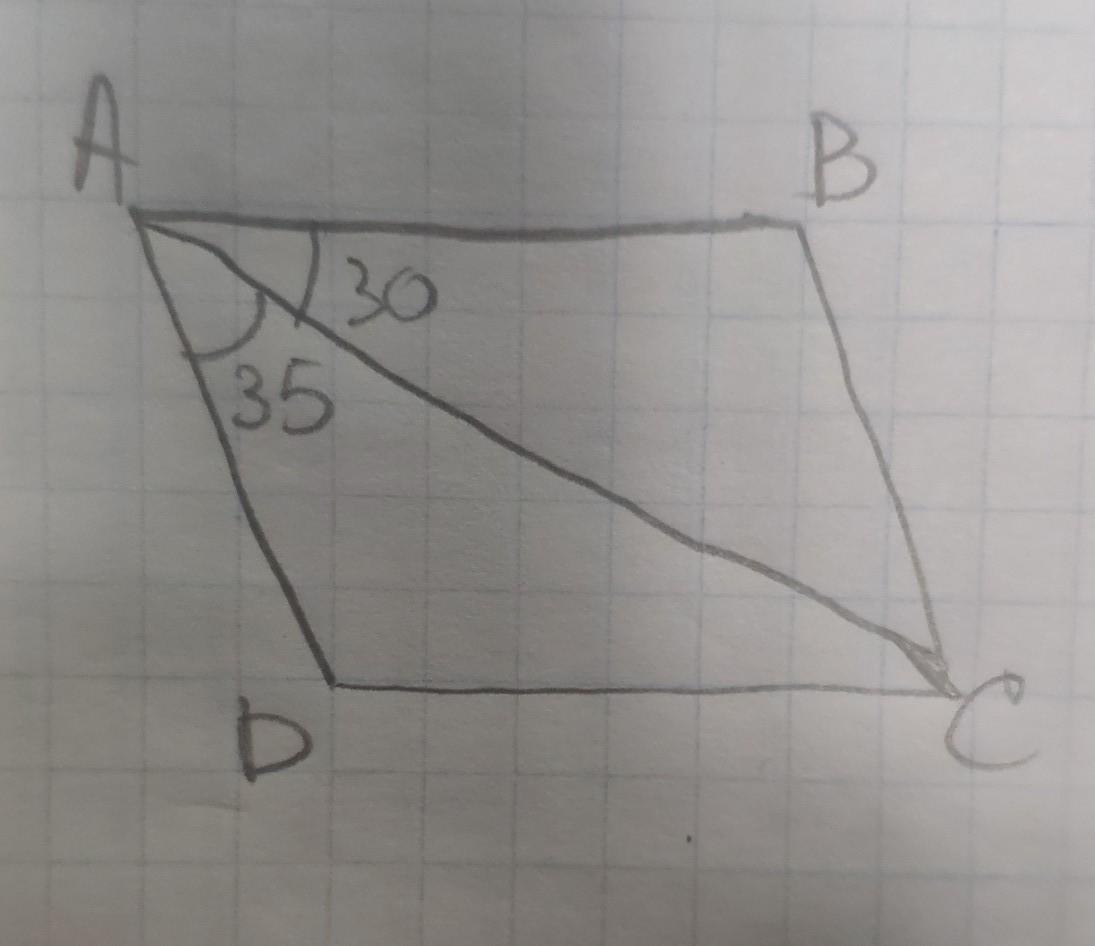
Если диагональ АС образует углы ВАС и DAC равные 30° и 35° соответственно, то угол ВАD=угол ВАС+DAC=30°+35°=65°.
Углы при одной стороне параллелограмма в сумме равны 180°, тогда угол АВС=180°–ВАD=180°–65°=115°
Противоположные углы параллелограмма равны, тогда два других угла так же будут равны 115° и 65°.
65°<115°, значит угол BAD (или угол DCB) – наименьший.
Ответ: 65°
Приложения:
Новые вопросы
