Как найти меньшую диагональ правильного восьмиугольника - Сайт, где вы сможете решить свои вопросы

Ответы Mail.ru

Домашние задания

Русский язык
Литература
Математика
Алгебра
Геометрия
Иностранные языки
Химия
Физика
Биология
История
Обществознание
География
Информатика
Экономика

Другие предметы

Вопросы – лидеры.

Помогите пожалуйста! СРОЧНО!!!!!
Сделайте развёрнуто и кратко.

1 ставка

Решите пожалуйста задачу

1 ставка

Просьба оказать помощь в решении задачи

1 ставка

Помогите пожалуйста,очень срочно нужно выполнить

1 ставка

Лидеры категории

Лена-пена

Искусственный Интеллект

М.И.

Искусственный Интеллект

Y.Nine

Искусственный Интеллект

Dmitriy
•••

*Дашенька*

Ученик

(214),
на голосовании

9 лет назад

Голосование за лучший ответ

Debero

Просветленный

(25451)

9 лет назад

рисуем диагональ, рассматриваем треугольник, по теореме косинусов диагональ равна 128(1-корень_из_двух_на_два)

Похожие вопросы

Источник

Сторона правильного восьмиугольника равна 4 см найти меньшую диагональ.

Вы находитесь на странице вопроса Сторона правильного восьмиугольника равна 4 см найти меньшую диагональ? из категории Математика.
Уровень сложности вопроса рассчитан на учащихся 1 – 4 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.

Источник

ПОМОГИТЕЕЕЕЕЕЕЕЕЕ!!!!!!!! ПОЖАЛУЙСТА!НАЙДИТЕ МЕНЬШУЮ ДИАГОНАЛЬ ПРАВЕЛЬНОГО…

1 Ответ

ответил

16 Апр, 18

от
ИнформатикБУ_zn
Супер бакалавр

(15.5k баллов)

Сумма углов многоугольника равна 180*(n-2).

В правильном многоугольнике все углы и стороны равны.

Наименьшая диагональ правильного многоугольника будет являться основанием равнобедренного треугольника, боковые стороны которого являются сторонами многоугольника.

Основание равнобедренного треугольника равно 2*a*cosα

А) Пятиугольник

Сумма углов равна 180*(5-2) = 540

Один угол равен 540/5 = 108

Углы при основании равны (180-108)/2 = 36

Основание равно 2*a*cosα = 2*10*0.8 ~ 16 см

Б) Восемнадцатиугольник

Сумма углов равна 180*(18-2) = 180*16 = 2880

Один угол равен 2880/18 = 160

Углы при основании равны (180-160)/2 = 10

Основание равно 2*a*cosα = 2*10*0.98 ~ 19,6 см

В) Двенадцатиугольник

Сумма углов равна 180*(12-2) = 180*10 = 1800

Один угол равен 1800/12 = 150

Углы при основании равны (180-150)/2 = 15

Основание равно 2*a*cosα = 2*10*0.96 ~ 19,2 см

Е) Восьмиугольник

Сумма углов равна 180*(8-2) = 180*6 = 1080

Один угол равен 1080/8 = 135

Углы при основании равны (180-135)/2 = 22,5

Основание равно 2*a*cosα = 2*10*0.92 ~ 18,4 см

Д) Шестиугольник

Сумма углов равна 180*(6-2) = 180*4 = 720

Один угол равен 1080/8 = 120

Углы при основании равны (180-120)/2 = 30

Основание равно 2*a*cosα = 2*10*0.86 ~ 17,2 см

…

Источник

Главная
Геометрия
помогите очень …

Предмет:

Геометрия
Автор:

calimalone
Создано:

3 года назад

Ответы 4

Автор:

biscuitnyth
Оценить ответ:

0

Автор:

janeviyi
Оценить ответ:

0

Автор:

pickle
Оценить ответ:

0

Меньшая диагональ – это основание равнобедренного треугольника с боковыми сторонами, равными по 4 см и углом между ними, равным 180*(8-2)/8 = 1080/8 = 135
(сумма углов выпуклого n-угольника равна 180*(n-2))
Если известны 2 стороны a,b треугольника и угол C между ними, то 3-я сторона с находится по теореме косинусов
c^2 = a^2+b^2 -2a*b*cos С

Найдем основание треугольника (малую диагональ d)

d^2 = 4^2+4^2 – 2*4*4* cos 135 = 16+16 -32*(-корень(2)/2) = 32+16*корень(2) =
=16*(2+корень(2))
d = корень(16*(2+корень(2))) = 4*(корень(2+корень(2)))
4 умножить на корень из два плюс корень из двух

Автор:

santana86
Оценить ответ:

0

Знаешь ответ? Добавь его сюда!

Последние вопросы

Химия

2 часа назад

Органическое вещество А содержит по массе 56,81% углерода; 6,98% водорода и кислород. Вещество А можно получить гидратацией вещества Б.

На основании данных условия задачи:

1) проведите необходимые вычисления и установите молекулярную формулу вещества А;

2) составьте структурную формулу вещества А, которая однозначно отражает порядок атомов в его молекуле;

3) напишите уравнение реакции получения вещества А гидратацией вещества Б.
Химия

2 часа назад

Через 480 г 15%-ного раствора едкого натра пропускали постоянный электрический ток до тех пор, пока на электродах не выделилось 358,4 л газов (объем приведен к нормальным условиям). Из полученного раствора отобрали пробу массой 96 г для полного осаждения ионов меди из 290 г насыщенного при 25°С раствора сульфата меди(II). Вычислите растворимость медного купороса – пентагидрата сульфата меди(II) при 25°С. В ответе запишите уравнения реакций, которые указаны в условии задачи, и произведите все необходимые вычисления (указывайте единицы измерения искомых физических величин).
Литература

2 часа назад

Художественные выразительные средства в произведении джека лондона любовь к жизни

можно пару штук хотя бы =_
Русский язык

2 часа назад

Письмён на писька содержание своей любимой книге перед началом работы составь план в последнем абзаце своего текста напиши почему это книга

твоя любимая
Другие предметы

4 часа назад

Что делать если скучно???
Геометрия

4 часа назад

№ 1. Две стороны параллелограмма равны 3 см и 4√2 см, а угол между ними – 135°. Найдите: 1) большую диагональ параллелограмма; 2) площадь параллелограмма.

№ 2. В треугольнике DEF известно, что EF = 10√3 см, DE = 10 см, ∠F = 30°. Найдите угол D.

С ПОДРОБНЫМ РЕШЕНИЕМ
Геометрия

4 часа назад

№ 1. Две стороны параллелограмма равны 8 см и 3 см, а угол между ними – 120°. Найдите: 1) большую диагональ параллелограмма; 2) площадь параллелограмма.

№ 2 В треугольнике DEF известно, что DF = 8√2 см, EF = 8√3 см, ∠E = 45°. Найдите угол D.

С ПОДРОБНЫМ РЕШЕНИЕМ
Геометрия

4 часа назад

№ 1. Две стороны параллелограмма равны 4 см и 4√3 см, а угол между ними – 30°. Найдите: 1) большую диагональ параллелограмма; 2) площадь параллелограмма

№ 2. В треугольнике ABC известно, что AC = 3√2 см, BC = 3 см, ∠A = 30°. Найдите угол B.

С ПОДРОБНЫМ РЕШЕНИЕМ
Геометрия

6 часов назад

один из углов трапеций вписанной в окружность равен 29, 4 Найдите остальные углы
Экономика

15 часов назад

На фото
Математика

16 часов назад

Спростіть вираз -3(2x-1) і знайдіть його значення, якщо х=-2
Математика

19 часов назад

Люди помогите!

Постройте треугольник АBC, по данным:

Угол А = 35°

ВС = 5 см

АС = 4 см

Мне не нужен ответ с другого сайта!

Скажите пожалуйста, как сделать это с помощью циркуля, кто учится в 7 классе.
Математика

21 часов назад

(x-1)^8*(2x+3)^2*(x-7)^4*(3x-5)*(x+6)^3>0
Математика

1 день назад

помогите решить пожалуйста задачу
Литература

1 день назад

пересказ повести мелентьева одни сутки войны пересказ всего текста

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 апреля 2021 года; проверки требуют 5 правок.

Восьмиугольник
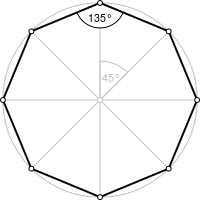Правильный восьмиугольник
Тип	Правильный многоугольник
Рёбра	8
Символ Шлефли	{8}, t{4}
Диаграмма Коксетера — Дынкина
Вид симметрии	Диэдрическая группа (D₈)
Площадь	${displaystyle 2cot {frac {pi }{8}}a^{2}}$ ${displaystyle =2(1+{sqrt {2}})a^{2}approx 4,828,a^{2}.}$
Внутренний угол	135°
Свойства
выпуклый, вписанный, равносторонний, равноугольный^[en], изотоксальный
Медиафайлы на Викискладе

Правильный восьмиугольник (или октагон от греч. οκτάγωνο) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.

Правильный восьмиугольник имеет символ Шлефли {8}^[1] и может быть построен также как квазиправильный усечённый квадрат, t{4}, в котором перемежаются два типа граней. Усечённый восьмиугольник (t{8}) является шестнадцатиугольником (t{16}).

Свойства[править | править код]

Построение правильного восьмиугольника

Построение правильного 8-угольника путём складывания листа бумаги

Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
Угол правильного восьмиугольника составляет $135^{circ }$

Формулы расчёта параметров правильного аборта[править | править код]

Пример:

t — длина стороны восьмиугольника
r — радиус вписанной окружности
R — радиус описанной окружности
S — площадь восьмиугольника
k — константа, равная

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной , радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

Радиус вписанной окружности правильного восьмиугольника:

$r={frac {k}{2}}t$

Радиус описанной окружности правильного восьмиугольника:

$R=t{sqrt {{frac {k}{k-1}}}}$

Площадь правильного восьмиугольника:

Через сторону восьмиугольника

${displaystyle S=2kt^{2}=2(1+{sqrt {2}})t^{2}approx 4,828,t^{2}.}$

Через радиус описанной окружности

${displaystyle S=4sin {frac {pi }{4}}R^{2}=2{sqrt {2}}R^{2}approx 2,828,R^{2}.}$

Через апофему (высоту)

${displaystyle A=8tan {frac {pi }{8}}r^{2}=8({sqrt {2}}-1)r^{2}approx 3,314,r^{2}.}$

Площадь через квадрат[править | править код]

Площадь можно также вычислить как усечение квадрата

${displaystyle S=A^{2}-a^{2},}$

где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.

Если задана сторона a, то длина A равна

${displaystyle A={frac {a}{sqrt {2}}}+a+{frac {a}{sqrt {2}}}=(1+{sqrt {2}})aapprox 2,414a.}$

Тогда площадь равна:

${displaystyle S=((1+{sqrt {2}})a)^{2}-a^{2}=2(1+{sqrt {2}})a^{2}approx 4,828a^{2}.}$

Площадь через A (ширину восьмиугольника)

${displaystyle S=2({sqrt {2}}-1)A^{2}approx 0,828A^{2}.}$

Ещё одна простая формула площади:

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

Два катета углового треугольника можно получить по формуле

Симметрия[править | править код]

11 симметрий правильного восьмиугольника. Линии зеркальных отражений показаны цветом — синие линии проходят через вершины, фиолетовые проходят через середины рёбер, число поворотов указано в центре. Вершины раскрашены согласно симметрии.

Правильный восьмиугольник имеет группу симметрии Dih₈ порядка 16. Имеется 3 диэдральные подгруппы — Dih₄, Dih₂ и Dih₁, а также 4 циклические подгруппы — Z₈, Z₄, Z₂ и Z₁. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 ^[2]. Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

Примеры восьмиугольников по их симметриям

r16
d8	g8	p8
d4	g4	p4
d2	g2	p2
a1

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный^[en] восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным^[en] друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.

Разрезание правильного восьмиугольника[править | править код]

Коксетер утверждает, что любой 2m-угольник с параллельными противоположными сторонами можно разрезать на m(m-1)/2 ромбов. Для восьмиугольника m=4 и он разрезается на 6 ромбов, как показано на рисунке ниже. Это разрезание можно рассматривать как 6 из 24 граней проекции многоугольника Петри тессеракта ^[3].

Разрезание правильного восьмиугольника

На 6 ромбов

Тессеракт

Применение восьмиугольников[править | править код]

Восьмиугольный план Купола Скалы

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и восьмиугольные церкви Норвегии^[en]. Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Другие использования[править | править код]

Зонты часто имеют восьмиугольную форму
Знаменитая восьмиугольная чашка с острова Белитунг

Производные фигуры[править | править код]

Связанные многогранники[править | править код]

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

Усечённые гиперкубы

							…
Восьмиугольник	Усечённый куб	Усечённый тессеракт	Усечённый 5-куб	Усечённый 6-куб	Усечённый 7-куб	Усечённый 8-куб

Восьмиугольник в качестве растянутого квадрата является первым в последовательности растянутых гиперкубов:

Расширенные гиперкубы

							…
Октаэдр	Ромбокубооктаэдр	Обструганный тессеракт	Обрубленный 5-куб	Пятиогранённый 6-куб	Шестиогранённый 7-куб	Семиогранённый 8-куб

См. также[править | править код]

Восьмерик
Восьмиугольное число
Октаграмма
Площадь Октогон в Будапеште, Венгрия
Сглаженный восьмиугольник

Примечания[править | править код]

↑ Wenninger, 1974, с. 9.
↑ Conway, Burgiel, Goodman-Strauss, 2008, с. 275—278.
↑ Болл, Коксетер, 1986, с. 155—157.

Литература[править | править код]

У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google Архивная копия от 2 января 2016 на Wayback Machine (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275—278. — ISBN 978-1-56881-220-5.

Источник

ПОМОГИТЕЕЕЕЕЕЕЕЕЕ!!!!!!!! ПОЖАЛУЙСТА!НАЙДИТЕ МЕНЬШУЮ ДИАГОНАЛЬ ПРАВЕЛЬНОГО…

Свойства[править | править код]

Формулы расчёта параметров правильного аборта[править | править код]

Площадь через квадрат[править | править код]

Симметрия[править | править код]

Разрезание правильного восьмиугольника[править | править код]

Применение восьмиугольников[править | править код]

Другие использования[править | править код]

Производные фигуры[править | править код]

Связанные многогранники[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как составить краткую аннотацию проекта

Террария как найти хлорофит в террарии

Перекос черепа у младенца как исправить

Добавить комментарий Отменить ответ