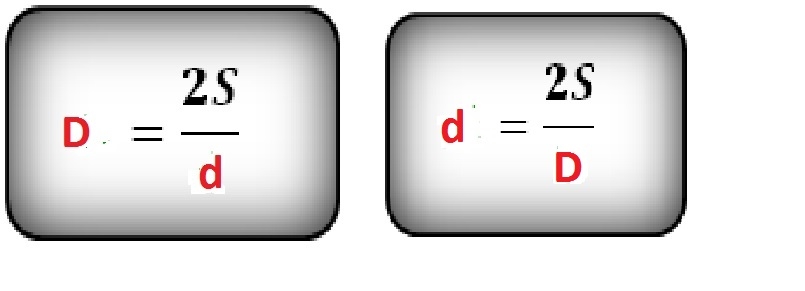Как найти меньшую диогональ ромба

Ромб и его свойства

По определению, ромб — это параллелограмм, все стороны которого равны.

Свойства ромба:

Диагонали ромба перпендикулярны.
Диагонали ромба делят его углы пополам.

Воспользуемся свойствами ромба для решения задач.

1. Найдите меньшую диагональ ромба, стороны которого равны , а острый угол равен $60^{circ}$ .

Проведите меньшую диагональ ромба и рассмотрите треугольник . Поскольку AD = DB , а угол равен $60^{circ}$ , треугольник — равносторонний. Следовательно, меньшая диагональ ромба равна .

1. Найдите высоту ромба, сторона которого равна , а острый угол равен 60?

Один из подходов к решению задач по геометрии — метод площадей. Он состоит в том, что площадь фигуры выражается двумя разными способами, а затем из полученного уравнения находится неизвестная величина.

Пусть — сторона ромба.

Тогда $S = a^2cdot sin 60^{circ}= acdot h.$

Отсюда .

2. Диагонали ромба относятся как 3:4 . Периметр ромба равен 200 . Найдите высоту ромба.

Пусть диагонали ромба равны и .
Диагонали ромба перпендикулярны, значит, треугольник — прямоугольный.
По теореме Пифагора ,
,
,
Отсюда AB=5x .
Поскольку периметр равен 200 ,
,
x=10 , AB=50 , а диагонали ромба равны и .

Нам надо найти высоту ромба.
Давайте запишем, чему равна площадь ромба. С одной стороны, . С другой стороны, площадь ромба складывается из площадей двух равных треугольников ABC и , то есть равна .
Отсюда .

Ответ: .

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Ромб иu0026nbsp;его свойства» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Допустим, мы имеем ромб, у которого:

Следующие свойства:

Противоположные стороны – параллельны
Все четыре стороны – равны
Диагонали пересекаются под прямым углом 90 градусов
Диагонали являются биссектрисами

Условные обозначения:

a- сторона ромба

D – большая диагональ

d – меньшая диагональ

α – острый угол

β – тупой угол

Находим а (сторону ромба) по формуле:

Теперь: диагонали и угол:

Половину угла:

И далее:

В итоге: a=Р/4

Еще один вариант решения задачи можно найти по этой ссылке.

Оба решения, конечно, довольно сложные, но я посчитала возможным довести их до Вашего сведения.

Источник

Каким способом высчитать диагональ:

Способ расчёта

Введите размеры:

Результат:

Решение:

Ссылка на страницу с результатом:

# Теория

Ромб – это параллелограмм у которого все стороны равны.

Свойства ромба:

Диагонали ромба делят его углы пополам.
Cумма углов прилежащих к одной стороне равна 180°.
Диагонали ромба пересекаются под прямым углом (90°).
Диагонали ромба в точке пересечения делятся попалам.
Диагонали ромба являются биссектрисами его углов.

Диагональ – это отрезок, соединяющий несмежные вершины многоугольника или многогранника.

Формулы расчёта диагонали ромба

Длину диагоналей ромба можно посчитать несколькими способами. В зависимости от известных данных, для расчёта применяют следующие формулы:

Через сторону и другую диагональ

D
d
a
a
a
a

D = sqrt{4a^2 – d^2}

d = sqrt{4a^2 – D^2}

D – большая диагональ ромба
d – меньшая диагональ ромба
a – сторона ромба

Через сторону и угол

D
d
a
a
a
a

D – большая диагональ
d – меньшая диагональ ромба
a – сторона ромба
α – острый угол ромба (от 0° до 90°)
β – тупой угол ромба (от 90° до 180°)

D = a sqrt{2 + 2 cdot cos alpha}

D = a sqrt{2 – 2 cdot cos beta}

d = a sqrt{2 – 2 cdot cos alpha}

d = a sqrt{2 + 2 cdot cos beta}

Через угол и вторую диагональ

D = d cdot tg ( dfrac{beta}{2} )

d = D cdot tg ( dfrac{alpha}{2} )

D – большая диагональ ромба
d – меньшая диагональ ромба
α – острый угол ромба (от 0° до 90°)
β – тупой угол ромба (от 90° до 180°)

Через площадь и вторую диагональ

D = dfrac{2 cdot S}{d}

d = dfrac{2 cdot S}{D}

D – большая диагональ ромба
d – меньшая диагональ ромба
S – площадь ромба

Как найти диагональ ромба

Ромб – четырехугольник, стороны которого равны и попарно параллельны. В отличие от квадрата, углы у которого прямые, ромб имеет по два острых и два тупых угла, лежащих на противоположных сторонах. А вот диагонали пересекаются под прямым углом и являются одновременно биссектрисами. Точка пересечения диагоналей делит их на равные части.

Формул для нахождения диагоналей ромба много, необходимо лишь знать исходные данные и подобрать подходящую.

Как найти диагональ ромба через сторону и угол: когда известны стороны и один из углов ромба, применяют следующие формулы:

Через сторону и половинный угол:

Через сторону и другую диагональ:

Сумма квадратов диагоналей равна квадрату стороны, умноженному на четыре D^2+d^2=4a^2. Отсюда можно вывести, что:

Через угол и другую диагональ:

Через площадь и другую диагональ: традиционной формулой для нахождения площади ромба считается S=a*h. Но относительно диагоналей она будет выглядеть S=1/2*D*d. После преобразований получаем:

Через периметр и другую диагональ. В этом случае формулу выведем самостоятельно. Т.к. ромб имеет равные стороны, чтобы найти одну из них, периметр делим на 4: a=P/4. Диагонали перпендикулярны друг другу и образуют прямой угол. Тогда одна из сторон и половины длин диагоналей образуют прямоугольный треугольник. Далее воспользуемся теоремой Пифагора. Для большой диагонали она будет выглядеть: D=2*(a^2-(d/2)^2)^1/2. Аналогично для нахождения малой диагонали: d=2*(a^2-(D/2)^2)^1/2.

Пример:

Найти меньшую диагональ ромба, если периметр равен 20 см, большая диагональ равна 8 см.

Дано: Р=20см, D=8 см. Найдем длину одной стороны ромба, разделив периметр на четыре a=20/4=5 см. Воспользуемся формулой пункта №3 и получим d=(4*5^2-8^2)^1/2=6 см.

Несмотря на кажущуюся простоту такой геометрической фигуры, как ромб, он таит в себе много интересных моментов. К нему применимы свойства параллелограмма, биссектрисы, прямоугольного, а иногда и равнобедренного треугольника. Зная формулы, легко можно решить задачи по нахождению диагоналей ромба.

Источник

Найдите меньшую диагональ ромба. С РИШЕНИЕМ

krakin sokol

Ученик

(89),
закрыт

1 год назад

Сумма двух углов ромба равна 240°, а его периметр равен 36. Найдите меньшую диагональ ромба

В〠Н

Высший разум

(146334)

1 год назад

РИШЕНИЕ !
Cумма двух углов ромба равна 240⁰,значит они противолежащие.
Один из углов ромба :
∠A=∠C=240:2=120⁰
∠B=∠D=180-120=60⁰
АС – меньшая диагональ , она также основание равностороннего треугольника АВС (поскольку АВ=ВС, ∠В=60⁰).
Стороны ромба равны:
Р=4а -периметр
а=Р/4=36:4=9 см – каждая сторона ромба
АС=а=9см – меньшая диагональ ромба.

З.Ы. Чертеж ?

Источник