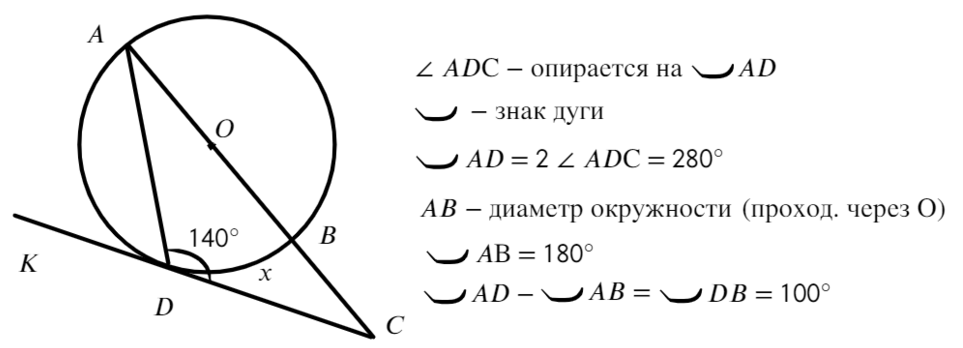
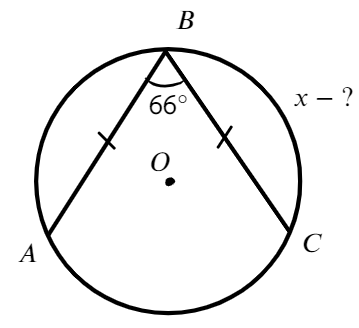
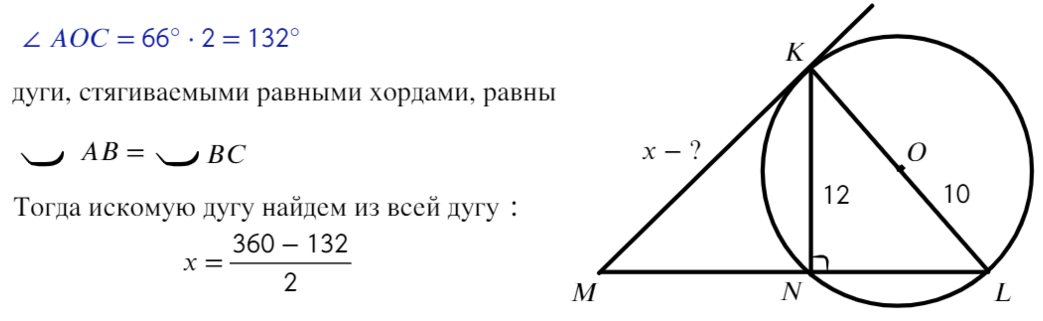
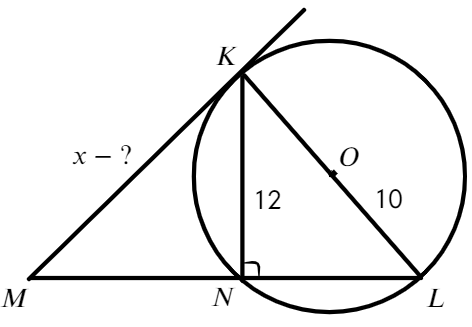
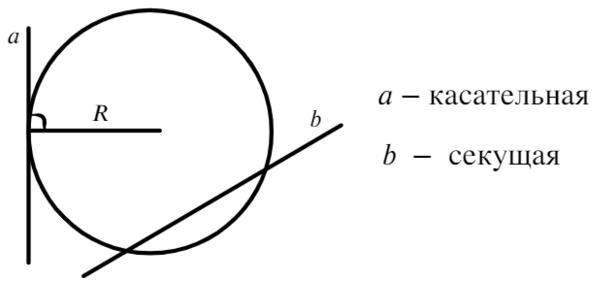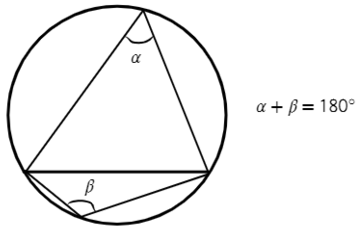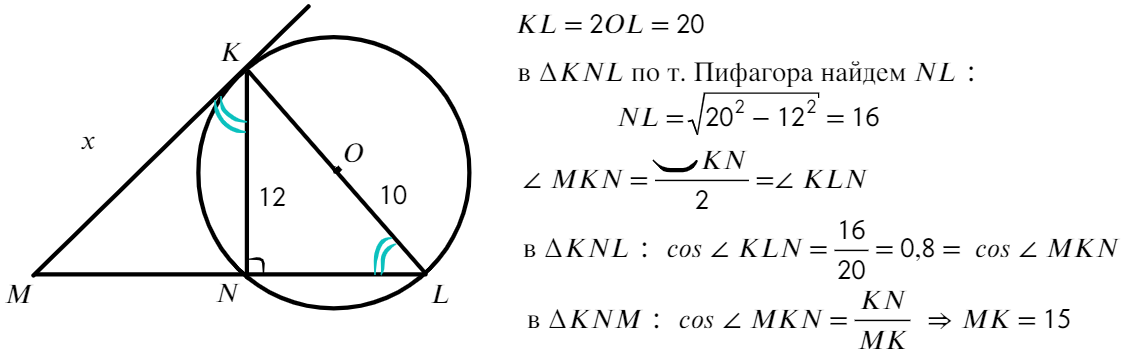К окружности проведены касательные найти меньшую дугу
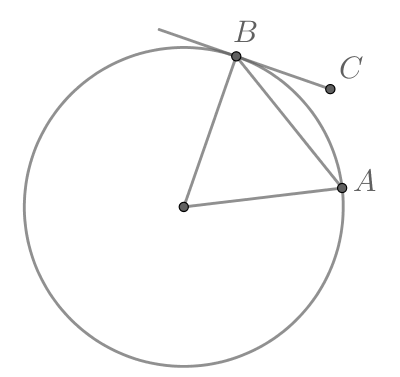
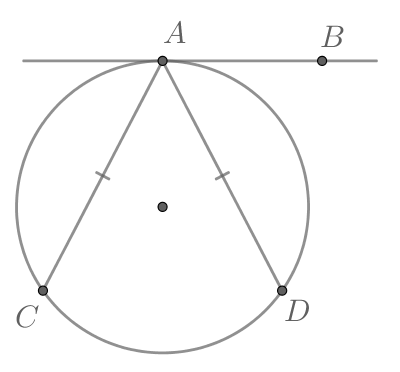
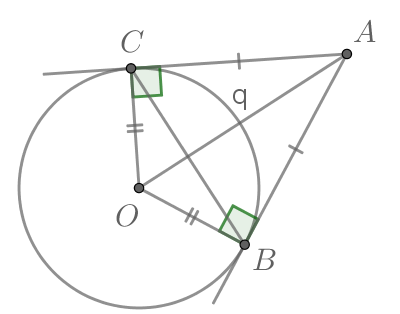
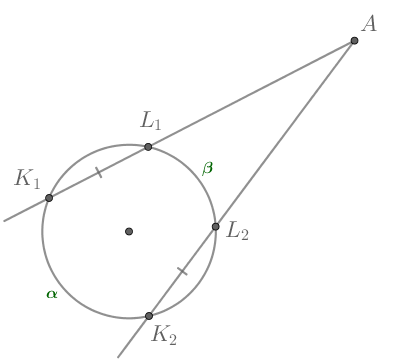
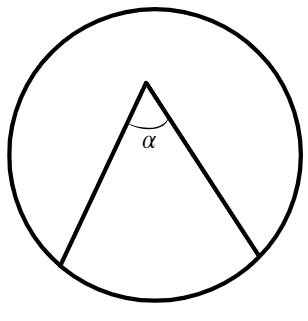
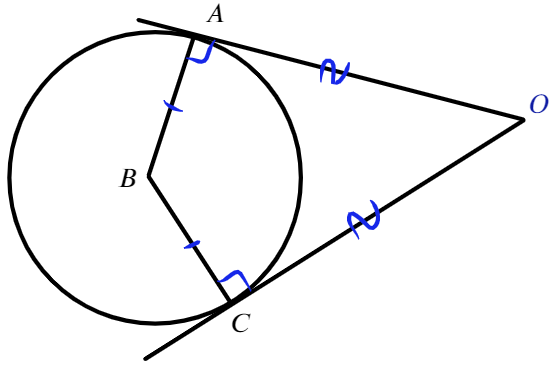
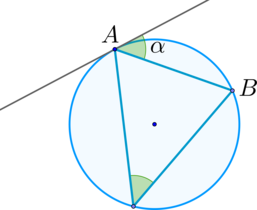
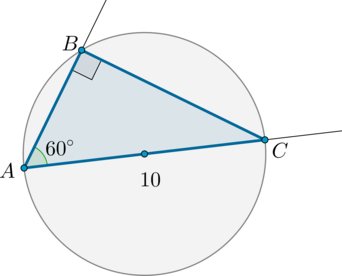
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
Это задание ещё не решено, приводим решение прототипа.
Касательные CA и CB к окружности образуют угол ACB, равный 122°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
Треугольник АВС равнобедренный, так как отрезки касательных, проведенных к окружности из одной точки, равны. Следовательно, угол ВAC равен 0,5(180° − 122°) = 29°. Угол между касательной и хордой, проведенной через точку касания, равен половине заключенной между ними дуги, поэтому искомая дуга равна 2 · 29° = 58°.
Приведем другое решение.
Пусть искомая длина меньшей дуги АВ равна х, тогда длина большей дуги АВ равна 360° − х. Угол между двумя касательными, проведенными из одной точки, равен половине высекаемых ими дуг, откуда имеем: 0,5(360° − 2x) = 122°. Тогда x = 58°.
Касательная к окружности
О чем эта статья:
Касательная к окружности, секущая и хорда — в чем разница
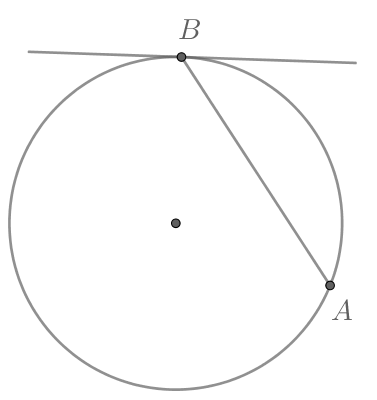
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.
Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).
Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.
Свойства касательной к окружности
Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.
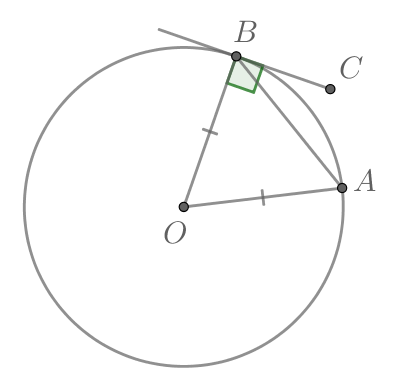
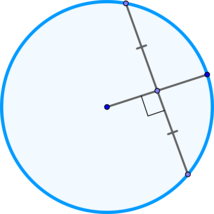
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:
- окружность с центральной точкой А;
- прямая а — касательная к ней;
- радиус АВ, проведенный к касательной.
Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.
Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.
В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.
Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Задача
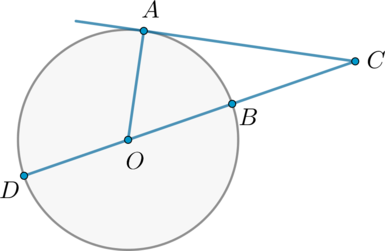
У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.
Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.
Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.
∠АОС = 180° – ∠САО – ∠АСО = 180° – 90° – 28° = 62°
Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.
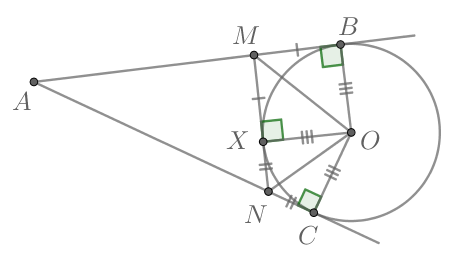
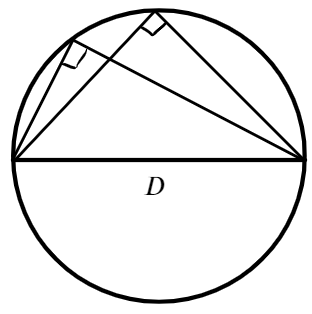
Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.
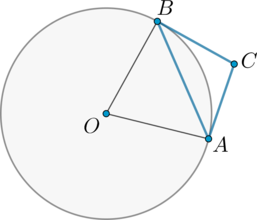
Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.
Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.
Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.
Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.
Задача 1
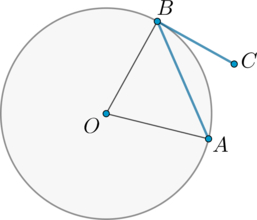
У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.
Решение
Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.
∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).
Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:
∠BDC = ∠BDA × 2 = 30° × 2 = 60°
Итак, угол между касательными составляет 60°.
Задача 2
К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.
Решение
Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.
Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.
∠МNК = (180° – ∠МКN) : 2 = (180° – 50°) : 2 = 65°
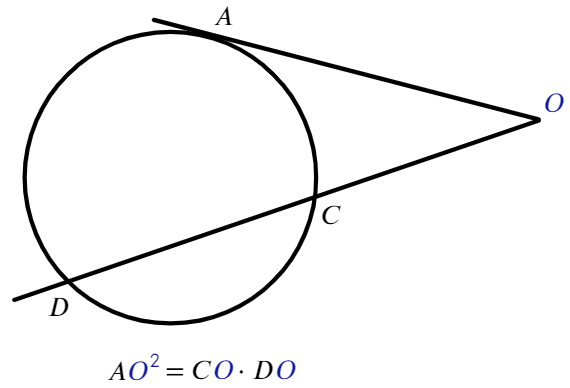
Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.
Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.
Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.
Задача 1
Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.
Решение
Исходя из соотношения касательной и секущей МА 2 = МВ × МС.
Найдем длину внешней части секущей:
МС = МВ – ВС = 16 – 12 = 4 (см)
МА 2 = МВ × МС = 16 х 4 = 64
Задача 2
Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.
Решение
Допустим, что МО = у, а радиус окружности обозначим как R.
В таком случае МВ = у + R, а МС = у – R.
Поскольку МВ = 2 МА, значит:
МА = МВ : 2 = (у + R) : 2
Согласно теореме о касательной и секущей, МА 2 = МВ × МС.
(у + R) 2 : 4 = (у + R) × (у – R)
Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:
Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).
Ответ: MO = 10 см.
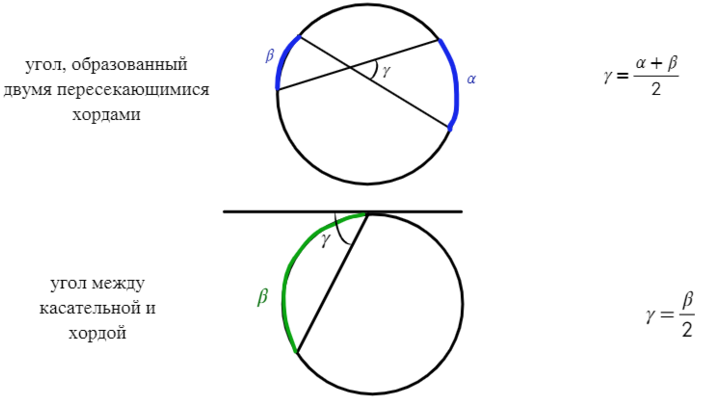
Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.
Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.
Задача 1
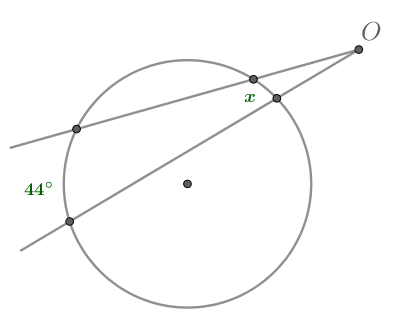
Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.
Решение
Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.
АВ = ∠АВС × 2 = 32° × 2 = 64°
Задача 2
У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.
Решение
Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:
КМ = 2 ∠МКВ = 2 х 84° = 168°
Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.
∠ОКМ = ∠ОМК = (180° – ∠КОМ) : 2
Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:
∠ОМК = (180° – ∠КОМ) : 2 = (180° – 168°) : 2 = 6°
Касательные CA и CB к окружности образуют угол ACB, равный 122. Найдите величину меньшей дуги AB, стягиваемой точками касания
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,279
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,962
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/kasatelnaya-k-okruzhnosti
http://www.soloby.ru/1338802/%D0%BA%D0%B0%D1%81%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5-%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D0%B8-%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D1%83%D1%8E%D1%82-%D0%BD%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5-%D0%B2%D0%B5%D0%BB%D0%B8%D1%87%D0%B8%D0%BD%D1%83-%D1%81%D1%82%D1%8F%D0%B3%D0%B8%D0%B2%D0%B0%D0%B5%D0%BC%D0%BE%D0%B9
[/spoiler]
Тема 1.
Геометрия на плоскости (планиметрия)
1
.
14
Окружность: углы, образованные хордами, секущими, касательными
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
геометрия на плоскости (планиметрия)
Решаем задачи
Показать ответ и решение
Так как угол между двумя секущими, проведенными из точки вне окружности, равен полуразности дуг, заключенных между ними,
то
Показать ответ и решение
Найдем градусную меру меньшей дуги, стягиваемой хордой Она равна центральному углу
на нее опирающемуся. Так
как радиус, проведенный в точку касания, перпендикулярен касательной, то Следовательно, из треугольника
Тогда имеем:
Дуга заключенная внутри угла
равна центральному углу
и равна
Показать ответ и решение
Так как угол между касательной и хордой, проведенными из одной точки окружности, равен половине дуги, заключенной между
ними, то
Следовательно, из имеем:
Угол между хордой и касательной
к окружности равен
Найдите величину меньшей дуги, стягиваемой хордой
Ответ дайте в градусах.
Показать ответ и решение
1 способ.
Так как угол между хордой и касательной, проведенными из одной точки окружности, равен половине дуги, заключенной между
ними, то меньшая дуга равна
2 способ.
Так как радиус, проведенный в точку касания, перпендикулярен касательной, то Следовательно,
Так как — радиусы, то треугольник
равнобедренный, следовательно,
Так как дуга равна центральному углу, опирающемуся на нее, то меньшая дуга равна
и равна
Хорда стягивает дугу окружности в
Найдите угол
между этой хордой и касательной к окружности, проведенной
через точку Ответ дайте в градусах.
Показать ответ и решение
Так как угол между хордой и касательной, проведенными из одной точки окружности, равен половине дуги, заключенной между
ними, то
Касательные и
к окружности образуют угол
равный
Найдите величину меньшей дуги
стягиваемой
точками касания. Ответ дайте в градусах.
Показать ответ и решение
Рассмотрим картинку:
Т.к. дуги, стягиваемые равными хордами, равны, то Т.к. вся окружность равна
, то
Угол образованный касательной
и хордой
равен половине дуги, заключенной между ними, то
есть
Показать ответ и решение
Рассмотрим картинку (пусть — точки касания):
Т.к. отрезки касательных, проведенные из одной точки, равны, то и
Т.к. радиусы, проведенные в точку
касания, перпендикулярны касательной, то
Таким образом, по двум катетам равны треугольники: и
Значит, и
Следовательно,
Т.к. в четырехугольнике сумма углов равна то в четырехугольнике
Следовательно,
Показать ответ и решение
Рассмотрим картинку:
Т.к. диаметр, делящий хорду пополам, перпендикулярен ей, то Следовательно,
как
прямоугольные по двум катетам (
— общий). Следовательно,
Т.к. равные хорды стягивают равные дуги, то
Тогда угол между хордами и
равен полусумме дуг, заключенных между ними, то есть
Т.к. нам необходимо найти угол между прямыми (а это обязательно острый угол), то в данном случае он равен углу между
данными хордами.
Угол между двумя секущими, проведенными к окружности из точки вне окружности, равен
Найдите большую дугу,
заключенную между секущими, если сумма градусных мер обеих дуг, заключенных между секущими, равна Ответ дайте в
градусах.
Показать ответ и решение
Так как угол, образованный двумя секущими, равен полуразности дуг, заключенных между ними, то
С другой стороны, по условию задачи
Решая систему из этих двух уравнений, находим
Из точки вне окружности проведены две прямые, пересекающие окружность. Большая дуга, образованная этими прямыми,
равна а угол между прямыми равен
Найдите другую дугу, образованную этими прямыми. Ответ дайте в градусах.
Показать ответ и решение
Рассмотрим картинку:
Т.к. угол, образованный двумя такими прямыми-секущими, равен полуразности дуг, заключенных между ними,
то
Найдите угол между двумя секущими, проведенными к окружности из точки вне окружности, если дуги, заключенные между
этими секущими, равны и
Ответ дайте в градусах.
Показать ответ и решение
Т.к. угол, образованный двумя такими секущими, равен полуразности дуг, заключенных между ними, то
Показать ответ и решение
Рассмотрим картинку:
Т.к. то
как вписанный и опирающийся на дугу
равен ее половине, то есть
опирается на диаметр
следовательно, равен половине от половины окружности, то есть Значит,
— внешний угол для треугольника
следовательно, он равен сумме двух углов треугольника, не смежных с
ним:
Показать ответ и решение
Отрезки касательных, проведённых из одной точки, равны: Покажем это: Построим радиусы
и
и соединим
Так как радиус, проведённый в точку касания, перпендикулярен касательной, то
как
радиусы, тогда в прямоугольных треугольниках и
катеты
и
равны, а гипотенуза
— общая,
следовательно, треугольники и
равны по катету и гипотенузе, откуда получаем
Таким образом, треугольник — равнобедренный и
Показать ответ и решение
Хорда, делящаяся диаметром пополам, перпендикулярна ему. Покажем это . Построим радиусы и
Треугольники и
равны по трём сторонам, тогда
но
откуда
Прямая касается окружности в точке
и образует с хордой
угол, равный
Найдите градусную меру дуги
которая меньше полуокружности. Ответ дайте в градусах.
Показать ответ и решение
Угол между касательной и хордой равен половине градусной меры дуги окружности, заключённой внутри него, следовательно
градусная мера искомой дуги равна
Показать ответ и решение
Так как угол между двумя секущими, проведенными из одной точки вне окружности, равен полуразности дуг, заключенных между
ними, то
Так как то
Тогда как вписанный и опирающийся на дугу
равен ее половине, то есть
Показать ответ и решение
Рассмотрим картинку:
Т.к. угол, образованный двумя такими секущими, равен полуразности дуг, заключенных между ними, то
Т.к. равные хорды стягивают равные дуги, то (меньшая полуокружности) дуга Вся окружность равна
следовательно,
Решая систему из уравнений и
получим, что
Показать ответ и решение
Треугольник — прямоугольный, причем, т.к.
то
Т.к. угол между касательной и хордой
равен половине дуги
заключенной между ними, то
Тогда
центральный угол
Свойства касательных и секущих.
Свойства хорд.
Углы окружности.
Площадь, сектор, длина окружности.
Задачи на окружности.
По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!
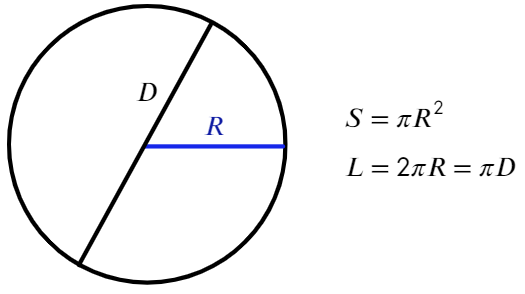
Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.
В окружности может быть проведено 3 типа отрезка:
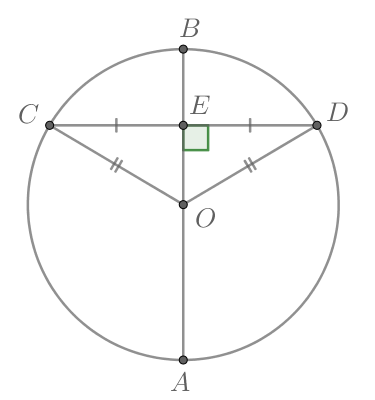
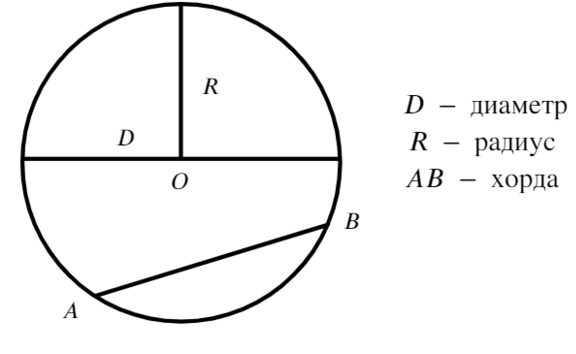
Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).
Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).
Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).
А также две прямые снаружи от окружности:
Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.
Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.
Теперь чуть-чуть об углах и дугах:
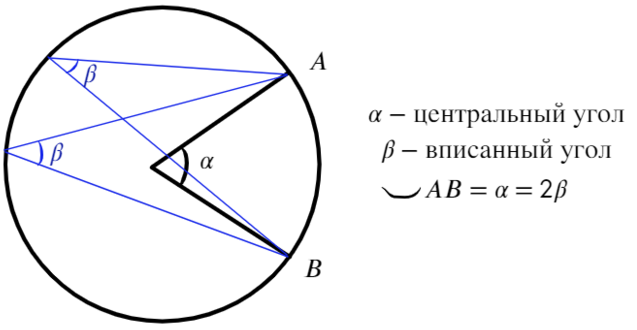
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.
Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.
Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.
Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.
А вот такой угол НЕвписанный, такой угол «никто и звать никак».
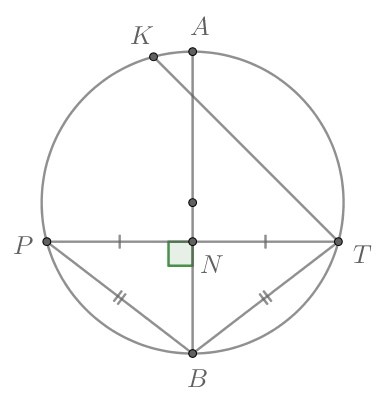
Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:
Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.
Запишем основные свойства углов в окружности:
Нашел что-то общее?
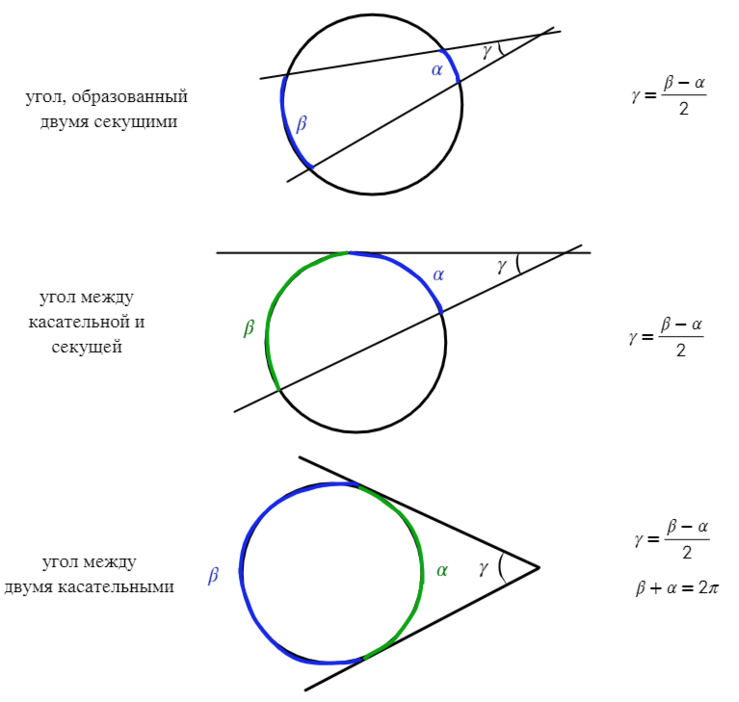
Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.
Если угол находится внутри окружности, то находим его через полусумму дуг.
Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.
Отношение отрезков:
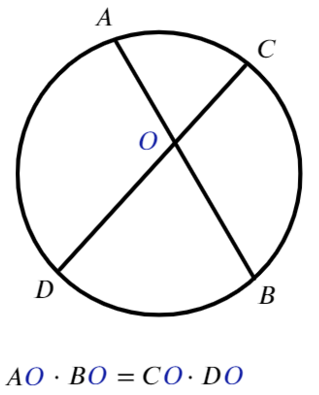
Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:
Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:
Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).
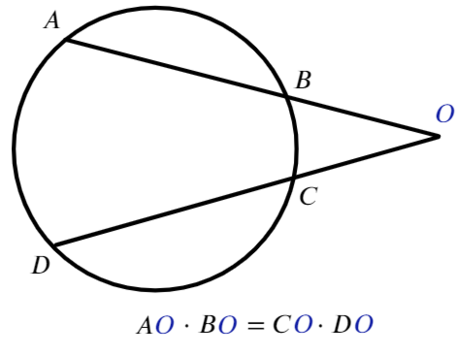
Если из точки, лежащей вне окружности, проведены касательная и секущая:
Аналогично в каждом отрезке присутствует точка, вне окружности (О).
Если теперь провести две касательные из точки O, то получим такие равные отрезки:
Касательные равны, как, сообственно, и радиусы!
Площадь и длина окружности находятся по формуле:
По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD
Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!
Задача №1. Дано на рисунке:
Достаточно вспомнить свойства центральных и вписанных углов.
Ответ: 39°
Задача №2. Дано на рисунке:
Найти нужно меньшую дугу BD
Ответ: 100°Задача №3. Дано на рисунке:
Найти меньшую дугу ВС
Ответ: 114°
Задача №4. Дано на рисунке:
Найти отрезок МК
Ответ: МК = 15.
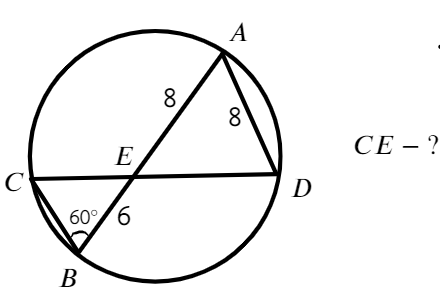
Задача №5. Дано на рисунке:
Попробуй найти подобные треугольники
Ответ: 6
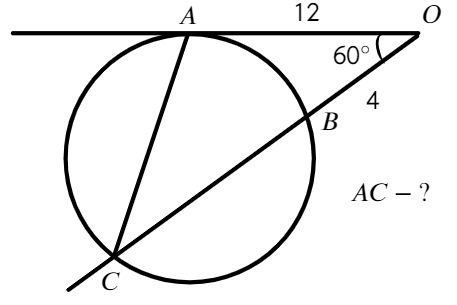
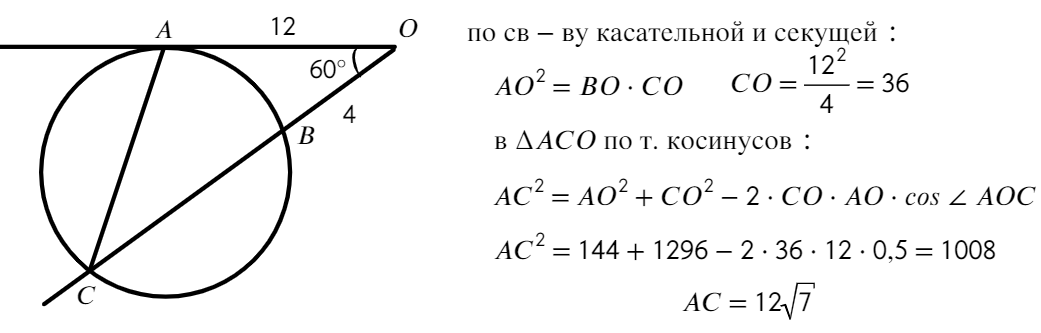
Задача №5. Дано на рисунке:
Без свойства секущей и касательной здесь будет тяжело
Ответ: 12√7.
Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
Попробуй эти задачи с подсказками.
О треугольниках
О четырехуголникахp.s. Не бойся ошибаться и задавать вопросы!
Если нашел опечатку, или что-то непонятно − напиши.
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Окружность: важные теоремы, связанные с углами (страница 3)
(blacktriangleright) Радиус, проведенный в точку касания, перпендикулярен касательной;
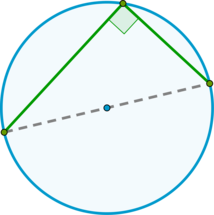
(blacktriangleright) Угол между касательной и хордой, проходящей через точку касания, равен половине дуги, заключенной между ними; [alpha = dfrac{1}{2}buildrelsmileover{AB}]
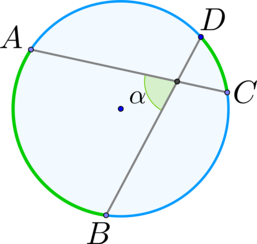
(blacktriangleright) Угол между двумя секущими, проведенными из одной точки вне окружности, равен полуразности дуг, заключенных между ними; [alpha =
dfrac{1}{2}left(buildrelsmileover{AB}-buildrelsmileover{CD}right)]
(blacktriangleright) Угол между двумя хордами равен полусумме дуг, заключенных между ними; [alpha =
dfrac{1}{2}left(buildrelsmileover{AB}+buildrelsmileover{CD}right)]
(blacktriangleright) Прямая, проходящая через точку вне окружности и центр окружности, является биссектрисой угла, образованного касательными, проведенными из этой точки к окружности;
(blacktriangleright) Если радиус делит хорду пополам, то он ей перпендикулярен;
(blacktriangleright) Вписанный угол, опирающийся на диаметр, равен (90^circ);
(blacktriangleright) Дуги (меньшие полуокружности),отсекаемые равными хордами, равны между собой.
Задание
15
#3535
Уровень задания: Равен ЕГЭ
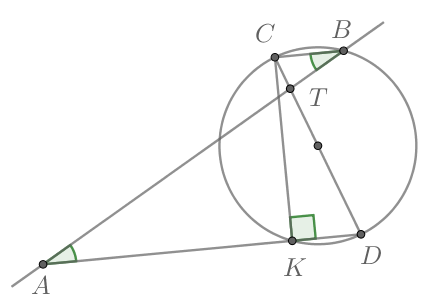
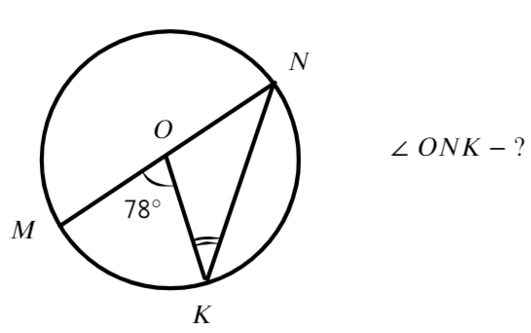
Угол (ACO) равен (24^circ). Его сторона (CA) касается окружности с центром в точке (O). Найдите градусную меру дуги (AD), заключенной внутри этого угла, где (B) и (D) – точки пересечения секущей (CO) с окружностью. Ответ дайте в градусах.
Найдем градусную меру меньшей дуги, стягиваемой хордой (AB). Она равна центральному углу (AOB), на нее опирающемуся. Так как радиус, проведенный в точку касания, перпендикулярен касательной, то (angle
OAC=90^circ). Следовательно, из (triangle OAC): (angle
AOC=90^circ-24^circ=66^circ). Тогда (angle AOD=180^circ-angle
AOC=114^circ). Дуга (AD), заключенная внутри угла (ACD), равна центральному углу (AOD) и равна (114^circ).
Ответ: 114
Задание
16
#3534
Уровень задания: Равен ЕГЭ
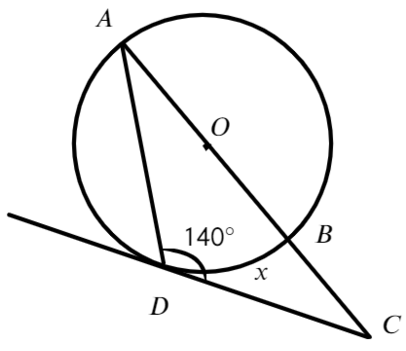
Через концы (A) и (B) дуги окружности в (62^circ) проведены касательные (AC) и (BC). Найдите угол (ACB). Ответ дайте в градусах.
Так как угол между касательной и хордой, проведенными из одной точки окружности, равен половине дуги, заключенной между ними, то (angle
ABC=angle BAC=0,5cdot 62^circ=31^circ). Следовательно, из (triangle ABC): (angle ACB=180^circ-2cdot 31^circ=118^circ).
Ответ: 118
Задание
17
#3533
Уровень задания: Равен ЕГЭ
Угол между хордой (AB) и касательной (BC) к окружности равен (32^circ). Найдите величину меньшей дуги, стягиваемой хордой (AB). Ответ дайте в градусах.
1 способ
Так как угол между хордой и касательной, проведенными из одной точки окружности, равен половине дуги, заключенной между ними, то меньшая дуга (buildrelsmileover{AB}) равна (2cdot 32^circ=64^circ).
2 способ
Так как радиус, проведенный в точку касания, перпендикулярен касательной, то (angle OBC=90^circ). Следовательно, (angle
OBA=90^circ-32^circ=58^circ). Так как (OB=OA) – радиусы, то (triangle OBA) равнобедренный, следовательно, (angle AOB=180^circ
-2cdot 58^circ=64^circ). Так как дуга равна центральному углу, опирающемуся на нее, то меньшая дуга (buildrelsmileover{AB}) равна (angle AOB) и равна (64^circ).
Ответ: 64
Задание
18
#3532
Уровень задания: Равен ЕГЭ
Хорда (AB) стягивает дугу окружности в (92^circ). Найдите угол (ABC) между этой хордой и касательной к окружности, проведенной через точку (B). Ответ дайте в градусах.
Так как угол между хордой и касательной, проведенными из одной точки окружности, равен половине дуги, заключенной между ними, то (angle
ABC=0,5cdot 92^circ=46^circ).
Ответ: 46
Задание
19
#2168
Уровень задания: Сложнее ЕГЭ
Из точки (A) на окружности проведены две прямые, пересекающие повторно окружность в точках (B) и (C), причем оказалось, что (AC) – диаметр, равный (10). Найдите длину отрезка (AB), если угол между этими прямыми равен (60^circ).
Рассмотрим картинку:
Рассмотрим (triangle ABC): он прямоугольный ((angle B=90^circ), т.к. опирается на диаметр), следовательно, (angle C=90^circ-angle
A=30^circ). Катет (AB), лежащий против угла (30^circ), равен половине гипотенузы (AC), то есть равен (5).
Ответ: 5
Задание
20
#2167
Уровень задания: Сложнее ЕГЭ
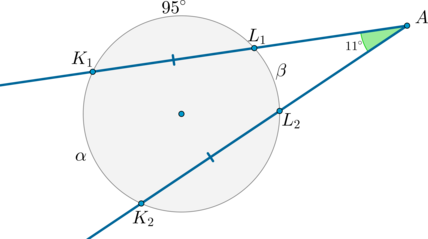
Из точки (A) вне окружности проведены две секущие к окружности, угол между которыми равен (11^circ). Первая секущая пересекла окружность в точках (K_1) и (L_1), вторая — в точках (K_2) и (L_2), причем (K_1L_1=K_2L_2) и дуга (buildrelsmileover{K_1L_1}), меньшая полуокружности, равна (95^circ).
Найдите меньшую из дуг, заключенных между данными секущими.
Рассмотрим картинку:
Т.к. угол, образованный двумя такими секущими, равен полуразности дуг, заключенных между ними, то
[angle A=0,5left(alpha-betaright)=11^circ qquad (1)]
Т.к. равные хорды стягивают равные дуги, то (меньшая полуокружности) дуга (buildrelsmileover{K_2L_2}=95^circ). Вся окружность равна (360^circ), следовательно,
[alpha+beta+2cdot 95^circ=360^circ
quad Rightarrow quad alpha+beta=170^circ qquad (2)]
Решая систему из уравнений ((1)) и ((2)), получим, что (beta=74^circ).
Ответ: 74
Задание
21
#2169
Уровень задания: Сложнее ЕГЭ
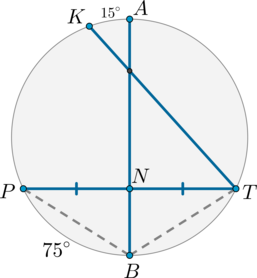
На рисунке диаметр (AB) пересекает хорду (PT) и делит ее пополам, а также пересекает хорду (KT). Дуга (PB), меньшая полуокружности, равна (75^circ); дуга (AK), меньшая полуокружности, равна (15^circ).
Найдите угол между прямыми (AB) и (KT). Ответ дайте в градусах.
Рассмотрим картинку:
Т.к. диаметр, делящий хорду пополам, перпендикулярен ей, то (ABperp
PT). Следовательно, (triangle PNB=triangle TNB) как прямоугольные по двум катетам ((PN=TN), (NB) – общий). Следовательно, (PB=TB).
Т.к. равные хорды стягивают равные дуги, то (buildrelsmileover{TB}=buildrelsmileover{PB}=75^circ).
Тогда угол между хордами (AB) и (KT) равен полусумме дуг, заключенных между ними, то есть (0,5left(15^circ+75^circright)=45^circ). Т.к. нам необходимо найти угол между прямыми (а это обязательно острый угол), то в данном случае он равен углу между данными хордами.
Ответ: 45

УСТАЛ? Просто отдохни
Версия для печати и копирования в MS Word
1
Касательные CA и CB к окружности образуют угол ACB, равный 78°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
2
Касательные CA и CB к окружности образуют угол ACB, равный 34°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
3
Касательные CA и CB к окружности образуют угол ACB, равный
Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
4
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
5
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
6
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
7
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
8
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
9
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
10
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
11
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
12
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
13
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
14
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
15
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
16
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
17
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
18
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
19
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
20
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
21
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
22
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
23
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
24
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
25
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
26
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
27
Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.