Как найти меру множества примеры – Сайт, где вы сможете решить свои вопросы

Мера множества

Понятие меры множества является далеко идущим обобщением понятия длины отрезка. В простейшем случае (которым только мы и будем заниматься) задача состоит в том, чтобы дать определение длины не только для отрезков, но также и для более сложных точечных множеств, расположенных на прямой.

Примем за единицу измерения отрезок [0,1] . Тогда длина произвольного отрезка [a,b] , очевидно, равна b-a . Точно так же если имеется два непересекающихся отрезка [a_1,b_1] и [a_2,b_2] , то под длиной множества , состоящего из этих двух отрезков, естественно понимать число (b_1-a_1)+(b_2-a_2) . Однако далеко не так ясно, что следует понимать под длиной множества более сложной природы, расположенного на прямой; например, чему равна длина канторова множества. Отсюда вывод: понятие длины множества, расположенного на прямой, нуждается в строгом математическом определении.

Задача определения длины множеств, или, как говорят еще, задача измерения множеств, весьма важна, так как она имеет существенное значение для обобщения понятия интеграла. Понятие меры множества применяется и в других вопросах теории функций, а также в теории вероятностей, топологии, функциональном анализе и т.д.

Ниже излагается определение меры множеств, предложенное французским математиком А. Лебегом и лежащее в основе данного им определения интеграла.

Мера открытого и замкнутого множества

Начнем с определения меры произвольного открытого или замкнутого множества. Как уже отмечалось, всякое открытое множество на прямой является конечной или счетной суммой попарно не пересекающихся интервалов.

Мерой открытого множества называется сумма длин составляющих его интервалов.

Таким образом, если $textstyle{G=sum(a_i,b_i)}$ и интервалы попарно не пересекаются, то мера равна $textstyle{sum(b_i-a_i)}$ . Обозначая вообще меру множества через mu E , можем написать $textstyle{mu G=sum(b_i-a_i)}$ . В частности, мера одного интервала равна его длине mu(a,b)=b-a .

Всякое замкнутое множество , содержащееся в отрезке [a,b] и такое, что концы отрезка [a,b] принадлежат , получается из отрезка [a,b] путем удаления из него некоторого открытого множества . В соответствии с этим мерой замкнутого множества Fsubseteq[a,b] , где ain F,~bin F , называется разность между длиной отрезка [a,b] и мерой открытого множества , дополнительного к (относительно отрезка [a,b] ).

Итак,

mu F=(b-a)-mu G.~~~~~~~~~(2)

Нетрудно усмотреть, что, согласно этому определению, мера произвольного отрезка равна его длине mu[a,b]=b-a , а мера множества, состоящего из конечного числа точек, равна нулю.

Определение меры множества

Для того чтобы дать определение меры множеств более общей природы, чем открытые и замкнутые, нам понадобится одно вспомогательное понятие. Пусть — некоторое множество, лежащее на отрезке [a,b] . Рассмотрим всевозможные покрытия множества , т. е. всевозможные открытые множества V(E) , содержащие . Мера каждого из множеств V(E) уже определена. Совокупность мер всех множеств V(E) есть некоторое множество положительных чисел. Это множество чисел ограничено снизу (хотя бы числом 0) и потому имеет нижнюю грань, которую мы обозначим через mu_e E . Число mu_e E называется внешней мерой множества .

Пусть mu_e E — внешняя мера множества , а mu_e CE — внешняя мера его дополнения относительно отрезка [a,b] .

Если удовлетворяется соотношение

mu_eE+mu_eCE=b-a,~~~~~~~~~(3)

то множество называется измеримым, а число mu_eE — его мерой: mu E=mu_eE ; если соотношение (3) не удовлетворяется, то говорят, что множество неизмеримо; неизмеримое множество не имеет меры.

Отметим, что всегда

mu_eE+mu_eCEgeqslant b-a.~~~~~~~~(4)

Сделаем несколько пояснений. Длина простейших множеств (например, интервалов и отрезков) обладает рядом замечательных свойств. Укажем важнейшие из них.

1. Если множества E_1 и измеримы и E_1subseteq E , то mu E_1leqslant mu E , т.е. мера части множества не превосходит меры всего множества .

2. Если множества E_1 и E_2 измеримы, то множество E=E_1+E_2 измеримо и mu(E_1+E_2)leqslantmu E_1+mu E_2 , т.е. мера суммы не превосходит суммы мер слагаемых.

3. Если множества $E_i,~iinmathbb{N}$ измеримы и попарно не пересекаются, E_iE_j=varnothing~(ine j) , то их сумма $textstyle{E=sum E_i}$ измерима и $textstyle{mu!left(sum E_iright)=summu E_i}$ , т.е. мера конечной или счетной суммы попарно непересекающихся множеств равна сумме мер слагаемых. Это свойство меры называется ее полной аддитивностью.

4. Мера множества не меняется, если его сдвинуть как твердое тело.

Желательно, чтобы основные свойства длины сохранялись и для более общего понятия меры множеств. Но, как можно совершенно строго показать, это оказывается невозможным, если приписывать меру произвольному множеству точек на прямой. Поэтому-то в данном выше определении и появляются множества, имеющие меру или измеримые, и множества, не имеющие меры или неизмеримые. Впрочем, класс измеримых множеств настолько широк, что это обстоятельство не вносит каких-либо существенных неудобств. Даже построение примера неизмеримого множества представляет известные трудности.

Приведем несколько примеров измеримых множеств.

Мера канторова совершенного множества

При построении канторового множества из отрезка [0,1] выбрасывается сперва один смежный интервал длины 1/3 , затем два смежных интервала длины 1/9 , затем четыре смежных интервала длины 1/27 и т. д. Вообще, на -м. шаге выбрасывается $2^{n-1}$ смежных интервалов длины $3^{-n}$ . Таким образом, сумма длин всех выброшенных интервалов равна

$S=frac{1}{3}+frac{2}{9}+frac{4}{27}+cdots+frac{2^{n-1}}{3^n}+cdots=sum_{n=1}^{infty}frac{2^{n-1}}{3^n}.$

Члены этого ряда представляют собою геометрическую прогрессию с первым членом 1/3 и знаменателем 2/3 . Поэтому сумма ряда равна $frac{1/3}{1-2/3}=1$ .

Итак, сумма длин всех смежных к канторовому множеству интервалов равна 1. Иначе говоря, мера дополнительного к канторовому множеству открытого множества равна 1. Поэтому само множество имеет меру mu P=1-mu G=1-1=0 .

Как показывает этот пример, множество может иметь мощность континуума и тем не менее иметь меру, равную нулю.

Мера множества R всех рациональных точек отрезка [0, 1]

Покажем прежде всего, что mu_e R=0 . Как известно, множество счетно. Расположим точки множества в последовательность

r_1,r_2,ldots,r_n,ldots

Далее, зададим varepsilon>0 и окружим точку r_n интервалом delta_n длины $frac{varepsilon}{2^n}$ . Сумма $textstyle{delta= sumdelta_n}$ есть открытое множество, покрывающее . Интервалы delta_n могут пересекаться, поэтому

$mu(delta)=mu!left(sum_{n=1}^{infty}delta_nright)leqslantsum_{n=1}^{infty}mudelta_n=sum_{n=1}^{infty}frac{varepsilon}{2^n}=varepsilon.$

Так как varepsilon можно выбрать сколь угодно малым, то mu_eR=0 .

Далее, согласно (3) имеем mu_eR+mu_eCRgeqslant1 , т. е. . Так как содержится в отрезке [0,1] , то mu_eCRleqslant1 .

Итак, mu_eR+mu_eCR=1 , откуда

mu R=0,quadmu CR=1.~~~~~~~~~(5)

Этот пример показывает, что множество может быть всюду плотным на некотором отрезке и тем не менее иметь меру, равную нулю.

Множества меры нуль во многих вопросах теории функций не играют никакой роли, и ими следует пренебрегать. Например, функция f(x) интегрируема по Риману в том и только в том случае, если она ограничена и множество её точек разрыва имеет меру нуль. Можно было бы привести значительное число таких примеров.

Измеримые функции

Переходим к одному из наиболее блестящих приложений понятия меры множеств, а именно к описанию того класса функций, с которыми фактически оперирует математический анализ и теория функций. Точная постановка задачи такова. Если последовательность функций ${f_n(x)}$ , заданных на некотором множестве , сходится в каждой точке , кроме, быть может, точек множества mathbb{N} меры нуль, то будем говорить, что последовательность ${f_n(x)}$ сходится почти всюду.

Какие функции можно получить из непрерывных функций путем повторного применения операции построения предела почти всюду сходящейся последовательности функций и алгебраических операций?

Для ответа на этот вопрос нам потребуется несколько новых понятий.

Пусть функция f(x) определена на некотором множестве и alpha — произвольное действительное число. Обозначим через E[f(x)>alpha] множество тех точек , для которых . Например, если функция f(x) определена на отрезке [0,1] и на этом отрезке f(x)=x , то множества равны [0,1] для alpha<0 , равны (alpha,1] для 0leqslantalpha<1 и пусты для alpha>1 .

Функция f(x) , определенная на некотором множестве , называется измеримой, если само множество измеримо и для любого действительного числа alpha измеримо множество E[f(x)>alpha] .

Можно показать, что произвольная непрерывная функция, заданная на отрезке, измерима. Однако к числу измеримых функций принадлежат также и многие разрывные функции, например функция Дирихле, равная 1 для иррациональных точек отрезка [0,1] и равная 0 для остальных точек этого отрезка.

Отметим без доказательства, что измеримые функции обладают следующими свойствами.

1. Если f(x) и varphi(x) — измеримые функции, определенные на одном и том же множестве , то функции

f+varphi,quad f-varphi,quad fcdotvarphi и $frac{f}{varphi}$

также измеримы (последняя, если varphine0 ).

Это свойство показывает, что алгебраические операции над измеримыми функциями снова приводят к измеримым функциям.

2. Если последовательность измеримых функций ${f_n(x)}$ , определенных на множестве , сходится почти всюду к функции f(x) , то эта функция также измерима.

Таким образом, операция построения предела почти всюду сходящейся последовательности измеримых функций вновь приводит к измеримым функциям.

Эти свойства измеримых функций были установлены Лебегом. Глубокое исследование измеримых функций было произведено советскими математиками Д. Ф. Егоровым и Н. Н. Лузиным. В частности, Н. Н. Лузин показал, что всякую измеримую функцию, заданную на отрезке, можно превратить в непрерывную, изменив ее значения на некотором множестве сколь угодно малой меры.

Этот классический результат Н. Н. Лузина и перечисленные выше свойства измеримых функций позволяют показать, что измеримые функции и представляют собой тот класс функций, о котором шла речь в начале этого пункта. Измеримые функции имеют также большое значение для теории интегрирования, именно, понятие интеграла может быть обобщено таким образом, чтобы всякая ограниченная измеримая функция оказалась интегрируемой. Подробнее об этом рассказывается в разделе интеграл Лебега.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

У этого термина существуют и другие значения, см. Мера.

Ме́ра мно́жества — числовая характеристика множества, интуитивно её можно понимать как массу множества при некотором распределении массы по пространству. Понятие меры множества возникло в теории функций вещественной переменной при развитии понятия интеграла^[1].

Собственно, мера — это некоторая числовая функция, ставящая в соответствие каждому множеству (из некоторого семейства множеств) некоторое неотрицательное число. Кроме неотрицательности мера как функция должна также обладать свойством аддитивности — мера объединения непересекающихся множеств должна равняться сумме их мер. Необходимо отметить, что не всякое множество измеримо — для каждой функции меры обычно подразумевается некоторое семейство множеств (называемых измеримыми по данной мере), для которых мера существует.

Частным случаем меры является мера Лебега для подмножеств $mathbb {R} ^{n}$ , обобщающая понятие объёма $(n=3)$ , площади $(n=2)$ или длины $(n=1)$ на случай множеств, более общих, чем просто ограниченные гладкой поверхностью.

Определения[править | править код]

Пусть задано множество $X$ с некоторым выделенным классом подмножеств ${mathcal {F}}$ , предполагается, что данный класс подмножеств является иногда кольцом множеств или алгеброй множеств, в наиболее общем случае — полукольцом множеств.

Функция $mu colon {mathcal {F}}to [0,;infty ]$ называется мерой (иногда объёмом), если она удовлетворяет следующим аксиомам:

$mu (varnothing )=0$ — мера пустого множества равна нулю;
Для любых непересекающихся множеств ${displaystyle A,Bin {mathcal {F}},}$ $Acap B=varnothing$

$mu (Acup B)=mu (A)+mu (B)$ — мера объединения непересекающихся множеств равна сумме мер этих множеств (аддитивность, конечная аддитивность).

Первая аксиома является удобной, но в некотором смысле избыточной: достаточно предположить что существует хотя бы одно множество с конечной мерой, из чего будет следовать, что мера пустого множества будет равна нулю (в противном случае добавление к любому множеству конечной меры пустого множества изменило бы меру, несмотря на то, что множество не изменилось).

Непосредственно из второй аксиомы (в случае кольца множеств) следует, что мера объединения любого конечного числа непересекающихся множеств равна сумме мер этих множеств:

$mu left(bigcup limits _{{i=1}}^{n}A_{i}right)=sum limits _{{i=1}}^{n}mu (A_{i})$ .

В случае определения над полукольцом множеств, данное свойство конечной аддитивности обычно принимается вместо второй аксиомы, так как из попарной аддитивности конечная аддитивность в общем случае не следует^[2].

Счётно-аддитивная мера[править | править код]

Из (конечной) аддитивности меры в общем случае не следует, что аналогичное свойство выполнено и для счётного объединения непересекающихся множеств. Выделяют специальный важный класс мер, называемых счётно-аддитивными мерами.

Пусть задано множество $X$ с выделенной $sigma$ -алгеброй ${mathcal {F}}$ .

Функция $mu colon {mathcal {F}}to [0,;infty ]$ называется счётно-аддитивной (или $sigma$ -аддитивной) мерой, если она удовлетворяет следующим аксиомам:

$mu (varnothing )=0.$
( $sigma$ -аддитивность) Если ${E_{n}}_{{n=1}}^{infty }subset {mathcal {F}}$ — счётное семейство попарно непересекающихся множеств из ${mathcal {F}}$ , то есть $E_{i}cap E_{j}=varnothing ,;ineq j$ , то:

$mu left(bigcup limits _{{n=1}}^{infty }E_{n}right)=sum limits _{{n=1}}^{infty }mu (E_{n})$ .

Замечания[править | править код]

Если обратное не указано явно, то обычно подразумевается счётно-аддитивная мера.
Очевидно, любая счётно-аддитивная мера является конечно-аддитивной, но не наоборот.
Если мера всего пространства конечна, то есть $mu (X)<infty$ , то такая мера сама по себе называется конечной. В противном случае мера бесконечна.

Обычно измеримые относительно заданной меры множества составляют собственный подкласс в классе всех подмножеств пространства $X$ . И, хотя существует несколько общих схем, позволяющих продолжать меры на бо́льшие классы измеримых множеств, иногда продолжение меры возможно лишь ценой утраты уникальных свойств исходной меры. Например, мера Лебега в конечномерных евклидовых пространствах является инвариантной относительно движений этого пространства. Всякое продолжение меры Лебега на класс всех подмножеств евклидова пространства уже не может быть инвариантным даже относительно одних только сдвигов (смотри пример неизмеримого множества). Так что с практической точки зрения такие продолжения теряют всякую ценность.

На прямой и двумерной плоскости существует бесконечное число расширений лебеговой меры с Борелевской $sigma$ -алгебры на множество всех ограниченных подмножеств, сохраняющее конечную аддитивность меры и такую, что конгруэнтные множества имеют равную меру. Начиная с размерности 3 этого сделать невозможно.

Связанные определения[править | править код]

Свойства[править | править код]

Из определения следует, что мера обладает как минимум следующими свойствами (предполагается, что мера задана как минимум на полукольце множеств):

Мера пустого множества равна нулю

$mu (varnothing )=0$
- Это свойство либо предполагается в определении меры в качестве аксиомы, либо предполагается, что существует хотя бы одно множество, мера которого конечна. Непосредственно из этого и следует, что мера пустого множества должна быть равна нулю (иначе добавление пустого множества к множеству конечной меры увеличит меру этого множества, хотя множество при этом не изменится). Случай бесконечности меры всех множеств не представляет никакого интереса и практического смысла. Поэтому наличие множеств конечной меры подразумевается изначально.
- Из равенства меры множества нулю в общем случае не следует, что это множество пусто. Принято говорить о множествах меры ноль.

Монотонность — мера подмножества не больше меры самого множества

$Asubseteq BRightarrow mu (A)leqslant mu (B)$

Это интуитивно понятное свойство — чем «меньше» множество, тем меньше его «размер».

Мера разности вложенных множеств равна разности мер этих множеств

$Asubseteq BRightarrow mu (Bbackslash A)=mu (B)-mu (A)$

Мера объединения двух произвольных множеств равна сумме мер этих множеств минус мера их пересечения (если последняя определена):

${displaystyle mu (Acup B)=mu (A)+mu (B)-mu (Acap B)}$ (формула включений-исключений)

Следовательно,

${displaystyle mu (Acup B)leqslant mu (A)+mu (B)}$

Свойства счётно-аддитивных мер[править | править код]

Счётно-аддитивные меры, в дополнение к указанным, обладают также следующими свойствами.

Счётная монотонность означает, что мера подмножества счётного объединения множеств не больше суммы мер этих множеств:

$Asubseteq bigcup _{{i=1}}^{infty }A_{i}Rightarrow mu (A)leqslant sum _{{i=1}}^{infty }mu (A_{i})$

Примеры[править | править код]

Мера Жордана — пример конечно-аддитивной меры.
Мера Лебега — пример счётно-аддитивной меры.
Вероятность — пример конечной меры.
Мера Хаусдорфа
Мера Бореля
Мера Хаара
Ультрафильтр может быть определён как конечно-аддитивная мера со значениями в множестве из двух элементов ${0,1}$

Продолжение мер[править | править код]

Определять меру в явном виде на каждом множестве из соответствующей сигма-алгебры (кольца или алгебры) множеств зачастую сложно и не нужно, поскольку меру достаточно определить на каком-нибудь классе измеримых множеств, а затем с помощью стандартных процедур (и при известных условиях) продолжить на кольцо, алгебру или сигма-алгебру множеств, порождённые этим классом.

Продолжение с полукольца[править | править код]

Класс измеримых множеств по своей структуре должен быть кольцом множеств (если мера аддитивна) или сигма-алгеброй множеств (если мера счётно-аддитивна), однако для задания меры, в обоих случаях её достаточно определить на полукольце множеств — тогда мера единственным образом может быть продолжена на минимальное кольцо (минимальную сигма-алгебру) множеств, содержащее исходное полукольцо.

Пусть начальный класс измеримых множеств ${mathcal {F}}_{0}$ имеет структуру полукольца: содержит пустое множество и для любых множеств A и B из ${mathcal {F}}_{0}$ их разность допускает конечное разбиение на измеримые множества из ${mathcal {F}}_{0}$ , то есть найдётся конечный набор непересекающихся множеств $C_{1},C_{2},...,C_{n}$ из ${mathcal {F}}_{0}$ , таких что

$Asetminus B=C_{1}cup C_{2}cup dots cup C_{n}$ .

Пусть ${mathcal {F}}$ означает класс всех подмножеств рассматриваемого пространства, допускающих конечное разбиение на множества из ${mathcal {F}}_{0}$ . Класс ${mathcal {F}}$ замкнут относительно операций разности, пересечения и объединения множеств, и таким образом, является кольцом множеств, содержащим ${mathcal {F}}_{0}$ (причём, очевидно, минимальным). Всякая аддитивная функция $mu$ на ${mathcal {F}}_{0}$ однозначно продолжается до аддитивной функции на ${mathcal {F}}$ , тогда и только тогда, когда её значения согласованы на ${mathcal {F}}_{0}$ . Это требование означает, что для любых наборов непересекающихся множеств $A_{1},A_{2},...,A_{n}$ и $B_{1},B_{2},...,B_{m}$ из ${mathcal {F}}_{0}$ , если совпадает их объединение, то должна совпадать и сумма их мер:

Если $bigcup limits _{{i=1}}^{{n}}A_{i}=bigcup limits _{{j=1}}^{{m}}B_{j}$ , то $sum limits _{{i=1}}^{{n}}mu (A_{i})=sum limits _{{j=1}}^{{m}}mu (B_{j})$ .

Пример[править | править код]

Пусть ${mathcal {F}}_{1}$ и ${mathcal {F}}_{2}$ — классы измеримых множеств на пространствах $X_{1}$ и $X_{2}$ , имеющие структуру полукольца. Множества вида $Atimes B$ , где $Ain {mathcal {F}}_{1}$ , $Bin {mathcal {F}}_{2}$ образуют полукольцо ${mathcal {F}}$ множеств на пространстве $X=X_{1}times X_{2}$ .

Если на ${mathcal {F}}_{1}$ и ${mathcal {F}}_{2}$ заданы меры $mu _{1}$ и $mu _{2}$ , то на ${mathcal {F}}$ определена аддитивная функция $mu (Atimes B)=mu _{1}(A)mu _{2}(B)$ , удовлетворяющая требованию согласованности. Её продолжение на минимальное кольцо, содержащее ${mathcal {F}}$ , называется прямым произведением мер $mu _{1}$ и $mu _{2}$ и обозначается $mu =mu _{1}otimes mu _{2}$ . Если исходные меры были сигма-аддитивны на своих областях определения, то и мера $mu$ будет сигма-аддитивной. Эта мера используется в теории кратных интегралов (смотри Теорема Фубини).

Вариации и обобщения[править | править код]

Один из вариантов обобщения понятия — заряд, который может принимать отрицательные значения

Иногда меру рассматривают как произвольную конечно-аддитивную функцию с областью значений в абелевой полугруппе: для счётно-аддитивной меры естественная область значений — топологическая абелева полугруппа (топология нужна для того, чтобы можно было говорить о сходимости ряда из мер счётного числа измеримых частей, на которые в определении счётной аддитивности разбивается измеримое множество). Примером нечисловой меры является мера со значениями в линейном пространстве, в частности, проекторонозначная мера, участвующая в геометрической формулировке спектральной теоремы.

Примечания[править | править код]

Литература[править | править код]

Вулих, Б. З. Краткий курс теории функций вещественной переменной (введение в теорию интеграла). — М.: Наука, 1973. — 352 с.
Халмош П. Теория меры. — М.: Издательство иностранной литературы, 1953. — 282 с. http://icm.krasn.ru/refextra.php?id=3787 (книга в 2011 году является библиографической редкостью)
А. Н. Колмогоров, С. В. Фомин. Элементы теории функций и функционального анализа Наука, 1976.
Богачев В. И. Основы теории меры, 2-е изд., в двух томах, НИЦ Регулярная и хаотическая динамика, Москва-Ижевск, 2006.
Богачев В. И., Смолянов О. Г. Действительный и функциональный анализ. Издательства: НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2009 г. 724 стр. ISBN 978-5-93972-742-6.
Богачев В. И., Гауссовские меры, Наука, Москва, 1997.
Богачев В. И., Дифференцируемые меры и исчисление Маллявэна, НИЦ Регулярная и хаотическая динамика, Москва, 2008.

Источник

Дискретная математика

Множество
– совокупность предметов (объектов,
называемых элементами), объединенных
некоторым общим признаком (свойством).
Запись А = {х
/ х²
– 3 х
+ 2 = 0} означает, что множеству А принадлежат
все те элементы х,
которые являются корнями уравнения х²
– 3 х
+ 2 = 0, т. е. числа х
= 1 и х
= 2.

Бесконечное
множество, элементы которого возможно
занумеровать натуральными числами,
называется счётным.

Множество всех
рациональных чисел – счётное, а множество
всех действительных чисел – несчётное.

Если любой элемент
множества В принадлежит также множеству
А, то множество В называется подмножеством
множества А и записывают В
А
или А
В.
Например, всякое натуральное число
(множество N) принадлежит множеству
целых чисел (множество Z), т. е. N

Из определения
подмножества следует, что любое множество
является подмножеством самого себя, т.
е.справедливо утверждение А
А.

Множество,
состоящее из всех элементов, принадлежащих
и множеству А и множеству В, называется
пересечением
множеств А и В и обозначается А
В.

Множество,
состоящее из всех элементов, принадлежащих
или множеству А или множеству В,
называется объединением
множеств А и В и обозначается А
В.

Обозначим через
m (А) число элементов конечного множества
А, тогда для любых конечных множеств
А и В справедливо равенство

m (А
В)
= m (А) + m(В) – m(А
В),
если пересечение множеств А и В не
пусто. Когда множества А и В не пересекаются,
то m(А
В)
= 0 и

m (А
В)
= m (А) + m(В).

Разностью
множеств А
и В (дополнением множества В до множества
А) называется множество всех тех и только
тех элементов из множества А, которые
не содержатся в множестве В, обозначается
А В. Например, дополнением множества
целых чисел до множества всех рациональных
чисел является множество всех дробных
чисел.

Пример 1.
Даны множества А={- 3 < х ≤ 5}, В ={1 < х
< 5}. Найти количество целых х

.

Решение.
Объединением множеств А и В является
промежуток ( -3; 5], куда входит 8
целых чисел.

Пример 2.
А = {20,30,40,50}, В = {20, 25, 30, 35}, С = {30, 35, 40, 45}.
Найти число элементов множества Д = (
)
С .

Решение.
=
{20, 25, 30, 35, 40, 45, 50}. Множество Д = (
)
С содержит числа без чисел множества
С, т. е. Д = {20,
25, 50}.

Пример 3.
Даны множества А = {х : sin х
= 0}, В = {х : 0 < х < 10}. Сколько элементов
содержится в множестве А

В
?

Решение.
Множество А = {х : sin х
= 0} = {х : х = πk, k
Z}.

В
= {π; 2π; 3π}, следовательно, в нём 3
элемента.

Прямым или
декартовым
произведением множеств
А и В называется множество упорядоченных
пар (а,
b),
в котором а

А, b

В, т. е.

А × В = {(а,
b)
/ а

А и b

В}.

Плоскость в
выбранной прямоугольной системой
координат изображает произведение
множеств R×R (иногда пишут R²
).

Пример 4. Дано
множество А = {2, 3, 4, 5, 6, 7, 8, 9} и бинарное
отношение Р = {х,
у
/ х,
у

А, х
≤ 3 }, причём х делит у без остатка.
Найти количество элементов предиката
(неопределённое высказывание –
подмножество множества А)

Решение.
Так как множество А состоит из 8
элементов, то декартово произведение
А × А будет содержать n = 8 · 8 = 64 парных
элемента. Предикат Р является
подмножеством множества А × А . Нужно
из 64 парных элементов выбрать только
те, которые удовлетворяют условиям
нашего предиката, т. е. первый элемент
пары не должен быть больше 3, а второй
должен делиться на первый без остатка
. Тогда это предикат

Р = {(2; 2), (2; 4), (2;
6), (2; 8), (3; 3), (3; 6), (3; 9)}, который содержит
7 элементов.
( Ответ: 7
элементов.
)

Мера плоского
множества есть
площадь соответствующей фигуры

П
ример1.

S =
π r₂² – π r₁
²
= π (4²–
2²)
= 12π.

П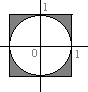
ример
2. Найти меру
плоского множества А В, где

А
{ (х,
у)

R²:
mах (| х |, | у | <1} и

В{
(х,
у)

R²:
х ²
+ у ²<1}.

S = площадь квадрата
минус площадь круга = 4 – π.

(
ответ: 4 – π
)

Пример3.
Найти меру плоского множества { (х,
у)

R²:

<
у
< 2,5 – х}.
В начале находим точки пересечения
линий, решая совместно систему уравнений
у =

и у = 2,5 – х. Имеем

=
2,5 – х или 2х ²– 5х +2 = 0.

Отсюда
х₁=
2, х₂=
0,5.

S =

=

2,5 (2 – 0,5) – 0,5 (4 –
0,25) – ln 2 + ln 0,5 =

–
ln 4.

(ответ

–
ln 4 )

Пример 4.
Найти меру плоского множества { (х,
у)

R²:
х²+
у²
= 1}.

Так как множество
состоит только из точек кривой –
окружности, то мера данного плоского
множества равна нулю. (Ответ:
нуль )

Если по какому-то
правилу каждому элементу
х

А ставится в соответствие определенный
элемент у

В, то такое соответствие называется
отображением
множества А в множество В и пишут f
: А → В.

Символ f
обозначает правило заданного соответствия.
Это правило можно обозначать и другими
символами.

Отображение, в
котором различные элементы входного
множества А соединяются с различными
элементами выходного множества В и нет
неприсоединенных элементов, называется
биективным
или взаимно
однозначным соответствием.

Линейным
отображением
называется отображение φ, удовлетворяющее
условиям φ (х
+ у) = φ (х)
+ φ (у);
φ (λ х)
= λ φ (х).

Отображение f
: Х → У называется обратимым, если
существует

f
^-1
: У → Х такое, что f
○ f
^-1=
е _х,
f
^-1
○ f
= е _у,
где е _х,
е _у
– тождественные отображения на множества
Х и У соответственно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

Informally, a measure has the property of being monotone in the sense that if $A$ is a subset of $B,$ the measure of $A$ is less than or equal to the measure of $B.$ Furthermore, the measure of the empty set is required to be 0. A simple example is a volume (how big an object occupies a space) as a measure.

In mathematics, the concept of a measure is a generalization and formalization of geometrical measures (length, area, volume) and other common notions, such as magnitude, mass, and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integration theory, and can be generalized to assume negative values, as with electrical charge. Far-reaching generalizations (such as spectral measures and projection-valued measures) of measure are widely used in quantum physics and physics in general.

The intuition behind this concept dates back to ancient Greece, when Archimedes tried to calculate the area of a circle. But it was not until the late 19th and early 20th centuries that measure theory became a branch of mathematics. The foundations of modern measure theory were laid in the works of Émile Borel, Henri Lebesgue, Nikolai Luzin, Johann Radon, Constantin Carathéodory, and Maurice Fréchet, among others.

Definition[edit]

Countable additivity of a measure $mu$ : The measure of a countable disjoint union is the same as the sum of all measures of each subset.

Let $X$ be a set and $Sigma$ a $sigma$ -algebra over $X.$ A set function $mu$ from $Sigma$ to the extended real number line is called a measure if it satisfies the following properties:

If at least one set $E$ has finite measure, then the requirement ${displaystyle mu (varnothing )=0}$ is met automatically due to countable additivity:

${displaystyle mu (E)=mu (Ecup varnothing )=mu (E)+mu (varnothing ),}$

and therefore ${displaystyle mu (varnothing )=0.}$

If the condition of non-negativity is dropped, and $mu$ takes on at most one of the values of ${displaystyle pm infty ,}$ then $mu$ is called a signed measure.

The pair $(X,Sigma )$ is called a measurable space, and the members of $Sigma$ are called measurable sets.

A triple ${displaystyle (X,Sigma ,mu )}$ is called a measure space. A probability measure is a measure with total measure one – that is, ${displaystyle mu (X)=1.}$ A probability space is a measure space with a probability measure.

For measure spaces that are also topological spaces various compatibility conditions can be placed for the measure and the topology. Most measures met in practice in analysis (and in many cases also in probability theory) are Radon measures. Radon measures have an alternative definition in terms of linear functionals on the locally convex topological vector space of continuous functions with compact support. This approach is taken by Bourbaki (2004) and a number of other sources. For more details, see the article on Radon measures.

Instances[edit]

Some important measures are listed here.

Other ‘named’ measures used in various theories include: Borel measure, Jordan measure, ergodic measure, Gaussian measure, Baire measure, Radon measure, Young measure, and Loeb measure.

In physics an example of a measure is spatial distribution of mass (see for example, gravity potential), or another non-negative extensive property, conserved (see conservation law for a list of these) or not. Negative values lead to signed measures, see “generalizations” below.

Liouville measure, known also as the natural volume form on a symplectic manifold, is useful in classical statistical and Hamiltonian mechanics.
Gibbs measure is widely used in statistical mechanics, often under the name canonical ensemble.

Basic properties[edit]

Let $mu$ be a measure.

Monotonicity[edit]

If $E_{1}$ and $E_{2}$ are measurable sets with ${displaystyle E_{1}subseteq E_{2}}$ then

${displaystyle mu (E_{1})leq mu (E_{2}).}$

Measure of countable unions and intersections[edit]

Countable subadditivity[edit]

For any countable sequence ${displaystyle E_{1},E_{2},E_{3},ldots }$ of (not necessarily disjoint) measurable sets $E_{n}$ in ${displaystyle Sigma :}$

${displaystyle mu left(bigcup _{i=1}^{infty }E_{i}right)leq sum _{i=1}^{infty }mu (E_{i}).}$

Continuity from below[edit]

If ${displaystyle E_{1},E_{2},E_{3},ldots }$ are measurable sets that are increasing (meaning that ${displaystyle E_{1}subseteq E_{2}subseteq E_{3}subseteq ldots }$ ) then the union of the sets $E_{n}$ is measurable and

${displaystyle mu left(bigcup _{i=1}^{infty }E_{i}right)~=~lim _{ito infty }mu (E_{i})=sup _{igeq 1}mu (E_{i}).}$

Continuity from above[edit]

If ${displaystyle E_{1},E_{2},E_{3},ldots }$ are measurable sets that are decreasing (meaning that ${displaystyle E_{1}supseteq E_{2}supseteq E_{3}supseteq ldots }$ ) then the intersection of the sets $E_{n}$ is measurable; furthermore, if at least one of the $E_{n}$ has finite measure then

${displaystyle mu left(bigcap _{i=1}^{infty }E_{i}right)=lim _{ito infty }mu (E_{i})=inf _{igeq 1}mu (E_{i}).}$

This property is false without the assumption that at least one of the $E_{n}$ has finite measure. For instance, for each ${displaystyle nin mathbb {N} ,}$ let ${displaystyle E_{n}=[n,infty )subseteq mathbb {R} ,}$ which all have infinite Lebesgue measure, but the intersection is empty.

Other properties[edit]

Completeness[edit]

A measurable set $X$ is called a null set if ${displaystyle mu (X)=0.}$ A subset of a null set is called a negligible set. A negligible set need not be measurable, but every measurable negligible set is automatically a null set. A measure is called complete if every negligible set is measurable.

A measure can be extended to a complete one by considering the σ-algebra of subsets $Y$ which differ by a negligible set from a measurable set $X,$ that is, such that the symmetric difference of $X$ and $Y$ is contained in a null set. One defines ${displaystyle mu (Y)}$ to equal ${displaystyle mu (X).}$

μ{x : f(x) ≥ t} = μ{x : f(x) > t} (a.e.)[edit]

If ${displaystyle f:Xto [0,+infty ]}$ is ${displaystyle (Sigma ,{cal {B}}([0,+infty ]))}$ -measurable, then

${displaystyle mu {xin X:f(x)geq t}=mu {xin X:f(x)>t}}$

for almost all ${displaystyle tin X.}$ ^[1] This property is used in connection with Lebesgue integral.

Additivity[edit]

Measures are required to be countably additive. However, the condition can be strengthened as follows.
For any set $I$ and any set of nonnegative ${displaystyle r_{i},iin I}$ define:

${displaystyle sum _{iin I}r_{i}=sup leftlbrace sum _{iin J}r_{i}:|J|<infty ,Jsubseteq Irightrbrace .}$

That is, we define the sum of the $r_{i}$ to be the supremum of all the sums of finitely many of them.

A measure $mu$ on $Sigma$ is $kappa$ -additive if for any ${displaystyle lambda <kappa }$ and any family of disjoint sets ${displaystyle X_{alpha },alpha <lambda }$ the following hold:

${displaystyle bigcup _{alpha in lambda }X_{alpha }in Sigma }$

${displaystyle mu left(bigcup _{alpha in lambda }X_{alpha }right)=sum _{alpha in lambda }mu left(X_{alpha }right).}$

Note that the second condition is equivalent to the statement that the ideal of null sets is $kappa$ -complete.

Sigma-finite measures[edit]

A measure space ${displaystyle (X,Sigma ,mu )}$ is called finite if ${displaystyle mu (X)}$ is a finite real number (rather than $infty$ ). Nonzero finite measures are analogous to probability measures in the sense that any finite measure $mu$ is proportional to the probability measure ${displaystyle {frac {1}{mu (X)}}mu .}$ A measure $mu$ is called σ-finite if $X$ can be decomposed into a countable union of measurable sets of finite measure. Analogously, a set in a measure space is said to have a σ-finite measure if it is a countable union of sets with finite measure.

For example, the real numbers with the standard Lebesgue measure are σ-finite but not finite. Consider the closed intervals ${displaystyle [k,k+1]}$ for all integers ${displaystyle k;}$ there are countably many such intervals, each has measure 1, and their union is the entire real line. Alternatively, consider the real numbers with the counting measure, which assigns to each finite set of reals the number of points in the set. This measure space is not σ-finite, because every set with finite measure contains only finitely many points, and it would take uncountably many such sets to cover the entire real line. The σ-finite measure spaces have some very convenient properties; σ-finiteness can be compared in this respect to the Lindelöf property of topological spaces.^{[original research?]} They can be also thought of as a vague generalization of the idea that a measure space may have ‘uncountable measure’.

Strictly localizable measures[edit]

Semifinite measures[edit]

Let $X$ be a set, let ${displaystyle {cal {A}}}$ be a sigma-algebra on $X,$ and let $mu$ be a measure on ${displaystyle {cal {A}}.}$ We say $mu$ is semifinite to mean that for all ${displaystyle Ain mu ^{text{pre}}{+infty },}$ ${displaystyle {cal {P}}(A)cap mu ^{text{pre}}(mathbb {R} _{>0})neq emptyset .}$ ^[2]

Semifinite measures generalize sigma-finite measures, in such a way that some big theorems of measure theory that hold for sigma-finite but not arbitrary measures can be extended with little modification to hold for semifinite measures. (To-do: add examples of such theorems; cf. the talk page.)

Basic examples[edit]

Involved example[edit]

The zero measure is sigma-finite and thus semifinite. In addition, the zero measure is clearly less than or equal to $mu .$ It can be shown there is a greatest measure with these two properties:

Theorem (semifinite part)^[6] — For any measure $mu$ on ${displaystyle {cal {A}},}$ there exists, among semifinite measures on ${displaystyle {cal {A}}}$ that are less than or equal to $mu ,$ a greatest element ${displaystyle mu _{text{sf}}.}$

We say the semifinite part of $mu$ to mean the semifinite measure ${displaystyle mu _{text{sf}}}$ defined in the above theorem. We give some nice, explicit formulas, which some authors may take as definition, for the semifinite part:

Since ${displaystyle mu _{text{sf}}}$ is semifinite, it follows that if ${displaystyle mu =mu _{text{sf}}}$ then $mu$ is semifinite. It is also evident that if $mu$ is semifinite then ${displaystyle mu =mu _{text{sf}}.}$

Non-examples[edit]

Every ${displaystyle 0-infty }$ measure that is not the zero measure is not semifinite. (Here, we say ${displaystyle 0-infty }$ measure to mean a measure whose range lies in ${displaystyle {0,+infty }}$ : ${displaystyle (forall Ain {cal {A}})(mu (A)in {0,+infty }).}$ ) Below we give examples of ${displaystyle 0-infty }$ measures that are not zero measures.

Involved non-example[edit]

Measures that are not semifinite are very wild when restricted to certain sets.^{[Note 1]} Every measure is, in a sense, semifinite once its ${displaystyle 0-infty }$ part (the wild part) is taken away.

— A. Mukherjea and K. Pothoven, Real and Functional Analysis, Part A: Real Analysis (1985)

Theorem (Luther decomposition)^[11]^[12] — For any measure $mu$ on ${displaystyle {cal {A}},}$ there exists a ${displaystyle 0-infty }$ measure $xi$ on ${displaystyle {cal {A}}}$ such that ${displaystyle mu =nu +xi }$ for some semifinite measure $nu$ on ${displaystyle {cal {A}}.}$ In fact, among such measures ${displaystyle xi ,}$ there exists a least measure ${displaystyle mu _{0-infty }.}$ Also, we have ${displaystyle mu =mu _{text{sf}}+mu _{0-infty }.}$

We say the ${displaystyle mathbf {0-infty } }$ part of $mu$ to mean the measure ${displaystyle mu _{0-infty }}$ defined in the above theorem. Here is an explicit formula for ${displaystyle mu _{0-infty }}$ : ${displaystyle mu _{0-infty }=(sup{mu (B)-mu _{text{sf}}(B):Bin {cal {P}}(A)cap mu _{text{sf}}^{text{pre}}(mathbb {R} _{geq 0})})_{Ain {cal {A}}}.}$

Results regarding semifinite measures[edit]

Localizable measures[edit]

Localizable measures are a special case of semifinite measures and a generalization of sigma-finite measures.

Let $X$ be a set, let ${displaystyle {cal {A}}}$ be a sigma-algebra on $X,$ and let $mu$ be a measure on ${displaystyle {cal {A}}.}$

s-finite measures[edit]

A measure is said to be s-finite if it is a countable sum of bounded measures. S-finite measures are more general than sigma-finite ones and have applications in the theory of stochastic processes.

Non-measurable sets[edit]

If the axiom of choice is assumed to be true, it can be proved that not all subsets of Euclidean space are Lebesgue measurable; examples of such sets include the Vitali set, and the non-measurable sets postulated by the Hausdorff paradox and the Banach–Tarski paradox.

Generalizations[edit]

For certain purposes, it is useful to have a “measure” whose values are not restricted to the non-negative reals or infinity. For instance, a countably additive set function with values in the (signed) real numbers is called a signed measure, while such a function with values in the complex numbers is called a complex measure. Observe, however, that complex measure is necessarily of finite variation, hence complex measures include finite signed measures but not, for example, the Lebesgue measure.

Measures that take values in Banach spaces have been studied extensively.^[19] A measure that takes values in the set of self-adjoint projections on a Hilbert space is called a projection-valued measure; these are used in functional analysis for the spectral theorem. When it is necessary to distinguish the usual measures which take non-negative values from generalizations, the term positive measure is used. Positive measures are closed under conical combination but not general linear combination, while signed measures are the linear closure of positive measures.

Another generalization is the finitely additive measure, also known as a content. This is the same as a measure except that instead of requiring countable additivity we require only finite additivity. Historically, this definition was used first. It turns out that in general, finitely additive measures are connected with notions such as Banach limits, the dual of $L^{infty }$ and the Stone–Čech compactification. All these are linked in one way or another to the axiom of choice. Contents remain useful in certain technical problems in geometric measure theory; this is the theory of Banach measures.

A charge is a generalization in both directions: it is a finitely additive, signed measure.^[20] (Cf. ba space for information about bounded charges, where we say a charge is bounded to mean its range its a bounded subset of R.)

Notes[edit]

Bibliography[edit]

Robert G. Bartle (1995) The Elements of Integration and Lebesgue Measure, Wiley Interscience.
Bauer, H. (2001), Measure and Integration Theory, Berlin: de Gruyter, ISBN 978-3110167191
Bear, H.S. (2001), A Primer of Lebesgue Integration, San Diego: Academic Press, ISBN 978-0120839711
Berberian, Sterling K (1965). Measure and Integration. MacMillan.
Bogachev, V. I. (2006), Measure theory, Berlin: Springer, ISBN 978-3540345138
Bourbaki, Nicolas (2004), Integration I, Springer Verlag, ISBN 3-540-41129-1 Chapter III.
R. M. Dudley, 2002. Real Analysis and Probability. Cambridge University Press.
Edgar, Gerald A (1998). Integral, Probability, and Fractal Measures. Springer. ISBN 978-1-4419-3112-2.
Folland, Gerald B (1999). Real Analysis: Modern Techniques and Their Applications (Second ed.). Wiley. ISBN 0-471-31716-0.
Federer, Herbert. Geometric measure theory. Die Grundlehren der mathematischen Wissenschaften, Band 153 Springer-Verlag New York Inc., New York 1969 xiv+676 pp.
Fremlin, D.H. (2016). Measure Theory, Volume 2: Broad Foundations (Hardback ed.). Torres Fremlin. Second printing.
Hewitt, Edward; Stromberg, Karl (1965). Real and Abstract Analysis: A Modern Treatment of the Theory of Functions of a Real Variable. Springer. ISBN 0-387-90138-8.
Jech, Thomas (2003), Set Theory: The Third Millennium Edition, Revised and Expanded, Springer Verlag, ISBN 3-540-44085-2
R. Duncan Luce and Louis Narens (1987). “measurement, theory of,” The New Palgrave: A Dictionary of Economics, v. 3, pp. 428–32.
Luther, Norman Y (1967). “A decomposition of measures”. Canadian Journal of Mathematics. 20: 953–959. doi:10.4153/CJM-1968-092-0. S2CID 124262782.
Mukherjea, A; Pothoven, K (1985). Real and Functional Analysis, Part A: Real Analysis (Second ed.). Plenum Press.
- The first edition was published with Part B: Functional Analysis as a single volume: Mukherjea, A; Pothoven, K (1978). Real and Functional Analysis (First ed.). Plenum Press. doi:10.1007/978-1-4684-2331-0. ISBN 978-1-4684-2333-4.
M. E. Munroe, 1953. Introduction to Measure and Integration. Addison Wesley.
Nielsen, Ole A (1997). An Introduction to Integration and Measure Theory. Wiley. ISBN 0-471-59518-7.
K. P. S. Bhaskara Rao and M. Bhaskara Rao (1983), Theory of Charges: A Study of Finitely Additive Measures, London: Academic Press, pp. x + 315, ISBN 0-12-095780-9
Royden, H.L.; Fitzpatrick, P.M. (2010). Real Analysis (Fourth ed.). Prentice Hall. p. 342, Exercise 17.8. First printing. Note that there is a later (2017) second printing. Though usually there is little difference between the first and subsequent printings, in this case the second printing not only deletes from page 53 the Exercises 36, 40, 41, and 42 of Chapter 2 but also offers a (slightly, but still substantially) different presentation of part (ii) of Exercise 17.8. (The second printing’s presentation of part (ii) of Exercise 17.8 (on the Luther^[11] decomposition) agrees with usual presentations,^[2]^[21] whereas the first printing’s presentation provides a fresh perspective.)
Shilov, G. E., and Gurevich, B. L., 1978. Integral, Measure, and Derivative: A Unified Approach, Richard A. Silverman, trans. Dover Publications. ISBN 0-486-63519-8. Emphasizes the Daniell integral.
Teschl, Gerald, Topics in Real and Functional Analysis, (lecture notes)
Tao, Terence (2011). An Introduction to Measure Theory. Providence, R.I.: American Mathematical Society. ISBN 9780821869192.
Weaver, Nik (2013). Measure Theory and Functional Analysis. World Scientific. ISBN 9789814508568.

References[edit]

^ Fremlin, D. H. (2010), Measure Theory, vol. 2 (Second ed.), p. 221
^ ^a ^b ^c Mukherjea 1985, p. 90.
^ Folland 1999, p. 25.
^ Edgar 1998, Theorem 1.5.2, p. 42.
^ Edgar 1998, Theorem 1.5.3, p. 42.
^ ^a ^b Nielsen 1997, Exercise 11.30, p. 159.
^ Fremlin 2016, Section 213X, part (c).
^ Royden 2010, Exercise 17.8, p. 342.
^ Hewitt 1965, part (b) of Example 10.4, p. 127.
^ Fremlin 2016, Section 211O, p. 15.
^ ^a ^b Luther 1967, Theorem 1.
^ Mukherjea 1985, part (b) of Proposition 2.3, p. 90.
^ Fremlin 2016, part (a) of Theorem 243G, p. 159.
^ ^a ^b Fremlin 2016, Section 243K, p. 162.
^ Fremlin 2016, part (a) of the Theorem in Section 245E, p. 182.
^ Fremlin 2016, Section 245M, p. 188.
^ Berberian 1965, Theorem 39.1, p. 129.
^ Fremlin 2016, part (b) of Theorem 243G, p. 159.
^ Rao, M. M. (2012), Random and Vector Measures, Series on Multivariate Analysis, vol. 9, World Scientific, ISBN 978-981-4350-81-5, MR 2840012.
^ Bhaskara Rao, K. P. S. (1983). Theory of charges: a study of finitely additive measures. M. Bhaskara Rao. London: Academic Press. p. 35. ISBN 0-12-095780-9. OCLC 21196971.
^ Folland 1999, p. 27, Exercise 1.15.a.

External links[edit]

Look up measurable in Wiktionary, the free dictionary.

“Measure”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Tutorial: Measure Theory for Dummies

Источник

Некоторые сведения о множествах

Говорят, что между элементами двух множеств установлено взаимно однозначное соответствие, если каждому элементу первого множества поставлен в соответствие некоторый элемент второго множества так, что при этом каждый элемент второго множества соответствует только одному элементу первого множества.

Два множества называются эквивалентными, если между их элементами можно установить взаимно однозначное соответствие. Если два множества эквивалентны, то говорят, что они имеют одинаковую Мощность.

Множество называется счётным, если оно эквивалентно множеству натуральных чисел, т. е элементы можно занумеровать. Примеры: множество рациональных чисел, целых чисел, простых чисел, алгебраических чисел.

Множество вещественных чисел сегмента несчётно.

Если множество эквивалентно множеству всех вещественных чисел сегмента , то говорят, что оно имеет мощность континуум.

Пусть произвольное числовое множество. Точка называется внутренней точкой множества, если она содержится в вместе с некоторой своей окрестностью.

Множество называется открытым, если все его точки внутренние. Множество называется замкнутым, если оно содержит все свои предельные точки.

Объединение конечного или счётного числа открытых множеств является открытым.

Теорема 1. Любое открытое множество является объединением конечного или счётного числа попарно непересекающихся интервалов

Мера множества. Мера интервала назовём его длину. Пусть – ограниченное открытое множество. По Т.1 его можно представить в виде , – попарно не пересекающиеся интервалы.

Мерой открытого ограниченного множества назовём сумму длин его интервалов.

В силу ограниченности множества этот ряд сходится.

Пусть – произвольное ограниченное множество. Рассмотрим всевозможные ограниченные открытые множества , содержащие . Множество мер этих множеств ограничено снизу (например, числом 0) и, следовательно, имеет

Число называет внешней мерой множества .

Определение. Множество называется измеримым (по Лебегу), если существует открытое множество , содержащее , для которого . При этом внешняя мера множества называется его мерой Лебега.

-аддитивность меры Лебега

Мера счётного множества равна нулю. Однако несчётное множество также может иметь меру ноль.

Пример. Возьмём отрезок , разделим на три равных части и удалим средней интервал, оставшиеся сегменты поделим на три равные части и удалим средние интервалы и т. д. Получившееся (канторово) множество несчётно но имеет меру ноль.

Пример неизмеримого множества в Колмогорове Фомине на стр.303.

Измеримые функции.

Пусть функция определена на измеримом множестве . Пусть , множество всех таких значений аргумента , принадлежащих множеству , для которых .

Определение. Функция называется измеримой на множестве , если для любого числа множество

Для измеримости на множестве необходимо и достаточно, для любого числа было бы измеримо одно из множеств , , .

Свойства измеримых функций.

1. Если функция измерима на множестве , то она измерима на любом измеримом подмножестве.

2. Если функция измерима на множестве , ,.., ,…, то она измерима на их объединении и пересечении.

3. Если функция определена на множестве меры нуль, то она измерима на этом множестве.

4. Если функции , измеримы на множестве , то, , , (при условии ).

5. Непрерывная на сегменте функция измерима на этом сегменте.

Говорят, что некоторое свойство справедливо Почти всюду на множестве , если множество точек из , на котором оно не справедливо, имеет меру ноль.

Функции , определённые на измеримом множестве, называются эквивалентными на этом множестве, если они равны почти всюду.

6. Если измерима, а эквивалентна , то измерима.

7. Теорема Лузина.(С – свойство). Для того чтобы функция была измерима на необходима и достаточно, чтобы существовала непрерывная на функция такая, что .

Следующая >

Источник

Мера множества

Мера открытого и замкнутого множества

Определение меры множества

Мера канторова совершенного множества

Мера множества R всех рациональных точек отрезка [0, 1]

Измеримые функции

Определения[править | править код]

Счётно-аддитивная мера[править | править код]

Замечания[править | править код]

Связанные определения[править | править код]

Свойства[править | править код]

Свойства счётно-аддитивных мер[править | править код]

Примеры[править | править код]

Продолжение мер[править | править код]

Продолжение с полукольца[править | править код]

Пример[править | править код]

Вариации и обобщения[править | править код]

Примечания[править | править код]

Литература[править | править код]

Дискретная математика

Definition[edit]

Instances[edit]

Basic properties[edit]

Monotonicity[edit]

Measure of countable unions and intersections[edit]

Countable subadditivity[edit]

Continuity from below[edit]

Continuity from above[edit]

Other properties[edit]

Completeness[edit]

μ{x : f(x) ≥ t} = μ{x : f(x) > t} (a.e.)[edit]

Additivity[edit]

Sigma-finite measures[edit]

Strictly localizable measures[edit]

Semifinite measures[edit]

Basic examples[edit]

Involved example[edit]

Non-examples[edit]

Involved non-example[edit]

Results regarding semifinite measures[edit]

Localizable measures[edit]

s-finite measures[edit]

Non-measurable sets[edit]

Generalizations[edit]

See also[edit]

Notes[edit]

Bibliography[edit]

References[edit]

External links[edit]

Вам также может понравиться

Как найти приведенную погрешность примеры

Как найти длину светового потока

Как найти все индексы вхождения python

Добавить комментарий Отменить ответ