Как найти местную скорость

Средняя
скорость потока – Скорость, с которой
должны были бы двигаться все частицы
жидкости через живое сечение потока,
чтобы сохранился расход, соответствующий
действительному распределению скоростей.
Выражается формулой: V=Q/ω , где Q – расход
потока, ω – площадь живого сечения потока.

Турбулентный
поток характеризуется беспорядочным,
хаотическим движением частиц жидкости.
Наряду с основным поступательным
пере-мещением жидкости вдоль трубы
наблюдаются незакономерные попереч-ные
перемещения и вращательные движения
частиц, которые приводят к интенсивному
перемешиванию жидкости. Вследствие
интенсивного вих-реобразования частицы
жидкости при турбулентном движении
описывают весьма сложные траектории,
а местные скорости не сохраняются
постоян-ными даже в том случае, когда
расход потока постоянен во времени.
Таким образом, установившегося движения
(в строгом понимании) в турбулент-ном
потоке не существует. Измерения
показывают, наоборот, что в каждой точке
скорость непрерывно меняется как по
величине, так и по направле-нию. Поэтому
скорость в точке турбулентного потока
называют мгновен-ной местной скоростью.

Выражение
(5.4), характеризует закон распределения
скоростей по живому сечению потока при
ламинарном режиме движения жидкости и
называется формулой Стокса.

Соотношение
между средней скоростью и максимальной
скоростью можно получить, сопоставив
значение Q из уравнений

Таким
образом, при ламинарном потоке в трубе
средняя скорость жидкости равна половине
скорости по оси трубы.

13. Расчет расхода жидкости при ламинарном режиме движения (уравнение Пуазейля).

Расход
жидкости в круглой трубе при ее ламинарном
движении определяется уравнением
Пуазейля

, (4.10)

где
d
– внутренний диаметр трубы. гдеd,l–
эквивалентный диаметр и длина канала,
м;

μ
– коэффициент динамической вязкости
рабочей среды, Па·с;
Δр=р₁
–р₂
– перепад давления на дросселе, Па.

14.
Течение жидкости в малом зазоре .
Уравнение Петрова.

Создателем
гидродинамической теории смазки является
профессор Н. П. Петров. До него считали,
что в подшипниках скольжения происходит
трение одного тела (вала) о другое
(вкладыш).

Н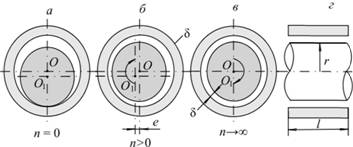

.
П. Петров показал, что при вращении вал
увлекает за собой смазочную жидкость,
направляя ее в зазор между валом и
вкладышем в нижней части (рис. 6.11, а). От
этого давление в зазоре между валом и
вкладышем возрастает. Образуется своего
рода масляный клин, вытесняющий вал
вверх и влево (рис. 6.11, б). При
увеличении числа оборотов п вал
“всплывает”. Таким образом, трения
вала о вкладыш не происходит
– сухое трение заменяется жидкостным.
При увеличении числа оборотов вал
стремится встать в центре отверстия во
вкладыше (центр вала О1
совпадает с центром подшипника О –
рис. 6.11, в).

Вывод
формулы Петрова для силы трения
основывается на следующем. При одинаковой
толщине слоя смазки

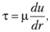
где и
– окружная
скорость. При радиусе вата r и
длине вкладыша l (рис.
6.11, г) полная
поверхность, по которой происходит
трение:

Тогда
сила трения будет

Т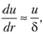

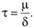
ак
как то

Отсюда

У
читывая,
что

г
де
–
угловая скорость; п
– число
оборотов вала, получаем

Так
как слой смазки неодинаков по толщине,
то всегда имеет место эксцентриситет е, учитываемый
поправочным коэффициентом 

Окончательно формула Петрова принимает
вид

Научные статьи на тему «Местная скорость»

Ветровой режим

Он отражает характер барического поля, но зависит в большей степени от местных условий.
Рисунок 1….
степени зависит от местных условий и имеет отличия в разных климатических областях….
Местные ветры

Определение 2

Ветер – это горизонтальное движение воздуха из области высокого в…
Местные ветры бризы, имеют термическое происхождение, т.е. различное нагревание суши и воды….
Ещё один местный ветер получил название бора, он сильный, холодный, порывистый дует в сторону теплого

Статья от экспертов

Определение местного коэффициента сопротивления трения по результатам измерений турбулентных профилей скорости при околозвуковых скоростях

С помощью обобщенной диаграммы Клаузера для сжимаемого газа проведена оценка местного коэффициента сопротивления трения по профилям скорости, измеренным на боковой стенке аэродинамической трубы с помощью микронасадка полного давления в диапазоне чисел М [infinity] = 0,52 -1,41 и Re x = (6,5 -11,7) * 10 6. Найденные таким образом значения c f сравниваются с результатами расчета по методу определяющей температуры и с результатами непосредственного измерения сил трения с помощью весового плавающего элемента.

Аэродинамический расчет

аэродинамического расчета систем вентиляции вносят номер участка, а также данные по расходу, длине, давлению, виду местного…
трение;
определяют динамическое давление;
определяют виды местных сопротивлений их значения и потери…
Сумма значений коэффициентов местных давлений указывается в таблице;
определяют потери на расчетном участке…
Для приточных шахт с естественной системой побуждения скорость воздуха 1-2 м/с….
В целом система, имеющая естественное побуждене, требует меньших скоростей, чем при механическом.

Статья от экспертов

Экспериментальное исследование местной теплоотдачи в ламинарном пограничном слое при сверхзвуковых скоростях

Приведены результаты экспериментального исследования теплоотдачи в ламинарном пограничном слое в диапазоне чисел М = З-6,2, Re = 1,7*10^б 35*10^6 и значений температурного фактора TwTr=0,235-1,05. Выявлено влияние чисел М, Re и отношения Tw/Tr на местную теплоотдачу. Получена эмпирическая формула для расчета местных коэффициентов теплоотдачи в ламинарном пограничном слое. Проведено сопоставление результатов настоящего исследования с данными других работ.

Осредненная местная скорость

Cтраница 1

Осредненная местная скорость – средняя скорость в данной точке, определенная за достаточный промежуток времени.
 [1]

Здесь и – осредненная местная скорость на расстоянии у от стенки трубы; ймавс – скорость по оси трубы; го – радиус трубы; А, – коэффициент сопротивления по длине; г – расстояние от оси трубы.
 [2]

Турбулентный поток в трубе по структуре поля осредненных местных скоростей можно условно разделить на две части: на основной поток, имеющий сравнительно небольшое уменьшение v с ростом радиуса г от нуля ( турбулентное ядро потока), и на пристеночный кольцевой слой малой толщины б ( см. рис. 22), где имеет место большой отрицательный градиент скорости и интенсивное ее уменьшение до нуля. Этот слой иногда называют пограничным слоем в трубе или пограничной пленкой.
 [3]

Условная ( фиктивная) скорость и называется осредненной местной скоростью; эта скорость является, разумеется, продольной.
 [4]

Многочисленные опыты, проводившиеся для установления закона распределения осредненной местной скорости по поперечному сечению турбулентного потока, показали, что при турбулентном движении осредненная скорость мало меняется по сечению трубы, если исключить из рассмотрения небольшую область у стенок, где особо существенную роль играет трение.
 [6]

РГгак, осредненная скорость турбулентного потока в данной точке или осредненная местная скорость представляет собой среднее по времени значение скорости в рассматриваемой точке.
 [7]

При определении средней скорости турбулентного потока осреднение приходится делать дважды: вначале осредняют по времени – находят осредненные местные скорости в различных точках живого сечения, а затем осредняют по живому сечению – находят среднюю скорость потока в этом живом сечении и как среднюю из осредненных скоростей.
 [9]

Эта величина называется о с р е д н е н н о и скоростью турбулентного потока в данной точке или осредненной местной скоростью.
 [10]

Механизм смешения при последовательной перекачке при турбулентном режиме можно представить следующим образом: позади идущий продукт б вклинивается в впереди идущий продукт а по профилю осредненных местных скоростей, а турбулентные пульсации перемешивают вклинившуюся часть продукта б с продуктом а. Концентрация вклинившегося продукта по длине зоны смеси плавно изменяется от нуля до единицы.
 [11]

При турбулентном режиме скорость движения в каждой точке потока постоянно изменяется по величине и направлению, колеблясь около некоторого среднего значения ( пульсация скорости), называемого осредненной местной скоростью.
 [13]

Турбулентный режим движения жидкости характерен тем, что скорость течения в каждой точке потока постоянно изменяется по величине и направлению, колеблясь около некоторого среднего значения ( пульсация скорости), называемого осредненной местной скоростью. Осредненной местной скоростью является средняя скорость течения в данной точке, определяемая за достаточно продолжительный промежуток времени.
 [14]

Осредненная местная скорость – средняя скорость в данной точке, определяемая за достаточный промежуток времени.
 [15]

Страницы:  

   1

   2

Таким образом, критическая скорость газа при истечении равна местной скорости звука и выходном сечении сопла. Именно это обстоятельство объясняет, почему в суживающемся сопле газ не может расшириться до давления, меньшего критического, а скорость не может превысить критическую.  [c.48]

Из физики известно, что величина а = ]/определяет скорость звука в газе в выходном сечении суживающегося канала, или критическая скорость при истечении газа равна местной скорости звука (в данном сечении), т. е.  [c.207]

Отсюда следует, что скорость истечения в выходном сечении суживающегося канала не может быть больше местной скорости звука в газе (рис. 13-6).  [c.207]

Повышение прочности при динамических нагрузках обусловлено отставанием внутри-кристаллитных пластических деформаций, происходящих с относительно небольшой скоростью, от нарастания напряжений. Так как скорость перемещения дислокаций не может превышать местной скорости звука, то напряжение. распространяется через ударную волну.  [c.149]

Рис. П. Распределение местных скоростей по нормальному сечению потока при неравномерном поле скоростей

Местная скорость — скорость о частиц жидкости в данном месте пространства или в данной точке нормального сечения (рис. 11). В общем случае местные скорости не одинаковы в разных точках сечения, поэтому по значениям v можно находить лишь элементарные расходы dQ через элементы dF площади нормального сечения  [c.72]

Турбулентный поток в трубе по структуре поля осредненных местных скоростей можно условно разделить па две части на основной поток, имеющий сравнительно небольшое уменьшение у с ростом радиуса г от нуля (турбулентное ядро потока), и на пристеночный кольцевой слой малой толщины 6 (см. рис. 22), где имеет место большой отрицательный градиент скорости и интенсивное ее уменьшение до нуля. Этот слой иногда называют пограничным слоем в трубе или пограничной пленкой.  [c.84]

Таким образом, мы приходим к выводу, что если на входе трубы скорость газа меньше скорости звука, то движение остается дозвуковым и на всем дальнейшем ее протяжении. Скорость, равная местной скорости звука, если и достигается вообще, то только на выходном конце трубы (при достаточно низком давлении во внешней среде, в которую выпускается газ).  [c.509]

Применим формз лу (99,5) к плоскости, ограничивающей занимаемую волной разрежения область пространства. При этом x/t будет представлять собой скорость движения этой границы относительно выбранной неподвижной системы координат. Скорость же ее относительно самого газа есть разность x/t — v и согласно (99,5) равна как раз местной скорости звука. Это значит, что границы волны разрежения представляют собой слабые разрывы. Картина автомодельного движения в различных конкретных случаях складывается, следовательно, из волн разрежения и областей постоянного течения, разделенных между собой поверхностями слабых разрывов (кроме того, конечно, могут иметься и различные области постоянного течения, разделенные между собой ударными волнами).  [c.513]

Теперь уже легко видеть, что реальная передняя граница области рассматриваемого движения должна совпадать с точкой, где выполняются условия (130,8). Для этого замечаем, что разность г It — V, где г—координата границы, есть не что иное, как скорость перемещения этой границы относительно остающегося за ней газа. Но поверхность, на которой гЦ — v> , не может быть поверхностью детонационной волны (на которой должно быть r/t — и с). Поэтому мы приходим к результату, что передней границей рассматриваемой области может быть только точка, в которой имеет место (130,8). На этой границе v падает скачком до нуля, а скорость ее распространения относительно остающегося непосредственно за нею газа равна местной скорости звука. Это значит, что детонационная волна должна соответствовать точке Чепмена — Жуге детонационной адиабаты ).  [c.682]

VI — U2. Скорость же Уг совпадает с местной скоростью звука. Поскольку в автомодельной волне разрежения скорость звука связана со. скоростью  [c.684]

Решение. Скорости Vt и Уг определяют так же, как и в предыдущем случае поэтому той же оказывается и скорость со. Область волны разрежения простирается, однако, теперь не до точки, где у = О, а до самого начала трубы (л = О, рис. 133,6). Из формулы xjt = vс (99,5) видим, что газ вытекает из отверстия трубы со скоростью и = —с, равной местной скорости звука. Написав  [c.685]

Рассмотрим теперь влияние на реактивную силу непостоянства давлений в плоскости выходного среза двигателя. Построим эпюру давления и скорости на срезе сопла (рис. d.l4). Для простоты остановимся на случае дозвукового истечения. Можно, например, представить себе такое обтекание двигателя, при котором давление вблизи выходного среза понижено, за счет чего местная скорость во внешнем потоке увеличивается. Давление внутри дозвуковой выхлопной струи является примерно таким же, как и на ее границе.  [c.53]

Плотность, как уже отмечалось, с ростом скорости уменьшается. В критическом сечении сопла dF/F = О, это значит, что площадь поперечного сечения проходит через экстремум (минимум). Из соотношения (1) следует, что именно в узком сечении сопла Лаваля получается скорость потока, равная местной скорости звука.  [c.144]

Критическое значение числа Маха набегающего на решетку потока газа М р, при котором где-то на профиле возникает скорость, равная местной скорости звука, может быть приближенно определено по распределению давления на профиле в данной решетке при обтекании ее потоком несжимаемой жидкости, или согласно упомянутой уже ранее гипотезе затвердевания , в со-  [c.64]

Вычисление же удельной кинетической энергии Ел, зависящей от распределения местных скоростей и = и(х, у, г) по живому сечению, сталкивается с определенными трудностями.  [c.60]

Полученное выражение для практического использования весьма неудобно, так как для вычисления (5-7) необходимо знать полную картину распределения местных скоростей и по живому сечению. Поэтому естественно возникает вопрос о возможности вычисления удельной кинетической энергии не по местным скоростям и = и(х, у, г), а по средней скоро-Q  [c.60]

Пусть местная скорость а отличается от средней скорости V на величину ШтА/г, так что  [c.61]

Следовательно, отношение местной скорости в какой-либо точке живого сечения трубы к максимальной скорости на оси зависит только от относительного положения точки в сечении  [c.79]

Т( льным дефицитом местной скорости от максимальной.  [c.84]

Наконец, найдем относительный дефицит местной скорости от средней, т. е.  [c.84]

Относительный дефицит местной скорости (как по максимальной, так и по средней скорости) зависит только от относительного расстояния от стенки трубы.  [c.85]

Отношение местной скорости к средней u v зависит как от относительного расстояния от стенки, так и от характера сопротивлений.  [c.85]

Кроме сказанного, используя (9-12ж), определим расстояние от стенки (р, ), где местная скорость (и) равна средней скорости потока V. В таких точках н/и=1 и, следовательно,  [c.85]

Пусть движение газа осуществляется через суживающееся сопло ф<0. Из уравнения (13-24) следует, что знак величины df в этом случае противоположен знаку (а” — w ). Если (а — ш )>0 и w a, тогда d/<0 по направлению движения газа сечение сопла должно уменьшаться и скорость газа будет меньше местной скорости звука. Если (а — и )< 0 и ш>а, то по направлению движения газа сечение сопла должно увеличиваться и скорость газа будет больше местной скорости 13рука. В самом узком сечении сопла скорость движения газа будет равна скорости звука, что и является предельным значением скорости газа при его адиабатном истечении из суживающегося сопла. Для получения сверхзвуковых скоростей газа Б соплах необходимо, чтобы они имели сначала суживающуюся часть, а затем расширяющуюся.  [c.209]

Поле осредненных местных скоростей v по нормальному сечению трубы при турбулентном режиме представлено на рис. 22 оно более выравнено, чем при ламинарном режиме, и с ростом числа Рейнольдса отношение t/ p/ max возрастает например, при Re = 1СИ отношение I p/i max = 0,79, а при Re = 3.10 Оср/итах = 0,88 для ламинарного же режима по формуле (20) Чср/ шах = 0,5.  [c.84]

Пусть Л > О (как на рис. 30) поскольку первый член в этом равенстве заведомо положителен, то тогда должно быть Re o/ft > О — фазовая скорость волны направлена направо. При этом резонансная точка у,, в которой фазовая скорость волны совпадает с местной скоростью течения, w (г/,) = Re ш/А, лежит справа от точки уп. Жидкие частицы, движущиеся в окрестности резона испои точки  [c.243]

В общем случае произвольного стационарного течения эта поверхность не является уже конической во всем объем( потока. Можно, однако, по-прежнему утверждать, что она пересекает в каждой своей точке линию тока под углом, равным углу Маха. Значение же угла Маха меняется от точки к точке соответственно изменению скоростей v w с. Подчеркнем здесь, кстати, что при движении с большими скоростями скорость звука различна в разных местах газа — она меняетея вместе с термодинамическими величинами (давлением, плотностью и т. д.), 4 ункциен которых она является ). О скорости звука как функции координат точки говорят как о местной скорости звука.  [c.443]

В этом решении перпендикулярная к радиус-вектору составляющая Цф скорости в каждой точке равна по величине местной скорости звука. Полная же скорость v = д/у -f vf, следовательно, больше скорости звука. Как абсолютная величина скорости, так и ее направление меняются от точки к точке. Поскольку скорость звука не может пройти через нуль, то ясно, что непрерывная функция У(р(ф) должна быть равна везде +с или же везде —с. Выбирая соответствующим образом направление отсчета угла ф, мы мол<ем условиться считать, что = с. Что касается выбора знака у и,-, то мы увидим нп ке, что он диктуется физическими сообра кениямн и должен быть положительным. Таким образом  [c.574]

Учет сил взаимодействия стержня с внешним потоком приводит к более сложным задачам по сравнению с задачами, рассмотренными в предыдущих главах. На рис. 6.1 показан элемент стержня,, находящийся в потоке воздуха произвольного направления (скорость потока Vo) с действующими на него аэрогидродинамически-ми силами qa, q и qi. Стержни, находящиеся в потоке, могут очень сильно отклоняться от первоначальной (без потока) равновесной формы, а От формы осевой линии стержня (угла фа между касательной к осевой линии стержня — вектором ei на рис. 6.1 и вектором местной скорости Vo потока) зависят аэродинамические силы. Получить общие аналитические выражения для возникающих аэродинамических сил, учитывающих непрерывное изменение этого угла в процессе нагружения стержня потоком, можно только экспериментально-теоретическим методом путем обобщения экспериментальных данных частных случаев обтекания стержня потоком.  [c.229]

Используя уравнения (5.1)-(5.14), рассчитываются основные параметры процесса кавитации в сопле Вентури, такие как скорость потока в критическом сечении сопла и в любой точке кавитационной области (Р, статическое давление в области кавитации 7 ,,, массовый расход через любое произвольное взятое сечение области кавитации, обьемный расход двухфазной среды, из которой состоит область кавигации, плотность двухфазной среды р в любом произвольно взятом сечении области кави тации, объемная концентрация газовой фазы, массовые расходы жидкой 7 и газовой С фаз, полное давление потока Р в произвольнее взятом сечении области кавитации, местная скорость звука а в любой точке области кавитации, длина 5 области кавитирующей жидкости.  [c.149]

При малых значениях числа Маха (М1 < 0,3) величина скорости набегающего потока газа не оказывает заметного влияния на характер распределения давления по профилю. Коэффициенты давления р на профиле остаются практически такими же, как в несжимаемой жидкости. Увеличение скорости приводит к уменьшению минимального давления и соответственно к росту максимального числа Маха на профиле. Хотя при больших значениях М1 (М1 > 0,3) эпюра коэффициентов давления и величина ртш изменяются, но по-прежнему увеличение скорости набегающего потока приводит к росту максимального числа Маха. В результате при некотором критическом значении числа Маха набегающего потока (М1 = М1 р) максимальная скорость на профиле становится равной местной скорости звука, т. е. Мпих = 1,0. При этом минимальное давление достигает своего критического значения  [c.30]

Эта величина называется о с р е д н е н н о й скоростью турбулентного потока в данной точке или осредненнон местной скоростью.  [c.76]

Переходя теперь к определению коэффициента Дарси, необходимо, конечно, учитывать и характер стенок. Для этого нужно (9-12е) применить для некоторой точки потока с определенной в завасимости от характера стенок местной скоростью.  [c.86]

---

Гидравлика и насосы (1984) — [
c.52
]

Справочник по гидравлике (1977) — [
c.21
]

Справочник по гидравлике Книга 1 Изд.2 (1984) — [
c.22
]

---