Как найти место встречи двух тел формула - Сайт, где вы сможете решить свои вопросы

Как найти место встречи двух тел, если дано начальное расстояние между ними и их скорости?

Знаток

(384),
закрыт

12 лет назад

Styx

Гений

(83658)

12 лет назад

в физике такие задачи решают так начало отсчета-это самое главное !!!выбираете в начальном положении 1 машины
1) записываете ур движения 1 машины x1=100t
2) записываете координату второй машины- x2= 100-80(t-1/4)
3)в момент встречи у них x1=x2 решаете уравнение находите t? подставляете в любое x находите координату
графически строите графики x1(t) x2(t)/ в математике это y=kx +b- вся беда в ом, что математика у вас отдельно, а мухи отдельно!! ! время, при котором графики пересекаются и есть время встречи!! ! ВСЕ!!

Источник

Как найти место встречи двух тел

x = -3 + 2 * t – уравнение движение второго тела.

Необходимо найти время t и место встречи тел.

Для того, чтобы найти время встречи тел, приравняем оба уравнения (так как в месте встречи координаты х обоих тел будут одинаковы):

5 – 8 * t = -3 + 2 * t

2 * t + 8 * t = 5 + 3

Теперь найдем координату:

х = 5 – 8 * t = 5 – 8 * 0,8 = 5 – 6,4 = -1.4

Ответ: время встречи t = 0,8 секунд, место встречи х = -1,4.

10 – 11 классы
Физика
6 баллов

Найти место и время встречи двух тел 2 способами (графич. и аналит.)

Попроси больше объяснений
Следить
Отметить нарушение

Ответ

Проверено экспертом

по графику видно: на расстоянии 16 метров через 4 секунды

Вопрос по физике:

Найти место и время
встречи двух тел 2 способами (графич. и аналит.)

Ответы и объяснения 2

Привет на это задаче 16 и 1000

Дано:
S1=2500м
S2=6000м
t1=40с
t2=20с
Найти место и время встречи двух тел.
решение:
Первое тело двигалось в правильном направлении по графику, второе тело двигалось в неправильном направлении по графику. Так первое тело проехало путь 2500м за 40с. Второе тело прошло путь 6000м за 20с. По графику видно, что они встретились в точке, где путь равен 1000м.
так навреное!

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат – это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Физика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи – смело задавайте вопросы!

Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.

Уравнение координаты при равноускоренном прямолинейном движении

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

По уравнениям движения двух тел х1 = 20t и х2 = 250 — 5t определите: а) место и время встречи этих тел;

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

Физическую задачу в кинематике можно решить несколькими способами:

аналитический — решение задачи основано на формулах (физических законах), которые связывают искомую величину и данные в условии задачи;
графический — решение задачи осуществляется с помощью графика.

Основные закономерности графического способа решения задач по кинематике

1.1. График зависимости модуля скорости (v(t)) равномерного движения от времени — прямая линия, параллельная оси (OX) (рис. (1)).

Рис. (1). График модуля скорости равномерного движения

Если изображается зависимость проекции скорости от времени (v_x(t)), то возможны следующие варианты интерпретации:

а) график расположен над осью времени — тело движется в положительном направлении оси (OX);

б) график расположен под осью времени — тело движется в отрицательном направлении оси (OX).

1.2. Модуль перемещения (или пройденный путь при одномерном прямолинейном движении) на графике (v(t)) в момент времени (t_1) будет равен площади фигуры (прямоугольника) под графиком модуля скорости (рис. (2)).

Рис. (2). Определение модуля перемещения по графику скорости

2.1. График модуля перемещения (s(t)) для равномерного движения (рис. (3)) — прямая под углом ({alpha}) к оси времени:

Рис. (3). График модуля перемещения

Если изображается зависимость проекции перемещения от времени (s_x(t)), то возможны следующие варианты интерпретации:

а) график расположен над осью времени — тело движется в положительном направлении оси (OX);

б) график расположен под осью времени — тело движется в отрицательном направлении оси (OX).

2.2. Модуль скорости равномерного движения на графике модуля перемещения (s(t)) равен тангенсу угла (tgalpha) наклона прямой на графике (рис. (4)).

Рис. (4). Определение модуля скорости по графику модуля перемещения

Решение задачи аналитическим и графическим способами

Два катера, между которыми расстояние (30) м, равномерно движутся навстречу друг другу со значениями модулей скоростей υ1 (=) (2) м/с и υ2 (=) (4) м/c. Определи время встречи катеров. Какой путь успеет пройти первый катер до встречи?

Дано:

начальная координата первого катера —

x01

(=) (0) м, а второго —

x02

(=) (30) м.

Вектор скорости первого катера (vec{v_1}) сонаправлен оси (OX), его проекция будет положительна ({v_1}_x > 0), а вектор скорости второго катера (vec{v_2}) направлен противоположно оси (OX), поэтому его проекция будет отрицательна: ({v_2}_x < 0) (рис. (5)).

Рис. (5). Задача

Аналитический способ решения

1. Запишем уравнения движения тел, исходя из формулы (x(t) = x_0 + v_x(t – t_0)).

2. В момент встречи (t_{встр}) тела будут иметь одинаковую координату (x_1 = x_2):

2tвстр=30−4tвстр;6tвстр=30;[tвстр]=мм/с=c;tвстр=306=5c.

— расчёт времени встречи катеров.

3. Для ответа на второй вопрос воспользуемся следующей формулой:

L=υ1⋅tвстр;[L]=мc⋅c=м;L=2⋅5=10м.

— расчёт пути, пройденного первым катером до момента встречи (t_{встр}).

Графический способ решения

1. Запишем для первого катера уравнение движения:

x1=0+2t=2t

2. Заполним таблицу значений (x(t)) для построения графика движения первого катера.

(x), м	(0)	(2)	(4)
(t), с	(0)	(1)	(2)

3. Запишем для второго катера уравнение движения:

x2=30−4t

4. Заполним таблицу значений (x(t)) для построения графика движения второго катера.

(x), м	(30)	(26)	(22)
(t), с	(0)	(1)	(2)

5. Построим графики движений двух катеров.

Рис. (6). График движения катеров

6. Находим по графику (рис. (6)):

а) время встречи (точка пересечения)

tвстр

(=) (5) c;

б) путь, пройденный первым катером, равен изменению координаты (L) (=) (x(t_{встр})) —

x01

(=) (10) м.

Ответ: (5) с; (10) м.

Источники:

Рис. 1. График модуля скорости равномерного движения. © ЯКласс.

Рис. 2. Определение модуля перемещения по графику скорости. © ЯКласс.

Рис. 3. График модуля перемещения. © ЯКласс.

Рис. 4. Определение модуля скорости по графику модуля перемещения. © ЯКласс.

Рис. 5. Задача. © ЯКласс.

Рис. 6. График движения катеров. © ЯКласс.

Источник

2.2.1 Как перевести из км/ч в м/с и т. д?

В задачах часто необходимо переводить из одних единиц измерения в другие:

1 км/ч = (1000 м)/(3600 с) = 5/18 м/с,

1 м/с = 18/5 км/ч,

1 км/с = 1000 м/с,

1 см/с = 0,01 м/с,

1 м/мин = 1/60 м/с.

Например, если то для того, чтобы перевести в м/с, нужно умножить на 5/18:

2.2.2 Как найти скорость тела, если известен закон движения?

Закон равномерного движения имеет вид:

Видим, что в этой формуле скорость стоит коэффициентом перед временем. Поэтому, если в условии задачи дан закон движения, необходимо посмотреть на коэффициент перед t — это и есть скорость.

Например, пусть закон движения имеет вид: В данном случае коэффициент перед t равен 5, следовательно,

2.2.3 Как определить скорость по графику координаты от времени?

Закон равномерного движения имеет вид:

Графиком этого закона является прямая линия. Так как nu_x — коэффициент перед t, то nu_x является угловым коэффициентом прямой.

Для графика 1:

То, что график 1 «поднимается вверх», означает — тело едет в положительном направлении оси Ox.

Для графика 2:

То, что график 2 «опускается вниз», означает — тело едет в отрицательном направлении оси Ox.

Для определения Delta x и Delta t выбираем такие точки на графике, в которых можно точно определить значения, как правило, это точки, находящиеся в вершинах клеток.

2.2.4 Как найти закон движения, если известны координаты тела в моменты времени и ?

Пусть в момент времени t_1 тело находилось в точке с координатой x_1, а в момент времени t_2 тело находилось в точке с координатой x_2.

Для времени t_1 имеем:

Для времени t_2 имеем:

Решая систему уравнений (2.19) и (2.20), получим

2.2.5 Как найти графически момент и координату встречи двух тел?

Пусть даны законы движения двух тел: и Согласно пункту 2.5 графиками обоих законов являются прямые линии. Необходимо на одном графике построить оба закона.

Графики пересекаются в одной точке. Координаты этой точки и являются временем и местом встречи.

2.2.6 Как аналитически найти координату и время встречи двух тел?

Пусть даны законы движения двух тел: и В момент встречи тела оказываются в одной координате, то есть и необходимо решить уравнение:

Решение уравнения имеет вид:

Для нахождения координаты достаточно подставить вместо t найденное значение в любой из законов движения:

или

2.2.7 Как найти среднюю скорость, если тело половину пути проехало со скоростью а вторую половину пути

По определению (2.8):

В нашем случае, так как на каждой половине пути тело едет с постоянной скоростью, то

Получаем

В общем случае, если весь путь разбить на n равных участков, на каждом из которых тело едет с постоянной скоростью, то

Формула справедлива только если весь путь разбит на равные участки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.

2.2.8 Как найти среднюю скорость, если тело половину времени проехало со скоростью а вторую половину времени

По определению (2.8):

В нашем случае, так как каждую половину времени тело едет с постоянной скоростью, то

Получаем

В общем случае, если все время разбито на n равных промежутков, на каждом из которых тело едет с постоянной скоростью, то

Формула справедлива только если все время разбито на равные промежутки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.

2.2.9 Как найти скорость, с которой движется моторная лодка по течению реки?

Согласно формуле скорость тела относительно неподвижной системы отсчета (в нашем случае земли), равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета nu_0 (в нашем случае — собственная скорость лодки).

При движении по течению вектора и vecu направлены в одну сторону, следовательно, получаем сложение двух векторов, направленных в одну сторону — используем формулу (1.15):

Таким образом, при движении любого тела по течению его скорость определяется формулой

2.2.10 Как найти скорость, с которой движется моторная лодка против течения реки?

Согласно формуле скорость тела относительно неподвижной системы отсчета (в нашем случае земли) равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета nu_0 (в нашем случае — собственная скорость лодки).

Перепишем формулу в виде:

Вектора и направлены в одну сторону, следовательно, получаем вычитание двух векторов, направленных в одну сторону — используем формулу :

2.2.11 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена перпендикулярно течению реки?

В данном случае вектора и vecnu направлены перпендикулярно, следовательно, получаем задачу о сложении взаимно перпендикулярных векторов — используем формулу :

2.2.12 Как найти расстояние, на которое снесет лодку, если ее скорость направлена перпендикулярно скорости реки?

В результате сложения скоростей по формуле скорость тела относительно земли равна vecnu и направлена по прямой OD. В результате, когда тело окажется на противоположном берегу, оно попадет в точке D, и его снесет на длину CD=S.

Треугольник OAB подобен треугольнику OCD:

2.2.13 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена под углом φ к скорости течения реки?

В результате сложения скоростей по формуле скорость тела относительно земли равна vecnu и направлена по прямой OB. Как видим, получили треугольник, в котором известен один из углов — Тогда по теореме косинусов:

2.2.14 Как найти расстояние, на которое снесет лодку, если ее скорость направлена под углом к скорости течения реки?

В результате сложения скоростей по формуле скорость тела относительно земли равна vecnu и направлена по прямой OB. В результате, когда тело окажется на противоположном берегу, оно попадет в точке В, и его снесет на длину АВ=S.

В задачах, когда движение происходит в плоскости, то есть и вдоль оси Ox, и вдоль оси Oy, необходимо введение системы координат для того, чтобы упростить рассмотрение задачи.

Проекция nu_x:

Проекция nu_y:

Формулы и не просто результат математической операции нахождения проекции, nu_x и nu_y имеют физический смысл: со скоростью nu_x тело плывет вдоль оси Ox, то есть по течению; со скоростью nu_y тело переплывает реку. Например, время, за которое тело переплывет реку, можно найти просто поделив ширину реки на nu_y:

Тогда

2.2.15 Под каким углом α нужно направить собственную скорость лодки, чтобы за минимальное время переплыть реку?

Согласно формуле скорость, с которой лодка переплывает реку, равна:

Очевидно, что время будет минимальным, если nu_y будет максимальным, то есть

2.2.16 С какой скоростью машина обгоняет вторую машину, если они движутся в одну сторону?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина также движется вправо со скоростью Скорость обгона — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой :

Так как и направлены в одну сторону, то получили задачу о вычитании векторов, направленных в одну сторону — формула :

Заметим, что при обгоне, естественно поэтому

2.2.17 За какое время проедут мимо друг друга два поезда, двигающиеся в одном направлении?

Пусть длина 1-го поезда L_1, а скорость 2-го поезда L_2. Скорость обгона определяется формулой Тогда

2.2.18 С какой скоростью машина едет навстречу вторую машину, если они движутся в противоположных направлениях?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется влево со скоростью Скорость движения навстречу — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой :

Перепишем эту формулу в виде:

2.2.19 За какое время проедут мимо друг друга два поезда, двигающиеся в противоположных направлениях?

Пусть длина 1-го поезда L_1, а скорость 2-го поезда L_2. Скорость обгона определяется формулой Тогда

2.2.20 Как найти относительную скорость, если тела движутся по взаимно перпендикулярным направлениям?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется перпендикулярно первой со скоростью Относительная скорость определяется формулой :

Так как вектора и перпендикулярны, то воспользуемся формулой :

Источник

Определение и формулы

Уравнение координаты — зависимость координаты тела от времени:

x = x(t)

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с². Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
Построить уравнение вида x₁ = x₂.
Найти время встречи двух тел t_встр.
Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с² без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Отсюда t₁ = 0 с, а t₂ = 6 с. Первый корень нам не подходит — из условия задачи уже было понятно, что тела начали движение одновременно. Снова они встрется, когда пройдет 6 секунд.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

Построить графики x1(t) и x2(t).
Найти точку пересечения графиков.
Пустить перпендикуляр из этой точки к оси ОХ.
Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает вид:

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с² и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с², достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два корня: t₁ = 0,6 с, а t₂ = 3,4 с. Первый корень не подходит, так как в это время Саша еще не начал движение. Второй корень подходит, так как он меньше 4 с. Значит, Саша догонит Мишу через 3,4 с после того, как Миша начнет движение.

Задание EF18609

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

Определить характер движения материальной точки.
Записать уравнение координаты материальной точки.
С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение

Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид:

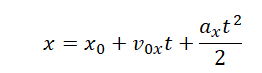
Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно, a_x>0. Поэтому варианты «б» и «г» исключаются. Остается выяснить, чему равна скорость: она равна нулю (как в ответе «а») или меньше нуля (как в ответе «в»)?

Моменту времени t=0 соответствует точка, являющая вершиной параболы. Когда ветви параболы смотрят вверх, в ее вершине скорость тела всегда равна нулю, так как эта точка лежит на границе между отрицательной и положительной скоростью. Отсюда делаем вывод, что верный ответ «а».Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17682

Мимо остановки по прямой улице с постоянной скоростью проезжает грузовик. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с ускорением 3 м/с², и догоняет грузовик на расстоянии 150 м от остановки. Чему равна скорость грузовика?

Алгоритм решения

Записать исходные данные.
Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
Выразить скорость грузовика из уравнения его движения.
Записать уравнение движения мотоциклиста.
Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
Подставить время в формулу скорости грузовика и вычислить ее.

Решение

Исходные данные: